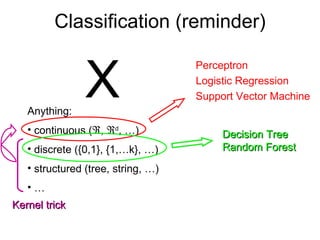
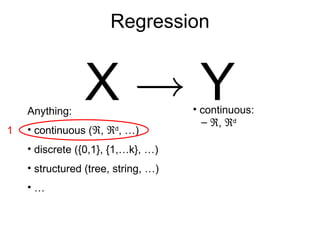
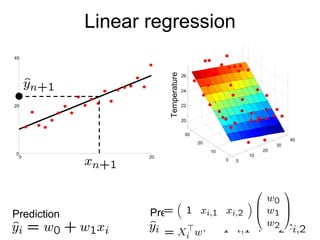
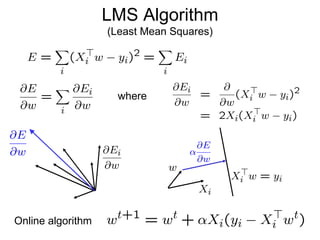
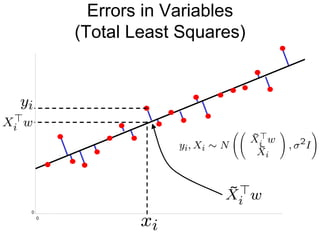
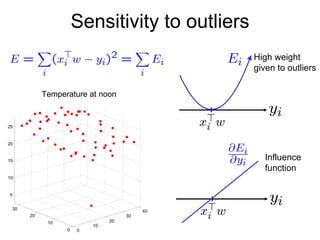
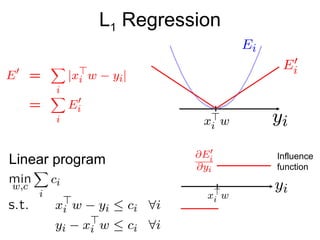
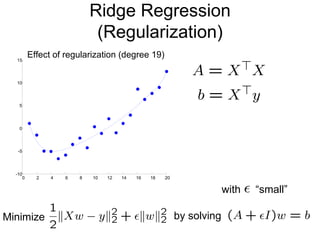
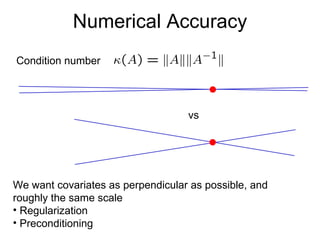
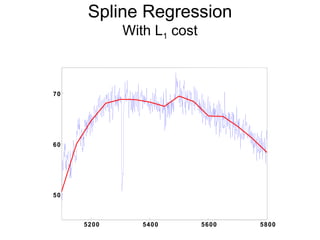
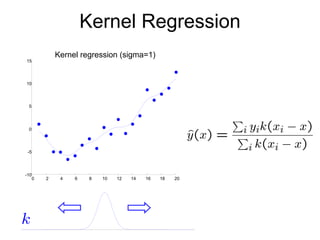
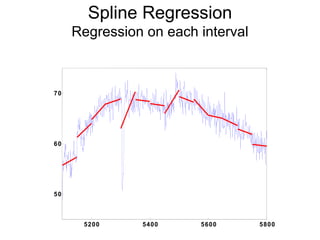
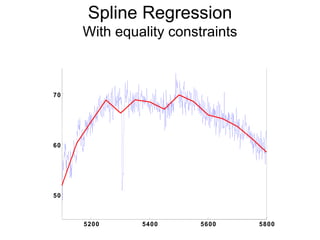
The document outlines various regression techniques including: 1) Ordinary Least Squares regression which finds the best fitting linear model by minimizing the sum of squared errors between predicted and actual values. 2) Overfitting can occur when the model learns from noise in the data. Regularization addresses this by imposing a penalty on complexity. 3) Kernel regression, spline regression, and Multiple Adaptive Regression Splines (MARS) allow for nonlinear relationships between variables.

1. Regression CS294 Practical Machine Learning Romain Thibaux 09/18/06

2. Outline Ordinary Least Squares regression Derivation from minimizing the sum of squares Probabilistic interpretation Online version (LMS) Overfitting and Regularization Numerical stability L 1 Regression Kernel Regression, Spline Regression Multiple Adaptive Regression Splines (MARS)

3. Classification (reminder) X ! Y Anything: continuous (  ,  d , …) discrete ({0,1}, {1,…k}, …) structured (tree, string, …) … discrete: {0,1} binary {1,…k} multi-class tree, etc. structured

4. Classification (reminder) X Anything: continuous (  ,  d , …) discrete ({0,1}, {1,…k}, …) structured (tree, string, …) …

5. Classification (reminder) X Anything: continuous (  ,  d , …) discrete ({0,1}, {1,…k}, …) structured (tree, string, …) … Perceptron Logistic Regression Support Vector Machine Decision Tree Random Forest Kernel trick

6. Regression X ! Y continuous:  ,  d Anything: continuous (  ,  d , …) discrete ({0,1}, {1,…k}, …) structured (tree, string, …) … 1

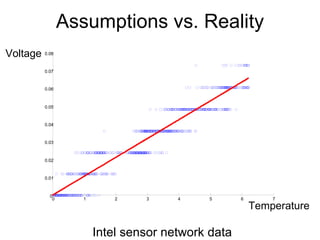
7. Examples Voltage ! Temperature Processes, memory ! Power consumption Protein structure ! Energy [next week] Robot arm controls ! Torque at effector Location, industry, past losses ! Premium

8. Linear regression 0 10 20 30 40 0 10 20 30 20 22 24 26 Temperature 0 10 20 0 20 40 [start Matlab demo lecture2.m] Given examples Predict given a new point

9. Linear regression 0 20 0 20 40 Temperature 0 10 20 30 40 0 10 20 30 20 22 24 26 Prediction Prediction

10. Ordinary Least Squares (OLS) 0 20 0 Error or “residual” Prediction Observation Sum squared error

11. Minimize the sum squared error Sum squared error Linear equation Linear system

12. Alternative derivation n d Solve the system (it’s better not to invert the matrix)

13. LMS Algorithm (Least Mean Squares) where Online algorithm

14. Beyond lines and planes everything is the same with still linear in 0 10 20 0 20 40

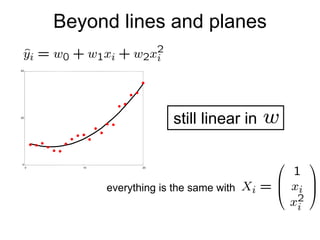
15. Geometric interpretation [Matlab demo] 0 10 20 0 100 200 300 400 -10 0 10 20

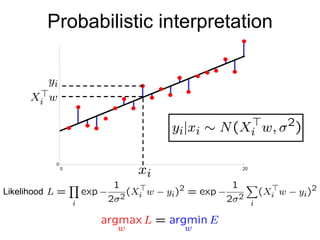
16. Ordinary Least Squares [summary] n d Let For example Let Minimize by solving Given examples Predict

17. Probabilistic interpretation 0 20 0 Likelihood

18. Assumptions vs. Reality Voltage Intel sensor network data Temperature 0 1 2 3 4 5 6 7 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08

19. Overfitting 0 2 4 6 8 10 12 14 16 18 20 -15 -10 -5 0 5 10 15 20 25 30 [Matlab demo] Degree 15 polynomial

20. Ridge Regression (Regularization) 0 2 4 6 8 10 12 14 16 18 20 -10 -5 0 5 10 15 Effect of regularization (degree 19) with “small” Minimize by solving

21. Probabilistic interpretation Likelihood Prior Posterior

22. Numerical Accuracy Condition number vs We want covariates as perpendicular as possible, and roughly the same scale Regularization Preconditioning

23. Errors in Variables (Total Least Squares) 0 0

24. Sensitivity to outliers High weight given to outliers Influence function 0 10 20 30 40 0 10 20 30 5 10 15 20 25 Temperature at noon

25. L 1 Regression Linear program Influence function

26. Kernel Regression 0 2 4 6 8 10 12 14 16 18 20 -10 -5 0 5 10 15 Kernel regression (sigma=1)

27. Spline Regression Regression on each interval 5200 5400 5600 5800 50 60 70

28. Spline Regression With equality constraints 5200 5400 5600 5800 50 60 70

29. Spline Regression With L 1 cost 5200 5400 5600 5800 50 60 70

30. 0 1 2 0 #requests per minute Time (days) 5000 Heteroscedasticity

31. MARS Multivariate Adaptive Regression Splines … on the board…

32. Further topics Generalized Linear Models Gaussian process regression Local Linear regression Feature Selection [next class]