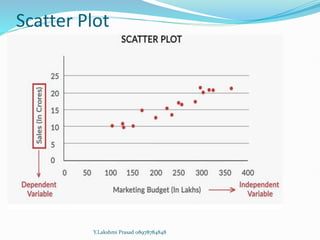
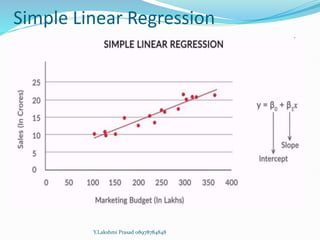
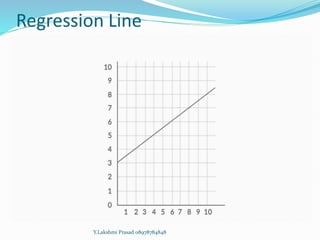
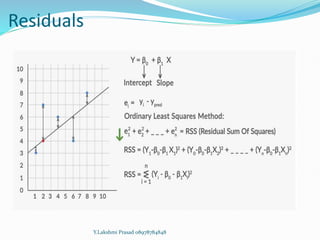
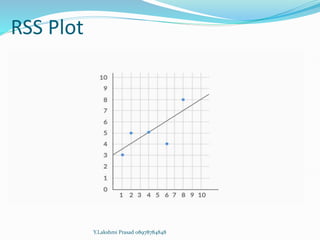
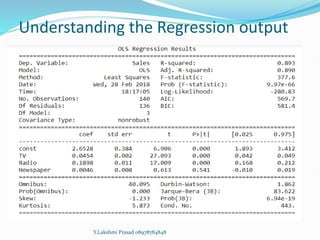
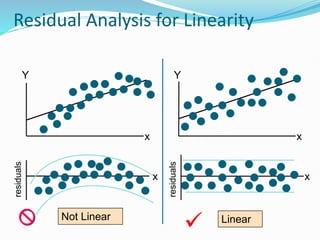
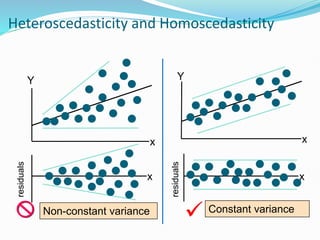
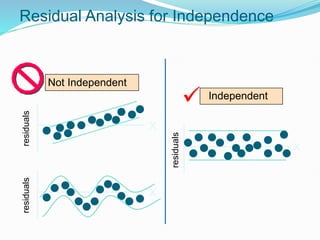
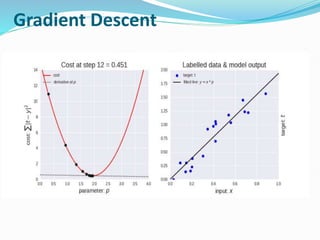
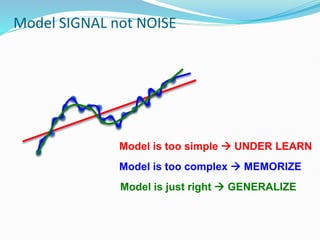
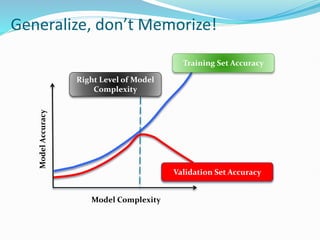
The document provides an overview of linear regression, covering concepts such as simple and multiple linear regression, the least squares method, and metrics for model evaluation like R-squared and residual sum of squares. It also discusses the assumptions underlying linear regression, issues related to multicollinearity, and techniques for variable selection such as Recursive Feature Elimination (RFE). Overall, the text serves as a comprehensive guide to understanding and implementing linear regression models.