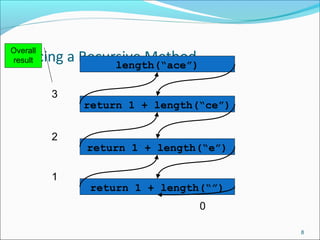
The document discusses recursion, which is when a function calls itself directly or indirectly. It provides examples of directly and indirectly recursive functions. It notes the requirements for a recursive solution, including having a base case and breaking the problem down into smaller subproblems of the same kind. The document gives examples of recursively finding the length and printing characters of a string. It also discusses tracing a recursive method call stack and defines the Fibonacci series recursively, providing an example recursive Fibonacci function that is inefficient due to redundant calls.

2. Recursion
“A function that either directly or indirectly make a
call to itself.”
Powerful and efficient programming tool.
Example of directly call
method1()
{
System.out.println(“We Are Anonymous.”)
method1();
}
2

3. Example of Indirect Call
A()
{
System.out.println(“Function ‘A’ Call”);
B();
}
B()
{
System.out.println(“Fuction B Call”);
A();
}
3

4. Requirements for Recursive Solution
 At least one “small” case that you can solve directly
 A way of breaking a larger problem down into:
 One or more smaller subproblems
 Each of the same kind as the original
 A way of combining subproblem results into an overall
solution to the larger problem
4

5. Recursive Design Example: Code
Recursive algorithm for finding length of a string:
public static int length (String str) {
if (str == null ||
str.equals(“”))
return 0;
else
return length(str.substring(1)) + 1;
}
5

6. Recursive Design Example: printChars
Recursive algorithm for printing a string:
public static void printChars
(String str) {
if (str == null ||
str.equals(“”))
return;
else
System.out.println(str.charAt(0));
printChars(str.substring(1));
}
6

7. Recursive Design Example: printChars2
Recursive algorithm for printing a string?
public static void printChars2
(String str) {
if (str == null ||
str.equals(“”))
return;
else
printChars2(str.substring(1));
System.out.println(str.charAt(0));
}
7

8. Tracing a Recursive Method
8
length(“ace”)
return 1 + length(“ce”)
return 1 + length(“e”)
return 1 + length(“”)
0
1
2
3
Overall
result

9. Recursive Definitions: Fibonacci Series
Definition of fibi, for integer i > 0:
fib1 = 1
fib2 = 1
fibn = fibn-1 + fibn-2, for n > 2
9

10. Fibonacci Series Code
public static int fib (int n) {
if (n <= 2)
return 1;
else
return fib(n-1) + fib(n-2);
}
This is straightforward, but an inefficient recursion ...
10

11. Efficiency of Recursion: Inefficient Fibonacci
11