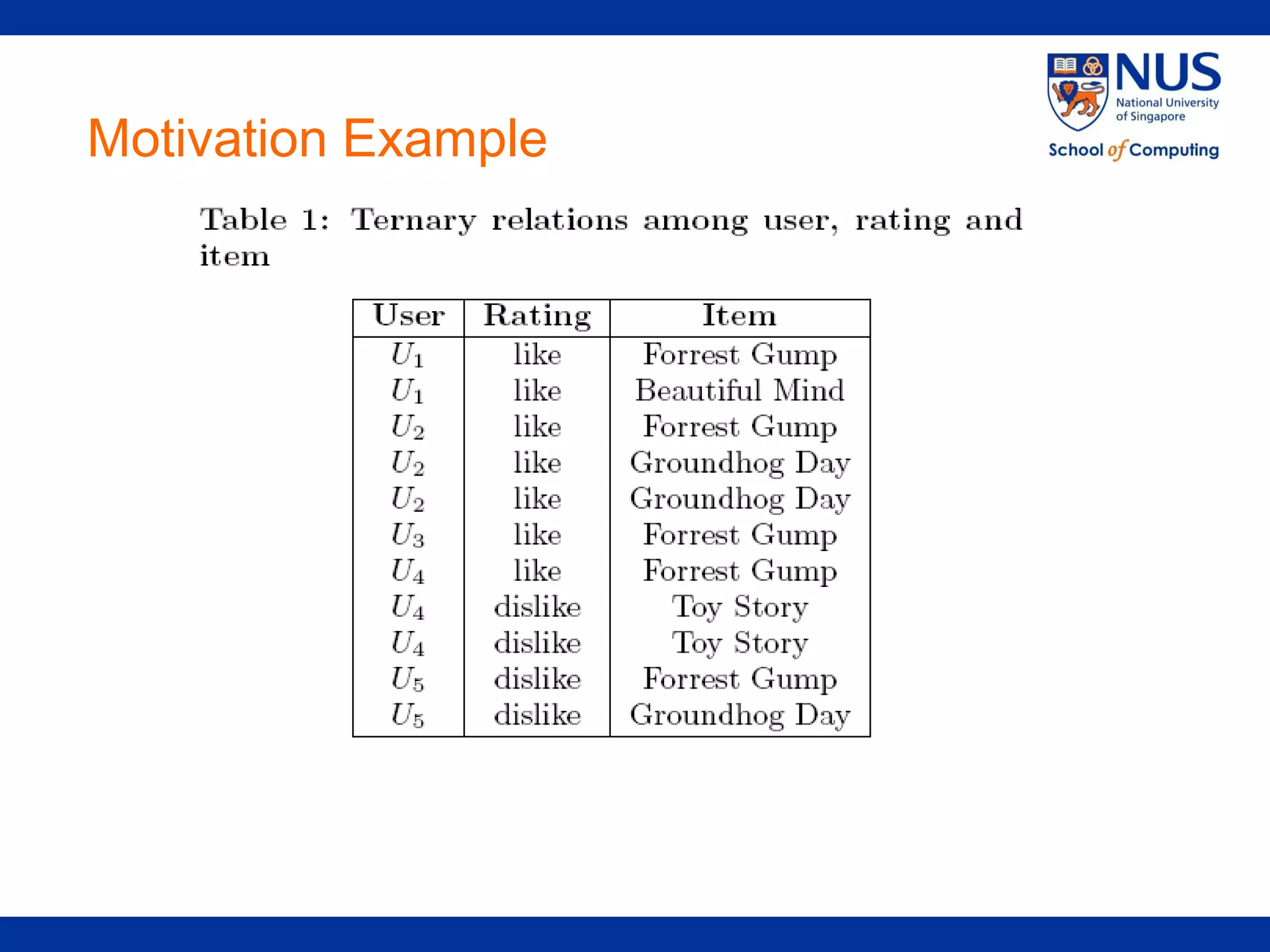
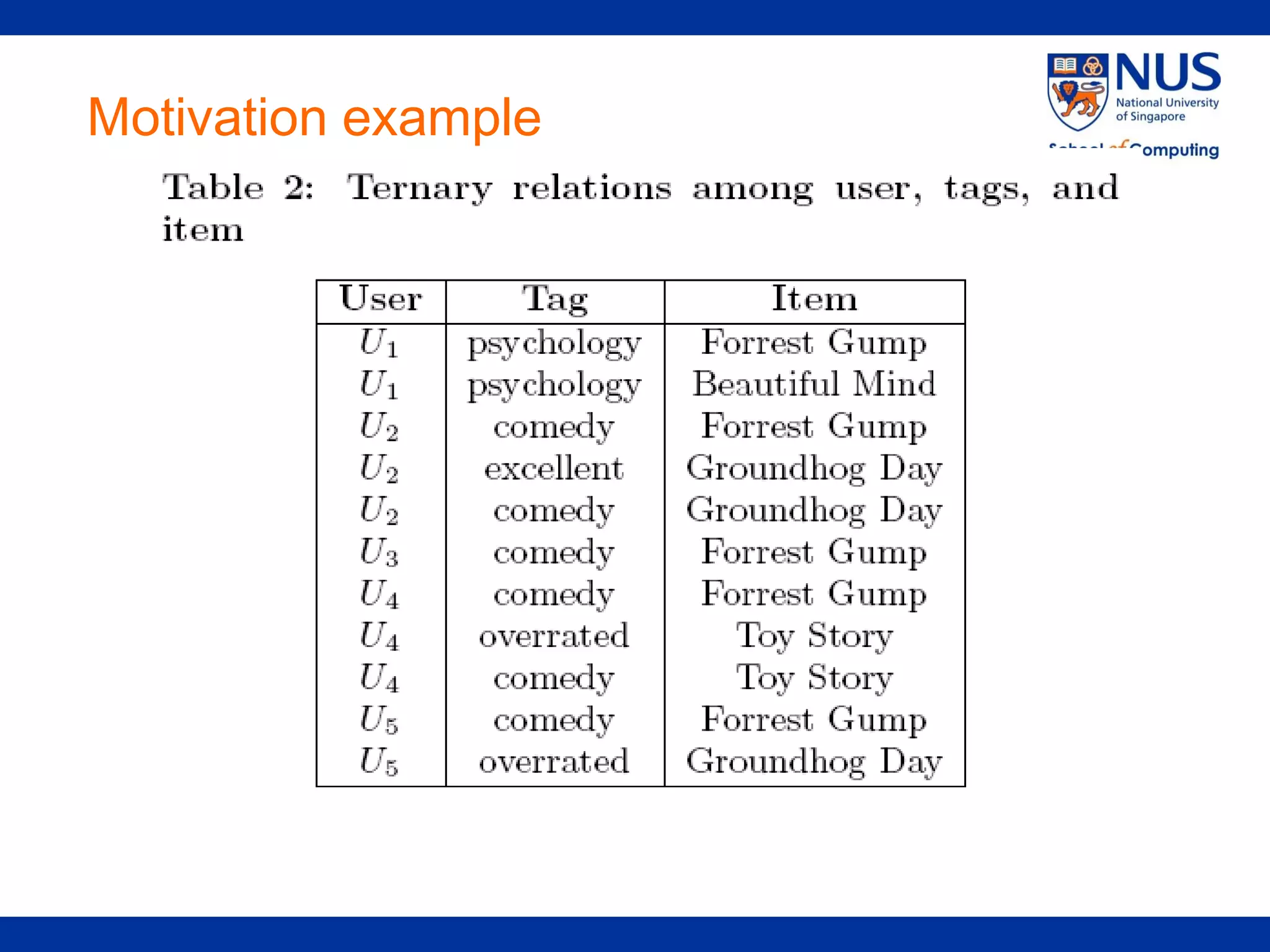
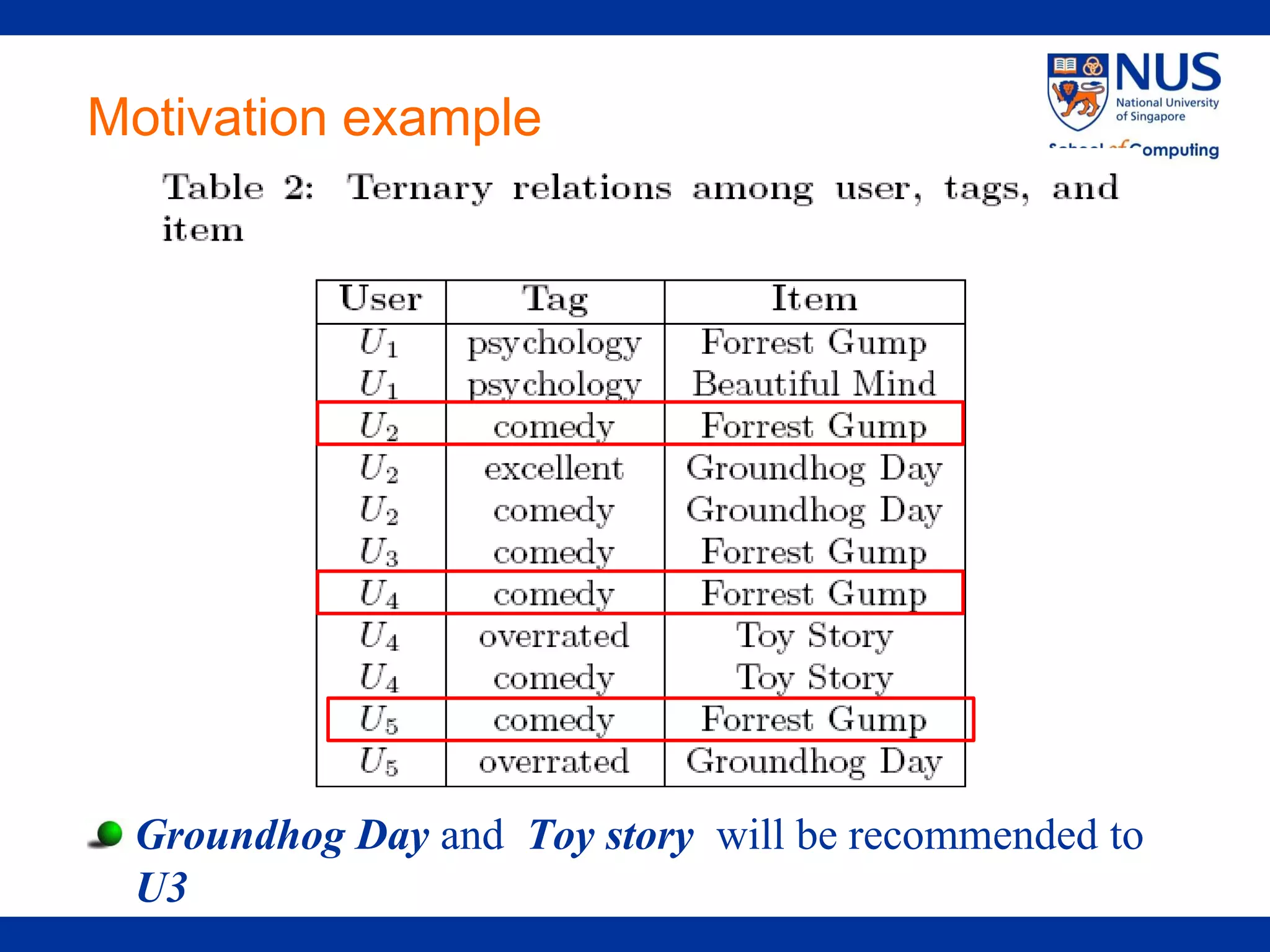
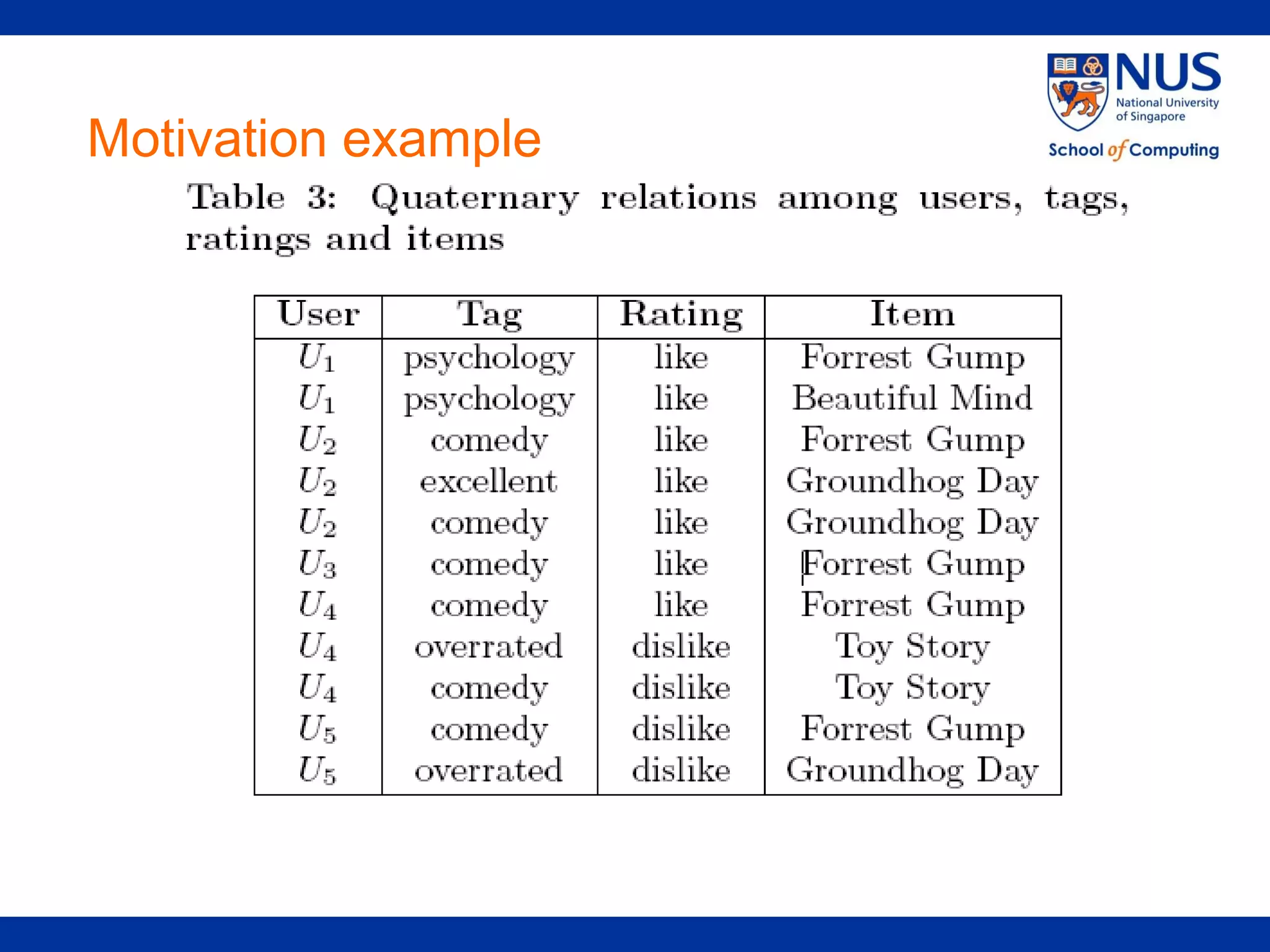
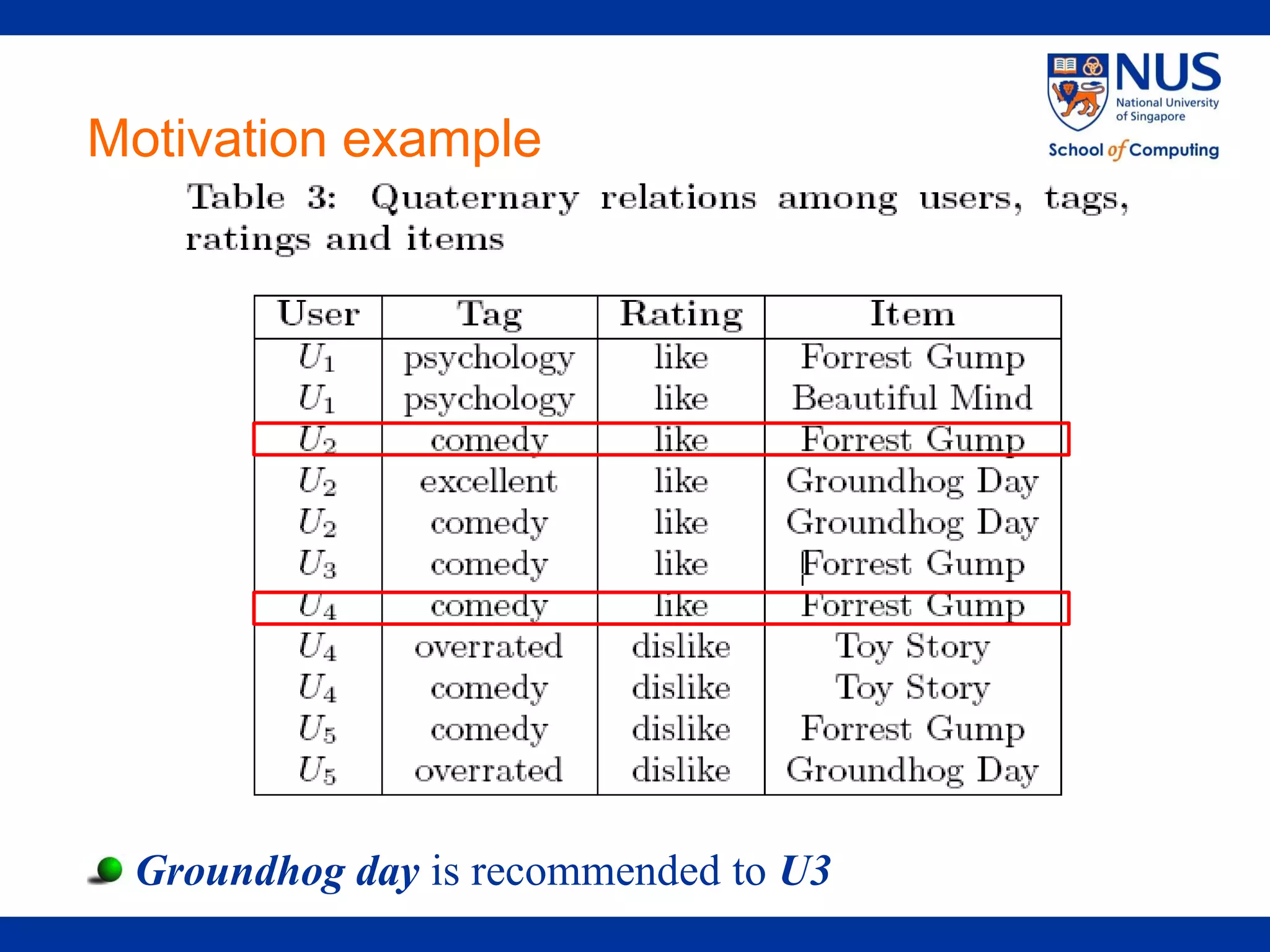
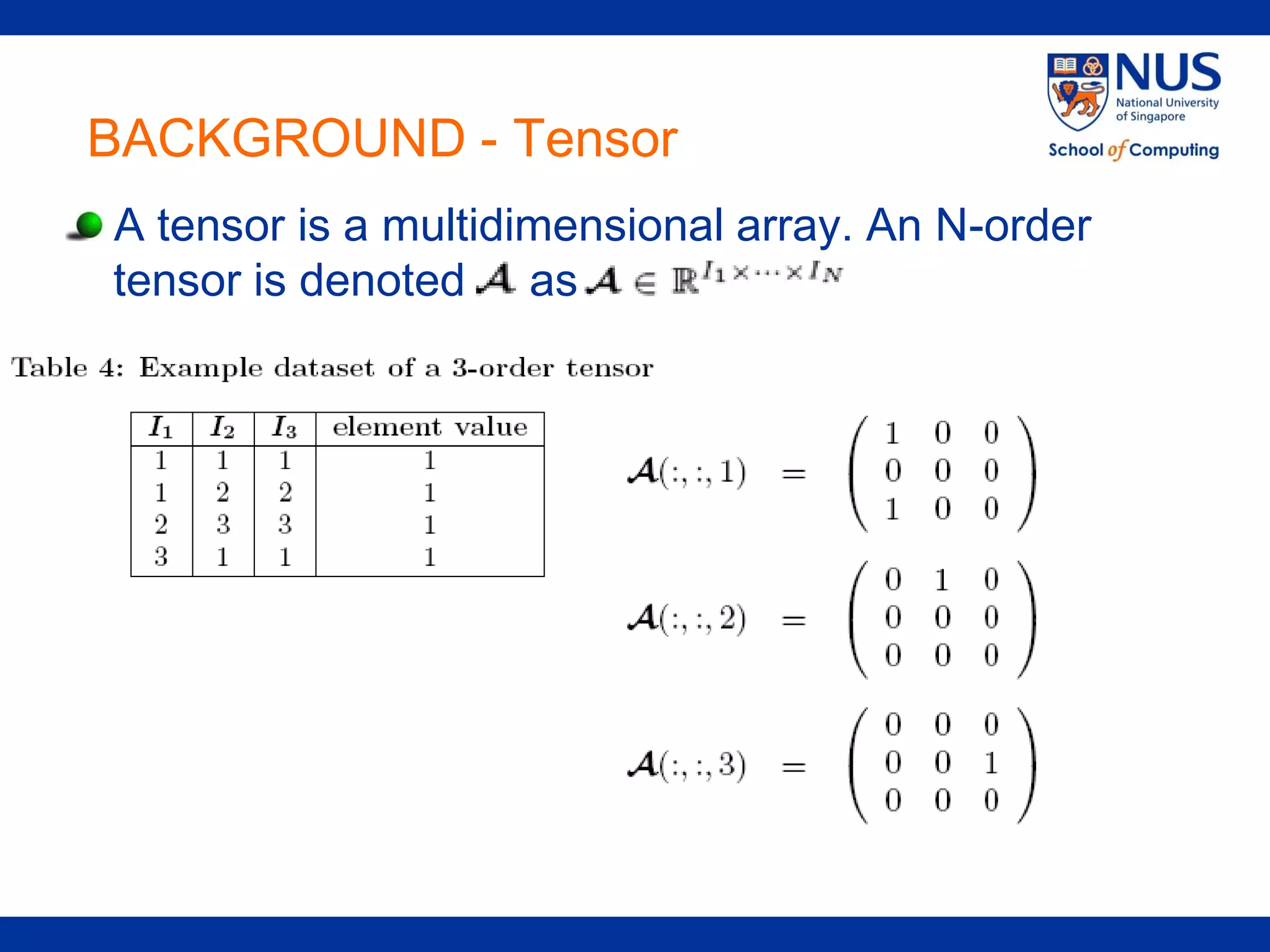
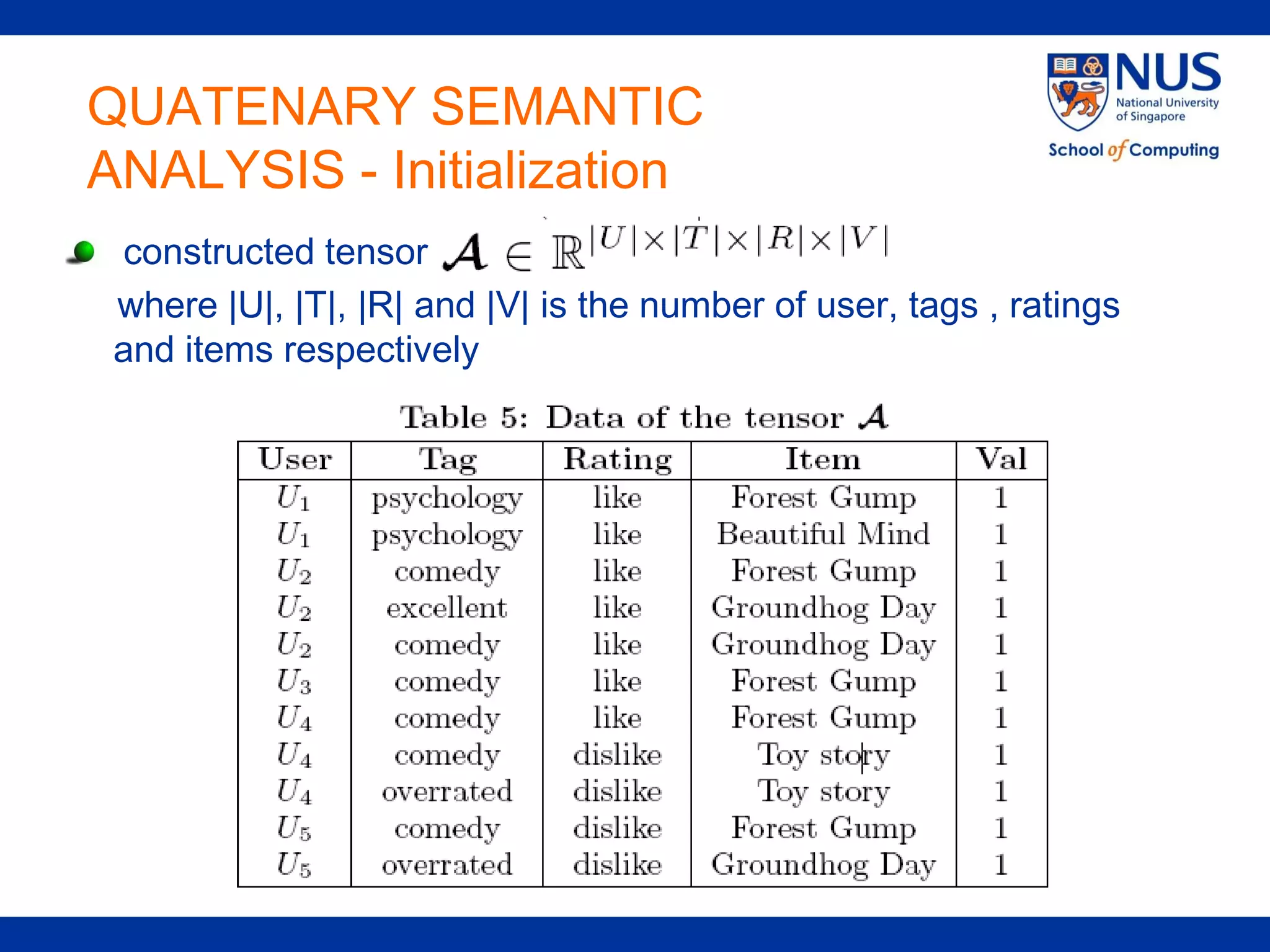
The document proposes a framework for recommendations based on analyzing relationships between users, items, tags, and ratings (quaternary relationships). It models these relationships using a 4-order tensor and applies Higher-Order Singular Value Decomposition (HOSVD) to reveal latent semantic associations. This allows generating recommendations for users, items, tags, and predicting ratings. Experimental results on a movie dataset show the proposed quaternary approach outperforms methods using only ternary relationships.

1. A Unified Framework for
Recommendations Based on
Quaternary Semantic Analysis
Wei Chen*, Wynne Hsu*, Mong Li Lee*
*School of Computing, National University of Singapore
1

2. Introduction
The amount of information on the web is increasing
at a lightning pace. E.g products in Amazon, videos
in Youtube, movies in Netflix
Recommendation is necessary.

3. Introduction
Recommendation systems are typically classified
according to four types :
 User recommendation
 Item recommendation
 Tag recommendation
 Item rating prediction

4. Related Work
Most of the work in recommendation systems
utilize only ternary relationships in generating
recommendations.
The collaborative filtering-based recommendation
systems use <user ,rating, items >
[B. Sarwar,WWW’01,SIGIR’09]
Tag-based recommendation systems utilize the
<users, tags, items >.

5. Motivation
We argue that recommendations based on ternary
relationships are not accurate as they would have
missed out important associations

6. Motivation Example

7. Motivation Example
Beautiful Mind and Groundhog day will be recommended to
U3

8. Motivation example

9. Motivation example
Groundhog Day and Toy story will be recommended to
U3

10. Motivation example

11. Motivation example
Groundhog day is recommended to U3

12. Motivation
The need of quaternary relationship is necessary. This
is reinforced by the following observations:
 Users may use the same tag for an item but have
different ratings for it.
 Items may have multiple tags indicating their different
facets.
 Some tags may carry implicit semantics that can reveal
the users’ preferences.

13. Overview of the paper
We propose a model: using tensor to model the
quaternary relationship.
Higher-Order Singular Value Decomposition
(HOSVD) is applied in the 4-order tensor to reveal
the latent semantic associations among users,
items, tags and ratings.

14. BACKGROUND - Tensor
A tensor is a multidimensional array. An N-order
tensor is denoted as

15. BACKGROUND – Tensor unfolding
The matrix unfolding of an N-order tensor
along the dimension i are vectors
obtained by keeping the index fixed while varying
the other indices.

16. BACKGROUND – n-mode product

17. BACKGROUND – HOSVD
HOSVD is a generalization of Singular Value
Decomposition (SVD) to higher-order tensors and
can be written as n-mode product
Where U(n) contain the orthonormal vectors (n-
mode singular vector) spanning the column space
of the A (n) , is the core tensor

18. BACKGROUND – HOSVD

19. BACKGROUND – HOSVD
With this, the core tensor can be
constructed as described in [L. D.,SIAM 2000], that is
and we can get:

20. BACKGROUND- Rank, Low Rank
Approximation

21. BACKGROUND
Suppose we want to get the RANK-(2,3,3)
approximation, we first retain the first ci column of
matrix U(i) at mode i as follows:

22. BACKGROUND –Tensor
Approximation
We can now construct the approximate core tensor
using

23. BACKGROUND
Finally, we obtain the RANK-(2,3,3) approximation

24. QUATENARY SEMANTIC
ANALYSIS
The main idea is to capture the underlying
relationships among users-tags-items-ratings by
reducing the rank of the original tensor to minimize
the effect of noise on the underlying population
and reduce spareness.

25. QUATENARY SEMANTIC
ANALYSIS - Initialization
Input: list of quadruples < users, tags, rating, items>;

26. QUATENARY SEMANTIC
ANALYSIS - Initialization
constructed tensor
where |U|, |T|, |R| and |V| is the number of user, tags , ratings
and items respectively

27. QUATENARY SEMANTIC
ANALYSIS
Calculate the matrix unfolding A(1) , A(2) , A(3) and
A(4) from Tensor
Perform SVD on each matrix unfolding and get the
left singular matrix U(1) , U(2) , U(3) and U(4)

28. QUATENARY SEMANTIC
ANALYSIS
Remove the least significant rows |U|-c1; |V |-c2; |T|-c3
and |R|-c4 from U(1);U(2);U(3); and U(4), respectively. We
choose c1= 4; c2 =4; c3 = 4; c4 = 2.

29. QUATENARY SEMANTIC
ANALYSIS
Calculate the approximate core tensor
Approximate the original tensor by:

30. QUATENARY SEMANTIC
ANALYSIS

31. QUATENARY SEMANTIC
ANALYSIS
Latent associations such as the newly added
quadruples in Table 6 may not be found if the
tensor data is sparse
We overcome this problem by applying a
smoothing technique to the tensor in Algorithm.

32. RECOMMENDATION
GENERATION

33. RECOMMENDATION
GENERATION

34. RECOMMENDATION
GENERATION

35. RECOMMENDATION
GENERATION

36. Experimental result – dataset
description
Datasets: Movielens Data
The first file contains users’ tags on different movies.
The second file contains users’ ratings on different
movies on a scale of 1 to 5.
By joining these two files over user and movie, we
obtain the quadruples < user; movie; tag; rating >.
After preprocessing, the dataset has 11122 tuples with
201 users, 501 movies, and 404 tags.

37. Experimental result – Item
Recommendation
Compare method:
 UPCC: User based recommendation
 IPCC: Item based recommendation
 Probabilistic Matrix Factorization (PMF)

38. Experimental result – Item
recommendation

39. Experimental result – Rating
Prediction

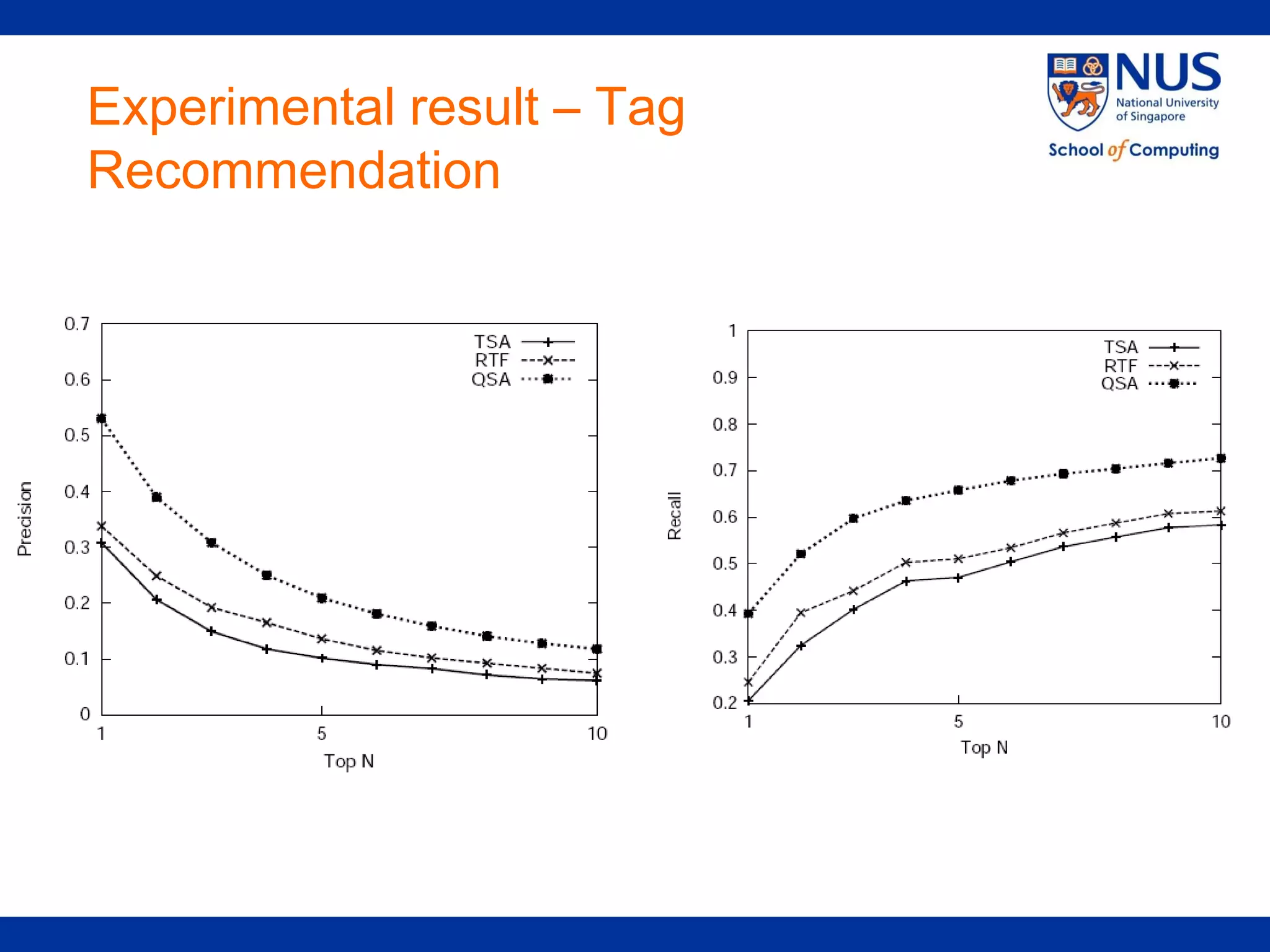
40. Experimental result – Tag
Recommendation
Compare method:
 TSA [TKDE10]: Ternary Semantic Analysis
 RTF [KDD.09]: Optimal ranking using tensor
factorization.

41. Experimental result – Tag
Recommendation

42. Experimental result – User
recommendation

43. Conclusion
We have shown that quaternary semantic analysis
can lead to more accurate recommendation.
We have proposed using a 4-order tensor to model
the four heterogeneous entities: users, items, tags
and ratings.
A unified framework is proposed that utilize
quaternary relation for user recommendation, item
recommendation, tag recommendation and rating
prediction.

44. Thank you very much!

Q/A
44