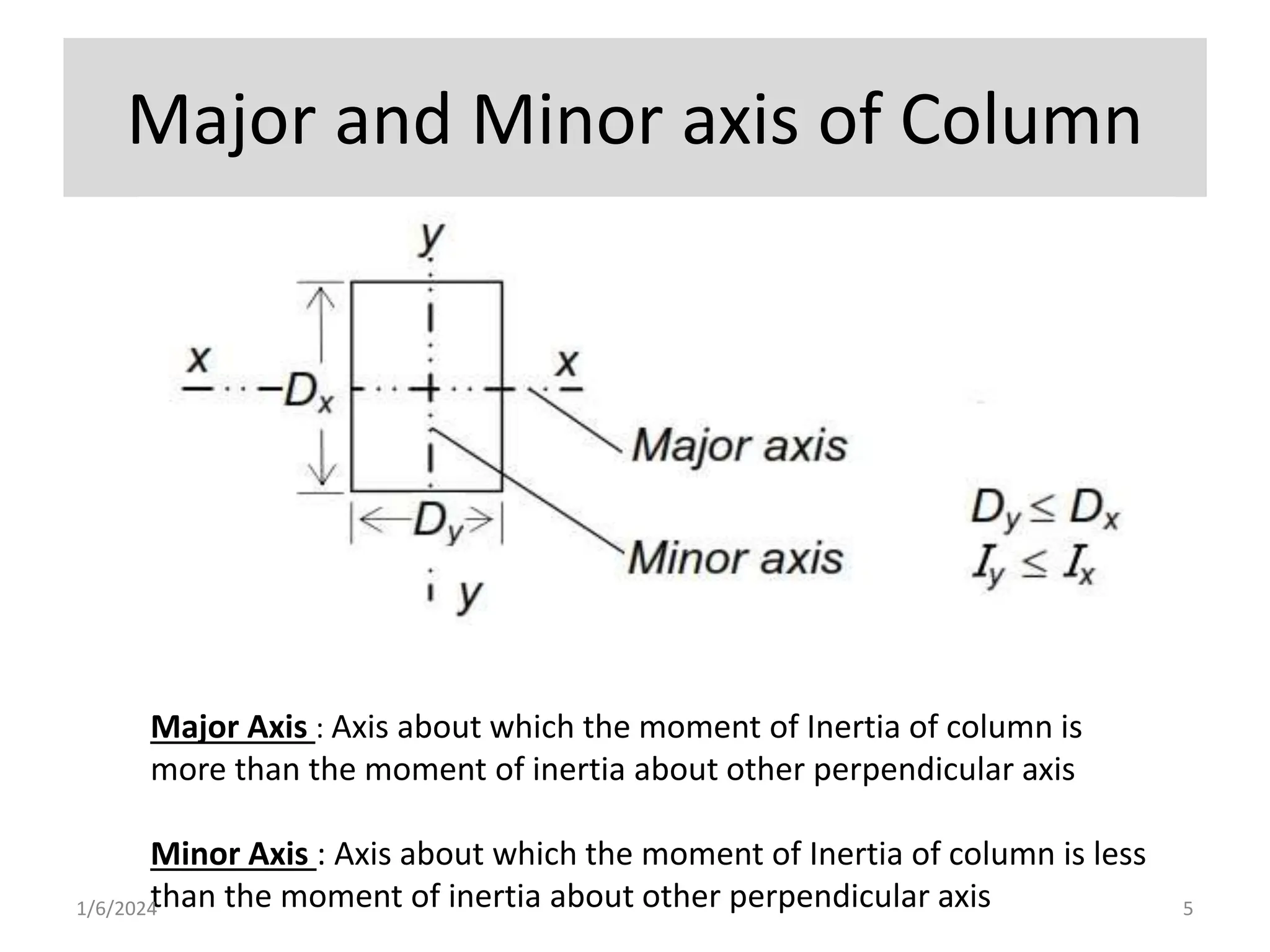
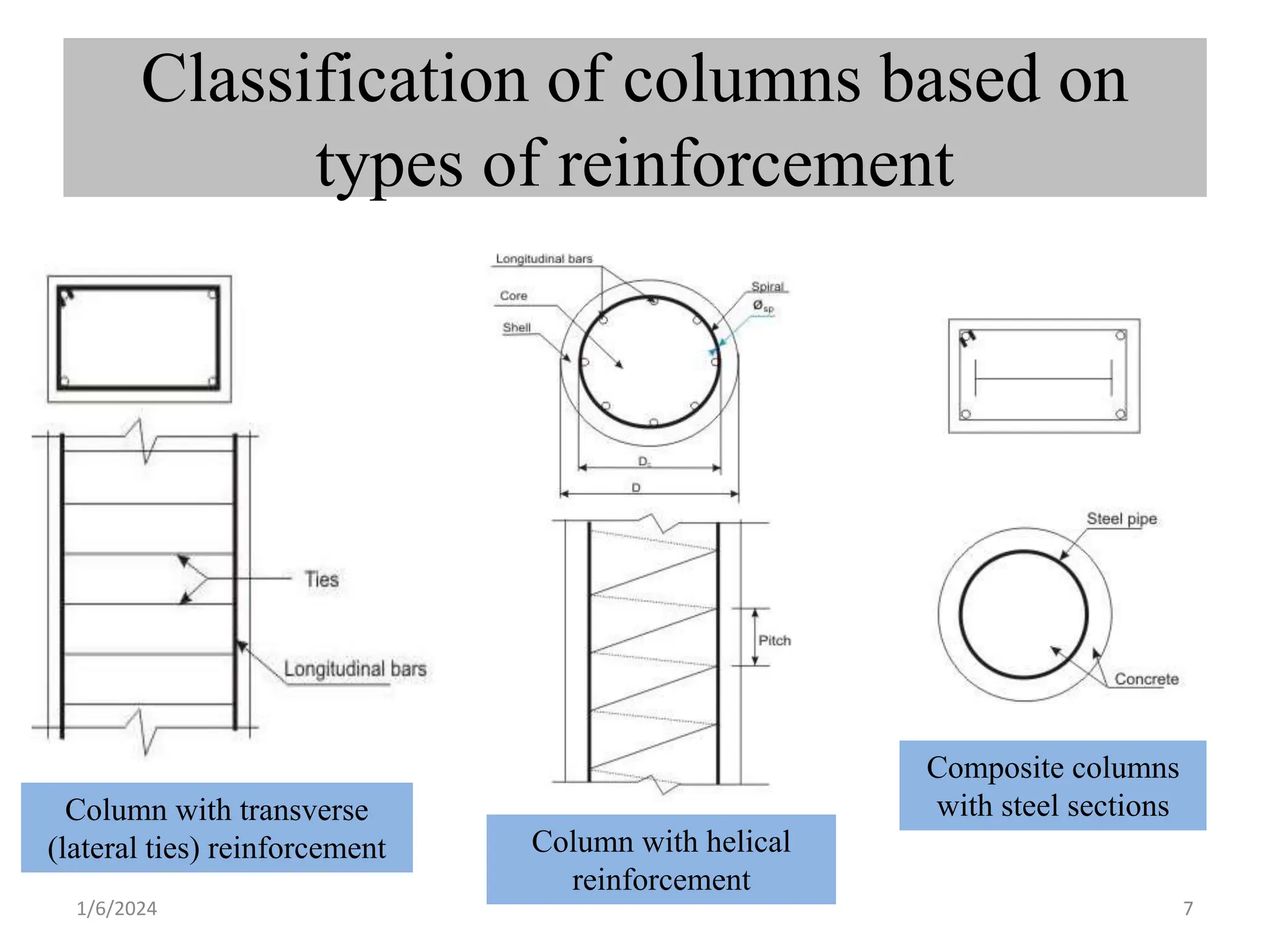
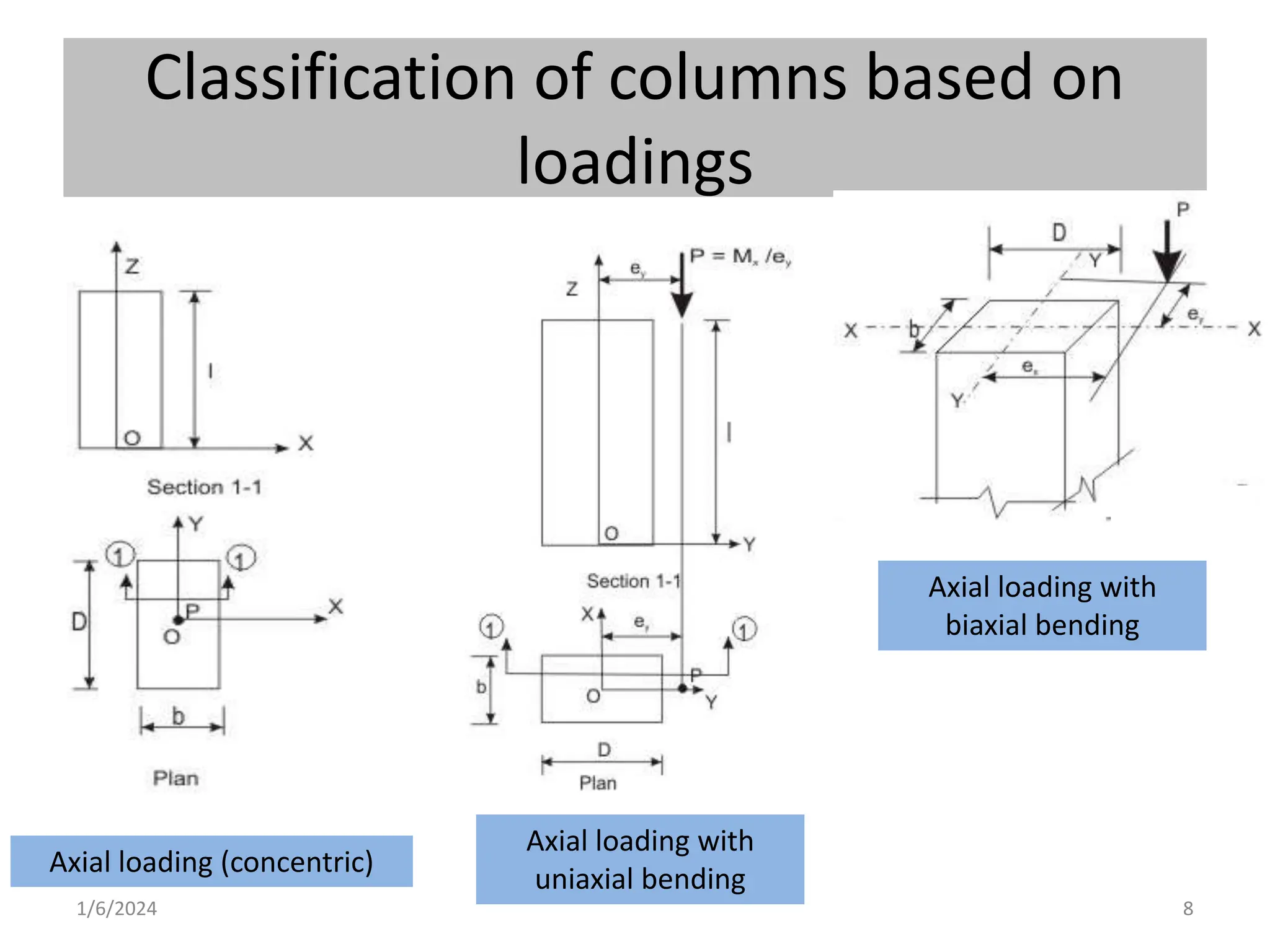
The document discusses various types of compression members including columns, pedestals, walls, and struts. It describes design considerations for compression members including strength and buckling resistance. It defines effective length as the vertical distance between points of inflection when the member buckles. Various classifications of columns are discussed based on loadings, slenderness ratio, and reinforcement type. Code requirements for longitudinal and transverse reinforcement as well as detailing are provided. Two examples of column design are included, one with axial load only and one with spiral reinforcement.

1. Compression Members
• Vertical Structural members
• Transmits axial compressive loads with or
without moment
• Design considerations
– Strength
– Buckling
• Examples : Pedestal, column, wall and strut
1/6/2024 1

2. • Effective length
– The vertical distance between the points of
inflection of the compression member in the
buckled configuration in a plane is termed as
effective length le of that compression member in
that plane. If l is the unsupported length, then
– Clause 25.2 of IS 456:2000 stipulates the effective
lengths of compression members
le = kl
1/6/2024 2

3. IS-456: Table 28:Effective length of
compression member
1/6/2024 3

4. IS-456: Table 28:Effective length of
compression member- Continue
1/6/2024 4

5. Major and Minor axis of Column
Major Axis : Axis about which the moment of Inertia of column is
more than the moment of inertia about other perpendicular axis
Minor Axis : Axis about which the moment of Inertia of column is less
than the moment of inertia about other perpendicular axis
1/6/2024 5

6. Compression Members
• Pedestal (IS 456:2000 cl. 26.5.3)
– l <= 3 times least horizontal dimension, say b
– other horizontal dimension <= 4 times b
• Column (IS 456:2000 cl. 25.3)
– unsupported length, l <= 60 times least
dimension, if restrained at both ends
• Wall (IS 456:2000 cl. 32.2.3)
– Effective height to thickness ratio <= 30
1/6/2024 6

7. Classification of columns based on
types of reinforcement
Column with transverse
(lateral ties) reinforcement Column with helical
reinforcement
Composite columns
with steel sections
1/6/2024 7

8. Classification of columns based on
loadings
Axial loading (concentric)
Axial loading with
uniaxial bending
Axial loading with
biaxial bending
1/6/2024 8

9. Column with axial loading (concentric)
Column with axial loads and uniaxial bending
Column with axial loads and biaxial bending
1/6/2024 9

10. Classification of columns based on
slenderness ratio
Mode Failure
Mode 1
Compression
Failure
• Occurs in short column
• No lateral deformation
• collapse due to material failure
Mode 2
Combine
compression
and bending
Failure
• Short column – combined effects of axial
load and bending
• Slender column – beam-column effect
under axial load
Mode 3
Buckling
Failure
• Failure due to elastic instability under
small loads without yielding of material
1/6/2024 10

11. Classification of columns based on
slenderness ratio
According to code (Cl.25.1.2)
•Short Column – (Lex/D) & (Ley/b) < 12
•Long Column – (Lex/D) OR (Ley/b) ≥ 12
Lex = Effective length in respect of the major axis
D = Depth w.r.t. major axis
Ley = Effective length in respect of the minor axis
b = Width of the member
1/6/2024 11

12. • cl. 25.3.1 the maximum unsupported length between
two restraints of a column to sixty times its least
lateral dimension.
l/d ≤ 60
• For cantilever columns, when one end of the column
is unrestrained, the unsupported length is restricted
to 100b2/D where b and D are as defined earlier
cl.25 Compression members
1/6/2024 12

13. Code Requirements on Reinforcement
and Detailing
Longitudinal reinforcement (cl.26.5.3.1)
• The minimum amount of steel should be at least 0.8% of the
gross cross-sectional area of the column required.
• The maximum amount of steel should be 4% of the gross
cross-sectional area of the column so that it does not exceed
6 per cent when bars from column below have to be lapped
with those in the column under consideration.
• Four and six are the minimum number of longitudinal bars in
rectangular and circular columns, respectively.
• The diameter of the longitudinal bars should be at least 12
mm.
1/6/2024 13

14. Code Requirements on Reinforcement
and Detailing
• Columns having helical reinforcement shall have at
least six longitudinal bars within and in contact with
the helical reinforcement. The bars shall be placed
equidistant around its inner circumference.
• The bars shall be spaced not exceeding 300 mm
along the periphery of the column.
• The amount of reinforcement for pedestal shall be at
least 0.15 per cent of the cross-sectional area
provided
1/6/2024 14

15. Code Requirements on Reinforcement
and Detailing
Transverse reinforcement (cl.26.5.3.2)
• A reinforced concrete compression member shall have transverse or
helical reinforcement so disposed that every longitudinal bar nearest
to the compression face has effective lateral support against
buckling subject to provisions given in cl.26.5.3.2(b)(Arrangement
of transverse reinforcement). The effective lateral support is given
by transverse reinforcement either in the form of circular rings or by
polygonal links (lateral ties) with internal angles not exceeding 1350.
• The pitch or spacing of lateral ties is limited to the least of:
– the least lateral dimension of the compression members;
– sixteen times the smallest diameter of the longitudinal reinforcement bar to
be tied; and
– 300 mm.
1/6/2024 15

16. Design of axially loaded columns
rm = 1.5 for Concrete
Stress = 0.67fck/1.5 = 0.446 fck
rm = 1.15 for Steel
Stress = fy/1.5 = 0.87fy
1/6/2024 16

17. • The stress corresponding to 0.002 strain in steel bars are as follows:
Grade of Steel Stress
Corresponding to
0.002 Strain
Fe250 0.87 fy
Fe 415 0.79 fy
Fe 500 0.75 fy
1/6/2024 17

18. Design of axially loaded columns
• The code adopts the critical value of 0.75 fy
for all grades of steel for finding out the pure
axial load carrying capacity of the column
Pu = 0.446 fck Ac + 0.75 fy As………….(1)
1/6/2024 18

19. Design of axially loaded columns
• Due to Rigid frame action, lateral loadings and
practical aspects of construction axially loaded
columns are subjected to bending moments.
• Minimum eccentricity as specified in code
(Clause 25.4) need to be considered
• emin Should be Greater of
– (unsupported length/500 + lateral dimension/30)
– 20 mm
1/6/2024 19

20. Design of axially loaded columns
• When emin does not exceed 0.05 times the lateral
dimension, code permits the use of following
simplified formula obtained by reducing Pu (Given in
equation 1 ) by approx. 10% (cl. 39.3)
Pu = 0.4 fck Ac + 0.67 fy As
1/6/2024 20

21. 𝑃𝑢 = 0.40𝑓𝑐𝑘𝐴𝑐 + 0.67𝑓𝑦𝐴𝑠
𝑃𝑢 = 0.40𝑓𝑐𝑘(𝐴𝑔−𝐴𝑠) + 0.67𝑓𝑦𝐴𝑠
𝑃𝑢 = 0.40𝑓𝑐𝑘𝐴𝑔(1 − 𝑝) + 0.67𝑓𝑦𝑝𝐴𝑔
• 𝐴𝑔= gross area of the section
• 𝑝= percentage of steel reinforcement
Design of axially loaded columns
1/6/2024 21

22. Compression Member with Helical
Reinforcement
• The strength of compression
members with helical reinforcement
shall be taken as 1.05 times the
strength of similar member with
lateral ties.
Pu = 1.05*(0.4 fck Ac + 0.67 fy As)
•The ratio of the volume of helical
reinforcement to the volume of the
core shall not be less than
0.36(Ag/Ac-1)*fck/fy
1/6/2024 22

23. • 𝑣𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 ℎ𝑒𝑙𝑖𝑐𝑎𝑙 𝑟𝑒𝑖𝑛𝑓𝑜𝑟𝑐𝑒𝑚𝑒𝑛𝑡
𝑣𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑐𝑜𝑟𝑒(𝑉𝑐)
≥ 0.36
𝐴𝑔
𝐴𝑐
− 1 ∗
𝑓𝑐𝑘
𝑓𝑦
• 𝑣𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 ℎ𝑒𝑙𝑖𝑐𝑎𝑙 𝑟𝑒𝑖𝑛𝑓𝑜𝑟𝑐𝑒𝑚𝑒𝑛𝑡 =
𝜋(𝐷𝑐−𝜑𝑠𝑝
)∗asp
• 𝑉𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑐𝑜𝑟𝑒 = 𝜋
4
∗ Dc2 ∗ 𝑆𝑣
•
𝜋(𝐷𝑐−𝜑𝑠𝑝
)∗asp
𝜋
4
∗Dc2∗Sv
≥ 0.36
𝐴𝑔
𝐴𝑐
− 1 ∗
𝑓𝑐𝑘
𝑓𝑦
Dc = Dia. of core
𝜑𝑠𝑝 = Dia. of spiral reinforcement
asp = Area of cross section of spiral reinforcement
Sv = pitch of spiral reinforcement
1/6/2024 23

24. Detailing of Reinforcement in Column
1/6/2024 24

25. Q. Design the reinforcement in a column of size 400 mm x 600 mm
subjected to an axial load of 2000 KN under service dead load and
live load. The column has an unsupported length of 4.0 m and
effectively held in position and restrained against rotation in both
ends. Use M 25 concrete and Fe 415 steel.
Slenderness Check
𝑙𝑒𝑥/𝐷𝑥 = 2600/600=4.33 < 12
𝑙𝑒𝑦/𝐷𝑦 = 2600/400=6.5 < 12
Hence it is a short column
Minimum Eccentricity
ex min = Greater of (lx/500+D/30) and 20 mm
= Greater of (4000/500 + 600/30) and 20 mm
= 28 mm and 20 mm => 28 mm
As per IS-456: Table 28,
Theoretical value = 0.5L
Recommended value =0.65L
=0.65*4000=2600
1/6/2024 25

26. ey min = Greater of (ly/500+Dy/30) and 20 mm
= Greater of (4000/500 + 400/30) and 20 mm
= 21.33 mm and 20 mm => 21.33 mm
0.05*Dx = 0.05*600 =30 mm > ex min (28mm)
0.05*Dy = 0.05*400 = 20 mm ~ ey min (21.33 mm)
• When emin does not exceed 0.05 times the lateral
dimension, code permits the use of simplified
formula.
1/6/2024 26

27. 𝑃𝑢 = 0.40𝑓𝑐𝑘𝐴𝑐 + 0.67𝑓𝑦
𝑃𝑢 = 0.40𝑓𝑐𝑘(𝐴𝑔 − 𝐴𝑠) + 0.67𝑓𝑦𝐴𝑠
3000*103 = 0.4 *25*(400 *600- As) + 0.67*415*As
As = 2238.39 mm2
Provide #6 Nos. 20 mm dia. Bars and #2 Nos. 16 mm dia. Bars
Hence Area provided = 2287 mm2
% Reinforcement Pt = (As/bd)*100
Pt = 0.953 > 0.8% & < 4% (cl. 26.5.3.2)……..OK.
Lateral Ties
Not less than…… i. φ/4 and
ii. 6 mm
Here φ is the largest bar diameter in the longitudinal reinforcement
Consider 8 mm dia. lateral ties which is currently being used in
field.
1/6/2024 27

28. Pitch ……. cl.26.5.3.2
i. the least lateral dimension of the column = 400 mm
ii. sixteen times the smallest diameter of longitudinal
reinforcement bar to be tied = 16(16) = 256 mm
iii. 300 mm
Use a pitch of 250 mm
1/6/2024 28

29. Design a reinforced concrete spiral column of 390
mm diameter subjected to an axial factored load of
1750 kN. The column is braced against side sway and
has unsupported length of 3.3 m. The concrete mix
and steel to be used in construction are of grades M25
and Fe415, respectively.
1/6/2024 29

30. 1/6/2024 30

31. Design of Spiral steel
Conside a bar dia. Of 8 mm and pitch Sv
Dia. Of the Core Dc = 390-40-40 = 310 mm
Dia. Of the helix Dsp = 390-40-40-8 = 302 mm
As per cl. 39.4.1
𝑣𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 ℎ𝑒𝑙𝑖𝑐𝑎𝑙 𝑟𝑒𝑖𝑛𝑓𝑜𝑟𝑐𝑒𝑚𝑒𝑛𝑡
𝑣𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑐𝑜𝑟𝑒(𝑉𝑐)
≥ 0.36
𝐴𝑔
𝐴𝑐
− 1 ∗
𝑓𝑐𝑘
𝑓𝑦
𝜋(𝐷𝑐−𝜑𝑠𝑝
)∗asp
𝜋
4
∗Dc2∗Sv
≥ 0.36
𝐴𝑔
𝐴𝑐
− 1 ∗
𝑓𝑐𝑘
𝑓𝑦
Dc = Dia. of core
φsp = Dia. of spiral reinforcement
asp = Area of cross section of spiral reinforcement
Sv = pitch of spiral reinforcement
1/6/2024 31

32. 1/6/2024 32

33. Detailing of Reinforcement
1/6/2024 33