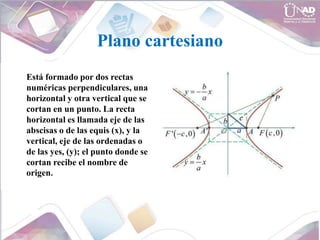
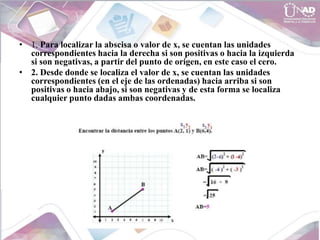
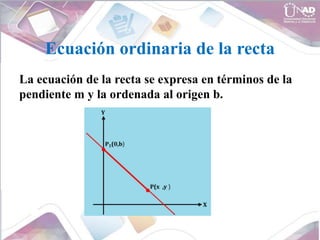
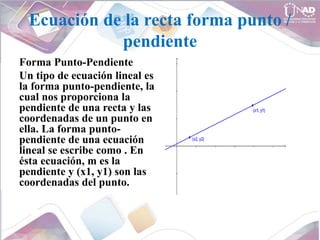
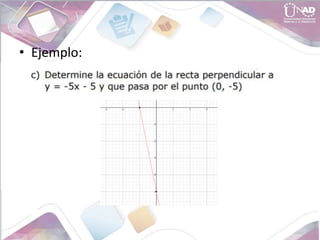
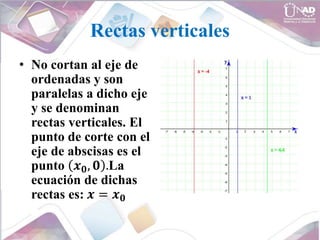
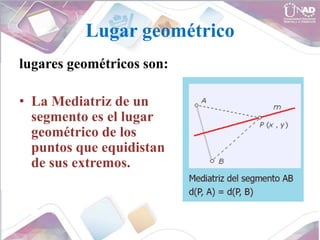
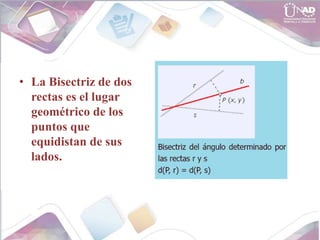
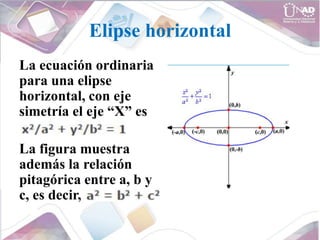
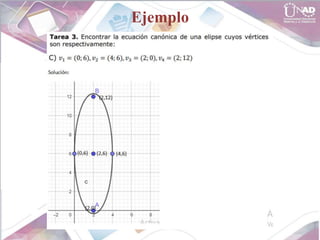
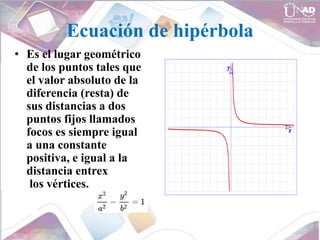
This document provides an overview of analytic geometry concepts including: - The Cartesian plane and using coordinates to locate points - Equations for lines including vertical, horizontal, and oblique lines - Geometric loci such as the midpoint and bisector - Equations for circles, parabolas, ellipses, and hyperbolas It includes examples of finding equations that model geometric shapes on the Cartesian plane.

1. Paso 4- unidad 3
Presentado por: María Elsa Rodríguez Zapata
Código de grupo: 551108_34
Tutor: WILSON FERNANDO MORENO
ALGEBRA, TRIGONOMETRIAY GEOMETRIA
ANALITICA
Universidad Nacional Abierta y a Distancia UNAD
Escuela de Ciencias de la Educación – ECEDU
Licenciatura en Matemáticas
Noviembre -2021

2. Unidad 3
Pensamiento
geométrico y analítico

3. Geometría
analítica

4. Estudia las figuras, sus
distancias, sus áreas, puntos de
intersección, ángulos de
inclinación, puntos de división,
volúmenes, etcétera.
Analiza con detalle los datos de
las figuras geométricas
mediante técnicas básicas del
análisis matemático y del
álgebra en un determinado
sistema de coordenadas.

5. Plano cartesiano
Está formado por dos rectas
numéricas perpendiculares, una
horizontal y otra vertical que se
cortan en un punto. La recta
horizontal es llamada eje de las
abscisas o de las equis (x), y la
vertical, eje de las ordenadas o
de las yes, (y); el punto donde se
cortan recibe el nombre de
origen.

6. Ubicación de puntos en el plano
cartesiano
Se forman asociando un valor del eje de las
equis a uno de las yes, respectivamente, esto
indica que un punto (P) se puede ubicar en el
plano cartesiano tomando como base sus
coordenadas, lo cual se representa como:
P (x, y)

7. • 1. Para localizar la abscisa o valor de x, se cuentan las unidades
correspondientes hacia la derecha si son positivas o hacia la izquierda
si son negativas, a partir del punto de origen, en este caso el cero.
• 2. Desde donde se localiza el valor de x, se cuentan las unidades
correspondientes (en el eje de las ordenadas) hacia arriba si son
positivas o hacia abajo, si son negativas y de esta forma se localiza
cualquier punto dadas ambas coordenadas.

8. Lugar geométrico
lugares geométricos son:
• La Mediatriz de un
segmento es el lugar
geométrico de los
puntos que equidistan
de sus extremos.

9. • La Bisectriz de dos
rectas es el lugar
geométrico de los
puntos que
equidistan de sus
lados.

10. • La Circunferencia
de centro C y radio r
es el lugar
geométrico de los
puntos cuya
distancia al centro
es r.

11. Ecuación ordinaria de la recta
La ecuación de la recta se expresa en términos de la
pendiente m y la ordenada al origen b.

12. Ecuación de la recta forma punto /
pendiente
Forma Punto-Pendiente
Un tipo de ecuación lineal es
la forma punto-pendiente, la
cual nos proporciona la
pendiente de una recta y las
coordenadas de un punto en
ella. La forma punto-
pendiente de una ecuación
lineal se escribe como . En
ésta ecuación, m es la
pendiente y (x1, y1) son las
coordenadas del punto.

13. • Ejemplo:

15. Rectas verticales
• No cortan al eje de
ordenadas y son
paralelas a dicho eje
y se denominan
rectas verticales. El
punto de corte con el
eje de abscisas es el
punto 𝒙𝟎, 𝟎 .La
ecuación de dichas
rectas es: 𝒙 = 𝒙𝟎

16. Rectas horizontales
• No cortan al eje de las
abscisas y, por tanto, son
paralelas a dicho eje y se
denominan rectas
horizontales. El punto de
corte con el eje de
ordenadas es el punto
(𝟎, 𝒚𝟎)La ecuación de
dichas rectas es:
𝒚 = 𝒚𝟎

17. Recta oblicua
• En ellas hay un punto
de corte con el eje de
abscisas (a,0) y otro
punto de corte con el
eje de ordenadas
(0,b). El valor (𝒂)
recibe el nombre de
abscisa en el origen,
mientras que el (𝒃)se
denomina ordenada
en el origen.

18. Elementos de las
cónicas

19. Ecuación de la circunferencia
Para hallar la circunferencia con centro en el
origen será necesario conocer el radio de esta o
un punto por donde pasa la circunferencia,
cuando se conoce el radio será más sencillo
puesto que la ecuación tendrá como estructura.
𝒙𝟐
+ 𝒚𝟐
= 𝒓𝟐
luego al hallar el radio únicamente conoceremos
la ecuación terminada, cuando conocemos un
punto de la circunferencia deberemos usar la
ecuación de distancia y hallaremos el radio.

20. Ecuación ordinaria de una
circunferencia dado su centro y
radio
• Dados las coordenadas del centro de la
circunferencia C(h, k) y el radio "r" de la misma,
podemos utilizar la siguiente ecuación para
determinar el valor de "y" correspondiente a un
valor de "x".

21. EJEMPLO:

23. Ecuaciones de la parábola
Es el lugar geométrico de todos los
puntos que equidistan de un punto fijo
llamado foco y de una recta fija llamada
directriz.
Una parábola cuyo eje de simetría sea
paralelo al eje de abcisas se expresa
mediante la ecuación:

24. Ecuación de la elipse
La elipse es el lugar geométrico de todos los
puntos de un plano, tales que la suma de las
distancias a otros dos puntos fijos llamados
focos es constante.

25. Elipse horizontal
La ecuación ordinaria
para una elipse
horizontal, con eje
simetría el eje “X” es
La figura muestra
además la relación
pitagórica entre a, b y
c, es decir,

26. Elipse vertical
Elipse centrada en el origen de coordenadas y eje mayor el eje
“Y”.
El eje mayor está en el eje de las y. Las intercepciones en x
son (±b, 0) y las intercepciones en y son (0, ±a).
El eje mayor está en el eje de las y.
Dese cuenta que el eje mayor es horizontal si el término 𝒙𝟐
tiene el denominador más grande y vertical si el término
𝒚𝟐tiene el denominador más grande. Ya que el más grande de
los dos denominadores es 𝒂𝟐, la longitud del eje mayor
siempre es 2a y la longitud del eje menor siempre es 2b. La
distancia del centro a cualquier foco es |c|.

27. Ejemplo

29. Ecuación de hipérbola
• Es el lugar geométrico
de los puntos tales que
el valor absoluto de la
diferencia (resta) de
sus distancias a dos
puntos fijos llamados
focos es siempre igual
a una constante
positiva, e igual a la
distancia entrex
los vértices.

30. Bibliografía
Rondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a
Distancia. Páginas 136 – 235. Recuperado de https://repository.unad.edu.co/handle/10596/11583​
Rondón, J. (2005) Matemática Básica. Bogotá D.C.: Universidad Nacional Abierta y a Distancia. Recuperado
de http://hdl.handle.net/10596/7425​
Ramírez, V. A. P., & Cárdenas, A. J. C. (2001). Matemática universitaria: conceptos y aplicaciones generales.
Vol. 1. San José, CR: Editorial Cyrano. Páginas 59 - 82. Recuperado de https://elibro-
net.bibliotecavirtual.unad.edu.co/es/ereader/unad/85383?page=66​
https://www.cecyt3.ipn.mx/ibiblioteca/mundodelasmatematicas/EcuacionesDeLaHiperbolaConCentroEnElOrig
en.html