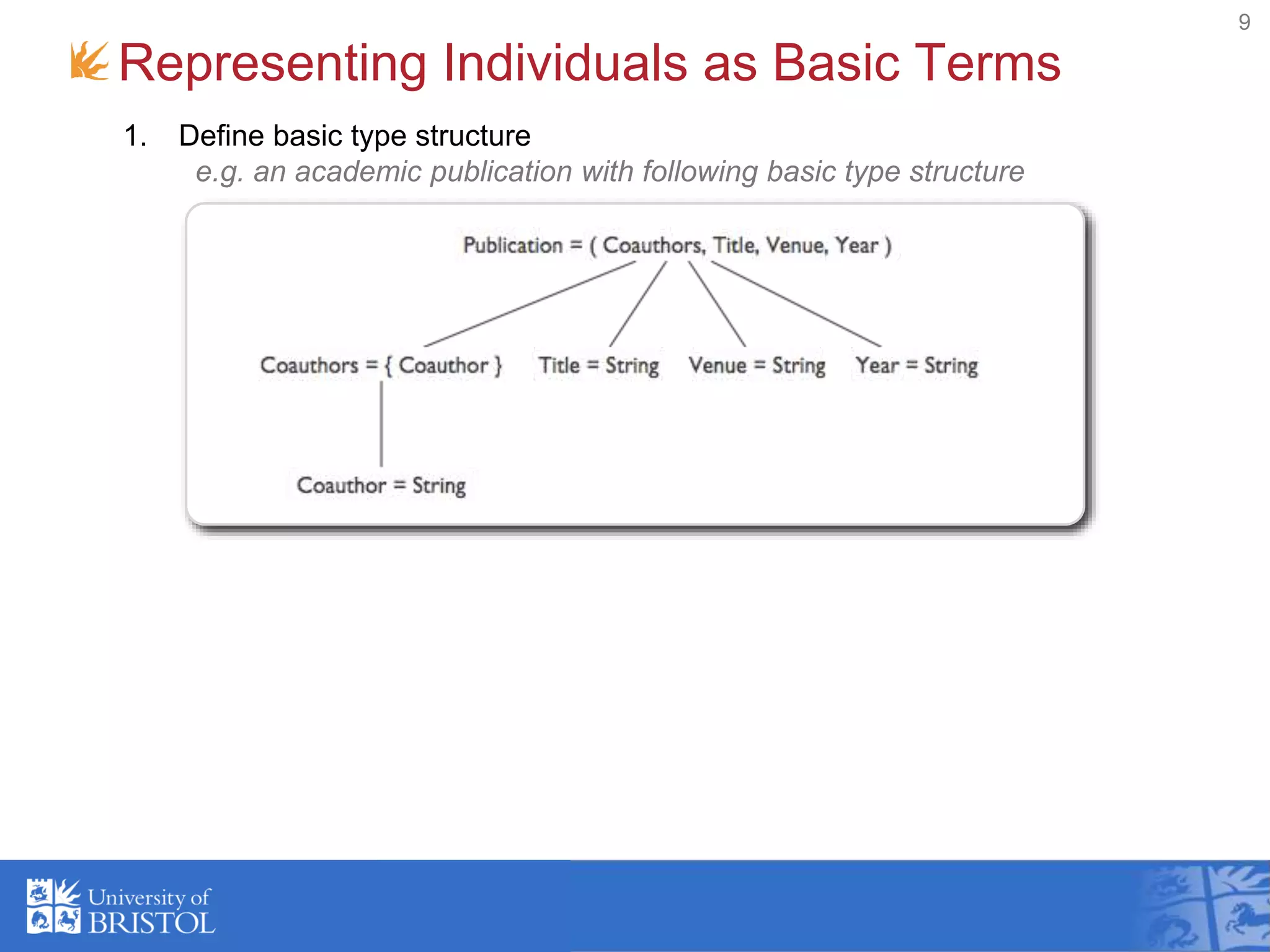
The document discusses querying and merging heterogeneous data using approximate joins based on higher-order terms, specifically addressing the integration of varied data sources like web pages and databases. It outlines a framework for relational joins tailored for basic terms, introduces basic term proximity-joins, and demonstrates its application in bibliographic data. The work presents a novel relational algebra that facilitates approximate querying and highlights its implications for data integration.

1. Querying and Merging Heterogeneous
Data by Approximate Joins on Higher-
Order Terms
Simon Price and Peter Flach
ILP 2008

2. Query heterogeneous data sources as if their data
were conveniently held in a single relational
database.
Example data sources:
• web pages
• digital libraries
• knowledge bases
• Semantic Web
• databases
Our Aim
2

3. Outline of this paper
1. Relational Joins (a quick review)
2. Basic Terms
3. Relational Joins for Basic Terms
4. Basic Term Proximity-Join
5. Application
3

4. Contribution of this work
Relational Algebra for Basic Terms
Basic Term Proximity-Join
Application to bibliographic data
4

5. 1. Relational Joins (a quick review)
5
1. Relational Joins (a quick review)
2. Basic Terms
3. Relational Joins for Basic Terms
4. Basic Term Proximity-Join
5. Application

6. θ-Join
6
publications
publication
#
title venue year
1 a b c
2 d e f
authors
author#
publication
#
name
1 1 p
2 1 q
3 2 r
publication
#
title venue year
1 a b c
author#
publication
#
name
1 1 p
publication
#
title venue year
2 d e f
author#
publication
#
name
3 2 r
publication
#
title venue year
1 a b c
author#
publication
#
name
2 1 q

7. 2. Basic Terms
7
1. Relational Joins (a quick review)
2. Basic Terms
3. Relational Joins for Basic Terms
4. Basic Term Proximity-Join
5. Application

8. Basic Terms
8
• Proposed by John Lloyd
• Family of typed-terms in higher-order logic
• Based on Church’s simple theory of types
• Data types representing:
• tuples
• structures - e.g. trees and graphs
• abstractions - e.g. sets and multisets (bags)
• Basic Terms and the “individuals-as-terms”
model
Lloyd, J. W.: Logic for Learning. Springer. New York
(2003)

9. Representing Individuals as Basic Terms
9
1. Define basic type structure
e.g. an academic publication with following basic type structure
2. Transform data instances to basic terms of that type
e.g. a publication record from the CORA bibliographic database
( { “Mitchell, T.”, “Thrun, S.” },
“Explanation-Based Learning: A Comparison of Symbolic and Neural Network
Approaches.”,
“In Proceedings of the Tenth International Conference on Machine Learning”,
“1993” )

10. 3. Relational Joins for Basic Terms
10
1. Relational Joins (a quick review)
2. Basic Terms
3. Relational Joins for Basic Terms
4. Basic Term Proximity-Join
5. Application

11. Upgrading Relational Joins for Basic Terms
11
1. Restate (a sub-set of) traditional relational algebra
1. Remove schematic metadata from the data itself
2. Make explicit the tuple item indexing function
2. Replace sets of tuples (relations) with sets of basic
terms (“basic term relations”)
3. Upgrade indexing function to index all types of basic
terms:
1. basic tuples (tuples of basic terms)
2. basic structures (e.g. lists and trees of basic terms)
3. basic abstractions (e.g. sets and multisets of basic terms)
4. any combination of the above three

12. Basic Term θ-Join (Example 1)
12
A = { ({p, q}, a, b, c),
({r}, d, e, f),
({s, t}, d, g, h) }
B = { ({p, q}, a, b, c),
({p, q}, d, e, f) }
{ ( ({p, q}, a, b, c), ({p, q}, a, b, c) ),
( ({r}, d, e, f), ({p, q}, d, e, f) ),
( ({s, t}, d, g, h), ({p, q}, d, e, f) ) }
Title = TitleA B =

13. Basic Term θ-Join (Example 2)
13
A = { ({p, q}, a, b, c),
({r}, d, e, f),
({s, t}, g, h, k) }
B = { ({p, q}, a, b, c),
({p, q}, d, e, f) }
{ ( ({p, q}, a, b, c), ({p, q}, a, b, c) ),
( ({p, q}, a, b, c), ({p, q}, d, e, f) ) }
Coauthors = CoauthorsA B =

14. Basic Term θ-Join (Example 3)
14
A = { ({p, q}, a, b, c),
({r}, d, e, f),
({s, t}, g, h, k) }
B = { ({p, q}, a, b, c),
({p, q}, d, e, f) }
{ ( ({p, q}, a, b, c), ({p, q}, a, b, c) ) }Publication = PublicationA B =

15. 4. Basic Term Proximity Join
15
1. Relational Joins (a quick review)
2. Basic Terms
3. Relational Joins for Basic Terms
4. Basic Term Proximity-Join
5. Application

16. Replacing Equality with Proximity
16
Proximity
Distance Threshold
is a dependency relation, but not an
equivalence relation.
i.e. proximity is reflexive and
symmetric but not necessarily
transitive. Due to:
Properties of Proximity
• dist is not constrained to have
an upper bound.
• Some normalising function
may be used,
usually into the closed
interval [0, 1].
• Or can normalise in feature
space (e.g. normalising
kernels).
Normalisation

17. Basic Term Proximity Join
• Basic Term Projection
• Basic Term θ-Restriction
• Basic Term Proximity Join
17
s is a basic subterm at type tree index i

18. 5. Application
18
1. Relational Joins (a quick review)
2. Basic Terms
3. Relational Joins for Basic Terms
4. Basic Term Proximity-Join
5. Application

19. • Given the ground truth
where
• The goal is to reconstruct V as V’ by choosing an appropriate s
Proximity joins on bibliographic publications
data
19

20. • Currently, ground truths for pairs of data sets are rare.
So, we choose with
• CORA-REFS publications data set (1881 instances)
• Data type is the one used in examples throughout this talk
• Example pair of instances that require approximate join:
CORA Data Set
20
( { “Mitchell, T.”, “Thrun, S.” },
“Explanation-Based Learning:
...”,
“In Proceedings of the Tenth
...”,
“1993” )
( { “Tom Mitchell”, “Sven Thrun”
},
“Explanation based learning:
...”,
“Proceedings of the 10th ...”,
“ ’93 ” )

21. Experiments on CORA data set
21
For each join:
1. Calculate pairwise distances
between all basic terms in
CORA
2. Construct a dendrogram
3. Calculate precision-recall at
each node in the dendrogram
i.e. plot a point on the p-r chart
for each node in the
dendrogram
e.g.
threshold = 120
TP FN
FP TN
Confusion Matrix
TP is no. pairs in same cluster
that should be in the same
cluster.
TN is no. pairs in different
clusters that should be in
different clusters.
FP is etc...

22. Proximity Joins on CORA Dataset
23
Publication
Publication.Coauthors
Publication.Title
Publication.Venue
Precision
Recall
• Distance derived from a kernel in the usual way
• Basic term kernel = default kernel for basic terms
• String kernel = p-spectrum kernel
• Default kernel = matching kernel

23. And finally...
24

24. Conclusion
26
• Relational Algebra for Basic Terms
• Combines relational model and basic terms in single
formalism
• Basic Term Proximity-Join
• Enables approximate querying and merging of basic terms
• Application to bibliographic data
• Shows potential for data integration
❦ ❦ ❦

25. Default Kernel for Basic Terms
27