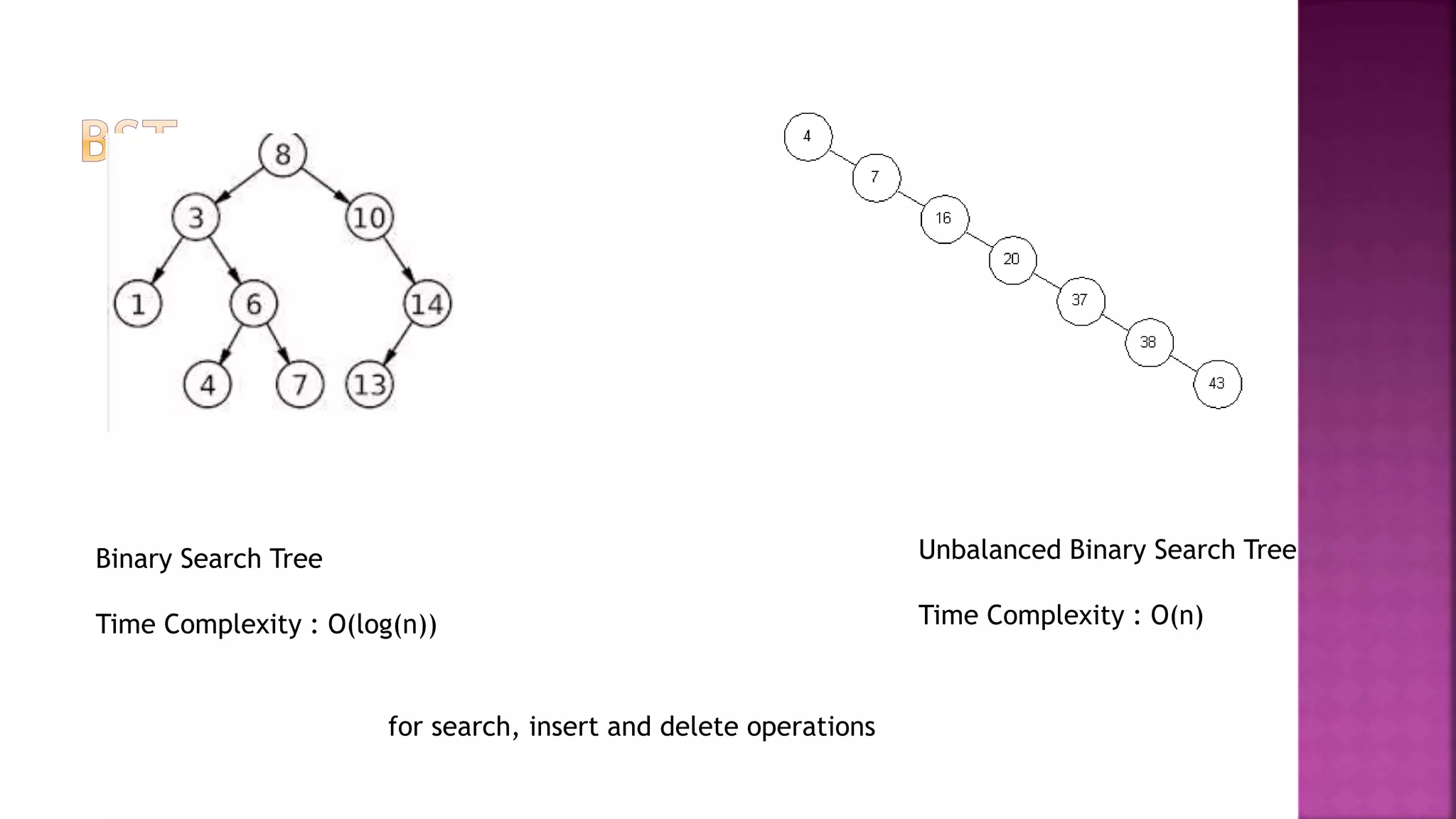
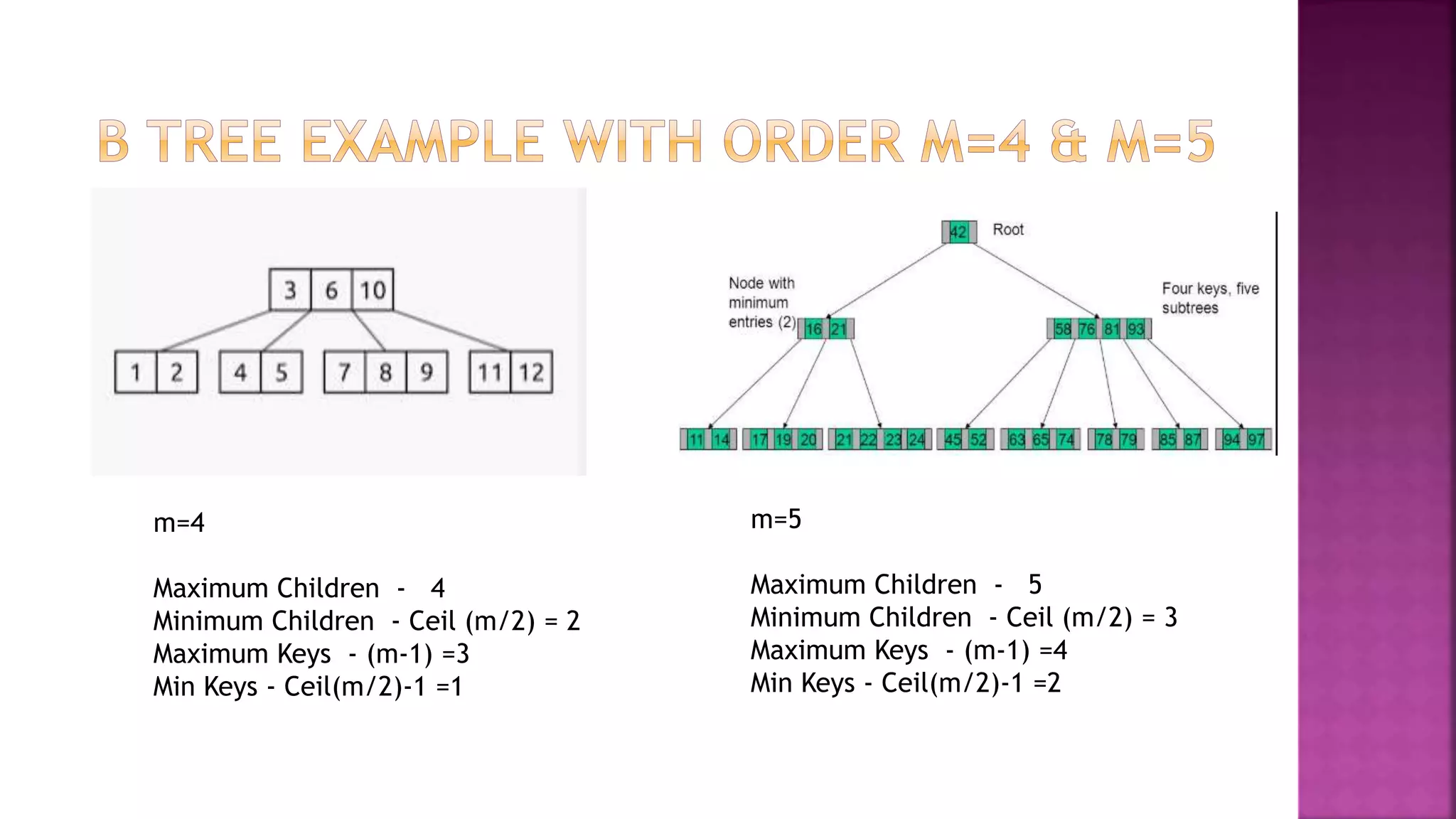
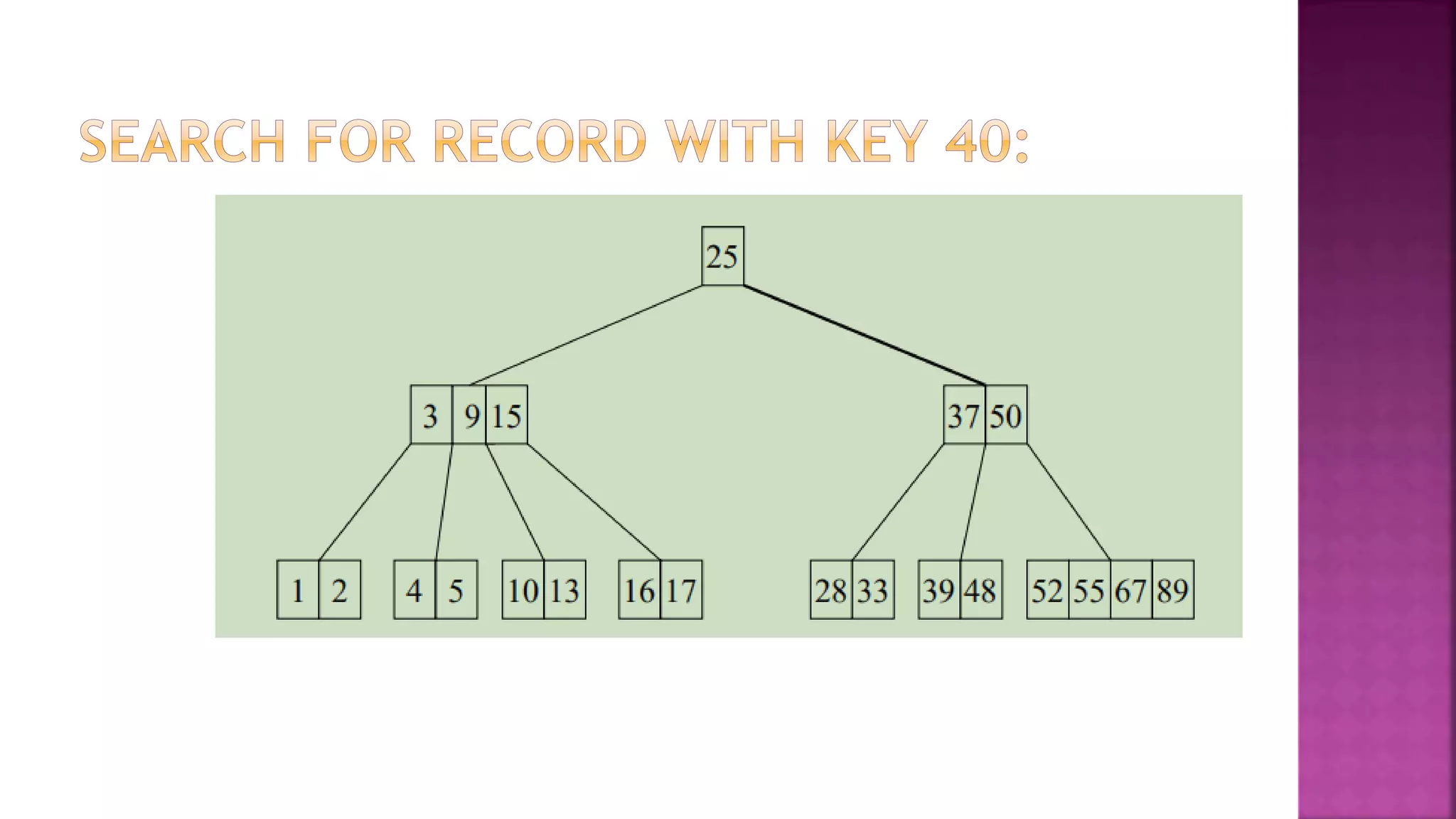
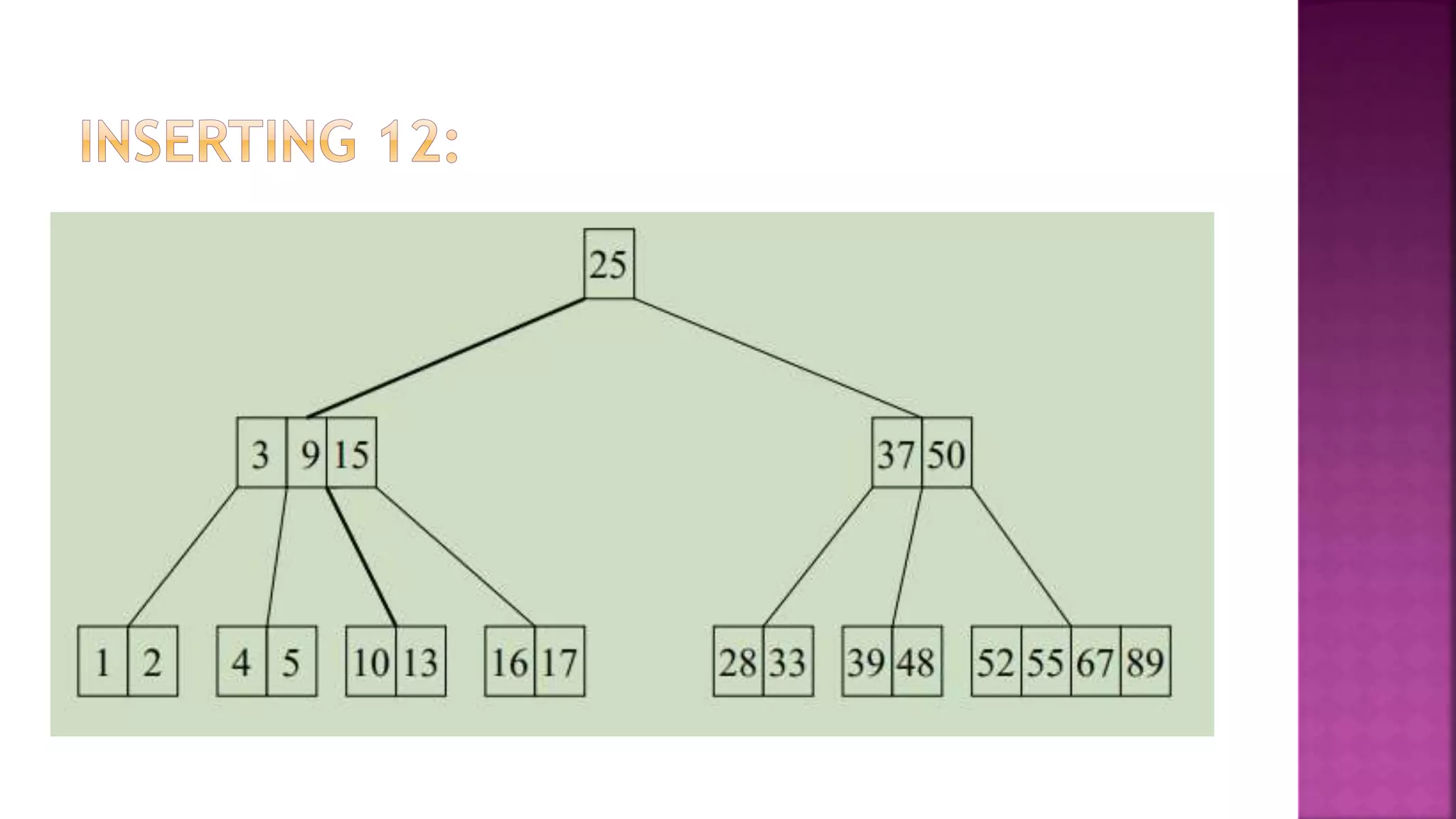
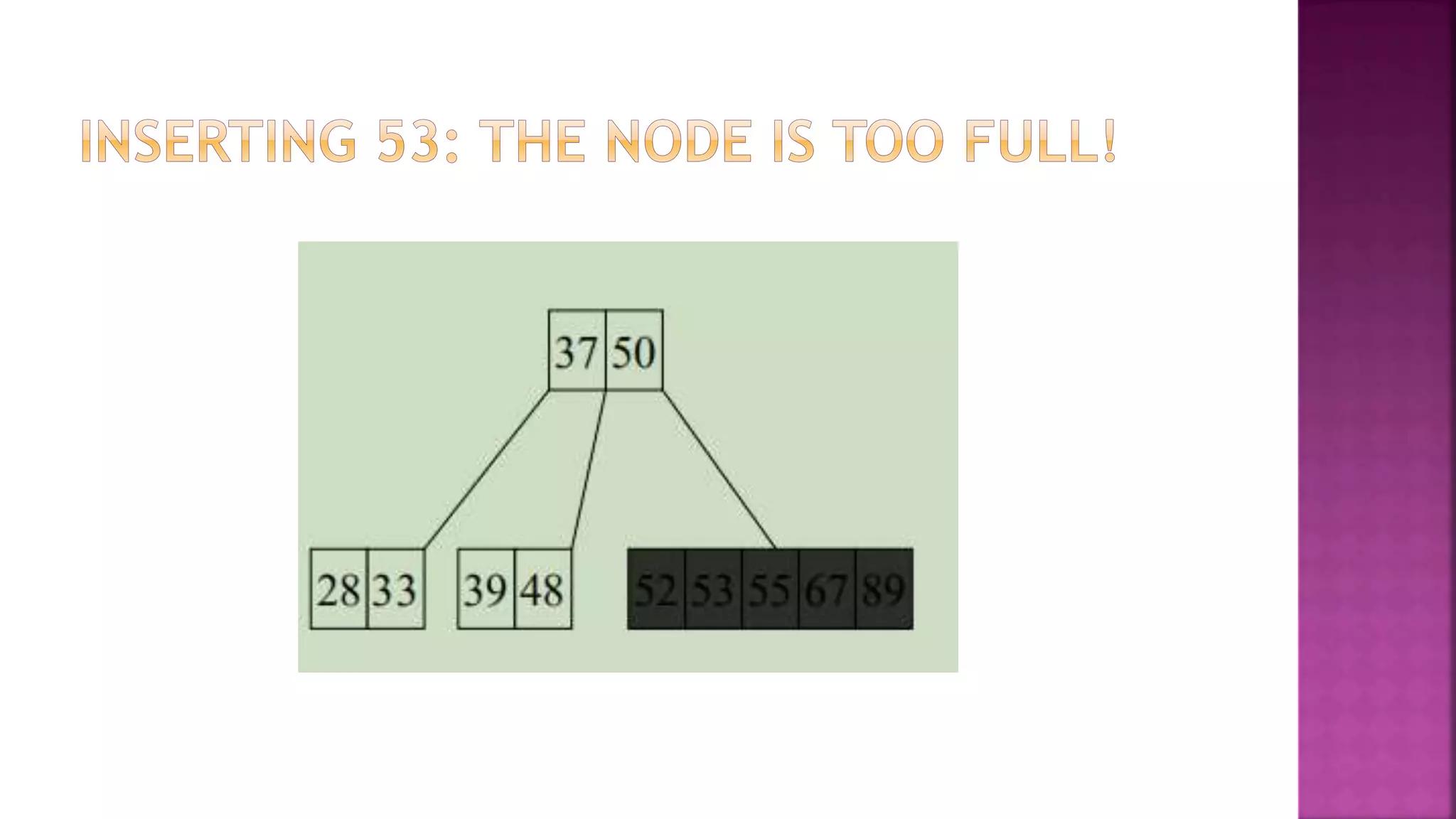
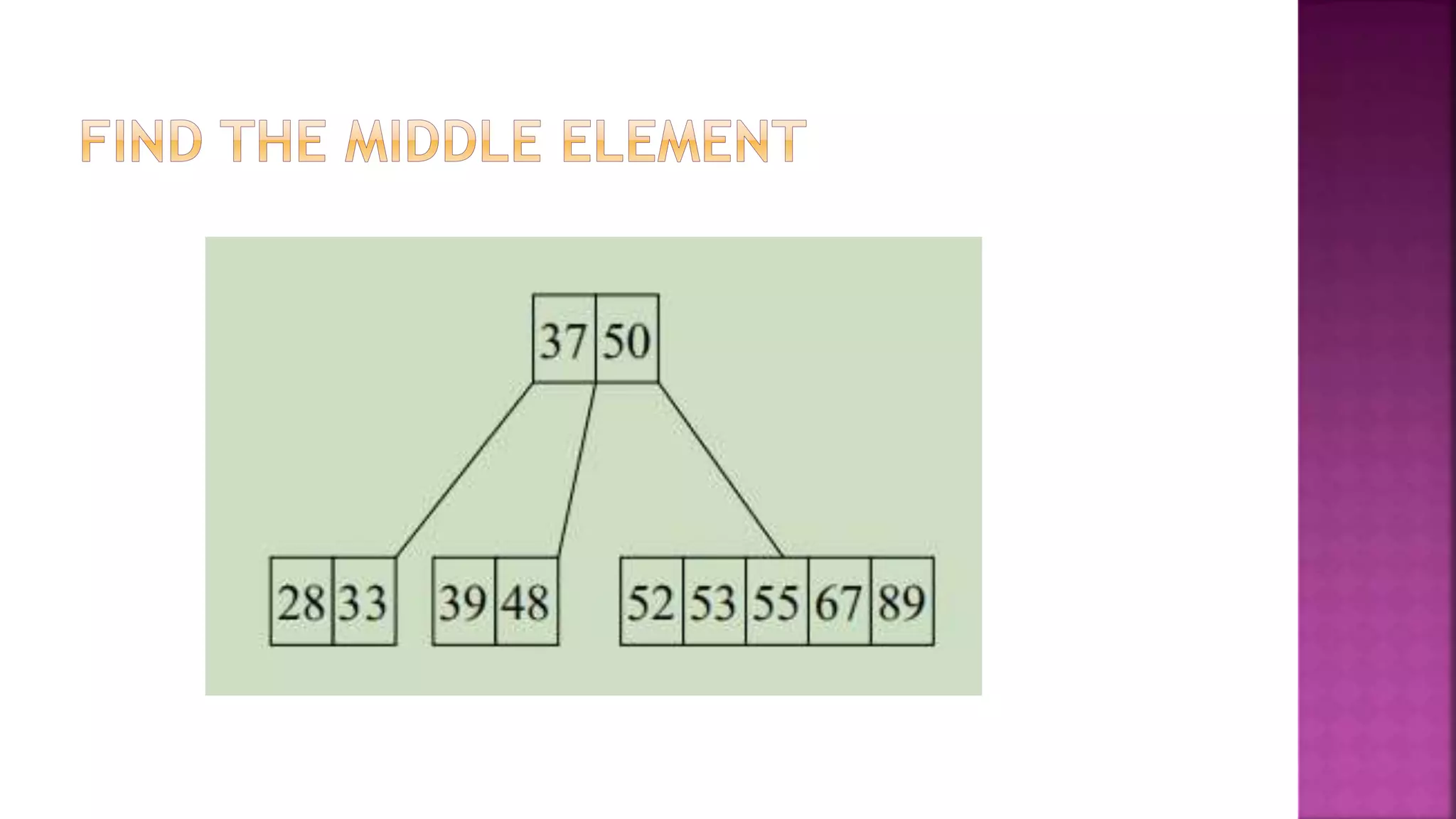
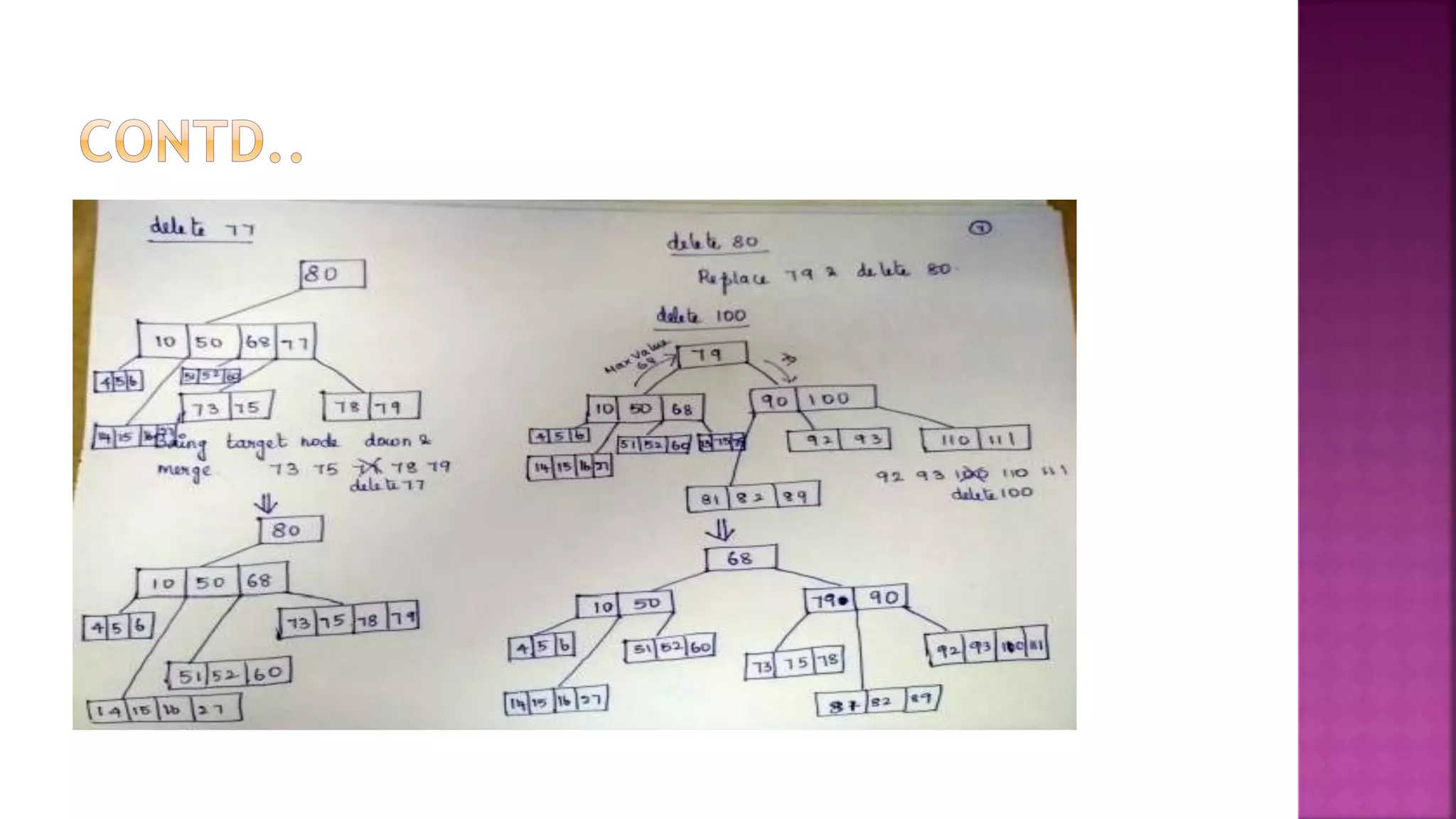
The document discusses trees and B-trees, which are data structures used to store and retrieve data efficiently. It notes that B-trees are well-suited for external memory as each node can hold multiple data items and child pointers. The key properties of B-trees are that each node has between m/2 and m child pointers and m-1 or fewer keys, ensuring the tree remains balanced during search, insertion, and deletion operations. An example of constructing a B-tree of order 4 from a sample data set is also provided.

1. Dr.P.Prittopaul
Assistant Professor
Dept of CSE
Velammal Engineering College
Velammal Engineering College
(An Autonomous Institution, Affiliated to Anna University, Chennai)
(Accredited by NAAC & NBA)

2.  In CS a tree is
 an Organizational Structure for the storage and retrieval of data.
 Height balanced binary search trees: AVL trees, red-black trees
search faster than in an average binary search tree because the tree is
guaranteed to have the smallest possible depth.
 Another kind of multi-way search trees . Optimises search in external
memory.

3.  Main memory (RAM)
 External (peripheral) storage: hard disk,
CD-ROM, tape, etc.
Different considerations are important in designing algorithms
and data structures for primary (main) versus secondary
(peripheral) memory.

4. Binary Search Tree
Time Complexity : O(log(n))
Unbalanced Binary Search Tree
Time Complexity : O(n)
for search, insert and delete operations

5.  Remedy is self balancing trees.
 Automatically adjust to itself to get balanced.
 eg Red black tree
 B-Tree

6.  Intro
 Invented by Rudolf Bayer and Ed McCreight in 1972 at Boeing Research
Labs.
 B-Tree is known as balanced m-way tree and used in external sorting.
 m-way node is were m=5 it describes that there should be m links and m-1
data.
 Algorithms and data structures for external memory as opposed to the
main memory

7.  A good example of a data structure for external memory is a
B-tree.
 Better than binary search trees if data is stored in external
memory (they are NOT better with in-memory data!).
 Each node in a tree should correspond to a block of data.
 Each node stores many data items and has many successors
(stores addresses of successor blocks).

8.  The tree has fewer levels but search for an item involves
more comparisons at each level.
 There is a single root node, which may have only one record
and two children (or none if the tree is empty).

9.  Each node has a maximum of M children and minimum of m/2 children
 Each node should have a fewer keys than children with a maximum of
m-1 keys
 Keys should be arranged in a defined order within the node
 Key to be inserted into a fullnode, the node is splitted into two nodes by
taking the median value.
 All Leaves are to be at same level.
 no empty subtrees

10. m=4
Maximum Children - 4
Minimum Children - Ceil (m/2) = 2
Maximum Keys - (m-1) =3
Min Keys - Ceil(m/2)-1 =1
m=5
Maximum Children - 5
Minimum Children - Ceil (m/2) = 3
Maximum Keys - (m-1) =4
Min Keys - Ceil(m/2)-1 =2

11.  Basic three opeartions
 Insertion
 Insertion will be done in the leaf nodes
 Deletion
 Search

20.  To insert elements in B tree element to be inserted is to be
scanned from left to right.
 If the order to construct an even order B tree then two sets
of tree is created

21.  Find the node where the item is to be inserted by following
the search procedure.
 If the node is not full, insert the item into the node in order.
 If the node is full, it has to be split.

22.  Construct a B-Tree of
order 4 with following set
of datas
5,3,21,9,1,13,2,7,10,12,4,8
m=4 max keys=m-1 =3

23. 5,3,21,9,1,13,2,7,10,12,4,8
m=4 max keys=m-1 =3

26.  The key to be deleted is called the target key
Two Possibilities
 Target key can be a leaf node
 Target Key can be in internal node

27.  Target key can be leaf node
Two Possibilities
 Leaf node contains more than min no of keys
 Leaf node contains min no of keys


28.  If the target key is internal node
