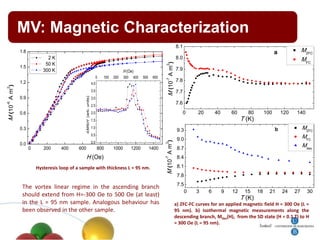
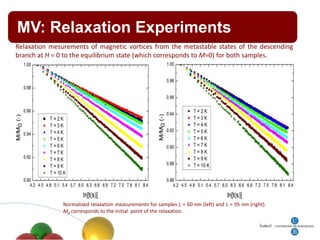
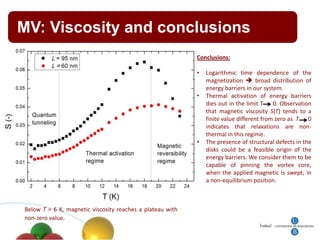
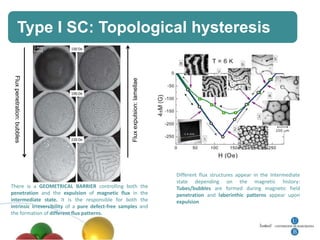
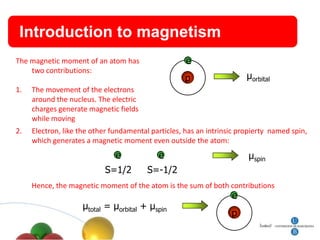
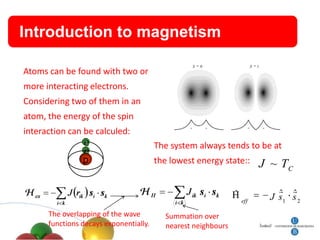
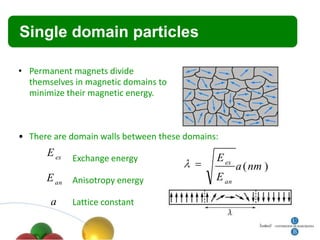
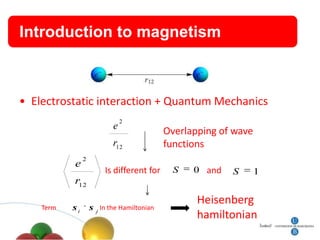
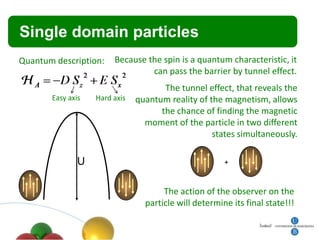
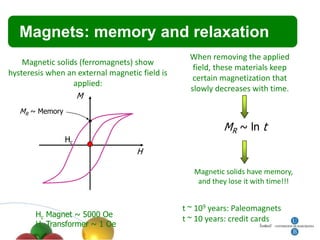
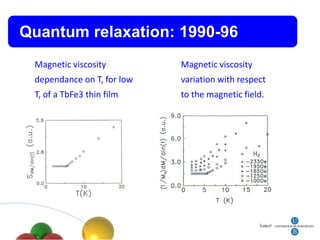
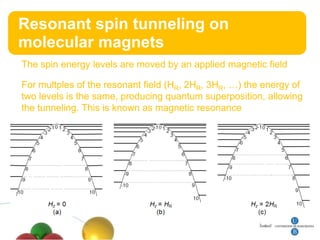
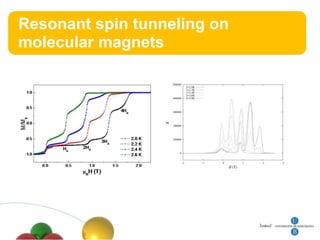
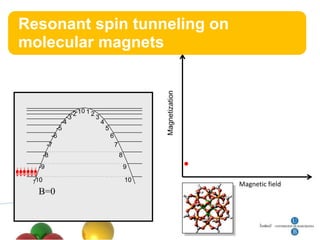
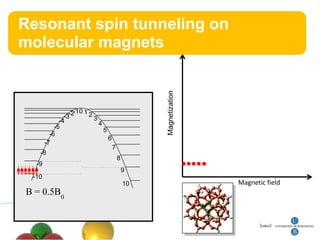
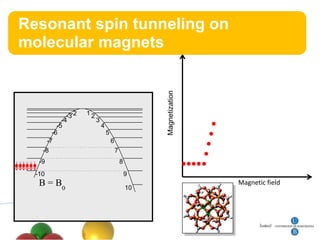
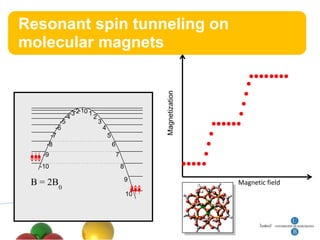
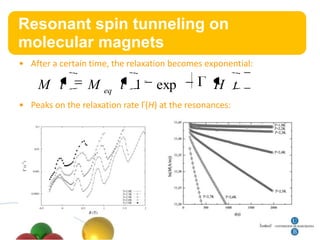
1. The document summarizes research on quantum effects in nanomagnetism, including single domain particles, molecular magnets, and superconductors. 2. It discusses quantum tunneling of magnetization in single domain particles and molecular magnets, where the spin can tunnel through an anisotropy barrier. 3. Resonant spin tunneling is observed in molecular magnets at certain magnetic field values where spin energy levels are degenerate, allowing quantum superposition and tunneling. 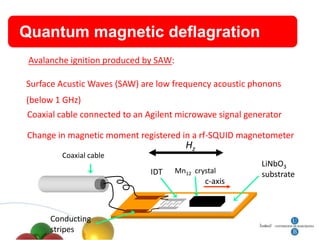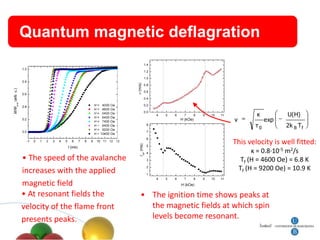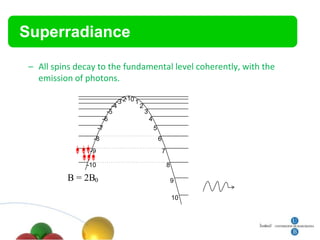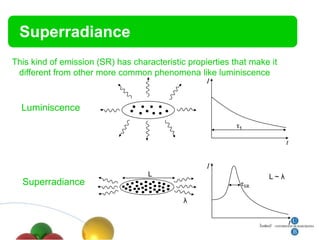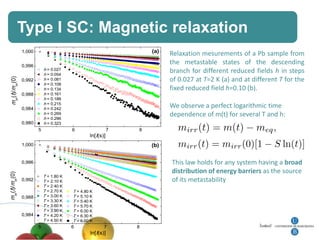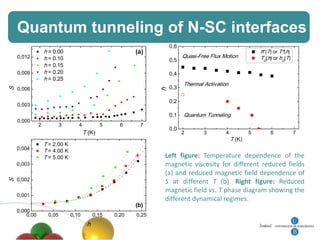4. Other topics covered include quantum magnetic deflagration, superradiance, magnetic vortices, and quantum effects in type-I superconductors such as topological hysteresis and flux penetration/expulsion patterns

1. QUANTUM NANOMAGNETISM
Proceedings of the International Conference Nanomaterials:
Applications and Properties
September 2012
Javier Tejada, Dept. Física Fonamental
Universitat de Barcelona

2. Contenidos
Content
Introduction to magnetism
Single Domain Particles
Quantum relaxation: 1990-96
Resonant spin tunneling: 1996-2010
Quantum magnetic deflagration
Superradiance
Free rotors
Magnetic vortices
Quantum effects in type-I superconductors

3. Introduction to magnetism
• Electrostatic interaction + Quantum Mechanics
2
e
Overlapping of wave
r12 functions
2
e
Is different for S 0 and S 1
r12
Heisenberg
Term si s In the Hamiltonian
j
hamiltonian

4. Introduction to magnetism
The magnetic moment of an atom has e
two contributions:
p μorbital
1. The movement of the electrons
around the nucleus. The electric
charges generate magnetic fields
while moving
2. Electron, like the other fundamental particles, has an intrinsic propierty named spin,
which generates a magnetic moment even outside the atom:
e e μspin
S=1/2 S=-1/2
Hence, the magnetic moment of the atom is the sum of both contributions
e
μtotal = μorbital + μspin
p

5. Título
Introduction to magnetism
S 0 S 1
Atoms can be found with two or
more interacting electrons.
Considering two of them in an
atom, the energy of the spin
interaction can be calculed:
e The system always tends to be at
e
p the lowest energy state:: J ~ TC
ˆ  
ˆ ˆ
eff
J s1 s 2
The overlapping of the wave Summation over
functions decays exponentially. nearest neighbours

6. Título
Introduction to magnetism
Existence of metastable
states
Magnetic Time dependent
hysteresis phenomena
Slow relaxation towards the free energy
minimum.
Global Non-linear
thermodynamic effects.
equilibrium.

7. Título
Single domain particles
• Permanent magnets divide
themselves in magnetic domains to
minimize their magnetic energy.
• There are domain walls between these domains:
E ex Exchange energy E ex
a (nm )
E an Anisotropy energy E an
a Lattice constant

8. Título
Single domain particles
E ex 3 5 The exchange energy is so high that
Tipically 10 10
E an it is difficult to do any non-uniform
rotation of the magnetization.
If the particle has R then no domain
walls can be formed. This is a SDP:
The probabilty of the flip E ex
exp( ) 0 and E ex Tc
of an individual spin is:
T
Hence, at low T, the magnetic moment is a
T Tc S ct
vector of constant modulus:

9. Single domain particles
The rotation of M as a whole needs certain energy called magnetic
anisotropy.
• Relativistic origin:
p
v
– Order of magnitude , with p even.
c
• Classic description:
– Energetic barrier of height: U
U (H )
U kV e T
Anisotropy Volume
constant

10. Single domain particles
Quantum description: Because the spin is a quantum characteristic, it
can pass the barrier by tunnel effect.
The tunnel effect, that reveals the
Easy axis Hard axis quantum reality of the magnetism, allows
the chance of finding the magnetic
moment of the particle in two different
states simultaneously.
U +
The action of the observer on the
particle will determine its final state!!!

11. Single domain particles
Important aspects of SDPs:
• Volume distribution: f R f V f U
• And orientations:
• Their magnetic moments tend to align with the applied magnetic
field.

12. Single domain particles
• The particles relax toward the equilibrium state:
t
M M0 1 S ln
0
Magnetic viscosity
• Thermal behaviour ( S T)
– At high temperatures it is easier to “jump” the barrier.
• Quantum behaviour (independent of T)
– Relaxation due to tunnel effect.

13. Magnets: memory and relaxation
When removing the applied
Magnetic solids (ferromagnets) show
field, these materials keep
hysteresis when an external magnetic field is
certain magnetization that
applied:
slowly decreases with time.
M
MR ~ Memory
MR ~ ln t
Hc
H
Magnetic solids have memory,
and they lose it with time!!!
t ~ 109 years: Paleomagnets
Hc Magnet ~ 5000 Oe
t ~ 10 years: credit cards
Hc Transformer ~ 1 Oe

14. Título
Quantum relaxation: 1990-96
Magnetic viscosity Magnetic viscosity
dependance on T, for low variation with respect
T, of a TbFe3 thin film to the magnetic field.

15. Título
Quantum relaxation: 1990-96

16. Resonant spin tunneling on
molecular magnets
• Identical to single domain particles
• Quantum objects
[M i , M j ] 2i M
B ijk k |M| ~ μB Quantum
[M i , M j ] M iM j
M jM i B
M k
|M| » μB Classic
Empirically, the magnetic moment is considered in a quantum way if
|M| ≤ 1000μB
2 2
H A
DS z
ES x
M(H,T) univocally determined by D and E

17. Resonant
Título spin tunneling on
molecular magnets
• Application of an external field: Zeeman term H S
- Longitudinal component of the field (H || easy axis)
Moves the levels.
- Transverse component of the field (H easy axis)
Allows tunnel effect.
• The tunnel effect is possible for certain values of the field;
resonant fields.

18. Resonant spin tunneling on
molecular magnets
The spin energy levels are moved by an applied magnetic field
For multples of the resonant field (HR, 2HR, 3HR, …) the energy of
two levels is the same, producing quantum superposition, allowing
the tunneling. This is known as magnetic resonance

19. Resonant
Título spin tunneling on
molecular magnets

20. Resonant spin tunneling on
molecular magnets
-2-10 1 2
-3 3
-4 4
-5 5
-6 6
-7 7
-8 8
-9 9
-10 10
Magnetic field
B=0

21. Resonant spin tunneling on
molecular magnets
-3-2-10 1 2
-4 3
-5 4
5
-6
6
-7
7
-8
8
-9
9
-10
10 Magnetic field
B = 0.5B0

22. Resonant spin tunneling on
molecular magnets
-3-2 12
-4 3
-5 4
-6 5
-7 6
-8 7
-9 8
-10 9
B = B0 10
Magnetic field

23. Resonant spin tunneling on
molecular magnets
-3-2-10 1
-4 2
-5 3
-6 4
-7 5
-8 6
-9 7
-10 8
9
B = 2B0 Magnetic field
10

24. Resonant
Título spin tunneling on
molecular magnets
• After a certain time, the relaxation becomes exponential:
M t M eq
t 1 exp H t
• Peaks on the relaxation rate Γ(H) at the resonances:

25. Quantum magnetic deflagration
Avalanche ignition produced by SAW:
Surface Acustic Waves (SAW) are low frequency acoustic phonons
(below 1 GHz)
Coaxial cable connected to an Agilent microwave signal generator
Change in magnetic moment registered in a rf-SQUID magnetometer
Hz
Coaxial cable
LiNbO3
IDT Mn12 crystal substrate
c-axis
Conducting
stripes

26. Quantum magnetic deflagration
κ U(H)
v exp
τ0 2k B T f
This velocity is well fitted:
κ = 0.8·10-5 m2/s
• The speed of the avalanche Tf (H = 4600 Oe) = 6.8 K
increases with the applied Tf (H = 9200 Oe) = 10.9 K
magnetic field
• At resonant fields the • The ignition time shows peaks at
velocity of the flame front the magnetic fields at which spin
presents peaks. levels become resonant.

27. Quantum magnetic deflagration

28. Superradiance
– All spins decay to the fundamental level coherently, with the
emission of photons.
-1
-3-2 0 1
-4 2
-5 3
-6 4
-7 5
-8 6
-9 7
-10 8
B = 2B0 9
10

29. Superradiance
This kind of emission (SR) has characteristic propierties that make it
different from other more common phenomena like luminiscence
I
Luminiscence
τ1
t
I
L L~λ
Superradiance τSR
λ
t

30. Milestones
Título
1896 Zeeman Effect (1)
1922 Stern–Gerlach Experiment (2)
1925 The spinning electron (3)
1928 Dirac equation (4)
1928 Quantum Magnetism (5)
1932 Isospin (6)
1940 Spin–statistics connection (7)

31. Milestones
Título
1946 Nuclear Magnetic Resonance (8)
1950s Development of Magnetic devices (9)
1950–1951 NMR for chemical analysis (10)
1951 Einstein–Podolsky–Rosen argument in spin
variables (11)
1964 Kondo effect (12)
1971 Supersimmetry (13)
1972 Superfluid helium-3 (14)

32. Milestones
Título
1973 Magnetic resonance imaging (15)
1976 NMR for protein structure determination (16)
1978 Dilute magnetic semiconductors (17)
1988 Giant magnetoresistance (18)
1990 Functional MRI (19)
1990 Proposal for spin field-effect transistor (20)
1991 Magnetic resonance force microscopy (21)

33. Milestones
Título
1996 Mesoscopic tunnelling of magnetization (22)
1997 Semiconductor spintronics (23)
© 2008 Nature Publishing Group

34. Magnetic Vortices (MV): Introduction
Vortex State
• The spin field splits into two well-differentiated
structures: 1) the vortex core consisting of a uniform
out-of-plane spin component (spatial extension
about the exchange length) and 2) the curling
magnetization field (in-plane spin component),
characterized by a non-zero vorticity value.
• The application of an in-plane magnetic field yields
the displacement of the vortex core perpendicularly
to the field direction.
• The vortex shows a special vibrational mode (called
gyrotropic mode) consisting of the displacement of
the vortex core as a whole, following a precessional
movement around the vortex centre. Its
characteristic frequency belongs to the subGHz
range.
Experimental set-up
We have studied several arrays of permalloy (Fe19Ni81) disks with diameter 2R = 1.5 μm and different
thickness (L = 60, 95 nm) under the application of an in-plane magnetic field up to 0.1 T in the range of
temperatures 2-300 K. Samples were prepared stacking four 5x5 mm2 arrays with parallel sides.

35. MV: Magnetic Characterization
Hysteresis loop of a sample with thickness L = 95 nm.
The vortex linear regime in the ascending branch
should extend from H=-300 Oe to 500 Oe (at least)
in the L = 95 nm sample. Analogous behaviour has a) ZFC-FC curves for an applied magnetic field H = 300 Oe (L =
been observed in the other sample. 95 nm). b) Isothermal magnetic measurements along the
descending branch, Mdes(H), from the SD state (H = 0.1 T) to H
= 300 Oe (L = 95 nm).

36. MV: Relaxation Experiments
Relaxation mesurements of magnetic vortices from the metastable states of the descending
branch at H = 0 to the equilibrium state (which corresponds to M=0) for both samples.
Normalized relaxation measurements for samples L = 60 nm (left) and L = 95 nm (right).
M0 corresponds to the initial point of the relaxation.

37. MV: Viscosity and conclusions
Conclusions:
• Logarithmic time dependence of the
magnetization  broad distribution of
energy barriers in our system.
• Thermal activation of energy barriers
dies out in the limit T 0. Observation
that magnetic viscosity S(T) tends to a
finite value different from zero as T 0
indicates that relaxations are non-
thermal in this regime.
• The presence of structural defects in the
disks could be a feasible origin of the
energy barriers. We consider them to be
capable of pinning the vortex core,
when the applied magnetic is swept, in
a non-equilibrium position.
Magnetic viscosity S versus temperature T for both samples.
Below T = 6 K, magnetic viscosity reaches a plateau with
non-zero value.

38. Type I SC: Topological hysteresis
Flux penetration: bubbles
Flux expulsion: lamellae
Different flux structures appear in the Intermediate
state depending on the magnetic history:
There is a GEOMETRICAL BARRIER controlling both the Tubes/bubbles are formed during magnetic field
penetration and the expulsion of magnetic flux in the penetration and laberinthic patterns appear upon
intermediate state. It is the responsible for both the expulsion
intrinsic irreversibility of a pure defect-free samples and
the formation of different flux patterns.

39. Type I SC: Magnetic relaxation
Relaxation mesurements of a Pb sample from
the metastable states of the descending
branch for different reduced fields h in steps
of 0.027 at T=2 K (a) and at different T for the
fixed reduced field h=0.10 (b).
We observe a perfect logarithmic time
dependence of m(t) for several T and h:
This law holds for any system having a broad
distribution of energy barriers as the source
of its metastability

40. Quantum tunneling of N-SC interfaces
Left figure: Temperature dependence of the
magnetic viscosity for different reduced fields
(a) and reduced magnetic field dependence of
S at different T (b). Right figure: Reduced
magnetic field vs. T phase diagram showing the
different dynamical regimes.