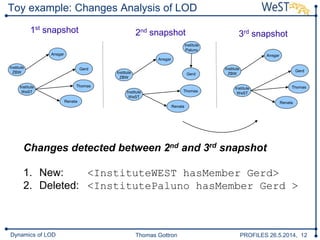
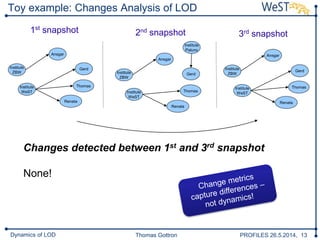
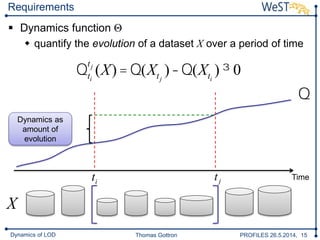
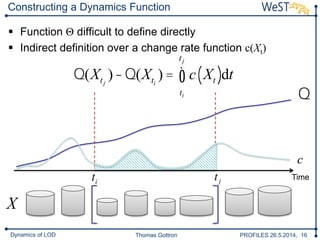
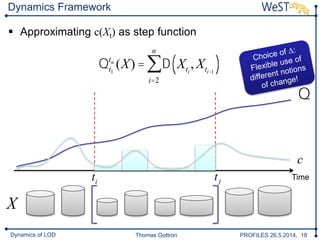
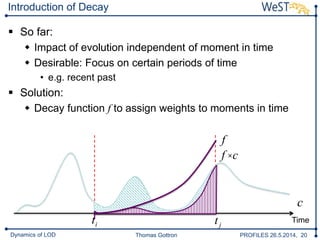
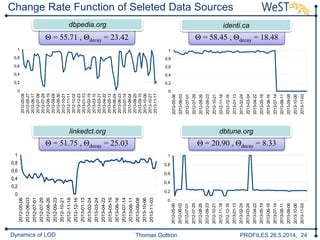
The document discusses a framework for analyzing the dynamics of Linked Open Data (LOD) sources, detailing methods for comparing data snapshots and measuring changes over time. It introduces dynamic functions and decay functions to quantify data evolution and improve change rate approximations through various metrics. The conclusion highlights the framework's configurability and the potential for future enhancements in change rate modeling and its implications for LOD updates.

1. Institute for Web Science & Technologies – WeST
From Changes to Dynamics:
Dynamics Analysis of Linked Open
Data Sources
Renata Dividino, Thomas Gottron
Ansgar Scherp, Gerd Gröner
May 26th, 2014
PROFILES Workshop, Crete

2. Thomas Gottron PROFILES 26.5.2014, 2Dynamics of LOD
Linked Data Evolves

3. Thomas Gottron PROFILES 26.5.2014, 3Dynamics of LOD
Linked Data Evolves
Time
Volume
Triples provided by data sources

4. Thomas Gottron PROFILES 26.5.2014, 4Dynamics of LOD
Effects on Indices and Caches

5. Thomas Gottron PROFILES 26.5.2014, 5Dynamics of LOD
Updates of Indices and Caches

6. Thomas Gottron PROFILES 26.5.2014, 6Dynamics of LOD
Change Metrics

7. Thomas Gottron PROFILES 26.5.2014, 7Dynamics of LOD
Change Metrics
 Comparison of two RDF data sets (e.g. from different
points in time)
 Xi : Set of triple statements
 Numeric expression for „distance“
 Example:
X1
X2
Δ 0,¥[ )
DJaccard X1, X2( ) =1-
X1 Ç X2
X1 È X2

8. Thomas Gottron PROFILES 26.5.2014, 8Dynamics of LOD
Toy example: Changes Analysis of LOD
1st snapshot
GerdInstitute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata

9. Thomas Gottron PROFILES 26.5.2014, 9Dynamics of LOD
Toy example: Changes Analysis of LOD
1st snapshot
GerdInstitute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
2nd snapshot
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
Paluno

10. Thomas Gottron PROFILES 26.5.2014, 10Dynamics of LOD
Toy example: Changes Analysis of LOD
Changes detected between 1st and 2nd snapshot
1. Deleted: <InstituteWEST hasMember Gerd>
2. New: <InstitutePaluno hasMember Gerd >
1st snapshot
GerdInstitute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
2nd snapshot
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
Paluno

11. Thomas Gottron PROFILES 26.5.2014, 11Dynamics of LOD
Toy example: Changes Analysis of LOD
1st snapshot
GerdInstitute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
2nd snapshot
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
Paluno
3rd snapshot
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata

12. Thomas Gottron PROFILES 26.5.2014, 12Dynamics of LOD
Toy example: Changes Analysis of LOD
1st snapshot 2nd snapshot 3rd snapshot
GerdInstitute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
Paluno
Changes detected between 2nd and 3rd snapshot
1. New: <InstituteWEST hasMember Gerd>
2. Deleted: <InstitutePaluno hasMember Gerd >

13. Thomas Gottron PROFILES 26.5.2014, 13Dynamics of LOD
Toy example: Changes Analysis of LOD
1st snapshot 2nd snapshot 3rd snapshot
GerdInstitute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
ZBW
Institute
WeST
Thomas
Gerd
Ansgar
Renata
Institute
Paluno
Changes detected between 1st and 3rd snapshot
None!

14. Thomas Gottron PROFILES 26.5.2014, 14Dynamics of LOD
A Framework for Linked Data
Dynamics

15. Thomas Gottron PROFILES 26.5.2014, 15Dynamics of LOD
Requirements
 Dynamics function Θ
 quantify the evolution of a dataset X over a period of time
Qti
tj
(X)= Q(Xtj
)-Q(Xti
) ³ 0
Q
Dynamics as
amount of
evolution
Timeti tj
X

16. Thomas Gottron PROFILES 26.5.2014, 16Dynamics of LOD
Constructing a Dynamics Function
 Function Θ difficult to define directly
 Indirect definition over a change rate function c(Xt)
Q(Xtj
)-Q(Xti
) = c Xt( )
ti
tj
ò dt
Time
Q
c
ti tj
X

17. Thomas Gottron PROFILES 26.5.2014, 17Dynamics of LOD
Change Rate Function
 Also c(Xt) not explicitely known!
 But can be approximated!
 Given snapshots of the data in small time intervals:
 The change rate can be approximated via change metrics:
D Xti
, Xti-1
( )
ti -ti-1
ti-1®ti
¾ ®¾¾ c Xti
( )=
d
dt
Q(Xti
)

18. Thomas Gottron PROFILES 26.5.2014, 18Dynamics of LOD
Dynamics Framework
 Approximating c(Xt) as step function
Timeti tj
Q
c
Qt1
tn
(X) = D Xti
, Xti-1
( )
i=2
n
å
X

19. Thomas Gottron PROFILES 26.5.2014, 19Dynamics of LOD
Use of Decay Functions

20. Thomas Gottron PROFILES 26.5.2014, 20Dynamics of LOD
Introduction of Decay
 So far:
 Impact of evolution independent of moment in time
 Desirable: Focus on certain periods of time
• e.g. recent past
 Solution:
 Decay function f to assign weights to moments in time
Time
c
ti tj
f
f ×c

21. Thomas Gottron PROFILES 26.5.2014, 21Dynamics of LOD
Implementing a Decay Function
 Exponential decay function:
 Incoporated in the framework:
 When using the step function approximation of c(Xt) :
f t( )= e-lt
Q(Xtj
)-Q(Xti
) = e
-l tj-t( )
×c Xt( )
ti
tj
ò dt
Qt1
tn
(X) = e
-l tn-ti( )
×D Xti
, Xti-1
( )
i=2
n
å

22. Thomas Gottron PROFILES 26.5.2014, 22Dynamics of LOD
Some Results

23. Thomas Gottron PROFILES 26.5.2014, 23Dynamics of LOD
Experiments
 84 snapshots (approx 1.5 years)
 652 data sources (PLD)
 Dynamics on data level

24. Thomas Gottron PROFILES 26.5.2014, 24Dynamics of LOD
Tabelle1
2012-05-06
2012-06-03
2012-07-01
2012-07-29
2012-08-26
2012-09-23
2012-10-21
2012-11-18
2012-12-16
2013-01-13
2013-02-24
2013-03-24
2013-04-22
2013-05-19
2013-06-16
2013-07-14
2013-08-11
2013-09-08
2013-10-06
2013-11-03
0
0,2
0,4
0,6
0,8
1
Change Rate Function of Seleted Data Sources
Tabelle1
2012-05-06
2012-05-27
2012-06-17
2012-07-08
2012-07-29
2012-08-19
2012-09-09
2012-09-30
2012-10-21
2012-11-11
2012-12-02
2012-12-23
2013-01-13
2013-02-19
2013-03-10
2013-03-31
2013-04-22
2013-05-12
2013-06-04
2013-06-23
2013-07-14
2013-08-04
2013-08-25
2013-09-15
2013-10-06
2013-10-27
2013-11-17
0
0,2
0,4
0,6
0,8
1
Θ = 55.71 , Θdecay = 23.42
dbpedia.org
Tabelle1
2012-05-06
2012-06-03
2012-07-01
2012-07-29
2012-08-26
2012-09-23
2012-10-21
2012-11-18
2012-12-16
2013-01-13
2013-02-24
2013-03-24
2013-04-22
2013-05-19
2013-06-16
2013-07-14
2013-08-11
2013-09-08
2013-10-06
2013-11-03
0
0,2
0,4
0,6
0,8
1
Θ = 58.45 , Θdecay = 18.48
identi.ca
Θ = 51.75 , Θdecay = 25.03
linkedct.org
Tabelle1
2012-05-06
2012-06-03
2012-07-01
2012-07-29
2012-08-26
2012-09-23
2012-10-21
2012-11-18
2012-12-16
2013-01-13
2013-02-24
2013-03-24
2013-04-22
2013-05-19
2013-06-16
2013-07-14
2013-08-11
2013-09-08
2013-10-06
2013-11-03
0
0,2
0,4
0,6
0,8
1
Θ = 20.90 , Θdecay = 8.33
dbtune.org

25. Thomas Gottron PROFILES 26.5.2014, 25Dynamics of LOD
Conclusion
Summary
 Framework to capture the dynamics of LOD data sources
 Configurable to use different change metrics
 Incorporation of a decay function
 Values align with intuitive definition
Future Work
 Better approximations of the change rate function
 Incorporation notion of dynamics in update strategies for
LOD indices and caches

26. Thomas Gottron PROFILES 26.5.2014, 26Dynamics of LOD
Thanks!
Contact:
Thomas Gottron
WeST – Institute for Web Science and Technologies
Universität Koblenz-Landau
gottron@uni-koblenz.de