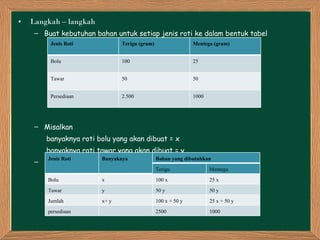
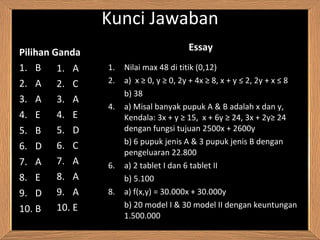
Dokumen ini membahas tentang program linier, termasuk konsep sistem pertidaksamaan linier dua variabel, penyelesaian model matematika dari masalah program linier, dan cara menentukan nilai optimum dengan metode grafik, termasuk uji titik pojok dan garis selidik. Contoh diberikan melalui masalah pembuatan roti oleh Farah dengan mengoptimalkan jumlah roti yang dapat dibuat berdasarkan kendala persediaan bahan. Metodologi untuk menemukan solusi optimum dijelaskan secara terperinci, beserta ilustrasi grafik dan langkah-langkah perhitungan.

1. OM SWASTYASTU Loading Loading Complete Power Point is starting up...

2. I Putu Yoga Semara Putra (2009.V.1.0163) I Wayan Winata Adi Putra (2009.V.1.0179) I Wayan Agus Aristana (2009.V.1.0197) Doni Dominggus (2009.V.1.0208) Nama kelompok :

3. Program Linier

4. STANDAR KOMPETENSI MENYELESAIKAN MASALAH PROGRAM LINIER

5. KOMPETENSI DASAR MENYELASIKAN SISTEM PERSAMAAN LINIER DUA VARIABEL MERANCANG MODEL MATEMATIKA DARI MASALAH PROGRAM LINIER MENEYELESAIKA MODEL MATEMATIKA DARI MASALAH PROGRAM LINIER DAN PENAFSIRANNYA

6. INDIKATOR MENGENAL ARTI SITEM PERTIDAKSAMAAN LINIER DUA VARIABEL MENENTUKAN PENYELESAIAN SISTEM PERTIDAKSAMAAN LINIER DUA VARIABLE MENGENAL MASALAH YANG MERUPAKAN PROGRAM LINIER MENENTUKAN FUNGSI OBJEKTIF DAN KENDALA DARI PROGRAM LINIER MENGGAMBAR DAERAH FISIBEL DARI PROGRAM LINIER MERUMUSKAN MODEL MATEMATIKA MASALAH PROGRAM LINIER MENENTUKAN NILAI OPTIMUM DARI FUNGSI OBJEKTIF MENAFSIRKAN SOLUSI DARI MASALAH PROGRAM LINIER

7. A. SISTEM PERTIDAKSAMAAN LINIER DUA VARIABEL DEFINISI PERTIDAKSAMAAN LINIER DUA VARIABEL ADALAH PERTDAKSAMAAN YANG MEMUAT DUA VARIABEL DAN PANGKAT TERTINGGI DARI VARIABEL TERSEBUT ADALAH SATU CONTOH : x + y ≤ 60 4x + y ≤ 90 a + 3b ≤ 300 2a + 2b ≤ 40

8. Menentukan Penyelesaian Sistem Pertidaksamaan Linier 2 Variabel Daerah himpunan penyelesaian sistem pertidaksamaan linier dua variabel merupakan irisan atau interseksi dari tiap daerah penyelesaian pertidaksamaan linier dua variabel yang menyusunnya

9. Diberikan pertidaksamaan : x + y ≤ 60 4x + y ≤ 90 Himpunan penyelesaiaannya dapat dicari dengan langkah – langkah sebagai berikut: Gambar garis x + y = 60 pada bidang cartesius dengan cara menghubungkan titik potong garis dengan sumbu X dan Sumbu Y x = 0 maka y = 60 y = 0 maka x = 60 Selanjutnya selidiki daerah yang merupakan himpunan penyelesaian x + y ≤ 60 Ambil titik selidik O(0,0), kemudian substitusi titik (0,0) ke pertidaksamaan x + y ≤ 60 diperoleh 0 + 0 ≤ 60 0 ≤ 60 Ketidaksamaan benar berarti titik O(0,0) terletak pada daerah himpunan penyelesaian pertidaksamaan x + y ≤ 60 Y X 60 60 x + y = 60 O

10. Jadi, daerah himpunan penyelesaian ditunjukan oleh daerah yang diarsir pada gambar Lakukan hal yang sama untuk pertidaksamaan 4x + y ≤ 90 x = 0 maka y = 90 y = 0 maka x = 22,5 Ambil titik selidik (0,0), substitusi titik (0,0) ke pertidaksamaan 4x + y ≤ 90 diperoleh 4.(0) + 0 ≤ 90 0 ≤ 90 Karena ketiksamaan bernilai benar berarti titik selidik (0,0) terletak pada daerah himpunan penyelesaian Y O X 60 60 O Y X 90 22,5

11. Jadi, daerah himpunan penyelesaian ditunjukan oleh daerah yang diarsir pada gambar Langkah selanjutnya adalah menggambarkan daerah himpunan penyelesaian pertidaksamaan x + y ≤ 60 dan 4x + y ≤ 90 dalam satu bidang cartesius, dan daerah yang terarsir dua kali adalah himpunan penyelesaiannya. O Y X 90 22,5 Y O X 60 60 90 22,5

12. B. FUNGSI TUJUAN (FUNGSI OBJEKTIF) BESERTA KENDALA Model Matematika Model matematika adalah hasil terjemahan permasalahan kedalam bahasa / lambang matematika. Fungsi Tujuan (Fungsi Objektif) Fungsi tujan adalah fungsi dari suatu keadaan yang hendak dicapai secara maksimum atau minimum Kendala Kendala adalah pertidaksamaan – pertidaksamaan linier yang memenuhi semua syarat yang diberikan

13. Contoh Farah akan membuat roti bolu dan roti tawar. Roti bolu membutuhkan 100 gram terigu dan 25 gram mentega. Roti jenis tawar membutuhkan 50 gram terigu dan 50 gram mentega. Farah mempunyai persedian bahan 2,5 Kg terigu 1Kg mentega. Farah akan membuat ro t i sebanyak – banyaknya. Tentukan model matematika dari masalah tersebut!

14. Langkah – langkah Buat kebutuhan bahan untuk setiap jenis roti ke dalam bentuk tabel Misalkan banyaknya roti bolu yang akan dibuat = x banyaknya roti tawar yang akan dibuat = y Maka tabel akan menjadi Jenis Roti Terigu (gram) Mentega (gram) Bolu 100 25 Tawar 50 50 Persediaan 2.500 1000 Jenis Roti Banyaknya Bahan yang dibutuhkan Terigu Mentega Bolu x 100 x 25 x Tawar y 50 y 50 y Jumlah x+ y 100 x + 50 y 25 x + 50 y persediaan 2500 1000

15. Karena x dan y mewakili banyaknya roti yang dibuat, maka nilainya harus bulat dan tidak negatif Jadi, x > 0 (i) y > 0 (ii) Persediaan terigu 2.500 gram, oleh karena itu penggunaan terigu tidak boleh lebih dari 2.500 gram. Jadi, 100 x + 50 y ≤ 2.500 atau 2x + y ≤ 50 (iii) Persediaan mentega 1000 gram, maka jumlah mentega yang digunakan memenuhi pertidaksamaan 25 x + 50 y ≤ 1000 atau x + 2 y ≤ 40 (iv) Farah ingin membuat roti bolu dan tawar sebanyak – banyaknya, dapat ditulis sebagai sebuah fungsi yaitu : f(x,y) = x+ y Kedua jenis roti akan dibuat sebanyak – banyaknya, maka pertidaksamaan (i), (ii), (iii) dan (iv) membentuk sistem pertidaksamaan yang harus dipenuhi untuk memaksimumkan f(x,y) = x + y

16. Sehingga model matematika untuk masalah farah adalah: Memaksimumkan (fungsi tujuan / fungsi objektif) f(x,y) = x + y Dengan syarat (kendala) x ≥ 0 y ≥ 0 2 x + y ≤ 50 x + 2 y ≤ 40

17. C. NILAI OPTIMUM DARI MASALAH PROGRAM LINIER Penyelesaian Optimum Penyelesaian optimum / masalah optimum adalah sebuah penyelesaian yang memberikan hasil terbaik dari berbagai kemungkinan penyelesaian Tujuan dari masalah program linier adalah mengoptimumkan fungsi tujuan f(x,y) = ax +by. Pada subbab ini hanya akan dijelaskan mengunakan metode grafik. Dalam metode grafik ada dua macam metode, yaitu: Metode uji titik pojok Metode garis selidik

18. 1. Metode uji titik pojok Dalam metode ini, untuk menentukan nilai optimum dengan menghitung ax + by pada tiap titik pojok atau tiap tititk yang dekat dengan titik pojok dari daerah himpunan penyelesaian Contoh Model matematika masalah Farah dalam membuat roti Memaksimumkan f(x,y) = x + y Dengan syarat / kendala : x ≥ 0 y ≥ 0 2x + y ≤ 50 x + 2y ≤ 40 Tentukan nilai maksimum dari fungsi objektif tersebut!

19. Langkah – langkah Gambar grafik daerah penyelesaian dari kendala – kendala yang diberikan dala bidang koordinat. dan namai titik –titik pojoknya dengan huruf alfabet Tentukan koordinat – koordinat titik pojok yang merupakan daerah penyelesaiannya O (0,0) A (25,0) C (0,20) 50 20 25 40 O A B C X Y

20. Langkah – langkah Titik B dapat dicari dengan menggunakan metode gabungan eliminasi dan substitusi. Karena titik B merupakan titik perpotongan antara garis 2x + y =50 dan garis x + 2y =40 Eliminasi variabel x 2x + y = 50 x1 2x +2y = 50 x + 2y = 40 x2 2x +4y = 80 -3y = -30 y = 10 Substitusi nilai y = 10 ke persamaan 2x + y = 50 maka 2x + 10 = 50 2x = 40 x = 20 Jadi koordianat titik B (20,10)

21. Langkah – langkah Langkah selanjutnya adalah menentukan nilai fungsi objektif pada masing – masing titik pojoknya f(x,y) = x + y O(0,0) maka f(x,y) = 0 + 0 = 0 A(25,0) maka f(x,y) = 25 + 0 = 25 B(20,10) maka f(x,y) = 20 + 10 = 30 C(0,20) maka f(x,y) = 0 + 20 = 20 Dari nilai fungsi objektif tersebut diperoleh Nilai maksimum = 30 dicapai pada titik (20,10) Nilai minimum = 0 dicapai pada titik (0,0) Nilai optimum pada permasalahan farah adalah nilai maksimum, karena Farah ingin membuat roti tawar dan bolu sebanyak – banyaknya . Jadi, Farah dapat membuat roti tawar sebanyak 20 buah dan bolu sebanyak 10 buah

22. 2 . Metode Garis Selidik Metode garis selidik lebih praktis dari metode uji titik pojok. Karena dalam metode uji titik pojok memerlukan ketelitian dan waktu yang agak lama untuk menghitung nilai fungsi objektif di masing – masing titik pojoknya Diberikan persamaan garis x + 2y = k Garis tersebut memotong sumbu X di (k,0) dan memotong sumbu Y di (0, k/2 ). Grafik garis x + 2y = k dilukis dengan menghubungkan titik (k,0) dan (0, k/2 ).

23. Gambar berikut merupakan grafik garis x + 2y = k untuk nlai – nilai k = 0, k = 2, k = 4, dan k = 6 Dari gambar terlihat, jika nilai k makin besar maka garis x + 2y = k makin menjauhi titik pangkal. Ini berarti himpunan garis- garis yang sejajar dengan persamaan x + 2y = k dapat dipakai untuk menyelediki nilai optimum (maksimum atau minimum) dari bentuk objektif f(x,y) = x + 2y . Sehingga garis dengan persamaan dinamakan garis selidik. Jadi, nilai optimum (maksimum atau minimum) bentuk objektif a x+by dapat diselidiki menggunakan garis selidik ax +by =k y x 3 2 1 0 2 4 6

24. Contoh Model matematika masalah Farah dalam membuat roti Memaksimumkan f(x,y) = x + y Dengan syarat / kendala : x ≥ 0 y ≥ 0 2x + y ≤ 50 x + 2y ≤ 40 Tentukan nilai maksimum dari fungsi objektif tersebut!

25. Langkah – langkah Gambarkan grafik daerah penyelesaiannya dari kendala – kendala yang diberikan dalam bidang koordinat. Tentukan persamaan garis selidik ax + by = k , untuk suatu k tertentu. Dari persamaan Farah diperoleh fungsi objektif f(x,y) = x +y Persamaan garis selidik x + y = k Ambil k = 1, diperoleh x + y = 1 50 20 25 40 O A X Y

26. Langkah – langkah Garis – garis yang sejajar dengan x + y = 1 adalah x + y = 2, x + y = 3, x + y = 4, x + y = 5, x+ y = 50 dan lain – lain Garis yang sejajar dengan garis x + y = 1 dan terletak paling dekat dengan titik pangkal (0,0) adalah garis yang melaui O(0,0). Garis itu adalah garis x + y = 0, sehingga titik O(0,0) merupakan titik pada daerah himpunan penyelesaian yang menyebabkan nilai x + y minimum. Nilai minimum dari fungsi objektif x + y adalah 0 + 0 = 0 50 20 25 40 O A B C X Y X + y = 0 X + y = 1 0 X + y = 2 0 X + y = 3 0

27. Langkah – langkah Garis yang sejajar dengan garis x + y = 1 dan terletak paling jauh dengan titik pangkal adalah garis yang melalui titik B (20,10). Garis itu adalah garis x + y = 30, sehingga titik B (20,10) merupakan titik pada daerah himpunan penyelesaian yang menyebabkan nilai x + y maksimum. Nilai maksimum dari fungsi objektif x + y adalah 20 + 10 = 30 Dalam permasalahan Farah di muka, Farah ingin membuat roti tawar dan bolu sebanyak – banyaknya. Jadi, farah dapat membuat roti tawar sebanyak 20 buah dan roti bolu sebanyak 10

28. Soal-Soal Program Linier 20 Soal Pilihan Ganda & 5 Soal Essay

29. Kunci Jawaban Pilihan Ganda B A A E B D A E D B S Essay Nilai max 48 di titik (0,12) a) x ≥ 0, y ≥ 0, 2y + 4x ≥ 8, x + y ≤ 2, 2y + x ≤ 8 b) 38 a) Misal banyak pupuk A & B adalah x dan y, Kendala: 3x + y ≥ 15, x + 6y ≥ 24, 3x + 2y≥ 24 dengan fungsi tujuan 2500x + 2600y b) 6 pupuk jenis A & 3 pupuk jenis B dengan pengeluaran 22.800 a) 2 tablet I dan 6 tablet II b) 5.100 a) f(x,y) = 30.000x + 30.000y b) 20 model I & 30 model II dengan keuntungan 1.500.000 A C A E D C A A A E

30. OM santi, santi, santi om