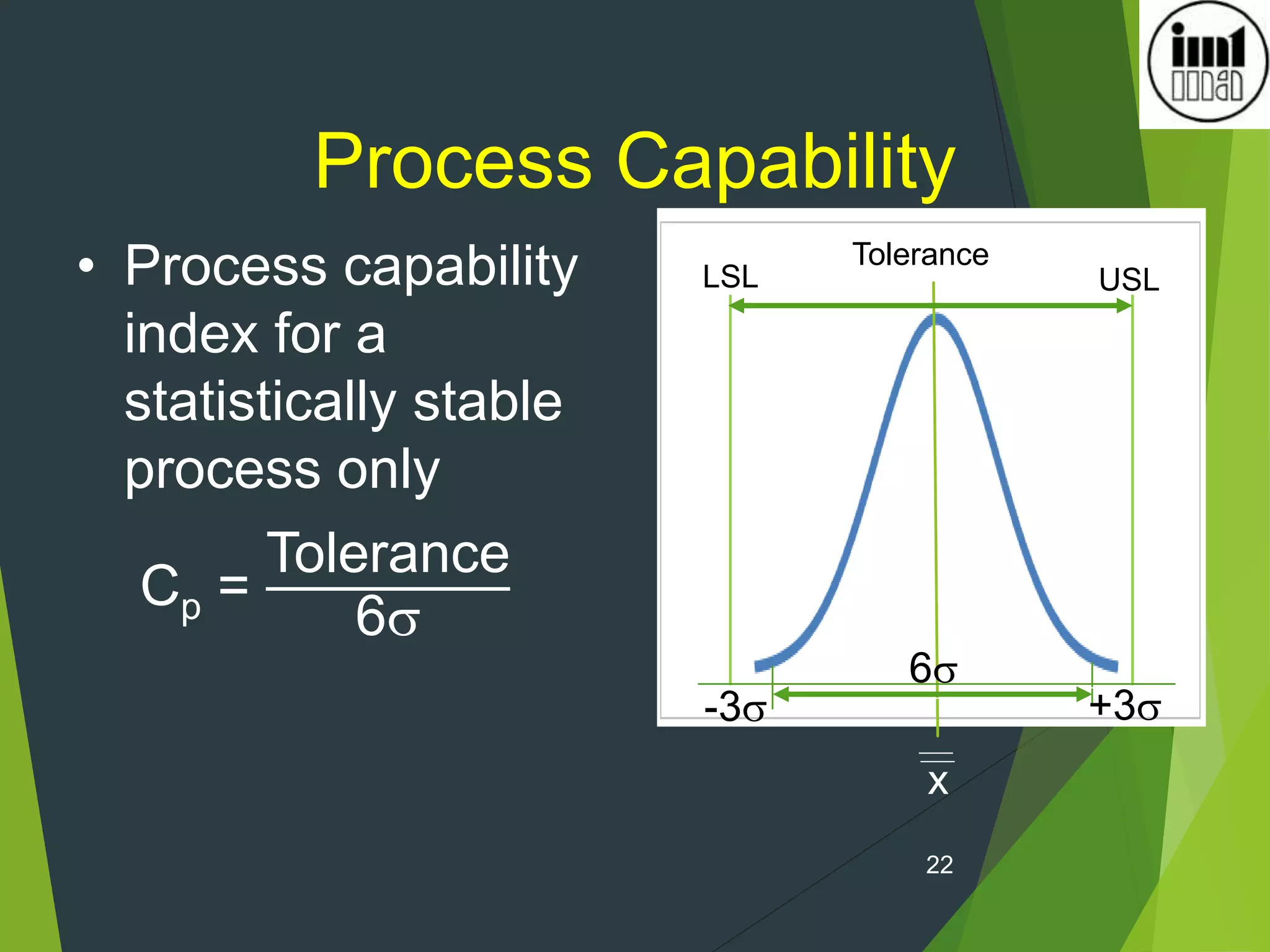
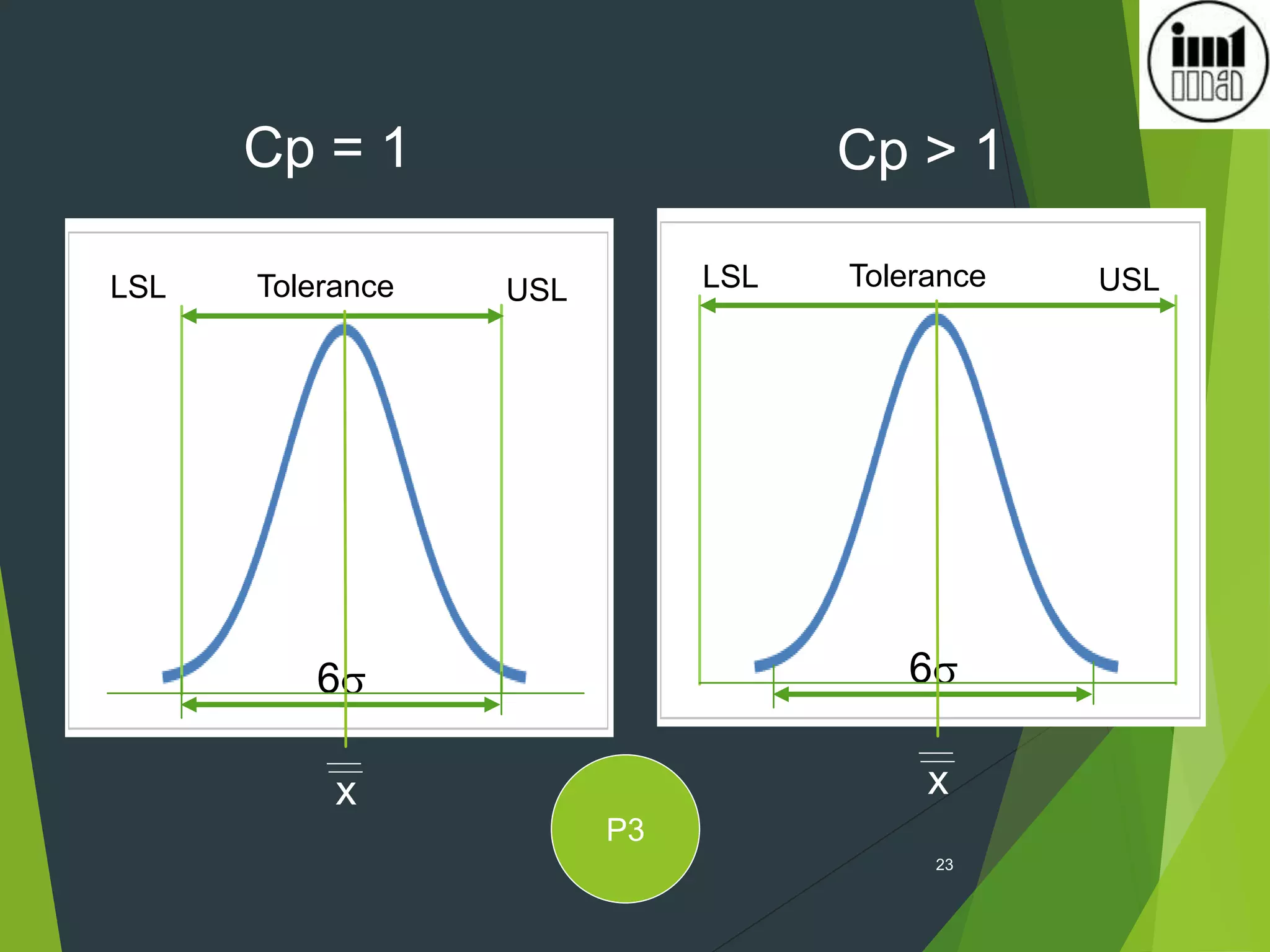
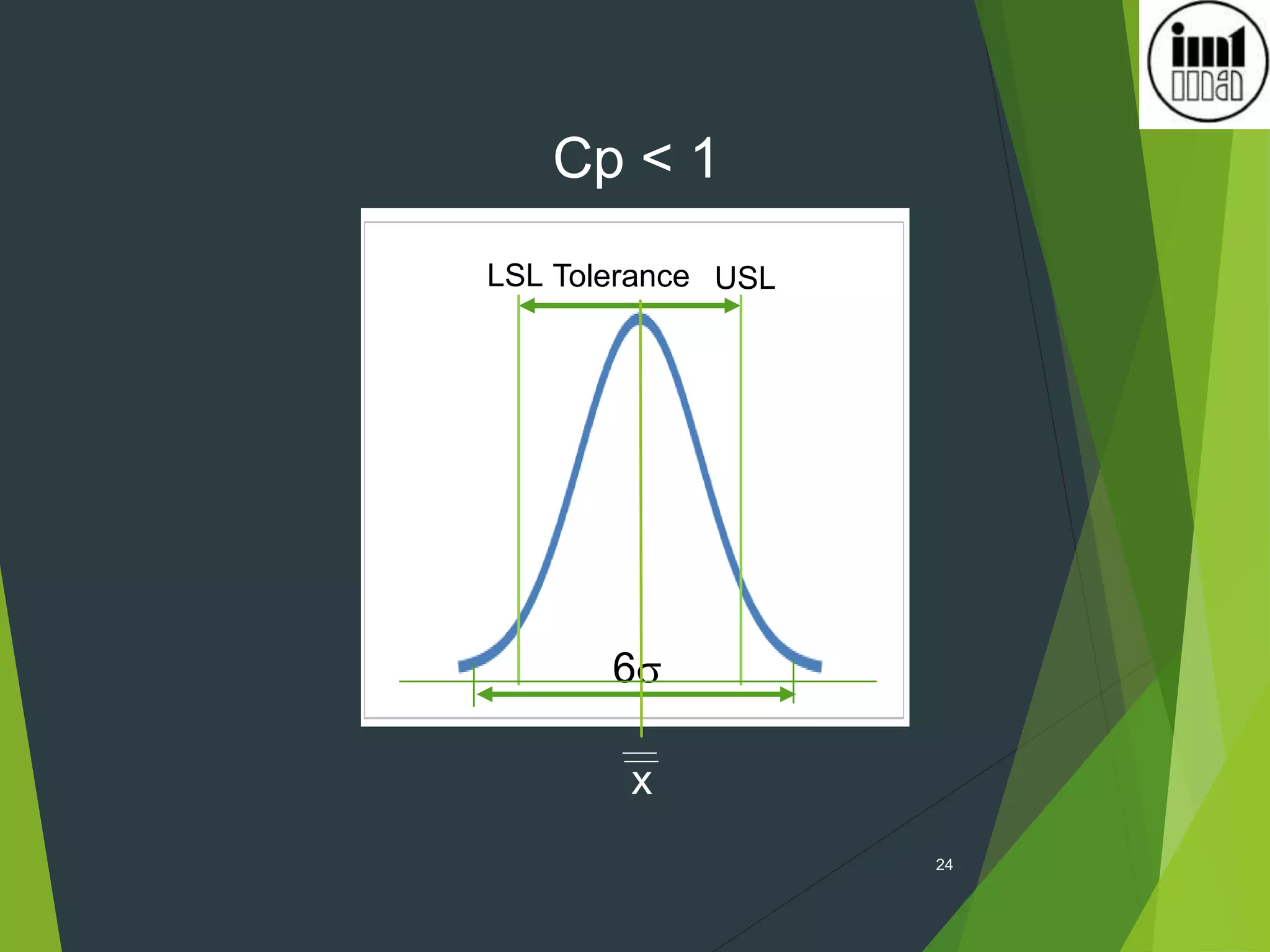
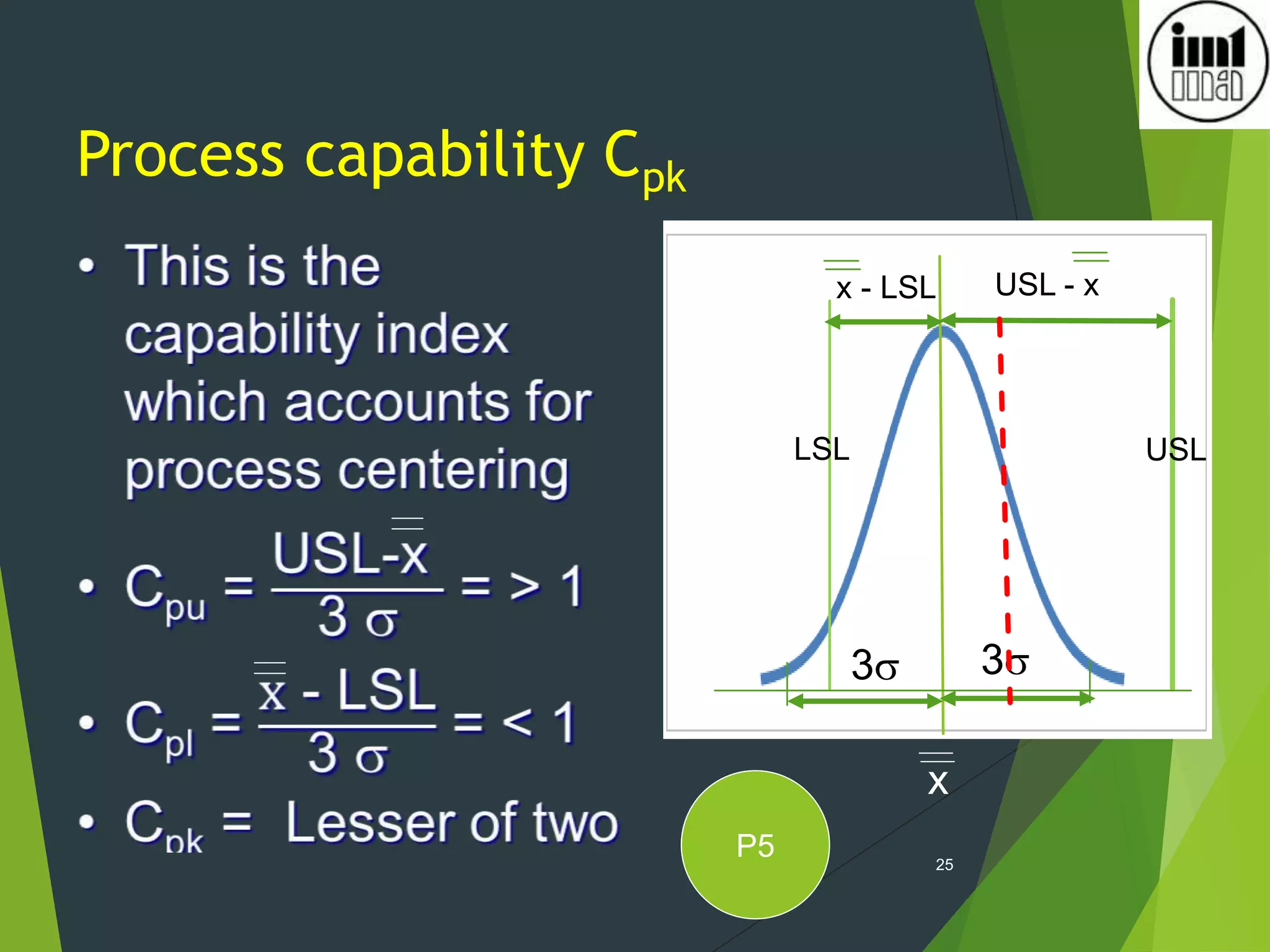
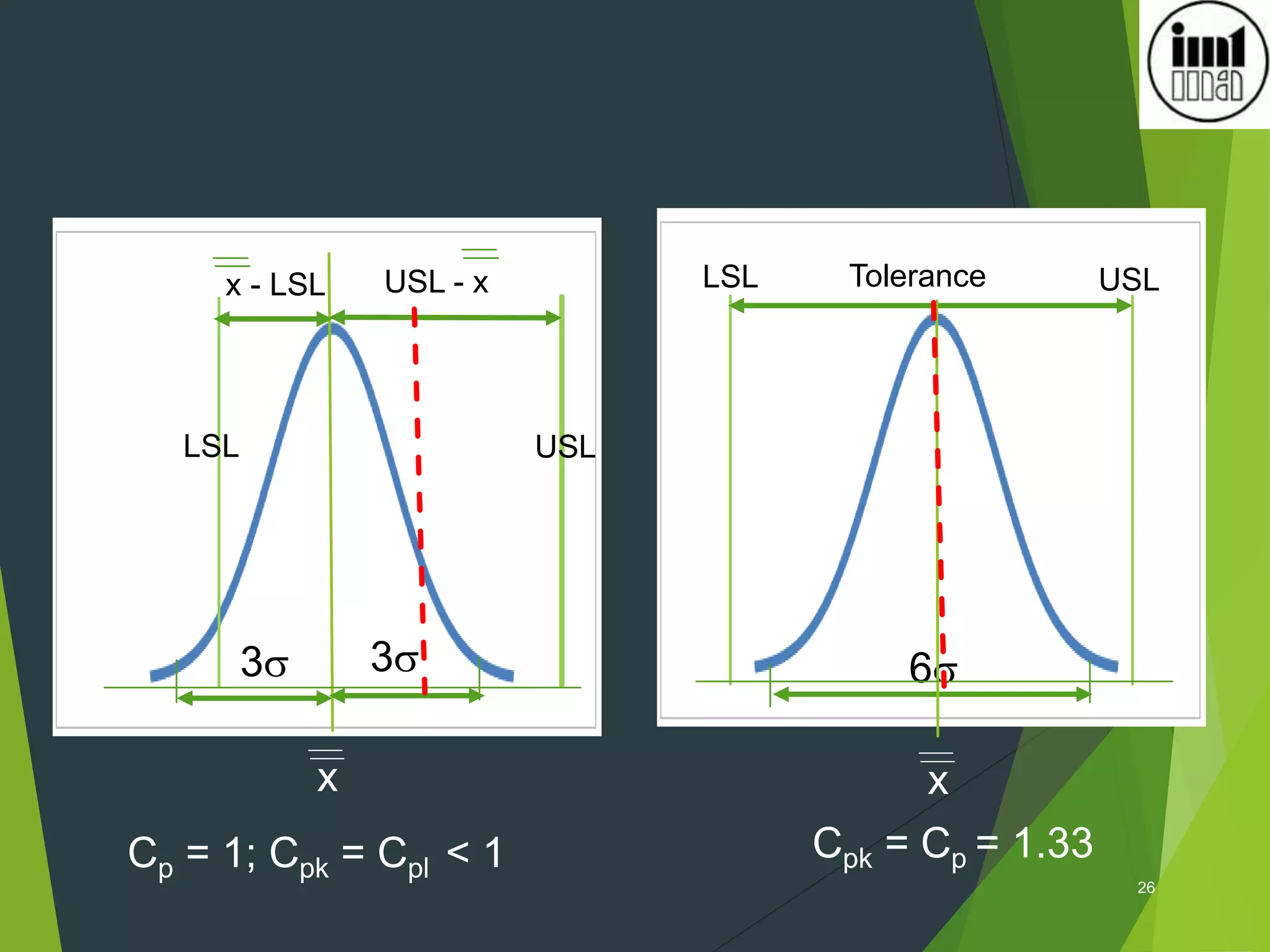
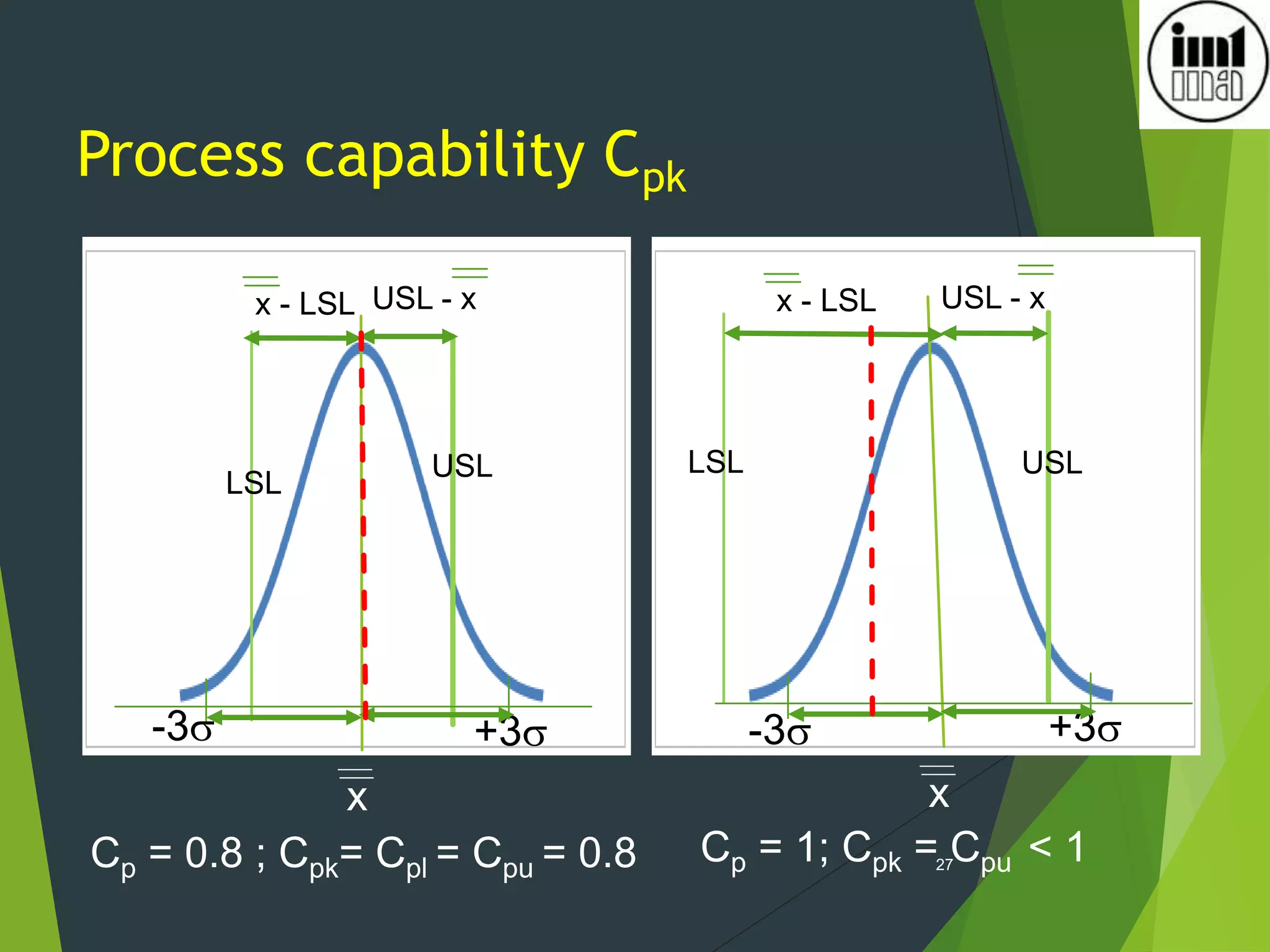
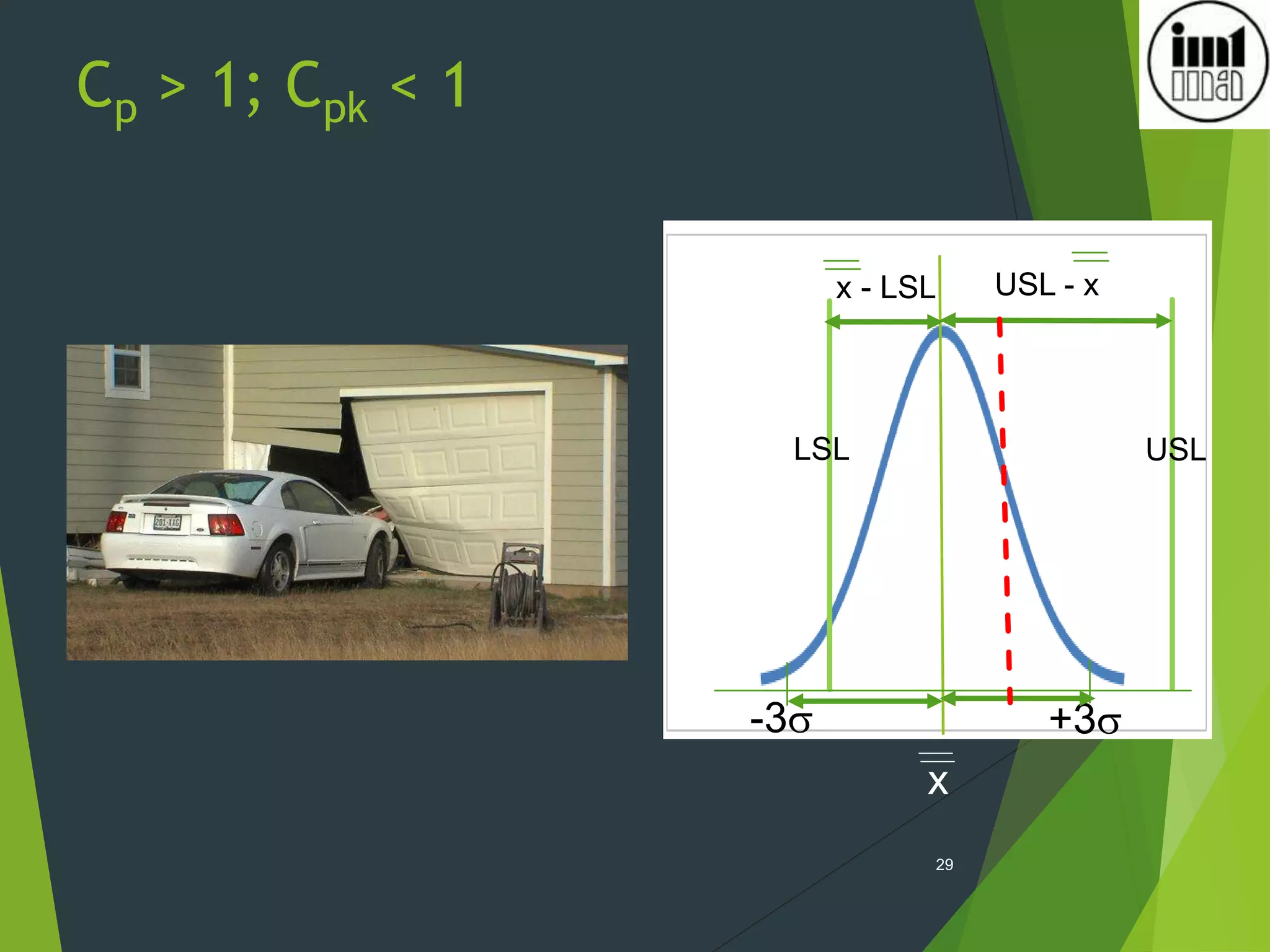
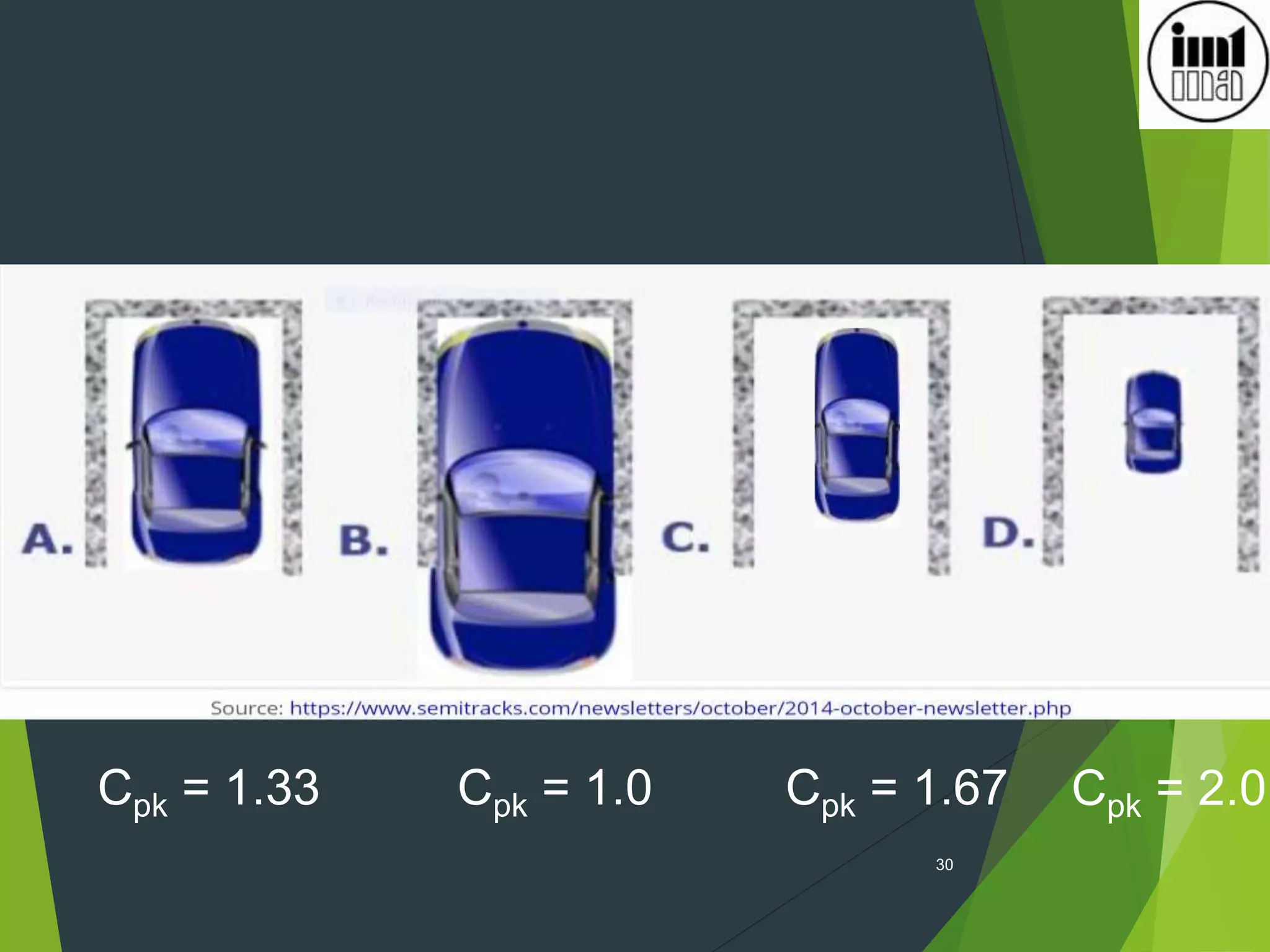
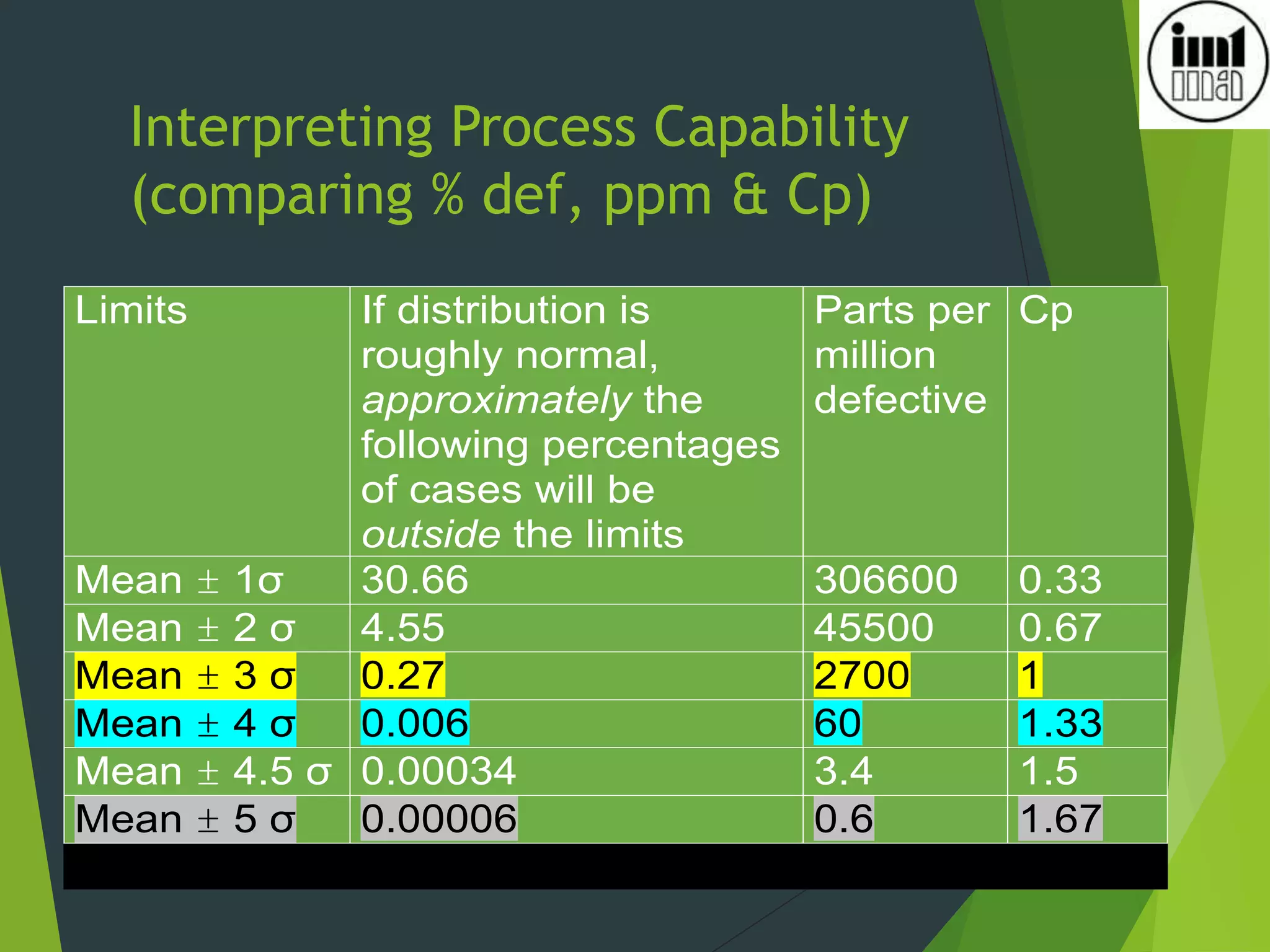
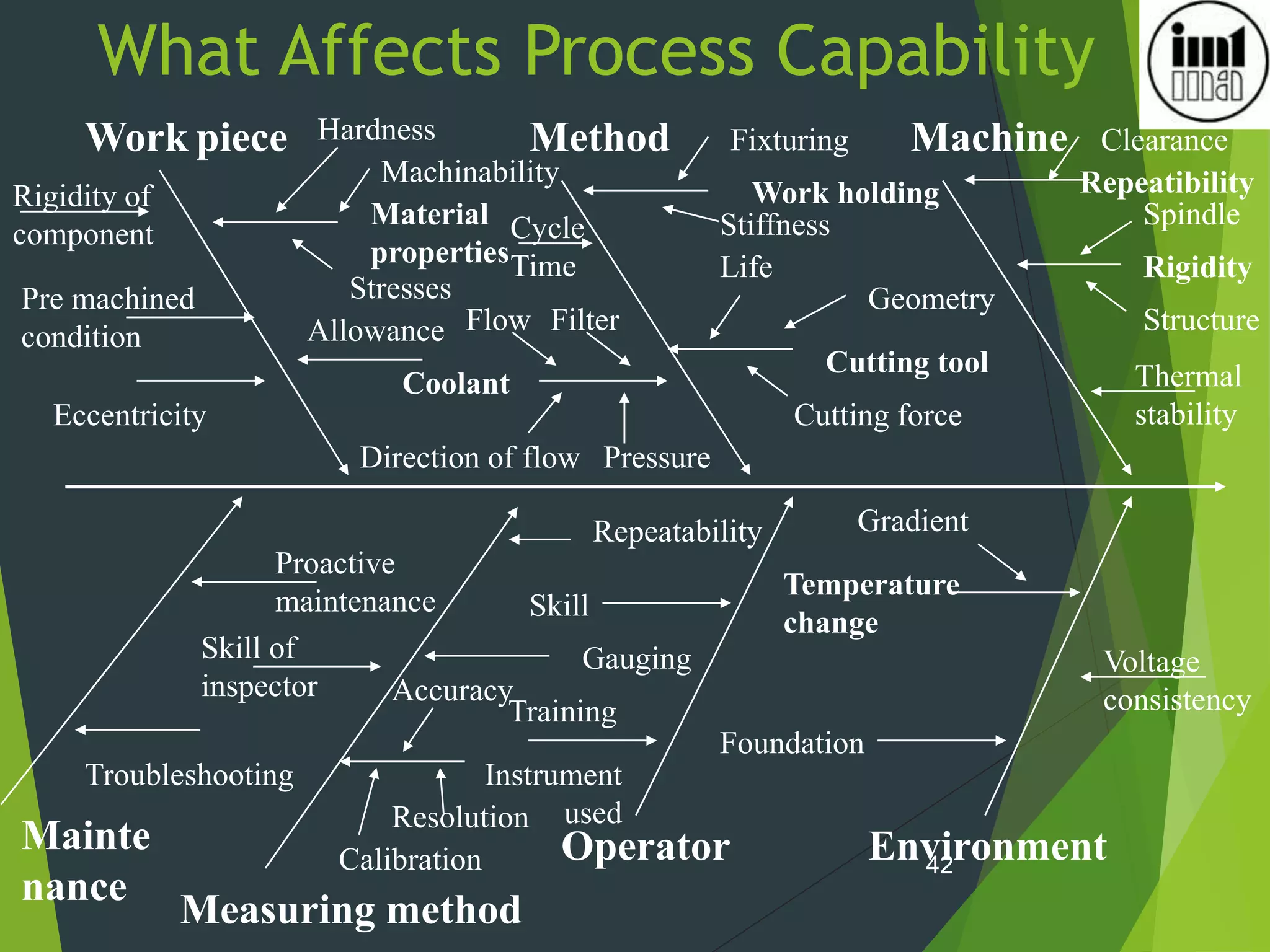
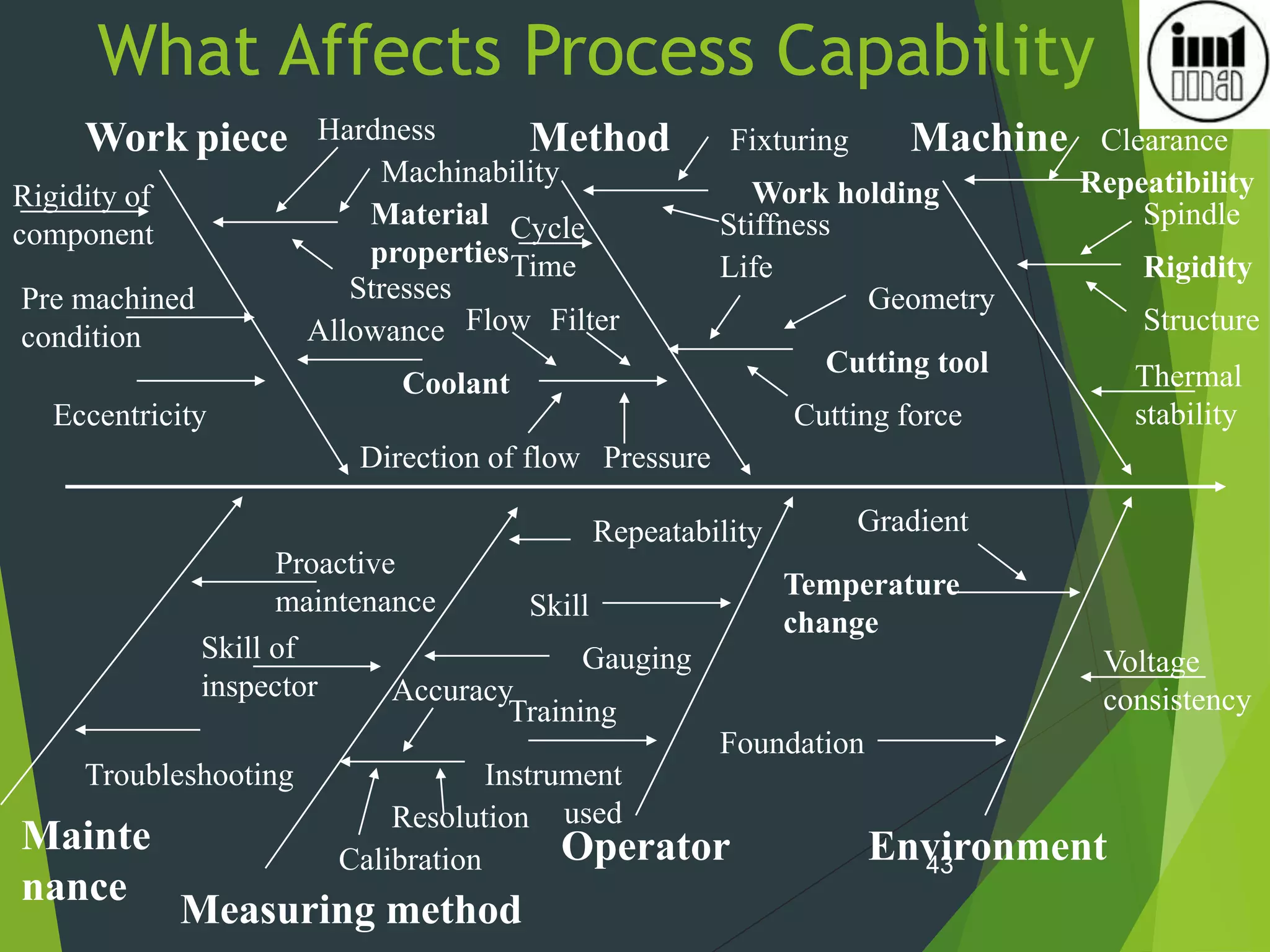
The document discusses fundamentals of process capability including: 1) Achieving process control is key to reducing variation and non-conforming parts to achieve quality and cost targets. 2) Process capability indices like Cp, Cpk measure how well a process performs versus specifications and a value of 1.33 or higher indicates a stable and capable process. 3) Many factors can impact a process's capability including the machine, environment, operator, material and more; conducting process capability studies helps evaluate a process and identify sources of variation.

1. Fundamentals of
Process Capability
Gautam Doshi
Productivity & Quality Improvement Services
Indian Machine Tool Manufacturers’ Association
1

2. Achieving World Class
Manufacturing
Quality & Cost Target
requires having your
process in control
2
Eliminate
Non –
Confirming
Parts
Reduce
Variation in
Manufacturing
Control
The
Process
Manufacturing excellence is a journey…
From elimination of non-conforming parts
to control of process
Cost
Quality

3. Where does quality come from?
 There is no direct
control for quality
 Quality results from the
Process that creates
products
 Variation in your Process
results in variation in
Quality
3
Process control drives
Quality control

4. 4
How consistent is Sachin?
• Sachin’s 9 consecutive inning’s score
• 40, 56, 38, 38,63, 59, 52, 49, 46

5. 5
Average
• average of all the above numbers =
( 40+56+38+ 63+59+52+49+46)/9
• = 49
• Average =(x1+x2+ ……..xn)/n = X

6. 6
Median = Half way point
• Sorting the nos..
• 63, 59, 56, 52, 49, 46, 40, 38, 38

7. 7
Measure of deviation
• Score Distance from mean (49)
• 40 9 = ( 40-49)
• 56 7 = (56-49)
• 38 11
• 38 11
• 63 14
• 59 10
• 52 3
• 49 0
• 46 3
Scores
40, 56, 38, 38,63,
59, 52, 49, 46

8. 8
Mean absolute deviation
• average of 9, 7,... 0, 3 = 7.556
• Sum of deviation / no of readings

9. 9
Variance
Variance
• Square each deviation and find the
mean
• (40-49)2+ …………..(46-49)2/n
• = 686/9 = 76.222
• Standard deviation is
• In this example std. Deviation 8.73

10. 10
Normal Distribution
• Some interesting
properties
• 68% of all the nos.. will
be within 2
• 95% of all the nos.. will
be in 4
• 99.73% of all the nos..
will be in 6
• Note this is true only
if the distribution is
normal
95.46
68.26
99.73
-2 -1
-3 1 2 3

11. 11
Sachin ‘s probability
• 68% of his scores will be within 40 to 57
• 95% of his scores will be within 32 to 66
• 99.73% of his scores will be within 23 to 75
• 0.27% of his scores will be less than 23 or
greater than 75
P1

12. Variations
12

13. Variations
13

14. 14
Who is a better shooter?
P2

15. 15
Definition of Process terms
 Inherent process variation - σ
 Estimated from control chart by
 Reflects only common causes
2
/d
R
σ 

16. 2
/d
R
σ 
16
Definition of Process terms
 Inherent process variation – σ (range method)
 Estimated from control chart by
 Reflects only common causes

17. Some definitions
 R This is the average of Range of
groups
 d2 is a constant based on group sample
size
  is an estimate of the standard
deviation of a stable process
  s is an estimate of the standard
deviation of a set of readings of a
parameter of a sample taken from a
large population
17

18. Factors
Sub
group
size
Factor
d2
Factor A2
for X bar
chart
Factor D3
for R bar
chart
Factor D4
for R bar
chart
2 1.128 1.88 0 3.27
3 1.693 1.02 0 2.57
4 2.059 0.73 0 2.28
5 2.326 0.58 0 2.11
6 2.534 0.48 0 2.00
7 2.704 0.42 0.08 1.92
8 2.847 0.37 0.14 1.86
9 2.970 0.34 0.18 1.82
10 3.078 0.31 0.22 1.78
18

19. 19
 Total process variation (formula method)
 Estimated by the standard deviation using
individual readings from control chart or process
study by
Definition of Process terms
s

 
1
2




n
x
x
s i


20. 20
Process Capability
• Process capability index for a
statistically stable process only
– Cp = Tolerance / 6 
• Short term process capability index

21. 21
Process Capability
• Process performance capability
index
– Pp = Tolerance / 6  s
• Long term process capability index

22. • Process capability
index for a
statistically stable
process only
Cp =
Tolerance
6
22
Process Capability
6
LSL USL
Tolerance
x
+3
-3

23. 23
6
LSL USL
Tolerance
x
6
LSL USL
Tolerance
x
Cp = 1 Cp > 1
P3

24. 24
6
LSL USL
Tolerance
x
Cp < 1

25. Process capability Cpk
25
3
x - LSL USL - x
x
3
USL
LSL
P5

26. 26
6
LSL USL
Tolerance
x
3
x - LSL USL - x
x
3
USL
LSL
Cp = 1; Cpk = Cpl < 1 Cpk = Cp = 1.33

27. Process capability Cpk
27
+3
x - LSL USL - x
x
-3
USL
LSL
+3
x - LSL USL - x
x
-3
USL
LSL
Cp = 0.8 ; Cpk= Cpl = Cpu = 0.8 Cp = 1; Cpk = Cpu < 1

28. 28
Cp = Cpk
P6

29. Cp > 1; Cpk < 1
29
+3
x - LSL USL - x
x
-3
USL
LSL

30. 30
Cpk = 1.33 Cpk = 1.0 Cpk = 1.67 Cpk = 2.0

31. Desired Cpk Values
• Cpk = 1.33 In production
• For Centre line shift
• Cpk = 1.67
• For new process
31
P7

32. 32
Example
• For a tolerance of say 25 microns
• For Cp = 1.33
• Cp = Tolerance / 6  , then  = 3.13
microns
• If the sample size is 5, d2 = 2.326 & R = 7
microns
• This means on an average the difference in
readings in your sample should not exceed
7 microns

33. 33
•For same tolerance of 25 microns
•For Cp = 1.67,  = 2.5 microns
•If the sample size is 5, d2 = 2.326 & R =
6 microns
•That means the Average R in say 5
components must be within 7 microns
for Cp = 1.33 and 6 microns for Cp =
1.67

34. 34
• For tolerance of 20 microns
• Average R must be within 5.8 microns
for Cp = 1.33
• R must be within 4.6 microns for Cp =
1.67
• In conclusion
• As tolerance becomes tighter, Range
becomes closer.
• As required Cp increases, Range
becomes closer

35. Machine Capability - Cm & Cmk
 Same formula as Cp & Cpk
 All input variables controlled well within specs
 Machine (e.g. degree of wear and choice of tooling);
 Measurement (e.g. resolution and GR&R of measuring
instrument);
 Operator (e.g. how experienced and careful he/she is);
 Material (e.g. variations in surface smoothness and hardness);
 Environment (e.g. variations in temperature, humidity and
voltage);
 Method (e.g. type of machining operation).
36

36. Machine Capability Trials
 Only variability of machine assessed
 All input variables controlled well within specs
Machine
Measurement (e.g. Gauge R & R within 10% of part
tol)
Operator (e.g. skilled operator);
Material (e.g. input raw material within tolerance);
Environment (e.g. no variations during trial);
Method (e.g. no changes in program, parameters &
cutting tool).

37. Conducting Process Capability Trials
 Warm up machine as per Supplier; time not to exceed 60 min.
 Machine 5 pieces & check Class A parameters. Readings to lie in
centre of tol. & range not to exceed 25% of tol. band
 Rectify if necessary
 Check all tools are new or freshly ground
 Machine 50 pieces; but not less than 30 pieces sequentially
 Pieces are numbered & measured
 No adjustments or offsets; in case of interruption - fresh trials
 Calculate Cmk using range method
 Check for freak readings
 If Cmk not acceptable locate & rectify source of variation &
reconduct trials.
 Fresh trials on all parameters affected by rectification

38. Exceptional Circumstances
? Machining time of a piece is too long
? Excessive tool wear
? Wear compensation may be given of a fixed amount after
specific number of pieces
? Wheel dressing and compensation may be given in grinding
machines
? Cmk value based on less than 30 pieces likely to be
erroneous & less than 10 pieces unreliable and
should not be used for machine acceptance

39. Trial Quantity Schedule
 Trial Pieces to be checked 100% and to be supplied
with inspection report. All pieces within tolerance
 In case picked up randomly from previous process,
then Cp of previous process should be established
Trials, Quantity and Schedule Quantity Date to reach
supplier’s
works
Setting trials at Supplier’s works 50 pieces
Fine tuning process capability before final
trials
100
pieces
Establishing process capability in presence
of buyer at supplier’s works
100
pieces

40. Trial Docket
 Warm up sequence from cold start : Note Spindle rpm and time
 In case tolerance is closer than 0.02 then note: shop floor ambient temperature
and machine foundation
 Include pre-machining & final workpiece drawing
 Include raw material size, spec. & inspection report
 Operation sheet
 Hard copy of CNC programe
 Tool layout on machine incl. Drg of special tools
 Clamping / workholding arrangement incl. Sketch
 Quality plan
 Inspection report of trial components with machine capability calculations

41. What Affects Process Capability
42
Machine
Repeatibility
Clearance
Rigidity
Spindle
Thermal
stability
Structure
Method
Work piece
Environment
Operator
Measuring method
Mainte
nance
Stresses
Material
properties
Allowance
Hardness
Machinability
Rigidity of
component
Pre machined
condition
Eccentricity
Temperature
change
Voltage
consistency
Gradient
Foundation
Skill
Training
Proactive
maintenance
Troubleshooting
Repeatability
Gauging
Instrument
used
Accuracy
Resolution
Calibration
Skill of
inspector
Work holding
Cutting tool
Coolant
Fixturing
Stiffness
Geometry
Life
Cutting force
Filter
Flow
Pressure
Direction of flow
Cycle
Time

42. What Affects Process Capability
43
Machine
Repeatibility
Clearance
Rigidity
Spindle
Thermal
stability
Structure
Method
Work piece
Environment
Operator
Measuring method
Mainte
nance
Stresses
Material
properties
Allowance
Hardness
Machinability
Rigidity of
component
Pre machined
condition
Eccentricity
Temperature
change
Voltage
consistency
Gradient
Foundation
Skill
Training
Proactive
maintenance
Troubleshooting
Repeatability
Gauging
Instrument
used
Accuracy
Resolution
Calibration
Skill of
inspector
Work holding
Cutting tool
Coolant
Fixturing
Stiffness
Geometry
Life
Cutting force
Filter
Flow
Pressure
Direction of flow
Cycle
Time

43. Recommendations
 Critical parameters (Class A) Cmk of 1.33 or better for
bilateral tolerances.
 Unilateral tolerances if classified as Critical (Class A) -
all measurements to lie within 80% tolerance
 Other parameters (Class B) - all measurements to lie
within tolerance
 Range method of calculation to be used

44. Recommendations for Auto
Companies
 Critical parameters (Class A) Cmk of 1.67 or better for
bilateral tolerances.
 Unilateral tolerances if classified as Critical (Class A) -
all measurements to lie within 60% - 70% of tolerance
 Other parameters (Class B) - all measurements to lie
within tolerance
 RMS (formula) method of calculation to be used

45. Interpreting Process Capability
(comparing % def, ppm & Cp)
46
Limits If distribution is
roughly normal,
approximately the
following percentages
of cases will be
outside the limits
Parts per
million
defective
Cp
Mean ± 1σ 30.66 306600 0.33
Mean ± 2 σ 4.55 45500 0.67
Mean ± 3 σ 0.27 2700 1
Mean ± 4 σ 0.006 60 1.33
Mean ± 4.5 σ 0.00034 3.4 1.5
Mean ± 5 σ 0.00006 0.6 1.67

46. Implication of Cpk = 1.67
Cp = 1.8
Component
tolerance
[microns]
Six Sigma
Variation
[microns]
Frequ
ency
272
(2σ)
Frequ
ency
380
(4σ)
Frequ
ency
399
(6σ)
Beyo
nd
6σ
Tot
al
40 22 7 14 22 1 400
30 16 5 10 16 1 400
20 11 3 7 11 1 400
10 5 1 3 5 1 400
47

47. One Sided & Unilateral
Tolerance
48
20.00 +0.10
P9

48. One sided tolerances
 If significant
characteristic is
roundness, surface,
flatness,
concentricity, etc
 Distribution is
skewed in one
direction – Not
Normal
49
Positive
Negative

49. Skewed distribution
 Formulae do not apply
 There is no agreed simple approach
 Companies take different approaches
 All sample values to fall within 80% of tol.
 All sample values to fall within 60% of tol.
 Mode + 3σ to lie within tolerance
 Use software to normalise data & calculate Cp
 Follow the approach of your company

50. Few Approaches to Unilateral Tolerances
 Box Cox Transformation of Data to
normalize it
 Johnson Transformation
 Fitting Pearson Curve

51. .
52
In Conclusion it is extremely
difficult & therefore costly to
maintain Cpk of 1.67 on
very close tolerances.
Designer must be extremely
careful in asking for high Cpk
on closely tolerated
dimension. Also monitoring of
such a process would
probably call for in process
quality control

52. 53
SPC never tells you
what to do to correct/
improve one’s Process
SPC only tells you if your
Process is under statistical
control or not. It is you who
decides if it needs
correction/ improvement

53. Gautam Doshi
Advisor
Indian Machine Tool Manufacturers’
Association
gpdoshi@gmail.com