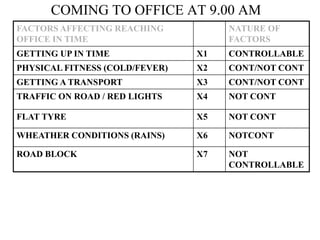
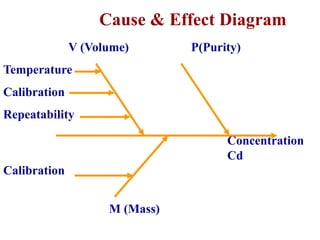
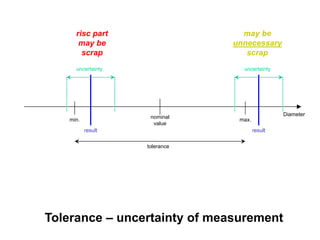
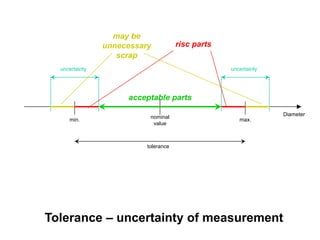
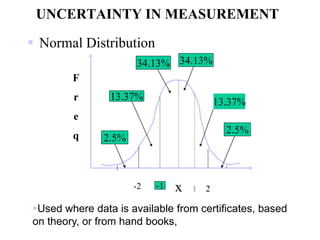
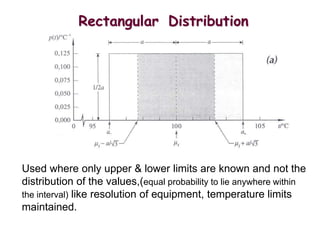
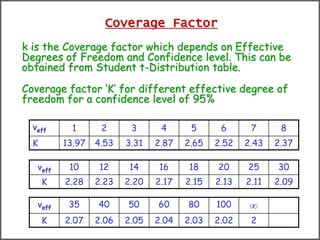
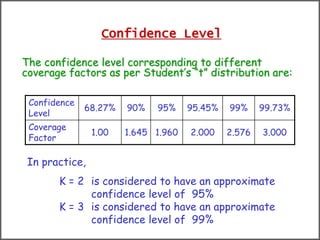
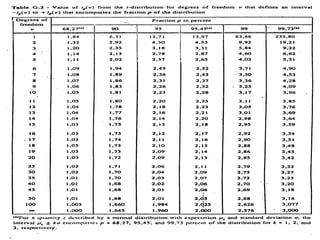
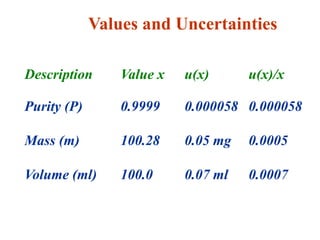
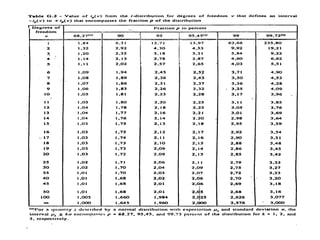
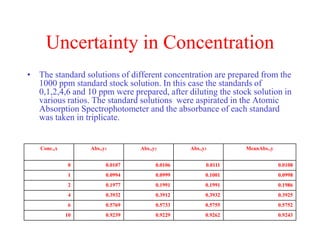
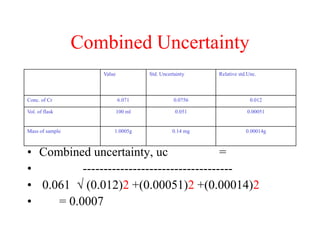
The document discusses the concepts of measurement uncertainty, including its definition, significance, and methods for estimation. It highlights the mandatory nature of establishing and reporting measurement uncertainty in laboratories and outlines various factors that contribute to uncertainty. The importance of understanding related terminologies, evaluating uncertainty, and following ISO/IEC 17025 standards for accreditation is also emphasized.