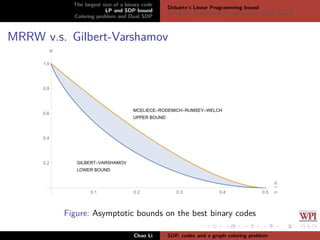
The document discusses the largest size of a binary error-correcting code and related problems, focusing on linear programming (LP) and semidefinite programming (SDP) bounds. It defines key concepts such as Hamming distance, binary codes, and provides an overview of established upper bounds and recent advancements in determining the maximum size of binary codes with specific lengths and distances. The work highlights the significance of these codes in maintaining high information rates while resisting noise during transmission.

1. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Semidefinite programming, binary codes and a
graph coloring problem
Chao Li
Advised by Prof. Martin
cli5@wpi.edu
May 12, 2015
Chao Li SDP, codes and a graph coloring problem

2. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Outline I
The largest size of a binary code
Binary codes
Problem introduction
LP and SDP bound
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Chao Li SDP, codes and a graph coloring problem

3. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Chao Li SDP, codes and a graph coloring problem

4. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Then Fn is the set of all binary strings with n bits.
Chao Li SDP, codes and a graph coloring problem

5. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Then Fn is the set of all binary strings with n bits.
Hamming distance: ∂(x, y) = k means xi = yi for exactly k
values of i. e.g. ∂(000111, 001001) = 3.
Chao Li SDP, codes and a graph coloring problem

6. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Then Fn is the set of all binary strings with n bits.
Hamming distance: ∂(x, y) = k means xi = yi for exactly k
values of i. e.g. ∂(000111, 001001) = 3.
A binary error-correcting code C of length n and distance d is
a collection of x ∈ Fn where ∂(x, y) ≥ d, ∀x = y ∈ C.
Chao Li SDP, codes and a graph coloring problem

7. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Then Fn is the set of all binary strings with n bits.
Hamming distance: ∂(x, y) = k means xi = yi for exactly k
values of i. e.g. ∂(000111, 001001) = 3.
A binary error-correcting code C of length n and distance d is
a collection of x ∈ Fn where ∂(x, y) ≥ d, ∀x = y ∈ C.
For example a code C = {0100, 1000, 0111} is a code of
length 4 and minimum Hamming distance 2.
Chao Li SDP, codes and a graph coloring problem

8. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Then Fn is the set of all binary strings with n bits.
Hamming distance: ∂(x, y) = k means xi = yi for exactly k
values of i. e.g. ∂(000111, 001001) = 3.
A binary error-correcting code C of length n and distance d is
a collection of x ∈ Fn where ∂(x, y) ≥ d, ∀x = y ∈ C.
For example a code C = {0100, 1000, 0111} is a code of
length 4 and minimum Hamming distance 2.
Is C the largest such code?
Chao Li SDP, codes and a graph coloring problem

9. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Binary codes
Let F = {0, 1} denote the binary field.
Then Fn is the set of all binary strings with n bits.
Hamming distance: ∂(x, y) = k means xi = yi for exactly k
values of i. e.g. ∂(000111, 001001) = 3.
A binary error-correcting code C of length n and distance d is
a collection of x ∈ Fn where ∂(x, y) ≥ d, ∀x = y ∈ C.
For example a code C = {0100, 1000, 0111} is a code of
length 4 and minimum Hamming distance 2.
Is C the largest such code?
A(4, 2) = 8 because we can choose
C = {0000, 0011, 0101, 0110, 1001, 1010, 1100, 1111}.
Chao Li SDP, codes and a graph coloring problem

10. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Our problem
Find the maximum size A(n, d) of a binary error-correcting
code C of length n and minimum distance d: ∂(x, y) ≥ d for
all x = y in C.
Chao Li SDP, codes and a graph coloring problem

11. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Our problem
Find the maximum size A(n, d) of a binary error-correcting
code C of length n and minimum distance d: ∂(x, y) ≥ d for
all x = y in C.
We require large codes with large minimum distance to
maintain high information rate while still allowing recovery
from channel noise.
Chao Li SDP, codes and a graph coloring problem

12. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Our problem
Find the maximum size A(n, d) of a binary error-correcting
code C of length n and minimum distance d: ∂(x, y) ≥ d for
all x = y in C.
We require large codes with large minimum distance to
maintain high information rate while still allowing recovery
from channel noise.
From 1950s forward, we have seen many constructions and
many upper bounds. But for most values of n and d, A(n, d)
is not known.
Chao Li SDP, codes and a graph coloring problem

13. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Binary codes
Problem introduction
Our problem
Find the maximum size A(n, d) of a binary error-correcting
code C of length n and minimum distance d: ∂(x, y) ≥ d for
all x = y in C.
We require large codes with large minimum distance to
maintain high information rate while still allowing recovery
from channel noise.
From 1950s forward, we have seen many constructions and
many upper bounds. But for most values of n and d, A(n, d)
is not known.
We will focus on a recently discovered upper bound.
Chao Li SDP, codes and a graph coloring problem

14. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Association scheme
An association scheme (X, R) with n classes consists of a finite set
X, of size v say, together with n + 1 relations Ri on X which,
viewed as n + 1 v × v adjacency matrices Di with entries 0 and 1,
satisfy
Di = Di
n
i=0
Di = J all ones matrix
D0 = I
Di Dj =
n
k=0
pk
ij Dk
Chao Li SDP, codes and a graph coloring problem

15. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
An example of an association scheme
1 2 3 4 5 6
1 0 1 1 2 3 3
2 1 0 1 3 2 3
3 1 1 0 3 3 2
4 2 3 3 0 1 1
5 3 2 3 1 0 1
6 3 3 2 1 1 0
Chao Li SDP, codes and a graph coloring problem

16. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Bose-Mesner algebra
Given an association scheme (X, R), the vector space
A =
n
t=0
αtDt | αt ∈ C
is closed under matrix multiplication and constitutes a subalgebra
of Cv×v whose dimension is n + 1. This is called the Bose-Mesner
algebra of the association scheme (X, R).
Note that A is also closed under entry-wise multiplication and
contains the identities, I and J, for both of these multiplications.
Chao Li SDP, codes and a graph coloring problem

17. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
An example
00 01
10 11
R0
00 01
10 11
R1
00 01
10 11
R2
Figure: Hamming scheme for n = 2
Chao Li SDP, codes and a graph coloring problem

18. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
An example
D0 =





1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1





D1 =





0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0





D2 =





0 0 0 1
0 0 1 0
0 1 0 0
1 0 0 0





{D0, D1, D2} is the usual basis of the Bose-Mesner algebra for the
previous Hamming scheme.
Chao Li SDP, codes and a graph coloring problem

19. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Eigenmatrix Q
The Bose-Mesner algebra admits a basis of positive semidefinite
matrices E0, E1, . . . , Ed and the change of basis matrix Q from Ai
to Ei is known as the second eigenmatrix and is given by
Qij = Kj(i) where Kj(x) is the Krawtchouk polynomial
Kj(x) :=
j
h=0
(−1)h
(q − 1)j−h x
h
n − x
j − h
where q = 2 in the binary case.
Chao Li SDP, codes and a graph coloring problem

20. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Characteristic vector
The characteristic vector x of a code C has one entry for each
c ∈ Fn, xc = 1 if c ∈ C; xc = 0 otherwise.
Chao Li SDP, codes and a graph coloring problem

21. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Characteristic vector
The characteristic vector x of a code C has one entry for each
c ∈ Fn, xc = 1 if c ∈ C; xc = 0 otherwise.
For example, for F2 = {00, 01, 10, 11}, a code C = {00, 01}
will have the characteristic vector [1, 1, 0, 0].
Chao Li SDP, codes and a graph coloring problem

22. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Characteristic vector
The characteristic vector x of a code C has one entry for each
c ∈ Fn, xc = 1 if c ∈ C; xc = 0 otherwise.
For example, for F2 = {00, 01, 10, 11}, a code C = {00, 01}
will have the characteristic vector [1, 1, 0, 0].
Define
ai =
1
|C|
x Ai x
Later we call this xC instead of x.
Chao Li SDP, codes and a graph coloring problem

23. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming constraints
xC Ai xC counts pairs of codewords at distance i.
Chao Li SDP, codes and a graph coloring problem

24. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming constraints
xC Ai xC counts pairs of codewords at distance i.
ai := 1
|C|xC Ai xC is the average number of codewords of
distance i from c ∈ C.
Chao Li SDP, codes and a graph coloring problem

25. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming constraints
xC Ai xC counts pairs of codewords at distance i.
ai := 1
|C|xC Ai xC is the average number of codewords of
distance i from c ∈ C.
Now define bj := 2n
|C| xC EjxC
Chao Li SDP, codes and a graph coloring problem

26. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming constraints
xC Ai xC counts pairs of codewords at distance i.
ai := 1
|C|xC Ai xC is the average number of codewords of
distance i from c ∈ C.
Now define bj := 2n
|C| xC EjxC
Clearly:
ai ≥ 0
a0 = 1
a1 = · · · = ad−1 = 0
n
i=0
ai = |C|
Chao Li SDP, codes and a graph coloring problem

27. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming constraints
Since Ej 0, x Ejx ≥ 0. So bj ≥ 0.
Chao Li SDP, codes and a graph coloring problem

28. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming constraints
Since Ej 0, x Ejx ≥ 0. So bj ≥ 0.
But we know
Ej =
1
2n
n
i=0
Kj(i)Ai
x Ejx =
1
2n
n
i=0
Kj(i)x Ai x
x Ejx =
|C|
2n
n
i=0
Qijai ≥ 0
bj =
n
i=0
ai Qij ≥ 0
Chao Li SDP, codes and a graph coloring problem

29. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear Programming formulation for code size
Then we obtain our LP formulation for code size:
max n
i=0ai
s.t. aQ≥ 0
a ≥ 0
a0 = 1
a1 = · · · = ad−1 = 0
Since every code C gives a feasible solution, with objective value
|C|, the summation of ai gives an upper bound on the maximum
size of any code C with length n and minimum distance d.
Chao Li SDP, codes and a graph coloring problem

30. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Implementation of the Linear Programming bound
We use C++ linked with CPLEX to formulate and solve the
linear programming model.
If we insist on exact solutions, our program can only solve
linear programming formulations up to n < 32, since when
n = 32 and d = 2 there will be overflow.
Chao Li SDP, codes and a graph coloring problem

31. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Analytic results
The results indicate A(n, d) = 2n−1 when d = 2,
A(n, d) ≈ 2n
n+1 when d = 3 and A(n, d) = 2 when d > 2n/3,
which can be proved as well.
So we can do linear programming without the computer.
Some bounds
Plotkin bound
Levenshtein bound
MRRW bound
Chao Li SDP, codes and a graph coloring problem

32. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
MRRW v.s. Gilbert-Varshamov
MCELIECE-RODEMICH-RUMSEY-WELCH
UPPER BOUND
GILBERT-VARSHAMOV
LOWER BOUND
0.1 0.2 0.3 0.4 0.5
d
n
0.2
0.4
0.6
0.8
1.0
R
Figure: Asymptotic bounds on the best binary codes
Chao Li SDP, codes and a graph coloring problem

33. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Semidefinite Programming (SDP)
Semidefinite programming is a new branch of conic
programming, developed since 1990s.
Chao Li SDP, codes and a graph coloring problem

34. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Semidefinite Programming (SDP)
Semidefinite programming is a new branch of conic
programming, developed since 1990s.
It searches for solutions on a section of a positive semidefinite
cone. Since the semidefinite cone is convex, it’s a convex
optimization problem.
Chao Li SDP, codes and a graph coloring problem

35. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Semidefinite Programming (SDP)
Semidefinite programming is a new branch of conic
programming, developed since 1990s.
It searches for solutions on a section of a positive semidefinite
cone. Since the semidefinite cone is convex, it’s a convex
optimization problem.
Inner product C, X = tr(C X).
Chao Li SDP, codes and a graph coloring problem

36. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Semidefinite Programming (SDP)
Semidefinite programming is a new branch of conic
programming, developed since 1990s.
It searches for solutions on a section of a positive semidefinite
cone. Since the semidefinite cone is convex, it’s a convex
optimization problem.
Inner product C, X = tr(C X).
We call Hermitian matrix X positive semidefinite if v Xv ≥ 0
for all v.
Chao Li SDP, codes and a graph coloring problem

37. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Semidefinite Programming (SDP)
Semidefinite programming is a new branch of conic
programming, developed since 1990s.
It searches for solutions on a section of a positive semidefinite
cone. Since the semidefinite cone is convex, it’s a convex
optimization problem.
Inner product C, X = tr(C X).
We call Hermitian matrix X positive semidefinite if v Xv ≥ 0
for all v.
X 0 means X is positive semidefinite.
Chao Li SDP, codes and a graph coloring problem

38. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Generic form of SDP formulation
The generic form of a SDP formulation is as follows:
max C, χ
s.t. Ai , χ = bi (1 ≤ i ≤ m)
Bj, χ ≤ dj (1 ≤ j ≤ k)
χ 0 ,
in which χ represents the semidefinite variable, a Hermitian v × v
matrix. Ai , Bj and C are constant matrices. bi and dj are constant
numbers.
Chao Li SDP, codes and a graph coloring problem

39. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Basis for Terwilliger algebra
Let α = (α0, α1, α2, α3), and let α n indicate that
n = α0 + α1 + α2 + α3 and all αi ≥ 0.
Chao Li SDP, codes and a graph coloring problem

40. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Basis for Terwilliger algebra
Let α = (α0, α1, α2, α3), and let α n indicate that
n = α0 + α1 + α2 + α3 and all αi ≥ 0.
Let α2 + α3 = i α1 + α3 = j α1 + α2 = k
Chao Li SDP, codes and a graph coloring problem

41. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Basis for Terwilliger algebra
Let α = (α0, α1, α2, α3), and let α n indicate that
n = α0 + α1 + α2 + α3 and all αi ≥ 0.
Let α2 + α3 = i α1 + α3 = j α1 + α2 = k
Define wt(x) be the Hamming distance between vector x and
the 0 vector, say ∂(0, x).
Chao Li SDP, codes and a graph coloring problem

42. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Basis for Terwilliger algebra
Let α = (α0, α1, α2, α3), and let α n indicate that
n = α0 + α1 + α2 + α3 and all αi ≥ 0.
Let α2 + α3 = i α1 + α3 = j α1 + α2 = k
Define wt(x) be the Hamming distance between vector x and
the 0 vector, say ∂(0, x).
Define
(Lα)x,y =
1 if wt(x) = i, wt(y) = j, ∂(x, y) = k
0 o.w.
be a Fn × Fn matrix. Where a Fn × Fn matrix means the
rows and columns of this matrix are both indexed by elements
of Fn.
Chao Li SDP, codes and a graph coloring problem

43. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Basis for Terwilliger algebra
Let α = (α0, α1, α2, α3), and let α n indicate that
n = α0 + α1 + α2 + α3 and all αi ≥ 0.
Let α2 + α3 = i α1 + α3 = j α1 + α2 = k
Define wt(x) be the Hamming distance between vector x and
the 0 vector, say ∂(0, x).
Define
(Lα)x,y =
1 if wt(x) = i, wt(y) = j, ∂(x, y) = k
0 o.w.
be a Fn × Fn matrix. Where a Fn × Fn matrix means the
rows and columns of this matrix are both indexed by elements
of Fn.
We call the set {Lα : ∀α n} the usual basis for Terwilliger
algebra.
Chao Li SDP, codes and a graph coloring problem

44. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Example for the basis of Terwilliger algebra
00 01
10 11
R0
00 01
10 11
R1
00 01
10 11
R2
00 01
10 11
R3
00 01
10 11
R4
00 01
10 11
R5
00 01
10 11
R6
Chao Li SDP, codes and a graph coloring problem

45. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
00 01
10 11
R7
00 01
10 11
R8
00 01
10 11
R9
Chao Li SDP, codes and a graph coloring problem

46. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Block diagonalization
Schrijver observes that Tn = { α n xαLα | ∀xα ∈ C} is a
C*-algebra hence there exists a unitary matrix U and positive
integers p0, q0, . . . , pm, qm such that U∗TnU is equal to the
collection of all block diagonal matrices. For M ∈ Tn,
M = α n xαLα:
U∗
MU =






C0 0 · · · 0
0 C1 · · · 0
...
...
...
...
0 0 · · · Cm






Chao Li SDP, codes and a graph coloring problem

47. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
in which Cj is a block diagonal matrix with qj repeated identical
blocks of order pk:
Ck =






Bk 0 · · · 0
0 Bk · · · 0
...
...
...
...
0 0 · · · Bk






Chao Li SDP, codes and a graph coloring problem

48. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
By deleting all repeated blocks, we obtain an algebra isomorphism:
ϕ(Tn) →






B0 0 · · · 0
0 B1 · · · 0
...
...
...
...
0 0 · · · Bm






Schrijver finds block Bk has size pk = n + 1 − 2k and is repeated
qk = n
k − n
k−1 times.
Chao Li SDP, codes and a graph coloring problem

49. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
The exact entries of Bk
Let
βk
α =
n
u=0
(−1)u−α3
u
α3
n − 2k
u − k
n − k − u
α2 + α3 − u
n − k − u
α1 + α3 − u
then we will get the kth block matrix Bk as a
(n − 2k + 1) × (n − 2k + 1) matrix:


α n
n − 2k
α2 + α3 − k
−1
2
n − 2k
α1 + α3 − k
−1
2
βk
αxα


n−k
α2+α3=k,α1+α3=k
Chao Li SDP, codes and a graph coloring problem

50. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Some notations
Define
ˇα(α) = (α0 + α2, 0, α1 + α3, 0)
´α(α) = (α0 + α1, 0, α2 + α3, 0)
ˆα(α) = (α0 + α3, 0, α1 + α2, 0)
Chao Li SDP, codes and a graph coloring problem

51. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Semidefinite matrices
Let C ⊆ Fn be a code, and Π be the set of all automorphisms π of
Fn. Let x be the characteristic vector of code C. Define
Π0 = {π ∈ Π : 0 ∈ π(C)}
Π1 = {π ∈ Π : 0 /∈ π(C)}
R =
1
|Π0| π∈Π0
xπ(C)xπ(C)
R =
1
|Π1| π∈Π1
xπ(C)xπ(C)
Chao Li SDP, codes and a graph coloring problem

52. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Let λα be the number of triples (x, y, z) ∈ C3, where
∂(x, y) = α2 + α3 ∂(x, z) = α1 + α3 ∂(y, z) = α1 + α2
Define
xα =
1
|C| n
α0,α1,α2,α3
λα (1)
Then we can show that
R =
α n
xαLα R =
|C|
2n − |C| α n
(xˆα − xα)Lα
are both positive semidefinite matrices.
Chao Li SDP, codes and a graph coloring problem

53. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Linear constraints
Along with the semidefinite conditions, Schrijver’s formulation has
the following linear constraints:
I xα(0) = 1
II 0 ≤ xα ≤ x´α, ∀α ∈ T and x´α + xˇα ≤ 1 + xα, ∀α ∈ T
III xα = xα if (α1, α2, α3) is a permutation of (α1, α2, α3)
IV xα = 0 if {α1 + α2, α2 + α3, α1 + α3} ∩ {1, . . . , d − 1} = ∅
Chao Li SDP, codes and a graph coloring problem

54. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Objective function
The objective function is to maximize |C| = α n
n
α2+α3
x´α.
Since
λ´α =



(x, y, z) ∈ C3
:
∂(x, y) = α2 + α3
∂(x, z) = 0
∂(y, z) = α2 + α3



Hence
´α
λ´α = |C|2
By substituting (1) into this, we obtain that
|C| =
α n
n
α2 + α3
x´α
Chao Li SDP, codes and a graph coloring problem

55. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Implementation of Schrijver’s SDP formulation
We use Matlab and CVX to model the previous SDP
formulation.
CVX is a convex optimization package used with Matlab
CVX has the capability modeling and solving semidefinite
programming models.
Chao Li SDP, codes and a graph coloring problem

56. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Implementation of Schrijver’s SDP formulation
We use Matlab and CVX to model the previous SDP
formulation.
CVX is a convex optimization package used with Matlab
CVX has the capability modeling and solving semidefinite
programming models.
We build the linear constraints III & IV implicitly when
validating the αs. Since x only depends on α, we eliminate
some αs when we enumerate all n+3
3 of them.
Chao Li SDP, codes and a graph coloring problem

57. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Implementation of Schrijver’s SDP formulation
We use Matlab and CVX to model the previous SDP
formulation.
CVX is a convex optimization package used with Matlab
CVX has the capability modeling and solving semidefinite
programming models.
We build the linear constraints III & IV implicitly when
validating the αs. Since x only depends on α, we eliminate
some αs when we enumerate all n+3
3 of them.
For constraint III, we assign them the same name if α is a
permutation of α in α1, α2 and α3.
Chao Li SDP, codes and a graph coloring problem

58. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
Delsarte’s Linear Programming bound
Schrijver’s Semidefinite Programming (SDP) Bound
Implementation of Schrijver’s SDP formulation
We use Matlab and CVX to model the previous SDP
formulation.
CVX is a convex optimization package used with Matlab
CVX has the capability modeling and solving semidefinite
programming models.
We build the linear constraints III & IV implicitly when
validating the αs. Since x only depends on α, we eliminate
some αs when we enumerate all n+3
3 of them.
For constraint III, we assign them the same name if α is a
permutation of α in α1, α2 and α3.
Constraint IV allows us to elimintate many variables.
Chao Li SDP, codes and a graph coloring problem

59. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Orthogonality graph
Observe that (±)1-vectors, u, v in Rn are orthogonal iff the
corresponding binary vectors are at Hamming distance n/2.
Chao Li SDP, codes and a graph coloring problem

60. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Orthogonality graph
Observe that (±)1-vectors, u, v in Rn are orthogonal iff the
corresponding binary vectors are at Hamming distance n/2.
The graph with all 01-tuples as vertices is called the
orthogonality graph if x ∼ y iff ∂(x, y) = n
2 . We denote this
by Ω(n). We note that Ω(n) is k-regular for k = n
n/2 .
Chao Li SDP, codes and a graph coloring problem

61. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
A quantum information game
The orthogonality graph coloring problem is inspired from a
quantum information game, expanding to classical bits.
Chao Li SDP, codes and a graph coloring problem

62. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
A quantum information game
The orthogonality graph coloring problem is inspired from a
quantum information game, expanding to classical bits.
Two players A and B are asked questions xA and xB, coded as
n-bit rings satisfying ∂(xA, xB) ∈ {0, n/2}. A and B win the
game if they give answers yA and yB, coded as binary string of
length r such that yA = yB ⇔ xA = xB. Galliard et al.
pointed out that whether or not the game can always be won
is equivalent to the question
χ(Ω(n)) ≤ r?
Chao Li SDP, codes and a graph coloring problem

63. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
The graph coloring problem
We want to find the minimum number of colors required to color
Ω(n) a priori, so that the two questions xA and xB are viewed as
two vertices of Ω(n) and A and B answer their respective questions
by giving the colors of the vertices xA and xB respectively, coded as
binary string of length log2(n) = r. If the two vertices have the
same color, then they win.
Chao Li SDP, codes and a graph coloring problem

64. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
The SDP formulation
De Klerk and Pasechnik give a very similar formulation based on
Schrijver’s code size upper bound formulation. The only difference
is in linear constraint IV:
xα = 0 if {α1 + α2, α1 + α3, α2 + α3} ∩ {n/2} = ∅
Chao Li SDP, codes and a graph coloring problem

65. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Implementation of the SDP formulation for graph coloring
problem
Just with moderate modification, we obtained our SDP
formulation for the graph coloring problem, and produce the same
results as de Klerk and Pasechnik did.
Chao Li SDP, codes and a graph coloring problem

66. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Duality form of semidefinite programming
max α uαxα
s.t. α xαBα C
xα ≥ 0
min C, χ
Bα, χ ≤ −uα
χ 0
Chao Li SDP, codes and a graph coloring problem

67. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Can we generate the dual SDP automatically
Based on our implementation we are able to transfer the
primal SDP to its dual problem.
Chao Li SDP, codes and a graph coloring problem

68. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Can we generate the dual SDP automatically
Based on our implementation we are able to transfer the
primal SDP to its dual problem.
We explicitly assign 1 to x0 and 0 to x1.
Chao Li SDP, codes and a graph coloring problem

69. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Can we generate the dual SDP automatically
Based on our implementation we are able to transfer the
primal SDP to its dual problem.
We explicitly assign 1 to x0 and 0 to x1.
We expand the block diagonal matrix by appending the linear
constraints to the end.
Chao Li SDP, codes and a graph coloring problem

70. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Can we generate the dual SDP automatically
Based on our implementation we are able to transfer the
primal SDP to its dual problem.
We explicitly assign 1 to x0 and 0 to x1.
We expand the block diagonal matrix by appending the linear
constraints to the end.
We split the positive semidefinite diagonal matrix into the
sum of constant matrices, which are the coefficients of xαs.
Chao Li SDP, codes and a graph coloring problem

71. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Can we generate the dual SDP automatically
Based on our implementation we are able to transfer the
primal SDP to its dual problem.
We explicitly assign 1 to x0 and 0 to x1.
We expand the block diagonal matrix by appending the linear
constraints to the end.
We split the positive semidefinite diagonal matrix into the
sum of constant matrices, which are the coefficients of xαs.
Finally we use the constant matrices to formulate the dual
SDP problem.
Chao Li SDP, codes and a graph coloring problem

72. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Implementation
Use the Matlab code to output the constraints and the
semidefinite cone to text files.
Use C++ program to parse the text files.
After parsing the text file, the C++ program obtains the
coefficient matrices and output them as text files.
Then we use another Matlab code to parse the text files of
the coefficient matrices and build the dual SDP problem.
Chao Li SDP, codes and a graph coloring problem

73. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Contribution and future work
Now we have obtained the dual SDP problem and can obtain
the optimal solution of it.
Chao Li SDP, codes and a graph coloring problem

74. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Contribution and future work
Now we have obtained the dual SDP problem and can obtain
the optimal solution of it.
Our program could easily build and solve the dual SDP
problems for small values of n.
Chao Li SDP, codes and a graph coloring problem

75. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Contribution and future work
Now we have obtained the dual SDP problem and can obtain
the optimal solution of it.
Our program could easily build and solve the dual SDP
problems for small values of n.
By comparing the optimal solution of the primal SDP and the
optimal solution of the dual SDP for different values of n, we
want to find the pattern behind them.
Chao Li SDP, codes and a graph coloring problem

76. The largest size of a binary code
LP and SDP bound
Coloring problem and Dual SDP
The graph coloring problem
The dual semidefinite programming (D-SDP) formulation
Contribution and future work
Now we have obtained the dual SDP problem and can obtain
the optimal solution of it.
Our program could easily build and solve the dual SDP
problems for small values of n.
By comparing the optimal solution of the primal SDP and the
optimal solution of the dual SDP for different values of n, we
want to find the pattern behind them.
Once the pattern is clear, we can try to prove it on paper for
arbitrarily large n.
Chao Li SDP, codes and a graph coloring problem