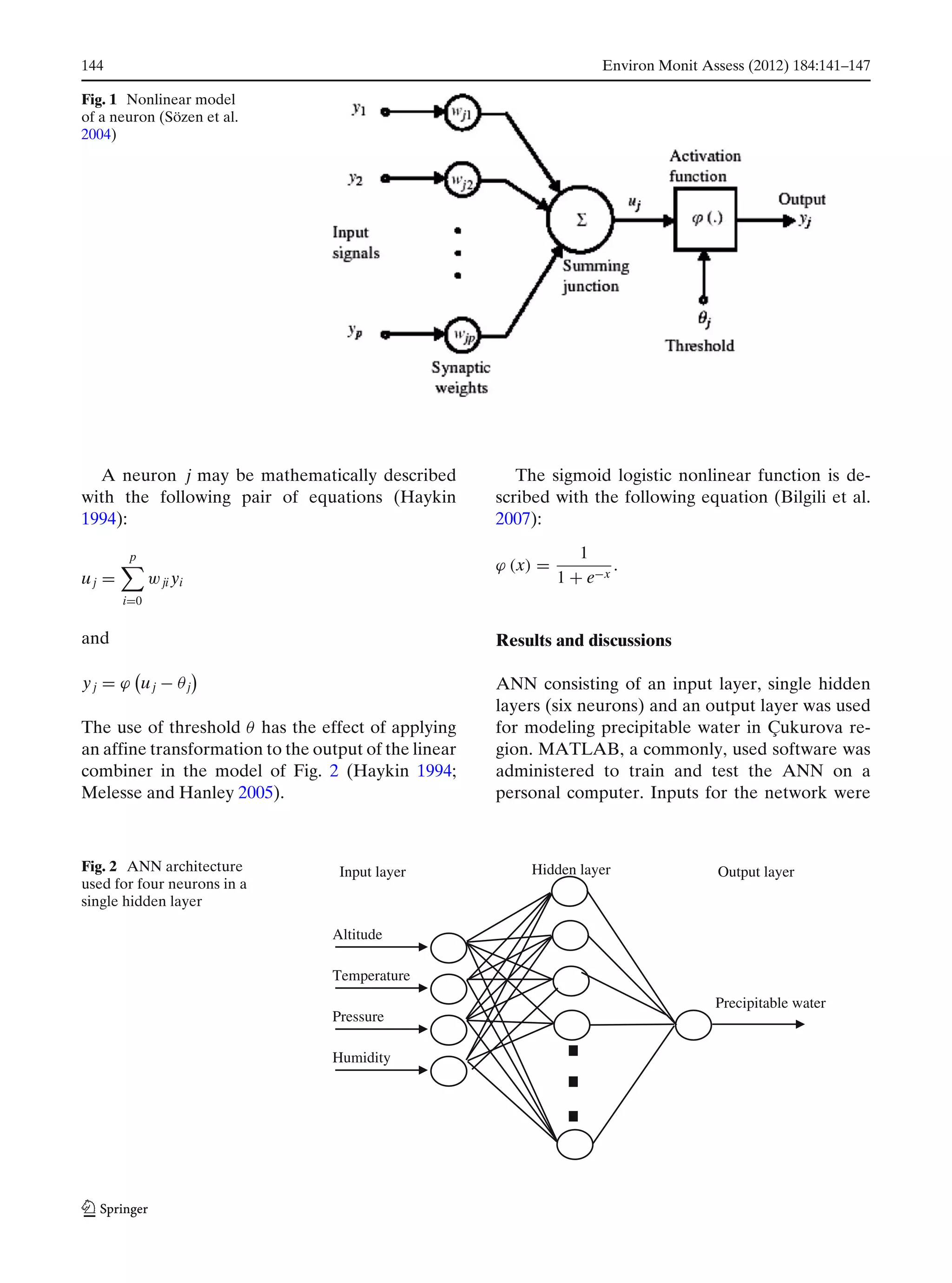
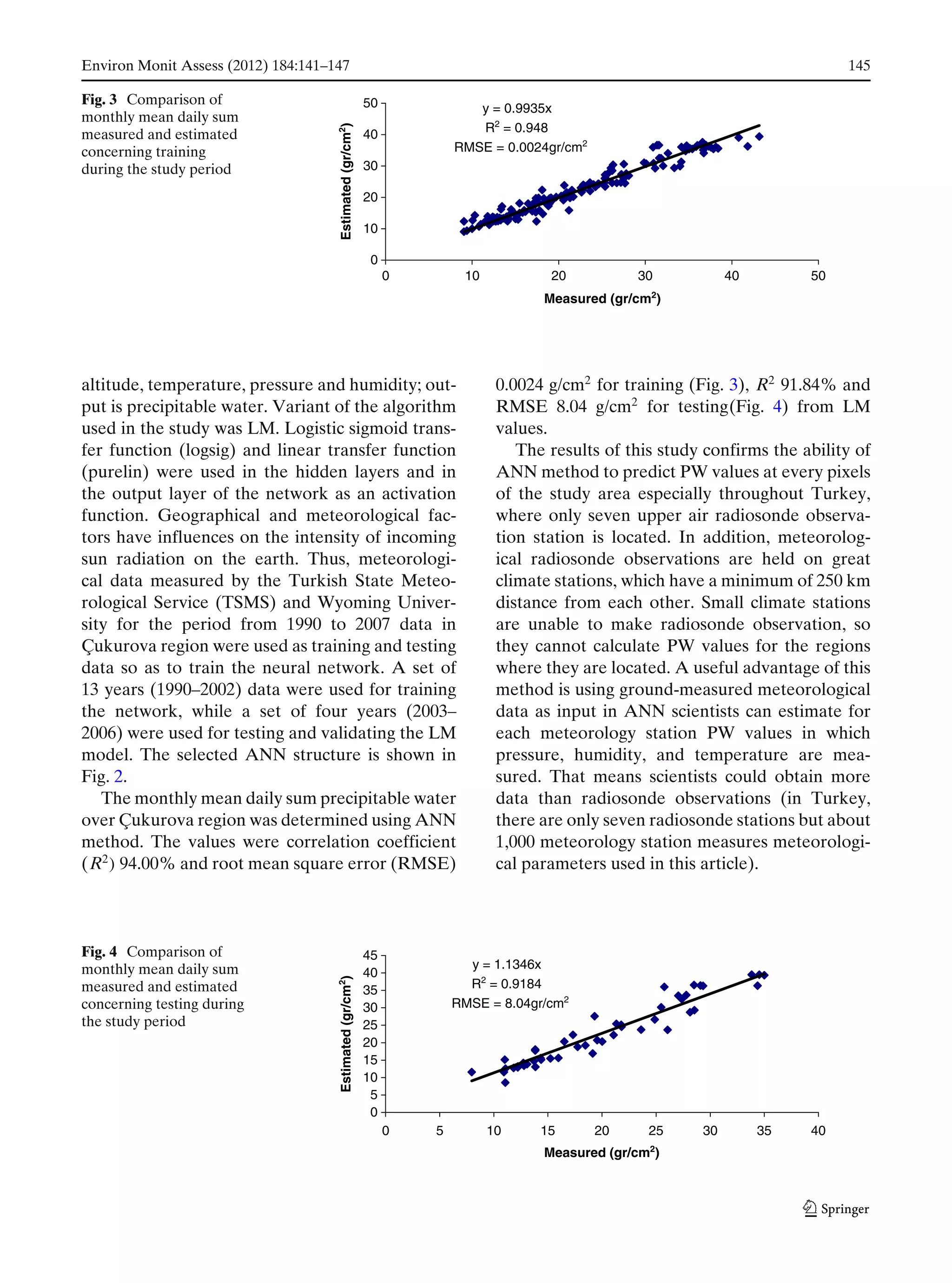
This document summarizes a study that used an artificial neural network to model and predict precipitable water values in the Çukurova region of Turkey. Meteorological and geographical data from 1990-2006 was used to train the neural network, with altitude, temperature, pressure, and humidity as inputs and precipitable water as the output. The neural network achieved a correlation of 94.0% between predicted and measured monthly mean precipitable water values for the training data and 91.8% for the testing data. The results demonstrated that an artificial neural network is effective at estimating precipitable water and can be used to predict values where observational data is limited.