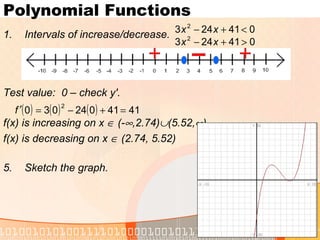
The document covers three topics: 1) Composite functions and finding f[g(0)] for a given function. 2) The derivative and its applications, including proving the derivative of a function and finding the equation of a tangent line. 3) Polynomial functions, including finding the y-intercept, x-intercepts, critical points and intervals of increase/decrease to sketch the graph of a polynomial function.

1. Unit 2 Review Composite Functions, Derivative, Polynomials

2. Composite Functions Find f[g(0)]. Given: Find an equation for:

3. The Derivative & Its Applications Remember that ‘the derivative’ of a function is another name for the slope, or rate of change of that function. It is also known as the ‘slope of the tangent line’ and ‘instantaneous rate of change.’ Ex: Prove, using the “definition of a derivative” that the derivative of is

4. The Derivative & Its Applications Ex: Find the equation of the tangent line of y=2x 3 -1 at x=2. Solution: First, we need to find the slope of this tangent line – the derivative of the function, when x=2. The next thing we need to do is find the y-coordinate of our original function when x=2. Then we come up with our equation of the line:

5. Polynomial Functions Consider the following function: Find the y-intercept. Find the x-intercept(s). Find the critical points and state whether each is a min. or max. Find the intervals of increase and decrease. Sketch the function.

6. Polynomial Functions Consider the following function: Find the y-intercept. Find the x-intercept(s) – use either long division or synthetic substitution. Find the critical points and state whether each is a min. or max – find the derivative; set it equal to zero; solve for x. Max or min? Plug into original function.

7. Polynomial Functions Intervals of increase/decrease. Test value: 0 – check y ′ . f(x) is increasing on x  (-  ,2.74)  (5.52,  ) f(x) is decreasing on x  (2.74, 5.52) 5. Sketch the graph.