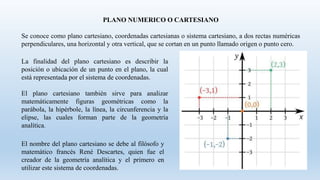
The document discusses the Cartesian plane and some of its key elements and uses in geometry. It defines the Cartesian plane as two perpendicular number lines that intersect at an origin point. It describes the axes, quadrants, coordinates, and how geometric shapes like circles and parabolas can be analyzed mathematically using the Cartesian plane. Circles are defined by a center point and radius, and their equations in the Cartesian plane are provided. Properties of parabolas and hyperbolas such as their foci, vertices, and equations are also outlined.

1. República Bolivariana De Venezuela
Ministerio Del Poder Popular Para La Educación Superior
Universidad Politécnica Territorial Del Estado Lara Andrés Eloy Blanco
(UPTAEB)
Barquisimeto Estado Lara
Integrantes
Keishmer Amaro C.I: 20.188.828
Sección: 0102
PNF Higiene Y Seguridad Laboral

2. PLANO NUMERICO O CARTESIANO
Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a dos rectas numéricas
perpendiculares, una horizontal y otra vertical, que se cortan en un punto llamado origen o punto cero.
La finalidad del plano cartesiano es describir la
posición o ubicación de un punto en el plano, la cual
está representada por el sistema de coordenadas.
El plano cartesiano también sirve para analizar
matemáticamente figuras geométricas como la
parábola, la hipérbole, la línea, la circunferencia y la
elipse, las cuales forman parte de la geometría
analítica.
El nombre del plano cartesiano se debe al filósofo y
matemático francés René Descartes, quien fue el
creador de la geometría analítica y el primero en
utilizar este sistema de coordenadas.

3. PARTES DEL PLANO CARTESIANO
Los elementos y características que conforman el plano
cartesiano son los ejes coordenados, el origen, los
cuadrantes y las coordenadas. A continuación, te
explicamos cada uno.
Se llaman ejes coordenados a las dos rectas
perpendiculares que se interconectan en un punto del
plano. Estas rectas reciben el nombre de abscisa y
ordenada.
Abscisa: el eje de las abscisas está dispuesto de manera
horizontal y se identifica con la letra “x”.
Ordenada: el eje de las ordenadas está orientado
verticalmente y se representa con la letra “y”.

4. Se llama origen al punto en el que se intersecan los ejes
“x” y “y”, punto al cual se le asigna el valor de cero (0).
Por ese motivo, también se conoce como punto cero
(punto 0). Cada eje representa una escala numérica que
será positiva o negativa de acuerdo a su dirección
respecto del origen.
Así, respecto del origen o punto 0, el segmento derecho
del eje “x” es positivo, mientras que el izquierdo es
negativo. Consecuentemente, el segmento ascendente del
eje “y” es positivo, mientras que el segmento descendente
es negativo.
ORIGEN O PUNTO 0

5. CUADRANTES DEL PLANO CARTESIANO
Se llama cuadrantes a las cuatro áreas que se forman por la
unión de las dos rectas perpendiculares. Los puntos del plano
se describen dentro de estos cuadrantes.
Los cuadrantes se enumeran tradicionalmente con números
romanos: I, II, III y IV.
Cuadrante I: la abscisa y la ordenada son positivas.
Cuadrante II: la abscisa es negativa y la ordenada positiva.
Cuadrante III: tanto la abscisa como la ordenada son
negativas.
Cuadrante IV: la abscisa es positiva y el ordenada negativa.

6. PUNTO MEDIO
Punto medio o punto equidistante: en matemática, es el punto que se encuentra a
la misma distancia de cualquiera de los extremos.
Definición
Antes debemos conocer que es un punto es una figura geométrica adimensional:
no tiene longitud, área, volumen, ni otro ángulo dimensional. No es un objeto
físico. Describe una posición en el espacio, determinada respecto de un sistema de
coordenadas preestablecido
Representación Grafica
En algunos textos de geometría se suele utilizar una pequeña cruz (+), círculo (o),
cuadrado o triángulo. A los puntos se les suele nombrar con una letra mayúscula:
A, B, C, etc. (a las rectas con letras minúsculas). La forma de representar un punto
mediante dos segmentos que se cortan (una pequeña “cruz” +) presupone que el
punto es la intersección. Cuando se representa con un pequeño círculo,
circunferencia, u otra figura geométrica, presupone que el punto es su centro.

7. DETERMINACIÓN GEOMÉTRICA
En el sistema de coordenadas cartesianas, se determina mediante las distancias ortogonales a los ejes
principales, que se indican con dos letras o números: (x, y) en el plano; y con tres en el espacio (x, y, z).
PUNTO MEDIO DE UN SEGMENTO
El punto medio del segmento AB, que llamaremos M, es un punto del segmento que dista lo mismo de A
que de B. Esto quiere decir que: Si es un segmento acotado, el punto medio es el que lo divide en dos
partes iguales. En ese caso, el punto medio es único y equidista de los extremos del segmento. Por
cumplir esta última condición, pertenece a la mediatriz del segmento.
El modo de obtener geométricamente el punto medio de un segmento, mediante regla y compás, consiste
en trazar dos arcos de circunferencia de igual radio, con centro en los extremos, y unir sus intersecciones
para obtener la recta mdiatriz. Esta «corta» al segmento en su punto medio.
Teorema Sea AB un segmento cuyos extremos tienen coordenadas A(xA; yA) ; B(xB; yB) entonces las
coordenadas del punto medio M(xM ; yM) de AB son:

8. ECUACIONES Y TRAZADO DE CIRCUNFERENCIAS
La circunferencia es el lugar geométrico de los puntos del plano
que equidistan de un punto fijo llamado centro (recordar que
estamos hablando del Plano Cartesiano y es respecto a éste que
trabajamos).
DETERMINACIÓN DE UNA CIRCUNFERENCIA
Una circunferencia queda determinada cuando conocemos:
a) Tres puntos de la misma, equidistantes del centro.
b) El centro y el radio.
c) El centro y un punto en ella.
d) El centro y una recta tangente a la circunferencia.

9. También podemos decir que la circunferencia es la línea
formada por todos los puntos que están a la misma
distancia de otro punto, llamado centro .
Esta propiedad es la clave para hallar la expresión
analítica de una circunferencia (la ecuación de la
circunferencia ).
Entonces, entrando en el terreno de la Geometría
Analítica , (dentro del Plano Cartesiano ) diremos que —
para cualquier punto, P (x, y) , de una circunferencia
cuyo centro es el punto C (a, b) y con radio r ─, la
ecuación ordinaria es (𝑥 ─ 𝑎)2 + (𝑦 ─ 𝑏)2= 𝑟2
¿Qué significa esto?
En el contexto de la Geometría Analítica
significa que una circunferencia graficada con un
centro definido (coordenadas) en el Plano
Cartesiano y con radio conocido la podemos
“ver” como gráfico y también la podemos
“transformar” o expresar como una ecuación
matemática.
Así podemos expresarla
Donde:
(d) Distancia CP = r
y
(𝑥 ─ 𝑎)2 + (𝑦 ─ 𝑏)2= 𝑟
Fórmula que elevada al cuadrado nos da
(𝑥 ─ 𝑎)2
+ (𝑦 ─ 𝑏)2
= 𝑟2
También se usa como
(𝑥 ─ ℎ)2
+(𝑦 ─ 𝑘)2
= 𝑟2
Asi la vemos

10. La ecuación anterior se conoce como ecuación ordinaria de la circunferencia. Para obtener la ecuación general
debemos desarrollar los binomios al cuadrado
DE LA ECUACIÓN ORDINARIAA LA ECUACIÓN GENERAL
𝑥2 ─ 2𝑎𝑥 + 𝑎2 + 𝑦2 ─ 2𝑏𝑦 + 𝑏2 ─ 𝑟2 = 0 ecuación que ordenada sería
𝑥2
+ 𝑦2
─ 2𝑎𝑥 ─ 2𝑏𝑦 + 𝑎2
+ 𝑏2
─ 𝑟2
= 0
Si para tener una ecuación más sintetizada hacemos las siguientes asignaciones:
─ 2𝑎 = 𝐷,
─ 2𝑏 = 𝐸,
𝑎2+ 𝑏2─ 𝑟2= f
la ecuación quedaría expresada de la forma:
𝑥2
+ 𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0 conocida como Ecuación General de la Circunferencia, la cual debe cumplir las
siguientes condiciones para serlo:
No existe término en xy

11. Los coeficientes de x 2 e y 2 son iguales.
Si 𝐷 = ─ 2𝑎 entonces a=
−𝐷
2
´Si 𝐸 = ─ 2𝑏 entonces a=
−𝐸
2
Si 𝐹 = 𝑎2
+ 𝑏2
─ 𝑟 2 entonces r = 𝑎2+ 𝑏2─ F
Además, otra condición necesaria para que una ecuación dada represente una circunferencia es que:
𝑎2
+ 𝑏2
─ F > 0 (𝑎2
+ 𝑏2
─ F debe ser mayor que cero)
Nota:
Para simplificar la ecuación general de la circunferencia ( 𝑥2+ 𝑦2─ 2ax ─ 2by + 𝑎2+ 𝑏2─ 𝑟2= 0) algunos textos o
docentes utilizan otra convención y hacen:
─ 2𝑎 = 𝐴,
─ 2𝑏 = 𝐵,
𝑎2+ 𝑏2─ 𝑟2 = 𝐶 para tener finalmente
𝑥2
+ 𝑦2
+ 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0 que es lo mismo que 𝑥2
+ 𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0

12. CONCEPTO DE HIPÉRBOLA Y SUS ELEMENTOS
Es el lugar geométrico de los puntos del plano cuya diferencia
de distancias a dos puntos fijos llamados focos es constante.
𝑃𝐹 − 𝑃𝐹′ = 2𝑎
Elementos de la hipérbola:
1. Focos: Son los puntos fijos F y F'.
2. Eje principal o real: Es la recta que pasa por los focos.
3. Eje secundario o imaginario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Vértices: Los puntos A y A' son los puntos de intersección de la
hipérbola con el eje focal.
Los puntos B y B' se obtienen como intersección del eje imaginario con la
circunferencia que tiene por centro uno de los vértices y de radio c.
6. Radios vectores: Son los segmentos que van desde un punto de la
hipérbola a los focos: PF y PF'.
7. Distancia focal: Es el segmento 𝐹𝐹′ de longitud 2c.
8. Eje mayor: Es el segmento 𝐴𝐴′ de longitud 2a.
9. Eje menor: Es el segmento 𝐵𝐵′ de longitud 2b.
10. Ejes de simetría: Son las rectas que contienen al eje real o al eje
imaginario.
11. Asíntotas: Son las rectas de ecuaciones:
12. Relación entre los semiejes:
y = −
𝑏
𝑎
𝑥 , 𝑦 =
𝑏
𝑎
𝑥
𝑐2
= 𝑎2
+ 𝑏2

13. ECUACIONES DE LA HIPÉRBOLA CON CENTRO
EN EL ORIGEN
La ecuación de la hipérbola se puede expresar cuando su
centro es O = (o1,o2) como:
Si la hipérbola tiene su centro en el origen, O = (0,0), su
ecuación es:
Además, los puntos de una hipérbola son los que cumplen
la ecuación general de la hipérbola:
siendo A, B, C, D y E escalares (números reales) y
necesariamente debe cumplir que los coeficientes de x2 y
y2 (A y C) son no nulos y tienen diferente signo.

14. CONCEPTO DE PARÁBOLA Y SUS ELEMENTOS
Una parábola queda definida por el conjunto de los
puntos del plano que equidistan de una recta fija y un
punto fijo:
Elementos de la parábola
• Foco: Es el punto fijo F.
• Directriz: Es la recta fija D.
• Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro p.
• Eje: La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el
eje de simetría de la parábola.
• Vértice: Es el punto medio entre el foco y la directriz. También se puede ver como el punto de
intersección del eje con la parábola.
• Radio vector: Es el segmento que une un punto cualquiera de la parábola con el foco.

15. ECUACIONES DE LA PARÁBOLA CON VÉRTICE EN
EL ORIGEN
Primeramente, estudiaremos la ecuación de la parábola para los
casos en que su vértice esté en el origen (coordenadas (0, 0) del
Plano Cartesiano), y según esto, tenemos cuatro posibilidades de
ecuación y cada una es característica.
Para iniciar nuestra explicación empezaremos con la parábola cuyo
vértice está en el origen, su eje focal o de simetría coincide con el
eje de las X (abscisas) y que está orientada (se abre) hacia la
derecha.
Por definición, sabemos que, en una parábola la distancia entre un
punto “P” (no confundir con el “parámetro p”), cualquiera de
coordenadas (x, y), y el foco “F” será igual a la distancia entre la
directriz (D) y dicho punto, como vemos en la figura:

16. De lo anterior resulta: 𝑃𝐷 = 𝑃𝐹 (trazo PD igual al trazo PF)
El trazo PD nace en el punto (x, y) y termina en el punto (–p, y) y
podemos usar la fórmula para calcular distancia entre dos puntos:
𝑃𝐷 = (𝑥 − (−𝑝))2+(𝑦 − 𝑦)2
𝑃𝐷 = (𝑥 − 𝑝)2
El trazo PF nace en el punto (x, y) y termina en el punto (p, 0), y
también podemos usar la fórmula para calcular la distancia entre
ellos:
𝑃𝐹 = (𝑥 − 𝑝)2+(𝑦 − 0)2
𝑃𝐹 = (𝑥 − 𝑝)2+𝑦2
Sustituyendo en la expresión de distancias 𝑃𝐷 = 𝑃𝐹 resulta:
(𝑥 − 𝑝)2 = (𝑥 − 𝑝)2+𝑦2
Elevando ambos miembros de la ecuación al cuadrado y
desarrollando, se tiene:
Simplificando términos semejantes y reordenando la
expresión, se obtiene:
𝑦2
= 4𝑝𝑥
que es ecuación de la parábola en su forma ordinaria o
canónica.
Esta ecuación tiene leves variaciones según sea la
orientación de la parábola (hacia donde se abre).
Veamos ahora las cuatro posibilidades:

17. PRIMERA POSIBILIDAD
La que ya vimos, cuando la parábola se abre hacia la
derecha (sentido positivo) en el eje de las abscisas “X”
Ecuacion de la parábola 𝑦2
= 4𝑝𝑥
Ecuacion de la directriz 𝑥 + 𝑝 = 0
SEGUNDA POSIBILIDAD
Cuando la parábola se abre hacia la izquierda (sentido
negativo) del eje de las abscisas “X”.
Ecuacion de la parábola 𝑦2
= −4𝑝𝑥
Ecuacion de la directriz 𝑥 − 𝑝 = 0

18. TERCERA POSIBILIDAD
Cuando la parábola se abre hacia arriba (sentido
positivo) en el eje de las ordenadas “Y” .
CUARTA POSIBILIDAD
Cuando la parábola se abre hacia abajo (sentido
negativo) en el eje de las ordenadas “Y”.
Ecuacion de la parábola 𝑦2
= 4𝑝𝑦
Ecuacion de la directriz y+𝑝 = 0
Ecuacion de la parábola 𝑦2
= −4𝑝𝑦
Ecuacion de la directriz y−𝑝 = 0

19. CONCEPTO Y ELEMENTOS DE LA ELIPSE
Es el lugar geométrico de los puntos del plano cuya suma de
distancias a dos puntos fijos llamados focos es constante.
𝑃𝐹 + 𝑃𝐹′ = 2𝑎
Elementos de la elipse:
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos:
PF y PF'.
6. Distancia focal: Es el segmento segmento de longitud 2c, c es el valor de la
semidistancia focal.
7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8. Eje mayor: Es el segmento segmento de longitud 2a, a es el valor del semieje
mayor.
9. Eje menor: Es el segmento segmento de longitud 2b, b es el valor del semieje
menor.
10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de
intersección de los ejes de simetría.
𝑎2
= 𝑐2
+𝑏2

20. ECUACIÓN DE LA ELIPSE
Ecuación de eje mayor horizontal centrada en un punto cualquiera
P(𝑥0, 𝑦0)
La ecuación de una elipse cuyo eje mayor es horizontal viene dada por:
Donde:
𝑥0, 𝑦0: Coordenadas x e y del centro de la elipse
a : Semieje de abcisas
b : Semieje de ordenadas. En nuestro caso debe cumplirse que b ⩽ a.

21. Ecuación de eje mayor vertical centrada en un punto cualquiera
P(𝑥0, 𝑦0)
La ecuación de una elipse cuyo eje mayor es vertical viene dada por:
Donde:
𝑥0, 𝑦0: Coordenadas x e y del centro de la elipse
a : Semieje de abcisas
b : Semieje de ordenadas. En nuestro caso debe cumplirse que b > a.
ECUACIÓN DE LA ELIPSE

22. Problemas resueltos de álgebra lineal
Autor: Francisco José Marcellán
Español, Jorge Arvesu Carballo,
Jorge Sánchez Ruiz
Editorial: Paraninfo
Encliclopedia Estudiantil Tutor
Autores: Carlos Gispert
Jose Gay
Jose A. Vidal
Editorial: Oceano
BLIBLIOGRAFIA
https://www.cecyt3.ipn.mx/ibiblioteca/mundodelasmatematicas/