The document describes a construction of a verifiable random function (VRF) that improves upon previous work. It directly constructs a VRF without using Goldreich-Levin hardcore bits, allows inputs of arbitrary size without encoding, and has proofs and keys consisting of a constant number of group elements. The security of the VRF relies on complexity assumptions in bilinear groups and it finds applications like non-interactive lotteries and compact e-cash schemes.

1. A Verifiable Random Function With Short Proofs and Keys Yevgeniy Dodis Aleksandr Yampolskiy (NYU) (Yale)

2. Outline Motivation Previous work Our constructions Extensions Conclusion

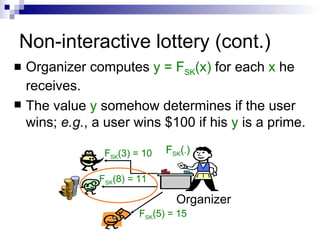
3. Non-interactive lottery [MR02] Lottery organizer has a secret function F SK ( . ) Each participant chooses a lottery ticket x and sends it to the organizer Organizer F SK ( . ) x 1 = 3 x 2 = 8 x 3 = 5

4. Non-interactive lottery (cont.) Organizer computes y = F SK (x) for each x he receives. The value y somehow determines if the user wins; e.g. , a user wins $100 if his y is a prime. F SK ( . ) F SK (3) = 10 F SK (8) = 11 F SK (5) = 15 Organizer

5. Non-interactive lottery (cont.) This scheme almost works except… Problem 1: We must ensure that users cannot bias the lottery; i.e. , F SK (x) should look random. Problem 2: What stops the organizer from lying about the true F SK (x) value?

6. Verifiable Random Function What we need is a verifiable random function (VRF) [MRV99] On input x , owner of secret key SK can compute y = F SK (x) together with proof  SK (x). The output y looks random. Yet the proof  SK (x) convinces every verifier that y is correct with respect to public key.

7. Previous work VRFs have many useful applications (non-interactive lottery, rZK, e-cash, verifiable transaction escrow). However, they are not very well studied [MRV99, Lys02, Dod03] Prior constructions are not very efficient. 

8. Previous work (cont.) Use an inefficient Goldreich-Levin hardcore bit [MRV99, Lys02] Construct a verifiable unpredictable function (VUF) , whose output is hard to guess but not necessarily random. Use Goldreich-Levin bit to convert a VUF into a VRF.

9. Previous work (cont.) Use an inefficient Goldreich-Levin hardcore bit [MRV99, Lys02] Inputs need to be encoded in a special way [MRV99, Lys02, Dod03] [MRV99]: inputs are first mapped into primes [Lys02, Dod03]: inputs are mapped to codewords of an error-correcting code

10. Previous work (cont.) Use an inefficient Goldreich-Levin hardcore bit [MRV99, Lys02] Inputs need to be encoded in a special way [MRV99, Lys02, Dod03] Proofs and keys are long [Lys02, Dod03] [Lys02, Dod03]: keys (PK, SK) and proofs  SK (x) consist of O(|x|) group elements.

11. Our work We construct a VRF directly without using the Goldreich-Levin hardcore bit. Inputs need not be encoded in any special way. Our proofs and keys consist of O(1) group elements regardless of the input size. 

12. Bilinear groups G, G 1 : cyclic groups of prime order p An admissible bilinear map e: G £ G  G 1 bilinear: 8 u,v 2 G and 8 x,y 2 Z e(u x , v y ) = e(u, v) xy non-degenerate: e(g, g) ≠ 1 efficiently computable Can construct such maps from Weil pairing on elliptic curves [JN01]

13. Compexity assumptions We make two assumptions: q-DHI assumption : given (g, g x , …, g (x q ) ), it is hard to compute g 1/x [MSK02] q-DBDHI assumption : given (g, g x , …, g (x q ) ), it is hard to distinguish e(g,g) 1/x from random [BB04] Hard = adversary running for s(k) steps is unlikely to succeed. Here, s(k)=  (poly(k)) and s(k)=o(2 k ) .

14. Our VUF Starting point: Boneh-Boyen signature [BB04] Algorithm Gen(1 k ): Pick s 2 R Z p * .The secret key is SK = s . The public key is PK = g s . Algorithm Sign SK (x): To sign x , compute y = g 1/(x+SK) . Algorithm Ver PK (x, y): Check that e(y, g x ¢ PK) = e(g, g). {

15. Our VUF (cont.) Boneh-Boyen signature is secure against non-adaptive queries (and uses stronger q-SDH assumption) A VUF must be secure against adaptive queries adversary challenger (PK, SK) PK x 1 x 2 x k … y 1 y 2 y k … adversary challenger (PK, SK) PK x i y i

16. Our VUF (cont.) Trick: Restrict input size to be small, a(k) =  (log s(k)) ( s(k) is the security) Then, we can enumerate all possible queries in less than s(k) time and give answers adaptively.

17. Our VUF (cont.) Boneh-Boyen signature becomes a verifiable unpredictable function (VUF) for small inputs We can use Goldreich-Levin bit to convert a VUF into a VRF, but this is very inefficient

18. Our VRF Instead, we construct a VRF directly: Algorithm Gen(1 k ): Pick s 2 R Z p * .The secret key is SK = s . The public key is PK = g s . Algorithm Prove SK (x) : Compute (F SK (x),  SK (x)) = (e(g,g) 1/(x+SK) , g 1/(x+SK) ) Algorithm Ver PK (x,y,  ): Verify that e(g x ¢ PK,  ) = e(g,g) and y = e(g,  ). { our VUF

19. Proof of security : big picture Our VRF is provably secure for inputs of small size, a(k) = O (log s(k)) . If there is an algorithm A that breaks the VRF in time t , with probability  , then there is an algorithm B that solves the q-DBDHI problem ( q=2 a(k) ) in time ¼ t/(2 a(k) ¢ poly(k)) , with probability  /2 a(k) .

20. Proof of security : big picture B A Construct reduction algorithm B that answers A ’s queries and then uses A ’s answers to solve the q-DBDHI instance (g, g  , …, g (  q ) ,  ) Is  = e(g,g) 1/   Challenger VRF game …

21. Proof of security : sketch Idea: Want to know if  = e(g,g) 1/  ? Guess that A can distinguish VRF value of x * from random. Prepare keys (PK, SK) such that SK =  - x* is unknown, yet we can correctly compute h F SK (x),  SK (x) i for any x ≠ x * . We construct  * from  such that F SK (x*) =  * if  = e(g,g) 1/  F SK (x*) = $ if  = $

22. Proof of security : sketch B A (g, g  , …, g (  q ) ,  ) Challenger We can then use A to distinguish the original  from random. (PK, SK) PK    is not e(g,g) 1/  not random x *

23. Extending the input size Our VRF is secure for small inputs, a(k)=  (log s(k)) . Inputs of arbitrary size are no problem! Just use a collision-resistant hash function H( ¢ ): {0,1} *  {0,1} a(k) . Trivially, composition F SK (H( ¢ )) is secure.

24. Extending the input size (cont.) Alternatively, we can truncate basic VRF’s output to a(k)-1 bits and use [MRV99] tree construction: 0 a-1 y=F(0 a ) z=F(0 a-1 1) F(z0) F(z1) F(y0) F(y1) F(F(y1)1) F(F(y1)0) 0 1 0 1 0 1 0 1 VRF value for x = 011

25. Efficiency Suppose a(k) = 160 bits, the length of SHA-1 digests. We then have: Group size Length of proofs and keys 160 bits, elliptic group >3,200 bytes [Dod03], [Lys02] 14,383 bits, Z n * 280,000 bytes [MRV99] 1,000 bits, elliptic group 125 bytes Our VRF

26. Compact e-cash [CHL05] Offline anonymous e-cash scheme. A user can withdraw a wallet of 2 l coins from the bank and later spend them. In best known schemes, withdraw and spend operations take O(2 l ¢ k) time ( k is the security parameter). In EuroCrypt ’05, [CHL05] used our VRF to construct a scheme whose withdraw/spend operations take O(l+k) time.

27. Conclusion We give a simple and efficient VRF construction. It can be instantiated with elliptic groups of reasonable size. Proofs and keys consist of only one group element regardless of the input size. Can obtain a VRF value on committed values. Our VRF can be made distributed and proactive.