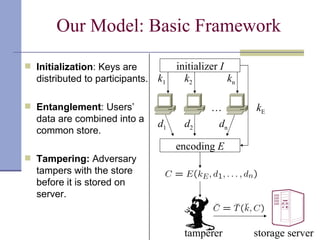
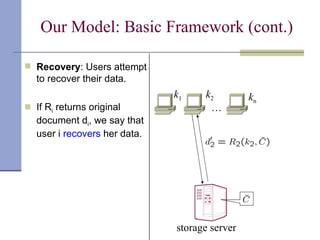
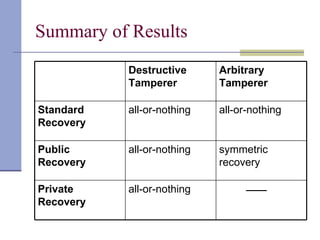
The document proposes a model for entangling users' data to protect remotely stored data from server corruption. It defines six adversary classes based on the recovery algorithm (standard, public, private) and corruption method (destructive, arbitrary). It shows all-or-nothing integrity is possible in the standard-recovery model by using message authentication codes, but not in public/private models as adversaries can modify the recovery algorithm. Symmetric recovery is possible in the public model if encoding is symmetric. All-or-nothing integrity is achievable against destructive adversaries by interpolating a polynomial of the data.

1. Towards a Theory of Data Entanglement James Aspnes, Joan Feigenbaum, Aleksandr Yampolskiy, and Sheng Zhong (Yale University)

2. Outline Motivation Dagster and Tangler Our model Notions of entanglement Possibility and impossibility results Conclusion

3. Goal: Protect Remotely Stored Data from the Server Question: Suppose you store your data on a remote server. How do you ensure that it is not corrupted by the server? Answer: Have your data entangled with some VIPs’ data so that corruption of your data  corruption of theirs.

4. Previous Work: Dagster [SW01] New Document  Encrypt c randomly chosen blocks Pool of blocks Analysis: Deleting a typical document  loss of O( c ) documents

5. Previous Work: Tangler [WM01] (0, New Document) 2 randomly chosen blocks Pool of n blocks Analysis: Deleting a typical document  loss of O ( (log n ) / n ) documents Interpolate degree-2 poly F() (x 1 ,F(x 1 )) (x 2 ,F(x 2 ))

6. Our Model: Basic Framework Initialization : Keys are distributed to participants. Entanglement : Users’ data are combined into a common store. Tampering: Adversary tampers with the store before it is stored on server. encoding E … d 1 d 2 d n initializer I k 1 k 2 k n k E tamperer storage server

7. Our Model: Basic Framework (cont.) Recovery : Users attempt to recover their data. If R i returns original document d i , we say that user i recovers her data. … k 1 k 2 k n storage server

8. Our Model : Classification Question: What can the adversary do to the data store? Answer: He can… tamper with the store tamper with the store and distribute a new recovery algorithm to all users ( upgrade attack ) encrypt the store and distribute his recovery algorithm only to a few select buddies ( superencryption attack )

9. Our Model : Classification (cont.) Classification based on recovery algorithm: Standard recovery algorithm Public recovery algorithm Private recovery algorithm … … …

10. Our Model : Classification (cont.) Classification based on corrupting algorithm: Destructive adversary that reduces entropy of the data store. Arbitrary adversary. Altogether, we have 6 (= 3 £ 2) adversary classes .

11. Our Definitions Fix encoding scheme , adversary , and recovery algorithms R i . Recovery vector summarizes which documents are recovered

12. Our Definitions (cont.) Data dependency: d i depends on d j if, with high probability, d i is recovered  d j is recovered: d 1 d 2 d 3 d 4 d 1 depends on d 2

13. Our Definitions (cont.) All-or-nothing integrity (AONI): every document depends on every other document: d 1 d 2 d 3 d 4

14. Our Definitions (cont.) Symmetric recovery: adversary cannot bias which documents are recovered

15. Possibility of AONI in Standard-Recovery Model All users use the standard recovery algorithm: for all i, R i =R. When combining data, mark data store using an unforgeable Message Authentication Code (MAC). Standard recovery algorithm checks MAC: If MAC is valid, recover data. If MAC is invalid, refuse to recover data.

16. Impossibility of AONI in Public and Private-Recovery Models If any users use the adversary’s recovery algorithm (for some i, R i ≠ R), AONI cannot be achieved Adversary modifies the data store so that old recovery algorithm does not work. And distributes a new recovery algorithm that flips a coin to decide whether to recover data or not.

17. Impossibility of AONI in Public and Private-Recovery Models (cont.) With high probability, not all coin flips will have same result. With high probability, some data are recovered while others are not. …

18. Possibility of Symmetric Recovery in Public-Recovery Model All users use adversary’s recovery algorithm: for all i, We can prevent targeted destruction of documents. Documents d 1 ,…, d n must appear i.i.d Encoding scheme must be symmetric:

19. Possibility of AONI for Destructive Adversaries We can achieve AONI in all recovery models if tamperer destroys entropy. When combining data, interpolate a polynomial using points (k i , d i ). Store = polynomial. AONI is achieved if sufficient entropy is removed. Many stores are mapped to single corrupted store.  With high probability, cannot recover every data item.

20. Summary of Results  all-or-nothing Private Recovery symmetric recovery all-or-nothing Public Recovery all-or-nothing all-or-nothing Standard Recovery Arbitrary Tamperer Destructive Tamperer

21. Future Work We have considered a single-round model. Allowing multiple rounds of storage/retrieval will be more realistic. What if data entanglement is combined with other techniques like replication? Will that help to defend data against untrusted server(s)?