physics_problem_workbooks.pdf.pdf

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem A 1
NAME ______________________________________ DATE _______________ CLASS ____________________
The Science of Physics
Problem A
METRIC PREFIXES
P R O B L E M
In Hindu chronology, the longest time measure is a para. One para equals
311 040 000 000 000 years. Calculate this value in megahours and in
nanoseconds.Write your answers in scientific notation.
S O L U T I O N
Given: 1 para = 311 040 000 000 000 years
Unknown: 1 para = ? Mh
1 para = ? ns
Express the time in years in terms of scientific notation. Then build conversion
factors from the relationships given in Table 3.
1 para = 3.1104 × 1014
years

365
1
.2
y
5
ea
d
r
ays
 × 
1
24
da
h
y
 × 
1 ×
1 M
10
h
6 h


365
1
.2
y
5
ea
d
r
ays
 × 
1
24
da
h
y
 × 
36
1
0
h
0 s
 × 
1 ×
1
1
n
0
s
−9s

Convert from years to megahours by multiplying the time by the first conversion
expression.
1 para = 3.1104 × 1014
years × 
365
1
.2
y
5
ea
d
r
ays
 × 
1
24
da
h
y
 × 
1 ×
1 M
10
h
6 h

=
Convert from years to nanoseconds by multiplying the time by the second con-
version expression.
1 para = 3.1104 × 1014
years × 
365
1
.2
y
5
ea
d
r
ays
 × 
1
24
da
h
y
 × 
36
1
0
h
0 s
 × 
1 ×
1
1
n
0
s
−9 s

= 9.8157 × 1030
ns
2.7266 × 1012
Mh
ADDITIONAL PRACTICE
1. One light-year is the distance light travels in one year. This distance is
equal to 9.461 × 1015
m. After the sun, the star nearest to Earth is Alpha
Centauri, which is about 4.35 light-years from Earth. Express this dis-
tance in
a. megameters.
b. picometers.

Holt Physics Problem Workbook
2
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. It is estimated that the sun will exhaust all of its energy in about ten
billion years. By that time, it will have radiated about 1.2 × 1044
J (joules)
of energy. Express this amount of energy in
a. kilojoules.
b. nanojoules.
3. The smallest living organism discovered so far is called a mycoplasm. Its
mass is estimated as 1.0 × 10–16
g. Express this mass in
a. petagrams.
b. femtograms.
c. attograms.
4. The “extreme” prefixes that are officially recognized are yocto, which in-
dicates a fraction equal to 10–24
, and yotta, which indicates a factor equal
to 1024
. The maximum distance from Earth to the sun is 152 100 000 km.
Using scientific notation, express this distance in
a. yoctometers (ym).
b. yottameters (Ym).
5. In 1993, the total production of nuclear energy in the world was
2.1 × 1015
watt-hours, where a watt is equal to one joule (J) per second.
Express this number in
a. joules.
b. gigajoules.
6. In Einstein’s special theory of relativity, mass and energy are equivalent.
An expression of this equivalence can be made in terms of electron volts
(units of energy) and kilograms, with one electron volt (eV) being equal
to 1.78 × 10–36
kg. Using this ratio, express the mass of the heaviest
mammal on earth, the blue whale, which has an average mass of
1.90 × 105
kg, in
a. mega electron volts.
b. tera electron volts.
7. The most massive star yet discovered in our galaxy is one of the stars
in the Carina Nebula, which can be seen from Earth’s Southern
Hemisphere and from the tropical latitudes of the Northern Hemisphere.
The star, designated as Eta Carinae, is believed to be 200 times as massive
as the sun, which has a mass of nearly 2 × 1030
kg. Find the mass of Eta
Carinae in
a. milligrams.
b. exagrams.
8. The Pacific Ocean has a surface area of about 166 241 700 km2
and an
average depth of 3940 m. Estimate the volume of the Pacific Ocean in
a. cubic centimeters.
b. cubic millimeters.

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem A 3
NAME ______________________________________ DATE _______________ CLASS ____________________
Motion in One Dimension
Problem A
AVERAGE VELOCITY AND DISPLACEMENT
P R O B L E M
The fastest fish, the sailfish, can swim 1.2 × 102
km/h. Suppose you have
a friend who lives on an island 16 km away from the shore. If you send
a message using a sailfish as a messenger, how long will it take for the
message to reach your friend?
S O L U T I O N
Given: vavg = 1.2 × 102
km/h
∆x = 16 km
Unknown: ∆t = ?
Use the definition of average speed to find ∆t.
vavg = 
∆
∆
x
t

Rearrange the equation to calculate ∆t.
∆t = 
v
∆
av
x
g

∆t = =
= 8.0 min

2.0
1
k
6
m
k
/
m
min

16 km

1.2 × 102

k
h
m


60
1
m
h
in


ADDITIONAL PRACTICE
1. The Sears Tower in Chicago is 443 m tall. Joe wants to set the world’s
stair climbing record and runs all the way to the roof of the tower. If Joe’s
average upward speed is 0.60 m/s, how long will it take Joe to climb from
street level to the roof of the Sears Tower?
2. An ostrich can run at speeds of up to 72 km/h. How long will it take an
ostrich to run 1.5 km at this top speed?
3. A cheetah is known to be the fastest mammal on Earth, at least for short
runs. Cheetahs have been observed running a distance of 5.50 × 102
m
with an average speed of 1.00 × 102
km/h.
a. How long would it take a cheetah to cover this distance at this speed?
b. Suppose the average speed of the cheetah were just 85.0 km/h.
What distance would the cheetah cover during the same time inter-
val calculated in (a)?

4
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. A pronghorn antelope has been observed to run with a top speed of
97 km/h. Suppose an antelope runs 1.5 km with an average speed of
85 km/h, and then runs 0.80 km with an average speed of 67 km/h.
a. How long will it take the antelope to run the entire 2.3 km?
b. What is the antelope’s average speed during this time?
5. Jupiter, the largest planet in the solar system, has an equatorial radius of
about 7.1 × 104
km (more than 10 times that of Earth). Its period of ro-
tation, however, is only 9 h, 50 min. That means that every point on
Jupiter’s equator “goes around the planet” in that interval of time. Calcu-
late the average speed (in m/s) of an equatorial point during one period
of Jupiter’s rotation. Is the average velocity different from the average
speed in this case?
6. The peregrine falcon is the fastest of flying birds (and, as a matter of fact,
is the fastest living creature). A falcon can fly 1.73 km downward in 25 s.
What is the average velocity of a peregrine falcon?
7. The black mamba is one of the world’s most poisonous snakes, and with
a maximum speed of 18.0 km/h, it is also the fastest. Suppose a mamba
waiting in a hide-out sees prey and begins slithering toward it with a
velocity of +18.0 km/h. After 2.50 s, the mamba realizes that its prey can
move faster than it can. The snake then turns around and slowly returns
to its hide-out in 12.0 s. Calculate
a. the mamba’s average velocity during its return to the hideout.
b. the mamba’s average velocity for the complete trip.
c. the mamba’s average speed for the complete trip.
8. In the Netherlands, there is an annual ice-skating race called the “Tour of
the Eleven Towns.” The total distance of the course is 2.00 × 102
km, and
the record time for covering it is 5 h, 40 min, 37 s.
a. Calculate the average speed of the record race.
b. If the first half of the distance is covered by a skater moving with
a speed of 1.05v, where v is the average speed found in (a), how
long will it take to skate the first half? Express your answer in hours
and minutes.

Problem B 5
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem B
AVERAGE ACCELERATION
P R O B L E M
In 1977 off the coast of Australia, the fastest speed by a vessel on the water
was achieved. If this vessel were to undergo an average acceleration of
1.80 m/s2
, it would go from rest to its top speed in 85.6 s.What was the
speed of the vessel?
S O L U T I O N
Given: aavg = 1.80 m/s2
∆t = 85.6 s
vi = 0 m/s
Unknown: vf = ?
Use the definition of average acceleration to find vf.
aavg = 
∆
∆
v
t
 = 
vf
∆
–
t
vi

Rearrange the equation to calculate vf.
vf = aavg ∆t + vi
vf =
1.80 
m
s2

85.6 s
+ 0 
m
s

= 154 
m
s

=
154 
m
s


3.60
1
×
h
103
s


1
1
0
k
3
m
m


= 554 
k
h
m

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. If the vessel in the sample problem accelerates for 1.00 min, what will
its speed be after that minute? Calculate the answer in both meters per
second and kilometers per hour.
2. In 1935, a French destroyer, La Terrible, attained one of the fastest
speeds for any standard warship. Suppose it took 2.0 min at a constant
acceleration of 0.19 m/s2
for the ship to reach its top speed after start-
ing from rest. Calculate the ship’s final speed.
3. In 1934, the wind speed on Mt. Washington in New Hampshire
reached a record high. Suppose a very sturdy glider is launched in this
wind, so that in 45.0 s the glider reaches the speed of the wind. If the

6
NAME ______________________________________ DATE _______________ CLASS ____________________
glider undergoes a constant acceleration of 2.29 m/s2
, what is the
wind’s speed? Assume that the glider is initially at rest.
4. In 1992, Maurizio Damilano, of Italy, walked 29 752 m in 2.00 h.
a. Calculate Damilano’s average speed in m/s.
b. Suppose Damilano slows down to 3.00 m/s at the midpoint in his
journey, but then picks up the pace and accelerates to the speed
calculated in (a). It takes Damilano 30.0 s to accelerate. Find the
magnitude of the average acceleration during this time interval.
5. South African frogs are capable of jumping as far as 10.0 m in one hop.
Suppose one of these frogs makes exactly 15 of these jumps in a time
interval of 60.0 s.
a. What is the frog’s average velocity?
b. If the frog lands with a velocity equal to its average velocity and
comes to a full stop 0.25 s later, what is the frog’s average
acceleration?
6. In 1991 at Smith College, in Massachusetts, Ferdie Adoboe ran
1.00 × 102
m backward in 13.6 s. Suppose it takes Adoboe 2.00 s to
achieve a velocity equal to her average velocity during the run. Find
her average acceleration during the first 2.00 s.
7. In the 1992 Summer Olympics, the German four-man kayak team cov-
ered 1 km in just under 3 minutes. Suppose that between the starting
point and the 150 m mark the kayak steadily increases its speed from
0.0 m/s to 6.0 m/s, so that its average speed is 3.0 m/s.
a. How long does it take to cover the 150 m?
b. What is the magnitude of the average acceleration during that
part of the course?
8. The highest speed ever achieved on a bicycle was reached by John
Howard of the United States. The bicycle, which was accelerated by
being towed by a vehicle, reached a velocity of +245 km/h. Suppose
Howard wants to slow down, and applies the brakes on his now freely
moving bicycle. If the average acceleration of the bicycle during brak-
ing is –3.0 m/s2
, how long will it take for the bicycle’s velocity to de-
crease by 20.0 percent?
9. In 1993, bicyclist Rebecca Twigg of the United States traveled 3.00 km
in 217.347 s. Suppose Twigg travels the entire distance at her average
speed and that she then accelerates at –1.72 m/s2
to come to a complete
stop after crossing the finish line. How long does it take Twigg to come
to a stop?
10. During the Winter Olympic games at Lillehammer, Norway, in 1994,
Dan Jansen of the United States skated 5.00 × 102
m in 35.76 s. Sup-
pose it takes Jansen 4.00 s to increase his velocity from zero to his
maximum velocity, which is 10.0 percent greater than his average ve-
locity during the whole run. Calculate Jansen’s average acceleration
during the first 4.00 s.
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem C 7
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem C
DISPLACEMENT WITH CONSTANT ACCELERATION
P R O B L E M
In England, two men built a tiny motorcycle with a wheel base (the dis-
tance between the centers of the two wheels) of just 108 mm and a wheel’s
measuring 19 mm in diameter. The motorcycle was ridden over a distance
of 1.00 m. Suppose the motorcycle has constant acceleration as it travels
this distance, so that its final speed is 0.800 m/s. How long does it take the
motorcycle to travel the distance of 1.00 m? Assume the motorcycle is ini-
tially at rest.
S O L U T I O N
Given: vf = 0.800 m/s
vi = 0 m/s
∆x = 1.00 m
Unknown: ∆t = ?
Use the equation for displacement with constant acceleration.
∆x = 
1
2
(vi + vf )∆t
Rearrange the equation to calculate ∆t.
∆t = 
v
2
f
∆
+
x
vi

∆t = = 
0
2
.
.
8
0
0
0
0
 s
= 2.50 s
(2)(1.00 m)

0.800 
m
s
 + 0 
m
s

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1993, Ileana Salvador of Italy walked 3.0 km in under 12.0 min. Sup-
pose that during 115 m of her walk Salvador is observed to steadily in-
crease her speed from 4.20 m/s to 5.00 m/s. How long does this increase
in speed take?
2. In a scientific test conducted in Arizona, a special cannon called HARP
(High Altitude Research Project) shot a projectile straight up to an alti-
tude of 180.0 km. If the projectile’s initial speed was 3.00 km/s, how long
did it take the projectile to reach its maximum height?
3. The fastest speeds traveled on land have been achieved by rocket-
powered cars. The current speed record for one of these vehicles is
about 1090 km/h, which is only 160 km/h less than the speed of
sound in air. Suppose a car that is capable of reaching a speed of

8
NAME ______________________________________ DATE _______________ CLASS ____________________
1.09 × 103
km/h is tested on a flat, hard surface that is 25.0 km long. The
car starts at rest and just reaches a speed of 1.09 × 103
km/h when it
passes the 20.0 km mark.
a. If the car’s acceleration is constant, how long does it take to make
the 20.0 km drive?
b. How long will it take the car to decelerate if it goes from its maxi-
mum speed to rest during the remaining 5.00 km stretch?
4. In 1990, Dave Campos of the United States rode a special motorcycle
called the Easyrider at an average speed of 518 km/h. Suppose that at
some point Campos steadily decreases his speed from 100.0 percent to
60.0 percent of his average speed during an interval of 2.00 min. What is
the distance traveled during that time interval?
5. A German stuntman named Martin Blume performed a stunt called “the
wall of death.” To perform it, Blume rode his motorcycle for seven
straight hours on the wall of a large vertical cylinder. His average speed
was 45.0 km/h. Suppose that in a time interval of 30.0 s Blume increases
his speed steadily from 30.0 km/h to 42.0 km/h while circling inside the
cylindrical wall. How far does Blume travel in that time interval?
6. An automobile that set the world record for acceleration increased speed
from rest to 96 km/h in 3.07 s. How far had the car traveled by the time
the final speed was achieved?
7. In a car accident involving a sports car, skid marks as long as 290.0 m
were left by the car as it decelerated to a complete stop. The police report
cited the speed of the car before braking as being “in excess of 100 mph”
(161 km/h). Suppose that it took 10.0 seconds for the car to stop. Esti-
mate the speed of the car before the brakes were applied. (REMINDER:
Answer should read,“speed in excess of . . .”)
8. Col. Joe Kittinger of the United States Air Force crossed the Atlantic
Ocean in nearly 86 hours. The distance he traveled was 5.7 × 103
km.
Suppose Col. Kittinger is moving with a constant acceleration during
most of his flight and that his final speed is 10.0 percent greater than his
initial speed. Find the initial speed based on this data.
9. The polar bear is an excellent swimmer, and it spends a large part of its
time in the water. Suppose a polar bear wants to swim from an ice floe to
a particular point on shore where it knows that seals gather. The bear
dives into the water and begins swimming with a speed of 2.60 m/s. By
the time the bear arrives at the shore, its speed has decreased to 2.20 m/s.
If the polar bear’s swim takes exactly 9.00 min and it has a constant de-
celeration, what is the distance traveled by the polar bear?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 9
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem D
VELOCITY AND DISPLACEMENT WITH CONSTANT ACCELERATION
P R O B L E M
Some cockroaches can run as fast as 1.5 m/s. Suppose that two cock-
roaches are separated by a distance of 60.0 cm and that they begin to run
toward each other at the same moment. Both insects have constant accel-
eration until they meet. The first cockroach has an acceleration of
0.20 m/s2
in one direction, and the second one has an acceleration of
0.12 m/s2
in the opposite direction. How much time passes before the
two insects bump into each other?
S O L U T I O N
Given: a1 = 0.20 m/s2
(first cockroach’s acceleration)
vi,1 = 0 m/s (first cockroach’s initial speed)
a2 = 0.12 m/s2
(second cockroach’s acceleration)
vi,2 = 0 m/s (second cockroach’s initial speed)
d = 60.0 cm = 0.60 m (initial distance between the insects)
Unknown: ∆x1 = ? ∆x2 = ? ∆t = ?
Choose an equation(s) or situation: Use the equation for displacement with
constant acceleration for each cockroach.
∆x1 = vi,1∆t + 
1
2
a1∆t2
∆x2 = vi,2∆t + 
1
2
a2∆t2
The distance the second cockroach travels can be expressed as the difference be-
tween the total distance that initially separates the two insects and the distance
that the first insect travels.
∆x2 = d – ∆x1
Rearrange the equation(s) to isolate the unknown(s): Substitute the expression
for the first cockroach’s displacement into the equation for the second cockroach’s
displacement using the equation relating the two displacements to the initial dis-
tance between the insects.
∆x2 = d – ∆x1 = d –
vi,1∆t + 
1
2
a1∆t2

= vi,2∆t + 
1
2
a2∆t2
The equation can be rewritten to express ∆t in terms of the known quantities. To
simplify the calculation, the terms involving the initial speeds, which are both
zero, can be removed from the equations.
d – 
1
2
a1∆t2
= 
1
2
a2∆t2
∆t = 
a1

2
+
d
a
2


1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

10
NAME ______________________________________ DATE _______________ CLASS ____________________
Substitute the values into the equation(s) and solve:
∆t =
= =
The final speeds for the first and second cockroaches are 0.38 m/s and 0.23 m/s,
respectively. Both of these values are well below the maximum speed for cock-
roaches in general.
1.9 s
1.2 m

0.32 m/s2
(2)(0.60 m)

0.20 
m
s2
 + 0.12 
m
s2

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1986, the first flight around the globe without a single refueling was
completed. The aircraft’s average speed was 186 km/h. If the airplane
landed at this speed and accelerated at −1.5 m/s2
, how long did it take
for the airplane to stop?
2. In 1976, Gerald Hoagland drove a car over 8.0 × 102
km in reverse. For-
tunately for Hoagland and motorists in general, the event took place on
a special track. During this drive, Hoagland’s average velocity was
about –15.0 m/s. Suppose Hoagland decides during his drive to go for-
ward. He applies the brakes, stops, and then accelerates until he moves
forward at same speed he had when he was moving backward. How
long would the entire reversal process take if the average acceleration
during this process is +2.5 m/s2
?
3. The first permanent public railway was built by George Stephenson
and opened in Cleveland, Ohio, in 1825. The average speed of the
trains was 24.0 km/h. Suppose a train moving at this speed accelerates
–0.20 m/s2
until it reaches a speed of 8.0 km/h. How long does it take
the train to undergo this change in speed?
4. The winding cages in mine shafts are used to move workers in and out
of the mines. These cages move much faster than any commercial ele-
vators. In one South African mine, speeds of up to 65.0 km/h are at-
tained. The mine has a depth of 2072 m. Suppose two cages start their
downward journey at the same moment. The first cage quickly attains
the maximum speed (an unrealistic situation), then proceeds to de-
scend uniformly at that speed all the way to the bottom. The second
cage starts at rest and then increases its speed with a constant accelera-
tion of magnitude 4.00 × 10–2
m/s2
. How long will the trip take for
each cage? Which cage will reach the bottom of the mine shaft first?
5. In a 1986 bicycle race, Fred Markham rode his bicycle a distance of
2.00 × 102
m with an average speed of 105.4 km/h. Markham and the
bicycle started the race with a certain initial speed.
a. Find the time it took Markham to cover 2.00 × 102
m.
b. Suppose a car moves from rest under constant acceleration. What
is the magnitude of the car’s acceleration if the car is to finish the
race at exactly the same time Markham finishes the race?
3. CALCULATE
4. EVALUATE

Problem D 11
NAME ______________________________________ DATE _______________ CLASS ____________________
6. Some tropical butterflies can reach speeds of up to 11 m/s. Suppose a
butterfly flies at a speed of 6.0 m/s while another flying insect some dis-
tance ahead flies in the same direction with a constant speed. The but-
terfly then increases its speed at a constant rate of 1.4 m/s2
and catches
up to the other insect 3.0 s later. How far does the butterfly travel dur-
ing the race?
7. Mary Rife, of Texas, set a women’s world speed record for sailing. In
1977, her vessel, Proud Mary, reached a speed of 3.17 × 102
km/h. Sup-
pose it takes 8.0 s for the boat to decelerate from 3.17 × 102
km/h to
2.00 × 102
km/h. What is the boat’s acceleration? What is the displace-
ment of the Proud Mary as it slows down?
8. In 1994, a human-powered submarine was designed in Boca Raton,
Florida. It achieved a maximum speed of 3.06 m/s. Suppose this sub-
marine starts from rest and accelerates at 0.800 m/s2
until it reaches
maximum speed. The submarine then travels at constant speed for an-
other 5.00 s. Calculate the total distance traveled by the submarine.
9. The highest speed achieved by a standard nonracing sports car is
3.50 × 102
km/h. Assuming that the car accelerates at 4.00 m/s2
, how
long would this car take to reach its maximum speed if it is initially at
rest? What distance would the car travel during this time?
10. Stretching 9345 km from Moscow to Vladivostok, the Trans-Siberian
railway is the longest single railroad in the world. Suppose the train is ap-
proaching the Moscow station at a velocity of +24.7 m/s when it begins a
constant acceleration of –0.850 m/s2
. This acceleration continues for 28
s. What will be the train’s final velocity when it reaches the station?
11. The world’s fastest warship belongs to the United States Navy. This ves-
sel, which floats on a cushion of air, can move as fast as 1.7 × 102
km/h.
Suppose that during a training exercise the ship accelerates +2.67 m/s2
,
so that after 15.0 s its displacement is +6.00 × 102
m. Calculate the
ship’s initial velocity just before the acceleration. Assume that the ship
moves in a straight line.
12. The first supersonic flight was performed by then Capt. Charles
Yeager in 1947. He flew at a speed of 3.00 × 102
m/s at an altitude of
more than 12 km, where the speed of sound in air is slightly less than
3.00 × 102
m/s. Suppose Capt. Yeager accelerated 7.20 m/s2
in 25.0 s to
reach a final speed of 3.00 × 102
m/s. What was his initial speed?
13. Peter Rosendahl rode his unicycle a distance of 1.00 × 102
m in 12.11 s.
If Rosendahl started at rest, what was the magnitude of his acceleration?
14. Suppose that Peter Rosendahl began riding the unicycle with a speed of
3.00 m/s and traveled a distance of 1.00 × 102
m in 12.11s. What would
the magnitude of Rosendahl’s acceleration be in this case?
15. In 1991, four English teenagers built an electric car that could attain a
speed 30.0 m/s. Suppose it takes 8.0 s for this car to accelerate from
18.0 m/s to 30.0 m/s. What is the magnitude of the car’s acceleration?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

12
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem E
FINAL VELOCITY AFTER ANY DISPLACEMENT
P R O B L E M
In 1970, a rocket-powered car called Blue Flame achieved a maximum
speed of 1.00 ( 103
km/h (278 m/s). Suppose the magnitude of the car’s
constant acceleration is 5.56 m/s2
. If the car is initially at rest, what is the
distance traveled during its acceleration?
S O L U T I O N
Given: vi = 0 m/s
vf = 278 m/s
a = 5.56 m/s2
Unknown: ∆x = ?
Choose an equation(s) or situation: Use the equation for the final velocity after
any displacement.
vf
2
= vi
2
+ 2a∆x
Rearrange the equation(s) to isolate the unknown(s):
∆x = 
vf
2
2
−
a
vi
2

∆x = =
Using the appropriate kinematic equation, the time of travel for Blue Flame is
found to be 50.0 s. From this value for time the distance traveled during the ac-
celeration is confirmed to be almost 7 km. Once the car reaches its maximum
speed, it travels about 16.7 km/min.
6.95 × 103
m
278 
m
s


2
−
0 
m
s


2

(2)
5.56 
m
s2


1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. In 1976, Kitty Hambleton of the United States drove a rocket-engine
car to a maximum speed of 965 km/h. Suppose Kitty started at rest
and underwent a constant acceleration with a magnitude of 4.0 m/s2
.
What distance would she have had to travel in order to reach the maxi-
mum speed?
2. With a cruising speed of 2.30 × 103
km/h, the French supersonic pas-
senger jet Concorde is the fastest commercial airplane. Suppose the
landing speed of the Concorde is 20.0 percent of the cruising speed. If
the plane accelerates at –5.80 m/s2
, how far does it travel between the
time it lands and the time it comes to a complete stop?

Problem E 13
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 3. The Boeing 747 can carry more than 560 passengers and has a maxi-
mum speed of about 9.70 × 102
km/h. After takeoff, the plane takes a
certain time to reach its maximum speed. Suppose the plane has a con-
stant acceleration with a magnitude of 4.8 m/s2
. What distance does the
plane travel between the moment its speed is 50.0 percent of maximum
and the moment its maximum speed is attained?
4. The distance record for someone riding a motorcycle on its rear wheel
without stopping is more than 320 km. Suppose the rider in this un-
usual situation travels with an initial speed of 8.0 m/s before speeding
up. The rider then travels 40.0 m at a constant acceleration of
2.00 m/s2
. What is the rider’s speed after the acceleration?
5. The skid marks left by the decelerating jet-powered car The Spirit of
America were 9.60 km long. If the car’s acceleration was –2.00 m/s2
,
what was the car’s initial velocity?
6. The heaviest edible mushroom ever found (the so-called “chicken of
the woods”) had a mass of 45.4 kg. Suppose such a mushroom is at-
tached to a rope and pulled horizontally along a smooth stretch of
ground, so that it undergoes a constant acceleration of +0.35 m/s2
. If
the mushroom is initially at rest, what will its velocity be after it has
been displaced +64 m?
7. Bengt Norberg of Sweden drove his car 44.8 km in 60.0 min. The
feature of this drive that is interesting is that he drove the car on two
side wheels.
a. Calculate the car’s average speed.
b. Suppose Norberg is moving forward at the speed calculated in
(a). He then accelerates at a rate of –2.00 m/s2
. After traveling
20.0 m, the car falls on all four wheels. What is the car’s final
speed while still traveling on two wheels?
8. Starting at a certain speed, a bicyclist travels 2.00 × 102
m. Suppose the
bicyclist undergoes a constant acceleration of 1.20 m/s2
. If the final
speed is 25.0 m/s, what was the bicyclist’s initial speed?
9. In 1994, Tony Lang of the United States rode his motorcycle a short
distance of 4.0 × 102
m in the short interval of 11.5 s. He started from
rest and crossed the finish line with a speed of about 2.50 × 102
km/h.
Find the magnitude of Lang’s acceleration as he traveled the 4.0 × 102
m
distance.
10. The lightest car in the world was built in London and had a mass of
less than 10 kg. Its maximum speed was 25.0 km/h. Suppose the driver
of this vehicle applies the brakes while the car is moving at its maxi-
mum speed. The car stops after traveling 16.0 m. Calculate the car’s
acceleration.

14
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem F
FALLING OBJECT
P R O B L E M
The famous Gateway to the West Arch in St. Louis, Missouri, is about
192 m tall at its highest point. Suppose Sally, a stuntwoman, jumps off the
top of the arch. If it takes Sally 6.4 s to land on the safety pad at the base
of the arch, what is her average acceleration? What is her final velocity?
S O L U T I O N
Given: vi = 0 m/s
∆y = –192 m
∆t = 6.4 s
Unknown: a = ?
vf = ?
Choose an equation(s) or situation: Both the acceleration and the final speed
are unknown. Therefore, first solve for the acceleration during the fall using the
equation that requires only the known variables.
∆y = vi ∆t + 
1
2
a ∆t2
Then the equation for vf that involves acceleration can be used to solve for vf .
vf = vi + a∆t
a = 
2(∆y
∆
–
t
v
2
i ∆t)

vf = vi + a∆t
=
vf = 0 
m
s
 +
–9.4 
m
s2

(6.4s) =
Sally’s downward acceleration is less than the free-fall acceleration at Earth’s sur-
face (9.81 m/s2
). This indicates that air resistance reduces her downward acceler-
ation by 0.4 m/s2
. Sally’s final speed, 60 ms2
, is such that, if she could fall at this
speed at the beginning of her jump with no acceleration, she would travel a dis-
tance equal to the arch’s height in just a little more than 3 s.
–6.0 × 101

m
s

–9.4 
m
s2

a = (2)
(–192 m)–
0 
m
s

(6.4s)


(6.4 s)2
1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. CALCULATE
4. EVALUATE

Problem F 15
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. ADDITIONAL PRACTICE
1. The John Hancock Center in Chicago is the tallest building in the United
States in which there are residential apartments. The Hancock Center is
343 m tall. Suppose a resident accidentally causes a chunk of ice to fall
from the roof. What would be the velocity of the ice as it hits the ground?
Neglect air resistance.
2. Brian Berg of Iowa built a house of cards 4.88 m tall. Suppose Berg
throws a ball from ground level with a velocity of 9.98 m/s straight up.
What is the velocity of the ball as it first passes the top of the card house?
3. The Sears Tower in Chicago is 443 m tall. Suppose a book is dropped
from the top of the building. What would be the book’s velocity at a
point 221 m above the ground? Neglect air resistance.
4. The tallest roller coaster in the world is the Desperado in Nevada. It has a
lift height of 64 m. If an archer shoots an arrow straight up in the air and
the arrow passes the top of the roller coaster 3.0 s after the arrow is shot,
what is the initial speed of the arrow?
5. The tallest Sequoia sempervirens tree in California’s Redwood National
Park is 111 m tall. Suppose an object is thrown downward from the top
of that tree with a certain initial velocity. If the object reaches the ground
in 3.80 s, what is the object’s initial velocity?
6. The Westin Stamford Hotel in Detroit is 228 m tall. If a worker on the
roof drops a sandwich, how long does it take the sandwich to hit the
ground, assuming there is no air resistance? How would air resistance af-
fect the answer?
7. A man named Bungkas climbed a palm tree in 1970 and built himself a
nest there. In 1994 he was still up there, and he had not left the tree for
24 years. Suppose Bungkas asks a villager for a newspaper, which is
thrown to him straight up with an initial speed of 12.0 m/s. When
Bungkas catches the newspaper from his nest, the newspaper’s velocity is
3.0 m/s, directed upward. From this information, find the height at
which the nest was built. Assume that the newspaper is thrown from a
height of 1.50 m above the ground.
8. Rob Colley set a record in “pole-sitting” when he spent 42 days in a bar-
rel at the top of a flagpole with a height of 43 m. Suppose a friend want-
ing to deliver an ice-cream sandwich to Colley throws the ice cream
straight up with just enough speed to reach the barrel. How long does it
take the ice-cream sandwich to reach the barrel?
9. A common flea is recorded to have jumped as high as 21 cm. Assuming
that the jump is entirely in the vertical direction and that air resistance is
insignificant, calculate the time it takes the flea to reach a height of 7.0 cm.

Problem A 17
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved. Two-Dimensional Motion andVectors
Problem A
FINDING RESULTANT MAGNITUDE AND DIRECTION
Cheetahs are, for short distances, the fastest land animals. In the course
of a chase, cheetahs can also change direction very quickly. Suppose a
cheetah runs straight north for 5.0 s, quickly turns, and runs 3.00 × 102
m
west. If the magnitude of the cheetah’s resultant displacement is 3.35 ×
102
m, what is the cheetah’s displacement and velocity during the first
part of its run?
S O L U T I O N
Given: ∆t1 = 5.0 s
∆x = 3.00 s × 102
m
d = 3.35 × 102
m
Unknown: ∆y = ? vy = ?
Diagram:
1. DEFINE
2. PLAN
3. CALCULATE
P R O B L E M
∆y = ?
∆x = 3.00 × 102 m
d = 3.35 × 102 m
N
Choose the equation(s) or situation: Use the Pythagorean theorem to subtract
one of the displacements at right angles from the total displacement, and thus
determine the unknown component of displacement.
d2
= ∆x2
+ ∆y2
Use the equation relating displacement to constant velocity and time, and use the
calculated value for ∆y and the given value for ∆t to solve for v.
∆v =
∆y2
= d2
– ∆x2
∆y =

d 2

–
∆
x2

vy =
Substitute the values into the equation(s) and solve: Because the value for ∆y
is a displacement magnitude, only the positive root is used (∆y 0).
∆y =

(3
.3

5

×

1

02

m

)2

−

(

3.

00

×

1

02

m

)2

=

1.
12
×
1
05
m
2
−
9
.0
0
×
1
04
m
2

∆y
∆t
∆y
∆t

18
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
4. EVALUATE
=

2.

2

×

1

04

m

=
vy = 
1.5
5
×
.0
10
s
2
m
 =
The cheetah has a top speed of 30 m/s, or 107 km/h. This is equal to about
67 miles/h.
3.0 × 101
m/s, north
1.5 × 102
m, north
ADDITIONAL PRACTICE
1. An ostrich cannot fly, but it is able to run fast. Suppose an ostrich runs
east for 7.95 s and then runs 161 m south, so that the magnitude of the
ostrich’s resultant displacement is 226 m. Calculate the magnitude of the
ostrich’s eastward component and its running speed.
2. The pronghorn antelope, found in North America, is the best long-
distance runner among mammals. It has been observed to travel at an av-
erage speed of more than 55 km/h over a distance of 6.0 km. Suppose the
antelope runs a distance of 5.0 km in a direction 11.5° north of east,
turns, and then runs 1.0 km south. Calculate the resultant displacement.
3. Kangaroos can easily jump as far 8.0 m. If a kangaroo makes five such
jumps westward, how many jumps must it make northward to have a
northwest displacement with a magnitude of 68 m? What is the angle of
the resultant displacement with respect to north?
4. In 1926, Gertrude Ederle of the United States became the first woman to
swim across the English channel. Suppose Ederle swam 25.2 km east
from the coast near Dover, England, then made a 90° turn and traveled
south for 21.3 km to a point east of Calais, France. What was Ederle’s re-
sultant displacement?
5. The emperor penguin is the best diver among birds: the record dive is
483 m. Suppose an emperor penguin dives vertically to a depth of 483 m
and then swims horizontally a distance of 225 m. What angle would the
vector of the resultant displacement make with the water’s surface? What
is the magnitude of the penguin’s resultant displacement?
6. A killer whale can swim as fast as 15 m/s. Suppose a killer whale swims in
one direction at this speed for 8.0 s, makes a 90° turn, and continues
swimming in the new direction with the same speed as before. After a cer-
tain time interval, the magnitude of the resultant displacement is 180.0 m.
Calculate the amount of time the whale swims after changing direction.
7. Woodcocks are the slowest birds: their average speed during courtship
displays can be as low as 8.00 km/h. Suppose a woodcock flies east for
15.0 min. It then turns and flies north for 22.0 min. Calculate the magni-
tude of the resultant displacement and the angle between the resultant
displacement and the woodcock’s initial displacement.

Problem B 19
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
ADDITIONAL PRACTICE
1. A common flea can jump a distance of 33 cm. Suppose a flea makes five
jumps of this length in the northwest direction. If the flea’s northward
displacement is 88 cm, what is the flea’s westward displacement.
Two-Dimensional Motion andVectors
Problem B
RESOLVING VECTORS
Certain iguanas have been observed to run as fast as 10.0 m/s. Suppose an
iguana runs in a straight line at this speed for 5.00 s. The direction of mo-
tion makes an angle of 30.0° to the east of north. Find the value of the
iguana’s northward displacement.
S O L U T I O N
Given: v = 10.0 m/s
t = 5.00 s
q = 30.0°
Unknown: ∆y = ?
Diagram:
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
P R O B L E M
Ν
30.0° d = v∆t
∆y
θ =
Choose the equation(s) or situation: The northern component of the vector is
equal to the vector magnitude times the cosine of the angle between the vector
and the northward direction.
∆y = d(cos q)
Use the equation relating displacement with constant velocity and time, and sub-
stitute it for d in the previous equation.
d = v∆t
∆y = v∆t(cos q)
∆y =
10.0 
m
s

(5.00 s)(cos 30.0°)
=
The northern component of the displacement vector is smaller than the displace-
ment itself, as expected.
43.3 m, north

20
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
2. The longest snake ever found was a python that was 10.0 m long. Sup-
pose a coordinate system large enough to measure the python’s length is
drawn on the ground. The snake’s tail is then placed at the origin and the
snake’s body is stretched so that it makes an angle of 60.0° with the posi-
tive x-axis. Find the x and y coordinates of the snake’s head. (Hint: The y-
coordinate is positive.)
3. A South-African sharp-nosed frog set a record for a triple jump by trav-
eling a distance of 10.3 m. Suppose the frog starts from the origin of a
coordinate system and lands at a point whose coordinate on the y-axis is
equal to −6.10 m. What angle does the vector of displacement make with
the negative y-axis? Calculate the x component of the frog.
4. The largest variety of grasshopper in the world is found in Malaysia.
These grasshoppers can measure almost a foot (0.305 m) in length and
can jump 4.5 m. Suppose one of these grasshoppers starts at the origin of
a coordinate system and makes exactly eight jumps in a straight line that
makes an angle of 35° with the positive x-axis. Find the grasshopper’s
displacements along the x- and y-axes. Assume both component dis-
placements to be positive.
5. The landing speed of the space shuttle Columbia is 347 km/h. If the shut-
tle is landing at an angle of 15.0° with respect to the horizontal, what are
the horizontal and the vertical components of its velocity?
6. In Virginia during 1994 Elmer Trett reached a speed of 372 km/h on his
motorcycle. Suppose Trett rode northwest at this speed for 8.7 s. If the
angle between east and the direction of Trett’s ride was 60.0°, what was
Trett’s displacement east? What was his displacement north?
7. The longest delivery flight ever made by a twin-engine commercial jet
took place in 1990. The plane covered a total distance of 14 890 km from
Seattle, Washington to Nairobi, Kenya in 18.5 h. Assuming that the plane
flew in a straight line between the two cities, find the magnitude of the
average velocity of the plane. Also, find the eastward and southward
components of the average velocity if the direction of the plane’s flight
was at an angle of 25.0° south of east.
8. The French bomber Mirage IV can fly over 2.3 × 103
km/h. Suppose this
plane accelerates at a rate that allows it to increase its speed from 6.0 ×
102
km/h to 2.3 × 103
km/h. in a time interval of 120 s. If this accelera-
tion is upward and at an angle of 35° with the horizontal, find the accel-
eration’s horizontal and vertical components.

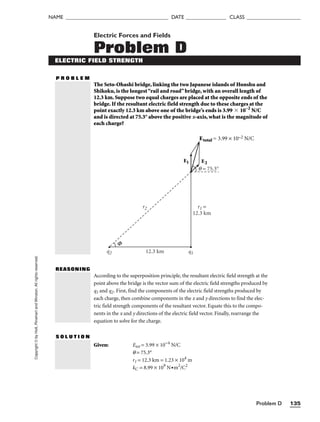
Problem C 21
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
P R O B L E M
Problem C
ADDING VECTORS ALGEBRAICALLY
The record for the longest nonstop closed-circuit flight by a model air-
plane was set in Italy in 1986. The plane flew a total distance of 1239 km.
Assume that at some point the plane traveled 1.25 × 103
m to the east, then
1.25 × 103
m to the north, and finally 1.00 × 103
m to the southeast. Calcu-
late the total displacement for this portion of the flight.
S O L U T I O N
Given: d1 = 1.25 × 103
m d2 = 1.25 × 103
m d3 = 1.00 × 103
m
Unknown: ∆xtot = ? ∆ytot = ? d = ? q = ?
Diagram:
1. DEFINE
2. PLAN
d3 = 1.00 × 103 m
d2 = 1.25 × 103 m
d1 = 1.25 × 103 m
∆xtot
∆ytot
dtot
45.0°
N
3. CALCULATE
Choose the equation(s) or situation: Orient the displacements with respect to
the x-axis of the coordinate system.
q1 = 0.00° q2 = 90.0° q3 = −45.0°
Use this information to calculate the components of the total displacement along
the x-axis and the y-axis.
∆xtot = ∆x1 + ∆x2 + ∆x3
= d1(cos q1) + d2(cos q2) + d3(cos q3)
∆ytot = ∆y1 + ∆y2 + ∆y3
= d1(sin q1) + d2(sin q2) + d3(sin q3)
Use the components of the total displacement, the Pythagorean theorem, and the
tangent function to calculate the total displacement.
d =

(∆
xt
ot
)2
+
(
∆
yt
ot
)2
q = tan−1

∆xtot = (1.25 × 103
m)(cos 0°) + (1.25 × 103
m)(cos 90.0°)
+(1.00 × 103
m)[cos (−45.0°)]
= 1.25 × 103
m + 7.07 × 102
m
= 1.96 × 103
m
∆ytot = (1.25 × 103
m)(sin 0°) + (1.25 × 103
m)(sin 90.0°)
+(1.00 × 103
m)[sin (−45.0°)]
= 1.25 × 103
m + 7.07 × 102
m
= 0.543 × 103
m
d =

(1
.9
6
×
1
03
m
)2
+
(
0.
54
3
×
1
03
m
)2

∆ytot

∆xtot

22
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
ADDITIONAL PRACTICE
1. For six weeks in 1992, Akira Matsushima, from Japan, rode a unicycle
more than 3000 mi across the United States. Suppose Matsushima is rid-
ing through a city. If he travels 250.0 m east on one street, then turns
counterclockwise through a 120.0° angle and proceeds 125.0 m north-
west along a diagonal street, what is his resultant displacement?
2. In 1976, the Lockheed SR-71A Blackbird set the record speed for any air-
plane: 3.53 × 103
km/h. Suppose you observe this plane ascending at this
speed. For 20.0 s, it flies at an angle of 15.0° above the horizontal, then
for another 10.0 s its angle of ascent is increased to 35.0°. Calculate the
plane’s total gain in altitude, its total horizontal displacement, and its re-
sultant displacement.
3. Magnor Mydland of Norway constructed a motorcycle with a wheelbase
of about 12 cm. The tiny vehicle could be ridden at a maximum speed
11.6 km/h. Suppose this motorcycle travels in the directions d1 and d2
shown in the figure below. Calculate d1 and d2, and determine how long
it takes the motorcycle to reach a net displacement of 2.0 × 102
m to the
right?
4. The fastest propeller-driven aircraft is the Russian TU-95/142, which can
reach a maximum speed of 925 km/h. For this speed, calculate the plane’s
resultant displacement if it travels east for 1.50 h, then turns 135° north-
west and travels for 2.00 h.
5. In 1952, the ocean liner United States crossed the Atlantic Ocean in less
than four days, setting the world record for commercial ocean-going ves-
sels. The average speed for the trip was 57.2 km/h. Suppose the ship
moves in a straight line eastward at this speed for 2.50 h. Then, due to a
strong local current, the ship’s course begins to deviate northward by
30.0°, and the ship follows the new course at the same speed for another
1.50 h. Find the resultant displacement for the 4.00 h period.
d =

3.
84
×
1
06
m
2
+
2
.9
5
×
1
05
m
2
=

4.
14
×
1
06
m
2

d =
q = tan−1

q =
The magnitude of the total displacement is slightly larger than that of the total
displacement in the eastern direction alone.
15.5° north of east
0.543 × 103
m

1.96 × 103
m
2.03 × 103
m
4. EVALUATE

Problem D 23
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
P R O B L E M
Problem D
PROJECTILES LAUNCHED HORIZONTALLY
A movie director is shooting a scene that involves dropping s stunt
dummy out of an airplane and into a swimming pool. The plane is 10.0 m
above the ground, traveling at a velocity of 22.5 m/s in the positive x di-
rection. The director wants to know where in the plane’s path the dummy
should be dropped so that it will land in the pool.What is the dummy’s
horizontal displacement?
S O L U T I O N
Given: ∆y = −10.0 m ay = −g = −9.81 m/s2
vx = 22.5 m/s
Unknown: ∆t = ? ∆x = ?
Diagram: The initial velocity vector of the
stunt dummy only has a horizontal
component. Choose the coordinate
system oriented so that the positive y
direction points upward and the pos-
itive x direction points to the right.
Choose the equation(s) or situation: The dummy drops with no initial vertical
velocity. Because air resistance is neglected, the dummy’s horizontal velocity re-
mains constant.
∆y = 
1
2
ay (∆t)2
∆x = vx∆t
∆t =

2
a
∆
y
y

First find the time it takes for the dummy to reach the ground.
∆t =

(
(
2
−
)
9
(
.
−
81
1

0
m
.0
/
m
s2)
)

= 1.43 s
Find out how far horizontally the dummy can travel during this period of time.
∆x = vx∆t = (22.5 m/s)(1.43 s)
=
The stunt dummy will have to drop from the plane when the plane is at a hori-
zontal distance of 32.2 m from the pool. The distance is within the correct order
of magnitude, given the other values in this problem.
32.2 m
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
vx
ay
y
x
−10.0m

24
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
ADDITIONAL PRACTICE
1. Florence Griffith-Joyner of the United States set the women’s world
record for the 200 m run by running with an average speed of 9.37 m/s.
Suppose Griffith-Joyner wants to jump over a river. She runs horizon-
tally from the river’s higher bank at 9.37 m/s and lands on the edge of the
opposite bank. If the difference in height between the two banks is 2.00
m, how wide is the river?
2. The longest banana split ever made was 7.320 km long (needless to say,
more than one banana was used). If an archer were to shoot an arrow
horizontally from the top of Mount Everest, which is located 8848 m
above sea level, would the arrow’s horizontal displacement be larger than
7.32 km? Assume that the arrow cannot be shot faster than 100.0 m/s,
that there is no air resistance, and that the arrow lands at sea level.
3. The longest shot on a golf tournament was made by Mike Austin in
1974. The ball went a distance of 471 m. Suppose the ball was shot hori-
zontally off a cliff at 80.0 m/s. Calculate the height of the cliff.
4. Recall Elmer Trett, who in 1994 reached a speed of 372 km/h on his mo-
torcycle. Suppose Trett drives off a horizontal ramp at this speed and
lands a horizontal distance of 40.0 m away from the edge of the ramp.
What is the height of the ramp? Neglect air resistance.
5. A Snorkel fire engine is designed for putting out fires that are well above
street level. The engine has a hydraulic lift that lifts the firefighter and a
system that delivers pressurized water to the firefighter. Suppose that the
engine cannot move closer than 25 m to a building that has a fire on its
sixth floor, which is 25 m above street level. Also assume that the water
nozzle is stuck in the horizontal position (an improbable situation). If
the horizontal speed of the water emerging from the hose is 15 m/s, how
high above the street must the firefighter be lifted in order for the water
to reach the fire?
6. The longest stuffed toy ever manufactured is a 420 m snake made by
Norwegian children. Suppose a projectile is thrown horizontally from a
height half as long as the snake and the projectile’s horizontal displace-
ment is as long as the snake. What would be the projectile’s initial speed?
7. Libyan basketball player Suleiman Nashnush was the tallest basketball
player ever. His height was 2.45 m. Suppose Nashnush throws a basket-
ball horizontally from a level equal to the top of his head. If the speed of
the basketball is 12.0 m/s when it lands, what was the ball’s initial speed?
(Hint: Consider the components of final velocity.)
8. The world’s largest flowerpot is 1.95 m high. If you were to jump hori-
zontally from the top edge of this flowerpot at a speed of 3.0 m/s, what
would your landing velocity be?

Problem E 25
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
P R O B L E M
Problem E
PROJECTILES LAUNCHED AT AN ANGLE
The narrowest strait on earth is Seil Sound in Scotland, which lies be-
tween the mainland and the island of Seil. The strait is only about 6.0 m
wide. Suppose an athlete wanting to jump“over the sea”leaps at an angle
of 35° with respect to the horizontal.What is the minimum initial speed
that would allow the athlete to clear the gap? Neglect air resistance.
S O L U T I O N
Given: ∆x = 6.0 m
q = 35°
ay = −g = −9.81 m/s2
Unknown: vi = ?
Diagram:
1. DEFINE
2. PLAN
∆x
v
= 6.00 m
θ = 35°
Choose the equation(s) or situation: The horizontal component of the athlete’s
velocity, vx, is equal to the initial speed multiplied by the cosine of the angle, q,
which is equal to the magnitude of the horizontal displacement, ∆x, divided by the
time interval required for the complete jump.
vx = vi cos q = 
∆
∆
x
t

At the midpoint of the jump, the vertical component of the athlete’s velocity, vy,
which is the upward vertical component of the initial velocity, vi sin q, plus
the component of velocity due to free-fall acceleration, equals zero. The time
required for this to occur is half the time necessary for the total jump.
vy = vi sin q + ay
∆
2
t

= 0
vi sin q =
−a
2
y ∆t

Rearrange the equation(s) to isolate the unknown(s): Express ∆t in the second
equation in terms of the displacement and velocity component in the first equation.
vi sin q =
−
2
ay


vi c
∆
o
x
s q


vi
2
=
2 si
−
n
a
q
y∆
c
x
os q

vi =

2 si
−
n
a
q
y

∆
c
x
os q

26
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
1. In 1993, Wayne Brian threw a spear a record distance of 201.24 m. (This
is not an official sport record because a special device was used to “elon-
gate” Brian’s hand.) Suppose Brian threw the spear at a 35.0° angle with
respect to the horizontal. What was the initial speed of the spear?
2. April Moon set a record in flight shooting (a variety of long-distance
archery). In 1981 in Utah, she sent an arrow a horizontal distance of
9.50 × 102
m. What was the speed of the arrow at the top of the flight if the
arrow was launched at an angle of 45.0° with respect to the horizontal?
3. In 1989 during overtime in a high school basketball game in Erie, Penn-
sylvania, Chris Eddy threw a basketball a distance of 27.5 m to score and
win the game. If the shot was made at a 50.0° angle above the horizontal,
what was the initial speed of the ball?
4. In 1978, Geoff Capes of the United Kingdom won a competition for
throwing 5 lb bricks; he threw one brick a distance of 44.0 m. Suppose
the brick left Capes’ hand at an angle of 45.0° with respect to the
horizontal.
a. What was the initial speed of the brick?
b. What was the maximum height reached by the brick?
c. If Capes threw the brick straight up with the speed found in (a),
what would be the maximum height the brick could achieve?
5. In 1991, Doug Danger rode a motorcycle to jump a horizontal distance
of 76.5 m. Find the maximum height of the jump if his angle with re-
spect to the ground at the beginning of the jump was 12.0°.
6. Michael Hout of Ohio can run 110.0 meter hurdles in 18.9 s at an aver-
age speed of 5.82 m/s. What makes this interesting is that he juggles three
balls as he runs the distance. Suppose Hout throws a ball up and forward
at twice his running speed and just catches it at the same level. At what
angle, q, must the ball be thrown? (Hint: Consider horizontal displace-
ments for Hout and the ball.)
ADDITIONAL PRACTICE
Substitute the values into the equation(s) and solve: Select the positive root for vi.
vi = =
By substituting the value for vi into the original equations, you can determine the
time for the jump to be completed, which is 0.92 s. From this, the height of the
jump is found to equal 1.0 m.
7.9 m/s
−(−9.81 m/s2
)(6.0 m)

(2)(sin 35°)(cos 35°)
4. EVALUATE
3. CALCULATE

Problem E 27
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved. 7. A scared kangaroo once cleared a fence by jumping with a speed of
8.42 m/s at an angle of 55.2° with respect to the ground. If the jump
lasted 1.40 s, how high was the fence? What was the kangaroo’s horizon-
tal displacement?
8. Measurements made in 1910 indicate that the common flea is an impres-
sive jumper, given its size. Assume that a flea’s initial speed is 2.2 m/s, and
that it leaps at an angle of 21° with respect to the horizontal. If the jump
lasts 0.16 s, what is the magnitude of the flea’s horizontal displacement?
How high does the flea jump?

Problem F
RELATIVE VELOCITY
P R O B L E M
The world’s fastest current is in Slingsby Channel, Canada, where the
speed of the water reaches 30.0 km/h. Suppose a motorboat crosses the
channel perpendicular to the bank at a speed of 18.0 km/h relative to the
bank. Find the velocity of the motorboat relative to the water.
S O L U T I O N
Given: vwb = 30.0 km/h along the channel (velocity of the water, w,
with respect to the bank, b)
vmb = 18.0 km/h perpendicular to the channel (velocity of the
motorboat, m, with respect to the bank, b)
Unknown: vmw = ?
Diagram:
1. DEFINE
2. PLAN
28
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved.
vwb
vmb
vmw
Choose the equation(s) or situation: From the vector diagram, the resultant
vector (the velocity of the motorboat with respect to the bank, vmb) is equal to
the vector sum of the other two vectors, one of which is the unknown.
vmw = vmb + vwb
Use the Pythagorean theorem to calculate the magnitude of the resultant velocity,
and use the tangent function to find the direction. Note that because the vectors
vmb and vwb are perpendicular to each other, the product that results from mul-
tiplying one by the other is zero. The tangent of the angle between vmb and vmw
is equal to the ratio of the magnitude of vwb to the magnitude of vmb.
vmw
2
= vmb
2
+ vwb
2
tanq = 
v
v
m
wb
b

vmw =

vm
b
2
+
v
w
b
2

q = tan−1

v
v
m
wb
b


Substitute the values into the equation(s) and solve: Choose the positive root
for vmw.
vmw = 1
8.
0

k
h
m


2
+

30
.0

k
h
m


2
= 35.0 
k
h
m

3. CALCULATE

Problem F 29
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
Allrights
reserved. The angle between vmb and vmw is as follows:
q = tan−1
=
The motorboat must move in a direction 59° with respect to vmb and against
the current, and with a speed of 35.0 km/h in order to move 18.0 km/h perpen-
dicular to the bank.
59.0° away from the
oncoming current
30.0 
k
h
m


18.0 
k
h
m

4. EVALUATE
ADDITIONAL PRACTICE
1. In 1933, a storm occurring in the Pacific Ocean moved with speeds
reaching a maximum of 126 km/h. Suppose a storm is moving north at
this speed. If a gull flies east through the storm with a speed of 40.0 km/h
relative to the air, what is the velocity of the gull relative to Earth?
2. George V Coast in Antarctica is the windiest place on Earth. Wind speeds
there can reach 3.00 × 102
km/h. If a research plane flies against the wind
with a speed of 4.50 × 102
km/h relative to the wind, how long does it
take the plane to fly between two research stations that are 250 km apart?
3. Turtles are fairly slow on the ground, but they are very good swimmers,
as indicated by the reported speed of 9.0 m/s for the leatherback turtle.
Suppose a leatherback turtle swims across a river at 9.0 m/s relative to
the water. If the current in the river is 3.0 m/s and it moves at a right
angle to the turtle’s motion, what is the turtle’s displacement with respect
to the river’s bank after 1.0 min?
4. California sea lions can swim as fast as 40.0 km/h. Suppose a sea lion be-
gins to chase a fish at this speed when the fish is 60.0 m away. The fish, of
course, does not wait, and swims away at a speed 16.0 km/h. How long
would it take the sea lion to catch the fish?
5. The spur-wing goose is one of the fastest birds in the world when it
comes to level flying: it can reach a speed of 90.0 km/h. Suppose two
spur-wing geese are separated by an unknown distance and start flying
toward each other at their maximum speeds. The geese pass each other
40.0 s later. Calculate the initial distance between the geese.
6. The fastest snake on Earth is the black mamba, which can move over a
short distance at 18.0 km/h. Suppose a mamba moves at this speed to-
ward a rat sitting 12.0 m away. The rat immediately begins to run away at
33.3 percent of the mamba’s speed. If the rat jumps into a hole just be-
fore the mamba can catch it, determine the length of time that the chase
lasts.

Problem A 31
NAME ______________________________________ DATE _______________ CLASS ____________________
Forces and the Laws of Motion
Problem A
DRAWING FREE-BODY DIAGRAMS
P R O B L E M
In the early morning, a park ranger in a canoe is observing wildlife on
the nearby shore. The Earth’s gravitational force on the ranger is 760 N
downward and its gravitational force on the boat is 190 N downward.
The water keeps the canoe afloat by exerting a 950 N force upward on it.
Draw a free-body diagram of the canoe.
S O L U T I O N
1. Identify the forces acting on the object and the directions of the forces.
• The Earth exerts a force of 190 N downward on the canoe.
• The park ranger exerts a force of 760 N downward on the canoe.
• The water exerts an upward force of 950 N on the canoe.
2. Draw a diagram to represent the isolated object.
The canoe can be represented by a simple outline, as shown in (a).
3. Draw and label vector arrows for all external forces acting on the object.
A free-body diagram of the canoe will show all the forces acting on the canoe
as if the forces are acting on the center of the canoe. First, draw and label the
gravitational force acting on the canoe, which is directed toward the center
of Earth, as shown in (b). Be sure that the length of the arrow approximately
represents the magnitude of the force.
Next, draw and label the downward force that is exerted on the boat by the
Earth’s gravitational attraction on the ranger, as shown in (c). Finally, draw
and label the upward force exerted by the water on the canoe as shown in (d).
Diagram (d) is the completed free-body diagram of the floating canoe.
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
(a)
(b)
(c) (d)
FEarth-on-canoe
FEarth-on-canoe FEarth-on-canoe
Fwater-on-canoe
Franger-on-canoe Franger-on-canoe

32
NAME ______________________________________ DATE _______________ CLASS ____________________
1. After a skydiver jumps from a plane, the only force initially acting on
the diver is Earth’s gravitational attraction. After about ten seconds of
falling, air resistance on the diver will have increased so that its magni-
tude on the diver is now equal in magnitude to Earth’s gravitational force
on the diver. At this time, a diver in a belly-down position will be falling
at a constant speed of about 190 km/h.
a. Draw a free-body diagram of the skydiver when the diver initially
leaves the plane.
b. Draw a free-body diagram of the skydiver at the tenth second of
the falling.
2. A chef places an open sack of flour on a kitchen scale. The scale reading
of 40 N indicates that the scale is exerting an upward force of 40 N on
the sack. The magnitude of this force equals the magnitude of the force
of Earth’s gravitational attraction on the sack. The chef then exerts an
upward force of 10 N on the bag and the scale reading falls to 30 N.
Draw a free-body diagram of the latter situation.
3. A music box within the toy shown below plays tunes when the toy is
pushed along the floor. As a child pushes along the handlebars with
a force of 5 N, the floor exerts a force of 13 N directly upward on the toy.
The Earth’s gravitational force on the toy is 10 N downward while inter-
actions between the wheels and the floor produce a backward force of
2 N on the toy as it moves. Draw a free-body diagram of the toy as it is
being pushed.
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem B 33
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem B
DETERMINING NET FORCE
P R O B L E M
The muscle responsible for closing the mouth is the strongest muscle in the
human body.It can exert a force greater than that exerted by a man lifting a
mass of 400 kg.Richard Hoffman of Florida recorded the force of biting at
4.33 103 N.If each force shown in the diagram below has a magnitude
equal to the force of Hoffman’s bite,determine the net force.
S O L U T I O N
Define the problem, and identify the variables.
Given: F1 = −4.33 × 103
N
F2 = 4.33 × 103
N
F3 = 4.33 × 103
N
Unknown: Fnet = ? qnet = ?
Diagram:
q = –60.0°
F1 = –4.33 × 103 N
F2 = 4.33 × 103 N
F3 = 4.33 × 103 N
Select a coordinate system, and apply it to the free-body diagram: Let F1 lie
along the negative y-axis and F2 lie along the positive x-axis. Now F3 must be re-
solved into x and y components.
Find the x and y components of all vectors: As indicated in the sketch, the angle
between F3 and the x-axis is 60.0°. Because this angle is in the quadrant bounded
by the positive x and negative y axes, it has a negative value.
F3,x
= F3(cos q) = (4.33 × 103
N) [cos (−60.0°)] = 2.16 × 103
N
F3,y
= F3(sin q) = (4.33 × 103
N) [sin (−60.0°)] = −3.75 × 103
N
Find the net external force in both the x and y directions.
For the x direction: ΣFx = F2 + F3,x = Fx,net
ΣFx = 4.33 × 103
N + 2.16 × 103
N = 6.49 × 103
N
For the y direction: ΣFy = F1 + F3,y = Fy,net
ΣFy = (−4.33 × 103
N) + (−3.75 × 103
N) = −8.08 × 103
N
Find the net external force.
Use the Pythagorean theorem to calculate Fnet. Use qnet = tan−1

F
F
x
y,
,
n
n
e
e
t
t

to find
the angle between the net force and the x-axis.
Fnet =

(F
x,
ne
t)
2
+
(
F
y,n
et
)

Fnet =

(6
.4
9
×
1
03
N
)2
+
(
−
8.
08
×
1
03
N
)2
=

10
.7
4
×
1
07
N
2

Fnet = 1.036 × 104
N
1. DEFINE
2. PLAN
3. CALCULATE

34
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. Joe Ponder, from North Carolina, once used his teeth to lift a pumpkin
with a mass of 275 kg. Suppose Ponder has a mass of 75 kg, and he
stands with each foot on a platform and lifts the pumpkin with an at-
tached rope. If he holds the pumpkin above the ground between the
platforms, what is the force exerted on his feet? (Draw a free-body dia-
gram showing all of the forces present on Ponder.)
2. In 1994, Vladimir Kurlovich, from Belarus, set the record as the world’s
strongest weightlifter. He did this by lifting and holding above his head
a barbell whose mass was 253 kg. Kurlovich’s mass at the time was
roughly 133 kg. Draw a free-body diagram showing the various forces
in the problem. Calculate the normal force exerted on each of
Kurlovich’s feet during the time he was holding the barbell.
3. The net force exerted by a woodpecker’s head when its beak strikes a
tree can be as large as 4.90 N, assuming that the bird’s head has a mass
of 50.0 g. Assume that two different muscles pull the woodpecker’s head
forward and downward, exerting a net force of 4.90 N. If the forces ex-
erted by the muscles are at right angles to each other and the muscle
that pulls the woodpecker’s head downward exerts a force of 1.70 N,
what is the magnitude of the force exerted by the other muscle? Draw a
free-body diagram showing the forces acting on the woodpecker’s head.
4. About 50 years ago, the San Diego Zoo, in California, had the largest go-
rilla on Earth: its mass was about 3.10 × 102
kg. Suppose a gorilla with this
mass hangs from two vines, each of which makes an angle of 30.0° with
the vertical. Draw a free-body diagram showing the various forces, and
find the magnitude of the force of tension in each vine.What would hap-
pen to the tensions if the upper ends of the vines were farther apart?
5. The mass of Zorba, a mastiff born in London, England, was measured
in 1989 to be 155 kg. This mass is roughly the equivalent of the com-
bined masses of two average adult male mastiffs. Suppose Zorba is
placed in a harness that is suspended from the ceiling by two cables that
are at right angles to each other. If the tension in one cable is twice as
large as the tension in the other cable, what are the magnitudes of the
two tensions? Assume the mass of the cables and harness to be negligi-
ble. Before doing the calculations, draw a free-body diagram showing
the forces acting on Zorba.
qnet = tan−1

−
6
8
.4
.0
9
8
×
×
1
1
0
0
3
3
N
N

=
The net force is larger than the individual forces, but it is not quite three times as
large as any one force, which would be the case if all three forces were acting in
one direction only. The angle is negative to indicate that it is in the quadrant
below the positive x-axis, where the values along the y-axis are negative. The net
force is 1.036 × 104
N at an angle of 51.2° below the positive x-axis.
−51.2°
4. EVALUATE

Problem C 35
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem C
NEWTON’S SECOND LAW
P R O B L E M
A 1.5 kg ball has an acceleration of 9.0 m/s2
to the left.What is the net
force acting on the ball?
S O L U T I O N
Given: m = 1.5 kg
a = 9.0 m/s2
to the left
Unknown: F = ?
Use Newton’s second law, and solve for F.
ΣF = ma
Because there is only one force,
ΣF = F
F = (1.5 kg)(9.0 m/s2
) = 14 N
F = 14 N to the left
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. David Purley, a racing driver, survived deceleration from 173 km/h to
0 km/h over a distance of 0.660 m when his car crashed. Assume that
Purley’s mass is 70.0 kg. What is the average force acting on him during
the crash? Compare this force to Purley’s weight. (Hint: Calculate the
average acceleration first.)
2. A giant crane in Washington, D. C. was tested by lifting a 2.232 × 106
kg
load.
a. Find the magnitude of the force needed to lift the load with a net
acceleration of 0 m/s2
.
b. If the same force is applied to pull the load up a smooth slope
that makes a 30.0° angle with the horizontal, what would be the
acceleration?
3. When the click beetle jumps in the air, its acceleration upward can be as
large as 400.0 times the acceleration due to gravity. (An acceleration
this large would instantly kill any human being.) For a beetle whose
mass is 40.00 mg, calculate the magnitude of the force exerted by the
beetle on the ground at the beginning of the jump with gravity taken
into account. Calculate the magnitude of the force with gravity ne-
glected. Use 9.807 m/s2
as the value for free-fall acceleration.

36
NAME ______________________________________ DATE _______________ CLASS ____________________
4. In 1994, a Bulgarian athlete named Minchev lifted a mass of 157.5 kg.
By comparison, his own mass was only 54.0 kg. Calculate the force act-
ing on each of his feet at the moment he was lifting the mass with an
upward acceleration of 1.00 m/s2
. Assume that the downward force on
each foot is the same.
5. In 1967, one of the high school football teams in California had a tackle
named Bob whose mass was 2.20 × 102
kg. Suppose that after winning a
game the happy teammates throw Bob up in the air but fail to catch
him. When Bob hits the ground, his average upward acceleration over
the course of the collision is 75.0 m/s2
. (Note that this acceleration has a
much greater magnitude than free-fall acceleration.) Find the average
force that the ground exerts on Bob during the collision.
6. The whale shark is the largest type of fish in the world. Its mass can be
as large as 2.00 × 104
kg, which is the equivalent mass of three average
adult elephants. Suppose a crane lifts a net with a 2.00 × 104
kg whale
shark off the ground. The net is steadily accelerated from rest over an
interval of 2.5 s until the net reaches a speed of 1.0 m/s. Calculate the
magnitude of the tension in the cable pulling the net.
7. The largest toad ever caught had a mass of 2.65 kg. Suppose a toad with
this mass is placed on a metal plate that is attached to two cables, as
shown in the figure below. If the plate is pulled upward so that it has a
net acceleration of 2.55 m/s2
, what is magnitude of the tension in the
cables? (The plate’s weight can be disregarded.)
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
q1
=45°
Fg =26 N
FT,1 FT,2
q2
=45°
8. In 1991, a lobster with a mass of 20.0 kg was caught off the coast of
Nova Scotia, Canada. Imagine this lobster involved in a friendly tug of
war with several smaller lobsters on a horizontal plane at the bottom of
the sea. Suppose the smaller lobsters are able to drag the large lobster,
so that after the large lobster has been moved 1.55 m its speed is
0.550 m/s. If the lobster is initially at rest, what is the magnitude of the
net force applied to it by the smaller lobsters? Assume that friction and
resistance due to moving through water are negligible.
9. A 0.5 mm wire made of carbon and manganese can just barely support
the weight of a 70.0 kg person. Suppose this wire is used to lift a 45.0 kg
load. What maximum upward acceleration can be achieved without
breaking the wire?

Problem C 37
NAME ______________________________________ DATE _______________ CLASS ____________________
10. The largest hydraulic turbines in the world have shafts with individual
masses that equal 3.18 × 105
kg. Suppose such a shaft is delivered to the
assembly line on a trailer that is pulled with a horizontal force of
81.0 kN. If the force of friction opposing the motion is 62.0 kN, what is
the magnitude of the trailer’s net acceleration? (Disregard the mass of
the trailer.)
11. An average newborn blue whale has a mass of 3.00 × 103
kg. Suppose
the whale becomes stranded on the shore and a team of rescuers tries
to pull it back to sea. The rescuers attach a cable to the whale and pull it
at an angle of 20.0° above the horizontal with a force of 4.00 kN. There
is, however, a horizontal force opposing the motion that is 12.0 percent
of the whale’s weight. Calculate the magnitude of the whale’s net accel-
eration during the rescue pull.
12. One end of the cable of an elevator is attached to the elevator car, and
the other end of the cable is attached to a counterweight. The counter-
weight consists of heavy metal blocks with a total mass almost the same
as the car’s. By using the counterweight, the motor used to lift and
lower the car needs to exert a force that is only about equal to the total
weight of the passengers in the car. Suppose the car with passengers has
a mass of 1.600 × 103
kg and the counterweight has a mass of 1.200 ×
103
kg. Calculate the magnitude of the car’s net acceleration as it falls
from rest at the top of the shaft to the ground 25.0 m below. Calculate
the car’s final speed.
13. The largest squash ever grown had a mass of 409 kg. Suppose you want
to push a squash with this mass up a smooth ramp that is 6.00 m long
and that makes a 30.0° angle with the horizontal. If you push the
squash with a force of 2080 N up the incline, what is
a. the net force exerted on the squash?
b. the net acceleration of the squash?
c. the time required for the squash to reach the top of the ramp?
14. A very thin boron rod with a cross-section of 0.10 mm × 0.10 mm can
sustain a force of 57 N. Assume the rod is used to pull a block along a
smooth horizontal surface.
a. If the maximum force accelerates the block by 0.25 m/s2
, find the
mass of the block.
b. If a second force of 24 N is applied in the direction opposite the
57 N force, what would be the magnitude of the block’s new
acceleration?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

38
NAME ______________________________________ DATE _______________ CLASS ____________________
15. A hot-air balloon with a total mass of 2.55 × 103
kg is being pulled
down by a crew tugging on a rope. The tension in the rope is 7.56 ×
103
N at an angle of 72.3° below the horizontal. This force is aided in
the vertical direction by the balloon’s weight and is opposed by a buoy-
ant force of 3.10 × 104
N that lifts the balloon upward. A wind blowing
from behind the crew exerts a horizontal force of 920 N on the balloon.
a. What is the magnitude and direction of the net force?
b. Calculate the magnitude of the balloon’s net acceleration.
c. Suppose the balloon is 45.0 m above the ground when the crew be-
gins pulling it down. How far will the balloon travel horizontally by
the time it reaches the ground if the balloon is initially at rest?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 39
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Forces and the Laws of Motion
Problem D
COEFFICIENTS OF FRICTION
P R O B L E M
A 20.0 kg trunk is pushed across the floor of a moving van by a horizontal
force. If the coefficient of kinetic friction between the trunk and the floor
is 0.255, what is the magnitude of the frictional force opposing the ap-
plied force?
S O L U T I O N
Given: m = 20.0 kg
mk = 0.255
g = 9.81 m/s2
Unknown: Fk = ?
Use the equation for frictional force, substituting mg for the normal force Fn.
Fk = mkFn = mkmg
Fk = (0.255)(20.0 kg)(9.81 m/s2
)
Fk = 50.0 N
ADDITIONAL PRACTICE
1. The largest flowers in the world are the Rafflesia arnoldii, found in
Malaysia. A single flower is almost a meter across and has a mass up to
11.0 kg. Suppose you cut off a single flower and drag it along the flat
ground. If the coefficient of kinetic friction between the flower and the
ground is 0.39, what is the magnitude of the frictional force that must
be overcome?
2. Robert Galstyan, from Armenia, pulled two coupled railway wagons a
distance of 7 m using his teeth. The total mass of the wagons was about
2.20 × 105
kg. Of course, his job was made easier by the fact that the
wheels were free to roll. Suppose the wheels are blocked and the coeffi-
cient of static friction between the rails and the sliding wheels is 0.220.
What would be the magnitude of the minimum force needed to move
the wagons from rest? Assume that the track is horizontal.
3. The steepest street in the world is Baldwin Street in Dunedin, New
Zealand. It has an inclination angle of 38.0° with respect to the hori-
zontal. Suppose a wooden crate with a mass of 25.0 kg is placed on
Baldwin Street. An additional force of 59 N must be applied to the crate
perpendicular to the pavement in order to hold the crate in place. If the
coefficient of static friction between the crate and the pavement is
0.599, what is the magnitude of the frictional force?

40
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. Now imagine that a child rides a wagon down Baldwin Street. In order
to keep from moving too fast, the child has secured the wheels of the
wagon so that they do not turn. The wagon and child then slide down
the hill at a constant velocity. What is the coefficient of kinetic friction
between the tires of the wagon and the pavement?
5. The steepest railroad track that allows trains to move using their own
locomotion and the friction between their wheels and the track is lo-
cated in France. The track makes an angle of 5.2° with the horizontal.
Suppose the rails become greasy and the train slides down the track
even though the wheels are locked and held in place with blocks. If the
train slides down the tracks with a constant velocity, what is the coeffi-
cient of kinetic friction between the wheels and track?
6. Walter Arfeuille of Belgium lifted a 281.5 kg load off the ground using
his teeth. Suppose Arfeuille can hold just three times that mass on a
30.0° slope using the same force. What is the coefficient of static fric-
tion between the load and the slope?
7. A blue whale with a mass of 1.90 × 105
kg was caught in 1947. What is
the magnitude of the minimum force needed to move the whale along
a horizontal ramp if the coefficient of static friction between the ramp’s
surface and the whale is 0.460?
8. Until 1979, the world’s easiest driving test was administered in Egypt.
To pass the test, one needed only to drive about 6 m forward, stop, and
drive the same distance in reverse. Suppose that at the end of the 6 m
the car’s brakes are suddenly applied and the car slides to a stop. If the
force required to stop the car is 6.0 × 103
N and the coefficient of ki-
netic friction between the tires and pavement is 0.77, what is the mag-
nitude of the car’s normal force? What is the car’s mass?
9. The heaviest train ever pulled by a single engine was over 2 km long.
Suppose a force of 1.13 × 108
N is needed to overcome static friction in
the train’s wheels. If the coefficient of static friction is 0.741, what is the
train’s mass?
10. In 1994, a 3.00 × 103
kg pancake was cooked and flipped in Manchester,
England. If the pancake is placed on a surface that is inclined 31.0° with
respect to the horizontal, what must the coefficient of kinetic friction
be in order for the pancake to slide down the surface with a constant
velocity? What would be the magnitude of the frictional force acting on
the pancake?

Problem E 41
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Forces and the Laws of Motion
Problem E
OVERCOMING FRICTION
P R O B L E M
In 1988, a very large telephone constructed by a Dutch telecommunica-
tions company was demonstrated in the Netherlands. Suppose this tele-
phone is towed a short distance by a horizontal force equal to 8670 N, so
that the telephone’s net acceleration is 1.30 m/s2
. Given that the coeffi-
cient of kinetic friction between the phone and the ground is 0.120, calcu-
late the mass of the telephone.
S O L U T I O N
Given: Fapplied = 8670 N
anet = 1.30 m/s2
mk = 0.120
g = 9.81 m/s2
Unknown: m = ?
Choose the equation(s) or situation: Apply Newton’s second law to describe the
forces acting on the telephone.
Fnet = manet = Fapplied − Fk
The frictional force, Fk, depends on the normal force, Fn, exerted on the tele-
phone. For a horizontal surface, the normal force equals the telephone’s weight.
Fk = mkFn = mk(mg)
Substituting the equation for Fk into the equation for Fnet provides an equation
with all known and unknown variables.
manet = Fapplied − mkmg
manet + mkmg = Fapplied
m(anet + mkg) = Fapplied
m = 
an
F
e
a
t
p
+
pli
m
ed
kg

Substitute the values into the equations and solve:
m =
m =
m = =
Because the mass is constant, the sum of the acceleration terms in the denomina-
tor must be constant for a constant applied force. Therefore, the net acceleration
decreases as the coefficient of friction increases.
3.50 × 103
kg
8670 N

2.48 m/s2
8670 N

1.30 m/s2
+ 1.18 m/s2
8670 N

1.30 m/s2
+ (0.120)(9.81 m/s2
)
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

42
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. Isaac Newton developed the laws of mechanics. Brian Newton put
those laws into application when he ran a marathon in about 8.5 h
while carrying a bag of coal. Suppose Brian Newton wants to remove
the bag from the finish line. He drags the bag with an applied horizon-
tal force of 130 N, so that the bag as a net acceleration of 1.00 m/s2
.
If the coefficient of kinetic friction between the bag and the pavement
is 0.158, what is the mass of the bag of coal?
2. The most massive car ever built was the official car of the General Sec-
retary of the Communist Party in the former Soviet Union. Suppose
this car is moving down a 10.0° slope when the driver suddenly applies
the brakes. The net force acting on the car as it stops is –2.00 × 104
N. If
the coefficient of kinetic friction between the car’s tires and the pave-
ment is 0.797, what is the car’s mass? What is the magnitude of the
normal force that the pavement exerts on the car?
3. Suppose a giant hamburger slides down a ramp that has a 45.0° incline.
The coefficient of kinetic friction between the hamburger and the
ramp is 0.597, so that the net force acting on the hamburger is 6.99 ×
103
N. What is the mass of the hamburger? What is the magnitude of
the normal force that the ramp exerts on the hamburger?
4. An extremely light, drivable car with a mass of only 9.50 kg was built in
London. Suppose that the wheels of the car are locked, so that the car
no longer rolls. If the car is pushed up a 30.0° slope by an applied force
of 80.0 N, the net acceleration of the car is 1.64 m/s2
. What is the coef-
ficient of kinetic friction between the car and the incline?
5. Cleopatra’s Needle, an obelisk given by the Egyptian government to
Great Britain in the nineteenth century, is 20+ m tall and has a mass of
about 1.89 × 105
kg. Suppose the monument is lowered onto its side
and dragged horizontally to a new location. An applied force of
7.6 × 105
N is exerted on the monument, so that its net acceleration is
0.11 m/s2
. What is the magnitude of the frictional force?
6. Snowfall is extremely rare in Dunedin, New Zealand. Nevertheless,
suppose that Baldwin Street, which has an incline of 38.0°, is covered
with snow and that children are sledding down the street. A sled and
rider move downhill with a constant acceleration. What would be the
magnitude of the sled’s net acceleration if the coefficient of kinetic fric-
tion between the snow and the sled’s runners is 0.100? Does the accel-
eration depend on the masses of the sled and rider?
7. The record speed for grass skiing was set in 1985 by Klaus Spinka, of
Austria. Suppose it took Spinka 6.60 s to reach his top speed after he
started from rest down a slope with a 34.0° incline. If the coefficient of
kinetic friction between the skis and the grass was 0.198, what was the
magnitude of Spinka’s net acceleration? What was his speed after 6.60 s?
ADDITIONAL PRACTICE

Problem A 43
NAME ______________________________________ DATE _______________ CLASS ____________________
Work and Energy
Problem A
WORK
P R O B L E M
The largest palace in the world is the Imperial Palace in Beijing, China.
Suppose you were to push a lawn mower around the perimeter of a rec-
tangular area identical to that of the palace, applying a constant horizon-
tal force of 60.0 N. If you did 2.05 × 105
J of work, how far would you have
pushed the lawn mower? If the Imperial Palace is 9.60 × 102
m long, how
wide is it?
S O L U T I O N
Given: F = 60.0 N
W = 2.05 × 105
J
x = 9.60 × 102
m
Unknown: d = ?
y = ?
Use the equation for net work done by a constant force.
W = Fd(cos q)
To calculate the width, y, recall that the perimeter of an area equals the sum of
twice its width and twice its length.
d = 2x + 2y
Rearrange the equations to solve for d and y. Note that the force is applied in the
direction of the displacement, so q = 0°.
d = 
F(c
W
os q)
 = 
(60
2
.
.
0
05
N
×
)(
1
c
0
o
5
s
J
0°)

d =
y = 
d −
2
2x
 =
y = = 
1.50 ×
2
103
m

y = 7.50 × 102
m
3.42 × 103
m − 1.92 × 103
m

2
3.42 × 103
m − (2)(9.60 × 102
m)

2
3.42 × 103
m
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. Lake Point Tower in Chicago is the tallest apartment building in the
United States (although not the tallest building in which there are
apartments). Suppose you take the elevator from street level to the roof
of the building. The elevator moves almost the entire distance at con-
stant speed, so that it does 1.15 × 105
J of work on you as it lifts the

44
NAME ______________________________________ DATE _______________ CLASS ____________________
entire distance. If your mass is 60.0 kg, how tall is the building?
Ignore the effects of friction.
2. In 1985 in San Antonio, Texas, an entire hotel building was moved several
blocks on 36 dollies. The mass of the building was about 1.45 × 106
kg. If
1.00 × 102
MJ of work was done to overcome the force of resistance that
was just 2.00 percent of the building’s weight, how far was the building
moved?
3. A hummingbird has a mass of about 1.7 g. Suppose a hummingbird
does 0.15 J of work against gravity, so that it ascends straight up with a
net acceleration of 1.2 m/s2
. How far up does it move?
4. In 1453, during the siege of Constantinople, the Turks used a cannon
capable of launching a stone cannonball with a mass of 5.40 × 102
kg.
Suppose a soldier dropped a cannonball with this mass while trying to
load it into the cannon. The cannonball rolled down a hill that made
an angle of 30.0° with the horizontal. If 5.30 × 104
J of work was done
by gravity on the cannonball as it rolled down a hill, how far did it roll?
5. The largest turtle ever caught in the United States had a mass of over
800 kg. Suppose this turtle were raised 5.45 m onto the deck of a re-
search ship. If it takes 4.60 × 104
J of work to lift the turtle this distance
at a constant velocity, what is the turtle’s weight?
6. During World War II, 16 huge wooden hangers were built for United
States Navy airships. The hangars were over 300 m long and had a maxi-
mum height of 52.0 m. Imagine a 40.0 kg block being lifted by a winch
from the ground to the top of the hangar’s ceiling. If the winch does 2.08
× 104
J of work in lifting the block, what force is exerted on the block?
7. The Warszawa Radio mast in Warsaw, Poland, is 646 m tall, making it
the tallest human-built structure. Suppose a worker raises some tools
to the top of the tower by means of a small elevator. If 2.15 × 105
J of
work is done in lifting the tools, what is the force exerted on them?
8. The largest mincemeat pie ever created had a mass of 1.02 × 103
kg.
Suppose that a pie with this mass slides down a ramp that is 18.0 m
long and is inclined to the ground by 10.0°. If the coefficient of kinetic
friction is 0.13, what is the net work done on the pie during its descent?
9. The longest shish kebab ever made was 881.0 m long. Suppose the meat
and vegetables need to be delivered in a cart from one end of this shish
kebab’s skewer to the other end. A cook pulls the cart by applying a
force of 40.00 N at an angle of 45.00° above the horizontal. If the force
of friction acting on the cart is 28.00 N, what is the net work done on
the cart and its contents during the delivery?
10. The world’s largest chandelier was created by a company in South
Korea and hangs in one of the department stores in Seoul, South Korea.
The chandelier’s mass is about 9.7 × 103
kg. Consider a situation in
which this chandelier is placed in a wooden crate whose mass is negli-
gible. The chandelier is then pulled along a smooth horizontal surface
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem A 45
NAME ______________________________________ DATE _______________ CLASS ____________________
by two forces that are parallel to the smooth surface, are at right angles
to each other, and are applied 45° to either side of the direction in
which the chandelier is moving. If each of these forces is 1.2 × 103
N,
how much work must be done on the chandelier to pull it 12 m?
11. The world’s largest flag, which was manufactured in Pennsylvania, has
a length of 154 m and a width of 78 m. The flag’s mass is 1.24 × 103
kg,
which may explain why the flag has never been flown from a flagpole.
Suppose this flag is being pulled by two forces: a force of 8.00 × 103
N
to the east and a force of 5.00 × 103
N that is directed 30.0° south of
east. How much work is done in moving the flag 20.0 m directly south?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

46
NAME ______________________________________ DATE _______________ CLASS ____________________
Work and Energy
Problem B
KINETIC ENERGY
P R O B L E M
Silvana Cruciata from Italy set a record in one-hour running by running
18.084 km in 1.000 h. If Cruciata’s kinetic energy was 694 J, what was her
mass?
S O L U T I O N
Given: ∆x = 18.084 km = 1.8084 × 104
m
∆t = 1.000 h = 3.600 × 103
s
KE = 694 J
Unknown: m = ?
Choose the equation(s) or situation: Use the definition of average velocity to
calculate Cruciata’s speed.
vavg = 
∆
∆
x
t

Use the equation for kinetic energy, using vavg for the velocity term, to solve for
m.
KE = 
1
2
 m vavg
2
Rearrange the equation(s) to isolate the unknown(s): Substitute the average
velocity equation into the equation for kinetic energy and solve for m.
m = 
v
2
a
K
vg
E
2
 = = 
2K
∆
E
x
∆
2
t2

m = =
If the average speed is rounded to 5.0 m/s, and the kinetic energy is rounded to
700 J, the estimated mass is 56 kg, which is close to the calculated value.
55.0 kg
(2)(694 J)(3.600 × 103
s)2

(1.8084 × 104
m)2
2KE


∆
∆
x
t


2
1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. In 1994, Leroy Burrell of the United States set what was then a new world
record for the men’s 100 m run. He ran the 1.00 × 102
m distance in 9.85 s.
Assuming that he ran with a constant speed equal to his average speed, and
his kinetic energy was 3.40 × 103
J, what was Burrell’s mass?
2. The fastest helicopter, the Westland Lynx, has a top speed of 4.00 ×
102
km/h. If its kinetic energy at this speed is 2.10 × 107
J, what is the
helicopter’s mass?

Problem B 47
NAME ______________________________________ DATE _______________ CLASS ____________________
3. Dan Jansen of the United States won a speed-skating competition at the
1994 Winter Olympics in Lillehammer, Norway. He did this by skating
500 m with an average speed of 50.3 km/h. If his kinetic energy was
6.54 × 103
J, what was his mass?
4. In 1987, the fastest auto race in the United States was the Busch Clash in
Daytona, Florida. That year, the winner’s average speed was about
318 km/h. Suppose the kinetic energy of the winning car was 3.80 MJ.
What was the mass of the car and its driver?
5. In 1995, Karine Dubouchet of France reached a record speed in downhill
skiing. If Dubouchet’s mass was 51.0 kg, her kinetic energy would have
been 9.96 × 104
J. What was her speed?
6. Susie Maroney from Australia set a women’s record in long-distance
swimming by swimming 93.625 km in 24.00 h.
a. What was Maroney’s average speed?
b. If Maroney’s mass was 55 kg, what was her kinetic energy?
7. The brightest, hottest, and most massive stars are the brilliant blue stars
designated as spectral class O. If a class O star with a mass of 3.38 × 1031
kg
has a kinetic energy of 1.10 × 1042
J, what is its speed? Express your answer
in km/s (a typical unit for describing the speed of stars).
8. The male polar bear is the largest land-going predator. Its height when
standing on its hind legs is over 3 m and its mass, which is usually
around 500 kg, can be as large as 680 kg. In spite of this bulk, a running
polar bear can reach speeds of 56.0 km/h.
a. Determine the kinetic energy of a running polar bear, using the
maximum values for its mass and speed.
b. What is the ratio of the polar bear’s kinetic energy to the kinetic
energy of Leroy Burrell, as given in item 1?
9. Escape speed is the speed required for an object to leave Earth’s orbit. It
is also the minimum speed an incoming object must have to avoid being
captured and pulled into an orbit around Earth. The escape speed for a
projectile launched from Earth’s surface is 11.2 km/s. Suppose a meteor
is pulled toward Earth’s surface and, as a meteorite, strikes the ground
with a speed equal to this escape speed. If the meteorite has a diameter of
about 3 m and a mass of 2.3 × 105
kg, what is its kinetic energy at the
instant it collides with Earth’s surface?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

48
NAME ______________________________________ DATE _______________ CLASS ____________________
Work and Energy
Problem C
WORK-KINETIC ENERGY THEOREM
P R O B L E M
The Great Pyramid of Khufu in Egypt, used to have a height of 147 m and
sides that sloped at an angle of 52.0° with respect to the ground. Stone
blocks with masses of 1.37 × 104
kg were used to construct the pyramid.
Suppose that a block with this mass at rest on top of the pyramid begins
to slide down the side. Calculate the block’s kinetic energy at ground level
if the coefficient of kinetic friction is 0.45.
S O L U T I O N
Given: m = 1.37 × 104
kg
h = 147 m
g = 9.81 m/s2
q = 52.0°
mk = 0.45
vi = 0 m/s
Unknown: KEf = ?
Choose the equation(s) or situation: The net work done by the block as it slides
down the side of the pyramid can be expressed by using the definition of work in
terms of net force. Because the net force is parallel to the displacement, the net
work is simply the net force multiplied by the displacement. It can also be ex-
pressed in terms of changing kinetic energy by using the work–kinetic energy
theorem.
Wnet = Fnetd
Wnet = ∆KE
The net force on the block equals the difference between the component of the
force due to free-fall acceleration along the side of the pyramid and the frictional
force resisting the downward motion of the block.
Fnet = mg(sin q) − Fk = mg(sin q) − mkmg(cos q)
The distance the block travels along the side of the pyramid equals the height of
the pyramid divided by the sine of the angle of the side’s slope.
h = d(sin q)
d = 
sin
h
q

Because the block is initially at rest, its initial kinetic energy is zero, and the
change in kinetic energy equals the final kinetic energy.
∆KE = KEf − KEi = KEf
1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem C 49
NAME ______________________________________ DATE _______________ CLASS ____________________
Rearrange the equation(s) to isolate the unknown(s): Combining these equa-
tions yields the following expression for the final kinetic energy.
KEf = Fnetd = mg(sin q − mk cos q)

sin
h
q


KEf = mgh
1 − 
ta
m
n
k
q


KEf = (1.37 × 104
kg)(9.81 m/s2
)(147 m)
1 − 
tan
0.
5
4
2
5
.0°


KEf = (1.37 × 104
kg)(9.81 m/s2
)(147 m)(1.00 − 0.35)
KEf = (1.37 × 104
kg)(9.81 m/s2
)(147 m)(0.65)
KEf =
Note that the net force, and thus the final kinetic energy, is about two-thirds of
what it would be if the side of the pyramid were frictionless.
1.3 × 107
J
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The tops of the towers of the Golden Gate Bridge, in San Francisco, are
227 m above the water. Suppose a worker drops a 655 g wrench from the
top of a tower. If the average force of air resistance is 2.20 percent of the
force of free fall, what will the kinetic energy of the wrench be when it
hits the water?
2. Bonny Blair of the United States set a world record in speed skating when
she skated 5.00 × 102
m with an average speed of 12.92 m/s. Suppose
Blair crossed the finish line at this speed and then skated to a stop. If the
work done by friction over a certain distance was −2830 J, what would
Blair’s kinetic energy be, assuming her mass to be 55.0 kg.
3. The CN Tower in Toronto, Canada, is 553 m tall, making it the tallest
free-standing structure in the world. Suppose a chunk of ice with a mass
of 25.0 g falls from the top of the tower. The speed of the ice is 30.0 m/s
as it passes the restaurant, which is located 353 m above the ground.
What is the magnitude of the average force due to air resistance?
4. In 1979, Dr. Hans Liebold of Germany drove a race car 12.6 km with an
average speed of 404 km/h. Suppose Liebold applied the brakes to reduce
his speed. What was the car’s final speed if −3.00 MJ of work was done by
the brakes? Assume the combined mass of the car and driver to be 1.00 ×
103
kg.
5. The summit of Mount Everest is 8848.0 m above sea level, making it the
highest summit on Earth. In 1953, Edmund Hillary was the first person
to reach the summit. Suppose upon reaching there, Hillary slid a rock
with a 45.0 g mass down the side of the mountain. If the rock’s speed is

50
NAME ______________________________________ DATE _______________ CLASS ____________________
27.0 m/s when it is 8806.0 m above sea level, how much work was done
on the rock by air resistance?
6. In 1990, Roger Hickey of California reached a speed 35.0 m/s on his
skateboard. Suppose it took 21 kJ of work for Roger to reach this speed
from a speed of 25.0 m/s. Calculate Hickey’s mass.
7. At the 1984 Winter Olympics, William Johnson of the United States
reached a speed of 104.5 km/h in the downhill skiing competition. Sup-
pose Johnson left the slope at that speed and then slid freely along a hori-
zontal surface. If the coefficient of kinetic friction between the skis and
the snow was 0.120 and his final speed was half of his initial speed, find
the distance William traveled.
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 51
NAME ______________________________________ DATE _______________ CLASS ____________________
Work and Energy
Problem D
POTENTIAL ENERGY
P R O B L E M
In 1993, Javier Sotomayor from Cuba set a record in the high jump by
clearing a vertical distance of 2.45 m. If the gravitational potential energy
associated with Sotomayor at the top point of his trajectory was 1.59
103
J, what was his mass?
S O L U T I O N
Given: h = 2.45 m
g = 9.81 m/s2
PEg = 1.59 × 103
J
Unknown: m = ?
Use the equation for gravitational potential energy, and rearrange it to solve
for m.
PEg = mgh
m = 
P
g
E
h
g

m = = 66.2 kg
(1.59 × 103
J)

9.81 
m
s2
s2
(2.45 m)
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1992, Ukrainian Sergei Bubka used a short pole to jump to a height
of 6.13 m. If the maximum potential energy associated with Bubka was
4.80 kJ at the midpoint of his jump, what was his mass?
2. Naim Suleimanoglu of Turkey has a mass of about 62 kg, yet he can lift
nearly 3 times this mass. (This feat has earned Suleimanoglu the nick-
name of “Pocket Hercules.”) If the potential energy associated with a
barbell lifted 1.70 m above the floor by Suleimanoglu is 3.04 × 103
J,
what is the barbell’s mass?
3. In 1966, a special research cannon built in Arizona shot a projectile to a
height of 180 km above Earth’s surface. The potential energy associated
with the projectile when its altitude was 10.0 percent of the maximum
height was 1.48 × 107
J. What was the projectile’s mass? Assume that
constant free-fall acceleration at this altitude is the same as at sea level.
4. The highest-caliber cannon ever built (though never used) is located in
Moscow, Russia. The diameter of the cannon’s barrel is about 89 cm,
and the cannon’s mass is 3.6 × 104
kg. Suppose this cannon were lifted
by airplane. If the potential energy associated with this cannon were

52
NAME ______________________________________ DATE _______________ CLASS ____________________
8.88 × 108
J, what would be its height above sea level? Assume that
constant free-fall acceleration at this altitude is the same as at sea level.
5. In 1987, Stefka Kostadinova from Bulgaria set a new women’s record in
high jump. It is known that the ratio of the potential energy associated
with Kostadinova at the top of her jump to her mass was 20.482 m2
/s2
.
What was the height of her record jump?
6. In 1992, David Engwall of California used a slingshot to launch a dart
with a mass of 62 g. The dart traveled a horizontal distance of 477 m.
Suppose the slingshot had a spring constant of 3.0 × 104
N/m. If the
elastic potential energy stored in the slingshot just before the dart was
launched was 1.4 × 102
J, how far was the slingshot stretched?
7. Suppose a 51 kg bungee jumper steps off the Royal Gorge Bridge, in
Colorado. The bridge is situated 321 m above the Arkansas River. The
bungee cord’s spring constant is 32 N/m, the cord’s relaxed length is
104 m, and its length is 179 m when the jumper stops falling. What is
the total potential energy associated with the jumper at the end of his
fall? Assume that the bungee cord has negligible mass.
8. Situated 4080 m above sea level, La Paz, Bolivia, is the highest capital in
the world. If a car with a mass of 905 kg is driven to La Paz from a loca-
tion that is 1860 m above sea level, what is the increase in potential
energy?
9. In 1872, a huge gold nugget with a mass of 286 kg was discovered in
Australia. The nugget was displayed for the public before it was melted
down to extract pure gold. Suppose this nugget is attached to the ceil-
ing by a spring with a spring constant of 9.50 × 103
N/m. The nugget is
released from a height of 1.70 m above the floor, and is caught when it
is no longer moving downward and is about to be pulled back up by
the elastic force of the spring.
a. If the spring stretches a total amount of 59.0 cm, what is the elas-
tic potential energy associated with the spring-nugget system?
b. What is the gravitational potential energy associated with the
nugget just before it is dropped?
c. What is the gravitational potential energy associated with the
nugget after the spring has stretched 59.0 cm?
d. What is the difference between the gravitational potential energy
values in parts (b) and (c)? How does this compare with your
answer for part (a)?
10. When April Moon set a record for flight shooting in 1981, the arrow
traveled a distance of 9.50 × 102
m. Suppose the arrow had a mass of
65.0 g, and that the angle at which the arrow was launched was 45.0°
above the horizontal.
a. What was the kinetic energy of the arrow at the instant it left
the bowstring?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 53
NAME ______________________________________ DATE _______________ CLASS ____________________
b. If the bowstring was pulled back 55.0 cm from its relaxed posi-
tion, what was the spring constant of the bowstring? (Hint:
Assume that all of the elastic potential energy stored in the bow-
string is converted to the arrow’s initial kinetic energy.)
c. Assuming that air resistance is negligible, determine the maxi-
mum height that the arrow reaches. (Hint: Equate the arrow’s ini-
tial kinetic energy to the sum of the maximum gravitational
potential energy associated with the arrow and the arrow’s kinetic
energy at maximum height.)
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

54
NAME ______________________________________ DATE _______________ CLASS ____________________
Work and Energy
Problem E
CONSERVATION OF MECHANICAL ENERGY
P R O B L E M
The largest apple ever grown had a mass of about 1.47 kg. Suppose you
hold such an apple in your hand.You accidentally drop the apple, then
manage to catch it just before it hits the ground. If the speed of the apple
at that moment is 5.42 m/s, what is the kinetic energy of the apple? From
what height did you drop it?
S O L U T I O N
Given: m = 1.47 kg
g = 9.81 m/s2
v = 5.42 m/s
Unknown: KE = ? h = ?
Choose the equation(s) or situation: Use the equations for kinetic and
gravitational potential energy.
KE = 
1
2
 mv2
PEg = mgh
The zero level for gravitational potential energy is the ground. Because the apple
ends its fall at the zero level, the final gravitational potential energy is zero.
PEg,f = 0
The initial gravitational potential energy is measured at the point from which the
apple is released.
PEg,i = mgh
The apple is initially at rest, so the initial kinetic energy is zero.
KEi = 0
The final kinetic energy is therefore:
KEf = 
1
2
 mv 2
PEg,i = (1.47 kg)(9.81 
m
s2
)h
KEf = 
1
2
(1.47 kg)
5.42 
m
s


2
Solving for KE yields the following result:
KE = KEf = 
1
2
(1.47 kg)
5.42 
m
s


2
= 21.6 J
1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. CALCULATE

Problem E 55
NAME ______________________________________ DATE _______________ CLASS ____________________
Now use the principle of conservation for mechanical energy and the calculated
quantity for KEf to evaluate h.
MEi = MEf
PEi + KEi = PEf + KEf
PEi + 0 J = 0 J + 21.6 J
mgh = 21.6 J
h = =
Note that the height of the apple can be determined without knowing the apple’s
mass. This is because the conservation equation reduces to the equation relating
speed, acceleration, and displacement: v2
= 2gh.
1.50 m
21.6 J

(1.47 kg)
9.81 
m
s2


Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. EVALUATE
ADDITIONAL PRACTICE
1. The largest watermelon ever grown had a mass of 118 kg. Suppose this
watermelon were exhibited on a platform 5.00 m above the ground. After
the exhibition, the watermelon is allowed to slide along to the ground
along a smooth ramp. How high above the ground is the watermelon at
the moment its kinetic energy is 4.61 kJ?
2. One species of eucalyptus tree, Eucalyptus regnens, grows to heights simi-
lar to those attained by California redwoods. Suppose a bird sitting on
top of one specimen of eucalyptus tree drops a nut. If the speed of the
falling nut at the moment it is 50.0 m above the ground is 42.7 m/s, how
tall is the tree? Do you need to know the mass of the nut to solve this
problem? Disregard air resistance.
3. In 1989, Michel Menin of France walked on a tightrope suspended under
a balloon nearly at an altitude of 3150 m above the ground. Suppose a
coin falls from Menin’s pocket during his walk. How high above the
ground is the coin when its speed is 60.0 m/s?
4. In 1936, Col. Harry Froboess of Switzerland jumped into the ocean from
the airship Graf Hindenburg, which was 1.20 × 102
m above the water’s
surface. Assuming Froboess had a mass of 72.0 kg, what was his kinetic
energy at the moment he was 30.0 m from the water’s surface? What was
his speed at that moment? Neglect the air resistance.
5. Suppose a motorcyclist rides a certain high-speed motorcycle. He reaches
top speed and then coasts up a hill. The maximum height reached by the
motorcyclist is 250.0 m. If 2.55 × 105
J of kinetic energy is dissipated by
friction, what was the initial speed of the motorcycle? The combined
mass of the motorcycle and motorcyclist is 250.0 kg.
6. The deepest mine ever drilled has a depth of 12.3 km (by contrast,
Mount Everest has height of 8.8 km). Suppose you drop a rock with a

56
NAME ______________________________________ DATE _______________ CLASS ____________________
mass of 120.0 g down the shaft of this mine. What would the rock’s ki-
netic energy be after falling 3.2 km? What would the potential energy as-
sociated with the rock be at that same moment? Assume no air resistance
and a constant free-fall acceleration.
7. Desperado, a roller coaster built in Nevada, has a vertical drop of 68.6 m.
The roller coaster is designed so that the speed of the cars at the end of
this drop is 35.6 m/s. Assume the cars are at rest at the start of the drop.
What percent of the initial mechanical energy is dissipated by friction?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem F 57
NAME ______________________________________ DATE _______________ CLASS ____________________
Work and Energy
Problem F
POWER
P R O B L E M
Martinus Kuiper of the Netherlands ice skated for 24 h with an average
speed of 6.3 m/s. Suppose Kuiper’s mass was 65 kg. If Kuiper provided
520 W of power to accelerate for 2.5 s, how much work did he do?
S O L U T I O N
Given: P = 520 W
∆t = 2.5 s
Unknown: W = ?
Use the equation for power and rearrange it to solve for work.
P = 
∆
W
t

W = P∆t = (520 W)(2.5 s) = 1300 J
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. The most powerful ice breaker in the world was built in the former So-
viet Union. The ship is almost 150 m long, and its nuclear engine gener-
ates 56 MW of power. How much work can this engine do in 1.0 h?
2. Reginald Esuke from Cameroon ran over 3 km down a mountain slope
in just 62.25 min. How much work was done if the power developed
during Esuke’s descent was 585.0 W?
3. The world’s tallest lighthouse is located in Japan and is 106 m tall. A
winch that provides 3.00 × 102
W of power is used to raise 14.0 kg of
equipment to the lighthouse top at a constant velocity. How long does it
take the equipment to reach the lighthouse top?
4. The first practical car to use a gasoline engine was built in London in
1826. The power generated by the engine was just 2984 W. How long
would this engine have to run to produce 3.60 × 104
J of work?
5. Dennis Joyce of the United States threw a boomerang and caught it at the
same location 3.0 min later. Suppose Joyce decided to work out while
waiting for the boomerang to return. If he expended 54 kJ of work, what
was his average power output during the workout?
6. In 1984, Don Cain threw a flying disk that stayed aloft for 16.7 s. Suppose
Cain ran up a staircase during this time, reaching a height of 18.4 m. If
his mass was 72.0 kg, how much power was needed for Cain’s ascent.

Problem A 59
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Momentum and Collisions
Problem A
MOMENTUM
P R O B L E M
The world’s most massive train ran in South Africa in 1989. Over 7 km
long, the train traveled 861.0 km in 22.67 h. Imagine that the distance was
traveled in a straight line north. If the train’s average momentum was
7.32 108
kg•m/s to the north, what was its mass?
S O L U T I O N
Given: ∆x = 861.0 km to the north
∆t = 22.67 h
pavg = 7.32 × 108

kg
s
•m
 to the north
Unknown: vavg = ? m = ?
Use the definition of average velocity to calculate vavg, and then substitute this
value for velocity in the definition of momentum to solve for mass.
vavg = 
∆
∆
x
t
 = 
(2
(
2
8
.6
6
7
1.
h
0
)
×
(3
1
6
0
0
3
0
m
s/
)
h)
 = 10.55 
m
s
 to the north
pavg = mvavg
m =
p
va
a
v
v
g
g
= = 6.94 × 107
kg
7.32 × 108

kg
s
•m



10.55 
m
s


ADDITIONAL PRACTICE
1. In 1987, Marisa Canofoglia, of Italy, roller-skated at a record-setting
speed of 40.3 km/h. If the magnitude of Canofoglia’s momentum was
6.60 × 102
kg•m/s, what was her mass?
2. In 1976, a 53 kg helicopter was built in Denmark. Suppose this heli-
copter flew east with a speed of 60.0 m/s and the total momentum of
the helicopter and pilot was 7.20 × 103
kg•m/s to the east. What was the
mass of the pilot?
3. One of the smallest planes ever flown was the Bumble Bee II, which had
a mass of 1.80 × 102
kg. If the pilot’s mass was 7.0 × 101
kg, what was
the velocity of both plane and pilot if their momentum was 2.08 ×
104
kg•m/s to the west?
4. The first human-made satellite, Sputnik I, had a mass of 83.6 kg and a
momentum with a magnitude of 6.63 × 105
kg•m/s. What was the
satellite’s speed?

60
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
5. Among the largest passenger ships currently in use, the Norway has
been in service the longest. The Norway is more than 300 m long, has a
mass of 6.9 × 107
kg, and can reach a top cruising speed of 33 km/h.
Calculate the magnitude of the ship’s momentum.
6. In 1994, a tower 22.13 m tall was built of Lego® blocks. Suppose a block
with a mass of 2.00 g is dropped from the top of this tower. Neglecting
air resistance, calculate the block’s momentum at the instant the block
hits the ground.

Problem B 61
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem B
FORCE AND IMPULSE
P R O B L E M
In 1993, a generator with a mass of 1.24 105
kg was flown from Ger-
many to a power plant in India on a Ukrainian-built plane. This consti-
tuted the heaviest single piece of cargo ever carried by a plane. Suppose
the plane took off with a speed of 101 m/s toward the southeast and then
accelerated to a final cruising speed of 197 m/s. During this acceleration,
a force of 4.00 105
N in the southeast direction was exerted on the gen-
erator. For how much time did the force act on the generator?
S O L U T I O N
Given: m = 1.24 × 105
kg
vi = 101 m/s to the southeast
vf = 197 m/s to the southeast
F = 4.00 × 105
N to the southeast
Unknown: ∆t = ?
Use the impulse-momentum theorem to determine the time the force acts on the
generator.
F ∆t = ∆p = mvf − mvi
∆t = 
mvf
F
− mvi

∆t =
∆t =
∆t = 
1.1
4
9
.0
×
0
1
×
07
10
k
5
g•
N
m/s

∆t = 29.8 s
2.44 × 107
kg•m/s − 1.25 × 107
kg•m/s

4.00 × 105
N
(1.24 × 105
kg)(197 m/s) − (1.24 × 105
kg)(101 m/s)

4.00 × 105
N
ADDITIONAL PRACTICE
1. In 1991, a Swedish company, Kalmar LMV, constructed a forklift truck
capable of raising 9.0 × 104
kg to a height of about 2 m. Suppose a mass
this size is lifted with an upward velocity of 12 cm/s. The mass is ini-
tially at rest and reaches its upward speed because of a net force of 6.0 ×
103
N exerted upward. For how long is this force applied?
2. A bronze statue of Buddha was completed in Tokyo in 1993. The statue
is 35 m tall and has a mass of 1.00 × 106
kg. Suppose this statue were to
be moved to a different location. What is the magnitude of the impulse
that must act on the statue in order for the speed to increase from 0 m/s

62
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
to 0.20 m/s? If the magnitude of the net force acting on the statue is
12.5 kN, how long will it take for the final speed to be reached?
3. In 1990, Gary Stewart of California made 177 737 jumps on a pogo
stick. Suppose that the pogo stick reaches a height of 12.0 cm with each
jump and that the average net force acting on the pogo stick during the
contact with the ground is 330 N upward. What is the time of contact
with the ground between the jumps? Assume the total mass of Stewart
and the pogo stick is 65 kg. (Hint: The difference between the initial
and final velocities is one of direction rather than magnitude.)
4. The specially designed armored car that was built for Leonid Brezhnev
when he was head of the Soviet Union had a mass of about 6.0 × 103
kg.
Suppose this car is accelerated from rest by a force of 8.0 kN to the east.
What is the car’s velocity after 8.0 s?
5. In 1992, Dan Bozich of the United States drove a gasoline-powered go-
cart at a speed of 125.5 km/h. Suppose Bozich applies the brakes upon
reaching this speed. If the combined mass of the go-cart and driver is
2.00 × 102
kg, the decelerating force is 3.60 × 102
N opposite the cart’s
motion, and the time during which the deceleration takes place is
10.0 s. What is the final speed of Bozich and the go-cart?
6. The “human cannonball” has long been a popular—and extremely
dangerous—circus stunt. In order for a 45 kg person to leave the can-
non with the fastest speed yet achieved by a human cannonball, a 1.6 ×
103
N force must be exerted on that person for 0.68 s. What is the
record speed at which a person has been shot from a circus cannon?
7. The largest steam-powered locomotive was built in the United States in
1943. It is still operational and is used for entertainment purposes. The
locomotive’s mass is 4.85 × 105
kg. Suppose this locomotive is traveling
northwest along a straight track at a speed of 20.0 m/s. What force
must the locomotive exert to increase its velocity to 25.0 m/s to the
northwest in 5.00 s?
8. With upward speeds of 12.5 m/s, the elevators in the Yokohama Land-
mark Tower in Yokohama, Japan, are among the fastest elevators in the
world. Suppose a passenger with a mass of 70.0 kg enters one of these
elevators. The elevator then goes up, reaching full speed in 4.00 s. Cal-
culate the net force that is applied to the passenger during the elevator’s
acceleration.
9. Certain earthworms living in South Africa have lengths as great as 6.0 m
and masses as great as 12.0 kg. Suppose an eagle picks up an earthworm
of this size, only to drop it after both have reached a height of 40.0 m
above the ground. By skillfully using its muscles, the earthworm man-
ages to extend the time during which it collides with the ground to
0.250 s. What is the net force that acts on the earthworm during its col-
lision with the ground? Assume the earthworm’s vertical speed when it
is initially dropped to be 0 m/s.

Problem C 63
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem C
STOPPING DISTANCE
P R O B L E M
The largest nuts (and, presumably, the largest bolts) are manufactured in
England. The nuts have a mass of 4.74 103
kg each, which is greater
than any passenger car currently in production. Suppose one of these
nuts slides along a rough horizontal surface with an initial velocity of
2.40 m/s to the right. If the force of friction acting on the nut is 6.8
103
N to the left, what is the change in the nut’s momentum after 1.1 s?
How far does the nut travel during its change in momentum?
S O L U T I O N
Given: m = 4.74 × 103
kg
vi = 2.40 m/s to the right = +2.40 m/s
F = 6.8 × 103
N to the left = −6.8 × 103
N
∆t = 1.1 s
Unknown: ∆p = ? ∆x = ?
Use the impulse-momentum theorem to calculate the change in momentum.
Use the definition of momentum to find vf, and then use the equation for stop-
ping distance to solve for ∆x.
∆p = F∆t = (−6.8 × 103
N)(1.1 s)
∆p =
∆p = mvf − mvi
vf = 
∆p +
m
mvi

vf =
vf = =
vf =
∆x = 
1
2
(vi + vf)∆t = 
1
2
(2.40 m/s + 0.82 m/s)(1.1 s) = 
1
2
(3.22 m/s)(1.1 s)
∆x = 1.8 m/s to the right
0.82 m/s to the right
3900 kg•m/s

4.74 × 103
kg
−7.5 ×103
kg•m/s + 1.14 × 104
kg•m/s

4.74 × 103
kg
−7.5 × 103
kg•m/s + (4.74 × 103
kg)(2.40 m/s)

4.74 × 103
kg
−7.5 × 103
kg•m/s to the right, or 7.5 × 103
kg•m/s to the left
ADDITIONAL PRACTICE
1. The most powerful tugboats in the world are built in Finland. These
boats exert a force with a magnitude of 2.85 × 106
N. Suppose one of
these tugboats is trying to slow a huge barge that has a mass of 2.0 ×
107
kg and is moving with a speed of 3.0 m/s. If the tugboat exerts its
maximum force for 21 s in the direction opposite to that in which the
barge is moving, what will be the change in the barge’s momentum? How
far will the barge travel before it is brought to a stop?

2. In 1920, a 6.5 × 104
kg meteorite was found in Africa. Suppose a me-
teorite with this mass enters Earth’s atmosphere with a speed of 1.0 km/s.
What is the change in the meteorite’s momentum if an average constant
force of –1.7 × 106
N acts on the meteorite for 30.0 s? How far does the
meteorite travel during this time?
3. The longest canoe in the world was constructed in New Zealand. The
combined mass of the canoe and its crew of more than 70 people was
2.03 × 104
kg. Suppose the canoe is rowed from rest to a velocity of
5.00 m/s to the east, at which point the crew takes a break for 20.3 s. If a
constant average retarding force of 1.20 × 103
N to the west acts on the
canoe, what is the change in the momentum of the canoe and crew? How
far does the canoe travel during the time the crew is not rowing?
4. The record for the smallest dog in the world belongs to a terrier who had
a mass of only 113 g. Suppose this dog runs to the right with a speed of
2.00 m/s when it suddenly sees a mouse. The dog becomes scared and
uses its paws to bring itself to rest in 0.80 s. What is the force required to
stop the dog? What is the dog’s stopping distance?
5. In 1992, an ice palace estimated to be 4.90 × 106
kg was built in Min-
nesota. Despite this sizable mass, this structure could be moved at a con-
stant velocity because of the small force of friction between the ice blocks
of its base and the ice of the lake upon which it was constructed. Imagine
moving the entire palace with a speed of 0.200 m/s on this very smooth,
icy surface. Once the palace is no longer being pushed, it coasts to a stop
in 10.0 s. What is the average force of kinetic friction acting on the
palace? What is the palace’s stopping distance?
6. Steel Phantom is a roller coaster in Pennsylvania that, like the Desperado
in Nevada, has a vertical drop of 68.6 m. Suppose a roller-coaster car
with a mass of 1.00 × 103
kg travels from the top of that drop without
friction. The car then decelerates along a horizontal stretch of track until
it comes to a stop. How long does it take the car to decelerate if the con-
stant force acting on it is –2.24 × 104
N? How far does the car travel
along the horizontal track before stopping? Assume the car’s speed at the
peak of the drop is zero.
7. Two Japanese islands are connected by a long rail tunnel that extends
horizontally underwater. Imagine a communication system in which a
small rail car with a mass of 100.0 kg is launched by a type of cannon in
order to transport messages between the two islands. Assume a rail car
from one end of the tunnel has a speed of 4.50 × 102
m/s, which is just
large enough for a constant frictional force of –188 N to cause the car to
stop at the other end of the tunnel. How long does it take for the car to
travel the length of the tunnel? What is the length of the tunnel?
64
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 65
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem D
CONSERVATION OF MOMENTUM
P R O B L E M
Kangaroos are good runners that can sustain a speed of 56 km/h
(15.5 m/s). Suppose a kangaroo is sitting on a log that is floating in a lake.
When the kangaroo gets scared, she jumps off the log with a velocity of
15 m/s toward the bank. The log moves with a velocity of 3.8 m/s away
from the bank. If the mass of the log is 250 kg, what is the mass of the
kangaroo?
S O L U T I O N
Given: vk,i = initial velocity of kangaroo = 0 m/s
vl,i = initial velocity of log = 0 m/s
vk,f = final velocity of kangaroo = 15 m/s toward bank = +15 m/s
vl,f = final velocity of log = 3.8 m/s away from bank = −3.8 m/s
ml = mass of log = 250 kg
Unknown: mk = mass of kangaroo = ?
Choose the equation(s) or situation: Because the momentum of the kangaroo-
log system is conserved and therefore remains constant, the total initial momen-
tum of the kangaroo and log will equal the total final momentum of the kanga-
roo and log.
mkvk,i + ml vl,i = mkvk, f + ml vl,f
The initial velocities of the kangaroo and log are zero, and therefore the initial
momentum for each of them is zero. It thus follows that the total final momen-
tum for the kangaroo and log must also equal zero. The momentum-conservation
equation reduces to the following:
mkvk,f + ml vl,f = 0
Rearrange the equation(s) and isolate the unknown(s):
mk = 
−m
vk
lv
,f
l,f

mk =
mk =
Because the log is about four times as massive as the kangaroo, its velocity is
about one-fourth as large as the kangaroo’s velocity.
63 kg
−(250 kg)(−3.8 m/s)

15 m/s
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

66
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. The largest single publication in the world is the 1112-volume set of
British Parliamentary Papers for 1968 through 1972. The complete set has
a mass of 3.3 × 103
kg. Suppose the entire publication is placed on a cart
that can move without friction. The cart is at rest, and a librarian is sit-
ting on top of it, just having loaded the last volume. The librarian jumps
off the cart with a horizontal velocity relative to the floor of 2.5 m/s to
the right. The cart begins to roll to the left at a speed of 0.05 m/s. Assum-
ing the cart’s mass is negligible, what is the librarian’s mass?
2. The largest grand piano in the world is really grand. Built in London, it
has a mass of 1.25 × 103
kg. Suppose a pianist finishes playing this piano
and pushes herself from the piano so that she rolls backwards with a
speed of 1.4 m/s. Meanwhile, the piano rolls forward so that in 4.0 s it
travels 24 cm at constant velocity. Assuming the stool that the pianist is
sitting on has a negligible mass, what is the pianist’s mass?
3. With a mass of 114 kg, Baby Bird is the smallest monoplane ever flown.
Suppose the Baby Bird and pilot are coasting along the runway when the
pilot jumps horizontally to the runway behind the plane. The pilot’s ve-
locity upon leaving the plane is 5.32 m/s backward. After the pilot jumps
from the plane, the plane coasts forward with a speed of 3.40 m/s. If the
pilot’s mass equals 60.0 kg, what is the velocity of the plane and pilot be-
fore the pilot jumps?
4. The September 14, 1987, issue of the New York Times had a mass of
5.4 kg. Suppose a skateboarder picks up a copy of this issue to have a look
at the comic pages while rolling backward on the skateboard. Upon realiz-
ing that the New York Times doesn’t have a “funnies” section, the skate-
boarder promptly throws the entire issue in a recycling container. The
newspaper is thrown forward with a speed of 7.4 m/s. When the skater
throws the newspaper away, he rolls backward at a speed of 1.4 m/s. If
the combined mass of the skateboarder and skateboard is assumed to be
50.0 kg, what is the initial velocity of the skateboarder and newspaper?
5. The longest bicycle in the world was built in New Zealand in 1988. It is
more than 20 m in length, has a mass of 3.4 × 102
kg, and can be ridden
by four people at a time. Suppose four people are riding the bike south-
east when they realize that the street turns and that the bike won’t make
it around the corner. All four riders jump off the bike at the same time
and with the same velocity (9.0 km/h to the northwest, as measured rela-
tive to Earth). The bicycle continues to travel forward with a velocity of
28 km/h to the southeast. If the combined mass of the riders is 2.6 ×
102
kg, what is the velocity of the bicycle and riders immediately before
the riders’ escape?
ADDITIONAL PRACTICE

Problem D 67
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 6. The largest frog ever found was discovered in Cameroon in 1989. The
frog’s mass was nearly 3.6 kg. Suppose this frog is placed on a skateboard
with a mass of 3.0 kg. The frog jumps horizontally off the skateboard to
the right, and the skateboard rolls freely in the opposite direction with a
speed of 2.0 m/s relative to the ground. If the frog and skateboard are ini-
tially at rest, what is the initial horizontal velocity of the frog?
7. In 1994, a pumpkin with a mass of 449 kg was grown in Canada. Sup-
pose you want to push a pumpkin with this mass along a smooth, hori-
zontal ramp. You give the pumpkin a good push, only to find yourself
sliding backwards at a speed of 4.0 m/s. How far will the pumpkin slide
3.0 s after the push? Assume your mass to be 60.0 kg.

Momentum and Collisions
Problem E
PERFECTLY INELASTIC COLLISIONS
P R O B L E M
The Chinese giant salamander is one of the largest of salamanders. Sup-
pose a Chinese giant salamander chases a 5.00 kg carp with a velocity of
3.60 m/s to the right and the carp moves with a velocity of 2.20 m/s in the
same direction (away from the salamander). If the speed of the salaman-
der and carp immediately after the salamander catches the carp is
3.50 m/s to the right, what is the salamander’s mass?
S O L U T I O N
Given: mc = mass of carp = 5.00 kg
vs,i = initial velocity of salamander = 3.60 m/s to the right
vc,i = initial velocity of carp = 2.20 m/s to the right
vf = final velocity = 3.50 m/s to the right
Unknown: ms = mass of salamander = ?
Use the equation for a perfectly inelastic collision and rearrange it to solve for ms.
msvs,i + mcvc,i = (ms + mc)vf
ms = 
mc
v
v
s
f
,
−
i −
m
v
c
f
vc,i

ms =
ms =
ms = 
6
0
.5
.1
k
0
g
m
•m
/s
/s

ms = 65 kg
17.5 kg•m/s − 11.0 kg•m/s

0.10 m/s
(5.00 kg)(3.50 m/s) − (5.00 kg)(2.20 m/s)

3.60 m/s − 3.50 m/s
68
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. Zorba, an English mastiff with a mass of 155 kg, jumps forward horizon-
tally at a speed of 6.0 m/s into a boat that is floating at rest. After the
jump, the boat and Zorba move with a velocity of 2.2 m/s forward. Cal-
culate the boat’s mass.
2. Yvonne van Gennip of the Netherlands ice skated 10.0 km with an aver-
age speed of 10.8 m/s. Suppose van Gennip crosses the finish line at her
average speed and takes a huge bouquet of flowers handed to her by a
fan. As a result, her speed drops to 10.01 m/s. If van Gennip’s mass is
63.0 kg, what is the mass of the bouquet?
ADDITIONAL PRACTICE

Problem E 69
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 3. The world’s largest guitar was built by a group of high school students in
Indiana. Suppose that this guitar is placed on a light cart. The cart and
guitar are then pushed with a velocity of 4.48 m/s to the right. One of the
students tries to slow the cart by stepping on it as it passes by her. The
new velocity of the cart, guitar, and student is 4.00 m/s to the right. If the
student’s mass is 54 kg, what is the mass of the guitar? Assume the mass
of the cart is negligible.
4. The longest passenger buses in the world operate in Zaire. These buses
are more than 30 m long, have two trailers, and have a total mass of 28 ×
103
kg. Imagine a safety test involving one of these buses and a truck
with a mass of 12 × 103
kg. The truck with an unknown velocity hits a
bus that is at rest so that the two vehicles move forward together with a
speed of 3.0 m/s. Calculate the truck’s velocity prior to the collision.
5. Sumo wrestlers must be very heavy to be successful in their sport, which
involves pushing the rival out of the ring. One of the greatest sumo
champions, Akebono, had a mass of 227 kg. The heaviest sumo wrestler
ever, Konishiki, at one point had a mass of 267 kg. Suppose these two
wrestlers are opponents in a match. Akebono moves left with a speed of
4.0 m/s, while Konishiki moves toward Akebono with an unknown
speed. After the wrestlers undergo an inelastic collision, both have a ve-
locity of zero. From this information, calculate Konishiki’s velocity be-
fore colliding with Akebono.
6. Louis Borsi, of London, built a drivable car that had a mass of 9.50 kg
and could move as fast as 24.0 km/h. Suppose the inventor falls out of
this car and the car proceeds driverless to the north at its maximum
speed. The inventor’s young daughter, who has a mass of 32.0 kg,
“catches” the car by jumping northward from a nearby stairway. The ve-
locity of the car and girl is 11.0 km/h to the north. What was the velocity
of Borsi’s daughter as she jumped in the car?
7. In 1990, Roger Hickey of California attained a speed of 89 km/h while
standing on a skateboard. Suppose Hickey is riding horizontally at his
stand-up speed when he catches up to another skateboarder, who is
moving at 69 km/h in the same direction. If the second skateboarder
steps sideways onto Hickey’s skateboard, the two riders move forward
with a new speed. Calculate this speed, assuming that both skateboarders
have equal, but unknown, masses and that the mass of the skateboard is
negligible.
8. The white shark is the largest carnivorous fish in the world. The mass of
a white shark can be as great as 3.0 × 103
kg. In spite of (or perhaps be-
cause of) the mass and ferocity of the shark, it is prized by commercial
and sports fishers alike. Suppose Joe, who is one of these fishers, goes to a
cliff that overlooks the ocean. To see if the sharks are biting, Joe drops a
2.5 × 102
kg fish as bait into the ocean below. As it so happens, a 3.0 ×
103
kg white shark is prowling the ocean floor just below the cliff. The

shark sees the bait, which is sinking straight down at a speed of
3.0 m/s. The shark swims upward with a speed of 1.0 m/s to swallow the
bait. What is the velocity of the shark right after it has swallowed the
bait?
9. The heaviest cow on record had a mass of 2.267 × 103
kg and lived in
Maine at the beginning of the twentieth century. Imagine that during an
agricultural exhibition, the cow’s owner puts the cow on a railed cart that
kg and pushes the cow and cart left to the stage
with a speed of 2.00 m/s. Another farmer puts his cow, which has a mass
of 1.800 × 103
kg, on an identical cart and pushes it toward the stage
from the opposite direction with a speed of 1.40 m/s. The carts collide
and stick together. What is the velocity of the cows after the collision?
70
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem F 71
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem F
KINETIC ENERGY IN PERFECTLY INELASTIC COLLISIONS
P R O B L E M
Alaskan moose can be as massive as 8.00 × 102
kg. Suppose two feuding
moose, both of which have a mass of 8.00 × 102
kg, back away and then
run toward each other. If one of them runs to the right with a speed of
8.0 m/s and the other runs to the left with a speed of 6.0 m/s, what
amount of kinetic energy will be dissipated after their inelastic collision?
S O L U T I O N
Given: m1 = mass of first moose = 8.00 × 102
kg
m2 = mass of second moose = 8.00 × 102
kg
v1,i = initial velocity of first moose = 8.0 m/s to the right
v2,i = initial velocity of second moose = 6.0 m/s to the left
= –6.0 m/s to the right
Unknown: ∆KE = ?
Use the equation for a perfectly inelastic collision.
m1v1,i + m2v2,i = (m1 + m2)vf
(8.00 × 102
kg)(8.0 m/s) + (8.00 × 102
kg)(–6.0 m/s)
= (2)(8.00 × 102
kg)vf
6.4 × 103
kg•m/s – 4.8 × 103
kg•m/s = (16.0 × 102
kg)vf
vf = 
1.6
16
×
.0
1
×
03
1
k
0
g
2
•
k
m
g
/s
 = 1.0 m/s to the right
Use the equation for kinetic energy to calculate the kinetic energy of each moose
before the collision and the final kinetic energy of the two moose combined.
Initial kinetic energy:
KEi = KE1,i + KE2,i = 
1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
KEi = 
1
2
(8.00 × 102
kg)(8.0 m/s)2
+ 
1
2
(8.00 × 102
kg)(−6.0 m/s)2
KEi = 2.6 × 104
J + 1.4 × 104
J = 4.0 × 104
J
Final kinetic energy:
KEf = KE1,f + KE2,f = 
1
2
(m1 + m2)vf
2
KEf =
KEf = 8.0 × 102
J
Change in kinetic energy:
∆KE = KEf − KEi = 8.0 × 102
J − 4.0 × 104
J =
By expressing ∆KE as a negative number, we indicate that the energy has left the
system to take a form other than mechanical energy.
−3.9 × 104
J
(2)(8.00 × 102
kg)(1.0 m/s)2

2

1. The hog-nosed bat is the smallest mammal on Earth: it is about the same
size as a bumblebee and has an average mass of 2.0 g. Suppose a hog-
nosed bat with this mass flies at 2.0 m/s when it detects a bug with a
mass of 0.20 g flying directly toward it at 8.0 m/s. What fraction of the
total kinetic energy is dissipated when it swallows the bug?
2. The heaviest wild lion ever measured had a mass of 313 kg. Suppose this
lion is walking by a lake when it sees an empty boat floating at rest near
the shore. The curious lion jumps into the boat with a speed of 6.00 m/s,
causing the boat with the lion in it to move away from the shore with a
speed of 2.50 m/s. How much kinetic energy is dissipated in this inelastic
collision.
3. The cheapest car ever commercially produced was the Red Bug Back-
board, which sold in 1922 in the United States for about $250. The car’s
mass was only 111 kg. Suppose two of these cars are used in a stunt crash
for an action film. If one car’s initial velocity is 9.00 m/s to the right and
the other car’s velocity is 5.00 m/s to the left, how much kinetic energy is
dissipated in the crash?
4. In 1986, four high school students built an electric car that could reach a
speed of 106.0 km/h. The mass of the car was just 60.0 kg. Imagine two
of these cars used in a stunt show. One car travels east with a speed of
106.0 km/h, and the other car travels west with a speed of 75.0 km/h. If
each car’s driver has a mass of 50.0 kg, how much kinetic energy is dissi-
pated in the perfectly inelastic head-on collision?
5. The Arctic Snow Train, built for the U.S. Army, has a mass of 4.00 × 105
kg
and a top speed of 32.0 km/h. Suppose such a train moving at its top
speed is hit from behind by another snow train with a mass of 1.60 ×
105
kg and a speed of 45.0 km/h in the same direction. What is the
change in kinetic energy after the trains’ perfect inelastic collision?
6. There was a domestic cat in Australia with a mass of 21.3 kg. Suppose
this cat is sitting on a skateboard that is not moving. A 1.80 × 10–1
kg
treat is thrown to the cat. When the cat catches the treat, the cat and
skateboard move with a speed of 6.00 × 10–2
m/s. How much kinetic en-
ergy is dissipated in the process? Assume one-dimensional motion.
7. In 1985, a spider with a mass of 122 g was caught in Surinam, South
America. (Recall that the smallest dog in the world had a smaller mass.)
Suppose a spider with this mass runs at a certain unknown speed when it
collides inelastically with another spider, which has a mass of 96.0 g and
is at rest. Find the fraction of the kinetic energy that is dissipated in the
perfect inelastic collision. Assume that the resting spider is on a low-
friction surface. Do you need to know the first spider’s velocity to calcu-
late the fraction of the dissipated kinetic energy?
72
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem G 73
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem G
ELASTIC COLLISIONS
P R O B L E M
American juggler Bruce Sarafian juggled 11 identical balls at one time in
1992.Each ball had a mass of 0.20 kg.Suppose two balls have an elastic head-
on collision during the act.The first ball moves away from the collision with
a velocity of 3.0 m/s to the right,and the second ball moves away with a veloc-
ity of 4.0 m/s to the left.If the first ball’s velocity before the collision is 4.0 m/s
to the left,what is the velocity of the second ball before the collision?
S O L U T I O N
Given: m1 = m2 = 0.20 kg
v1,i = initial velocity of ball 1 = 4.0 m/s to the left
= −4.0 m/s to the right
v1,f = final velocity of ball 1 = 3.0 m/s to the right
v2,f = final velocity of ball 2 = 4.0 m/s to the left
= –4.0 m/s to the right
Unknown: v2,i = initial velocity of ball 2 = ?
Choose the equation(s) or situation: Use the equation for the conservation of
momentum to determine the initial velocity of ball 2. Because both balls have
identical masses, the mass terms cancel.
m1v1,i + m2v2,i = m1v1,f + m2v2,f
v1,i + v2,i = v1,f + v2, f
v2,i = v1,f + v2,f − v1,i
v2,i = 3.0 m/s − 4.0 m/s − (−4.0 m/s)
v2,i =
Confirm your answer by making sure that kinetic energy is also conserved.

1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
= 
1
2
m1v1,f
2
+ 
1
2
m2v2,f
2
v1,i
2
+ v2,i
2
= v1,f
2
+ v2,f
2
(−4.0 m/s)2
+ (3.0 m/s)2
= (3.0 m/s)2
+ (−4.0 m/s)2
16 m2
/s2
+ 9.0 m2
/s2
= 9.0 m2
/s2
+ 16 m2
/s2
25 m2
/s2
= 25 m2
/s2
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The moon’s orbital speed around Earth is 3.680 × 103
km/h. Suppose the
moon suffers a perfectly elastic collision with a comet whose mass is 50.0
percent that of the moon. (A partially inelastic collision would be a much

more realistic event.) After the collision, the moon moves with a speed of
–4.40 × 102
km/h, while the comet moves away from the moon at 5.740
× 103
km/h. What is the comet’s speed before the collision?
2. The largest beet root on record had a mass of 18.40 kg. The largest cab-
bage on record had a mass of 56.20 kg. Imagine these two vegetables
traveling in opposite directions. The cabbage, which travels 5.000 m/s to
the left, collides with the beet root. After the collision, the cabbage has a
velocity of 6.600 × 10–2
m/s to the left, and the beet root has a velocity of
10.07 m/s to the left. What is the beet root’s velocity before the perfectly
elastic collision?
3. The first astronaut to walk in outer space without being tethered to a
spaceship was Capt. Bruce McCandless. In 1984, he used a jet backpack,
which cost about $15 million to design, to move freely about the exterior
of the space shuttle Challenger. Imagine two astronauts working in outer
space. Suppose they have equal masses and accidentally run into each
other. The first astronaut moves 5.0 m/s to the right before the collision
and 2.0 m/s to the left afterwards. If the second astronaut moves 5.0 m/s
to the right after the perfectly elastic collision, what was the second astro-
naut’s initial velocity?
4. Speeds as high as 273 km/h have been recorded for golf balls. Suppose a
golf ball whose mass is 45.0 g is moving to the right at 273 km/h and
strikes another ball that is at rest. If after the perfectly elastic collision the
golf ball moves 91 km/h to the left and the other ball moves 182 km/h to
the right, what is the mass of the second ball?
5. Jana Novotna of what is now the Czech Republic has the strongest serve
among her fellow tennis players. In 1993, she sent the ball flying with a
speed of 185 km/h. Suppose a tennis ball moving to the right at this speed
hits a moveable target of unknown mass. After the one-dimensional, per-
fectly elastic collision, the tennis ball bounces to the left with a speed of
80.0 km/h. If the tennis ball’s mass is 5.70 × 10–2
kg, what is the target’s
mass? (Hint: Use the conservation of kinetic energy to solve for the sec-
ond unknown quantity.)
6. Recall the two colliding snow trains in item 5 of the previous section.
Suppose now that the collision between the two trains is perfectly elastic
instead of inelastic. The train with a 4.00 × 105
kg and a velocity of
32.0 km/h to the right is struck from behind by a second train with a
mass of 1.60 × 105
kg and a velocity of 36.0 km/h to the right. If the first
train’s velocity increases to 35.5 km/h to the right, what is the final veloc-
ity of the second train after the collision?
7. A dump truck used in Canada has a mass of 5.50 × 105
kg when loaded
and 2.30 × 105
kg when empty. Suppose two such trucks, one loaded and
one empty, crash into each other at a monster truck show. The trucks are
supplied with special bumpers that make a collision almost perfectly
elastic. If the trucks hit each other at equal speeds of 5.00 m/s and the
less massive truck recoils to the right with a speed of 9.10 m/s, what is
the velocity of the full truck after the collision?
74
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem A 75
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Circular Motion and Gravitation
Problem A
CENTRIPETAL ACCELERATION
P R O B L E M
Calculate the orbital radius of the Earth,if its tangential speed is 29.7 km/s
and the centripetal acceleration acting on Earth is 5.9 10–3
m/s2
.
S O L U T I O N
Given: vt = 29.7 km/s ac = 5.9 × 10−3
m/s2
Unknown: r = ?
Use the centripetal acceleration equation written in terms of tangential speed.
Rearrange the equation to solve for r.
ac = 
v
r
t
2

r = 
v
a
t
c
2
 = 
(2
5
9
.9
.7
×
×
1
1
0
0
−3
3
m
m
/
/
s
s
2
)2
 = 1.5 × 1011
m = 1.5 × 108
km
ADDITIONAL PRACTICE
1. The largest salami in the world, made in Norway, was more than 20 m
long. If a hungry mouse ran around the salami’s circumference with a
tangential speed of 0.17 m/s, the centripetal acceleration of the mouse
was 0.29 m/s2
. What was the radius of the salami?
2. An astronomer at the equator measures the Doppler shift of sunlight at
sunset. From this, she calculates that Earth’s tangential velocity at the
equator is 465 m/s. The centripetal acceleration at the equator is 3.41 ×
10−2
m/s2
. Use this data to calculate Earth’s radius.
3. In 1994, Susan Williams of California blew a bubble-gum bubble
with a diameter of 58.4 cm. If this bubble were rigid and the centripetal
acceleration of the equatorial points of the bubble were 8.50 × 10−2
m/s2
,
what would the tangential speed of those points be?
4. An ostrich lays the largest bird egg. A typical diameter for an ostrich
egg at its widest part is 12 cm. Suppose an egg of this size rolls down a
slope so that the centripetal acceleration of the shell at its widest part is
0.28 m/s2
. What is the tangential speed of that part of the shell?
5. A waterwheel built in Hamah, Syria, has a radius of 20.0 m. If the tan-
gential velocity at the wheel’s edge is 7.85 m/s, what is the centripetal
acceleration of the wheel?
6. In 1995, Cathy Marsal of France cycled 47.112 km in 1.000 hour. Calcu-
late the magnitude of the centripetal acceleration of Marsal with re-
spect to Earth’s center. Neglect Earth’s rotation, and use 6.37 × 103
km as
Earth’s radius.

76
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Circular Motion and Gravitation
Problem B
CENTRIPETAL FORCE
P R O B L E M
The royal antelope of western Africa has an average mass of only 3.2 kg.
Suppose this antelope runs in a circle with a radius of 30.0 m. If a force of
8.8 N maintains this circular motion, what is the antelope’s tangential
speed?
S O L U T I O N
Given: m = 3.2 kg
r = 30.0 m
Fc = 8.8 N
Unknown: vt = ?
Use the equation for centripetal force, and rearrange it to solve for tangential speed.
Fc = 
m
r
vt
2

vt = 
F
m
c
r

= 
(8
.8
N
3
.
)
2
(
3
k
0
g
.
0
m
)

= 82

m
s
2
2


vt = 9.1 m/s
1. Gregg Reid of Atlanta, Georgia, built a motorcycle that is over 4.5 m
long and has a mass of 235 kg. The force that holds Reid and his motor-
cycle in a circular path with a radius 25.0 m is 1850 N. What is Reid’s
tangential speed? Assume Reid’s mass is 72 kg.
2. With an average mass of only 30.0 g, the mouse lemur of Madagascar is
the smallest primate on Earth. Suppose this lemur swings on a light
vine with a length of 2.4 m, so that the tension in the vine at the bot-
tom point of the swing is 0.393 N. What is the lemur’s tangential speed
at that point?
3. In 1994, Mata Jagdamba of India had very long hair. It was 4.23 m long.
Suppose Mata conducted experiments with her hair. First, she deter-
mined that one hair strand could support a mass of 25 g. She then at-
tached a smaller mass to the same hair strand and swung it in the hori-
zontal plane. If the strand broke when the tangential speed of the mass
reached 8.1 m/s, how large was the mass?
4. Pat Kinch used a racing cycle to travel 75.57 km/h. Suppose Kinch
moved at this speed around a circular track. If the combined mass of
Kinch and the cycle was 92.0 kg and the average centripetal force was
12.8 N, what was the radius of the track?
ADDITIONAL PRACTICE

Problem B 77
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 5. In 1992, a team of 12 athletes from Great Britain and Canada rappelled
446 m down the CN Tower in Toronto, Canada. Suppose an athlete
with a mass of 75.0 kg, having reached the ground, took a joyful swing
on the 446 m-long rope. If the speed of the athlete at the bottom point
of the swing was 12 m/s, what was the centripetal force? What was the
tension in the rope? Neglect the rope’s mass.

78
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem C
GRAVITATIONAL FORCE
P R O B L E M
The sun has a mass of 2.0 1030
kg and a radius of 7.0 105
km.What
mass must be located at the sun’s surface for a gravitational force of
470 N to exist between the mass and the sun?
S O L U T I O N
Given: m1 = 2.0 × 1030
kg
r = 7.0 × 105
km = 7.0 × 108
m
G = 6.673 × 10−11
N•m2
/kg2
Fg = 470 N
Unknown: m2 = ?
Use Newton’s universal law of gravitation, and rearrange it to solve for the second
mass.
Fg = G 
m1
r2
m2

m2 = =
m2 = 1.7 kg
(470 N)(7.0 × 108
m)2

6.673 × 10−11

N
k
•
g
m
2
2

(2.0 × 1030
kg)
Fg r2

G m1
ADDITIONAL PRACTICE
1. Deimos, a satellite of Mars, has an average radius of 6.3 km. If the gravi-
tational force between Deimos and a 3.0 kg rock at its surface is 2.5 ×
10–2
N, what is the mass of Deimos?
2. A 3.08 × 104
kg meteorite is on exhibit in New York City. Suppose this
meteorite and another meteorite are separated by 1.27 × 107
m (a dis-
tance equal to Earth’s average diameter). If the gravitational force be-
tween them is 2.88 × 10−16
N, what is the mass of the second meteorite?
3. In 1989, a cake with a mass of 5.81 × 104
kg was baked in Alabama.
Suppose a cook stood 25.0 m from the cake. The gravitational force ex-
erted between the cook and the cake was 5.0 × 10−7
N. What was the
cook’s mass?
4. The largest diamond ever found has a mass of 621 g. If the force of
gravitational attraction between this diamond and a person with a
mass of 65.0 kg is 1.0 × 10–12
N, what is the distance between them?

Problem C 79
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 5. The passenger liners Carnival Destiny and Grand Princess, built re-
cently, have a mass of about 1.0 × 108
kg each. How far apart must
these two ships be to exert a gravitational attraction of 1.0 × 10−3
N on
each other?
6. In 1874, a swarm of locusts descended on Nebraska. The swarm’s mass
was estimated to be 25 × 109
kg. If this swarm were split in half and the
halves separated by 1.0 × 103
km, what would the magnitude of the
gravitational force between the halves be?
7. Jupiter, the largest planet in the solar system, has a mass 318 times that
of Earth and a volume that is 1323 times greater than Earth’s. Calculate
the magnitude of the gravitational force exerted on a 50.0 kg mass on
Jupiter’s surface.

80
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem D
PERIOD AND SPEED OF AN ORBITING OBJECT
P R O B L E M
A satellite in geostationary orbit rotates at exactly the same rate as Earth,
so the satellite always remains in the same position relative to Earth’s
surface. The period of Earth’s rotation is 23 hours, 56 minutes, and
4 seconds.What is the altitude of a satellite in geostationary orbit?
S O L U T I O N
Given: T = 23:56:04 = 86 164 s
Unknown: rs = ?
Choose an equation or situation: Use the equation for the period of an object
in circular orbit, and rearrange the equation to solve for r.
T = 2p
G
r
m
3

T2
= 4p2

G
r
m
3

r3
=
G
4
m
p
T
2
2

r =
3

G
4
m
p
T
2
2

Use Table 1 in your textbook to find Earth’s mass (m) and radius (re).
re = 6.38 × 106
m (from Table 1)
m = 5.97 × 1024
kg (from Table 1)
Once you have found the total radius of the orbit (r), you can subtract Earth’s
radius (re) to find the altitude of the satellite (rs).
rs = r − re
Substitute the values into the equations and solve:
r =
3
= 4.22 × 107
m
rs = r − re = (4.22 × 107
m) − (6.38 × 106
m) =
A satellite in geostationary orbit is at an altitude of 3.58 × 107
m = 35,800 km.
3.58 × 107
m
6.673 × 10−11
N p
k
m
g
2
2

(5.97 × 1024
kg) (86 164 s)2

4p 2
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 81
NAME ______________________________________ DATE _______________ CLASS ____________________
1. The period of Mars’ rotation is 24 hours, 37 minutes, and 23 seconds.
At what altitude above Mars would a “Mars-stationary” satellite orbit?
2. Pluto’s moon, Charon, has an orbital period of 153 hours. How far is
Charon from Pluto?
3. The orbital radius of a satellite in geostationary orbit is 4.22 × 107
m
(see sample problem on previous page). What is the orbital speed of a
satellite in geostationary orbit?
4. Earth’s moon orbits Earth at a mean distance of 3.84 × 108
m. What is
the moon’s orbital speed?
5. Earth’s moon orbits Earth at a mean distance of 3.84 × 108
m. What is
the moon’s orbital period? Express your answer in Earth days.
6. Use data from Table 1 in your textbook to calculate the length of
Neptune’s “year” (the period of its orbit around the Sun). Express
your answer in Earth years.
7. The asteroid (45)Eugenia has a small moon named S/1998(45)1. The
moon orbits Eugenia once every 4.7 days at a distance of 1.19 x 103
km.
What is the mass of (45)Eugenia?
8. V404 Cygni is a dark object orbited by a star in the constellation
Cygnus. Many astronomers believe the object is a black hole. Suppose
the star’s orbit has a mean radius of 2.30 × 1010
m and a period of 6.47
days. What is the mass of the black hole? How many times larger is the
mass of the black hole than the mass of the sun?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights

82
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem E
TORQUE
P R O B L E M
A beam that is hinged near one end can be lowered to stop traffic at a rail-
road crossing or border checkpoint. Consider a beam with a mass of
12.0 kg that is partially balanced by a 20.0 kg counterweight. The coun-
terweight is located 0.750 m from the beam’s fulcrum.A downward force
of 1.60 102
N applied over the counterweight causes the beam to move
upward. If the net torque on the beam is 29.0 N•m when the beam makes
an angle of 25.0° with respect to the ground, how long is the beam’s
longer section? Assume that the portion of the beam between the coun-
terweight and fulcrum has no mass.
S O L U T I O N
Given: mb = 12.0 kg
mc = 20.0 kg
dc = 0.750 m
Fapplied = 1.60 × 102
N
tnet = 29.0 N•m
q = 90.0° − 25.0° = 65.0°
g = 9.81 m/s2
Unknown: l = ?
Diagram:
Choose the equation(s) or situation: Apply the definition of torque to each
force and add up the individual torques.
t = F d (sin q)
tnet = ta + tb + tc
where ta = counterclockwise torque produced by applied force = Fapplied dc (sin q)
tb = clockwise torque produced by weight of beam
= −mb g
(sin q)
tc = counterclockwise torque produced by counterweight
= mc g dc (sin q)
tnet = Fapplied dc (sin q) − mb g
(sin q) + mc g dc (sin q)
Note that the clockwise torque is negative, while the counterclockwise torques are
positive.
l

2
l

2
mbg
dc
θ

1. DEFINE
2. PLAN

Problem E 83
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Rearrange the equation(s) to isolate the unknown(s):
mb g
= (Fapplied + mc g) dc −

s
t
in
ne
q
t


l =
l =
l =
l =
l =
l =
l =
For a constant applied force, the net torque is greatest when q is 90.0° and de-
creases as the beam rises. Therefore, the beam rises fastest initially.
3.99 m
(2)(235 N•m)

(12.0 kg)(9.81 m/s2
)
(2)(2.67 × 102
N•m − 32.0 N•m]

(12.00 kg)(9.81 m/s2
)
(2) [356 N)(0.750 m) − 32.0 N•m]

(12.0 kg)(9.81 m/s2
)
(2) [(1.60 × 102
N + 196 N)(0.750 m) − 32.0 N•m]

(12.0 kg)(9.81 m/s2
)
(2)([1.60 × 102
N + (20.0 kg)(9.81 m/s2
)] (0.750 m) − 
2
s
9
i
.
n
0
6
N
5.
•
0
m
°



(12.0 kg)(9.81 m/s2
)
2(Fapplied + mc g)dc − 
s
t
in
ne
q
t



mb g
l

2
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The nests built by the mallee fowl of Australia can have masses as large as
3.00 × 105
kg. Suppose a nest with this mass is being lifted by a crane. The
boom of the crane makes an angle of 45.0° with the ground. If the axis of
rotation is the lower end of the boom at point A, the torque produced by
the nest has a magnitude of 3.20 × 107
N•m. Treat the boom’s mass as
negligible, and calculate the length of the boom.
2. The pterosaur was the most massive flying dinosaur. The average mass for
a pterosaur has been estimated from skeletons to have been between 80.0
and 120.0 kg. The wingspan of a pterosaur was greater than 10.0 m. Sup-
pose two pterosaurs with masses of 80.0 kg and 120.0 kg sat on the middle
and the far end, respectively, of a light horizontal tree branch. The
pterosaurs produced a net counterclockwise torque of 9.4 kN•m about
the end of the branch that was attached to the tree. What was the length of
the branch?

84
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. A meterstick of negligible mass is fixed horizontally at its 100.0 cm mark.
Imagine this meterstick used as a display for some fruits and vegetables
with record-breaking masses. A lemon with a mass of 3.9 kg hangs from
the 70.0 cm mark, and a cucumber with a mass of 9.1 kg hangs from the x
cm mark. What is the value of x if the net torque acting on the meterstick
is 56.0 N•m in the counterclockwise direction?
4. In 1943, there was a gorilla named N’gagi at the San Diego Zoo. Suppose
N’gagi were to hang from a bar. If N’gagi produced a torque of –1.3 ×
104
N•m about point A, what was his weight? Assume the bar has negligi-
ble mass.
5. The first—and, in terms of the number of passengers it could carry, the
largest—Ferris wheel ever constructed had a diameter of 76 m and held
36 cars, each carrying 60 passengers. Suppose the magnitude of the
torque, produced by a ferris wheel car and acting about the center of the
wheel, is –1.45 × 106
N•m. What is the car’s weight?
6. In 1897, a pair of huge elephant tusks were obtained in Kenya. One tusk
had a mass of 102 kg, and the other tusk’s mass was 109 kg. Suppose both
tusks hang from a light horizontal bar with a length of 3.00 m. The first
tusk is placed 0.80 m away from the end of the bar, and the second, more
massive tusk is placed 1.80 m away from the end. What is the net torque
produced by the tusks if the axis of rotation is at the center of the bar? Ne-
glect the bar’s mass.
7. A catapult, a device used to hurl heavy objects such as large stones, con-
sists of a long wooden beam that is mounted so that one end of it pivots
freely in a vertical arc. The other end of the beam consists of a large hol-
lowed bowl in which projectiles are placed. Suppose a catapult provides
an angular acceleration of 50.0 rad/s2
to a 5.00 × 102
kg boulder. This can
be achieved if the net torque acting on the catapult beam, which is 5.00 m
long, is 6.25 × 105
N•m.
a. If the catapult is pulled back so that the beam makes an angle of
10.0° with the horizontal, what is the magnitude of the torque pro-
duced by the 5.00 × 102
kg boulder?
b. If the force that accelerates the beam and boulder acts perpendicu-
larly on the beam 4.00 m from the pivot, how large must that force
be to produce a net torque of 6.25 × 105
N•m?

Problem A 85
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
NAME ______________________________________ DATE _______________ CLASS ____________________
Fluid Mechanics
Problem A
BUOYANT FORCE
P R O B L E M
The highest natural concentration of salts in water are found in the
evaporating remnants of old oceans, such as the Dead Sea in Israel. Sup-
pose a swimmer with a volume of 0.75 m3
is able to float just beneath the
surface of water with a density of 1.02 103
kg/m3
. How much extra
mass can the swimmer carry and be able to float just beneath the surface
of the Dead Sea, which has a density of 1.22 103
kg/m3
?
S O L U T I O N
Given: V = 0.75 m3
r1 = 1.02 × 103
kg/m3
r2 = 1.22 × 103
kg/m3
Unknown: m′ = ?
Choose the equation(s) or situation: In both bodies of water, the buoyant force
equals the weight of the floating object.
FB,1 = Fg,1
r1Vg = mg
FB,2 = Fg,2
r2Vg = (m + m′)g = r1Vg + m′g
m′ = (r2 − r1)V
m′ = (1.22 × 103
kg/m3
− 1.02 × 103
kg/m3
)(0.75 m3
)
m′ = (0.20 × 103
kg/m3
)(0.75 m3
)
m′ =
The mass that can be supported by buoyant force increases with the difference in
fluid densities.
150 kg
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The heaviest pig ever raised had a mass of 1158 kg. Suppose you placed
this pig on a raft made of dry wood. The raft completely submerged in
water so that the raft’s top surface was just level with the surface of the
lake. If the raft’s volume was 3.40 m3
, what was the mass of the raft’s dry
wood? The density of fresh water is 1.00 × 103
kg/m3
.
2. La Belle, one of four ships that Robert La Salle used to establish a French
colony late in the seventeenth century, sank off the coast of Texas. The
ship’s well-preserved remains were discovered and excavated in the
1990s. Among those remains was a small bronze cannon, called a min-
ion. Suppose the minion’s total volume is 4.14 × 10−2
m3
. What is the

86
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
NAME ______________________________________ DATE _______________ CLASS ____________________
minion’s mass if its apparent weight in sea water is 3.115 × 103
N? The
density of sea water is 1.025 × 103
kg/m3
.
3. William Smith built a small submarine capable of diving as deep as
30.0 m. The submarine’s volume can be approximated by that of a cylin-
der with a length of 3.00 m and a cross-sectional area of 0.500 m2
. Sup-
pose this submarine dives in a freshwater river and then moves out to
sea, which naturally consists of salt water. What mass of fresh water must
be added to the ballast to keep the submarine submerged? The density
of fresh water is 1.000 × 103
kg/m3
, and the density of sea water is
1.025 × 103
kg/m3
.
4. The largest iceberg ever observed had an area of 3.10 × 104
km2
, which is
larger than the area of Belgium. If the top and bottom surfaces of the ice-
berg were flat and the thickness of the submerged part was 0.84 km, how
large was the buoyant force acting on the iceberg? The density of sea
water equals 1.025 × 103
kg/m3
.
5. A cannon built in 1868 in Russia could fire a cannonball with a mass of
4.80 × 102
kg and a radius of 0.250 m. When suspended from a scale and
submerged in water, a cannonball of this type has an apparent weight of
4.07 × 103
N. How large is the buoyant force acting on the cannonball?
The density of fresh water is 1.00 × 103
kg/m3
.
6. The tallest iceberg ever measured stood 167 m above the water. Suppose
that both the top and the bottom of this iceberg were flat and the thick-
ness of the submerged part was estimated to be 1.50 km. Calculate the
density of the ice. The density of sea water equals 1.025 × 103
kg/m3
.
7. The Russian submarines of the “Typhoon” class are the largest sub-
marines in the world. They have a length of 1.70 × 102
m and an average
diameter of 13.9 m. When submerged, they displace 2.65 × 107
kg of sea
water. Assume that these submarines have a simple cylindrical shape. If a
“Typhoon”-class submarine has taken on enough ballast that it descends
with a net acceleration of 2.00 m/s2
, what is the submarine’s density dur-
ing its descent?
8. To keep Robert La Salle’s ship La Belle well preserved, shipbuilders are re-
constructing the ship in a large tank filled with fresh water. Polyethylene
glycol, or PEG, will then be slowly added to the water until a 30 percent
PEG solution is formed. Suppose La Belle displaces 6.00 m3
of liquid
when submerged. If the ship’s apparent weight decreases by 800 N as the
PEG concentration increases from 0 to 30 percent, what is the density of
the final PEG solution? The density of fresh water is 1.00 × 103
kg/m3
.

Problem B 87
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
NAME ______________________________________ DATE _______________ CLASS ____________________
Fluid Mechanics
Problem B
PRESSURE
P R O B L E M
The largest helicopter in the world, which was built in Russia, has a mass
of 1.03 103
kg. If you placed this helicopter on a large piston of a hy-
draulic lift, what force would need to be applied to the small piston in
order to slowly lift the helicopter? Assume that the weight of the heli-
copter is distributed evenly over the large piston’s area, which is
1.40 102
m2
. The area of the small piston is 0.80 m2.
S O L U T I O N
Given: m = 1.03 × 105
kg
A1 = 1.40 × 102
m2
A2 = 0.80 m2
g = 9.81 m/s2
Unknown: F2 = ?
Use the equation for pressure to equate the two opposing pressures in terms of
force and area.
P = 
A
F
 P1 = P2

A
F1
1
 = 
A
F2
2

F2 = F1 
A
A
2
1
 = mg

A
A
2
1


F2 = (1.03 × 105
kg)(9.81 m/s2
)

1.4
0
0
.8
×
0
1
m
02
2
m2


F2 = 5.8 × 103
N
ADDITIONAL PRACTICE
1. Astronauts and cosmonauts have used pressurized spacesuits to explore
the low-pressure regions of space. The pressure inside one of these suits
must be close to that of Earth’s atmosphere at sea level so that the space
explorer may be safe and comfortable. The pressure on the outside of the
suit is a fraction of 1.0 Pa. Clearly, pressurized suits are made of ex-
tremely sturdy material that can tolerate the stress from these pressure
differences. If the average interior surface area of a pressurized spacesuit
is 3.3 m2
, what is the force exerted on the suit’s material? Assume that the
pressure outside the suit is zero and that the pressure inside the suit is
1.01 × 105
Pa.
2. A strange idea to control volcanic eruptions is developed by a daydream-
ing engineer. The engineer imagines a giant piston that fits into the

NAME ______________________________________ DATE _______________ CLASS ____________________
88
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
volcano’s shaft, which leads from Earth’s surface down to the magma
chamber. The piston controls an eruption by exerting pressure that is
equal to or greater than the pressure of the hot gases, ash, and magma
that rise from the magma chamber through the shaft. The engineer as-
sumes that the pressure of the volcanic material is 4.0 × 1011
Pa, which is
the pressure in Earth’s interior. If the material rises into a cylindrical
shaft with a radius of 50.0 m, what force is needed on the other side of
the piston to balance the pressure of the volcanic material?
3. The largest goat ever grown on a farm had a mass of 181 kg; on the other
hand, the smallest “pygmy” goats have a mass of only about 16 kg. Imag-
ine an agricultural show in which a large goat with a mass of 181 kg
exerts a pressure on a hydraulic-lift piston that is equal to the pressure
exerted by three pygmy goats, each of which has a mass of 16.0 kg. The
area of the piston on which the large goat stands is 1.8 m2
. What is the
area of the piston on which the pygmy goats stand?
4. The greatest load ever raised was the offshore Ekofisk complex in the
North Sea. The complex, which had a mass of 4.0 × 107
kg, was raised
6.5 m by more than 100 hydraulic jacks. Imagine that his load could have
been raised using a single huge hydraulic lift. If the load had been placed
on the large piston and a force of 1.2 × 104
N had been applied to the
small piston, which had an area of 5.0 m2
, what must the large piston’s
area have been?
5. The pressure that can exist in the interior of a star due to the weight of
the outer layers of hot gas is typically several hundred billion times
greater than the pressure exerted on Earth’s surface by Earth’s atmos-
phere. Suppose a pressure equal to that estimated for the sun’s interior
(2.0 × 1016
Pa) acts on a spherical surface within a star. If a force of
1.02 N × 1031
N produces this pressure, what is the area of the surface?
What is the sphere’s radius r? (Recall that a sphere’s surface area equals
4pr2
.)
6. The eye of a giant squid can be more than 35 cm in diameter—the
largest eye of any animal. Giant squid also live at depths greater than a
mile below the ocean’s surface. At a depth of 2 km, the outer half of a
giant squid’s eye is acted on by an external force of 4.6 × 106
N. Assum-
ing the squid’s eye has a diameter of 38 cm, what is the pressure on the
eye? (Hint: Treat the eye as a sphere.)
7. The largest tires in the world, which are used for certain huge dump
trucks, have diameters of about 3.50 m. Suppose one of these tires has a
volume of 5.25 m3
and a surface area of 26.3 m2
. If a force of 1.58 × 107
N
acts on the inner area of the tire, what is the absolute pressure inside the
tire? What is the gauge pressure on the tire’s surface?

NAME ______________________________________ DATE _______________ CLASS ____________________
Problem C 89
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Fluid Mechanics
Problem C
PRESSURE AS A FUNCTION OF DEPTH
P R O B L E M
In 1969, a whale dove and remained underwater for nearly 2 h. Evidence
indicates that the whale reached a depth of 3.00 km, where the whale sus-
tained a pressure of 3.03 107
Pa. Estimate the density of sea water.
S O L U T I O N
Given: h = 3.00 km = 3.00 × 103
m
P = 3.03 × 107
Pa
Po = 1.01 × 105
Pa
g = 9.81 m/s2
Unknown: r = ?
Use the equation for fluid pressure as a function of depth, and rearrange it to solve
for density.
P = Po + rgh
r = 
P
g
−
h
Po

r =
r =
r = 1.03 × 103
kg/m3
3.02 × 107
Pa

(9.81 m/s2
)(3.00 × 103
m)
(3.03 × 107
Pa) − (1.01 × 105
Pa)

(9.81 m/s2
)(3.00 × 103
m)
ADDITIONAL PRACTICE
1. In 1994, a 16.8 m tall oil-filled barometer was constructed in Belgium.
Suppose the barometer column was 80.0 percent filled with oil. What
was the density of the oil if the pressure at the bottom of the column was
2.22 × 105
Pa and the air pressure at the top of the oil column was 1.01 ×
105
Pa?
2. One of the lowest atmospheric pressures ever measured at sea level was
8.88 × 104
Pa, which existed in hurricane Gilbert in 1988. This same
pressure can be found at a height 950 m above sea level. Use this infor-
mation to estimate the density of air.
3. In 1993, Francisco Ferreras of Cuba held his breath and took a dive that
lasted more than 2 min. The maximum pressure Ferreras experienced
was 13.6 times greater than atmospheric pressure. To what depth did
Ferreras dive? The density of sea water is 1.025 × 103
kg/m3
.
4. A penguin can endure pressures as great as 4.90 × 106
Pa. What is the
maximum depth to which a penguin can dive in sea water?

90
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
NAME ______________________________________ DATE _______________ CLASS ____________________
5. In 1942, the British ship Edinburgh, which was carrying a load of 460
gold ingots, sank off the coast of Norway. In 1981, all of the gold was re-
covered from a depth of 245 m by a team of 12 divers. What was the
pressure exerted by the ocean’s water at that depth?
6. In 1960, a bathyscaph descended 10 916 m below the ocean’s surface.
What was the pressure exerted on the bathyscaph at that depth?

Problem A 91
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Heat
Problem A
P R O B L E M
S O L U T I O N
TEMPERATURE CONVERSION
The temperature at the surface of the sun is estimated to be 5.97 × 103
K.
Express this temperature in degrees Fahrenheit and in degrees Celsius.
Given: T = 5.97 × 103
K
Unknown: TF = ? TC = ?
Use the Celsius-Fahrenheit and Celsius-Kelvin temperature conversion equations.
TC = T − 273.15 = (5.97 × 103
− 0.27 × 103
)K =
TF = 
9
5
TC + 32.0 = 
9
5
(5.70 × 103
) + 32.0°F = 1.03 × 104
°F
5.70 × 103
K
ADDITIONAL PRACTICE
1. Usually, people die if their body temperature drops below 35°C. There
was one case, however, of a two-year-old girl who had been accidentally
locked outside in the winter. She survived, even though her body temper-
ature dropped as low as 14°C. Express this temperature in kelvins and in
degrees Fahrenheit.
2. In experiments conducted by the United States Air Force, subjects en-
dured air temperatures of 4.00 × 102
°F. Express this temperature in
degrees Celsius and in kelvins.
3. The temperature of the moon’s surface can reach 117°C when exposed to
the sun and can cool to −163°C when facing away from the sun. Express
this temperature change in degrees Fahrenheit.
4. Because of Venus’ proximity to the sun and its thick, high-pressure
atmosphere, its temperature can rise to 860.0°F. Express this temperature
in degrees Celsius.
5. On January 22, 1943, the air temperature at Spearfish, South Dakota, rose
49.0°F in 2 min to reach a high temperature of 7.00°C. What were the ini-
tial and final temperatures in degrees Fahrenheit? What was the tempera-
ture in degrees Celsius before the temperature increase?
6. In 1916, Browning, Montana, experienced a temperature decrease of 56°C
during a 24 h period. The final temperature was −49°C. Express in kelvins
the temperatures at the beginning and the end of the 24 h period.
7. In 1980, Willie Jones of Atlanta, Georgia, was hospitalized with heat-
stroke, having a body temperature of 116°F. Fortunately, he survived.
Express Willie’s body temperature in kelvins.

P R O B L E M
Heat
Problem B
CONSERVATION OF ENERGY
The moon has a mass of 7.3 × 1022
kg and an average orbital speed of
1.02 × 103
m/s. Suppose all of the moon’s kinetic energy goes into in-
creasing the internal energy of a quantity of water at a temperature of
100.0°C. If it takes 2.26 × 106
J to vaporize 1.00 kg of water that is initially
at 100.0°C, what mass of this water can be vaporized?
S O L U T I O N
Given: mm = mass of moon = 7.3 × 1022
kg
vm = speed of moon = 1.02 × 103
m/s
k = energy needed to vaporize 1 kg of water = 2.26 × 106
J
Unknown: mw = mass of water vaporized = ?
Choose the equation(s) or situation: Use the equation for energy conservation,
including a term for the change in internal energy.
∆PE + ∆KE + ∆U = 0
The moon’s kinetic energy alone is taken into consideration. Therefore ∆PE
equals zero. Because all of the moon’s kinetic energy is transferred to the water’s
internal energy, the moon’s final kinetic energy is also zero.
∆KE + ∆U = KEf − KEi + ∆U = 0 − KEi + ∆U = 0
∆U = KEi = 
1
2
mm(vm)2
To find the mass of water that will be vaporized, the change in internal energy
must be divided by the conversion constant, k.
mw = 
∆
k
U
 = 
mm
2
(v
k
m)2

mw = =
The mass of the water vaporized is only 23 percent of the moon’s mass. This sug-
gests that a smaller object moving with the moon’s speed would vaporize a mass
of water only 0.23 times as large as its own mass. Because the water is already at
its boiling point, this result indicates that a considerable amount of energy goes
into the process of vaporization.
1.7 × 1022
kg
(7.3 × 1022
kg)(1.02 × 103
m/s)2

2(2.26 × 106
J/kg)
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
92
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. A British-built Hovercraft
—a vehicle that cruises on a cushion of air—
kg and can attain a speed of 120.0 km/h. Sup-
pose this vehicle slows down from 120.0 km/h to 90.0 km/h and that the

Problem B 93
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. change in its kinetic energy is used to raise the temperature of a quantity
of water by 10.0°C. Knowing that 4186 J is required to raise the tempera-
ture of 1.00 kg of water by 1.00°C, calculate the mass of the heated water.
2. The Westin Stamford Hotel in Detroit is 228 m tall. Suppose a piece of
ice, which initially has a temperature of 0.0°C, falls from the hotel roof
and crashes to the ground. Assuming that 50.0 percent of the ice’s me-
chanical energy during the fall and collision is absorbed by the ice and
that 3.33 × 105
J is required to melt 1.00 kg of ice, calculate the fraction
of the ice’s mass that would melt.
3. The French-built Concorde, the fastest passenger jet plane, is known to
travel with a speed as great as 2.333 × 103
km/h. Suppose the plane travels
horizontally at an altitude of 4.000 × 103
m and at maximum speed when
a fragment of metal breaks free from the plane. The metal has, of course,
the same horizontal speed as the plane, and when it lands on the ground,
it will have absorbed 1.00 percent of its total mechanical energy. If it takes
355 J to raise the temperature of 1.00 kg of this metal by 1.00°C, how
great a temperature change will the metal fragment experience from the
time it breaks free from the Concorde to the time it lands on the ground?
Ignore air resistance.
4. Mount Everest is the world’s highest mountain. Its height is 8848 m. Sup-
pose a steel alpine hook were to slowly slide off the summit of Everest
and fall all the way to the base of the mountain. If 20.0 percent of the
hook’s mechanical energy is absorbed by the hook as internal energy, cal-
culate the final temperature of the hook. Assume that the hook’s initial
temperature is −18.0°C and that the hook’s temperature increases by
1.00°C for every 448 J/kg that is added.
5. The second tallest radio mast in the world is located near Fargo, North
Dakota. The tower, which has an overall height of 629 m, was built in just
one month by a team of 11 workers. Suppose one of these builders left a
3.00 g copper coin on the top of the tower. During extremely windy
weather, the coin falls off the tower and reaches the ground at the tower’s
base with a speed of 42 m/s. If the coin absorbs 5.0 percent of its total me-
chanical energy, by how much does the coin’s internal energy increase?
6. In 1993, Russell Bradley carried a load of bricks with a total mass of
312 kg up a ramp that had a height of 2.49 m. Suppose Bradley puts the
load on the ramp and then pushes the load off the edge with a horizontal
speed of 0.50 m/s. If the bricks absorb half their total mechanical energy,
how much does their internal energy change?
7. Angel Falls, the highest waterfall in the world, is located in Venezuela. Es-
timate the height of the waterfall, assuming that the water that falls the
complete distance experiences a temperature increase of 0.230°C. In
your calculation, assume that the water absorbs 10.0 percent of its me-
chanical energy and that 4186 J is needed to raise the temperature of 1.00
kg of water by 1.00°C.

P R O B L E M
Heat
Problem C
CALORIMETRY
In 1990, the average rate for use of fresh water in the United States was
approximately 1.50 × 107
kg each second. Suppose a group of teenagers
build a really big calorimeter and that they place in it a mass of water
equal to the mass of fresh water consumed in 1.00 s. They then use a test
sample of gold with a mass equal to that of the United States gold reserve
for 1992. Initially, the gold has a temperature of 80.0°C and the water has a
temperature of 1.00°C. If the final equilibrium temperature of the gold
and water is 2.30°C, what is the mass of the gold?
S O L U T I O N
Given: Tf = 2.30°C mwater = mw = 1.50 × 107
kg
Tgold = Tg = 80.0°C Twater = Tw = 1.00°C
cp,gold = cp,g = 129 J/kg•°C cp,water = cp,w = 4186 J/kg•°C
Unknown: mgold = mg = ?
Choose the equation(s) or situation: Equate the energy removed from the gold
to the energy absorbed by the water.
energy removed from metal = energy absorbed by water
–cp,gmg(Tf – Tg) = cp,wmw(Tf − Tw)
mg =
mg =
mg = =
Although the masses of the gold sample and water are unrealistic, the tempera-
tures are entirely reasonable, indicating that temperature is an intrinsic variable
of matter that is independent of the quantity of a substance. The small increase
in the water’s temperature and the large decrease in the gold’s temperature is the
result of the water having both a larger mass and a larger specific heat capacity.
8.14 × 106
kg
(4186 J/kg•°C)(1.50 × 107
kg)(1.30°C)

(129 J/kg•°C)(77.7°C)
(4186 J/kg•°C)(1.50 × 107
kg)(2.30°C − 1.00°C)

(129 J/kg•°C)(80.0°C − 2.30°C)
cp,wmw(Tf − Tw)

cp,g(Tg – Tf )
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. In 1992, the average rate of energy consumption in the United States was
about 2.8 × 109
W. Suppose all of the copper produced in the United
States in 1992 is placed in the giant calorimeter used in the sample
94
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem 10C 95
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. problem. The quantity of energy transferred by heat from the copper to
the water is equal to the energy used in the United States during 1.2 s of
1992. If the initial temperature of the copper is 26.0°C, and the final
temperature is 21.0°C, what is the mass of the copper?
2. In 1992, a team of firefighters pumped 143 × 103
kg of water in less than
four days. What mass of wood can be cooled from a temperature of
280.0°C to one of 100.0°C using this amount of water? Assume that the
initial temperature of the water is 20.0°C and that all of the water has a
final equilibrium temperature of 100.0°C, but that none of the water is
vaporized. Use 1.700 × 103
J/kg•°C for the specific heat capacity of wood.
3. One of the nuclear generators at a power plant in Lithuania has a nomi-
nal power of 1.450 GW, making it the most powerful generator in the
world. Nippon Steel Corporation in Japan is the world’s largest steel pro-
ducer. Between April 1, 1993, and March, 31, 1994, Nippon Steel’s mills
produced 25.1 × 109
kg of steel. Suppose this entire quantity of steel is
heated and then placed in the giant calorimeter used in the sample prob-
lem. If the quantity of energy transferred by heat from the steel to the
water equals 1.00 percent of all the energy produced by the Lithuanian
generator in a year, what is the temperature change of the steel? Assume
that the specific heat capacities of steel and iron are the same.
4. In 1994, to commemorate the 200th anniversary of a beverage company,
a giant bottle was constructed and filled with 2.25 × 103
kg of the com-
pany’s lemonade. Suppose the lemonade has an initial temperature of
28.0°C when 9.00 × 102
kg of ice with a temperature of −18.0°C is added
to it. What is the lemonade’s temperature at the moment the tempera-
ture of the ice reaches 0.0°C? Assume that the lemonade has the same
specific heat capacity as water.
5. The water in the Arctic Ocean has a total mass of 1.33 × 1019
kg. The
average temperature of the water is estimated to be 4 .000°C. What
would the temperature of the water in the Arctic Ocean be if the
energy produced in 1.000 × 103
y by the world’s largest power plant
(1.33 × 1010
W) were transferred by heat to it?
6. There is a little island off the shore of Brazil where the weather is ex-
tremely consistent. From 1911 to 1990, the lowest temperature on the is-
land was 18°C (64°F) and the highest temperature was 32°C (90°F). It is
known that the liquid in a standard can of soft drink absorbs 20.8 kJ of
energy when its temperature increases from 18.0°C to 32.0°C. If the soft
drink has a mass of 0.355 kg, what is its specific heat capacity?
7. The lowest temperature ever recorded in Alaska is −62°C. The highest
temperature ever recorded in Alaska is 38°C. Suppose a piece of metal
with a mass of 180 g and a temperature of −62.0°C is placed in a
calorimeter containing 0.500 kg of water with a temperature of 38.0°C. If
the final equilibrium temperature of the metal and water is 36.9°C, what
is the specific heat capacity of the metal? Use the calculated value of the
specific heat capacity and Table 4 in your textbook to identify the metal.

P R O B L E M
Heat
Problem D
HEAT OF PHASE CHANGE
The world’s deepest gold mine, which is located in South Africa, is over
3 km deep. Every day, the mine transfers enough energy by heat to the
mine’s cooling systems to melt 3.36 × 107
kg of ice at 0.0°C. If the energy
output from the mine is increased by 2.0 percent, to what final tempera-
ture will the 3.36 × 107
kg of ice-cold water be heated?
S O L U T I O N
Given: mice = mwater = m = 3.36 × 107
kg
Ti = 0.0°C
Lf = 3.33 × 105
J/kg
cp,w = 4186 J/(kg•°C)
Q = energy added to water = (2.0 × 10−2
)Q
Unknown: Tf = ?
Choose the equation(s) or situation: First, determine the amount of energy
needed to melt 3.36 × 107
kg of ice by using the equation for the heat of fusion.
Q = miceLf = mLf
The energy added to the now liquid ice (Q) can then be determined.
Q = (2.0 × 10−2
)Q = (2.0 × 10−2
)mLf
Finally, the energy added to the water equals the product of the water’s mass, spe-
cific heat capacity, and change in temperature.
Q = mcp,w(Tf − Ti) = (2.0 × 10−2
)mLf
Tf = + Ti = (2.0 × 10−2
) 
cp
L
,
f
w
 + Ti
Tf = (2.0 × 10−2
) + 0.0°C =
Note that the result is independent of the mass of the ice and water. The amount
of energy needed to raise the water’s temperature by 1°C is a little more than
1 percent of the energy required to melt the ice.
1.6°C
(3.33 × 10−5
J/kg)

(4186 J/kg•°C)
(2.0 × 10−2
)mLf

mcp,w
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
96
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. Lake Superior contains about 1.20 × 1016
kg of water, whereas Lake Erie
contains only 4.8 × 1014
kg of water. Suppose aliens use these two lakes
for cooking. They heat Lake Superior to 100.0°C and freeze Lake Erie to

Problem D 97
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 0.0°C. Then they mix the two lakes together to make a “lake shake.”What
would be the final temperature of the mixture? Assume that the entire
energy transfer by heat occurs between the lakes.
2. The lowest temperature measured on the surface of a planetary body in the
solar system is that of Triton, the largest of Neptune’s moons. The surface
temperature on this distant moon can reach a low of −235°C. Suppose an
astronaut brings a water bottle containing 0.500 kg of water to Triton. The
water’s temperature decreases until the water freezes, then the temperature
of the ice decreases until it is in thermal equilibrium with Triton at a tem-
perature of −235°C. If the energy transferred by heat from the water to Tri-
ton is 471 kJ, what is the value of the water’s initial temperature?
3. Suppose that an ice palace built in Minnesota in 1992 is brought into con-
tact with steam with a temperature of 100.0°C. The temperature and mass
of the ice palace are 0.0°C and 4.90 × 106
kg, respectively. If all of the steam
liquefies by the time all of the ice melts, what is the mass of the steam?
4. In 1992,1.804 × 106
kg of silver was produced in the United States.What
mass of ice must be melted so that this mass of liquid silver can solidify? As-
sume that both substances are brought into contact at their melting tempera-
tures.The latent heat of fusion for silver is 8.82 × 104
J/kg.
5. The United States Bullion Depository at Fort Knox, Kentucky, contains
almost half a million standard mint gold bars, each with a mass of
12.4414 kg. Assuming an initial bar temperature of 5.0°C, each bar will
melt if it absorbs 2.50 MJ of energy transferred by heat. If the specific
heat capacity of gold is 129 J/kg •°C and the melting point of gold is
1063°C, calculate the heat of fusion of gold.
6. The world’s largest piggy bank has a volume of 7.20 m3
. Suppose the bank
is filled with copper pennies and that the pennies occupy 80.0 percent of
the bank’s total volume. The density of copper is 8.92 × 103
kg/m3
.
a. Find the total mass of the coins in the piggy bank.
b. Consider the mass found in (a). If these copper coins are brought
to their melting point, how much energy must be added to the
coins in order to melt 15 percent of their mass? The latent heat of
fusion for copper is 1.34 × 105
J/kg.
7. The total mass of fresh water on Earth is 3.5 × 1019
kg. Suppose all this
water has a temperature of 10.0°C. Suppose the entire energy output of
the sun is used to bring all of Earth’s fresh water to a boiling temperature
of 100.0°C, after which the water is completely vaporized.
a. How much energy must be added to the fresh water through heat in
order to raise its temperature to the boiling point and vaporize it?
b. If the rate at which energy is transferred from the sun is 4.0 × 1026
J/s,
how long will it take for the sun to provide sufficient energy for the
heating and vaporization process?

Problem A 99
NAME ______________________________________ DATE _______________ CLASS ____________________
Thermodynamics
Problem A
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
WORK DONE ON OR BY A GAS
Suppose 2.4 × 108
J of work was required to inflate 1.6 million balloons
that were released at one time in 1994. If each balloon was filled at a con-
stant pressure that was 25 kPa in excess of atmospheric pressure, what
was the change in volume for each balloon?
S O L U T I O N
Given: W = 2.4 × 108
J
P = 25 kPa = 2.5 × 104
Pa
n = number of balloons = 1.6 × 106
Unknown: ∆V = ?
Use the definition of work in terms of changing volume. The total volume
change involves 1.6 million balloons, so the volume change of one balloon must
be multiplied by n = 1.6 × 106
.
W = nP∆V
∆V = 
n
W
P
 = = 6.0 × 10−3
m3
2.4 × 108
J

(1.6 × 106
)(2.5 × 104
N/m2
)
ADDITIONAL PRACTICE
1. The largest glass bottle made by the method of glass-blowing was over
2 m tall. Suppose the net pressure used to expand the bottle to full vol-
ume was 5.1 kPa. If 3.6 × 103
J of work was done in expanding the bottle
from an initial volume of 0.0 m3
, what was the final volume?
2. Russell Bradley carried 207 kg of bricks 3.65 m up a ladder. If the amount
of work required to perform that task is used to compress a gas at a con-
stant pressure of 1.8 × 106
Pa, what is the change in volume of the gas?
3. Nicholas Mason inflated a weather balloon using just the power of his
lungs. The balloon’s final radius was 1.22 m. If 642 kJ of work was done
to inflate the balloon, at what net pressure was the balloon inflated?
4. Calculate the pressure needed to inflate a sphere that has a volume equal
to that of the sun assuming that the work done was 3.6 × 1034
J. The
sun’s radius is 7.0 × 105
km.
5. In 1979, an extremely low pressure of 87 kPa was measured in a storm over
the Pacific Ocean. Suppose a gas is compressed at this pressure and its vol-
ume decreases by 25.0 × 10−3
m3
. How much work is done by the gas?
6. Susan Williams, of California, blew a bubble-gum bubble with a radius
of 29.2 cm. If this were done with a constant net pressure of 25.0 kPa, the
work done could have been used to launch a model airplane. If the air-
plane’s mass were 160.0 g, what would have been the launch speed?

100
NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. The heaviest snake ever found had a mass of 227 kg and measured
8.45 m in length. Suppose a sample of a gas with an initial internal en-
ergy of 42.0 kJ performs an amount of work equal to that needed to lift
the snake to a height equal to its length. If 4.00 kJ of energy is transferred
Thermodynamics
Problem B
THE FIRST LAW OF THERMODYNAMICS
In 1992, residents of Arkansas consumed, on average, 11.4 L of gasoline
per vehicle per day. If this amount of gasoline burns completely in a pure
combustion reaction, it will release 4.3 × 108
J of energy. Suppose this
amount of energy is transferred by heat from a quantity of gas confined
in a very large cylinder. The cylinder, however, is equipped with a piston,
and shortly after the energy is transferred by heat from the cylinder, work
is done on the gas. The magnitude of the energy transferred by work is
equal to one-third the magnitude of the energy transferred by heat. If the
initial internal energy of the gas is 1.00 × 109
J, what is the final internal
energy of the gas?
S O L U T I O N
Given: Ui = 1.00 × 109
J Q = −4.3 × 108
J
W = Q/3 = −(4.3 × 108
J)/3 = −1.4 × 108
J
Work is done on the gas, so work, W, has a negative value and increases the inter-
nal energy of the gas. Energy is transferred from the gas by heat, Q, which re-
duces the gas’ internal energy. Therefore, Q must have a negative value.
Unknown: Uf = ?
Choose the equation(s) or situation: Apply the first law of thermodynamics
using the definition of the change in internal energy (∆U = Uf − Ui) and the
values for the energy transferred by heat, Q, and work, W, to find the value for
the final internal energy.
∆U = Q − W
Uf − Ui = Q − W
Uf = Q − W + Ui
Uf = (−4.3 × 108
J) − (−1.4 × 108
J) + (1.00 × 109
J)
Uf =
The final internal energy is less than the initial internal energy because three
times as much energy was transferred away from the gas by heat as was trans-
ferred to the gas by work done on the gas.
7.1 × 108
J
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

Problem B 101
NAME ______________________________________ DATE _______________ CLASS ____________________
to the gas by heat during the lifting process, what will be the final inter-
nal energy of the gas?
2. The most massive cannon ever built was made in Russia in 1868. This
cannon had a mass in excess of 1.40 × 105
kg and could fire cannonballs
with masses up to 4.80 × 102
kg. If the gunpowder in the cannon burned
very quickly (adiabatically), forming compressed gas in the barrel, then
the gas would expand and perform work on the cannonball. Suppose the
initial speed of one of these cannonballs is 2.00 × 102
m/s.
a. How much work is done by the expanding gas?
b. If the internal energy of the gas is 12.0 MJ when the cannonball
leaves the barrel, what is the initial internal energy of the gas im-
mediately after all of the powder burns?
3. The world’s largest jelly, which had a mass of about 4.00 × 104
kg, was
made in Australia in 1981.
a. How much energy must be transferred by heat from the jelly in order
for its temperature to decrease 20.0°C? Assume that the specific heat
capacity of the jelly equals that of water.
b. Suppose all this energy is transferred by heat to a sample of gas. At
the same time, the gas does 1.64 × 109
J of work on its surround-
ings. What is the net change in the internal energy of the gas?
4. The surface of Lake Ontario is 75.0 m above sea level. The mass of water
in the lake is about 1.64 × 1015
kg. Imagine an enormous sample of gas
that performs an amount of work capable of lifting Lake Ontario 75.0 m
and that also transfers to the lake enough energy by heat to vaporize the
entire lake. If the initial temperature of the lake water is 6.0°C and the
internal energy of the gas decreases by 90.0 percent, what is the final
internal energy of the gas?
5. An average elephant has a mass of 5.00 × 103
kg. Contrary to popular be-
lief, elephants are not slow; they can achieve speeds of up to 40.0 km/h.
Imagine a sample of gas that does an amount of work equal to the work
required for an average elephant to move from rest to its maximum
speed. If the initial internal energy of the gas, 2.50 × 105
J, is to be dou-
bled, how much energy must be transferred to the gas by heat?
6. The rate of nuclear energy production in the United States in 1992 was
about 5.9 × 109
J/s. Suppose one second’s worth of this energy is trans-
ferred by heat to an ideal gas. How much work must be done on or by
this gas so that the net increase in its internal energy is 2.6 × 109
J?
7. Dan Koko, a professional stuntman, jumped onto an air pad from a
height of almost 1.00 × 102
m. His impact speed was about 141 km/h.
a. If all of Koko’s kinetic energy was transferred by heat to the air in
the air pad after the inelastic collision with the air pad, how much
work was done?
b. Assuming that the initial internal energy of the air in the pad is
40.0 MJ, determine the percent increase in the internal energy of
this air after Koko’s jump. Assume that Koko’s mass was 76.0 kg.
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

102
NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Thermodynamics
Problem C
HEAT-ENGINE EFFICIENCY
In 1989, Brendan Keenoy ran up 1760 steps in the CN Tower in Toronto,
reaching a height of 342 m in 7 min 52 s. Suppose the amount of work
done by Keenoy is done by a heat engine. The engine’s input energy is
1.34 MJ, and its efficiency is 0.18. How much energy is exhausted from,
and how much work is done by the engine?
S O L U T I O N
Given: Qh = 1.34 MJ = 1.34 × 106
J eff = 0.18
Unknown: Qc = ? Wnet = ?
Use the equation for the efficiency of a heat engine, expressed in terms of Qh and
Wnet. The net work equals the work done in climbing the tower (mgh).
Qc = Qh (1 − eff ) = (1.34 × 106
J)(1 − 0.18) = (1.34 × 106
J)(0.82)
Qc =
Wnet = Qh − Qc = 1.34 × 106
J − 1.1 × 106
J = 2.4 × 105
J
1.1 × 106
J
ADDITIONAL PRACTICE
1. The oldest working steam engine was designed in 1779 by James Watt.
Suppose this engine’s efficiency is 8.0 percent. How much energy must be
transferred by heat to the engine’s surroundings if 2.5 kJ is transferred by
heat into the engine? How much work is done?
2. In 1894, the first turbine-driven ship was designed. Suppose the ships
turbine’s had an efficiency of 16 percent. How much energy would have
been exhausted by the turbines if the input energy was 2.0 × 109
J and
the net power was 1.5 MW?
3. A steam engine built in 1812 still works at its original site in England. The
engine delivers 19 kW of net power. If the engine’s efficiency is 6.0 percent,
how much energy must be transferred by heat to the engine in 1.00 h?
4. The first motorcycle was built in Germany in 1885, and it could reach a
speed of 19 km/h. The output power of the engine was 370 W. If the engine’s
efficiency was 0.19, what was the input energy after 1.00 min?
5. A fairly efficient steam engine was built in 1840. It required burning only
0.80 kg of coal to perform 2.6 MJ of net work. Calculate the engine’s effi-
ciency if burning coal releases 32.6 MJ of energy per kilogram of coal.
6. The world’s tallest mobile crane can lift 3.00 × 104
kg to a height of
1.60 × 102
m. What is the efficiency of a heat engine that does the same
task while losing 3.60 × 108
J of energy by heat to the surroundings?

Problem A 103
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Vibrations andWaves
Problem A
HOOKE’S LAW
The pygmy shrew has an average mass of 2.0 g. If 49 of these shrews are
placed on a spring scale with a spring constant of 24 N/m, what is the
spring’s displacement?
S O L U T I O N
Given: m = mass of one shrew = 2.0 g = 2.0 × 10−3
kg
n = 49
g = 9.81 m/s2
k = 24 N/m
Unknown:
Choose the equation(s) or situation: When the shrews are attached to the
spring, the equilibrium position changes. At the new equilibrium position, the
net force acting on the shrews is zero. So the spring force (given by Hooke’s law)
must be equal to and opposite the weight of the shrews.
Fnet = 0 = Felastic + Fg
Felastic = −kx
Fg = −mtotg = −nmg
−kx − nmg = 0
x = 
−n
k
mg

x =
x =
Forty-nine shrews of 2.0 g each provide a total mass of about 0.1 kg, or a weight
of just under 1 N. From the value of the spring constant, a force of 1 N should
displace the spring by 1/24 of a meter, or about 4 cm. This indicates that the final
result is consistent with the rest of the data.
−4.0 × 10−2
m
−(49)(2.0 × 10−3
kg)(9.81 m/s2
)

(24 N/m)
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
P R O B L E M
ADDITIONAL PRACTICE
1. The largest meteorite of lunar origin reportedly has a mass of 19 g. If the
meteorite placed on a scale whose spring constant is 83 N/m, what is the
compression of the spring?

104
NAME ______________________________________ DATE _______________ CLASS ____________________
2. In 1952, a great rainfall hit the island of Reunion in the Indian Ocean. In
less than 24 h, 187 kg of rain fell on each square meter of soil. If a 187 kg
mass is placed on a scale that has a spring constant of 1.53 × 104
N/m,
how far is the spring compressed?
3. The largest tigers, and therefore the largest members of the cat family, are
the Siberian tigers. Male Siberian tigers are reported to have an average
mass of about 389 kg. By contrast, a variety of very small cat that is na-
tive to India has an average adult mass of only 1.5 kg. Suppose this small
cat is placed on a spring scale, causing the spring to be extended from its
equilibrium position by 1.2 mm. How far would the spring be extended
if a typical male Siberian tiger were placed on the same scale?
4. The largest known crab is a giant spider crab that had a mass of 18.6 kg.
The distance from the end of one of this crab’s claws to the end of the
other claw measured about 3.7 m. If this particular giant spider crab
were hung from an elastic band so that the elongation of the band was
equal to the crab’s claw span, what would be the spring constant of the
elastic band?
5. The CN Tower in Toronto, Canada, is 533 m tall, making it the world’s
tallest free-standing structure. Suppose an unusually long bungee cord is
attached to the top of the CN Tower. The equilibrium length of the cord
is equal to one-third the height of the tower. When a test mass of 70.0 kg
is attached, the cord stretches to a length that equals two-thirds of the
tower’s height. From this information, determine the spring constant of
the bungee cord.
6. The largest ruby in the world may be found in New York. This ruby is
109 mm long, 91 mm wide, and 58 mm thick, making its volume about
575 cm3
. (By comparison, the world’s largest diamond, the Star of Africa,
has a volume of just over 30 cm3
.)
a. If the ruby is attached to a vertically hanging spring with a spring con-
stant of 2.00 × 102
N/m so that the spring is stretched 15.8 cm what is
the gravitational force pulling the spring?
b. What is the mass of the jewel?
7. Mauna Kea on the island of Hawaii stands 4200 m above sea level. How-
ever, when measured from the island’s sea-submerged base, Mauna Kea
has a height of 10 200 m, making it the tallest single mountain in the
world. If you have a 4.20 × 103
m elastic cord with a spring constant of
3.20 × 10−2
N/m, what force would stretch the spring to 1.02 × 104
m?
8. Rising 348 m above the ground, La Gran Piedra in Cuba is the tallest
rock on Earth. Suppose an elastic band 2.00 × 102
m long hangs vertically
off the top of La Gran Piedra. If the band’s spring constant is 25.0 N/m,
how large must a mass be if, when it is attached to the band, it causes the
band to stretch all the way to the ground?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem B 105
NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem B
SIMPLE HARMONIC MOTION OF A SIMPLE PENDULUM
Two friends in France use a pendulum hanging from the world’s highest
railroad bridge to exchange messages across a river. One friend attaches a
letter to the end of the pendulum and releases it so that the pendulum
swings across the river to the other friend. The bridge is 130.0 m above
the river. How much time is needed for the letter to make one swing
across the river? Assume the river is 16.0 m wide.
S O L U T I O N
Given: L = 130.0 m ag = g = 9.81 m/s2
Unknown: t = time required for pendulum to cross river = T/2 =?
Use the equation for the period of a simple pendulum. Then divide the period by
two to find the time of one swing across the river. The width of the river is not
needed to calculate the answer, but it must be small compared to the length of
the pendulum in order to use the equations for simple harmonic motion.
T = 2p

a
L
g

= 2p
9
1
.
8
3
1

0.
m
0

m
/
s2

= 22.9 s
t = 
T
2
 = 
22
2
.9 s
 = 11.4 s
ADDITIONAL PRACTICE
1. An earthworm found in Africa was 6.7 m long. If this worm were a sim-
ple pendulum, what would its period be?
2. The shortest venomous snake, the spotted dwarf adder, has an average
length of 20.0 cm. Suppose this snake hangs by its tail from a branch and
holds a heavy prey with its jaws, simulating a pendulum with a length of
15.0 cm. How long will it take the snake to swing through one period?
3. If bamboo, which can grow 88 cm in a day, is grown for four days and then
used to make a simple pendulum, what will be the pendulum’s period?
4. A simple pendulum with a frequency of 6.4 × 10−2
Hz is as long as the
largest known specimen of Pacific giant seaweed. What is this length?
5. The deepest permafrost is found in Siberia, Russia. Suppose a shaft is
drilled to the bottom of the frozen layer, and a simple pendulum with a
length equal to the depth of the shaft oscillates within the shaft. In 1.00 h
the pendulum makes 48 oscillations. Find the depth of the permafrost.
6. Ganymede, the largest of Jupiter’s moons, is also the largest satellite in
the solar system. Find the acceleration of gravity on Ganymede if a sim-
ple pendulum with a length of 1.00 m has a period of 10.5 s.

106
NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Vibrations andWaves
Problem C
SIMPLE HARMONIC MOTION OF A MASS-SPRING SYSTEM
A large pearl was found in the Philippines in 1934.Suppose the pearl is
placed on a spring scale whose spring constant is 362 N/m.If the scale’s plat-
form oscillates with a frequency of 1.20 Hz,what is the mass of the pearl?
S O L U T I O N
Given: k = 362 N/m f = 1.20 Hz
Unknown: m = ?
Use the equation for the period of a mass-spring system. Then express the period
in terms of frequency (T = 1/f ).
T = 2p
m
k

= 
1
f

m = 
4p
k
2
f2
 = 
4p
3
2
(
6
1
2
.2
N
0
/
H
m
z)2
 = 6.37 kg
ADDITIONAL PRACTICE
1. The hummingbird makes a humming sound with its wings, which beat
with a frequency of 90.0 Hz. Suppose a mass is attached to a spring with
a spring constant of 2.50 × 102
N/m. How large is the mass if its oscilla-
tion frequency is 3.00 × 10−2
times that of a hummingbird’s wings?
2. In 1986, a 35 × 103
kg watch was demonstrated in Canada. Suppose this
watch is placed on a huge trailer that rests on a lightweight platform, and
that oscillations equal to 0.71 Hz are induced. Find the trailer’s mass if the
platform acts like a spring scale with a spring constant equal to 1.0 × 106
N/m.
3. A double coconut can grow for 10 years and have a mass of 20.0 kg. If a
20.0 kg double coconut oscillates on a spring 42.7 times each minute,
what is the spring constant of the spring?
4. The monument commemorating the Battle of San Jacinto in Texas
stands almost 2.00 × 102
m and is topped by a 2.00 × 105
kg star. Imagine
that a 2.00 × 105
kg mass is placed on a spring platform. The platform re-
quires 0.80 s to oscillate from the top to the bottom positions. What is
the spring constant of the spring supporting the platform?
5. Suppose a 2662 kg giant seal is placed on a scale and produces a 20.0 cm
compression. If the seal and spring system are set into simple harmonic
motion, what is the period of the oscillations?
6. On average, a newborn human’s mass is just over 3.0 kg. However, in
1955, a 10.2 kg boy was born in Italy. Suppose this baby is placed in a crib
hanging from springs with a total spring constant of 2.60 × 102
N/m. If
the cradle is rocked with simple harmonic motion, what is its period?

Problem D 107
NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem D
WAVE SPEED
The world’s largest guitar, which was built by high school students in In-
diana, has strings that are 9.0 m long. The fundamental vibration that
can be induced on each string has a wavelength equal to twice the string’s
length. If the wave speed in a string is 9.0 102
m/s, what is the frequency
of vibration?
S O L U T I O N
Given: f = 50.0 Hz L = 9.0 m
Unknown: v = ?
Use the equation for the speed of a wave. The wavelength is equal to twice the
length of the string (l = 2L).
v = fl = f(2L) = (50.0 Hz)[(2)(9.0 m)] = 9.0 × 102
m/s
ADDITIONAL PRACTICE
1. The speed of sound in sea water is about 1530 m/s. If a sound wave has a
frequency of 2.50 × 102
Hz, what is its wavelength in sea water?
2. Cicadas produce a sound that has a frequency of 123 Hz. What is the
wavelength of this sound in the air? The speed of sound in air is 334 m/s.
3. Human fingers are very sensitive, detecting vibrations with amplitudes as
low as 2.0 × 10–5
m. Consider a sound wave with a wavelength exactly
1000 times greater than the lowest amplitude detectable by fingers. What
is this wave’s frequency?
4. A nineteenth-century fisherman’s cottage in England is only 2.54 m long.
Suppose a fisherman whistles inside the cottage, producing a note that has
a wavelength that exactly matches the length of the house. What is the
whistle’s frequency? The speed of sound in air is 334 m/s.
5. The lowest vocal note in the classical repertoire is low D (f = 73.4 Hz),
which occurs in an aria in Mozart’s opera Die Entführung aus dem Serail.
If low D has a wavelength of 4.50 m, what is the speed of sound in air?
6. The highest-pitched sound that a human ear can detect is about 21 kHz.
On the other hand, dolphins can hear ultrasound with frequencies up to
280 kHz. What is the speed of sound in water if the wavelength of ultra-
sound with a frequency of 2.80 × 105
Hz is 0.510 cm? How long would it
take this sound wave to travel to a dolphin 3.00 km away?

Problem A 109
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Sound
Problem A
P R O B L E M
INTENSITY OF SOUND WAVES
Kåre Walkert of Sweden reportedly snores loudly, with a record intensity
of 4.5 × 10–8
W/m2
. Suppose the intensity of Walkert’s snores are mea-
sured 0.60 m from her mouth.What is the power associated with the
record snore?
S O L U T I O N
Given: Intensity = 4.5 × 10−8
W/m2
r = 0.60 m
Unknown: P = ?
Use the equation for the intensity of a spherical wave.
Intensity = 
4p
P
r2

P = 4pr2
(Intensity) = 4p(0.60 m)2
(4.5 × 10−8
W/m2
)
P = 2.0 × 10−7
W
ADDITIONAL PRACTICE
1. Blue whales are the loudest creatures; they can emit sound waves with an
intensity of 3.0 × 10−3
W/m2
. If this intensity is measured 4.0 m from its
source, what power is associated with the sound wave?
2. The whistling sound that is characteristic of the language known as“silbo,”
which is used on the Canary Island of Gomera, is detectable at 8.0 km. Use
the spherical wave approximation to find the power of a whistler’s sound.
Sound intensity at the hearing threshold is 1.0 × 10−12
W/m2
.
3. Estimate how far away a cicada can be heard if the lowest audible inten-
sity of the sound it produces is 1.0 × 10−12
W/m2
and the power of a
cicada’s sound source is 2.0 × 10−6
W.
4. Howler monkeys, found in Central and South America, can emit a sound
that can be heard by a human several miles away. The power associated
with the sound is roughly 3.0 × 10−4
W. If the threshold of hearing of a
human is assumed to be 1.1 × 10−13
W/m2
, how far away can a howler
monkey be heard.
5. In 1983, Roy Lomas became the world’s loudest whistler; the power of
his whistle was 1.0 × 10−4
W. What was the sound’s intensity at 2.5 m?
6. In 1988, Simon Robinson produced a sound having an intensity level of
2.5 × 10−6
W/m2
at a distance of 2.5 m. What power was associated with
Robinson’s scream?

P R O B L E M
Sound
Problem B
HARMONICS
The tallest load-bearing columns are part of the Temple of Amun in
Egypt, built in 1270 B.C. Find the height of these columns if a standing
wave with a frequency of 47.8 Hz is generated in an open pipe that is as
tall as the columns. The sixth harmonic is generated. The speed of sound
in air is 334 m/s.
S O L U T I O N
Given: f6 = 47.8 Hz v = 334 m/s
n = number of the harmonic = 6
Unknown: L = ?
When the pipe is open, the wavelength associated with the first harmonic (funda-
mental frequency) is twice the length of the pipe.
fn = n 
2
v
L
 n = 1, 2, 3, . . .
L = n 
2
v
fn
 = (6) 
2
(
(
3
4
3
7
4
.8
m
H
/s
z
)
)
 = 21.0 m
ADDITIONAL PRACTICE
1. A 47.0 m alphorn was made in Idaho in 1989. An alphorn behaves like a
pipe with one end closed. If the frequency of the fifteenth harmonic is
26.7 Hz, how long is the alphorn? The speed of sound in air is 334 m/s.
2. A fully functional acoustic guitar over 8.0 m in length is on display in
Bristol, England. Suppose the speed of waves on the guitar’s strings is
5.00 × 102
m/s. If a third harmonic is generated on a string, so that the
sound produced in air has a wavelength of 3.47 m, what is the length of
the string? The speed of sound in air is 334 m/s.
3. The unsupported flagpole built for Canada’s Expo 86 has a height of
86 m. If a standing wave with a 19th harmonic is produced in an 86 m
open pipe, what is its frequency? The speed of sound in air is 334 m/s.
4. A power-plant chimney in Spain is 3.50 × 102
m high. If a standing wave
with a frequency of 35.5 Hz is generated in an open pipe with a length
equal to the chimney’s height and the 75th harmonic is present, what is
the speed of sound?
5. The world’s largest organ was completed in 1930 in Atlantic City, New
Jersey. Its shortest pipe is 4.7 mm long. If one end of this pipe is closed,
what is the number of harmonics created by an ultrasound with a wave-
length of 3.76 mm?
110
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem A 111
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Light and Reflection
Problem A
P R O B L E M
ELECTROMAGNETIC WAVES
The atoms in an HCl molecule vibrate like two charged balls attached to the
ends of a spring.If the wavelength of the emitted electromagnetic wave is
3.75 m,what is the frequency of the vibrations?
S O L U T I O N
Given: l = 3.75 × 10−6
m
c = 3.00 × 108
m/s
Unknown: f = ?
Use the wave speed equation, and solve for l.
c = fl
f = 
l
c
 = 
3
3
.
.
0
7
0
5
×
×
1
1
0
0
8
−6
m
m
/s
 = 8.00 × 1013
Hz
ADDITIONAL PRACTICE
1. New-generation cordless phones use a 9.00 × 102
MHz frequency and can
be operated up to 60.0 m from their base. How many wavelengths of the
electromagnetic waves can fit between your ear and a base 60.0 m away?
2. The highest directly measured frequency is 5.20 × 1014
Hz, corresponding
to one of the transitions in iodine-127. How many wavelengths of elec-
tromagnetic waves with this frequency could fit across a dot on a book
page? Assume the dot is 2.00 × 10−4
m in diameter.
3. Commercial trucks cause about 18 000 lane-change and merging accidents
per year in the United States. To prevent many of them, a warning system
covering blind spots is being developed. The system uses electromagnetic
waves of frequency 2.40 × 1010
Hz.What is the wavelength of these waves?
4. A typical compact disc stores information in tiny pits on the disc’s surface.
A typical pit size is 1.2 m. What is the frequency of electromagnetic waves
that have a wavelength equal to the typical CD pit size?
5. A new antiterrorist technique detects the differences in electromagnetic
waves emitted by humans and by weapons made of metal, plastic, or
ceramic. One possible range of wavelengths used with this technique is
from 2.0 mm to 5.0 mm. Calculate the associated range of frequencies.
6. The U.S. Army’s loudest loudspeaker is almost 17 m across and is trans-
ported on a special trailer. The sound is produced by an electromagnetic
coil that can generate a minimum frequency of 10.0 Hz. What is the wave-
length of these electromagnetic waves?

P R O B L E M
Light and Reflection
Problem B
IMAGING WITH CONCAVE MIRRORS
Lord Rosse, who lived in Ireland in the nineteenth century, built a reflect-
ing telescope called the Leviathan. Lord Rosse used it for astronomical
observations and discovered the spiral form of galaxies. Suppose the
Leviathan’s mirror has a focal length of 2.50 m.Where would you place
an object in front of the mirror in order to form an image at a distance of
3.75 m? What would the magnification be? If the image height were
6.0 cm, what would the object height be?
S O L U T I O N
Given: f = +2.50 m q = +3.75 m
h = 6.0 cm
The mirror is concave, so f is positive. The object is in front of
the mirror, so q is positive.
Unknown: p = ? M = ?
Diagram:
Choose the equation(s) or situation: Use the mirror equation for focal length
and the magnification formula.

p
1
 + 
1
q
 = 
1
f
 M = − 
p
q


p
1
 = 
1
f
 − 
1
q


p
1
 = 
2.5
1
0 m
 − 
3.7
1
5 m
 = 
0
1
.4
m
00
 − 
0
1
.2
m
67
 = 
0
1
.1
m
33

p = 7.50 m
1
2
q = ?
3
3
2
C F
1
p = 7.50 m
f = 2.50 m
1. DEFINE
2. PLAN
3. CALCULATE
112
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem B 113
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In Alaska, the top of Mount McKinley has been seen from the top of
Mount Sanford, a distance of 370 km. An object is 3.70 × 102
km from a
giant concave mirror. If the focal length of the mirror is 2.50 × 102
km
what are the object distance and the magnification?
2. A human hair is about 80.0 mm thick. If one uses a concave mirror with a
focal length of 2.50 cm and obtains an image of −59.0 cm, how far has
the hair been placed from the mirror? What is the magnification of the
hair?
3. A mature blue whale may have a length of 28.0 m. How far from a con-
cave mirror with a focal length of 30.0 m must a 7.00-m-long baby blue
whale be placed to get a real image the size of a mature blue whale?
4. In 1950 in Seattle, Washington, there was a Christmas tree 67.4 m tall.
How far from a concave mirror having a radius of curvature equal to
12.0 m must a person 1.69 m tall stand to form a virtual image equal to
the height of the tree? Will the image be upright or inverted?
5. A stalagmite that is 32 m tall can be found in a cave in Slovakia. If a con-
cave mirror with a focal length of 120 m is placed 180 m from this stalag-
mite, how far from the mirror will the image form? What is the size of
the image? Is it upright or inverted? real or virtual?
6. The eye of the Atlantic giant squid has a diameter of 5.00 × 102
mm. If
the eye is viewed in a concave mirror with a radius of curvature equal to
the diameter of the eye and the eye is 1.000 × 103
mm from the mirror,
how far is the image from the mirror? What is the size of the image? Is
the image real or virtual?
7. Quick Bird is the first commercial satellite designed for forming high-
resolution images of objects on Earth. Suppose the satellite is 1.00 ×
102
km above the ground and uses a concave mirror to form a primary
image of a 1.00 m object. If the image size is 4.00 mm and the image is
inverted, what is the mirror’s radius of curvature?
8. A stalactite with a length of 10.0 m was found in Brazil. If the stalactite is
placed 18.0 m in front of a concave mirror, a real image 24.0 m tall is
formed. Calculate the mirror’s radius of curvature.
Substitute the values for p and q to find the magnification of the image and h′ to
find the object height.
M = − 
3
7
.
.
7
5
5
0
m
m
 =
h = − 
p
q
h′
 = − 
(7.50 m
3.7
)(
5
0
m
.060 m)
 =
The image appears between the focal point (2.50 m) and the center of curvature,
is smaller than the object, and is inverted (–1 M 0). These results are con-
firmed by the ray diagram. The image is therefore real.
0.12 m
−0.500
4. EVALUATE

P R O B L E M
Problem C
CONVEX MIRRORS
The largest jellyfish ever caught had tentacles up to 36 m long, which is
greater than the length of a blue whale. Suppose the jellyfish is located in
front of a convex spherical mirror 36.0 m away. If the mirror has a focal
length of 12.0 m, how far from the mirror is the image? What is the image
height of the jellyfish?
S O L U T I O N
Given: f = −12.0 m p = +36.0 m
h = 36 m
The mirror is convex, so f is negative. The object is in front of
the mirror, so p is positive.
Unknown: q = ? M = ?
Diagram:
Choose the equation(s) or situation: Use the mirror equation for focal length
and the magnification formula.

p
1
 + 
1
q
 = 
1
f
 M = − 
p
q


1
q
 = 
1
f
 − 
p
1


1
q
 = − 
12.
1
0m
 − 
36.
1
0 m
 = − 
0.
1
08
m
33
 − 
0.
1
02
m
78
 − 
0.
1
11
m
11

q =
Substitute the values for p and q to find the magnification of the image and h to
find the image height.
M = − 
−
3
9
6
.0
.0
01
m
m
 =
h′
= − 
q
p
h
 = − 
(− 9.0
(
0
3
1
6.
m
0 m
)(3
)
6 m)
 = 9.001 m
0.250
−9.001 m
p = 36.0 m
2 2
3
3
1
F C
f =–12.0 m
q = ?
1
1. DEFINE
2. PLAN
3. CALCULATE
114
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem C 115
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
The image appears between the focal point (–12.0 m) and the mirror’s surface, as
confirmed by the ray diagram. The image is smaller than the object (M 1) and
is upright (M 0), as is also confirmed by the ray diagram.
1. The radius of Earth is 6.40 × 103
km. The moon is about 3.84 × 105
km
away from Earth and has a diameter of 3475 km. The Pacific Ocean sur-
face, which can be considered a convex mirror, forms a virtual image of
the moon. What is the diameter of that image?
2. A 10 g thread of wool was produced by Julitha Barber of Australia in
1989. Its length was 553 m. Suppose Barber is standing a distance equal
to the thread’s length from a convex mirror. If the mirror’s radius of cur-
vature is 1.20 × 102
m, what will the magnification of the image be?
3. Among the many discoveries made with the Hubble Space Telescope are
four new moons of Saturn, the largest being just about 70.0 km in diam-
eter. Suppose this moon is covered by a highly reflective coating, thus
forming a spherical convex mirror. Another moon happens to pass by at
a distance of 1.00 × 102
km. What is the image distance?
4. The largest scale model of the solar system was built in Peoria, Illinois. In
this model the sun has a diameter of 11.0 m. The real diameter of the sun
is 1.4 × 106
km. What is the scale to which the sun’s size has been reduced
in the model? If the model’s sun is a reflecting sphere, where in front of
the sphere is the object located?
5. Bob Henderson of Canada built a model railway to a scale of 1:1400.
How far from a convex mirror with a focal length of 20.0 mm should a
full-size engine be placed so that the size of its virtual image is the same
as that of the model engine?
6. The largest starfish ever discovered had a diameter of 1.38 m. Suppose
an object of this size is placed 6.00 m in front of a convex mirror. If the
image formed is just 0.900 cm in diameter (the size of the smallest
starfish), what is the radius of curvature of the mirror?
7. In 1995, a functioning replica of the 1936 Toyota Model AA sedan was
made in Japan. The model is a mere 4.78 mm in length. Suppose an ob-
ject measuring 12.8 cm is placed in front of a convex mirror with a focal
length of 64.0 cm. If the size of the image is the same as the size of the
model car, how far is the image from the mirror’s surface?
8. Some New Guinea butterflies have a wingspan of about 2.80 × 102
mm.
However, some butterflies which inhabit the Canary Islands have a
wingspan of only 2.00 mm. Suppose a butterfly from New Guinea is
placed in front a convex mirror. The image produced is the size of a but-
terfly from the Canary Islands. If the image is 50.0 cm from the mirror’s
surface, what is the focal length of the mirror?

Problem A 117
NAME ______________________________________ DATE _______________ CLASS ____________________
Refraction
Problem A
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
SNELL’S LAW
The smallest brilliant-cut diamond has a mass of about 15 µg and a height
of just 0.11 mm.Suppose a ray of light enters the diamond from the air
and,upon contact with one of the gem’s facets,refracts at an angle of 22.2°.
If the angle of incidence is 65.0°,what is the diamond’s index of refraction?
S O L U T I O N
Given: qi = 65.0° qr = 22.2° ni = 1.00
Unknown: nr = ?
Use the equation for Snell’s law.
nisin qi = nrsin qr
nr = ni
s
s
i
i
n
n
q
q
r
i
= (1.00)
(
(
s
s
i
i
n
n
6
2
5
2
.
.
0
2
°
°
)
)
 = 2.40
ADDITIONAL PRACTICE
1. Extra dense flint glass has one of the highest indices of refraction of any
type of glass. Suppose a beam of light passes from air into a block of
extra dense flint glass. If the light has an angle of incidence of 72° and an
angle of refraction of 34°, what is the index of refraction of the glass?
2. The index of refraction of a clear oil is determined by passing a beam of light
through the oil and measuring the angles of incidence and refraction. If the
light in air approaches the oil’s surface at an angle of 47.9° to the normal
and moves into the oil at an angle of 29.0° to the normal, what is the oil’s
index of refraction? Assume the index of refraction for air is 1.00.
3. Someone on a glass-bottom boat shines a light through the glass into the
water below. A scuba diver beneath the boat sees the light at an angle of
17° with respect to the normal. If the glass’s index of refraction is 1.5 and
the water’s index of refraction is 1.33, what is the angle of incidence with
which the light passes from the glass into the water? What is the angle of
incidence with which the light passes from the air into the glass?
4. A beam of light is passed through a layer of ice into a fresh-water lake
below. The angle of incidence for the light in the ice is 55.0°, while the
angle of refraction for the light in the water is 53.8°. Calculate the index of
refraction of the ice, using 1.33 as the index of refraction of fresh water.
5. An arrangement of three glass blocks with indices of refraction of 1.5,
1.6, and 1.7 are sandwiched together. A beam of light enters the first
block from air at an angle of 48° with respect to the normal. What is the
angle of refraction after the light enters the third block?

NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Refraction
Problem B
LENSES
Suppose the smallest car that is officially allowed on United States roads
is placed upright in front of a converging lens. The lens, which has a focal
length of 1.50 m, forms an image 75.0 cm tall and 2.00 m away. Calculate
the object distance, the magnification, and the object height.
S O L U T I O N
Given: q = +2.00 m f = +1.50 m h′ = −0.750 m
The image is behind the lens, so q is positive. The lens is con-
verging, so the focal length is positive (f 0). The image is in-
verted, so h′ is negative.
Unknown: p = ? M = ? h = ?
Diagram:
Choose the equation(s) or situation: Use the thin-lens equation to calculate
the image distance. Then use the equation for magnification to calculate the
magnification and the object height.

1
f
 = 
p
1
 + 
1
q
 M = −
p
q
 = 
h
h
′


p
1
 = 
1
f
 − 
1
q


p
1
 = 
1.5
1
0 m
 − 
2.0
1
0 m
 = 
0
1
.6
m
67
 − 
0
1
.5
m
00
 = 
0
1
.1
m
67
 p =
M = −
p
q
 = − 
(
(
2
6
.
.
0
0
0
0
m
m
)
)
 =
h = 
M
h′
 = 
(−
(−
0.
0
7
.
5
3
0
33
m
)
)
 =
Because −1 M 1, the image must form at a distance less than 2f but greater
than f, which is the case. At this position the image is real and inverted.
2.25 m
−0.333
6.00 m
1
3
2
1
F
F
2F
2F
3
2
p = ?
f = 1.50 m
f
q = 2.00 m
h = ?
h' = –0.750 m
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
118 Holt Physics Problem Workbook

Problem B 119
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
1. The National Museum of Photography, Film Television, in England,
has a huge converging lens with a diameter of 1.37 m and a focal length
of 8.45 m. Suppose you use this lens as a magnifying glass. At what dis-
tance would a friend have to stand for the friend’s image to appear 25 m
in front of the lens? What is the image magnification?
2. The largest of seals is the elephant seal, while the smallest seal, the
Galápagos fur seal, is only 1.50 m in length. Suppose you use a diverg-
ing lens with a focal length of 8.58 m to observe an elephant seal. The
elephant seal’s image turns out to have the exact length of a Galápagos
fur seal and forms 6.00 m in front of the lens. How far away is the ele-
phant seal, and what is its length?
3. The common musk turtle, also called a “stinkpot,” has a length of
7.60 cm at maturity. Suppose a turtle with this length is placed in front
of a diverging lens that has a 14.0 cm focal length. If the turtle’s image
is 4.00 cm across, how far is the turtle from the lens? How far is the tur-
tle’s image from the lens?
4. The largest mammal on land, the elephant, can reach a height of 3.5 m.
The largest mammal in the sea, however, is much bigger. A blue whale,
which is also the largest animal ever to have lived on Earth, can be as
long as 28 m. If you use a diverging lens with a focal length of 10.0 m to
look at a 28.0-m-long blue whale, how far must you be from the whale
to see an image equal to an elephant’s height (3.50 m)?
5. The largest scorpions in the world live in India. The smallest scorpions
live on the shore of the Red Sea and are only about 1.40 cm in length.
Suppose a diverging lens with a focal length of 20.0 cm forms an image
that is 1.40 cm wide. If the image is 19.00 cm in front of the lens, what
is the object distance and size?
6. The ocean sunfish, Mola mola, produces up to 30 × 106
eggs at a time.
Each egg is about 1.3 mm in diameter. How far from a magnifying glass
with a focal length of 6.0 cm should an egg be placed to obtain an
image 5.2 mm in size? How far is it between the image and the lens?
7. In 1992, Thomas Bleich of Austin, Texas, produced a photograph nega-
tive of about 3500 attendants at a concert. The negative was more than
7 m long. Bleich used a panoramic camera with a lens that had a focal
length of 26.7 cm. Suppose this camera is used to take a picture of just
one concert attendant. If the attendant is 3.00 m away from the lens, how
far should the film be from the lens? What is the image magnification?
8. Komodo dragons, or monitors, are the largest lizards, having an average
length of 2.25 m. This is much shorter than the largest crocodiles. If a
crocodile is viewed through a diverging lens with a focal length of
5.68 m, its image is 2.25 m long. If the crocodile is 12.0 m from this
lens, what is the image distance? How long is the crocodile?

120
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
9. The body of the rare thread snake is as thin as a match, and the longest
specimen ever found was only 108 mm long. If a thread snake of this
length is placed a distance equal to four times its length from a diverg-
ing lens and the lens has a focal length of 216 mm, how long is the
snake’s image? How far from the lens is the image?
10. Tests done by the staff of Popular Photography magazine revealed that
the zoom lenses available in stores have a focal length different from
what is written on them. Suppose one of these lenses, which is identi-
fied as having a focal length of 210 mm, yields an upright image of an
object located 117 mm away. If the image magnification is 2.4, what is
the true focal length of the lens?
11. In 1994, a model car was made at a scale of 1:64. This car traveled more
than 600 km in 24 h, setting a record. If this model car is placed under
an opaque projector, a real image will be projected. Suppose the image
on the screen has the same size as the actual, full-scale car. If the screen
is 12 m from the lens, what is the focal length of the lens? Is the image
upright or inverted?
12. The tallest man in history, Robert Wadlaw, was 2.72 m tall. The smallest
woman in history, Pauline Musters, had a height of 0.55 m. Suppose
Wadlaw is 5.0 m away from a converging lens. If his image is the same
size as Musters, what is the focal length of the lens?
13. Hummingbirds eggs, which have an average size of 10.0 mm, are the
smallest eggs laid by any bird. Suppose an egg is placed 12.0 cm from a
magnifying glass. A virtual image with a magnification of 3.0 is pro-
duced. What is the focal length of the lens?
14. In 1876, the Daily Banner, a newspaper printed in Roseberg, Oregon,
had pages that were 7.60 cm wide. What would be the width of this
newspaper’s image if the newspaper were placed 16.0 cm from a diverg-
ing lens with a focal length of 12.0 cm?
15. Estimates show that the largest dinosaurs were 48 m long. Suppose you
take a trip back in time with a camera that has a focal length of 110 mm.
Coming across a specimen of the largest dinosaur, you take its picture,
but to be safe and inconspicuous you take it from a distance of 120 m.
What length will the image have on the film?
16. The smallest spiders in the world are only about 0.50 mm across. On
the other hand, the goliath tarantula, of South America, can have a leg
span of about 280 mm. Suppose you use a diverging lens with a focal
length of 0.80 m to obtain an image that is 0.50 mm wide of an object
that is 280 mm wide. How far is the object from the lens? How far is the
image from the lens?

Problem C 121
NAME ______________________________________ DATE _______________ CLASS ____________________
P R O B L E M
Rutile, TiO2, has one of the highest indices of refraction: 2.80. Suppose
the critical angle between rutile and an unknown liquid is 33.6°.What is
the liquid’s index of refraction?
S O L U T I O N
Given: qc = 33.6°
ni = 2.80
Unknown: nr = ?
Use the equation for critical angle.
sin qc = 
n
n
r
i

nr = ni sin qc = (2.80)(sin 33.6°) = 1.54
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Refraction
Problem C
CRITICAL ANGLE
ADDITIONAL PRACTICE
1. Light moves from glass into a substance of unknown refraction index. If the
critical angle for the glass is 46° and the index of refraction for the glass is
1.5, what is the index of refraction of the other substance?
2. The largest uncut diamond had a mass of more than 600 g. Eventually, the
diamond was cut into several pieces. Suppose one of those pieces is a cube
with sides 1.00 cm wide. If a beam of light were to pass from air into the
diamond with an angle of incidence equal to 75.0°, the angle of refraction
would be 23.3°. From this information, calculate the index of refraction
and the critical angle for diamond in air.
3. A British company makes optical fibers that are 13.6 km in length. If the
critical angle for the fibers in air is 42.1°, what is the index of refraction of
the fiber material?
4. In 1996, the Fiberoptic Link Around the Globe (FLAG) was started. It
initially involves placing a 27 000 km fiber optic cable at the bottom of
the Mediterranean Sea and the Indian Ocean. Suppose the index of re-
fraction of this fiber is 1.56 and the index of refraction of sea water 1.36,
what is critical angle for internal reflection in the fiber?
5. The world’s thinnest glass is 0.025 mm thick. If the index of refraction
for this glass is 1.52, what is the critical angle of ocean water? How far
will a ray of light travel in the glass if it undergoes one internal reflection
at the critical angle?

Problem A 123
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Interference and Diffraction
Problem A
INTERFERENCE AND DIFFRACTION
P R O B L E M
To help prevent cavities, scientists at the University of Rochester have de-
veloped a method for melting tooth enamel without disturbing the inner
layers, or pulp, of the tooth. To accomplish this, short pulses from a laser
are used. These laser pulses, which are in the microwave portion of the
electromagnetic spectrum, have a wavelength of 9.3 µm. Suppose this
laser is operated continuously with a double-slit arrangement. If the slits
have a separation of 45 µm, at what angle will the third-order maximum
be observed?
S O L U T I O N
Given: l = 9.3 m = 9.3 × 10−6
m
d = 45 m = 45 × 10−6
m
m = 3
Unknown: q = ?
Choose the equation(s) or situation: Because a maximum (bright) fringe is ob-
served, the equation for constructive interference should be used.
dsin q = ml
q = sin−1

m
d
l


q = sin−1

3(
4
9
5
.3
×
×
1
1
0
0
−
−
6
6
m
m)


q =
The angle at which the third-order maximum appears is 38° from the central
maximum. Although the wavelength of the electromagnetic radiation is large
compared with that of visible light, the separation of the slits is much larger than
it would be in a visible-light double-slit setup. If the same slit separation that is
used with visible light (typically on the order of a few micrometers) were used
with microwave radiation, the interference pattern would not appear because
even for m = 1, sin q would be greater than one. This indicates that the condi-
tions for first-order constructive interference would not exist.
38°
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. Comet Hale-Bopp, which came close to Earth in 1997, has a complex
chemical composition. To understand it, scientists analyzed radiation
emitted from the comet’s nucleus. Carbon atoms in the comet emitted

radiation with a wavelength of 156.1 nm. Using a double-slit apparatus
with a slit separation of 1.20 × 103
nm to measure these wavelengths, at
what angle would a fifth-order maximum be observed?
2. A typical optic fiber has a thickness of only 6.00 × 103
nm. Consider a
beam from a standard He-Ne laser that has a wavelength equal to
633 nm. Suppose this beam is incident upon two parallel slits that are
separated by a distance equal to the width of a typical optic fiber. What is
the angle at which the first dark fringe would be observed?
3. The smallest printed and bound book, which contains the children’s
story “Old King Cole,” was published in 1985. The book’s width is about
0.80 mm. Imagine a double-slit apparatus with a separation equal to the
width of this book. What wavelength would produce a third-order mini-
mum at an angle of 1.6°?
4. The water in Earth’s atmosphere blocks most of the infrared waves com-
ing from space. In order to observe light of this wavelength, the Kuiper
Airborne Observatory has been developed. The observatory consists of
an optical telescope mounted inside a modified C-141 aircraft. The plane
flies at altitudes where the relative humidity is very low and where the in-
coming infrared radiation has not yet been significantly absorbed. Sup-
pose a double-slit arrangement with a 15.0 mm slit separation is used to
analyze infrared waves received by the telescope and that a second-order
maximum is observed at 19.5°. Determine the wave’s wavelength.
5. In 1995, Pan Xixing, of China, set a record for miniature writing by plac-
ing the text of a Chinese proverb on a human hair. If blue light with a
wavelength of 443 nm passes through two slits separated by a distance
equal to the width of an average character in that proverb, the fourth-
order minimum would be observed at an angle of 2.27°. Determine the
average width of each character.
6. A way to detect termites inside wooden structures has been developed at
the University of Minnesota. A detector perceives the high-frequency
sound waves produced by the termites’ chewing. These waves are then
converted into electromagnetic signals. Suppose these signals are at
“long” radio wavelengths and that a giant double-slit apparatus has been
built to observe interference of these radio waves. If the waves have a fre-
quency of 60.0 kHz, what would be the required slit separation for
observing the fourth-order maximum at 52.0°?
7. The Federal Communications Commission (FCC) assigns radio fre-
quencies to broadcasters to prevent stations close to each other from
transmitting at the same frequency. One reserved portion of the radio
spectrum is just beyond commercial FM frequencies and is used by
weather satellites. These broadcast at frequencies close to 137 MHz.
Suppose radiation with this frequency is incident on a double-slit
apparatus and that a second-order maximum is observed at 60.0°.
What is the slit separation? What is the highest order maximum that can
be observed for this radiation and with this apparatus?
124
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem B 125
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Interference and Diffraction
Problem B
DIFFRACTION GRATINGS
P R O B L E M
Two graduate students from the University of Nevada have developedVene-
tian blinds that open and close automatically by use of a solar sensor.Open
blinds let in infrared radiation,which increases the temperature of the
room.Consider the blinds as a type of diffraction grating with a line separa-
tion equal to 5.0 cm.Suppose the infrared waves pass through this grating
so that the third-order maximum is observed at an angle of 0.69°.What is
the wavelength of the infrared radiation?
S O L U T I O N
Given: q = 0.69°
d = 5.0 cm = 5.0 × 10−2
m
m = 3
Unknown: l = ?
Choose the equation(s) or situation: Use the equation for a diffraction grating.
dsin q = ml
l =
ds
m
in q

l =
l =
The electromagnetic radiation that is diffracted slightly by the Venetian blinds is
in the infrared portion of the spectrum. To increase the angle at which the dif-
fraction fringes appear, it would be necessary to narrow the spacing between the
slats in the blinds.
2.0 × 10−4
m = 0.20 mm
(5.0 × 10−2
m)(sin 0.69°)

3
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. In 1996, a phone call was placed from the U.S. National Military Com-
mand Center to the U.S. Atlantic Command, 304 km away. The phone
signal, however, traveled 120 750 km because it was transmitted via a
Milstar communication satellite. The satellite uses superhigh-frequency
electromagnetic radiation to ensure reliable communication that is se-
cured against eavesdropping. Assume these waves are passed through a
diffraction grating with 1.00 × 102
lines/m. The first-order maximum
appears at an angle of 30.0°. Determine the wavelength and frequency of
the electromagnetic waves.

2. Micropipette tubes with an outer diameter of 0.02 mm are used in research
with living cells. Imagine a diffraction grating with a line separation of
0.020 mm. If this grating is used to analyze electromagnetic radiation, what
wavelength would produce a third-order maximum at an angle of 12°?
3. Most stars are believed to be very nearly spherical, but R Cassiopeiae is
much closer to having an oblong, or oval, shape. This remarkable fact was
discovered by photographing its image in the orange region of the visible
spectrum (at a wavelength of 714 nm). Suppose this radiation is passed
through a diffraction grating so that it produces a third-order maximum
at an angle of 12.0°. What is the line separation in the grating?
4. In 1995, a satellite called the X Ray Timing Explorer (XTE) was launched
by NASA. The satellite can analyze X rays coming from hot matter sur-
rounding massive and often compact objects, such as neutron stars and
black holes. Because X rays have such short wavelengths, the only diffrac-
tion gratings with sufficiently small slit separations are crystal lattices. In
crystals, the separation between atoms is small enough to diffract X rays.
Suppose X rays with a wavelength of 40.0 nm are incident on a crystal
lattice that has a “line” separation of 150.0 nm. At what angle will the
second-order maximum occur?
5. Electromagnetic radiation comes to Earth from hydroxyl radicals in giant
molecular clouds in space. The frequency of this radiation is 1612 MHz,
which is close to the microwave frequencies used for aircraft communi-
cations. Filtering out this background noise is an important task. Sup-
pose a technique similar to visible spectroscopy is performed with ambi-
ent microwave radiation using a microwave radio telescope. These waves
could be directed toward a large diffraction grating so that their wave-
lengths and intensities could be analyzed. If the grating’s line separation
is 45.0 cm, at what angle would the first-order maximum occur for mi-
crowaves with a frequency of 1612 MHz?
6. A new astronomical facility is set for completion on Mount Wilson, in
Georgia, by 1999. Named the Center for High Angular Resolution Astron-
omy (CHARA) Array, it comprises five telescopes whose individual im-
ages will be analyzed by computer. The resulting data will then be used to
form a single high-resolution image of distant galaxies. The technique is
similar to what is currently being done with radio telescopes. The CHARA
Array will be used to observe radiation in the infrared portion of the
spectrum with wavelengths as short as 2200 nm. Suppose 2200 nm light
passes through a diffraction grating with 64 × 103
lines/m and produces a
fringe at an angle of 34.0°. What order maximum will the fringe be?
7. A new technology to improve the image quality of large-screen televi-
sions has been developed recently. The entire screen would consist of tiny
cells, each equipped with a movable mirror. The mirrors would change
positions relative to the incoming signal, providing a brighter image. The
entire screen would look like a diffraction grating with 250 000 lines/m.
Imagine shining red light with a wavelength of 750 nm onto this grating.
What order maximum would be observed at an angle of 48.6°?
126
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem A 127
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Electric Forces and Fields
Problem A
COULOMB’S LAW
P R O B L E M
Suppose you separate the electrons and protons in a gram of hydrogen
and place the protons at Earth’s North Pole and the electrons at Earth’s
South Pole. How much charge is at each pole if the magnitude of the elec-
tric force compressing Earth is 5.17 × 105
N? Earth’s diameter is 1.27 × 107
m.
S O L U T I O N
Given: Felectric = 5.17 × 105
N
r = 1.27 × 107
m
kC = 8.99 × 109
N•m2
/C2
Unknown: q = ?
Choose the equation(s) or situation: Rearrange the magnitude of the electric
force using Coulomb’s law.
q = 
F
el
e
k
c
C
tr
ic
r2


Substitute the values into the equation(s) and solve: .
q =
q =
The electrons and the protons have opposite signs, so the electric force between
them is attractive. The large size of the force (equivalent to the weight of a
52 700 kg mass at Earth’s surface) indicates how strong the attraction between
opposite charges in atoms is.
9.63 × 104
C
(5.17 × 105
N)(1.27 × 107
m)2

8.99 × 109
N•m2
/C2
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The safe limit for beryllium in air is 2.0 × 10−6
g/m3
, making beryllium
one of the most toxic elements. The charge on all electrons in the Be
contained in 1 m3
of air at the safe level is about 0.085 C. Suppose this
charge is placed 2.00 km from a second charge. Calculate the value of
the second charge if the magnitude of the electric force between the two
charges is 8.64 × 10−8
N.
2. Kalyan Ramji Sain, of India, had a mustache that measured 3.39 m from
end to end in 1993. Suppose two charges, q and 3q, are placed 3.39 m
apart. If the magnitude of the electric force between the charges is
2.4 × 10−6
N, what is the value of q?

3. The remotest object visible to the unaided eye is the great galaxy Messier
31 in the constellation Andromeda. It is located 2.4 × 1022
m from Earth.
(By comparison, the sun is only about 1.5 × 1011
m away.) Suppose two
clouds containing equal numbers of electrons are separated by a distance
of 2.4 × 1022
m. If the magnitude of the electric force between the clouds
is 1.0 N, what is the charge of each cloud?
4. In 1990, a French team flew a kite that was 1034 m long. Imagine two
charges, +2.0 nC and −2.8 nC, at opposite ends of the kite. Calculate
the magnitude of the electric force between them. If the separation of
charges is doubled, what absolute value of equal and opposite charges
would exert the same electric force?
5. Betelgeuse, one of the brightest stars in the constellation of Orion, has
a diameter of 7.0 × 1011
m (500 times the diameter of the sun). Con-
sider two compact clouds with opposite charge equal to 1.0 × 105
C. If
these clouds are located 7.0 × 1011
m apart, what is the magnitude of
the electric force of attraction between them?
6. An Italian monk named Giovanni Battista Orsenigo was also a dentist.
From 1868 to 1903 he extracted exactly 2 000 744 teeth, which on average
amounts to about 156 teeth per day. Consider a group of protons equal
to the total number of teeth. If this group is divided in half, calculate the
charge of each half. Also calculate the magnitude of the electric force that
would result if the two groups of charges are placed 1.00 km apart.
7. The business district of London has about 4000 residents. However,
every business day about 320 000 people are there. Consider a group of
4.00 × 103
protons and a group of 3.20 × 105
electrons that are 1.00 km
apart. Calculate the magnitude of the electric force between them.
Calculate the magnitude of the electric force if each group contains
3.20 × 105
particles and if the separation distance remains the same.
8. In 1994, element 111 was discovered by an international team of physi-
cists. Its provisional name was unununium (Latin for “one-one-one”).
Find the distance between two equal and opposite charges, each having
a magnitude equal to the charge of 111 protons, if the magnitude of the
electric force between them is 2.0 × 10−28
N.
9. By 2005, the world’s tallest building will be the International Finance
Center in Taipei, Republic of China. Suppose a 1.00 C charge is placed
at both the base and the top of the International Finance Center. If the
magnitude of the electric force stretching the building is 4.48 × 104
N,
how tall is the International Finance Center?
10. A 44 000-piece jigsaw puzzle was assembled in France in 1992. Sup-
pose the puzzle were square in shape, and that a 5.00 nC charge is
placed at the upper right corner of the puzzle and a charge of
−2.50 nC is placed at the lower left corner. If the magnitude of the
electric force the two charges exert on each other were 1.18 × 10–11
N,
what would be the distance between the two charges? What would be
the length of the puzzle’s sides?
128
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem B 129
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem B
THE SUPERPOSITION PRINCIPLE
P R O B L E M
The cinema screen installed at the Science Park, in Taejon, Korea, is 24.7 m
high and 33.3 m wide. Consider the arrangement of charges shown below.
If q1 = 2.00 nC, q2 = −3.00 nC, and q3 = 4.00 nC, find the magnitude and
direction of the resultant electric force on q1.
REASONING
According to the superposition principle, the resultant force on the charge q1 is
the vector sum of the forces exerted by q2 and q3 on q1. First find the force ex-
erted on q1 by each charge, then use the Pythagorean theorem to find the magni-
tude of the resultant force on q1. Take the ratio of the resultant y component to
the resultant x component, and then take the arc tangent of that quantity to find
the direction of the resultant force on q1.
Given: q1 = 2.00 nC = 2.00 × 10−9
C
q2 = −3.00 nC = −3.00 × 10−9
C
q3 = 4.00 nC = 4.00 × 10−9
C
r1,2 = 24.7 m
r1,3 = 33.3 m
kC = 8.99 × 109
N•m2
/C2
Unknown: F1,tot = ?
Diagram:
S O L U T I O N
q1 = 2.0 nC
q2 = −3.0 nC
q3 = 4.0 nC
r1,2 = 24.7 m
r1,3 = 33.3 m
F1,2
F1,3
F1,2 F1,2
F1,3
F1,3
F1,tot
q1 q1
1. Calculate the magnitude of the forces with Coulomb’s law:
F2,1 = kC 
(
q
r2
2
,
q
1)
1
2
 = 8.99 × 109

N
C
•m
2
2

F2,1 = 8.84 × 10−11
N
F3,1 = kC 
(
q
r3
3
,
q
1)
1
2
 = 8.99 × 109

N
C
•m
2
2

F3,1 = 6.49 × 10−11
N
(4.00 × 10−9
C)(2.00 × 10−9
C)

(33.3 m)2
(3.00 × 10−9
C)(2.00 × 10−9
C)

(24.7 m)2

2. Determine the direction of the forces by analyzing the signs of the charges:
The force F2,1 is attractive because q1 and q2 have opposite signs. F2,1 is
directed along the positive y-axis, so its sign is positive.
The force F3,1 is repulsive because q1 and q3 have the same sign. F3,1 is
directed toward the negative x-axis, so its sign is negative.
3. Find the x and y components of each force:
For F2,1: Fx = F3,1 = −6.49 × 10−11
N; Fy = 0
For F3,1: Fy = F2,1 = 8.84 × 10−11
N; Fx = 0
4. Calculate the magnitude of the total force acting in both directions:
Fx,tot = Fx = −6.49 × 10−11
N
Fy,tot = Fy = 8.84 × 10−11
N
5. Use the Pythagorean theorem to find the magnitude of the resultant force:
F1,tot =

(F
x,
to
t)
2
+
(
F
y,t
ot
)2
=

(−
6.
49
×
1
0−
11
N
)2
+
(
8.
84
×
1
0−
11
N
)2

F1,tot =
6. Use a suitable trigonometric function to find the direction of the resultant
force:
In this case, you can use the inverse tangent function.
tanq = 
F
F
x
y,
,
t
t
o
o
t
t
 = = −1.36
q = tan−1
(−1.36) =
7. Evaluate your answer:
The resultant force makes an angle of 53.7° to the left and above the x-axis.
−53.7°
(8.84 × 10−11
N)

(−6.49 × 10−11 N)
1.10 × 10−10
N
ADDITIONAL PRACTICE
1. In 1919 in Germany, a train of eight kites was flown 9740 m above the
ground. This distance is 892 m higher than Mount Everest. Consider the
arrangement of charges located at the various heights shown below. If
q1 = 2.80 mC, q2 = −6.40 mC, and q3 = 48.0 mC, find the magnitude and
direction of the resultant electric force acting on q1.
q2 = −6.40 mC
q3 = 48.0 mC
r1,2 = 892 m
r1,3 = 9740 m
q1 = 2.80 mC
2. In 1994, a group of British and Canadian athletes performed a rope slide
off the top of Mount Gibraltar, in Canada. The speed of the sliders at
130
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem B 131
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. times exceeded 160 km/h. The total length of the slide was 1747 m. Sup-
pose several sliders are located on the rope as shown. Due to friction, they
acquire the electric charges shown. Find the magnitude and direction of the
resultant electric force acting on the athlete at the far right of the diagram.
3. In 1913, a special postage stamp was issued in China. It was 248 mm long
and 70.0 mm wide. Suppose equal charges of 1.0 nC are placed in the
corners of this stamp. Find the magnitude and direction of the resultant
electric force acting on the upper right corner (assume the widest part of
the stamp is aligned with the x-axis).
4. In 1993, a chocolate chip cookie was baked in Arcadia, California. It con-
tained about three million chips and was 10.7 m long and 8.7 m wide.
Suppose four charges are placed in the corners of that cookie as follows:
q1 = −12.0 nC at the lower left corner, q2 = 5.6 nC at the upper left corner,
q3 = 2.8 nC at the upper right corner, and q4 = 8.4 nC at the lower right
corner. Find the magnitude and direction of the resultant electric force
acting on q1.
5. In 1988, a giant firework was exploded at the Lake Toya festival, in Japan.
The shell had a mass of about 700 kg and produced a fireball 1.2 km in
diameter. Consider a circle with this diameter. Suppose four charges are
placed on the circle’s perimeter so that the lines between them form a
square with sides parallel to the x- or y-axes. The charges have the follow-
ing strengths and locations: q1 = 16.0 mC at the upper left “corner,”
q2 = 2.4 mC at the upper right corner, q3 = −3.2 mC at the lower right
corner, and q4 = −4.0 mC at the lower left corner. Find the magnitude
and direction of the resultant electric force acting on q1. (Hint: Find the
distances between the charges first.)
6. American athlete Jesse Castenada walked 228.930 km in 24 h in 1976,
setting a new record. Consider an equilateral triangle with a perimeter
equal to the distance Castenada walked. Suppose the charges are placed
at the following vertices of the triangle: q1 = 8.8 nC at the bottom left
vertex, q2 = −2.4 nC at the bottom right vertex, and q3 = 4.0 nC at the
top vertex. Find the magnitude and direction of the resultant electric force
acting on q1.
q1 = 2.0 nC
q3 = 4.0 nC
q4 = 5.5 nC
r1,2 = 5.00 × 102 m
r1,4
=1747m
q2 = 3.0 nC
r1,3 = 1.00 × 103 m

Electric Forces and Fields
Problem C
EQUILIBRIUM
P R O B L E M
In 1955, a water bore that was 2231 m deep was drilled in Montana.
Consider two charges, q2 = 1.60 mC and q1, separated by a distance equal
to the depth of the well. If a third charge, q3 = 1.998 µC, is placed 888 m
from q2 and is between q2 and q1, this third charge will be in equilibrium.
What is the value of q1?
S O L U T I O N
1. DEFINE
2. PLAN
Given: q2 = 1.60 mC = 1.60 × 10−3
C
q3 = 1.998 mC = 1.998 × 10−6
C
r3,2 = 888 m
r3,1 = 2231 m − 888 m = 1342 m
r2,1 = 2231 m
kC = 8.99 × 109
N•m2
/C2
Unknown: q1 = ?
Diagram:
3. CALCULATE
4. EVALUATE
q2 = 1.60 mC
q3 = 1.998 mC
r3,1 = 1342 m
r2,1 = 2231 m
r3,2 = 888 m
q1
Choose the equation(s) or situation: The force exerted on q3 by q2 will be op-
posite the force exerted on q3 by q1. The resultant force on q3 must be zero in
order for the charge to be in equilibrium. This indicates that F3,1 and F3,2 must
be equal to each other.
F3,1 = kC
(
q
r3
3
,
q
1)
1
2

and F3,2 = kC
(
q
r3
3
,
q
2)
2
2


F3,1 = F3,2
kC
(
q
r3
3
,
q
1)
1
2

= kC
(
q
r3
3
,
q
2)
2
2


Rearrange the equation(s) to isolate the unknown(s): q3 and kC cancel.
q1 = q2
r
r
3
3
,
,
1
2


2
q1 = (1.60 × 10−3
C)

1
8
3
8
4
8
2
m
m


2
= 3.65 × 10−3
C
q1 =
Because q1 is a little more than twice as large as q2, the third charge (q3) must be
farther from q1 for the forces on q3 to balance.
3.65 mC
132
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem C 133
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
1. Hans Langseth’s beard measured 5.33 m in 1927. Consider two charges,
q1 = 2.50 nC and an unspecified charge, q2, are separated 5.33m. A
third charge of 1.0 nC is placed 1.90 m away from q1. If the net electric
force on this third charge is zero, what is q2?
2. The extinct volcano Olympus Mons, on Mars, is the largest mountain
in the solar system. It is 6.00 102
km across and 24 km high. Suppose
a charge of 75 mC is placed 6.0 102
km from a unspecified charge. If
a third charge of 0.10 mC is placed 24 km from the first charge and the
net electric force on this third charge is zero, how large is the unspeci-
fied charge?
3. Earth’s mass is about 6.0 × 1024
kg, while the moon’s mass is
7.3 × 1022
kg. What equal charges must be placed on Earth and the
moon to make the net force between them zero?
4. In 1974, an emerald with a mass of 17.23 kg was found in Brazil. Sup-
pose you want to hang this emerald on a string that is 80.0 cm long and
has a breaking strength of 167.6 N. To hang the jewel safely, you remove
a certain charge from the emerald and place it at the pivot point of the
string. What is the minimum possible value of this charge?
5. Little Pumpkin, a miniature horse owned by J. C. Williams, Jr., of South
Carolina, had a mass of about 9.00 kg. Consider Little Pumpkin on a
twin-pan balance. If the mass on the other pan is 8.00 kg and r equals
1.00 m, what equal and opposite charges must be placed as shown in the
diagram below to maintain equilibrium?
6. The largest bell that is in use today is in Mandalay, Myanmar, formerly
called Burma. Its mass is about 92 × 103
kg. Suppose the bell is sup-
ported in equilibrium as shown in the figure below. Calculate the value
for the charge q.
m
+q
−q
r
m = 92 × 103 kg
l1 = 1.0 m
+q
−q
r = 2.5 m
l2 = 8.0 m

7. In more than 30 years, Albert Klein, of California, drove 2.5 106
km
in one automobile. Consider two charges, q1 2.0 C and q2 6.0 C,
separated by Klein’s total driving distance. A third charge, q3 4.0 C, is
placed on the line connecting q1 and q2. How far from q1 should q3 be
placed for q3 to be in equilibrium?
8. A 55 mC charge and a 137 mC charge are separated by 87 m. Where
must a 14 mC charge be placed between these other two charges in
order for the net electric force on it to be zero?
9. In 1992, a Singapore company made a rope that is 56 cm in diameter
and has an estimated breaking strength of 1.00 × 108
N. Suppose this
rope is used to connect two strongly charged asteroids in space. If the
charges of the asteroids are q1 = 1.80 × 104
C and q2 = 6.25 × 104
C,
what is the minimum length that the rope can have and still remain in-
tact? Neglect the effects of gravity.
10. The CN Tower, in Toronto, Canada, is 553 m tall. Suppose two balls,
each with a mass of 5.00 kg and a charge of 40.0 mC, are placed at the
top and bottom of the tower, respectively. The ball at the top is then
dropped. At what height is the acceleration on the ball zero?
11. Mycoplasma is the smallest living organism known. Its mass has an esti-
mated value of 1.0 × 10−16
g. Suppose two specimens of this organism
are placed 1.0 m apart and one electron is placed on each. If the
medium through which the Mycoplasma move exerts a resistive force
on the organisms, how large must that force be to balance the force of
electrostatic repulsion?
12. The parasitic wasp Carapractus cinctus has a mass of 5.0 × 10−6
kg,
which makes it one of the smallest insects in the world. If two such
wasps are given equal and opposite charges with an absolute value of
2.0 × 10−15
C and are placed 1.00 m from each other on a horizontal
smooth surface, what extra horizontal force must be applied to each
wasp to keep it from sliding? Take into account both gravitational and
electric forces between the wasps.
13. In 1995, a single diamond was sold for more than $16 million. It was not
the largest diamond in the world, but its mass was an impressive 20.0 g.
Consider such a diamond resting on a horizontal surface. It is known
that if the diamond is given a charge of 2.0 mC and a charge of at least
–8.0 mC is placed on that surface at a distance of 1.7 m from it, then the
diamond will barely keep from sliding. Calculate the coefficient of static
friction between the diamond and the surface.
134
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 135
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem D
ELECTRIC FIELD STRENGTH
P R O B L E M
The Seto-Ohashi bridge, linking the two Japanese islands of Honshu and
Shikoku, is the longest“rail and road”bridge, with an overall length of
12.3 km. Suppose two equal charges are placed at the opposite ends of the
bridge. If the resultant electric field strength due to these charges at the
point exactly 12.3 km above one of the bridge’s ends is 3.99 10–2
N/C
and is directed at 75.3° above the positive x-axis, what is the magnitude of
each charge?
REASONING
According to the superposition principle, the resultant electric field strength at the
point above the bridge is the vector sum of the electric field strengths produced by
q1 and q2. First, find the components of the electric field strengths produced by
each charge, then combine components in the x and y directions to find the elec-
tric field strength components of the resultant vector. Equate this to the compo-
nents in the x and y directions of the electric field vector. Finally, rearrange the
equation to solve for the charge.
Given: Etot = 3.99 × 10−4
N/C
q = 75.3°
r1 = 12.3 km = 1.23 × 104
m
kC = 8.99 × 109
N•m2
/C2
S O L U T I O N
q2 12.3 km q1
Φ
E1 E2
Etotal = 3.99 × 10–2 N/C
q = 75.3°
r1 =
12.3 km
r2

Unknown: q1 = ? q2 = ?
The distance r2 must be calculated from the information in the diagram. Because r2
forms the hypotenuse of a right triangle whose sides equal r1, it follows that
r2 =

(r
1)
2
+
(
r1
)2
=

2(
r1
)2
= 1.74 × 104
m
The angle that r2 makes with the coordinate system equals the inverse tangent of
the ratio of the vertical to the horizontal components. Because these components
are equal,
tan f = 1.00, or f = 45.0°
1. Find the x and y components of each electric field strength vector:
At this point, the direction of each component must be taken into account.
For E1: Ex,1 = 0
Ey,1 = E1 = 
(
k
r
C
1
q
)2
1

For E2: Ex,2 = E2 cos (45.0°) =
Ey,2 = E2 sin (45.0°) =
2. Calculate the magnitude of the total electric field strength in both the
x and y directions:
Ex,tot = Ex,1 + Ex,2 = = Etot cos (75.3°)
Ey,tot = Ey,1 + Ey,2 = 
(
k
r
C
1
q
)
1
2
 + = Etot sin (75.3°)
5. Rearrange the equation(s) to isolate the unknown(s):
q2 =
q2 = q1 = 4.82 10–4
C
(3.99 × 10−2
N/C)cos(75.3°)

2
(1.74 104
m)2

8.99 109
N•m2
/C2
Etot cos (75.3°)

2
(r2)2

kC
kCq2


2
(r2)2
kCq2


2
(r2)2
kCq2


2
(r2)2
kCq2


2
(r2)2
136
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 137
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
1. The world’s largest tires have a mass of almost 6000 kg and a diameter of
3.72 m each. Consider an equilateral triangle with sides that are 3.72 m
long each. If equal positive charges are placed at the points on either end
of the triangle’s base, what is the direction of the resultant electric field
strength vector at the top vertex? If the magnitude of the electric field
strength at the top vertex equals 0.145 N/C, what are the two quantities
of charge at the base of the triangle?
2. The largest fountain is found at Fountain Hills, Arizona. Under ideal
conditions, the 8000 kg column of water can reach as high as 190 m.
Suppose a 12 nC charge is placed on the ground and another charge of
unknown quantity is located 190 m above the first charge. At a point on
the ground 120 m from the first charge, the horizontal component of the
resultant electric field strength is found to be Ex = 1.60 × 10−2
N/C.
Using this information, calculate the unknown quantity of charge.
3. Pontiac Silverdome Stadium, in Detroit, Michigan, is the largest air-
supported building in the world. Suppose a charge of 18.0 mC is placed
at one end of the stadium and a charge of −12.0 mC is placed at the other
end of the stadium. If the electric field halfway between the charges is
22.3 N/C, directed toward the –12.0 mC charge, what is the length of the
stadium?
4. In 1897, a Ferris wheel with a diameter of 86.5 m was built in London.
The wheel held 10 first-class and 30 second-class cabins, and each cabin
was capable of carrying 30 people. Consider two cabins positioned
exactly opposite each other. Suppose one cabin has an unbalanced charge
of 4.8 nC and the other cabin has a charge of 16 nC. At what distance
from the 4.8 nC charge along the diameter of the wheel would the
strength of the resultant electric field be zero?
5. Suppose three charges of 3.6 mC each are placed at three corners of the
Imperial Palace in Beijing, China, which has a length of 960 m and a width
of 750 m. What is the strength of the electric field at the fourth corner?
6. The world’s largest windows, which are in the Palace of Industry and
Technology in Paris, France, have a maximum width of 218 m and a
maximum height of 50.0 m. Consider a rectangle with these dimensions.
If charges are placed at its corners, as shown in the figure below, what
is the electric field strength at the center of the rectangle? The value of
q is 6.4 nC.
q
3q
q
2q
E
50.0 m
218 m
θ

Problem A 139
NAME ______________________________________ DATE _______________ CLASS ____________________
Electrical Energy and Current
Problem A
POTENTIAL ENERGY AND POTENTIAL DIFFERENCE
P R O B L E M
As a charge moves 39.0 cm in the direction of a uniform electric field, its
potential energy changes by 1.86 × 10−3
J. The magnitude of the electric
field is 177 N/C.Find the potential difference between the starting position
and final position of the charge.What is the charge on the moving particle?
S O L U T I O N
Given: ∆PEelectric = −1.86 × 10−3
J d = 0.390 m
E = 177 N/C
Unknown: ∆V = ? q = ?
The potential difference is the magnitude of E times the displacement.
∆V = −Ed = −(177 N/C)(0.390 m)
Use the equation for the change in electrical potential energy.
∆PEelectric = −qEd
Rearrange to solve for q, and insert values.
q = −
∆PE
E
e
d
lectric
= −
q = 2.69 × 10−5
C
(−1.86 × 10−3
J)

(177 N/C)(0.390 m)
∆V = −69.0 V
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. What is the potential difference between a point 0.48 mm from a
charge of 2.9 nC and a point at infinity?
2. The potential energy of an electron (q = −1.6 × 10−19
C) increases
by 3.3 × 10−15
J when it moves 3.5 cm parallel to a uniform electric
field. What is the magnitude of the electric field through which the
electron passes?
3. A charged particle gains 3.1 × 10−12
J of potential energy when it moves
4.7 cm through a uniform electric field. The potential difference across
this distance is −73 V.
a. What is the magnitude of the electric field?
b. What is the magnitude of the charge on the particle?

140
NAME ______________________________________ DATE _______________ CLASS ____________________
4. A charged particle moves through a distance of 9.35 m parallel to a
uniform electric field. The electrical potential energy of the particle
increases by 3.17 × 10−10
J as it moves. The electric field has a magni-
tude of 1.25 × 105
N/C.
a. What is the charge on the particle?
b. What is the potential difference between the starting and
final positions?
5. There is an electric field close to the surface of Earth. This field points
toward the surface and has a magnitude of about 1.5 × 102
N/C. A
charge moves perpendicularly toward the surface of Earth through a
distance of 439 m, the height of the Sears Tower in Chicago, Illinois.
During this trip, the electric potential energy of the charge decreases
by 3.7 × 10−8
J.
a. What is the charge on the moving particle?
b. What is the potential difference between the top of the
Sears Tower and the ground?
c. What is the electric potential of the charge at its final position?
6. Two parallel plates are separated by a distance of 0.077 cm. Between the
plates is a uniform electric field having a magnitude of 6.5 × 102
N/C.
What is the magnitude of the potential difference between the plates?
7. A proton (q = 1.6 × 10−19
C) moves 3.75 m in the direction of a uni-
form electric field having a field strength of 383 N/C.
a. What is the magnitude of the potential difference between
the initial and final positions of the proton?
b. What is the change in the electrical potential energy of
the proton?
8. A negative ion (q = −4.8 × 10−19
C) moves 0.63 cm through a uniform
electric field in a direction opposite to the direction of the field. The
magnitude of the electric field is 279 volts per meter.
a. What is the change in the electrical potential energy of the ion?
b. What is the electric potential at the final position of the ion?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem B 141
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem B
CAPACITANCE
P R O B L E M
Consider a parallel-plate capacitor the size of Nauru, an island with an
area of just 21 km2
. If 110 V is applied across the capacitor to store 55 J of
electrical potential energy, what is the capacitance of this capacitor? If
the area of its plates is the same as the area of Nauru, what is the plate
separation?
S O L U T I O N
Given: A = 21 km2
= 21 × 106
m2
PEelectric = 55 J
∆V = 110 V
e0 = 8.85 × 10−12
C2
/N•m2
Unknown: C = ? d = ?
To determine capacitance and the plate separation, use the definition for capaci-
tance energy and the equation for a parallel-plate capacitor.
PEelectric = 
1
2
C(∆V)2
C =
2
(
P
∆
E
V
ele
)
c
2
tric
=
(
2
1
(
1
5
0
5
V
J
)
)
2
=
C = e0 
A
d

d = e0 
C
A

d =
8.85 × 10−12

N
C
•m
2
2


d = 2.0 × 10−2
m = 2.0 cm
(21 × 106
m2
)

(9.1 × 10−3
F)
9.1 × 10−3
F
ADDITIONAL PRACTICE
1. To improve the short-range acceleration of an electric car, a capacitor
may be used. Charge is stored on the capacitor’s surface between a
porous composite electrode and electrolytic fluid. Such a capacitor can
provide a potential difference of nearly 3.00 × 102
V. If the energy
stored in this capacitor is 17.1 kJ, what is the capacitance?
2. A huge capacitor bank powers the large Nova laser at Lawrence Liver-
more National Lab, in California. Each capacitor can store 1450 J of
electrical potential energy when a potential difference of 1.0 × 104
V is
applied across its plates. What is the capacitance of this capacitor?

142
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. Air becomes a conductor if the electric field across it exceeds
3.0 × 106
V/m. What is the maximum charge that can be accumulated
on an air-filled capacitor with a 0.2 mm plate separation and a plate
area equal to the area of the world’s largest painting (6.7 × 103
m2
)?
4. The world’s largest hamburger, which was made in Wyoming, had a
radius of about 3.1 m. Suppose you build an air-filled parallel-plate
capacitor with an area equal to that of the hamburger and a plate sepa-
ration of 1.0 mm. The largest electric field that air can sustain before its
insulating properties break down and it begins conducting electricity is
3.0 MV/m. What is the maximum charge that you will be able to store
in the capacitor?
5. In 1987, an ultraviolet flash of light was produced at the Los Alamos
National Lab. For 1.0 ps, the power of the flash was 5.0 × 1015
W. If all
of this energy was provided by a battery of charged capacitors with a
total capacitance of 0.22 F, what was the potential difference across
these capacitors?
6. The International Exposition Center in Cleveland, Ohio, covers
2.32 × 105
m2
. If a capacitor with this same area and a plate separa-
tion of 1.5 cm is charged to 0.64 mC, what is the energy stored in
the capacitor?
7. In 1990, a pizza with a radius of 18.0 m was made in South Africa. Sup-
pose you make an air-filled capacitor with parallel plates whose area is
equal to that of the pizza. If a potential difference of 575 V is applied
across this capacitor, it will store just 3.31 J of electrical potential en-
ergy. What are the capacitance and plate separation of this capacitor?
8. When the keys on a computer keyboard are pressed, the plate separation
of small parallel-plate capacitors mounted under the keys changes from
about 5.00 mm to 0.30 mm. This causes a change in capacitance, which
triggers the electronic circuitry. If the area of the plates is 1.20 cm2
, find
the change in the capacitance. Is it positive or negative?
9. Tristan da Cunha, a remote island inhabited by a few hundred people,
has an area of 98 km2
. Suppose a 0.20 F parallel-plate capacitor with a
plate area equal to 98 km2
is built. What is the plate separation?
10. The largest apple pie ever made was rectangular in shape and had an
area of 7.0 m × 12.0 m. Consider a parallel-plate capacitor with this
area. Assume that the capacitor is filled with air and the distance be-
tween the plates is 1.0 mm.
a. What is the capacitance of the capacitor?
b. What potential difference would have to be placed across the ca-
pacitor for it to store 1.0 J of electrical potential energy?

Problem B 143
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 11. The largest lasagna in the world was made in California in 1993. It had
an area of approximately 44 m2
. Imagine a parallel-plate capacitor with
this area that is filled with air. If a potential difference of 30.0 V is
placed across the capacitor, the stored charge is 2.5 mC.
a. Calculate the capacitance of the capacitor.
b. Calculate the distance that the plates are separated.
c. Calculate the electrical potential energy that is stored in the
capacitor.

144
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem C
CURRENT
P R O B L E M
Amtrak introduced an electric train in 2000 that runs between New York
and Boston.With a travel time of 3.00 h, the train is not superfast, but it is
comfortable, very safe, and environmentally friendly. Find the charge
passing through the engine during the trip if the feeding current is 1.80 ×
102
A.
S O L U T I O N
Given: ∆t = 3.00 h = 1.08 × 104
s
I = 1.80 × 102
A
Unknown: ∆Q = ?
Use the equation for electric current.
I = 
∆
∆
Q
t

∆Q = I∆t = (1.80 × 102
A)(1.08 × 104
s) = 1.94 × 106
C
ADDITIONAL PRACTICE
1. An 8.00 × 106
kg electromagnet built in Switzerland draws a current of
3.00 × 102
A. How much charge passes through the magnet in 2.4 min?
2. On July 16, 2186, a total solar eclipse lasting 7 min, 29 s, will be observed
over the mid-Atlantic Ocean. During the eclipse, an observer may need a
flashlight to see. If the flashlight draws a current of 0.22 A, how much
charge will pass through the light bulb during the eclipse?
3. The National Institute of Standards and Technology has built a clock that
is off by only 3.3 ms a year. Consider a current of 0.88 A in a wire. How
many electrons pass through a cross-section of the wire in 3.3 × 10−6
s?
4. In England, a miniature electric bicycle has been constructed. The Ni-Cd
batteries help the rider pedal for up to 3.00 h. If a charge of 1.51 × 104
C
passes through the motor during those 3.00 h, what is the current?
5. Because high-temperature superconducting cables cannot sustain high
currents, their applicability is limited. However, a prototype of a high-
temperature superconductor that can transfer a charge of 1.8 × 105
C in
6.0 min has been constructed. To what current does this correspond?
6. In 1994, a prototype of what was claimed to be the first “practical” elec-
tric car was introduced. Recharging the batteries is not very practical,
though. Calculate the average time needed to recharge the car’s batteries
if a 13.6 A current carries 4.40 × 105
C to the batteries.

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem D 145
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem D
RESISTANCE
P R O B L E M
A medical belt pack with a portable laser for in-the-field medical purposes
has been constructed. The laser draws a current of 2.5 A and the circuitry
resistance is 0.6 Ω.What is the potential difference across the laser?
S O L U T I O N
Given: I = 2.5 A R = 0.6 Ω
Unknown: ∆V = ?
Use the definition of resistance.
∆V = IR = (2.5 A)(0.6 Ω) = 1.5 V
ADDITIONAL PRACTICE
1. Electric eels, found in South America, can provide a potential difference
of 440 V that draws a current of 0.80 A through the eel’s prey. Calculate
the resistance of the circuit (the eel and prey).
2. It is claimed that a certain camcorder battery can provide a potential dif-
ference of 9.60 V and a current of 1.50 A. What is the resistance through
which the battery must be discharged?
3. A prototype electric car is powered by a 312 V battery pack. What is the
resistance of the motor circuit when 2.8 × 105
C passes through the cir-
cuit in 1.00 h?
4. In 1992, engineers built a 2.5 mm long electric motor that can be driven
by a very low emf. What is the potential difference if it draws a 3.8 A cur-
rent through a 0.64 Ω resistor?
5. A team from Texas AM University has built an electric sports car with a
maximum motor current of 2.4 × 103
A. Determine the potential differ-
ence that provides this current if the circuit resistance is 0.30 Ω.
6. Stanford University scientists have constructed the Orbiting Picosatellite
Automated Launcher (OPAL). OPAL can launch disposable “picosatel-
lites” the size of hockey pucks. Each picosatellite will be powered by a
3.0 V battery for about an hour. If the satellite’s circuitry were to have a
resistance of 16 Ω, what current would be drawn by the satellite?
7. For years, California has been striving for all zero-emission vehicles on
its roads. In 1995, a street bus with a range of 120 km was built. This bus
is powered by batteries delivering 6.00 × 102
V. If the circuit resistance is
4.4 Ω, what is the current in the bus’s circuit?

Problem E
ELECTRIC POWER
P R O B L E M
In 1994, a group of students at Lawrence Technological University, in
Southfield, Michigan, built a car that combines a conventional diesel en-
gine and an electric direct-current motor. The power delivered by the
motor is 32 kW. If the resistance of the car’s circuitry is 8.0 Ω, find the
current drawn by the motor.
S O L U T I O N
Given: P = 32 kW = 3.2 × 104
W
R = 8.0 Ω
Unknown: I = ?
Because power and resistance are known, use the second form of the power equa-
tion to solve for I.
P = I2
R
I = 
R
P

= 
(3

.2
(
8
×
.0
1
Ω
0

4
)

W

)

= 63 A
ADDITIONAL PRACTICE
1. A flying source of light is being developed that will consist of a metal-
halide lamp lifted by a helium-filled balloon. The maximum power rat-
ing for the lamp available for the device is 12 kW. If the lamp’s resistance
is 2.5 × 102
Ω, what is the current in the lamp?
2. The first American hybrid electric bus operated in New York in 1905.
The gasoline-fueled generator delivered 33.6 kW to power the bus. If the
generator supplied an emf of 4.40 × 102
V, how large was the current?
3. A compact generator has been designed that can jump-start a car, though
the generator’s mass is only about 10 kg. Find the maximum current that
the generator can provide at 12.0 V if its maximum power is 850 W.
4. Fuel cells combine gaseous hydrogen and oxygen to effectively and
cleanly produce energy. Recently, German engineers produced a fuel cell
that can generate 4.2 × 1010
J of electricity in 1.1 × 103
h. What potential
difference would this fuel cell place across a 40.0 Ω resistor?
5. Omega, a laser built at the University of Rochester, New York, generated
6.0 × 1013
W for 1.0 ns in 1995. If this power is provided by 8.0 × 106
V
placed across the circuit, what is the circuit’s resistance?
6. In 1995, Los Alamos National Lab developed a model electric power
plant that used geothermal energy. Find the plant’s projected power
output if the plant produces a current of 6.40 × 103
A at 4.70 × 103
V.
146
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem F 147
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Electrical Energy and Current
Problem F
ELECTRIC POTENTIAL
P R O B L E M
The longest railway platform is in Kharagpur,India.Suppose you place two
charges, −8.1 × 10−8
C and −2.4 × 10−7
C,at opposite ends of this platform.
The electric potential at a point 6.60 × 102
m from the greater charge is
−7.5V. What is the distance between the charges?
S O L U T I O N
Given: q1 = −8.1 × 10−8
C
q2 = −2.4 × 10−7
C
r2 = 6.60 × 102
m
V = −7.5 V
kC = 8.99 × 109
N• m2
/C2
Unknown: d = ?
Use the equation for the electric potential near a point charge.
r1 = d − r2
V = kC 
q
r
 = kC
q
r1
1
 + 
q
r2
2

= kC
d
q
−
1
r2
 + 
q
r2
2



k
V
C
 − 
q
r2
2
 = 
d
q
−
1
r2

d = + r2
d =
−

+ 660 m
d = + 660 m
d = 
−4
−
.7
8.
×
1 ×
10
1
−
0
1
−
0
8
C
C
/m
 + 660 m = 830 m
−8.1 × 10−8
C

[−8.3 × 10−10 C/m + 3.6 × 10−10 C/m]
(−2.4 × 10−8
C)

660 m
−7.5 V

(8.99 × 109 N•m2/C2)
q1


k
V
c
 − 
q
r2
2


−8.1 × 10−8
C
1. The Sydney Harbour Bridge, in Australia, is the world’s widest long-span
bridge. Suppose two charges, −12.0 nC and −68.0 nC, are separated by
the width of the bridge. The electric potential along a line between the
charges at a distance of 16.0 m from the −12.0 nC charge is −25.3 V. How
far apart are the charges?
ADDITIONAL PRACTICE

148
NAME ______________________________________ DATE _______________ CLASS ____________________
2. The Hughes H4 Hercules, nicknamed the Spruce Goose, has a wingspan
of 97.5 m, which is greater than the wingspan of any other plane. Sup-
pose two charges, 18.0 nC and 92.0 nC, are placed at the tips of the
wings. If an electric potential of 53.3 V is measured at a certain point
along the wings, how far is that point from the 92.0 nC charge?
3. A Canadian company has developed a scanning device that can detect
drugs, explosives, and even cash that are being smuggled across state
borders. The scanner uses accelerated protons to generate gamma rays,
which can easily penetrate through most substances that are less than a
few centimeters thick. At the heart of the scanner is a compact power
supply that can produce an electric potential as large as 1.0 × 106
V. Find
the value of a point charge q that would create an electric potential of
1.0 × 106
V at a distance of 12 cm.
4. Gravitational potential and electric potential are described by similar
mathematical equations. Suppose Earth has a uniform distribution of pos-
itive charge on its surface. A test particle with a mass of 1.0 kg and a charge
of 1.0 C is placed at some distance from Earth. What must the total charge
on Earth’s surface be for the test particle to experience equal gravitational
and electric potentials? (Hint: Obtain the equation for gravitational poten-
tial by comparing the gravitational force equation from Section 7I to
Coulomb’s law for electrostatic force. Assume that the entire charge on
Earth’s surface can be treated as a point charge at Earth’s center.)
5. Overall, the matter in the sun is electrically neutral. However, the tem-
peratures within the sun are too high for electrons to remain with posi-
tively charged nuclei for more than a fraction of a second. Suppose the
positive and negative charges in the sun could be separated into two
clouds with a separation of 1.5 × 108
km, which is equal to the average
distance between Earth and the sun.
a. Calculate the charge in each cloud. Assume that the sun, which has
a mass of 1.97 × 1030
kg, consists entirely of hydrogen. The mass of
one hydrogen atom is 1.67 × 10−27
kg.
b. Calculate the electric potential for the two clouds at a distance of
1.1 × 108
km (the distance between the sun and Venus) from the
proton cloud.
6. The freight station at Hong Kong’s waterfront is the largest multilevel in-
dustrial building in the world. The station is 292 m long and 276 m wide,
and inside there are more than 26 km of roadways. Consider a rectangle
that is 292 m long and 276 m wide. If charges +1.0q, −3.0q, +2.5q, and
+4.0q are placed at the vertices of this rectangle, what is the electric
potential at the rectangle’s center? The value of q is 64 nC.
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem F 149
NAME ______________________________________ DATE _______________ CLASS ____________________
7. The largest premechanical earthwork was built about 700 years ago in
Africa along the boundaries of the Benin Empire. The total length of the
earthwork is estimated to be 16 000 km. Consider an equilateral triangle
in space formed by three equally charged asteroids with charges of
7.2 × 10−2
C. If the length of each side of the triangle is 1.6 × 104
km,
what is the electric potential at the midpoint of any one of the sides?
8. The Royal Dragon restaurant in Bangkok, Thailand, can seat over 5000
customers, making it the largest restaurant in the world. The area of the
restaurant is equal to that of a square with sides measuring 184 m each. If
three charges, each equal to 25.0 nC, are placed at three vertices of this
square, what is the electric potential at the fourth vertex?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

150
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem G
COST OF ELECTRICAL ENERGY
P R O B L E M
In 1995, the fortune of Sir Muda Hassanal Bolkiah, Sultan of Brunei, was
estimated at $37 billion. Suppose this money is used to pay for the energy
used by an ordinary 1.0 kW microwave oven at a rate of $0.086/kW•h.
How long can the microwave oven be powered?
S O L U T I O N
Given: Cost of energy = $0.086/kW•h P = 1.0 kW
Purchase power = $37 × 109
Unknown: ∆t = ?
First, calculate the number of kilowatt-hours that can be purchased by dividing
the total amount of money ($) by the cost of energy ($/kW•h). Then divide the
energy used (kW•h) by the power (kW) to find the time.
Energy = ($37 × 109
)

1
$
k
0
W
.08
•
6
h

= 4.3 × 1011
kW•h
∆t = 
Ene
P
rgy
 = 
(4.3 ×
(1
1
.0
01
k
1
W
kW
)
•h)
 = 4.3 × 1011
h = 4.9 My
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. The ten reactors of the nuclear power station in Fukushima, Japan, pro-
duce 8.8 × 109
W of electric power. If you have $1.0 × 106
, how many hours
of the station’s energy output can you buy? Assume a price of $0.081/kW•h.
2. A power plant in Hawaii produces electricity by using the difference in
temperature between surface water and deep-ocean water. The plant pro-
duces 104 kW. Suppose this energy is sold at a rate of $0.120/kW•h. For
how long would $18 000 worth of this energy last?
3. For basketball fans, a flexible light source that can be attached around any
basketball hoop rim has been developed. This source reportedly lasts for
1.0 × 104
h. How much power will this light source provide over its lifetime
if its overall cost of operation is $23 and the energy cost is $0.086/kW•h?
4. Fluorescent lamps with resistances that can be adjusted from 80.0 Ω to
400.0 Ω are being produced. If such a lamp is connected to a 110 V emf
source, how much will it cost to operate the lamp at its maximum rated
power for 24 h? The cost of energy is $0.086/kW•h.
5. A solar-cell installation that can convert 15.5 percent of the sun’s energy
into electricity has been built. The device delivers 1.0 kW of power. If it
produces energy at a cost of $0.080/kW•h, how much energy must the
sun provide to produce $1000.00 worth of energy?

Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Problem A 151
NAME ______________________________________ DATE _______________ CLASS ____________________
Circuits and Circuit Elements
Problem A
RESISTORS IN SERIES
P R O B L E M
A particular electronic-code lock provides over 500 billion combinations.
Moreover, it can sustain an electric shock of 1.25 × 105
V. Suppose this
potential difference is applied across a series connection of the following
resistors: 11.0 kΩ, 34.0 kΩ, and 215 kΩ.What is the equivalent resistance
for the circuit? What current would pass through the resistors?
S O L U T I O N
Given: R1 = 11.0 kΩ = 11.0 × 103
Ω
R2 = 34.0 kΩ = 34.0 × 103
Ω
R3 = 215 kΩ = 215 × 103
Ω
∆V = 1.25 × 105
V
Unknown: Req = ? I = ?
Choose the equation(s) or situation: Because the resistors are in series, the
equivalent resistance can be calculated from the equation for resistors in series.
Req = R1 + R2 + R3
The equation relating potential difference, current, and resistance can be used to
calculate the current.
∆V = IReq
I = 
R
∆
e
V
q

Req = (11.0 × 103
Ω + 34.0 × 103
Ω + 215 × 103
Ω)
Req =
I = 
(
(
2
1
.
.
6
2
0
5
×
×
1
1
0
0
5
5
Ω
V)
)
 =
For resistors connected in series, the equivalent resistance should be greater than
the largest resistance in the circuit.
2.60 × 105
Ω 2.15 × 105
Ω
0.481 A
2.60 × 105
Ω
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The Large Optics Diamond Turning Machine at the Lawrence Livermore
National Lab in California can cut a human hair lengthwise 3000 times!
That would produce pieces with a cross-sectional area of 10−7
mm2
. A
1.0 m long silver wire with this cross-sectional area would have a resistance

152
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
of 160 kΩ. Consider three pieces of silver wire connected in series. If their
lengths are 2.0 m, 3.0 m, and 7.5 m, and the resistance of each wire is pro-
portional to its length, what is the equivalent resistance of the connection?
2. Most of the 43 × 103
kg of gold that sank with the British ship HMS Lau-
rentis in 1917 has been recovered. If this gold were drawn into a wire
long enough to wrap around Earth’s equator five times, its electrical re-
sistance would be about 5.0 × 108
Ω. Consider three resistors with resis-
tances that are exactly 1/3, 2/7, and 1/5 the resistance of the gold wire.
What equivalent resistance would be produced by connecting all three
resistors in series?
3. A 3 mm thick steel wire that stretches for 5531 km has a resistance of
about 82 kΩ. If you connect in series three resistors with the values
16 kΩ, 22 kΩ, and 32 kΩ, what value must the fourth resistor have for
the equivalent resistance to equal 82 kΩ?
4. The largest operating wind generator in the world has a rotor diameter
of almost 100 m. This generator can deliver 3.2 MW of power. Suppose
you connect a 3.0 kΩ resistor, a 4.0 kΩ resistor, and a 5.0 kΩ resistor in
series. What potential difference must be applied across these resistors in
order to dissipate power equal to 1.00 percent of the power provided by
the generator? What is the current through the resistors? (Hint: Recall
the relation between potential difference, resistance, and power.)
5. The resistance of loudspeakers varies with the frequency of the sound
they produce. For example, one type of speaker has a minimum resis-
tance of 4.5 Ω at low frequencies and 4.0 Ω at ultra-low frequencies, and
it has a peak resistance of 16 Ω at a high frequency. Consider a set of re-
sistors with resistances equal to 4.5 Ω, 4.0 Ω, and 16.0 Ω. What values of
the equivalent resistance can be obtained by connecting any two of them
in different series connections?
6. Standard household potential difference in the United States is 1.20 × 102
V.
However, many electric companies allow the residential potential difference
to increase up to 138 V at night. Suppose a 2.20 × 102
Ω resistor is con-
nected to a constant potential difference.A second resistor is provided in an
alternate circuit so that when the potential difference rises to 138 V, the sec-
ond resistor connects in series with the first resistor. This changes the resis-
tance so that the current in the circuit is unchanged.What is the value of
the second resistor?
7. The towers of the Golden Gate Bridge, in San Francisco, California, are
about 227 m tall. The supporting cables of the bridge are about 90 cm
thick. A steel cable with a length of 227 m and a thickness of 90 cm
would have a resistance of 3.6 × 10−5
Ω. If a 3.6 × 10−5
Ω resistor is con-
nected in series with an 8.4 × 10−6
Ω resistor, what power would be dissi-
pated in the resistors by a 280 A current? (Hint: Recall the relation be-
tween current, resistance, and power.)

Problem B 153
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem B
RESISTORS IN PARALLEL
P R O B L E M
A light bulb in a camper’s flashlight is labeled 2.4 V, 0.70 A. Find the
equivalent resistance and the current if three of these light bulbs are
connected in parallel to a standard C size 1.5 V battery.
S O L U T I O N
Given: ∆V1 = 2.4 V I1 = 0.70 A
∆V2 = 2.4 V I2 = 0.70 A
∆V3 = 2.4 V I3 = 0.70 A
∆V = 1.5 V
Unknown: Req = ? I = ?
Choose the equation(s) or situation: Because the resistors (bulbs) are in parallel,
the equivalent resistance can be calculated from the equation for resistors in parallel.

R
1
eq
 = 
R
1
1
 + 
R
1
2
 + 
R
1
3

To calculate the individual resistances, use the definition of resistance.
∆Vn = InRn
The following form of the equation can be used to calculate the current.
∆V = IReq
Rn = 
∆
I
V
n
n
 I = 
R
∆
e
V
q

R1 = 
∆
I
V
1
1
 = 
(
(
0
2
.
.
7
4
0
V
A
)
)
 = 3.4 Ω
R2 = 
∆
I
V
2
2
 = 
(
(
0
2
.
.
7
4
0
V
A
)
)
 = 3.4 Ω
R3 = 
∆
I
V
3
3
 = 
(
(
0
2
.
.
7
4
0
V
A
)
)
 = 3.4 Ω

R
1
eq
 = 
R
1
1
 + 
R
1
2
 + 
R
1
3
 = 
(3.4
3
Ω)
 = 
0
1
.8
Ω
8

Req =
I = 
(
(
1
1
.
.
1
5
Ω
V)
)
 =
For resistors connected in parallel, the equivalent resistance should be less than
the smallest resistance in the circuit.
1.1 Ω 3.4 Ω
1.4 V
1.1 Ω
1. DEFINE
2. PLAN
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. CALCULATE
4. EVALUATE

154
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. A certain full-range loudspeaker has a maximum resistance of 32 Ω at
45 Hz, a resistance of 5.0 Ω for most audible frequencies, and a resistance
of only 1.8 Ω at 20 kHz. Consider three resistors with resistances of
1.8 Ω, 5.0 Ω, and 32 Ω. Find the equivalent resistance if they are
connected in parallel.
2. The Large Electron Positron ring, near Geneva, Switzerland, is one of the
biggest scientific instruments on Earth. The circumference of the ring is
27 km. A copper wire with this length and a cross-sectional area of 1 mm2
will have a resistance of about 450 Ω. Consider a parallel connection of
three resistors with resistances equal to 1.0, 2.0, and 0.50 times the resis-
tance of the copper wire, respectively. What is the equivalent resistance?
3. Cars on the Katoomba Scenic Railway are pulled along by winding ca-
bles, and at one point, they move along a 310 m span that makes an angle
of 51° with the horizontal. A 310 m steel cable that is 4 cm thick would
have an estimated resistance of 2.48 × 10−2
Ω. An equivalent resistance
of 6.00 × 10−3
Ω can be obtained if two resistors, one having the same
resistance as the steel cable, are connected in parallel. Find the resistance
of the second resistor.
4. In 1992 in Atlanta, 1 724 000 United States quarters were placed side by
side in a straight line. Suppose these quarters were stacked to form a
cylindrical tower. If the influence of the air gaps between coins is negligi-
ble, the resistance of the tower can be estimated easily. Find the resistance
if the parallel connection of four resistors that have resistances equal to
exactly 1, 3, 7, and 11 times the tower’s resistance yields an equivalent
resistance of 6.38 × 10−2
Ω.
5. The largest piece of gold ever found had a mass of about 70 kg. If you
were to draw this mass of gold out into a thin wire with a cross-sectional
area of 2.0 mm2
, the wire would have a length of 1813 km. The wire
would also have a resistance per unit length of 1.22 × 10−2
Ω/m.
a. What is the resistance of the wire?
b. Suppose the wire were cut into pieces having resistance of exactly
1/2, 1/4, 1/5, and 1/20 of the wire’s resistance, respectively. If these
pieces are reconnected in parallel, what is the equivalent resistance
of the four pieces?
6. A powerful cordless drill uses a 14.4 V battery to deliver 225 W of power.
Treating the drill as a resistor, find its resistance. If a single 14.4 V battery
is connected to four “drill” resistors that are connected in parallel, what
are the equivalent resistance and the battery current?
7. The total length of the telephone wires in the Pentagon is 3.22 × 105
km.
Suppose these wires have a resistance of 1.0 × 10−2
Ω/m. If all the wires
are cut into 1.00 × 103
km pieces and all pieces are connected in parallel
to a AA battery (∆V = 1.50 V), what would the current through the wires
be? Assume that a AA battery can sustain this current.

Problem C 155
NAME ______________________________________ DATE _______________ CLASS ____________________
Problem C
EQUIVALENT RESISTANCE
P R O B L E M
A certain amplifier can drive five channels with a load of 8.0 Ω each.
Consider five 8.0 Ω resistors connected as shown.What is the equivalent
resistance?
R1 = 8.0 Ω
R3 = 8.0 Ω
R2 = 8.0 Ω
R5 = 8.0 Ω
R4 = 8.0 Ω
REASONING
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Divide the circuit into groups of series and parallel resistors. This way, the meth-
ods presented in determining equivalent resistance for resistors in series and par-
allel can be used to calculate the equivalent resistance for each group.
S O L U T I O N
1. Redraw the circuit as a group of resistors along one side of the circuit.
Bends in a wire do not affect the circuit and do not need to be represented in a
schematic diagram. Redraw the circuit without corners, keeping the arrange-
ment of the circuit elements the same and disregarding the emf source.
2. Identify components in series, and calculate their equivalent resistance.
At this stage, there are no resistors in series.
3. Identify components in parallel, and calculate their equivalent resistance.
Resistors in group (a) are in parallel. For group (a):

Re
1
q,a
 = 
R
1
1
 + 
R
1
2
 = 
(8.0
2
Ω)
 = 
0
1
.2
Ω
5

Req,a = 4.0 Ω
R1 = 8.0 Ω
Req
R5 = 8.0 Ω
R4 = 8.0 Ω
R3 = 8.0 Ω
R2 = 8.0 Ω
Req,a
Req,b
(a)
(b)
(c)

156
NAME ______________________________________ DATE _______________ CLASS ____________________
4. Repeat steps 2 and 3 until the resistors in the circuit are reduced to a
single equivalent resistance.
Resistors in group (b) are in series.
Req,b = Req,a + R3 + R4 = 4.0 Ω + 8.0 Ω + 8.0 Ω = 20.0 Ω
Resistors in group (c) are in parallel.

R
1
eq
 = 
Re
1
q,b
 + 
R
1
5
 = 
(20.
1
0 Ω)
 + 
(8.0
1
Ω)
 = 
0.
1
05
Ω
00
 + 
0
1
.1
Ω
2

Req =

0
1
.1
Ω
7


−1
= 5.9 Ω
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1993, the gold reserves in the United States were about 8.490 × 106
kg.
If all that gold were made into a thick wire with a cross-sectional area
of 1 cm2
, its total resistance would be about 6.60 × 102
Ω. If the same
operation were applied to the gold reserves of Germany, France, and
Switzerland, the resistances would be 2.40 × 102
Ω, 2.00 × 102
Ω, and
2.00 × 102
Ω, respectively. Now consider all four resistors connected as
shown in the circuit diagram below. Find the equivalent resistance.
2. In 1920, there was an electric car that could travel at about 40 km/h and
that had about a 45 km range. The car was powered by a 24 V battery.
Suppose this battery is connected to a combination of resistors, as shown
in the circuit diagram below. What is the battery current?
R1 = 2.0 Ω R2 = 4.0 Ω
R3 = 6.0 Ω
R4 = 3.0 Ω
∆V = 24 V
R1 = 6.60 × 102 Ω R2 = 2.40 × 102 Ω
R4 = 2.00 × 102 Ω
R3 = 2.00 × 102 Ω

Problem C 157
NAME ______________________________________ DATE _______________ CLASS ____________________
3. By adding water to the Enviro-Gen portable power pack, the device can
generate 12 V for up to 40.0 h. If this device powers a combination of
small appliances with the resistances shown in the circuit diagram below,
what will be the net current for the circuit?
4. In 1995, the most powerful wind generator in the United States was the
Z-40, which has a rotor diameter of 40 m. The machine is capable of
producing 5.00 × 102
A at 1.00 × 103
V, assuming 100 percent efficiency.
Suppose a direct current of 5.00 × 102
A is produced when a potential
difference of 1.00 × 103
V is placed across a circuit of resistors, as shown
in the diagram below. What is the equivalent resistance of the circuit?
What is the power dissipated in the circuit?
5. The longest-lasting battery in the world is at Oxford University, in
England. It was built in 1840 and was still working in 1977, producing
a 1.0 × 10−8
A current. The battery provided a potential difference of
2.00 × 103
V. If the battery is connected to a group of resistors, as shown
in the circuit diagram below, find the value of the equivalent resistance
and the value of r.
R1 = r R2 = 3r
R3 = 2r R4 = 4r
∆V = 2.00 × 103 V
R1 = 1.5 Ω
R2 = 3.0 Ω
R3 = 1.0 Ω
∆V = 1.00 × 103 V
R1 = 2.5 Ω R2 = 3.5 Ω
R3 = 3.0 Ω
R4 = 4.0 Ω
R5 = 1.0 Ω
∆V = 12 V
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

158
NAME ______________________________________ DATE _______________ CLASS ____________________
6. During World War II, a high-powered searchlight was produced that had
a power rating of 6.0 × 105
W. Assuming a potential difference of 220 V
across the searchlight, find the resistance of the light bulb in that search-
light. Find the equivalent resistance for several of these light bulbs
connected as shown in the circuit diagram below. What is the total power
dissipated in the circuit?
R1 R2
R3
R4 R5
R6
∆V = 220 V
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem D 159
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
NAME ______________________________________ DATE _______________ CLASS ____________________
CURRENT IN AND POTENTIAL DIFFERENCE ACROSS A RESISTOR
P R O B L E M
Problem D
REASONING
First find the equivalent resistance of the circuit. From this, determine the total
circuit current. Then rebuild the circuit in steps, calculating the current and po-
tential difference for the equivalent resistance of each group until the current in
and potential difference across the specified 8.0 Ω resistor are known.
S O L U T I O N
1. Determine the equivalent resistance of the circuit.
The equivalent resistance, which was calculated in the sample problem of the
previous section, is 5.7 Ω.
2. Calculate the total current in the circuit.
Substitute the potential difference and equivalent resistance in ∆V = IR, and
rearrange the equation to find the current delivered by the battery.
I = 
R
∆
e
V
q
 = 
(
(
1
5
2
.9
.0
Ω
V
)
)
 = 2.0 A
3. Determine a path from the equivalent resistance found in step 1 to the
specified resistor.
Review the path taken to find the equivalent resistance in the diagram below,
and work backward through this path. The equivalent resistance for the entire
circuit is the same as the equivalent resistance for group (c). The top resistors
in group (c), in turn, form the equivalent resistance for group (b), and the
rightmost resistor in group (b) is the specified 8.0 Ω resistor.
R1 = 8.0 Ω
Req
R5 = 8.0 Ω
R4 = 8.0 Ω
R3 = 8.0 Ω
R2 = 8.0 Ω
Req,a
Req,b
(a)
(b)
(c)
For the circuit from the previous section’s sample problem, determine
the current in and potential difference across the 8.0 Ω resistor (R4) in
the figure below.
R1 = 8.0 Ω
R2 = 8.0 Ω
R3 = 8.0 Ω R4 = 8.0 Ω
R5 = 8.0 Ω
∆V = 12.0 V

NAME ______________________________________ DATE _______________ CLASS ____________________
160
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. Follow the path determined in step 3, and calculate the current in and po-
tential difference across each equivalent resistance. Repeat this process
until the desired values are found.
Regroup, evaluate, and calculate.
Replace the circuit’s equivalent resistance with group (c), as shown in the fig-
ure. The resistors in group (c) are in parallel, so the potential difference across
each resistor is equal to the potential difference across the equivalent resistance,
which is 12.0 V. The current in the equivalent resistance in group (b) can now
be calculated using ∆V = IR.
Given: ∆V = 12.0 V Req,b = 20.0 Ω
Unknown: Ib = ?
Ib = 
R
∆
e
V
q,b
 = 
(
(
2
1
0
2
.
.
0
0
Ω
V)
)
 = 0.600 A
Regroup, evaluate, and calculate.
Replace the 20.0 Ω resistor with group (b). The resistors R3, Req,b, and R4 in
group (b) are in series, so the current in each resistor is the same as the cur-
rent in the equivalent resistance, which equals 0.600 A.
Ib =
The potential difference across the 8.0 Ω resistor at the right can be calculated
using ∆V = IR.
Given: Ib = 0.600 A R4 = 8.0 Ω
Unknown: ∆V = ?
∆V = IR = (0.600 A)(8.0 Ω) =
The current through the specified resistor is 0.600 A, and the potential differ-
ence across it is 4.8 V.
4.8 V
0.600 A
ADDITIONAL PRACTICE
1. Recall from the previous section the high-powered searchlight with the
power rating of 6.0 × 105
W. For a potential difference of 220 V placed
across the light bulb of this searchlight, you found a value for the bulb’s
resistance. You also determined the equivalent resistance for the circuit
shown in the figure below.
a. Calculate the potential difference across and current in the search-
light bulb labeled R3.
R1 R2
R3
R4 R5
R6
∆V = 220 V

Problem D 161
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
NAME ______________________________________ DATE _______________ CLASS ____________________
b. Calculate the potential difference across and current in the search-
c. Calculate the potential difference across and current in the search-
2. Recall the portable power pack that can provide 12 V for 40.0 h. The
device powers a combination of small appliances with the resistances
shown in the circuit diagram below. In the previous section, you calcu-
lated the equivalent resistance and net current for this circuit.
a. Calculate the potential difference across and current in the 1.0 Ω
appliance.
b. Calculate the potential difference across and current in the 2.5 Ω
appliance.
c. Calculate the potential difference across and current in the 4.0 Ω
appliance.
d. Calculate the potential difference across and current in the 3.0 Ω
appliance.
3. Recall the longest-lasting battery in the world, which was constructed at
Oxford University in 1840. In 1977, the terminal voltage of the battery
was 2.00 × 103
V. Suppose the battery is placed in the circuit shown in the
diagram below. Determine the equivalent resistance of the circuit, and
then find the following:
a. the potential difference and current in the 5.0 Ω resistor (R4).
b. the potential difference and current in the 2.0 Ω resistor (R3).
c. the potential difference and current in the 7.0 Ω resistor (R5).
d. the potential difference and current in the 3.0 × 101
Ω resistor (R7).
R2 = 3.0 Ω R3 = 2.0 Ω
R4 = 5.0 Ω
R1 = 15 Ω
R5 = 7.0 Ω R6 = 3.0 Ω
R7 = 3.0 × 101 Ω
∆V = 2.00 × 103 V
R1 = 2.5 Ω R2 = 3.5 Ω
R3 = 3.0 Ω
R4 = 4.0 Ω
R5 = 1.0 Ω
∆V = 12 V

Problem A 163
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Magnetism
Problem A
PARTICLES IN A MAGNETIC FIELD
P R O B L E M
A proposed shock absorber uses the properties of tiny magnetizable par-
ticles suspended in oil. In the presence of a magnetic field, the particles
form chains, making the liquid nearly solid. Suppose this liquid is acti-
vated by a magnetic field with a magnitude of 0.080 T.What force will a
particle with a charge of 2.0 × 10−11
C experience if it moves perpendicu-
lar to the magnetic field with a speed of 4.8 cm/s?
S O L U T I O N
Given: q = 2.0 × 10−11
C
v = 4.8 cm/s = 4.8 × 10−2
m/s
B = 0.080 T = 8.0 × 10−2
T = 8.0 × 10−2
N/A•m
Unknown: Fmagnetic = ?
Use the equation for the magnitude of a magnetic field.
B = 
Fma
q
g
v
netic

Fmagnetic = qvB
Fmagnetic = (2.0 × 10−11
C)( 4.8 × 10−2
m/s)(8.0 × 10−2
N/A•m)
Fmagnetic = 7.7 × 10−14
N
ADDITIONAL PRACTICE
1. In 1995, construction began on the world’s most powerful electromag-
net, which will be capable of producing a magnetic field with a strength
of 45 T. If an electron enters this field at a right angle with a speed of
7.5 × 106
m/s, what will be the magnetic force acting on the electron?
2. Transrapid, the world’s first train using magnetic field levitation, is de-
signed to glide 1.0 cm above the track at speeds of up to 450 km/h. Sup-
pose a charged particle with a charge of 12 × 10−9
C and a speed of
450 km/h moves at right angles to a 2.4 T magnetic field. What is the
magnetic force acting on the particle?
3. Europe’s fastest train can move at speeds of up to 350 km/h. What is the
magnetic force on a particle with a 36 nC charge that travels 350 km/h at
a 30.0° angle with respect to Earth’s magnetic field? Assume the strength
of Earth’s magnetic field is 7.0 × 10−5
T. (Hint: Recall that a magnetic field
affects only the velocity component perpendicular to the field.)
4. The U.S. Navy plans to use electromagnetic catapults to launch planes
from aircraft carriers. These catapults will be able to accelerate a 45 ×
103
kg plane to a launch speed of 260 km/h. If an electron travels at a

164
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
speed of 2.60 × 102
km/h perpendicular to a magnetic field, so that the
force acting on the electron is 3.0 × 10−17
N, what is the magnetic field
strength?
5. A solar-powered vehicle developed at Massachusetts Institute of Technol-
ogy can reach an average speed of 60.0 km/h. Due to the presence of
Earth’s magnetic field, a magnetic force acts on the electrons that move
through the car’s circuitry. Suppose an electron moves at 60.0 km/h per-
pendicular to Earth’s magnetic field. If a 2.0 × 10−22
N force acts on the
electron, what is the magnetic field strength at that location?
6. By 1905, a locomotive powered by an electric motor (which was in turn
powered by an internal-combustion engine) cruised between the East
Coast and West Coast. Suppose a particle with a charge of 88 × 10−9
C
moves at the same speed as the locomotive in a 0.32 T magnetic field. If
the magnetic force on the particle is 1.25 × 10−6
N, what is the particle’s
(and locomotive’s) speed?
7. NASA plans a shuttle launch system, called MagLifter, that would speed
up the spacecraft using superconducting magnets. A space shuttle would
be accelerated along a track 4.0 km long. At the end of the track, the speed
of the shuttle would be great enough to place it into orbit around Earth.
a. At what speed is an electron moving in a powerful 6.4 T magnetic
field if it experiences a force of 2.76 × 10−16
N?
b. If this is the shuttle’s final speed at the end of the track, how long
does it take the shuttle to glide along the track, assuming that the
shuttle undergoes constant acceleration from rest?
8. The mass spectrometer is a device that was first used to separate the differ-
ent isotopes of an element. In a mass spectrometer, ionized atoms with the
same speed enter a region in which a strong magnetic field is maintained.
The field, which is perpendicular to the plane in which the atoms move,
exerts a force that keeps the atoms in a circular path. Because all of the
atoms have the same charge and speed, the magnetic force exerted on them
is the same. However, the atoms have slightly different masses, and there-
fore the centripetal acceleration on each varies slightly. The centripetal
force depends on the speed of the atoms and the radius of the circular path
the atoms follow. Isotopes with larger masses have trajectories with larger
radii. As a result, the more-massive isotopes are detected farther from the
center of the apparatus than isotopes with smaller masses.
a. Suppose the magnetic field in a mass spectrometer has a field
strength of 0.600 T and that two lithium atoms, each with a single
positive charge of 1.60 × 10−19
C and a speed of 2.00 × 105
m/s, enter
that field. What is the magnetic force exerted on these two atoms?
b. If the masses of the atoms are 9.98 × 10−27
kg and 11.6 × 10−27
kg,
respectively, what will be the difference in the radius for each
atom’s path? (Hint: The magnetic force equals the force required to
keep the atoms in a circular path.)

Problem B 165
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Magnetism
Problem B
FORCE ON A CURRENT-CARRYING CONDUCTOR
P R O B L E M
S O L U T I O N
Given: B = 1.0 × 103
T
Fmagnetic = 1.6 × 102
N
l = 25 cm = 0.25 m
Unknown: I = ?
Use the equation for force on a current-carrying conductor perpendicular to a
magnetic field.
I = 
Fma
B
g
l
netic

I = = 0.64 A
1.6 × 102
N

(1.0 × 103
T)(0.25 m)
ADDITIONAL PRACTICE
1. In 1964, a magnet at the Francis Bitter National Magnet Laboratory
created a magnetic field with a magnitude of 22.5 T. Ten megawatts of
power was required to generate this field. If a wire that is 12 cm long
and that carries a current of 8.4 × 10−2
A is placed in this field at a right
angle to the field, what is the force acting on it?
2. One of the subway platforms in downtown Chicago is 1066 m long.
Suppose the current in one of the service wires below the platform is
0.80 A. What is the magnitude of Earth’s magnetic field at that location
if the field exerts a force of 6.3 × 10−2
N on the wire? Assume the cur-
rent is perpendicular to the field.
3. The distance between the pylons of the power line across the Ameralik
Fjord in Greenland is 5.376 km. If this length of wire carries a current
of 12 A and experiences a force of 3.1 N because of Earth’s magnetic
field, what is the magnitude of the field in that region? Assume the wire
makes an angle of 38° with the field. (Hint: Only the component of the
magnetic field that is perpendicular to the current contributes to the
magnetic force.)
4. In February 1996, NASA extended a 21.0 km conducting tether from the
space shuttle Columbia in order to see how much power could be gener-
ated by interacting with Earth’s magnetic field. Suppose the
In March 1967, a 1000 T magnetic field was obtained in a lab for a frac-
tion of a second. Maximum sustained fields presently do not exceed 50 T.
If a 25 cm long wire is perpendicular to a 1.0 × 103
T magnetic field
and the magnetic force on the wire is 1.6 × 102
N, what is the current
in the wire?

166
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
magnetic field at the shuttle’s location has a magnitude of 6.40 × 10−7
T.
What current must be induced in the tether, located perpendicular to
the field, to create a magnetic force of 1.80 × 10−2
N?
5. Magnetic fields are created by the currents in home appliances. Sup-
pose the magnetic field in the vicinity of an electric blow-dryer has a
magnitude of about 2.5 × 10−4
T. If a wire 4.5 cm long in such a blow-
dryer experiences a magnetic force of 3.6 × 10−7
N, what current must
exist in the wire? Assume the wire is perpendicular to the field.
6. At Sandia National Laboratories, in Albuquerque, New Mexico, an inter-
esting project has been developed. Engineers have proposed a train that
will roll on existing rails and use existing wheels but be propelled by mag-
netic forces. Suppose such a train is pushed by a 5.0 × 105
N force and re-
sults from the interaction between a current in many wires and a magnetic
field with a magnitude of 3.8 T that is oriented perpendicular to the wires.
Find the total length of the wires if they carry a 2.00 × 102
A current.
7. The largest electric sign used for advertising was set on the Eiffel
Tower, in Paris. It was lighted by 250 000 bulbs, which required an im-
mense number of electric cables. Find the total length of those cables if
a single straight cable of identical length experiences a force of 16.1 N
in Earth’s magnetic field. Assume the magnitude of the magnetic field
is 6.4 × 10−5
T and the wire, carrying a current of 2.8 A, is placed
perpendicular to the field.
8. Cows have four stomachs, so if a cow swallows a nail, it is hard to re-
move it. To extract the nail, a veterinarian gives the cow a strong mag-
net to swallow. Suppose that such a “cow magnet” has a magnetic field
magnitude of 0.040 T. If a 55 cm straight length of wire located near
the magnet carries a current of 0.10 A and is positioned so that the
angle between the magnetic field lines and the current is 45°, what is
the magnetic force that the current will experience? (Hint: Only the
component of the magnetic field that is perpendicular to the current
contributes to the magnetic force.)
9. For many years, the strongest magnetic field ever produced had a mag-
nitude of 38 T. Suppose a straight wire with a length of 2.0 m is located
perpendicular to this field. What current would have to pass through
the wire in order for the magnetic force to equal the weight of a gradu-
ate student with a mass of 75 kg?
10. The longest straight span of railroad tracks stretches 478 km in south-
western Australia. Suppose an electric current is sent through one of
the rails and that a force of 0.40 N is exerted by Earth’s magnetic field.
If the magnetic field has a strength of 7.50 × 10−5
T at that location and
is perpendicular to the rail, how large is the current?

Problem A 167
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Electromagnetic Induction
Problem A
INDUCED emf AND CURRENT
P R O B L E M
In 1994,a unicycle with a wheel diameter of 2.5 cm was ridden 3.6 m in Las
Vegas,Nevada.Suppose the wheel has 200 turns of thin wire wrapped
around its rim,creating loops with the same diameter as the wheel.An emf
of 9.6 mV is induced when the wheel is perpendicular to a magnetic field
that steadily decreases from 0.68 T to 0.24 T.For how long is the emf
induced?
S O L U T I O N
Given: N = 200 turns
D = 2.5 cm = 2.5 × 10−2
m
Bi = 0.68 T
Bf = 0.24 T
emf = 9.6 mV = 9.6 × 10−3
V
q = 0.0°
Unknown: ∆t = ?
Choose the equation(s) or situation: Use Faraday’s law of magnetic induction to
find the induced emf in the coil. Only the magnetic field strength changes with time.
emf = −N
∆q
∆t
m
= −
N∆[A
∆
B
t
cos q]
= −NA cos q 
∆
∆
B
t

Use the equation for the area of a circle to calculate the area (A).
A = pr2
= p

D
2


2
∆t = −NA cos q 
e
∆
m
B
f

Substitute values into the equation(s) and solve:
A = p
2.5 × 1
2
0−2
m


2
= 4.9 × 10−4
m2
∆t = −(200)(4.9 × 10−4
m2
)[cos 0.0°]
(0
(
.
9
2
.
4
6
T
×
−
10
0
−
.
3
68
V
T
)
)

∆t =
The induced emf is directed through the coiled wire so that the magnetic field
produced opposes the decrease in the applied magnetic field. The rate of this
change is indicated by the positive value of time.
4.5 s
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

168
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. The Pentagon covers an area of 6.04 × 105
m2
, making it one of the
world’s largest office buildings. Suppose a huge loop of wire is placed on
the ground so that it covers the same area as the Pentagon. If the loop is
pulled at opposite ends so that its area decreases, an emf will be induced
because of the component of Earth’s magnetic field that is perpendicular
to the ground. If the field component has a strength of 6.0 × 10−5
T and
the average induced emf in the loop is 0.80 V, how much time passes be-
fore the loop’s area is reduced by half?
2. A Japanese-built Ferris wheel has a diameter of 100.0 m and can carry
almost 500 people at a time. Suppose a huge magnet is used to create
a field with an average strength of 0.800 T perpendicular to the wheel.
The magnet is then pulled away so that the field steadily decreases to
zero over time. If the wheel is a single conducting circular loop and the
induced emf is 46.7 V, find the time needed for the magnetic field to
decrease to zero.
3. In 1979, a potential difference of about 32.0 MV was measured in a lab in
Tennessee. The maximum magnetic fields, obtained for very brief periods
of time, had magnitudes around 1.00 × 103
T. Suppose a coil with exactly
50 turns of wire and a cross-sectional area of 4.00 × 10−2
m2
is placed per-
pendicular to one of these extremely large magnetic fields, which quickly
drops to zero. If the induced emf is 32.0 MV, in how much time does the
magnetic field strength decrease from 1.00 × 103
T to 0.0 T?
4. The world’s largest retractable roof is on the SkyDome in Toronto,
Canada. Its area is 3.2 × 104
m2
, and it takes 20 min for the roof to fully
retract. If you have a coil with exactly 300 turns of wire that changes its
area from 0.0 m2
to 3.2 × 104
m2
in 20.0 min, what will be the emf in-
duced in the coil? Assume that a uniform perpendicular magnetic field
with a strength of 4.0 × 10−2
T passes through the coil.
5. At Massachusetts Institute of Technology, there is a specially shielded
room in which extremely weak magnetic fields can be measured. As of
1994, the smallest field measured had a magnitude of 8.0 × 10−15
T.
Suppose a loop having an unknown number of turns and an area equal
to 1.00 m2
is placed perpendicular to this field and the magnitude of the
field strength is increased tenfold in 3.0 × 10−2
s. If the emf induced is
equal to −1.92 × 10−11
V, how many turns are in the loop?
6. An electromagnet that has a mass of almost 8.0 × 106
kg was built at the
CERN particle physics research facility in Switzerland. As part of the de-
tector in one of the world’s largest particle accelerators, this magnet cre-
ates a fairly large magnetic field with a magnitude of 0.50 T. Consider a
coil of wire that has 880 equal turns. Suppose this loop is placed perpen-
dicular to the magnetic field, which is gradually decreased to zero in 12 s.
If an emf of 147 V is induced, what is the area of the coil?

Problem B 169
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
Problem B
rms CURRENT AND emf
P R O B L E M
In 1945, turbo-electric trains in the United States were capable of speeds
exceeding 160 km/h. Steam turbines powered the electric generators,
which in turn powered the driving wheels. Each generator produced
enough power to supply an rms potential difference of 6.0 × 103
V across
an 18 Ω resistor.What was the maximum potential difference across the
resistor? What was the maximum current in the resistor? What was the
rms current in the resistor? What was the generator’s power output?
S O L U T I O N
Given: ∆Vrms = 6.0 × 103
V R = 18 Ω
Unknown: ∆Vmax = ? Imax = ? Irms = ? P = ?
Choose the equation(s) or situation: Use the equation relating maximum and
rms potential differences to calculate the maximum potential difference. Use the
definition of resistance to calculate the maximum current, then use the equation
relating maximum and rms currents to calculate rms current. Power can be cal-
culated from the product of rms current and rms potential difference.
∆Vmax =

2
(∆Vrms)
Imax = 
∆V
R
max

Irms = 
I

ma
2

x

P = ∆VrmsIrms
∆Vmax = (1.41)(6.0 × 103
V)
=
Imax = 
(8.5
(1
×
8
1
Ω
03
)
V)

=
Irms = (0.707)(4.7 × 102
A)
=
P = (6.0 × 103
V)(3.3 × 102
A)
=
To determine whether severe rounding errors occurred through the various cal-
culations, obtain the product of the maximum current and maximum potential
difference. The product of ∆Vmax and Imax should equal 2P, which for this prob-
lem equals 4.0 × 106
W.
2.0 × 106
W
3.3 × 102
A
4.7 × 102
A
8.5 × 103
V
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

170
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1963, the longest single-span “rope way” for cable cars opened in Cali-
fornia. The rope way stretched about 4 km from the Coachella Valley to
Mount San Jacinto. Suppose the rope way, which is actually a steel cable,
becomes icy. To de-ice the cable, you can connect its two ends to a
120 V (rms) generator. If the resistance of the cable is 6.0 × 10−2
Ω,
a. what will the rms current in the cable be?
b. what will the maximum current in the cable be?
c. what power will be dissipated by the cable, thus melting the ice?
2. In 1970, a powerful sound system was set up on the Ontario Motor
Speedway in California to make announcements to more than 200 000
people over the noise of 50 racing cars. The acoustic power of that system
was 30.8 kW. If the system was driven by a generator that provided an
rms potential difference of 120.0 V and only 10.0 percent of the supplied
power was transformed into acoustic power, what was the maximum
current in the sound system?
3. Modern power plants typically have outputs of over 10 × 106
kW. But in
1905, the Ontario Power Station, built on the Niagara River, produced
only 1.325 × 105
kW. Consider a single generator producing this power
when it is connected to a single load (resistor). If the generated rms po-
tential difference is 5.4 × 104
V, what is the maximum current and the
value of the resistor?
4. Stability of potential difference is a major concern for all high-emf
sources. In 1996, James Cross of the University of Waterloo in Canada,
constructed a compact power supply that produces a stable potential dif-
ference of 1.024 × 106
V. It can provide 2.9 × 10−2
A at this potential dif-
ference. If these values are the rms quantities for an alternating current
source, what are the maximum potential difference and current?
5. Certain species of catfish found in Africa have “power plants” similar to
those of electric eels. Though the electricity generated is not as powerful
as that of some eels, the electric catfish can discharge 0.80 A with a po-
tential difference of 320 V. Consider an ac generator in a circuit with a
load. If its maximum values for potential difference and current are the
same as the potential difference and current for the catfish, what are the
rms values for the potential difference and current? What is the resis-
tance of the load?
6. A wind generator installed on the island of Oahu, Hawaii, has a rotor
that is about 100 m in diameter. When the wind is strong enough, the
generator can produce a maximum current of 75 A in a 480 Ω load. Find
the rms potential difference across the load.
7. The world’s first commercial tidal power plant, built in France, has a power
output of only 6.2 × 104
kW, produced by 24 generators. Find the power
produced by each generator. If one of these generators is connected to a
120 kΩ resistor, find the rms and maximum currents in it.

Problem C 171
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
Problem C
TRANSFORMERS
P R O B L E M
The span between the pylons for the power line serving the Buksefjorden
Hydro Power Station, in Greenland, is about 5 km. These power lines
carry electricity at a high potential difference, which is then stepped-
down to the standard European household potential difference of 220 V.
If the transformer that does this has a primary with 1.5 × 105
turns and a
secondary with 250 turns, what is the potential difference across the pri-
mary? (Note: Reduction of potential difference usually takes place over
several steps, not one.)
S O L U T I O N
Given: N1 = 1.5 × 105
turns N2 = 250 turns
∆V2 = 220 V
Unknown: ∆V1 = ?
Choose the equation(s) or situation: Use the transformer equation.

∆
∆
V
V
2
1
 = 
N
N
2
1

∆V1 = ∆V2 
N
N
2
1

∆V1 = (220 V) 
(1.
(
5
2
×
50
10
tu
5
r
t
n
u
s
r
)
ns)

∆V1 =
The primary should have 130 kV. The step-down factor for the transformer is
600:1.
1.3 × 105
V
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The most powerful electromagnet in the world uses 24 MW of power.
Consider a transformer that transmits 24 MW of power. The primary
has 5600 turns, and the secondary has 240 turns. If the secondary poten-
tial difference is 4.1 kV, what is the primary potential difference?
2. In 1990, New Jersey was the most densely populated state in the United
States, with 403 people per square kilometer. Consider a transformer with
74 turns in the primary and 403 turns in the secondary. If a 650 V potential
difference exists between the terminals of the secondary, what is the poten-
tial difference between the terminals of the primary?

172
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. In 1992, a battery whose longest dimension was 70 nm was made at the
University of California at Irvine. It produced a 2.0 × 10−2
V potential
difference for almost an hour. Suppose an ac generator producing this
potential difference is connected to a transformer that contains exactly
400 turns in the primary and exactly 3600 turns in the secondary. If this
emf is created between the terminals of the primary of a step-up trans-
former, what is the potential difference between the terminals of the sec-
ondary? If the 2.0 × 10−2
V is applied to the secondary instead, what is
the potential difference created between the terminals of the primary?
4. The hydraulic turbines installed at the third power plant at Grand
Coulee, in Washington, are almost 10 m in diameter. Each turbine is
large enough to produce a current of 1.0 × 103
A at 765 kV. If a trans-
former steps this potential difference down to 540 kV and the primary
contains 2.8 × 103
turns, how many turns must be in the secondary?
5. In 1965, the biggest power failure to date left about 30 million people in
the dark for several hours. About 200 000 km2
, including Ontario,
Canada, and several northeastern states in the United States were af-
fected. Such failures can usually be avoided because all major electric
grids are interconnected. Transformers are needed in these connections.
For example, a transformer can increase the potential difference from
230 kV to 345 kV, which is the typical potential difference for transmis-
sion lines in the United States. If the primary in such a step-up trans-
former has 1.2 × 104
turns, how many turns are in the secondary?
6. The sunroof on some cars doubles as a solar battery. In strong sunlight, it
produces about 20.0 W of power.
a. If this power is transmitted by the primary of a transformer with
120 V across it, what is the current in the primary?
b. What is the potential difference across the secondary if the primary
contains only 36 percent of the number of turns in the secondary?
7. Electric cars, though still few in number, are appearing on the roads. By
using a 220 V potential difference to recharge their batteries instead of
the standard 120 V, the cars could be recharged in 3 to 6 h. One process,
developed at the Electric Power Research Institute in California, suggests
using 220 V outlets with a 30.0 A charging current. If a transformer is
used to increase the potential difference from 120 V to 220 V, what is the
current in the primary? How many turns does the primary have if the
secondary has 660 turns?

Problem A 173
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Atomic Physics
Problem A
QUANTUM ENERGY
P R O B L E M
Free-electron lasers can be used to produce a beam of light with variable
wavelength. Because the laser can produce light with wavelengths as long
as infrared waves or as short as X rays, its potential applications are much
greater than for a laser that can produce light of only one wavelength.
If such a laser produces photons of energies ranging from 1.034 eV to
620.6 eV, what are the minimum and the maximum wavelengths corre-
sponding to these photons?
S O L U T I O N
Given: E1 = 1.034 eV
= (1.034 eV)
1.60 × 10−19

e
J
V

= 1.65 × 10−19
J
E2 = 620.6 eV
= (620.6 eV)
1.60 × 10−19

e
J
V

= 9.93 × 10−17
J
h = 6.63 × 10−34
J•s
c = 3.00 × 108
m/s
Unknown: lmin = ? lmax = ?
Use the equation for the energy of a quantum of light. Use the relationship
between the frequency and wavelength of electromagnetic waves.
E = hf
f = 
l
c

Substitute for f in the first equation, and rearrange to solve for wavelength.
E = 
h
l
c

l = 
h
E
c

Substitute values into the equation.
lmax =
lmax = 1.21 × 10−6
m
lmax =
lmin =
lmin = 2.00 × 10−9
m
lmin = 2.00 nm
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

(9.93 × 10−17 J)
1210 nm
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

(1.65 × 10−19
J)

174
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1974, IBM researchers announced that X rays with energies of
1.29 × 10−15
J had been guided through a “light pipe” similar to optic
fibers used for visible and near-infrared light. Calculate the wavelength
of one of these X-ray photons.
2. Some strains of Mycoplasma are the smallest living organisms. The wave-
length of a photon with 6.6 × 10−19
J of energy is equal to the length of
one Mycoplasma. What is that wavelength?
3. Of the various types of light emitted by objects in space, the radio signals
emitted by cold hydrogen atoms in regions of space that are located be-
tween stars are among the most common and important. These signals
occur when the“spin”angular momentum of an electron in a hydrogen
atom changes orientation with respect to the“spin”angular momentum of
the atom’s proton. The energy of this transition is equal to a fraction of an
electron-volt, and the photon emitted has a very low frequency. Given that
the energy of these radio signals is 5.92 × 10−6
eV, calculate the wavelength
of the photons.
4. The camera with the fastest shutter speed in the world was built for re-
search with high-power lasers and can expose individual frames of film
with extremely high frequency. If the frequency is the same as that of a
photon with 2.18 × 10−23
J of energy, calculate its magnitude.
5. Wireless “cable” television transmits images using radio-band photons
with energies of around 1.85 × 10−23
J. Find the frequency of these
photons.
6. In physics, the basic units of measurement are based on fundamental phys-
ical phenomena. For example, one second is defined by a certain transition
in a cesium atom that has a frequency of exactly 9 192 631 770 s−1
. Find
the energy in electron-volts of a photon that has this frequency. Use
the unrounded values for Planck’s constant (h = 6.626 0755 × 10−34
J•s)
and for the conversion factor between joules and electron volts (1 eV =
1.602 117 33 × 10−19
J).
7. Consider an electromagnetic wave that has a wavelength equal to 92 cm,
a length that corresponds to the longest ear of corn grown to date. What
is the frequency corresponding to this wavelength? What is its photon
energy? Express the answer in joules and in electron-volts.
8. The slowest machine in the world, built for testing stress corrosion, can
be controlled to operate at speeds as low as 1.80 × 10−17
m/s. Find the
distance traveled at this speed in 1.00 year. Calculate the energy of the
photon with a wavelength equal to this distance.

Problem B 175
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Atomic Physics
Problem B
THE PHOTOELECTRIC EFFECT
P R O B L E M
Ultraviolet radiation, which is part of the solar spectrum, causes a photo-
electric effect in certain materials. If the kinetic energy of the photoelec-
trons from an aluminum sample is 5.6 × 10−19
J and the work function of
aluminum is about 4.1 eV, what is the frequency of the photons that pro-
duce the photoelectrons?
S O L U T I O N
Given: KEmax = 5.6 × 10−19
J = 3.5 eV
hft = 4.1 eV
h = 6.63 × 10−34
J•s = 4.14 × 10−15
eV•s
c = 3.00 × 108
m/s
Unknown: f = ?
Use the equation for the maximum kinetic energy of an ejected photoelectron to
calculate the frequency of the photon.
KEmax = 
h
l
c
 − hft
f = 
KEma
h
x + hft

f =
f = 1.8 × 1015
Hz
[3.5 eV + 4.1 eV]

4.14 × 10−15
eV/s
ADDITIONAL PRACTICE
1. The melting point of mercury is about −39°C, which makes it convenient
for many applications, such as thermometers and thermostats. Mercury
also has some unusual applications, such as in “liquid mirrors.” By spin-
ning a pool of mercury, a perfect parabolic surface can be obtained for
use as a concave mirror. If the surface of mercury is exposed to light, a
photoelectric effect can be observed. If the work function of mercury is
4.5 eV, what is the frequency of photons that produce photoelectrons
with kinetic energies of 3.8 eV?
2. The largest all-metal telescope mirror, which was used in Lord Rosse’s
telescope, the Leviathan, was produced in 1845 from a copper-tin alloy.
The work function of the surface of that mirror can be estimated as
4.3 eV. Calculate the frequency of the photons that would produce
photoelectrons having a kinetic energy of 3.2 eV.

176
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. Values for the work function have been experimentally determined for
most nonradioactive, elemental metals. The smallest work function,
which is 2.14 eV, belongs to the element cesium. The largest work func-
tion, which is 5.9 eV, belongs to the element selenium.
a. What is the wavelength of the photon that will just have the thresh-
old energy for cesium?
b. What is the wavelength of the photon that will just have the thresh-
old energy for selenium?
4. Carbon is a nonmetal, yet it is a conductor of electricity, and it exhibits
photoelectric properties. Calculate the work function and the threshold
frequency for carbon if photons with a wavelength of 2.00 × 102
nm pro-
duce photoelectrons moving at a speed of 6.50 × 105
m/s.
5. Two giant water jugs made in 1902 for the Maharaja of Jaipur, India, are
the largest single-piece silver items on Earth. Each jug has a capacity of
about 8 m3
and a mass of more than 240 kg. If the surface of one of these
jugs is exposed to UV light that has a frequency of 2.2 × 1015
Hz, a pho-
toelectric effect is observed. If the photoelectrons have 4.4 eV of kinetic
energy, find the work function and the threshold frequency of silver.
6. Rhenium is one of the rarest elements on Earth. Estimates indicate that on
average there is less than 1 mg of rhenium in a kilogram of Earth’s crust
and about 4 ng of rhenium in a liter of sea water. Rhenium also has one of
the highest work functions of any metal. Suppose that a rhenium sample is
exposed to light with a wavelength of 2.00 × 102
nm and that photoelec-
trons with kinetic energies of 0.46 eV are emitted. Using this information,
calculate the work function and threshold frequency for rhenium.
7. Sodium-vapor lamps, which are widely used in streetlights, produce yel-
low light with a principal wavelength of 589 nm. Would this sodium light
cause a photoelectric effect on the surface of solid sodium (hft = 2.3 eV)?
If the answer is yes, what is the energy of those photoelectrons? If the an-
swer is no, how much energy does the photon lack?
8. Lithium’s unusual electric properties make it an ideal material for high-
capacity batteries. The purity of a thin lithium foil, used in a lithium-
polymer “sandwich” to create an efficient battery for solar-powered cars,
is extremely important. One way to assess a metal’s purity is by means of
the photoelectric effect. If the work function of lithium is 2.3 eV, what is
the kinetic energy of the photoelectrons produced by violet light with a
wavelength of 410 nm?
9. Lead and zinc are vital elements in the construction of electric batteries.
For example, the largest battery in the world, in use in California, is a
lead-acid battery, while the most durable battery in the world, working
continuously since 1840, is a zinc-sulfur battery. Zinc and lead have simi-
lar work functions: 4.3 eV and 4.1 eV, respectively. Suppose certain pho-
tons have just enough energy to cause a photoelectric effect in zinc. If the
same photons were to strike the surface of lead, what would be the speed
of the photoelectrons?

Problem C 177
NAME ______________________________________ DATE _______________ CLASS ____________________
Atomic Physics
Problem C
INTERPRETING ENERGY-LEVEL DIAGRAMS
P R O B L E M
Although neutral lithium has three electrons, two of the electrons are in
the n 1 energy level, which is filled. The third electron is in the n 2
energy level, and behaves like the single electron in a hydrogen atom,
except that the nucleus has a 3 charge and the two inner electrons
partially shield the stronger attraction of the nucleus. Of the various
possible energy levels that can be occupied by one or more of lithium's
electrons, the simplest one for the single outer electron is shown below.
E4 E = 4.53 eV
E3 E = 3.84 eV
E2 E = 1.85 eV
E1 E = 0 eV
An electron in a lithium atom drops from an energy level to E1. If the
photon emitted has a wavelength of 323.7 nm, which energy level did
the electron initially occupy, and what is its value (in eV) relative to E1?
Assume that the ground state E1 has an energy of 0 eV.
S O L U T I O N
Given: λ = 323.7 nm
Efinal = E1 = 0 eV
Unknown: Einitial = ?
Choose the equation(s) or situation: Calculate the energy of the emitted
photon, and equate this to the difference between the energy levels.
E = hf
c = fλ
E =
h
λ
c

E = Einitial − Efinal = Einitial − E1
Einitial = E + E1 =
h
λ
c
+ E1
Einitial = ×
10
1
9
m
nm
×
1.60
1
×
e
1
V
0−19
J
+ 0 eV
Einitial = 3.84 eV + 0 eV = 3.84 eV
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

323.7 nm
1. DEFINE
2. PLAN
3. CALCULATE
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.

178
NAME ______________________________________ DATE _______________ CLASS ____________________
1. Using the energy diagram for lithium shown in the Sample problem,
determine which energy level provides the initial state for an electron
that, in dropping to energy E1, produces photon with the wavelength
671.9 nm.
2. Aluminum has electrons that fill the orbitals of the two lowest energy
states, and another pair of electrons that fill the 3s level. This leaves one
unpaired electron in the 3p that can behave in certain transitions like
the single electron of the hydrogen atom. A diagram of some of these
transitions is shown below.
E4 E = 5.24 eV
E3 E = 4.69 eV
E2 E = 3.15 eV
E1 E = 0 eV
If an electron drops from the E4 energy level to E1, what is the wave-
length of the emitted photon?
3. Calculate the wavelength of a photon emitted between the E3 and E1
energy levels of an aluminum atom.
4. Calculate the wavelength of a photon emitted between the E2 and E1
energy levels of an aluminum atom.
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
The photon drops from the energy level that is 3.84 eV higher than the ground
state E1, which according to the energy diagram is the level with energy E3. It is
this transition in the lithium atom that causes the emission of the photon with
wavelength 323.7 nm.
4. EVALUATE

Problem D 179
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Atomic Physics
Problem D
DE BROGLIE WAVES
P R O B L E M
In 1974, the most massive elementary particle known was the y¢ particle,
which has a mass of about four times the mass of a proton. If the de
Broglie wavelength is 3.615 × 10−11
m when it has a speed of 2.80 × 103
m/s, what is the particle’s mass?
S O L U T I O N
Given: l = 3.615 × 10−11
m v = 2.80 × 103
m/s
h = 6.63 × 10−34
J•s
Unknown: m = ?
Use the equation for the de Broglie wavelength.
m = 
l
h
v
 = = 6.55 × 10−27
Kg
(6.63 × 10−34
J•s)

(3.615 × 10−11
m)(2.80 × 103
m/s)
ADDITIONAL PRACTICE
1. The world’s smallest watch, made in Switzerland, has a fifteen-jewel
mechanism and is less than 5 mm wide. When this watch has a speed of
3.2 m/s, its de Broglie wavelength is 3.0 × 10−32
m. What is the mass of the
watch?
2. Discovered in 1983, Z° was still the most massive particle known in 1995.
If the de Broglie wavelength of the Z° particle is 6.4 × 10−11
m when the
particle has a speed of 64 m/s, what is the particle’s mass?
3. Although beryllium, Be, is toxic, the Be2+
ion is harmless. When a Be2+
ion is accelerated through a potential difference of 240 V, the ion’s de
Broglie wavelength is 4.4 × 10−13
m. What is the mass of the Be2+
ion?
4. In 1972, a powder with a particle size of 2.5 nm was produced. At what
speed should a neutron move to have a de Broglie wavelength of 2.5 nm?
5. The graviton is a hypothetical particle that is believed to be responsible
for gravitational interactions. Although its existence has not been proven,
cosmological observations and theories indicate that its mass, which is
theoretically zero, has an upper limit of 7.65 × 10−70
kg. What speed must
a graviton have for its de Broglie wavelength to be 5.0 × 1032
m? (Gravi-
tons are predicted to have a speed equal to that of light.)
6. The average mass of the bee hummingbird is about 1.6 g. What is the de
Broglie wavelength of this variety of hummingbird if it is flying at 3.8 m/s?
7. In 1990, Dale Lyons ran 42 195 m, in 3 h, 47 min, while carrying a spoon
with an egg in it. What was Lyons’ average speed during the run? If the
egg’s mass was 0.080 kg, what was its de Broglie wavelength?

Problem A 181
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Subatomic Physics
Problem A
BINDING ENERGY
P R O B L E M
Each egg of Caraphractus cinctus, a parasitic wasp, has a mass of about
2.0 × 10−10
kg. Consider the formation of 16
8O from H atoms and neu-
trons. How many nuclei of 16
8O must be formed to produce a mass defect
equal to the mass of one Caraphractus cinctus egg? What is the total bind-
ing energy of these 16
8O nuclei? The atomic mass of 16
8O is 15.994 915 u.
S O L U T I O N
Given: megg = 2.0 × 10−10
kg
element formed = 16
8O
Z = 8 N = 16 − 8 = 8
atomic mass of 16
8O = 15.994 915 u
atomic mass of H = 1.007 825 u
mn = 1.008 665 u
Unknown: ∆m = ?
n = number of 16
8O nuclei formed = ?
total Ebind = ?
Choose the equation(s) or situation: First find the mass defect using the equa-
tion for mass defect.
∆m = Z(atomic mass of H) + Nmn − atomic mass
To determine the number of oxygen-16 nuclei that must be formed to produce a
total mass defect equal to the mass of a Caraphractus cinctus egg, calculate the
ratio of the mass of one egg to the mass defect.
the number of 16
8O nuclei formed = n = 
m
∆
e
m
gg

Finally, to find the total binding energy of all 16
8O nuclei, use the equation for the
binding energy of a nucleus and multiply it by n.
total Ebind = nEbind = n∆mc2
total Ebind = n∆m(931.49 MeV/u)
∆m = 8(1.007 825 u) + 8(1.008 665 u) − 15.994 915 u
∆m = 8.062 600 u + 8.069 320 u − 15.994 915 u
∆m = 0.137 005 u
n = 
(2
(
.
0
0
.1
×
37
10
0
−
0
1
5
0
u
k
)
g)


1.66 ×
1
1
u
0−27 kg

=
total Ebind = (8.8 × 1017
)(0.137 005 u)(931.49 MeV/u)
total Ebind = 1.1 × 1020
MeV
8.8 × 1017
nuclei
1. DEFINE
2. PLAN
3. CALCULATE

182
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1993, the United States had more than 100 operational nuclear reactors
producing about 30 percent of the world’s nuclear energy, or 610 TW•h.
a. Find the mass defect corresponding to a binding energy equal to
that energy output.
b. How many 2
1H nuclei would be needed to provide this mass defect?
c. How many 56
26Fe nuclei would be needed to provide this mass defect?
d. How many 226
88Ra nuclei would be needed to provide this mass defect?
2. In 1976, Montreal hosted the Summer Olympics. To complete the new
velodrome, the 4.1 × 107
kg roof had to be raised 10.0 cm to be placed in
the exact position.
a. Find the energy needed to raise the roof.
b. Find the mass of 56
26Fe that is formed when an amount of energy
equal to that calculated in part (a) is obtained from binding H atoms
and neutrons in iron-56 nuclei.
3. Nuclear-energy production worldwide was 2.0 × 103
TW•h in 1993.What
mass of 235
92U releases an equivalent amount of energy in the form of binding
energy?
4. In 1993, the United States burned about 2.00 × 108
kg of coal to produce
about 2.1 × 1019
J of energy. Suppose that instead of burning coal, you
obtain energy by forming coal (12
6C) out of H atoms and neutrons. What
amount of coal must be formed to provide 2.1 × 1019
J of energy? As-
sume 100 percent efficiency.
5. The sun radiates energy at a rate of 3.9 × 1026
J/s. Suppose that all the
sun’s energy occurs because of the formation of 4
2He from H atoms and
neutrons. Find the number of reactions that take place each second.
6. Sulzer Brothers, a Swiss company, made powerful diesel engines for the
container ships built for American President Lines. The power of each
12-cylinder engine is about 42 MW. Suppose the turbines use the forma-
tion of 14
7N for the energy-releasing process. What mass of nitrogen
would have to be formed to provide enough energy for 24 h of continu-
ous work? Assume the turbines are 100 percent efficient.
7. A hundred years ago, the most powerful hydroelectric plant in the world
produced 3.84 × 107
W of electric power. Find the total mass of 12
6C
atoms that must be formed each second from H atoms and neutrons to
produce the same power output.
For every nucleus of 16
8O formed, the mass defect is 0.137 005 u, and the mass of
the nucleus formed is 15.994 915 u. When ∆m has a total value of 2.0 × 10−10
kg,
8.8 × 1017
nuclei, or 2.3 × 10−8
kg of 16
8O will have formed.
4. EVALUATE

Problem B 183
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. Subatomic Physics
Problem B
NUCLEAR DECAY
P R O B L E M
The most stable radioactive nuclide known is tellurium-128. It was
discovered in 1924, and its radioactivity was proven in 1968. This isotope
undergoes two-step beta decay.Write the equations that correspond to
this reaction.
S O L U T I O N
Given: 128
52Te → −1
0
e + X + v

X → −1
0
e + Z + v

Unknown: the daughter elements X and Z
The mass numbers and atomic numbers on both sides of the expression must be
the same so that both charge and mass are conserved during the course of this
particular decay reaction.
Mass number of X = 128 − 0 = 128
Atomic number of X = 52 − (−1) = 53
The periodic table shows that the nucleus with an atomic number of 53 is iodine, I.
Thus, the first step of the process is as follows:
128
52Te → −1
0
e + 128
53I + v

A similar approach for the second beta decay reaction gives the following equa-
tion. Again, the emission of an electron does not change the mass number of the
nucleus. It does, however, change the atomic number by 1.
Mass number of Z = 128 − 0 = 128
Atomic number of Z = 53 − (−1) = 54
The periodic table shows that the nucleus with an atomic number of 54 is xenon,
Xe. Thus the next step of the process is as follows:
128
53I → −1
0
e + 128
54Xe + v

The complete two-step reaction is described by the two balanced equations below.
128
52Te → −1
0
e + 128
53I + v

128
53I → −1
0
e + 128
54Xe + v

ADDITIONAL PRACTICE
1. Standard nuclear fission reactors use 235
92U for fuel. However, the supply
of this uranium isotope is limited. Its concentration in natural uranium-
238 is low, and the cost of enrichment is high. A good alternative is the
breeder reactor in which the following reaction sequence occurs: 238
92U
captures a neutron, and the resulting isotope emits a −1
0
e particle to form

239
93Np. This nuclide emits a second −1
0
e particle to form 239
94Pu, which is
fissionable and can be used as an energy-producing material. Write bal-
anced equations for each of the reactions described.
2. Radon has the highest density of any gas. Under normal conditions
radon’s density is about 10 kg/m3
. One of radon’s isotopes undergoes
two alpha decays and then one beta decay (b−
) to form 212
83Bi. Write the
equations that correspond to these reaction steps.
3. Every element in the periodic table has isotopes, and cesium has the
most: as of 1995, 37 isotopes of cesium had been identified. One of ce-
sium’s most stable isotopes undergoes beta decay (b−
) to form 135
56Ba.
Write the equation describing this beta-decay reaction.
4. Fission is the process by which a heavy nucleus decomposes into two
lighter nuclei and releases energy. Uranium-235 undergoes fission when
it captures a neutron. Several neutrons are produced in addition to the
two light daughter nuclei. Complete the following equations, which de-
scribe two types of uranium-235 fission reactions.
235
92U + 1
0n → 144
56Ba + 89
36Kr + ____
235
92U + 1
0n → 140
54Xe + ____ + 21
0n
5. The maximum safe amount of radioactive thorium-228 in the air is
2.4 × 10–19
kg/m3
, which is equivalent to about half a kilogram distrib-
uted over the entire atmosphere. One reason for this substance’s high
toxicity is that it undergoes alpha decay in which gamma rays are pro-
duced as well. Write the equation corresponding to this reaction.
6. The 1930s were notable years for nuclear physics. In 1931, Robert Van de
Graaff built an electrostatic generator that was capable of creating the
high potential differences needed to accelerate charged particles. In 1932,
Ernest O. Lawrence and M. Stanley Livingston built the first cyclotron. In
the same year, Ernest Cockcroft and John Walton observed one of the
first artificial nuclear reactions. Complete the following equation for the
nuclear reaction observed by Cockcroft and Walton.
1
1
p + 7
3Li → ____ + 4
2He
7. Among the naturally occurring elements, astatine is the least abundant,
with less than 0.2 g present in Earth’s entire crust. The isotope 217
85At
accounts for only about 5 × 10−9
g of all astatine. However, this highly
radioactive isotope contributes nothing to the natural abundance of
astatine because when it is created, it immediately undergoes alpha
decay. Write the equation for this decay reaction.
184
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem C 185
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
Subatomic Physics
Problem C
MEASURING NUCLEAR DECAY
P R O B L E M
Tellurium-128, the most stable of all radioactive nuclides, has a half-life
of about 1.5 × 1024
years. Determine the decay constant of 128
52Te. How
long would it take for 75 percent of a sample of this isotope to decay?
S O L U T I O N
Given: T1/2 = 1.5 × 1024
year
N = 1.00 − 0.75 = 0.25 = 25 percent remaining
Unknown: l = ? t = ?
Choose the equation (s) or situation: To calculate the decay constant, use the
equation for determining a half-life.
T1/2 = 
0.6
l
93

After 75 percent of the original sample decays, 25 percent, or one-fourth, of the
parent nuclei remain. The rest of the nuclei have decayed into daughter nuclei. By
definition, after the elapsed time of one half-life, half of the parent nuclei remain.
After two half-lives, one fourth (or half of one-half) of the parent nuclei remain.
The time for 75 percent of the original sample to decay is therefore two half-lives.
t = 2(T1/2)
l = 
0
T
.6
1
9
/2
3

l = 
(1.5 ×
0
1
.6
0
9
2
3
4
year)
 =
t = 2(1.5 × 1024
year) =
Because the half-life of tellurium-128 is on the order of 1024
years, the decay
constant is on the order of the reciprocal of the half-life, or 10−24
year. This
corresponds to one decay event per year for a mole (127.6 g) of pure
tellurium-128.
3.0 × 1024
year
4.6 × 10−24
year−1
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
1. In 1995, an Ethiopian athlete, Halie Gebrselassie, ran 10 km in 26 min,
43.53 s. Lead-214 has a half-life similar to Gebrselassie’s run time. Find
the decay constant for 214
82Pb. What percent of a sample of this isotope
would decay in a time interval equal to five times Gebrselassie’s run time?

2. Thorium-228, the most toxic of radioactive substances, has a half-life of
1.91 years. How long would it take for a sample of this isotope to de-
crease its toxicity by 93.75 percent?
3. In 1874, a huge cloud of locusts covered Nebraska, occupying an area of
almost 5.00 × 105
km2
. The number of insects in that cloud was esti-
mated as 1013
. Consider a sample of 144
56Ba, which has a half-life of 11.9 s,
containing 1.00 × 1013
atoms. Approximately how long would it take for
1.25 × 1012
atoms to remain?
4. The oldest living tree in the world is a bristlecone pine in California
named Methuselah. Its estimated age is 4800 years. Suppose a sample of
226
88Ra began to decay at the time the pine began to grow. What percent of
the sample would remain now? The half-life for 226
88Ra is 1600 years.
5. The oldest fish on record is an eel that lived to the age of 88 years in a
museum aquarium in Sweden. After that period of time, only about 
1
1
6
 of
a sample of 214
82Pb would be left. Find the decay constant for 210
82Pb.
6. In 1994, Peter Hogg sailed across the Pacific Ocean on his trimaran Aotea
in 34 days, 6 h, and 26 min. During that time period, only about 
5
1
12
 of a
sample of radon-222 would not decay. Estimate the decay constant of
222
86Rn in (days)−1
.
7. Lithium-5 is the least stable isotope known. Its mean lifetime is
4.4 × 10−22
s. Use the definition of a radionuclide’s mean lifetime as the
reciprocal of the decay constant (T = 1/l) to calculate the half-life of
lithium-5.
186
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem A 187
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. AdvancedTopics
Problem A
ANGULAR DISPLACEMENT
P R O B L E M
The diameter of the outermost planet,Pluto,is just 2.30 103
km.If a
space probe were to orbit Pluto near the planet’s surface,what would the
arc length of the probe’s displacement be after it had completed eight orbits?
S O L U T I O N
Given: r = 
2.30 ×
2
103
km
 = 1.15 × 103
km
∆q = 8 orbits = 8(2p rad) = 16p rad
Unknown: ∆s = ?
Use the angular displacement equation and rearrange to solve for ∆s.
∆q = 
∆
r
s

∆s = r ∆q = (1.15 × 103
km)(16p rad) = 5.78 × 104
km
ADDITIONAL PRACTICE
1. A neutron star can have a mass three times that of the sun and a radius
as small as 10.0 km. If a particle travels +15.0 rad along the equator of a
neutron star, through what arc length does the particle travel? Does the
particle travel in the clockwise or counterclockwise direction from the
viewpoint of the neutron star’s “north” pole?
2. John Glenn was the first American to orbit Earth. In 1962, he circled
Earth counterclockwise three times in less that 5 h aboard his spaceship
Friendship 7. If his distance from the Earth’s center was 6560 km, what
arc length did Glenn and his spaceship travel through?
3. Jupiter’s diameter is 1.40 × 105
km. Suppose a space vehicle travels
along Jupiter’s equator with an angular displacement of 1.72 rad.
a. Through what arc length does the space vehicle move?
b. How many orbits around Earth’s equator can be completed if the
vehicle travels at the surface of the Earth through this arc length
around Earth? Use 6.37 × 103
km for Earth’s radius.
4. In 1981, the space shuttle Columbia became the first reusable spacecraft
to orbit Earth. The shuttle’s total angular displacement as it orbited
Earth was 225 rad. How far from Earth’s center was Columbia if it
moved through an arc length of 1.50 × 106
km? Use 6.37 × 103
km for
Earth’s radius.
5. Mercury, the planet closest to the sun, has an orbital radius of 5.8 × 107
km. Find the angular displacement of Mercury as it travels through an arc
length equal to the radius of Earth’s orbit around the sun (1.5 × 108
km).

188
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. From 1987 through 1988, Sarah Covington-Fulcher ran around the
United States, covering a distance of 1.79 × 104
km. If she had run that
distance clockwise around Earth’s equator, what would her angular dis-
placement have been? (Earth’s average radius is 6.37 × 103
km).

Problem B 189
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem B
ANGULAR VELOCITY
P R O B L E M
In 1975, an ultrafast centrifuge attained an average angular speed of 2.65
104
rad/s.What was the centrifuge’s angular displacement after 1.5 s?
S O L U T I O N
Given: wavg = 2.65 × 104
rad/s
∆t = 1.5 s
Unknown: ∆q = ?
Use the angular speed equation and rearrange to solve for ∆q.
wavg = 
∆
∆
q
t

∆q = wavg ∆t = (2.65 × 104
rad/s)(1.5 s)
∆q = 4.0 × 104
rad
ADDITIONAL PRACTICE
1. The largest steam engine ever built was constructed in 1849. The en-
gine had one huge cylinder with a radius of 1.82 m. If a beetle were to
run around the edge of the cylinder with an average angular speed of
1.00 × 10–1
rad/s, what would its angular displacement be after 60.0 s?
What arc length would it have moved through?
2. The world’s largest planetarium dome is 30 m in diameter. What would
your angular displacement be if you ran around the perimeter of this
dome for 120 s with an average angular speed of 0.40 rad/s?
3. The world’s most massive magnet is located in a research center in
Dubna, Russia. This magnet has a mass of over 3.0 × 107
kg and a ra-
dius of 30.0 m. If you were to run around this magnet so that you trav-
eled 5.0 × 102
m in 120 s, what would your average angular speed be?
4. A floral clock in Japan has a radius of 15.5 m. If you ride a bike around
the clock, making 16 revolutions in 4.5 min, what is your average angu-
lar speed?
5. A revolving globe with a radius of 5.0 m was built between 1982 and
1987 in Italy. If the globe revolves with the same average angular speed
as Earth, how long will it take for a point on the globe’s equator to
move through 0.262 rad?
6. A water-supply tunnel in New York City is 1.70 × 102
km long and has
a radius of 2.00 m. If a beetle moves around the tunnel’s perimeter with
an average angular speed of 5.90 rad/s, how long will it take the beetle
to travel a distance equal to the tunnel’s length?

AdvancedTopics
Problem C
ANGULAR ACCELERATION
P R O B L E M
A self-propelled Catherine wheel (a spinning wheel with fireworks along
its rim) with a diameter of 20.0 m was built in 1994. Its maximum angu-
lar speed was 0.52 rad/s. How long did the wheel undergo an angular ac-
celeration of 2.6 10–2
rad/s2
in order to reach its maximum angular
speed?
S O L U T I O N
Given: w1 = 0 rad/s
w2 = 0.52 rad/s
aavg = 2.6 × 10−2
rad/s2
Unknown: ∆t = ?
Use the angular acceleration equation and rearrange to solve for ∆t.
aavg = 
∆
∆
w
t

∆t = 
a
∆
a
w
vg
 = 
w2
a
−
av
w
g
1
 = = 2.0 × 101
s
0.52 rad/s − 0 rad/s

2.6 × 10−2
rad/s2
190
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. Peter Rosendahl of Sweden rode a unicycle with a wheel diameter of
2.5 cm. If the wheel’s average angular acceleration was 2.0 rad/s2
, how
long would it take for the wheel’s angular speed to increase from
0 rad/s to 9.4 rad/s?
2. Jupiter has the shortest day of all of the solar system’s planets. One ro-
tation of Jupiter occurs in 9.83 h. If an average angular acceleration of
–3.0 × 10–8
rad/s2
slows Jupiter’s rotation, how long does it take for
Jupiter to stop rotating?
3. In 1989, Dave Moore of California built the Frankencycle, a bicycle
with a wheel diameter of more than 3 m. If you ride this bike so that
the wheels’ angular speed increases from 2.00 rad/s to 3.15 rad/s in
3.6 s, what is the average angular acceleration of the wheels?
4. In 1990, David Robilliard rode a bicycle on the back wheel for more
than 5 h. If the wheel’s initial angular speed was 8.0 rad/s and Robilliard
tripled this speed in 25 s, what was the average angular acceleration?
5. Earth takes about 365 days to orbit once around the sun. Mercury, the
innermost planet, takes less than a fourth of this time to complete one
revolution. Suppose some mysterious force causes Earth to experience
an average angular acceleration of 6.05 × 10–13
rad/s2
, so that after

Problem C 191
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 12.0 days its angular orbital speed is the same as that of Mercury. Cal-
culate this angular speed and the period of one orbit.
6. The smallest ridable tandem bicycle was built in France and has a
length of less than 40 cm. Suppose this bicycle accelerates from rest so
that the average angular acceleration of the wheels is 0.800 rad/s2
. What
is the angular speed of the wheels after 8.40 s?

AdvancedTopics
Problem D
ANGULAR KINEMATICS
P R O B L E M
In 1990, a pizza with a radius of 18.7 m was baked in South Africa. Sup-
pose this pizza was placed on a rotating platform. If the pizza accelerated
from rest at 5.00 rad/s2
for 25.0 s, what was the pizza’s final angular speed?
S O L U T I O N
Given: wi = 0 rad/s
a = 5.00 rad/s2
∆t = 25.0 s
Unknown: wf = ?
Use the rotational kinematic equation relating final angular speed to initial angu-
lar speed, angular acceleration, and time.
wf = wi + a∆t
wf = 0 rad/s + (5.00 rad/s2
)(25.0 s)
wf = 125 rad/s
192
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. In 1987, Takayuki Koike of Japan rode a unicycle nonstop for 160 km in
less than 7 h. Suppose at some point in his trip Koike accelerated
downhill. If the wheel’s angular speed was initially 5.0 rad/s, what
would the angular speed be after the wheel underwent an angular ac-
celeration of 0.60 rad/s2
for 0.50 min?
2. The moon orbits Earth in 27.3 days. Suppose a spacecraft leaves the
moon and follows the same orbit as the moon. If the spacecraft has a
constant angular acceleration of 1.0 × 10–10
rad/s2
, what is its angular
speed after 12 h of flight? (Hint: At takeoff, the spaceship has the same
angular speed as the moon.)
3. African baobab trees can have circumferences of up to 43 m. Imagine
riding a bicycle around a tree this size. If, starting from rest, you
travel a distance of 160 m around the tree with a constant angular ac-
celeration of 5.0 × 10–2
rad/s2
, what will your final angular speed be?
4. In 1976, Kathy Wafler produced an unbroken apple peel 52.5 m in
length. Suppose Wafler turned the apple with a constant angular
acceleration of –3.2 × 10–5
rad/s2
, until her final angular speed was
0.080 rad/s. Assuming the apple was a sphere with a radius of 8.0 cm,
calculate the apple’s initial angular speed.

Problem D 193
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 5. In 1987, a giant hanging basket of flowers with a mass of 4000 kg was
constructed. The radius of the basket was 3.0 m. Suppose this basket
was placed on the ground and an admiring spectator ran around it to
see every detail again and again. At first the spectator’s angular speed
was 0.820 rad/s, but he steadily decreased his speed to 0.360 rad/s by
the time he had traveled 20.0 m around the basket. Find the spectator’s
angular acceleration.
6. One of the largest scientific devices in the world is the particle accelera-
tor at Fermilab, in Batavia, Illinois. The accelerator consists of a giant
ring with a radius of 1.0 km. Suppose a maintenance engineer drives
around the accelerator, starting at an angular speed of 5.0 × 10–3
rad/s
and accelerating at a constant rate until one trip is completed in
14.0 min. Find the engineer’s angular acceleration.
7. With a diameter of 207.0 m, the Superdome in New Orleans, Louisiana,
is the largest “dome” in the world. Imagine a race held along the Super-
dome’s outside perimeter. An athlete whose initial angular speed is
7.20 × 10–2
rad/s runs 12.6 rad in 4 min 22 s. What is the athlete’s con-
stant angular acceleration?
8. In 1986, Fred Markham rode a bicycle that was pulled by an automo-
bile 200 m in 6.83 s. Suppose the angular speed of the bicycle’s wheels
increased steadily from 27.0 rad/s to 32.0 rad/s. Find the wheels’ angu-
lar acceleration.
9. Consider a common analog clock. At midnight, the hour and minute
hands coincide. Then the minute hand begins to rotate away from the
hour hand. Suppose you adjust the clock by pushing the hour hand
clockwise with a constant acceleration of 2.68 × 10–5
rad/s2
. What is the
angular displacement of the hour hand after 120.0 s? (Note that the un-
accelerated hour hand makes one full rotation in 12 h.)
10. Herman Bax of Canada grew a pumpkin with a circumference of 7 m.
Suppose an ant crawled around the pumpkin’s “equator.” The ant
started with an angular speed of 6.0 × 10–3
rad/s and accelerated
steadily at a rate of 2.5 × 10–4
rad/s2
until its angular speed was tripled.
What was the ant’s angular displacement?
11. Tal Burt of Israel rode a bicycle around the world in 77 days. If Burt
could have ridden along the equator, his average angular speed would
have been 9.0 × 10–7
rad/s. Now consider an object moving with this an-
gular speed. How long would it take the object to reach an angular speed
of 5.0 × 10–6
rad/s if its angular acceleration was 7.5 × 10–10
rad/s2
?
12. A coal-burning power plant in Kazakhstan has a chimney that is nearly
500 m tall. The radius of this chimney is 7.1 m at the base. Suppose a
factory worker takes a 500.0 m run around the base of the chimney. If
the worker starts with an angular speed of 0.40 rad/s and has an angu-
lar acceleration of 4.0 × 10–3
rad/s2
, how long will the run take?

AdvancedTopics
Problem E
TANGENTIAL SPEED
P R O B L E M
In about 45 min, Nicholas Mason inflated a weather balloon using only
lung power. If a fly, moving with a tangential speed of 5.11 m/s, were to
make exactly 8 revolutions around this inflated balloon in 12.0 s, what
would the balloon’s radius be?
S O L U T I O N
Given: vt = 5.11 m/s
∆q = 8 rev
∆t = 12.0 s
Unknown: w = ? r = ?
Use ∆q and ∆t to calculate the fly’s angular speed. Then rearrange the tangential
speed equation to determine the balloon’s radius.
w = 
∆
∆
q
t
 = = 4.19 rad/s
vt = rw
r = 
w
vt
 = 
4
5
.1
.1
9
1
r
m
ad
/
/
s
s
 = 1.22 m
(8 rev)
2p 
r
r
a
e
d
v



12.0 s
194
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
ADDITIONAL PRACTICE
1. The world’s tallest columns, which stand in front of the Education
Building in Albany, New York, are each 30 m tall. If a fly circles a col-
umn with an angular speed of 4.44 rad/s, and its tangential speed is
4.44 m/s, what is the radius of the column?
2. The longest dingoproof wire fence stretches across southeastern Aus-
tralia. Suppose this fence were to have a circular shape. A rancher driv-
ing around the perimeter of the fence with a tangential speed of
16.0 m/s has an angular speed of 1.82 × 10–5
rad/s. What is the fence’s
radius and length (circumference)?
3. The smallest self-sustaining gas turbine has a tiny wheel that can rotate
at 5.24 × 103
rad/s. If the wheel rim’s tangential speed is 131 m/s, what
is the wheel’s radius?
4. Earth’s average tangential speed around the sun is about 29.7 km/s. If
Earth’s average orbital radius is 1.50 × 108
km, what is its angular or-
bital speed in rad/s?

Problem E 195
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 5. Two English engineers designed a ridable motorcycle that was less than
12 cm long. The front wheel’s diameter was only 19.0 mm. Suppose this
motorcycle was ridden so that the front wheel had an angular speed of
25.6 rad/s. What would the tangential speed of the front wheel’s rim
have been?

AdvancedTopics
Problem F
TANGENTIAL ACCELERATION
P R O B L E M
In 1988, Stu Cohen made his kite perform 2911 figure eights in just 1 h. If
the kite made a circular“loop”with a radius of 1.5 m and had a tangential
, what was the kite’s angular acceleration?
S O L U T I O N
Given: r = 1.5 m at = 0.6 m/s2
Unknown: a = ?
Apply the tangential acceleration equation, solving for angular acceleration.
at = ra
a = 
a
r
t
 = 
0.
1
6
.5
m
m
/s2
 = 0.4 rad/s2
196
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. The world’s largest aquarium, at the EPCOT center in Orlando, Florida,
has a radius of 32 m. Bicycling around this aquarium with a tangential
, what would your angular acceleration be?
2. Dale Lyons and David Pettifer ran the London marathon in less than
4 h while bound together at one ankle and one wrist. Suppose they
made a turn with a radius of 8.0 m. If their tangential acceleration was
−1.44 m/s2
, what was their angular acceleration?
3. In 1991, Timothy Badyna of the United States ran 10 km backward in
just over 45 min. Suppose Badyna made a turn, so that his angular
speed decreased 2.4 × 10–2
rad/s in 6.0 s. If his tangential acceleration
was –0.16 m/s2
, what was the radius of the turn?
4. Park Bong-tae of South Korea made 14 628 turns of a jump rope in
1.000 h. Suppose the rope’s average angular speed was gained from rest
during the first turn and that the rope during this time had a tangential
. What was the radius of the rope’s circular path?
5. To “crack” a whip requires making its tip move at a supersonic speed.
Kris King of Ohio achieved this with a whip 56.24 m long. If the tip of
this whip moved in a circle and its angular speed increased from
6.00 rad/s to 6.30 rad/s in 0.60 s, what would the magnitude of the tip’s
tangential acceleration be?
6. In 1986 in Japan, a giant top with a radius of 1.3 m was spun. The top
remained spinning for over an hour. Suppose these people accelerated
the top from rest so that the first turn was completed in 1.8 s. What was
the tangential acceleration of points on the top’s rim?
ADDITIONAL PRACTICE

Problem G 197
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem G
ROTATIONAL EQUILIBRIUM
P R O B L E M
In 1960, a polar bear with a mass of 9.00 × 102
kg was discovered in
Alaska. Suppose this bear crosses a 12.0 m long horizontal bridge that
spans a gully. The bridge consists of a wide board that has a uniform
mass of 2.50 × 102
kg and whose ends are loosely set on either side of the
gully.When the bear is two-thirds of the way across the bridge, what is
the normal force acting on the board at the end farthest from the bear?
S O L U T I O N
Given: mb = mass of bridge = 2.50 × 102
kg
mp = mass of polar bear = 9.00 × 102
kg
l = length of bridge = 12.0 m
g = 9.81 m/s2
Unknown: Fn,1 = ?
Diagram:
Choose the equation(s) or situation:
Apply the first condition of equilibrium: The unknowns in this problem are the
normal forces exerted upward by the ground on either end of the board. The known
quantities are the weights of the bridge and the polar bear. All of the forces are in the
vertical (y) direction.
Fy = Fn,1 + Fn,2 − mbg − mpg = 0
Because there are two unknowns and only one equation, the solution cannot be
obtained from the first condition of equilibrium alone.
Choose a point for calculating net torque: Choose the end of the bridge farthest
from the bear as the pivot point. The torque produced by Fn,1 will be zero.
Apply the second condition of equilibrium: The torques produced by the bridge’s
and polar bear’s weights are clockwise and therefore negative. The normal force on
the end of the bridge opposite the axis of rotation exerts a counterclockwise (positive)
torque.
tnet = −(mbg)db − (mpg)dp + Fn,2d2 = 0
12.0 m
Fn,1 Fn,2
mp
mb
1. DEFINE
2. PLAN

The lever arm for the bridge’s weight (db) is the distance from the bridge’s
center of mass to the pivot point, or half the bridge’s length. The lever arm for the
polar bear is two-thirds the bridge’s length. The lever arm for the normal force
farthest from the pivot equals the entire length of the bridge.
db = 
1
2
l , dp = 
2
3
l , d2 = l
The torque equation thus takes the following form:
tnet = − − + Fn,2l = 0
Rearrange the equation(s) to isolate the unknowns:
Fn,2 = + =

m
2
b
 + 
2
3
mp

g
Fn,1 = mb g + mp g − Fn,2
Fn,2 =

2.50 ×
2
102
kg
 + 
(2)(9.00
3
× 102
kg)

(9.81 m/s2
)
Fn,2 = (125 kg + 6.00 × 102
kg)(9.81 m/s2
)
Fn,2 = (725 kg)(9.81 m/s2
)
Fn,2 = 7.11 × 103
N
Fn,1 = (2.50 × 102
kg)(9.81 m/s2
) + (9.00 × 102
kg)(9.81 m/s2
)
− 7.11 × 103
N
Fn,1 = 2.45 × 103
N + 8.83 × 103
N − 7.11 × 103
N
Fn,1 =
The sum of the upward normal forces exerted on the ends of the bridge must
equal the weight of the polar bear and the bridge. (The individual normal forces
change as the polar bear moves across the bridge.)
(4.17 kN + 7.11 kN) = (2.50 × 102
kg + 9.00 × 102
kg)(9.81 m/s2
)
11.28 kN = 11.28 × 103
N
4.17 × 103
N
2mp gl

3l
mb gl

2l
2mp gl

3
mb gl

2
ADDITIONAL PRACTICE
3. CALCULATE
4. EVALULATE
1. The heaviest sea sponge ever collected had a mass of 40.0 kg, but after
drying out, its mass decreased to 5.4 kg. Suppose two loads equal to the
wet and dry masses of this giant sponge hang from the opposite ends of a
horizontal meterstick of negligible mass and that a fulcrum is placed
70.0 cm from the larger of the two masses. How much extra force must
be applied to the end of the meterstick with the smaller mass in order to
provide equilibrium?
2. A Saguaro cactus with a height of 24 m and an estimated age of 150 years
was discovered in 1978 in Arizona. Unfortunately, a storm toppled it in
1986. Suppose the storm produced a torque of 2.00 × 105
N•m that
acted on the cactus. If the cactus could withstand a torque of only
198
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem G 199
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 1.2 × 105
N•m, what minimum force could have been applied to the cac-
tus keep it standing? At what point and in what direction should this
force have been applied? Assume that the cactus itself was very strong
and that the roots were just pulled out of the ground.
3. In 1994, John Evans set a record for brick balancing by holding a load of
bricks with a mass of 134 kg on his head for 10 s. Another, less extreme,
method of balancing this load would be to use a lever. Suppose a board
with a length of 7.00 m is placed on a fulcrum and the bricks are set on
one end of the board at a distance of 2.00 m from the fulcrum. If a force
is applied at a right angle to the other end of the board and the force has
a direction that is 60.0° below the horizontal and away from the bricks,
how great must this force be to keep the load in equilibrium? Assume the
board has negligible mass.
4. In 1994, a vanilla ice lollipop with a mass of 8.8 × 103
kg was made in
Poland. Suppose this ice lollipop was placed on the end of a lever 15 m in
length. A fulcrum was placed 3.0 m from the lollipop so that the lever
made an angle of 20.0° with the ground. If the force was applied perpen-
dicular to the lever, what was the smallest magnitude this force could
have and still lift the lollipop? Neglect the mass of the lever.
5. The Galápagos fur seals are very small. An average adult male has a mass
of 64 kg, and a female has a mass of only 27 kg. Suppose one average
adult male seal and one average adult female seal sit on opposite ends of
a light board that has a length of 3.0 m. How far from the male seal
should the board be pivoted in order for equilibrium to be maintained?
6. Goliath, a giant Galápagos tortoise living in Florida, has a mass of 3.6 ×
102
kg. Suppose Goliath walks along a heavy board above a swimming
pool. The board has a mass of 6.0 × 102
kg and a length of 15 m, and it is
placed horizontally on the edge of the pool so that only 5.0 m of it ex-
tends over the water. How far out along this 5.0 m extension of the board
can Goliath walk before he falls into the pool?
7. The largest pumpkin ever grown had a mass of 449 kg. Suppose this
pumpkin was placed on a platform that was supported by two bases
5.0 m apart. If the left base exerted a normal force of 2.70 × 103
N on the
platform, how far must the pumpkin have been from the platform’s left
edge? The platform had negligible mass.
8. In 1991, a giant stick of Brighton rock (a type of rock candy) was made
in England. The candy had a mass of 414 kg and a length of 5.00 m.
Imagine that the candy was balanced horizontally on a fulcrum. A child
with a mass of 40.0 kg sat on one end of the stick. How far must the ful-
crum have been from the child in order to maintain equilibrium?

AdvancedTopics
Problem H
NEWTON’S SECOND LAW FOR ROTATION
P R O B L E M
The giant sequoia General Sherman in California has a mass of about 2.00
106
kg,making it the most massive tree in the world.Its height of 83.0 m
is also impressive.Imagine a uniform bar with the same mass and length as
the tree.If this bar is rotated about an axis that is perpendicular to and
passes through the bar’s midpoint,how large an angular acceleration would
result from a torque of 4.60 107
N•m? (Note:Assume the bar is thin.)
S O L U T I O N
Given: M = 2.00 × 106
kg
l = 83.0 m
t = 4.60 × 107
N•m
Unknown: a × ?
Calculate the bar’s moment of inertia using the formula for a thin rod with the
axis of rotation at its center.
I = 
1
1
2
 M l 2
= 
1
1
2
 (2.00 × 106
kg)(83.0 m)2
= 1.15 × 109
kg•m2
Now use the equation for Newton’s second law for rotating objects. Rearrange the
equation to solve for angular acceleration.
t = Ia
a = 
t
I
 = 
(
(
1
4
.1
.6
5
0
×
×
1
1
0
0
9
7
k
N
g•
•
m
m
2
)
)
 = 4.00 × 10−2
rad/s2
ADDITIONAL PRACTICE
1. One of the largest Ferris wheels currently in existence is in Yokohama,
Japan. The wheel has a radius of 50.0 m and a mass of 1.20 × 106
kg. If
a torque of 1.0 × 109
N•m is needed to turn the wheel from a state of
rest, what would the wheel’s angular acceleration be? Treat the wheel as
a thin hoop.
2. In 1992, Jacky Vranken from Belgium attained a speed of more than
250 km/h on just the back wheel of a motorcycle. Assume that all of the
back wheel’s mass is located at its outer edge. If the wheel has a mass of
22 kg and a radius of 0.36 m, what is the wheel’s angular acceleration
when a torque of 5.7 N•m acts on the wheel?
3. In 1995, a fully functional pencil with a mass of 24 kg and a length of
2.74 m was made. Suppose this pencil is suspended at its midpoint and
a force of 1.8 N is applied perpendicular to its end, causing it to rotate.
What is the angular acceleration of the pencil?
200
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem H 201
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 4. The turbines at the Grand Coulee Third Power Plant in the state of
Washington have rotors with a mass of 4.07 × 105
kg and a radius of
5.0 m each. What angular acceleration would one of these rotors have if
a torque of 5.0 × 104
N•m were applied? Assume the rotor is a uniform
disk.
5. J. C. Payne of Texas amassed a ball of string that had a radius of 2.00 m.
Suppose a force of 208 N was applied tangentially to the ball’s surface
in order to give the ball an angular acceleration of 3.20 × 10–2
rad/s2
.
What was the ball’s moment of inertia?
6. The heaviest member of British Parliament ever was Sir Cyril Smith.
Calculate his peak mass by finding first his moment of inertia from the
following situation. If Sir Cyril were to have ridden on a merry-go-
round with a radius of 8.0 m, a torque of 7.3 × 103
N•m would have
been needed to provide him with an angular acceleration of 0.60 rad/s2
.
7. In 1975, a centrifuge at a research center in England made a carbon-
fiber rod spin about its center so fast that the tangential speed of the
rod’s tips was about 2.0 km/s. The length of the rod was 15.0 cm. If it
took 80.0 s for a torque of 0.20 N•m to bring the rod to rest from its
maximum speed, what was the rod’s moment of inertia?
8. The largest tricycle ever built had rear wheels that were almost 1.70 m
in diameter. Neglecting the mass of the spokes, the moment of inertia
of one of these wheels is equal to that of a thin hoop rotated about its
symmetry axis. Find the wheel’s moment of inertia and its mass if a
torque of 125 N•m is applied to the wheel so that in 2.0 s the wheel’s
angular speed increases from 0 rad/s to 12 rad/s.
9. In 1990, a cherry pie with a radius of 3.00 m and a mass of 17 × 103
kg
was baked in Canada. Suppose the pie was placed on a light rotating
platform attached to a motor. If this motor brought the angular speed
of the pie from 0 rad/s to 3.46 rad/s in 12 s, what was the torque the
motor must have produced? Assume the mass of the platform was neg-
ligible and the pie was a uniformly solid disk.
10. In just over a month in 1962, a shaft almost 4.00 × 108
m deep and with
a radius of 4.0 m was drilled in South Africa. The mass of the soil taken
out was about 1.0 × 108
kg. Imagine a rigid cylinder with a mass, ra-
dius, and length equal to these values. If this cylinder rotates about its
symmetry axis so that it undergoes a constant angular acceleration
from 0 rad/s to 0.080 rad/s in 60.0 s, how large a torque must act on the
cylinder?
11. In 1993, a bowl in Canada was filled with strawberries. The mass of the
bowl and strawberries combined was 2390 kg, and the moment of iner-
tia about the symmetry axis was estimated to be 2.40 × 103
kg•m2
. Sup-
pose a constant angular acceleration was applied to the bowl so that it
made its first two complete rotations in 6.00 s. How large was the
torque that acted on the bowl?

12. A steel ax with a mass of 7.0 × 103
kg and a length of 18.3 m was made
in Canada. If Paul Bunyan were to take a swing with such an ax, what
torque would he have to produce in order for the blade to have a tan-
gential acceleration of 25 m/s2
? Assume that the blade follows a circle
with a radius equal to the ax handle’s length and that nearly all of the
mass is concentrated in the blade.
202
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem I 203
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem I
CONSERVATION OF ANGULAR MOMENTUM
P R O B L E M
The average distance from Earth to the moon is 3.84 105
km. The aver-
age orbital speed of the moon when it is at its average distance from
Earth is 3.68 103
km/h. However, in 1912 the average orbital speed was
3.97 103
km/h, and in 1984 it was 3.47 103
km/h. Calculate the dis-
tances that correspond to the 1912 and 1984 orbital speeds, respectively.
S O L U T I O N
Given: ravg = 3.84 × 105
km
vavg = 3.68 × 103
km/h
v1 = 3.97 × 103
km/h
v2 = 3.47 × 103
km/h
Unknown: r1 = ? r2 = ?
Choose the equation(s) or situation: Because there are no external torques, the
angular momentum of the Earth-moon system is conserved.
Lavg = L1 = L2
Iavg wavg = I1 w1 = I2 w2
If the moon is treated as a point mass revolving around a central axis, its moment
of inertia is simply mr2
, and the conservation of momentum expression takes the
following form:
mmoon (vavg)2

v
ra
a
v
v
g
g

= mmoon (r1)2

v
r1
1

= mmoon (r2)2

v
r2
2


Because the mass of the moon is unchanged, the mass term cancels, and the
equation reduces to the following:
ravg vavg = r1 v1 = r2 v2
r1 = 
ravg
v1
vavg
 r2 = 
ravg
v2
vavg

r1 = =
r2 = =
Because angular momentum is conserved in the absence of external torques, the
tangential orbital speed of the moon is greater than its average value when the
moon is closer to Earth. Similarly, the smaller tangential orbital speed occurs
when the moon is farther from Earth.
4.07 × 105
km
(3.84 × 105
km)(3.68 × 103
km/h)

(3.47 × 103
km/h)
3.56 × 105
km
(3.84 × 105
km)(3.68 × 103
km/h)

(3.97 × 103
km/h)
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

1. Encke’s comet revolves around the sun in a period of just over three years
(the shortest period of any comet). The closest it approaches the sun is
4.95 × 107
km, at which time its orbital speed is 2.54 × 105
km/h. At what
distance from the sun would Encke’s comet have a speed equal to 1.81 ×
105
km/h?
2. In 1981, Sammy Miller reached a speed of 399 km/h on a rocket-
powered ice sled. Suppose the sled, moving at its maximum speed, was
hooked to a post with a radius of 0.20 m by a light cord with an un-
known initial length. The rocket engine was then turned off, and the sled
began to circle the post with negligible resistance as the cord wrapped
around the post. If the speed of the sled after 20 turns was 456 km/h,
what was the length of the unwound cord?
3. Earth is not a perfect sphere, in part because of its rotation about its axis.
A point on the equator is in fact over 21 km farther from Earth’s center
than is the North pole. Suppose you model Earth as a solid clay sphere
with a mass of 25.0 kg and a radius of 15.0 cm. If you begin rotating the
sphere with a constant angular speed of 4.70 × 10–3
rad/s (about the same
as Earth’s), and the sphere continues to rotate without the application of
any external torques, what will the change in the sphere’s moment of in-
ertia be when the final angular speed equals 4.74 × 10–3
rad/s?
4. In 1971, a model plane built in the Soviet Union by Leonid Lipinsky
reached a speed of 395 km/h. The plane was held in a circular path by a
control line. Suppose the plane ran out of gas while moving at its maxi-
mum speed and Lipinsky pulled the line in to bring the plane home
while it continued in a circular path. If the line’s initial length is 1.20 ×
102
m and Lipinsky shortened the line by 0.80 m every second, what was
the plane’s speed after 32 s?
5. The longest spacewalk by a team of astronauts lasted more than 8 h. It
was performed in 1992 by three crew members from the space shuttle
Endeavour. Suppose that during the walk two astronauts with equal
masses held the opposite ends of a rope that was 10.0 m long. From the
point of view of the third astronaut, the other two astronauts rotated
about the midpoint of the rope with an angular speed of 1.26 rad/s. If
the astronauts shortened the rope equally from both ends, what was their
angular speed when the rope was 4.00 m long?
6. In a problem in the previous section, a cherry pie with a radius of 3.00 m
and a mass of 17 × 103
kg was rotated on a light platform. Suppose that
when the pie reached an angular speed of 3.46 rad/s there was no net
torque acting on it. Over time, the filling in the pie began to move out-
ward, changing the pie’s moment of inertia. Assume the pie acted like a
uniform, rigid, spinning disk with a mass of 16.80 × 103
kg combined
with a 0.20 × 103
kg particle. If the smaller mass shifted from a position
2.50 m from the center to one that was 3.00 m from the center, what was
the change in the angular speed of the pie?
ADDITIONAL PRACTICE
204
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem J 205
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem J
CONSERVATION OF MECHANICAL ENERGY
P R O B L E M
In 1990, Eddy McDonald of Canada completed 8437 loops with a yo-yo in
an hour, setting a world record.Assume that the yo-yo McDonald used
had a mass of 6.00 10–2
kg.The yo-yo descended from a height of 0.600 m
down a vertical string and had a linear speed of 1.80 m/s by the time it
reached the bottom of the string. If its final angular speed was 82.6 rad/s,
what was the yo-yo’s moment of inertia?
S O L U T I O N
Given: m = 6.00 × 10−2
kg h = 0.600 m
vf = 1.80 m/s wf = 82.6 rad/s
g = 9.81 m/s2
Unknown: I = ?
Choose the equation(s) or situation: Apply the principle of conservation of
mechanical energy.
MEi = MEf
Initially, the system possesses only gravitational potential energy.
MEi = PEg = mgh
When the yo-yo reaches the bottom of the string, this potential energy has been
converted to translational and rotational kinetic energy.
MEf = KEtrans + KErot = 
1
2
mvf
2
+ 
1
2
Iwf
2
Equate the initial and final mechanical energy.
mgh = 
1
2
mvf
2
+ 
1
2
Iwf
2

1
2
Iwf
2
= mgh – 
1
2
mvf
2
I = 
2 mgh
w
−
f
2
mvf
2
 = 
m(2g
w
h
f
−
2
vf
2
)

I =
I = =
Assuming that the yo-yo can be approximated by a solid disk with a central axis of
rotation, the yo-yo’s moment of inertia is described by the equation I = 
1
2
MR2
.
From the calculated value for I, the yo-yo’s radius can be found to be 5.0 cm.
R = 
M
2
I

= = 0.050 m
(2)(7.6 × 10−5
kg•m2
)

6.00 × 10−2
kg
7.6 × 10−5
kg•m2
(6.00 × 10−2
kg)(8.6 m2
/s2
)

(82.6 rad/s)2
(6.00 × 10−2
kg)[(2) (9.81 m/s2
)(0.600 m) − (1.80 m/s)2
]

(82.6 rad/s)2
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE

1. In 1993, a group of students in England made a giant yo-yo that was 10 ft
in diameter and had a mass of 407 kg. With the use of a crane, the yo-yo
was launched from a height of 57.0 m above the ground. Suppose the lin-
ear speed of the yo-yo at the end of its descent was 12.4 m/s. If the angu-
lar speed at the end of the descent was 28.0 rad/s, what was the yo-yo’s
moment of inertia?
2. In 1994, a bottle over 3 m in height and with a radius at its base of 0.56 m
was made in Australia. Treat the bottle as a thin-walled cylinder rotating
about its symmetry axis, which has the same rotational properties as a
thin hoop rotating about its symmetry axis. What is the linear speed that
the bottle acquires after rolling down a slope with a height of 5.0 m? Do
you need to know the mass of the bottle?
3. In 1988, a cheese with a mass of 1.82 × 104
kg was made in Wisconsin.
Suppose the cheese had a cylindrical shape. The cheese was set to roll
along a horizontal road with an undetermined speed. The road then
went uphill, and the cheese rolled up the hill until its vertical displace-
ment was 1.2 m, at which point it came to a stop. Assuming that there
was no slipping between the rim of the cheese and the ground, calculate
the initial linear speed of the cheese.
4. In 1982, a team of ten people rolled a cylindrical barrel with a mass of
64 kg for almost 250 km without stopping. Imagine that at some point
during the trip the barrel was stopped at the crest of a steep hill. The bar-
rel was accidentally released and rolled down the hill. If the linear speed
of the barrel at the bottom of the slope was 12.0 m/s, how high was the
hill? Assume that the barrel’s moment of inertia was equal to 0.80 mr 2
.
5. A potato with a record-breaking mass of 3.5 kg was grown in 1994. Sup-
pose a child saw this potato and decided to pretend it was a soccer ball.
The child kicked the potato so that it rolled without slipping at a speed of
5.4 m/s. The potato rolled up a slope with a 30.0° incline. Assuming that
the potato could be approximated as a uniform, solid sphere with a ra-
dius of 7.0 cm, what was the distance along the slope that the potato
rolled before coming to a stop?
6. In 1992, an artificial egg with a mass of 4.8 × 103
kg was made in Aus-
tralia. Assume that the egg is a solid sphere with a radius of 2.0 m. Calcu-
late the minimum height of a slope that the egg rolls down if it is to
reach an angular speed of 5.0 rad/s at the bottom of the slope. What is
the translational kinetic energy of the egg at the bottom of the slope?
7. An onion grown in 1994 had a record-breaking mass of 5.55 kg. Assume
that this onion can be approximated by a uniform, solid sphere. Suppose
the onion rolled down an inclined ramp that had a height of 1.40 m.
What was the onion’s rotational kinetic energy? Assume that there was
no slippage between the ramp and the onion’s surface.
ADDITIONAL PRACTICE
206
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem K 207
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem K
BERNOULLI’S EQUATION
P R O B L E M
The widest road tunnel in the world is located in California. The tunnel
has a cross-sectional area of about 4.00 × 102
m2
. On the other hand, the
Three Rivers water tunnel in Georgia has a cross-sectional area of only
8.0 m2
. Imagine connecting together two tunnels with areas equal to
these along a flat region and setting fresh water to flow at 4.0 m/s in the
narrower tunnel. If the pressure in the wider tunnel is 1.10 × 105
Pa, what
is the pressure in the narrower tunnel?
S O L U T I O N
1. DEFINE
2. PLAN
Given: A1 = 8.0 m2
A2 = 4.00 × 102
m2
r = 1.00 × 103
kg/m3
v1 = 4.0 m/s
P2 = 1.10 × 105
Pa
Unknown: P1 = ?
Choose the equation(s) or situation: Because this problem involves fluid flow, it
requires the application of Bernoulli’s equation.
P1 + 
1
2
rv1
2
+ rgh1 = P2 + 
1
2
rv2
2
+ rgh2
The flow of water is horizontal, so h1 and h2 are equal.
P1 + 
1
2
rv1
2
= P2 + 
1
2
rv2
2
To find the speed of the flowing water in the wider tunnel, use the continuity
equation.
A1v1 = A2v2
Substitute this equation for v2 into Bernoulli’s equation.
P1 + 
1
2
rv1
2
= P2 + 
1
2
r

A
A
1
2
v1
2
P1 = P2 + 
1
2
rv1
2

A
A
1
2


2
−1

P1 = 1.10 × 105
Pa
+ 
1
2
(1.00 × 103
kg/m3
)(4.0 m/s)2

4.00
8.
×
0
1
m
02
2
m2


2
−1

P1 = 1.10 × 105
Pa + (8.0 × 103
N•m/m3
)(4.0 × 10−4
− 1)
P1 = 1.10 × 105
Pa − (8.0 × 103
Pa)(0.9996)
P1 = 1.10 × 105
Pa − 8.0 × 103
Pa
P1 = 1.02 × 105
Pa
3. CALCULATE

208
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. EVALUATE
ADDITIONAL PRACTICE
1. The Chicago system of sewer tunnels has a total length of about 200 km.
The tunnels are all at the same level and vary in diameter from less than
3 m to 10 m. Consider a connection between a wide tunnel and a narrow
tunnel. The pressure in the wide tunnel is 12 percent greater than the
pressure in the narrow one, and the speeds of flowing water in the wide
and the narrow tunnels are 0.60 m/s and 4.80 m/s, respectively. Based on
this information, find the pressure in the wide tunnel.
2. A certain New York City water-supply tunnel is almost 170 km long, is all
at the same level, and has a diameter of 4.10 m. Suppose water flows
through the tunnel at a speed of 3.0 m/s until it reaches a narrow section
where the tunnel’s diameter is 2.70 m. The pressure in the narrow section
is 82 kPa. Use the continuity equation to find the water’s speed in the
narrow section of the tunnel. Then find the pressure in the wide portion
of the tunnel.
3. An enormous open vat owned by a British cider company has a volume
of nearly 7000 m3
. If a small hole is drilled halfway down the side of this
vat when it is full of cider, the cider will hit the ground 19.7 m away from
the bottom of the vat. How tall is the vat?
4. The tallest cooling tower in the world is in Germany. Consider a water
pipe coming down from the top of the tower. The pipe is punctured near
the bottom, which causes the water to flow from the puncture hole with
a speed of 59 m/s. How high is the tower? Assume the pressure inside the
pipe is equal to the pressure outside the pipe.
5. A water tower built in Oklahoma has a capacity of 1893 m3
and is about
66.0 m high. Suppose a little hole with a cross-sectional area of 10.0 cm2
is drilled near the bottom of the tower’s water tank. At what speed does
the water initially flow through the hole? Assume that the air pressure in-
side and outside the tank is the same.
6. The Nurek Dam, in Tajikistan, is the tallest dam in the world—its height
is more than 300 m. Suppose the difference in water levels on the oppo-
site sides of the dam is 3.00 × 102
m. If a small crack appears in the dam
near the lower water level, at what speed will the water stream leave the
crack? Assume the air pressure on either side of the dam is the same.
7. The world’s largest litter bin has a volume of more than 40 m3
and is
6.0 m tall. If this bin is filled with water and then a hole with an area of
0.16 cm2
is drilled near the bottom, at what speed will the water leave the
bin? Assume that the water level in the bin drops slowly and that the bin
is open to the air.
The pressure of the water increases when it flows into the wider tunnel. The
speed of the water’s flow decreases, as indicated by the continuity equation.
v2 = (4.0 m/s)(8/400) = 8 × 10−2
m/s

Problem L 209
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem L
THE IDEAL GAS LAW
P R O B L E M
A hot-air balloon named Double Eagle V traveled a record distance of
more than 8000 km from Japan to California in 1981. The volume of the
balloon was 1.13 104
m3
. If the balloon contained 2.84 1029
gas parti-
cles that had an average temperature of 355 K, what was the absolute
pressure of the gas in the balloon?
S O L U T I O N
Given: V = 1.13 × 104
m3
N = 2.84 × 1029
particles
T = 355 K
kB = 1.38 × 10−23
J/K
Unknown: P = ?
Choose the equation(s) or situation: To find the pressure of the gas, use the
ideal gas law.
PV = NkBT
P = 
Nk
V
BT

P =
P =
The pressure inside the balloon is about 20 percent greater than standard air
pressure. This pressure corresponds to the higher temperature of the air in the
balloon. The hot air’s temperature is also nearly 20 percent greater than 300 K.
1.23 × 105
Pa
(2.84 × 1029
particles)(1.38 × 10−23
J/K)(355 K)

1.13 × 104
m3
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. The official altitude record for a balloon was set in 1961 by two Ameri-
can officers piloting a high-altitude helium balloon with a volume of 3.4
× 105
m3
. Assume that the temperature of the gas was 280 K. If the bal-
loon contained 1.4 × 1030
atoms of helium, find the absolute pressure in
the balloon at the maximum altitude of 35 km.
2. The estimated number of locusts that made up a swarm that infested
Nebraska in 1874 was 1.2 × 1013
. This number was about 7000 times the
total human population of Earth back then and about 2000 times the total
human population today. It is, however, only a few billionths of the number
of molecules in a liter of gas. If a container with a volume of 1.0 × 10−3
m3

210
NAME ______________________________________ DATE _______________ CLASS ____________________
is filled with 1.2 × 1013
gas molecules maintained at a temperature
of 300.0 K, what is the pressure of the gas in the container?
3. In terms of volume, the largest pyramid in the world is not in Egypt but
in Mexico. The Pyramid of the Sun at Teotihuacan has a volume of 3.3 ×
106
m3
. If you fill a balloon to this same volume with 1.5 × 1032
mole-
cules of nitrogen at a temperature of 360 K, what will the absolute pres-
sure of the gas be?
4. A snow palace more than 30 m high was built in Japan in 1994. Suppose
a container with the same volume as this snow palace is filled with 1.00 ×
1027
molecules. If the temperature of the gas is 2.70 × 102
K and the gas
pressure is 36.2 Pa, what is the volume of the gas?
5. Suppose the volume of a balloon decreases so that the temperature of the
balloon decreases from 280 K to 240 K and its pressure drops from 1.6 ×
104
Pa to 1.7 × 104
Pa. What is the new volume of the gas?
6. The longest navigable tunnel in the world was built in France. Suppose
the entire tunnel, which has a cross-sectional area of 2.50 × 102
m2
, is
filled with air at a temperature of 3.00 × 102
K and a pressure of 101 kPa.
If the tunnel contains 4.34 × 1031
molecules, what is the volume and
length of the tunnel?
7. A balloon is filled with 7.36 × 104
m3
of hot air. If the pressure inside the
balloon is 1.00 × 105
Pa and there are 1.63 × 1030
particles of air inside,
what is the average temperature of the air inside the balloon?
8. In 1993, a group of American researchers drilled a 3053 m shaft in the
ice sheet of Greenland. Suppose the cross-sectional area of the shaft is
0.040 m2
. If the air in the shaft consists of 3.6 × 1027
molecules at an
average pressure of 105 kPa, what is the air’s average temperature?
9. The cylinder of the largest steam engine had a radius of 1.82 m. Suppose
the length of the cylinder is six times the radius. Steam at a pressure of
2.50 × 106
Pa and a temperature of 495 K enters the cylinder when the
piston has reduced the volume in the cylinder to 3.00 m3
. The piston is
then pushed outward until the volume of the steam in the cylinder is
57.0 m3
. If the pressure of the steam after expansion is 1.01 × 105
Pa,
what is the temperature of the steam?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Problem M 211
NAME ______________________________________ DATE _______________ CLASS ____________________
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
Problem M
INDUCTION IN GENERATORS
P R O B L E M
InVirginia,a reversible turbine was built to serve as both a power genera-
tor and a pump.When operating as a generator,the turbine can deliver al-
most 5 × 108
W of power.The normal angular speed of the turbine rotor is
26.9 rad/s.Suppose the generator produces a maximum emf of 12 kV at
this angular speed.If the generator’s magnetic field strength is 0.12 T,how
many turns of wire,each with an area of 40.0 m2
,are used in the generator?
S O L U T I O N
Given: w = 26.9 rad/s
B = 0.12 T
A = 40.0 m2
maximum emf = 12 kV = 12 × 103
V
Unknown: N = ?
Choose the equation(s) or situation: Use the maximum emf equation for a
generator.
maximum emf = NBAw
N = 
maxim
AB
u
w
m emf

N = =
Although the magnetic field of the generator is fairly large and the area of the
loops is very large, several turns of wire are needed to produce a large maximum
emf. This gives some indication that at least one—and often several—of the
physical attributes of a generator must be large to induce a sizable emf.
93 turns
(12 × 103
V)

(40.0 m2)(0.12 T)(26.9 rad/s)
1. DEFINE
2. PLAN
3. CALCULATE
4. EVALUATE
ADDITIONAL PRACTICE
1. A gas turbine with rotors that are 5.0 cm in diameter was built in 1989.
The turbine’s rotors spin with a frequency of 833 Hz. Suppose a coil of
wire has a cross-sectional area equal to that of the turbine rotor. This coil
turns with the same frequency as the turbine rotor and is perpendicular
to a 8.0 × 10−2
T magnetic field. If the maximum emf induced in the coil
is 330 V, how many turns of wire are there in the coil?

212
NAME ______________________________________ DATE _______________ CLASS ____________________
2. A company in Michigan makes solar-powered lawn mowers. The batter-
ies can run a 3 kW motor for over an hour, and the blades spin at
335 rad/s, which is about 30 percent faster than the blades on a gasoline-
powered mower. Suppose the kinetic energy of rotation of the blades is
used to generate electricity. The generator is built so that the coil turns
at 335 rad/s, creating a maximum emf of 214 V. The coil is placed in a
8.00 × 10−2
T magnetic field. Each of the turns of wire on the rotating
coil has an area of 0.400 m2
. Use this information to calculate the num-
ber of turns of wire.
3. Tom Archer designed a self-propelled vertical Catherine wheel (its rim is
used to mount fireworks) that was 19.3 m in diameter. In 1994, the wheel
was successfully demonstrated. It made a few turns at an average angular
speed of 0.52 rad/s. If a similar wheel with exactly 40 turns of wire
wrapped around the rim is placed in a uniform magnetic field and ro-
tated about an axis that is along the wheel’s diameter, an emf will be gen-
erated. Suppose the maximum induced emf is 2.5 V. If the angular speed
of the wheel’s rotation is 0.52 rad/s, what is the magnitude of the mag-
netic field strength?
4. The Garuda, an airplane propeller designed in Germany in 1919, was
6.90 m across and had an angular speed of 57.1 rad/s during flight. Con-
sider a generator producing a maximum emf of 8.00 × 103
V. If the rotor
has 236 square turns, each with 6.90 m sides, and if the angular speed of
rotation equals 57.1 rad/s, what is the magnitude of the magnetic field in
which the rotor must be turned?
5. In Japan, a 5 mm long working model of a car has been built. The motor,
less than 1 mm long, uses a coil with 1000 turns of wire and is powered
by a 3.0 V emf source. Consider a mini-generator that uses a coil with ex-
actly 1000 turns of wire, each with an area of 8.0 cm2
. If the coil is placed
in a 2.4 × 10−3
T magnetic field, what is the angular speed in rad/s
needed to produce a maximum emf of 3.0 V?
6. In 1995, a turbine was built that had a rotor shaft suspended magnetically,
almost fully eliminating friction. This allows the extremely high angular
speeds needed to create a large emf to be achieved. Suppose the turbine
turns a coil that contains exactly 640 turns of wire, each with an area of
0.127 m2
. This generator produces a maximum emf of 24.6 kV while ro-
tating in a 8.00 × 10−2
T magnetic field. What is the angular speed in rad/s
of the coil?
7. At the University of Virginia is a centrifuge whose rotor is magnetically
supported in a vacuum; this allows for extremely low retarding forces.
The frequency of rotation of this centrifuge is 1.0 × 103
Hz. Consider an
electrical generator with this same frequency. The coil is placed in a
magnetic field that has a magnitude of 0.22 T. If the coil of the generator
has 250 circular loops, each with a 12 cm radius, what is the maximum
emf that can be induced?
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

The Science of Physics
Problem Workbook Solutions
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. distance = 4.35 light years
distance = 4.35 light years × 
9.4
1
6
l
1
ig
×
ht
1
y
0
e
1
a
5
r
m
 = 4.12 × 1016
m
a. distance = 4.12 × 1016
m × 
1
10
M
6 m
m
 =
b. distance = 4.12 × 1016
m × 
10
1
−
p
12
m
m
 = 4.12 × 1028
pm
4.12 × 1010
Mm
Additional Practice A
Givens Solutions
2. energy = 1.2 × 1044
J
a. energy = 1.2 × 1044
J × 
1
1
0
k
3
J
J
 =
b. energy = 1.2 × 1044
J × 
1
1
0−
n
9
J
J
 = 1.2 × 1053
nJ
1.2 × 1041
kJ
6. m = 1.90 × 105
kg
m = 1.90 × 105
kg × 
1.78 ×
1
1
e
0
V
−36 kg
 = 1.07 × 1041
eV
a. m = 1.07 × 1041
eV × 
1
10
M
6 e
e
V
V
 =
b. m = 1.07 × 1041
eV × 
1
1
01
T
2
e
e
V
V
 = 1.07 × 1029
TeV
1.07 × 1035
MeV
4. distance = 152 100 000 km
a. distance = 152 100 000 km × 
1
1
00
k
0
m
m
 × 
10
1
−
y
2
m
4 m
 =
b. distance = 152 100 000 km × 
1
1
00
k
0
m
m
 × 
1
1
02
Y
4
m
m
 = 1.521 × 10−13
Ym
1.521 × 1035
ym
5. energy = 2.1 × 1015
W•h
a. energy = 2.1 × 1015
W•h × 
1
1
J
W
/s
 × 
36
1
0
h
0 s
 =
b. energy = 7.6 × 1018
J × 
1
1
0
G
9
J
J
 = 7.6 × 109
GJ
7.6 × 1018
J
3. m = 1.0 × 10−16
g
a. m = 1.0 × 10−16
g × 
1
1
01
P
5
g
g
 =
b. m = 1.0 × 10−16
g × 
10
1
−1
fg
5 g
 =
c. m = 1.0 × 10−16
g × 
10
1
−
a
1
g
8 g
 = 1.0 × 102
ag
0.10 fg
1.0 × 10−31
Pg
Section Two — Problem Workbook Solutions II Ch. 1–1

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
7. m = (200)(2 × 1030
kg) =
4 × 1032 kg
a. m = 4 × 1032
kg × × =
b. m = 4 × 1032
kg × 
1
1
0
k
3
g
g
 × 
1
1
01
E
8
g
g
 = 4 × 1017
Eg
4 × 1038
mg
103
mg
ᎏ
1 g
103
g
ᎏ
1 kg
Givens Solutions
8. area = 166 241 700 km2
depth = 3940 m
V = volume = area × depth
V = (166 241 700 km2
)(3940 m) ×

1
1
00
k
0
m
m


2
V = 6.55 × 1017
m3
a. V = 6.55 × 1017
m3
× 
10
1
6
m
cm
3
3
 =
b. V = 6.55 × 1017
m3
× 
10
1
9
m
m
3
m3
 = 6.55 × 1026
mm3
6.55 × 1023
cm3
Holt Physics Solution Manual
II Ch. 1–2

Motion In One
Dimension
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. ∆x = 443 m
vavg = 0.60 m/s
∆t = 
v
∆
av
x
g
 = 
0
4
.6
4
0
3
m
m
/s
 = 740 s = 12 min, 20 s
Givens Solutions
2. vavg = 72 km/h
∆x = 1.5 km
∆t = 

v
∆
av
x
g
 = = 75 s
1.5 km

72 
k
h
m


36
1
0
h
0 s


3. ∆x = 5.50 × 102
m
vavg = 1.00 × 102
km/h
vavg = 85.0 km/h
a. ∆t = 
v
∆
av
x
g
 = =
b. ∆x = ∆vavg∆t
∆x = (85.0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(19.8 s) = 468 m
19.8 s
5.50 × 102
m

1.00 × 102

k
h
m


36
1
0
h
0 s


1
1
00
k
0
m
m


4. ∆x1 = 1.5 km
v1 = 85 km/h
∆x1 = 0.80 km
v2 = 67 km/h
a. ∆ttot = ∆t1 + ∆t2 = 
∆
v
x
1
1
 + 
∆
v
x
2
2

∆ttot = + = 64 s + 43 s =
b. vavg = = = = 77 km/h
2.3 km

(107 s)

36
1
0
h
0 s


1.5 km + 0.80 km

(64 s + 43 s)

3
1
60
h
0


∆x1 + ∆x2

∆t1 + ∆t2
107 s
0.80 km

67 
k
h
m


36
1
0
h
0 s


1.5 km

85 
k
h
m


36
1
0
h
0 s


5. r = 7.1 × 104
km
∆t = 9 h, 50 min
∆x =2πr
vavg = = =
vavg =
4.5 × 108
m

(590 min)

1
6
m
0
i
s
n


4.5 × 108
m

(540 min + 50 min)

1
6
m
0
i
s
n


2π(7.1 × 107
m)

(9 h)

60
1
m
h
in

+ 50 min

1
6
m
0
i
s
n


∆x

∆t
vavg =
Thus the average speed = 1.3 × 104
m/s.
On the other hand, the average velocity for this point is zero, because the point’s dis-
placement is zero.
1.3 × 104
m/s

II Ch. 2–2
Givens Solutions
6. ∆x = –1.73 km
∆t = 25 s
7. vavg,1 = 18.0 km/h
∆t1 = 2.50 s
∆t2 = 12.0 s
a. ∆x1 = vavg,1∆t1 = (18.0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(2.50s) = 12.5 m
∆x2 = –∆x1 = –12.5 m
vavg,2 = 
∆
∆
x
t2
2
 = 
–
1
1
2
2
.
.
0
5
s
m
 =
b. vavg,tot = 
∆
∆
x
t
1
1
+
+
∆
∆
x
t2
2
 = 
12.
2
5
.5
m
0
+
s +
(−
1
1
2
2
.0
.5
s
m)
 = =
c. total distance traveled = ∆x1 – ∆x2 = 12.5 m – (–12.5 m) = 25.0 m
total time of travel = ∆t1 + ∆t2 = 2.50 s + 12.0 s = 14.5 s
average speed = 
to
t
t
o
a
t
l
a
d
l
i
t
s
i
t
m
an
e
ce
 = 
2
1
5
4
.
.
0
5
m
s
 = 1.72 m/s
0.0 m/s
0.0 m

14.5 s
–1.04 m/s
8. ∆x = 2.00 × 102
km
∆t = 5 h, 40 min, 37 s
vavg⬘ = (1.05)vavg
∆x⬘ = 
1
2
∆x
a. vavg = 
∆
∆
x
t
 = = 
2.0
2
0
0
×
43
1
7
05
s
m

vavg =
b. ∆t = = = 9.73 × 103
s

2.00 ×
2
105
m



(1.05)
9.79 
m
s


∆x⬘

vavg⬘
9.79 m/s = 35.2 km/h
2.00 × 105
m

5 h

360
h
0 s

+
40 min

m
60
in
s

+ 37 s

vavg = = 
–1.73
2
×
5
1
s
03
m
 = –69 m/s = –250 km/h
∆x

∆t
∆t = (9.73 × 103
s)

36
1
0
h
0 s

= 2.70 h
(0.70 h)

60
1
m
h
in

= 42 min
∆t = 2 h, 42 min
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. vi = 0 km/h = 0 m/s
aavg = 1.8 m/s2
∆t = 1.00 min
vf = aavg ∆t + vi = (1.80 m/s2
)(1.00 min)

1
6
m
0
i
s
n

+ 0 m/s =
vf = 108 m/s = (108 m/s)

36
1
0
h
0 s


1
1
0
k
3
m
m

= 389 km/h
108 m/s
Additional Practice B
Givens Solutions
2. ∆t = 2.0 min
aavg = 0.19 m/s2
vi = 0 m/s
vf = aavg ∆t + vi = (0.19 m/s2
) (2.0 min)

1
6
m
0
i
s
n

+ 0 m/s = 23 m/s
3. ∆t = 45.0 s
aavg = 2.29 m/s2
vi = 0 m/s
vf = aavg ∆t + vi = (2.29 m/s2
)(45.0 s) + 0 m/s = 103 m/s
5. ∆x = (15 hops)

1
1
0
h
.0
o
m
p


= 1.50 × 102
m
∆t = 60.0 s
∆tstop = 0.25 s
vf = 0 m/s
vi = vavg = +2.50 m/s
a. vavg = 
∆
∆
x
t
 = 
1.50
60
×
.0
10
s
2
m
 =
b. aavg = 
v
∆
f
t
−
sto
v
p
i
 = 
0 m/s
0
−
.2
2
5
.5
s
0 m/s
 = 
−
0
2
.2
.5
5
0
m
m
/
/
s
s
 = −1.0 × 101
m/s2
+2.50 m/s
6. ∆x = 1.00 × 102
m, backward
= −1.00 × 102
m
∆t = 13.6 s
∆t⬘ = 2.00 s
vi = 0 m/s
vf = vavg
vavg = 
∆
∆
x
t
 = 
−1.00
13
×
.6
1
s
02
m
 = −7.35 m/s
aavg = 
vf
∆
−
t⬘
vi
 = = 3.68 m/s2
−7.35 m/s − 0 m/s

2.00 s
7. ∆x = 150 m
vi = 0 m/s
vf = 6.0 m/s
vavg = 3.0 m/s
a. ∆t = 
v
∆
av
x
g
 = 
3
1
.
5
0
0
m
m
/s
 =
b. aavg = 
vf
∆
−
t
vi
 = 
6.0
5
m
.0
/s
×
−
1
0
01
m/s
 = 0.12 m/s2
5.0 × 101
s
4. ∆x = 29 752 m
∆t = 2.00 h
vi = 3.00 m/s
vf = 4.13 m/s
∆t = 30.0 s
a. vavg = 
∆
∆
x
t
 = =
b. aavg = 
∆
∆
v
t
 = = 
1.
3
1
0
3
.0
m
s
/s
 = 3.77 × 10−2
m/s2
4.13 m/s − 3.00 m/s

30.0 s
4.13 m/s
29 752 m

(2.00 h)

36
1
0
h
0 s


II Ch. 2–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
8. vi = +245 km/h
aavg = −3.0 m/s2
vf = vi −(0.200) vi
Givens Solutions
9. ∆x = 3.00 km
∆t = 217.347 s
aavg = −1.72 m/s2
vf = 0 m/s
vi = vavg = 
∆
∆
x
t
 = = 13.8 m/s
tstop = 
vf
aa
−
vg
vi
 = = = 8.02 s
−13.8 m/s

−1.72 m/s2
0 m/s − 13.8 m/s

−1.72 m/s2
3.00 × 103
m

217.347 s
10. ∆x = +5.00 × 102
m
∆t = 35.76 s
vi = 0 m/s
∆t⬘ = 4.00 s
vmax = vavg + (0.100) vavg
vf = vmax = (1.100)vavg = (1.100)

∆
∆
x
t

= (1.100)

5.0
3
0
5
×
.7
1
6
0
s
2
m

= +15.4 m/s
aavg = 
∆
∆
t
v
⬘
 = 
vf
∆
−
t⬘
vi
 = = + 3.85 m/s2
15.4 m/s − 0 m/s

4.00 s
1. ∆x = 115 m
vi = 4.20 m/s
vf = 5.00 m/s
∆t = 
vi
2∆
+
x
vf
 = 
4.20
(
m
2)
/
(
s
1
+
15
5.
m
00
)
m/s
 = 
(2
9
)
.
(
2
1
0
1
m
5
/
m
s
)
 = 25.0 s
Additional Practice C
2. ∆x = 180.0 km
vi = 3.00 km/s
vf = 0 km/s
∆t = 
vi
2∆
+
x
vf
 = = 
3
3
.
6
0
0
0
.0
km
km
/s
 = 1.2 × 102
s
(2)(180.0 km)

3.00 km/s + 0 km/s
3. vi = 0 km/h
vf = 1.09 × 103
km/h
∆x = 20.0 km
∆x = 5.00 km
vi = 1.09 × 103
km/h
vf = 0 km/h
a. ∆t = 
vi
2
+
∆x
vf
 =
∆t = =
b. ∆t = 
vi
2
+
∆x
vf
 =
∆t = = 33.0 s
10.0 × 103
m

(1.09 × 103
km/h)

36
1
0
h
0 s


1
1
00
k
0
m
m


(2)(5.00 × 103
m)

(1.09 × 103
km/h + 0 km/h)

36
1
0
h
0 s


1
1
00
k
0
m
m


132 s
40.0 × 103
m

(1.09 × 103
km/h)

36
1
0
h
0 s


1
1
00
k
0
m
m


(2)(20.0 × 103
m)

(1.09 × 103
km/h + 0 km/h)

36
1
0
h
0 s


1
1
00
k
0
m
m


vi =
245 
k
h
m


36
1
0
h
0 s


1
1
0
k
3
m
m

= +68.1 m/s
vf = (1.000 − 0.200) vi = (0.800)(68.1 m/s) = +54.5 m/s
∆t = 
vf
aa
−
vg
vi
 = 
54.5 m
−3
/s
.0
−
m
6
/
8
s
.
2
1 m/s
 = = 4.5 s
−13.6 m/s

− 3.0 m/s2

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 4. vi = vavg = 518 km/h
vf = (0.600) vavg
∆t = 2.00 min
vavg =
518 
k
h
m


60
1
m
h
in


1
1
0
k
3
m
m

= 8.63 × 103
m/min
∆x = 
1
2
(vi + vf)∆t = 
1
2
[vavg + (0.600) vavg]∆t = 
1
2
(1.600)(8.63 × 103
m/min)(2.00 min)
∆x = 13.8 × 103
m = 13.8 km
Givens Solutions
5. ∆t = 30.0 s
vi = 30.0 km/h
vf = 42.0 km/h
∆x = 
1
2
(vi + vf)∆t = 
1
2
(30.0 km/h + 42.0 km/h)

36
1
0
h
0 s

(30.0 s)
∆x = 
1
2

72.0 
k
h
m


36
1
0
h
0 s

(30.0 s)
∆x = 3.00 × 10−1
km = 3.00 × 102
m
1. vi = 186 km/h
vf = 0 km/h = 0 m/s
a = −1.5 m/s2
∆t = 
vf −
a
vi
 = = 
−
−
5
1
1
.5
.7
m
m
/s
/
2
s
 = 34 s
0 m/s − (186 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m



−1.5 m/s2
Additional Practice D
6. vf = 96 km/h
vi = 0 km/h
∆t = 3.07 s
∆x = 
1
2
(vi + vf)∆t = 
1
2
(0 km/h + 96 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(3.07 s)
∆x = 
1
2

96 × 103

m
h

(8.53 + × 10−4
h) = 41 m
7. ∆x = 290.0 m
∆t = 10.0 s
vf = 0 km/h = 0 m/s
vi = 
2
∆
∆
t
x
 − vf = 
(2)(
1
2
0
9
.
0
0
.0
s
m)
 − 0 m/s =
(Speed was in excess of 209 km/h.)
58.0 m/s = 209 km/h
8. ∆x = 5.7 × 103
km
∆t = 86 h
vf = vi + (0.10) vi
vf + vi = 
2
∆
∆
t
x

vi (1.00 + 0.10) + vi = 
2
∆
∆
t
x

vi = 
(2)
(
(
2
5
.
.
1
7
0
×
)(
1
8
0
6
3
h
k
)
m)
 = 63 km/h
9. vi = 2.60 m/s
vf = 2.20 m/s
∆t = 9.00 min
∆x = 
1
2
(vi + vf)∆t = 
1
2
(2.60 m/s + 2.20 m/s)(9.00 min)

m
60
in
s

= 
1
2
(4.80 m/s)(5.40 × 102
s)
∆x = 1.30 × 103
m = 1.30 km
2. vi = −15.0 m/s
vf = 0 m/s
a = +2.5 m/s2
vi = 0 m/s
vf = +15.0 m/s
a = +2.5 m/s
For stopping:
∆t1 = 
vf
a
− vi
 = 
0 m/s
2
−
.5
(−
m
1
/
5
s
.
2
0 m/s)
 = 
1
2
5
.5
.0
m
m
/s
/
2
s
 = 6.0 s
For moving forward:
∆t2 = 
vf
a
− vi
 = = 
1
2
5
.5
.0
m
m
/s
/
2
s
 = 6.0 s
∆ttot = ∆t1 + ∆t2 = 6.0 s + 6.0 s = 12.0 s
15.0 m/s − 0.0 m/s

2.5 m/s2

II Ch. 2–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. vi = 24.0 km/h
vf = 8.0 km/h
a = −0.20 m/s2
∆t = 
vf −
a
vi

∆t =
∆t = = 22 s
−16.0 
k
h
m


36
1
0
h
0 s


1
1
0
k
3
m
m



−0.20 m/s2
(8.0 km/h − 24.0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m



−0.20 m/s2
4. v1 = 65.0 km/h
vi,2 = 0 km/h
a2 = 4.00 × 10−2
m/s2
∆x = 2072 m
For cage 1:
∆x = v1∆t1
∆t1 = 
∆
v1
x
 = =
For cage 2:
∆x = vi,2∆t2 + 
1
2
a2∆t2
2
Because vi,2 = 0 km/h,
∆t2 = 
2
a
∆
2
x

= 
4.
0
(2
0
)
×
(
2
1
0
0
7
−
2
2
m
m
)
/s
2

=
Cage 1 reaches the bottom of the shaft in nearly a third of the time required for cage 2.
322 s
115 s
2072 m

(65.0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m


5. ∆x = 2.00 × 102
m
v = 105.4 km/h
vi,car = 0 m/s
a. ∆t = = =
b. ∆x = vi,car ∆t + 
1
2
acar∆t2
acar = 
2
∆
∆
t2
x
 = 
(2)(2
(
.
6
0
.
0
83
×
s
1
)
0
2
2
m)
 = 8.57 m/s2
6.83 s
2.00 × 102
m

105.4 
k
h
m


36
1
0
h
0 s


1
1
0
k
3
m
m


∆x

v
Givens Solutions
7. vi = 3.17 × 102
km/h
vf = 2.00 × 102
km/h
∆t = 8.0 s
a = 
vf
∆
−
t
vi
 =
a = =
∆x = vi∆t + 
1
2
a∆t2
= (3.17 × 102
km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(8.0 s) + 
1
2
(−4.1 m/s2
)(8.0 s)2
∆x = (7.0 × 102
m) + (−130 m) = +570 m
−4.1 m/s2
(−117 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m



8.0 s
(2.00 × 102
km/h − 3.17 × 102
km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m



8.0 s
6. vi = 6.0 m/s
a = 1.4 m/s2
∆t = 3.0 s
∆x = vi∆t + 
1
2
a∆t2
= (6.0 m/s)(3.0 s) + 
1
2
(1.4 m/s2
)(3.0 s)2
= 18 m + 6.3 m = 24 m

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
10. vi = 24.0 m/s
a = −0.850 m/s2
∆t = 28.0 s
vf = vi + a∆t = 24.0 m/s + (− 0.850 m/s2
)(28.0 s) = 24.0 m/s − 23.8 m/s = +0.2 m/s
Givens Solutions
11. a = +2.67 m/s2
∆t = 15.0 s
∆x = +6.00 × 102
m
vi ∆t = ∆x − 
1
2
a∆t2
vi = 
∆
∆
x
t
 − 
1
2
a∆t = 
6.00
15
×
.0
10
s
2
m
 − 
1
2
(2.67 m/s2
)(15.0 s) = 40.0 m/s − 20.0 m/s = +20.0 m/s
12. a = 7.20 m/s2
∆t = 25.0 s
vf = 3.00 × 102
ms
vi = vf − a∆t
vi =(3.00 × 102
m/s) − (7.20 m/s2
)(25.0 s) = (3.00 × 102
m/s) − (1.80 × 102
m/s)
vi = 1.20 × 102
m/s
13. vi = 0 m/s
∆x = 1.00 × 102
m
∆t = 12.11 s
∆x = vi∆t + 
1
2
a∆t2
Because vi = 0 m/s,
a = 
2
∆
∆
t2
x
 = 
(2)(
(
1
1
.0
2
0
.1
×
1
1
s)
0
2
2
m)
 = 1.36 m/s2
8. vi = 0 m/s
vf = 3.06 m/s
a = 0.800 m/s2
∆t2 = 5.00 s
∆t1 = 
vf
a
− vi
 = 
3.0
0
6
.
m
80
/
0
s
m
−
/
0
s2
m/s
 = 3.82
∆x1 = vi∆t1 + 
1
2
a∆t1
2
= (0 m/s) (3.82 s) + 
1
2
(0.800 m/s2
) (3.82 s)2
= 5.84 m
∆x2 = vf∆t2 = (3.06 m/s)(5.00 s) = 15.3 m
∆xtot = ∆x1 + ∆x2 = 5.84 m + 15.3 m = 21.1 m
9. vf = 3.50 × 102
km/h
vi = 0 km/h = 0 m/s
a = 4.00 m/s2
∆t = 
(vf
a
− vi)
 = =
∆x = vi∆t + 
1
2
a∆t2
= (0 m/s)(24.3 s) + 
1
2
(4.00 m/s2
)(24.3 s)2
∆x = 1.18 × 103
m = 1.18 km
24.3 s
(3.50 × 102
km/h − 0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m



(4.00 m/s2)
14. vi = 3.00 m/s
∆x = 1.00 × 102
m
∆t = 12.11 s
a = 
2(∆x
∆
−
t2
vi∆t)
 =
a =
a = 
(
(
2
1
)
2
(
.
6
1
4
1
m
s)2
)
 = 0.87 m/s2
(2)(1.00 × 102
m − 36.3 m)

(12.11 s)2
(2)[1.00 × 102
m − (3.00 m/s)(12.11 s)]

(12.11 s)2
15. vf = 30.0 m/s
vi = 18.0 m/s
∆t = 8.0 s
a = 
vf
∆
−
t
vi
 = = 
12
8
.0
.0
m
s
/s
 = 1.5 m/s2
30.0 m/s − 18.0 m/s

8.0 s

II Ch. 2–8
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. vi = 0 km/h
vf = 965 km/h
a = 4.0 m/s2
∆x = 
vf
2
2
−
a
vi
2
 =
∆x = 
7.19
8
×
.0
1
m
04
/
m
s2
2
/s2
 = 9.0 × 103
m = 9.0 km
(965 km/h)2
− (0 km/h)2

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(4.0 m/s2)
2. vi = (0.20) vmax
vmax = 2.30 × 103
km/h
vf = 0 km/h
a = −5.80 m/s2
∆x = 
vf
2
2
−
a
vi
2
 =
∆x = 
−1.6
−
3
11
×
.6
1
m
04
/
m
s2
2
/s2
 = 1.41 × 103
m = 1.41 km
(0 km/h)2
− (0.20)2
(2.30 × 103
km/h)2

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(−5.80 m/s2)
3. vf = 9.70 × 102
km/h
vi = (0.500)vf
a = 4.8 m/s2
∆x = 
vf
2
2
−
a
vi
2
 =
∆x =
∆x =
∆x = = 5.7 × 103
m = 5.7 km
5.45 × 104
m2
/s2

9.6 m/s2
(7.06 × 105
km2
/h2
)

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(4.8 m/s2)
(9.41 × 105
km2
/h)2
−2.35 × 105
km2
/h2
)

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(4.8 m/s2)
(9.70 × 102
km/h)2
−(0.50)2
(9.70 × 102
km/h)2

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(4.8 m/s2)
Additional Practice E
Givens Solutions
4. vi = 8.0 m/s
∆x = 40.0 m
a = 2.00 m/s2
vf =

2a
∆
x
+
v
i
2
=

(2
)(
2.
0
m
/s
2
)
(4
0.
m
)
+
(
8.
0
m
/s
)2
=

1.
60
×
1
02
m
2
/
s2
+
6
4
m
2
/
s2

vf =

22
4
m
2
/
s2
= ± 15 m/s = 15 m/s
5. ∆x = +9.60 km
a = −2.0 m/s2
vf = 0 m/s
vi = vf
2
−
2
a∆
x
= (0
m
/s
)2
−
(
2)
(−
2.
0
m
/s
2
)
(9
.6
0
×
1
03
m
)

vi =

3.
84
×
1
04
m
2
/
s2
= ±196 m/s = +196 m/s
7. ∆x = 44.8 km
∆t = 60.0 min
a = −2.0 m/s2
∆x = 20.0 m
vi = 12.4 m/s
a. vavg = 
∆
∆
x
t
 = =
b. vf =

2a
∆
x
+
v
i
2
=

(2
)(
−
2.
0
m
/s
2)
(2
0.
0
m
)
+
(
12
.4
m
/s
)2

vf =

(−
80
.0
m
2/
s2
)
+
1
54
m
2/
s2
=

74
m
2
/
s2
= ±8.6 m/s = 8.6 m/s
12.4 m/s
44.8 × 103
m

(60.0 min)(60 s/min)
6. a = +0.35 m/s2
vi = 0 m/s
∆x = 64 m
vf =

2a
∆
x
+
v
i
2
=

(2
)(
0.
35
m
/s
2
)
(6
4
m
)
+
(
0
m
/s
)2

vf =

45
m
2s
2
= ±6.7 m/s = +6.7 m/s

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. ∆y = −443 m + 221 m
= −222 m
a = −9.81 m/s2
vi = 0 m/s
vf =

2a
∆
y
−
v
i
2
=

(2
)(
−
9.
81
m
/s
2)
(−
22
2
m
)
−
(
0
m
/s
)2
=

43
60
m
2
/
s2

vf = ±66.0 m/s = −66.0 m/s
Givens Solutions
4. ∆y = +64 m
a = −9.81 m/s2
∆t = 3.0 s
∆y = vi∆t + 
1
2
a∆t2
vi = = = 
64 m
3.
+
0
4
s
4 m

vi = 
1
3
0
.
8
0
m
s
 = 36 m/s initial speed of arrow = 36 m/s

3.0 s

∆t
5. ∆y = −111 m
∆t = 3.80 s
a = −9.81 m/s2
∆y = vi ∆t + 
1
2
a∆t2
vi = = =
vi = 
−
3
4
.
0
8
.
0
2
s
m
 = −10.6 m/s
−111 m + 70.8 m

3.80 s

3.80 s

∆t
9. ∆x = 4.0 × 102
m
∆t = 11.55
vi = 0 km/h
vf = 2.50 × 102
km/h
1. ∆y = −343 m
a = −9.81 m/s2
vi = 0 m/s
vf =

2a
∆
y
+
v
i
2
=

(2
)(
−
9.
81
m
/s
2)
(−
34
3
m
)
+
(
0
m
/s
)2
=

67
30
m
2
/
s2

vf = ±82.0 m/s = −82.0 m/s
Additional Practice F
2. ∆y = +4.88 m
vi = +9.98 m/s
a = −9.81 m/s2
vf =

2a
∆
y
+
v
i
2
=

(2
)(
−
9.
81
m
/s
2)
(4
.8
8
m
)
+
(
9.
98
m
/s
)2
=

−
95
.7
m
2
/
s2
+
9
9.
6
m
2
/
s2

vf =

3.
90
m
2
/
s2
= ±1.97 m/s = ±1.97 m/s
a = 
vf
2
2∆
−
x
vi
2
 =
a = 
4.8
8
2
.0
×
×
1
1
0
0
3
2
m
m
2
/s2
 = 6.0 m/s2
(2.50 × 102
km/h)2
− (0 km/h)2

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(4.0 × 102
m)
8. ∆x = 2.00 × 102
m
a = 1.20 m/s2
vf = 25.0 m/s
vi =

vf
2
−
2
a∆
x
=

(2
5.
0
m
/s
)2
−
(
2)
(1
.2
0
m
/s
2
)
(2
.0
0
×
1
02
m
)

vi =

62
5
m
2
/
s2
−
4
.8
0
×
1
02
m
2
/
s2

vi =

14
5
m
2
/
s2
= ±12.0 m/s = 12.0 m/s
10. vi = 25.0 km/h
vf = 0 km/h
∆x = 16.0 m
a = 
vf
2
2∆
−
x
vi
2
 =
a = = −1.51 m/s2
−4.82 m2
/s2

32.0 m
(0 km/h)2
− (25.0 km/h)2

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2

(2)(16.0 m)
64 m − 
1
2
(−9.81 m/s2
)(3.0 s)2
∆y − 
1
2
a∆t2
−111 m − 
1
2
(−9.81 m/s2)(3.80 s)2
∆y − 
1
2
a∆t2

II Ch. 2–10
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
9. ∆ymax = +21 cm
a = −9.81 m/s2
vf = 0 m/s
∆y = +7.0 cm
vi =

vf
2
−
2
a
∆
ym
ax
=

(0
m
/s
)2
−
(2
)(
−9
.8
1
m
/s
2)
(2
.1
×
1
0−
1
m
)
=

4.
1
m
2
/
s2

vi = +2.0 m/s
For the flea to jump +7.0 cm = +7.0 × 10−2
m = ∆y,
∆y = vi∆t + 
1
2
a∆t2
or 
1
2
a∆t2
+ vi∆t − ∆y = 0
Solving for ∆t by means of the quadratic equation,
∆t =
∆t =
∆t = =
∆t = = 0.37 s or 0.04 s
To choose the correct value for ∆t, insert ∆t, a, and vi into the equation for vf .
vf = a∆t + vi = (−9.81 m/s2
)(0.37 s) + 2.0 m/s
vf = (−3.6 m/s) + 2.0 m/s = −1.6 m/s
vf = a∆t + vi = (−9.81 m/s2
)(0.04 s) + 2.0 m/s
vf = (−0.4 m/s) + 2.0 m/s = +1.6 m/s
Because vf is still directed upward, the shorter time interval is correct. Therefore,
∆t = 0.04 s
2.0 m/s ± 1.6 m/s

9.81 m/s2
2.0 m/s ±

2.
6
m
2
/
s2


9.81 m/s2
−2.0 m/s ±

4.
0
m
2
/
s2
−
1
.4
m
2
/
s2


−9.81 m/s2
−2.0 m/s ±

(2
.0
m
/s
)2
−
(
2)
(−
9.
81
m
/s
2)
(−
7.
0
×
1
0−
2
m
)


−9.81 m/s2
−vi ±
(v
i)
2
−
4

2
a


(−
∆
y
)


2

2
a


6. ∆y = −228 m
a = −9.81 m/s2
vi = 0 m/s
When vi = 0 m/s,
∆t =

2
a
∆

y

= =
In the presence of air resistance, the sandwich would require more time to fall be-
cause the downward acceleration would be reduced.
6.82 s
(2)(−228 m)

−9.81 m/s2
Givens Solutions
7. vi = 12.0 m/s, upward =
+12.0 m/s
vf = 3.0 m/s, upward =
+3.0 m/s
a = −9.81 m/s2
yi = 1.50 m
∆y = 
vf
2
2
−
a
vi
2
 = =
∆y = = 6.88 m
height of nest from ground = h
∆y = h − yi h = ∆y + yi = 6.88 m + 1.50 m = 8.38 m
−135 m2
/s2

−19.6 m/s2
9.0 m3
/s2
− 144 m2
/s2

(2)(−9.81 m/s2
)
(3.0 m/s)2
− (12.0 m/s)2

(2)(−9.81 m/s2)
8. ∆y = +43 m
a = −9.81 m/s2
vf = 0 m/s
Because it takes as long for the ice cream to fall from the top of the flagpole to the
ground as it does for the ice cream to travel up to the top of the flagpole, the free-fall
case will be calculated.
Thus, vi = 0 m/s, ∆y = −43 m, and ∆y = 
1
2
a∆t2
.
∆t = 
2
a
∆
y

= = 3.0 s
(2)(−43 m)

−9.81 m/s2

Two-Dimensional
Motion and Vectors
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. ∆tx = 7.95 s
∆y = 161 m
d = 226 m
d2
= ∆x2
+ ∆y2
∆x =

d
2
−
∆
y
2
=

(2
26
m
)2
−
(
16
1
m
)2
=

5.
11
×
1
04
m
2
−
2
.5
9
×
1
04
m
2

∆x =

2.
52
×
1
04
m
2
= 159 m
∆x =
v = 
∆
∆
t
x
x
 = 
1
7
5
.9
9
5
m
s
 = 20.0 m/s
159 m
Givens Solutions
2. d1 = 5.0 km
θ1 = 11.5°
d2
= 1.0 km
q2 = −90.0°
∆xtot = d1(cos q1) + d2(cos q2) = (5.0 km)(cos 11.5°) + (1.0 km)[cos(−90.0°)]
∆xtot = 4.9 km
∆ytot = d1(sin q1) + d2(sin q2) = (5.0 km)(sin 11.5°) + (1.0 km)[sin(−90.0°
)]
= 1.0 km − 1.0 km
∆ytot = 0.0 km
d =

(∆
xt
ot
)2
+
(
∆
yt
ot
)2
=

(4
.9
k
m
)2
+
(
0.
0
km
)2

d =
q = tan−1

∆
∆
x
yt
t
o
o
t
t

= tan−1

0
4
.
.
0
9
k
k
m
m

= 0.0°
, or due east
4.9 km
3. ∆x = 5 jumps
1 jump = 8.0 m
d = 68 m
d2
= ∆x2
+ ∆y2
∆y =

d
2
−
∆
x
2
=

(6
8
m
)2
−
[
(5
)(
8.
0
m
)]
2
=

4.
6
×
1
03
m
2
−
1
.6
×
1
03
m
2

∆y =

3.
0
×
1
03
m
= 55 m
number of jumps northward = 
8.0
5
m
5
/
m
jump
 = 6.9 jumps =
q = tan−1

∆
∆
x
y

= tan−1

(5)
5
(
5
8.
m
0 m)

= 36° west of north
7 jumps
4. ∆x = 25.2 km
∆y = 21.3 km
d =

∆
x
2
+
∆
y
2
=

(2
5.
2
km
)2
+
(
21
.3
k
m
)2

d =

63
5
km
2
+
4
54
k
m
2
=

10
89
k
m
2

d =
q = tan−1

∆
∆
x
y

= tan−1

2
2
1
5
.
.
3
2
k
k
m
m


q = 42.6° south of east
33.00 km

II Ch. 3–2
Givens Solutions
5. ∆y = −483 m
∆x = 225 m
q = tan−1

∆
∆
x
y

= tan−1

2
−
2
4
5
8
m
3

= −65.0° =
d =

∆
x
2
+
∆
y
2
=

(2
25
m
)2
+
(
−
48
3
m
)2

d =

5.
06
×
1
04
m
2
+
2
.3
3
×
1
05
m
2
=

2.
84
×
1
05
m
2

d = 533 m
65.0° below the waters surface
6. v = 15.0 m/s
∆tx = 8.0 s
d = 180.0 m
d2
= ∆x2
+ ∆y2
= (v∆tx)2
+ (v∆ty)2
d2
= v2
(∆tx
2
+ ∆ty
2
)
∆ty = 
d
v


2
−
∆
tx
2
= 
1
1
5
8
.
0
0
.
0
m
m
/
s


2
−
(
8.
0
s)
2
=

14
4
s2
−
6
4
s2
=

8.
0
×
1
01
s
2

∆ty = 8.9 s
7. v = 8.00 km/h
∆tx = 15.0 min
∆ty = 22.0 min
d =

∆
x
2
+
∆
y
2
=

(v
∆
tx
)2
+
(
v∆
ty
)2

= v

∆
tx
2
+
∆
ty
2

d = (8.00 km/h)

60
1
m
h
in


(1
5.
0
m
in
)2
+
(
22
.0
m
in
)2

d = (8.00 km/h)

60
1
m
h
in


22
5
m
in
2
+
4
84
m
in
2

d =

8
6
.
0
00
m
k
i
m
n


70
9
m
in
2
=
q = tan−1

∆
∆
x
y

= tan−1

v
v
∆
∆
t
t
x
y

= tan−1

∆
∆
t
t
x
y

= tan−1

2
1
2
5
.
.
0
0
m
m
i
i
n
n


q = 55.7° north of east
3.55 km
1. d = (5)(33.0 cm)
∆y = 88.0 cm
q = sin−1

∆
d
y

= sin−1

(5)
8
(
8
3
.
3
0
.0
cm
cm)

=
∆x = d(cos q) = (5)(33.0 cm)(cos 32.2°) = 1.40 × 102
cm to the west
32.2° north of west
2. q = 60.0°
d = 10.0 m
∆x = d(cos q) = (10.0 m)(cos 60.0°) =
∆y = d(sin q) = (10.0 m)(sin 60.0°) = 8.66 m
5.00 m
3. d = 10.3 m
∆y = −6.10 m
Finding the angle between d and the x-axis yields,
q1 = sin−1

∆
d
y

= sin−1

−
1
6
0
.
.
1
3
0
m
m

= −36.3°
The angle between d and the negative y-axis is therefore,
q = −90.0 − (−36.3°) = −53.7°
q =
d2
+ ∆x2
+ ∆y
2
∆x =

d
2
−
∆
y2
=

(1
0.
3
m
)2
−
(
−
6.
10
m
)

2
=

10
6
m
2
−
3
7.
2
m
2
=

69
m
2

∆x = ±8.3 m
53.7° on either side of the negative y-axis
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
4. d = (8)(4.5 m)
q = 35°
∆x = d(cos q) = (8)(4.5 m)(cos 35°) =
∆y = d(sin q) = (8)(4.5 m)(sin 35°) = 21 m
29 m
5. v = 347 km/h
q = 15.0°
vx = v(cos q) = (347 km/h)(cos 15.0°) =
vy = v(sin q) = (347 km/h)(sin 15.0°) = 89.8 km/h
335 km/h
6. v = 372 km/h
∆t = 8.7 s
q = 60.0°
d = v∆t = (372 km/h)

36
1
0
h
0 s

(103
m/km)(8.7 s) = 9.0 × 102
m
∆x = d(cos q) = (9.0 × 102
m)(cos 60.0°) =
∆y = d(sin q) = (9.0 × 102
m)(sin 60.0°) = 780 m north
450 m east
7. d = 14 890 km
q = 25.0°
∆t = 18.5 h
vavg = 
∆
d
t
 = 
1.48
1
9
8
×
.4
1
5
0
h
4
km
 =
vx = vavg(cos q) = (805 km/h)(cos 25.0°) =
vy = vavg(sin q) = (805 km/h)(sin 25.0°) = 340 km/h south
730 km/h east
805 km/h
8. vi = 6.0 × 102
km/h
vf = 2.3 × 103
km/h
∆t = 120 s
q = 35° with respect to
horizontal
a = 
∆
∆
v
t
 = 
vf
∆
−
t
vi

a =
a =
a = 3.9 m/s2
ax = a(cos q) = (3.9 m/s2
)(cos 35°) =
ay = a(sin q) = (3.9 m/s2
)(sin 35°) = 2.2 m/s2
vertically
3.2 m/s2
horizontally
(1.7 × 103
km/h)

36
1
0
h
0 s

(103
m/km)

1.2 × 102
s
(2.3 × 103
km/h − 6.0 × 102
km/h)

36
1
0
h
0 s

(103
m/km)

1.2 × 102 s
1. ∆x1 = 250.0 m
d2 = 125.0 m
q2 = 120.0°
∆x2 = d2(cos q2) = (125.0 m)(cos 120.0°) = −62.50 m
∆y2 = d2(sin q2) = (125.0 m)(sin 120.0°) = 108.3 m
∆xtot = ∆x1 + ∆x2 = 250.0 m − 62.50 m = 187.5 m
∆ytot = ∆y1 + ∆y2 = 0 m + 108.3 m = 108.3 m
d =

(∆
xt
ot
)2
+
(
∆
yt
ot
)2
=

(1
87
.5
m
)2
+
(
10
8.
3
m
)2

d =

3.
51
6
×
1
04
m
2
+
1
.1
73
×
1
04
m
2
=

4.
68
9
×
1
04
m
2

d =
q = tan−1

∆
∆
x
yt
t
o
o
t
t

= tan−1

1
1
0
8
8
7
.
.
3
5
m
m

= 30.01° north of east
216.5 m

II Ch. 3–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. v = 3.53 × 103
km/h
∆t1 = 20.0 s
∆t2 = 10.0 s
q1 = 15.0°
q2 = 35.0°
∆x1 = v∆t1(cos q1)
∆x1 = (3.53 × 103
km/h)

36
1
0
h
0 s

(103
m/km)(20.0 s)(cos 15.0°) = 1.89 × 104
m
∆y1 = v∆t1(sin q1)
∆y1 = (3.53 × 103
km/h)

36
1
0
h
0 s

(103
m/km)(20.0 s)(sin 15.0°) = 5.08 × 103
m
∆x2 = v∆t2(cos q2)
∆x2 = (3.53 × 103
km/h)

36
1
0
h
0 s

(103
m/km)(10.0 s)(cos 35.0°) = 8.03 × 103
m
∆y2 = v∆t2(sin q2)
∆y2 = (3.53 × 103
km/h)

36
1
0
h
0 s

(103
m/km)(10.0 s)(sin 35.0°) = 5.62 × 103
m
∆ytot = ∆y1 + ∆y2 = 5.08 × 103
m + 5.62 × 103
m =
∆xtot = ∆x1 + ∆x2 = 1.89 × 104
m + 8.03 × 103
m =
d =

(∆
xt
ot
)2
+
(
∆
yt
ot
)2
=

(2
.6
9
×
1
04
m
)2
+
(
1.
07

×
1
04
m
)2

d =

7.
24
×
1
08
m
2
+
1
.1
1
×
1
08
m
2
=

8.

35

×

1

08

m

d =
q = tan−1

∆
∆
x
yt
t
o
o
t
t

= tan−1

1
2
.
.
0
6
7
9
×
×
1
1
0
0
4
4
m
m


q = 21.7° above the horizontal
2.89 × 104
m
2.69 × 104
m
1.07 × 104
m
Givens Solutions
3. ∆x1 + ∆x2 = 2.00 × 102
m
∆y1 + ∆y2 = 0
q1 = 30.0°
q2 = −45.0°
v = 11.6 km/h
∆y1 = d1(sin q1) = −∆y2 = −d2(sin q2)
d1 = −d2 
s
s
i
i
n
n
q
q
2
1

= −d2
si
s
n
i
(
n
−
3
4
0
5
.
.
0
0
°
°)

= 1.41d2
∆x1 = d1(cos q1) = (1.41d2)(cos 30.0°) = 1.22d2
∆x2 = d2(cos q2) = d2[cos(−45.0°)] = 0.707d2
∆x1 + ∆x2 = d2(1.22 + 0.707) = 1.93d2 = 2.00 × 102
m
d2 =
d1 = (1.41)d2 = (1.41)(104 m) =
v = 11.6 km/h = (11.6 km/h)

36
1
0
h
0 s

(103
m/km) = 3.22 m/s
∆t1 = 
d
v
1
 =

3
1
.2
4
2
7
m
m
/s

= 45.7 s
∆t2 = 
d
v
2
 =

3
1
.2
0
2
4
m
m
/s

= 32.3 s
∆ttot = ∆t1 + ∆t2 = 45.7 s + 32.3 s = 78.0 s
147 m
104 m

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
5. v = 57.2 km/h
∆t1 = 2.50 h
∆t2 = 1.50 h
θ2 = 30.0°
d1 = v∆t1 = (57.2 km/h)(2.50 h) = 143 km
d2 = v∆t2 = (57.2 km/h)(1.50 h) = 85.8 km
∆tot = d1 + d2(cos q2) = 143 km + (85.8 km)(cos 30.0°) = 143 km + 74.3 km = 217 km
∆ytot = d2(sin q2) = (85.8 km)(sin 30.0°) = 42.9 km
d =

(∆
xt
ot
)2
+
(
∆
yt
ot
)2
=

(2
17
k
m
)2
+
(
42
.9
k
m
)

d =

4.
71
×
1
04
k
m
2
+
1
.8
4
×
1
03
k
m
2
=

4.
89
×
1
04
k
m
2

d =
q = tan−1

∆
∆
x
yt
t
o
o
t
t

= tan−1

4
2
2
1
.
7
9
k
k
m
m

221 km
1. vx = 9.37 m/s
∆y = −2.00 m
ay = −g = −9.81 m/s2
∆t = 
2
a
∆
y
y

= 
∆
vx
x

∆x = vx 
2
a
∆
y
y

= (9.37 m/s) 
(
(
2
−
)
9
(
.
−
8
2
1

.0
m
0
/
m
s2
)
)

= 5.98 m
The river is 5.98 m wide.
4. v = 925 km/h
∆t1 = 1.50 h
∆t2 = 2.00 h
q2 = 135°
d1 = v∆t1 = (925 km/h)(103
m/km)(1.50 h) = 1.39 × 106
m
d2 = v∆t2 = (925 km/h)(103
m/km)(2.00 h) = 1.85 × 106
m
∆x1 = d1 = 1.39 × 106
m
∆y1 = 0 m
∆x2 = d2(cos q2) = (1.85 × 106
m)(cos 135°) = −1.31 × 106
m
∆y2 = d2(sin q2) = (1.85 × 106
m)(sin 135°) = 1.31 × 106
m
∆xtot = ∆x1 + ∆x2 = 1.39 × 106
m + (− 1.31 × 106
m) = 0.08 × 106
m
∆ytot = ∆y1 + ∆y2 = 0 m + 1.31 × 106
m = 1.31 × 106
m
d =

(∆
xt
ot
)2
+
(
∆
yt
ot
)2
=

(0
.0
8
×
1
06
m
)2
+
(
1.
31
×
1
06
m
)2

d =

6
×
1
09
m
2
+
1
.7
2
×
1
01
2
m
2
=

1.
73
×
1
01
2
m
2

d =
q = tan−1

∆
∆
x
yt
t
o
o
t
t

= tan−1

1
0
.
.
3
0
1
8
×
×
1
1
0
0
6
6
m
m

= 86.5° = 90.0° − 3.5°
q = 3.5° east of north
1.32 × 106
m = 1.32 × 103
km
Givens Solutions
2. ∆x = 7.32 km
∆y = −8848 m
ay = −g = −9.81 m/s2
∆t = 
2
a
∆
y
y

= 
∆
vx
x

vx = 
2
a
∆
y
y

∆x =

(
(
2
−
)
9
(−
.8
8
1
8
m
48
/s
m
2
)
)

(7.32 × 103
m) =
No. The arrow must have a horizontal speed of 172 m/s, which is much greater than
100 m/s.
172 m/s

II Ch. 3–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. vx = 372 km/h
∆x = 40.0 m
ay = −g = −9.81 m/s2
∆t = 
∆
vx
x

∆y = 
1
2
ay (∆t)2
= 
ay
2
(
v
∆
x
x
2
)2
 =
∆y = −0.735 m
The ramp is 0.735 m above the ground.
(−9.81 m/s2
)(40.0 m)2

(2)
(372 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m


2
5. ∆x = 25 m
vx = 15 m/s
ay = −g = −9.81 m/s2
h = 25 m
∆t = 
∆
vx
x

∆y = 
1
2
ay (∆t)2
= 
ay
2
(
v
∆
x
x
2
)2
 =
∆y = h − h′ = −14 m
h′ = h − ∆y = 25 m − (−14 m)
= 39 m
(−9.81 m/s2
)(25 m)2

(2)(15 m/s)2
6. l = 420 m
∆y =
∆x = l
ay = −g = −9.81 m/s2
−l

2
7. ∆y = −2.45 m
v = 12.0 m/s
ay = −g = −9.81 m/s2
vy
2
= 2ay∆y
v2
= vx
2
+ vy
2
= vx
2
+ 2ay∆y
vx =

v2 − 2a
y∆y
=

(12.0 m
/s)2
− (
2)(−9.8
1 m/s2
)(−2.45
m)

vx =

14
4
m
2
/
s2
−
4
8.
1
m
2
/
s2

=

96
m
2
/
s2

vx = 9.8 m/s
3. ∆x = 471 m
vi = 80.0 m/s
ay = −g = −9.81 m/s2
∆t = 
∆
vx
x

∆y = 
1
2
ay (∆t)2
= 
ay
2
(
v
∆
x
x
2
)2
 = = −1.70 × 102
m
The cliff is 1.70 × 102
m high.
(−9.81 m/s2
)(471 m)2

(2)(80.0 m/s)2
Givens Solutions
∆t = 
2
a
∆
y
y

= 
∆
vx
x

vx = 
2
a
∆
y
y

∆x = 
(
(
−
2
9
)(
.8
−
1
2
1
m
0
/
m
s2
)
)

(420 m) = 64 m/s

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
1. ∆x = 201.24 m
q = 35.0°
ay = −g = −9.81 m/s2
∆y = vi (sin q)∆t + 
1
2
ay(∆t)2
= vi (sin q) + 
1
2
ay∆t = 0
∆x = vi(cos q)∆t
∆t = 
vi(c
∆
o
x
s q)

vi(sin q) = −
1
2
ay
vi(c
∆
o
x
sq)


vi =

2(sin
−a
q
y
)(
∆
c
x
os q
)

=

vi = 45.8 m/s
−(−9.81 m/s2
)(201.24 m)

(2)(sin 35.0°)(cos 35.0°)
2. ∆x = 9.50 × 102
m
q = 45.0°
ay = −g = −9.81 m/s2
Using the derivation shown in problem 1,
vi =

2(sin
−a
q
y
)(
∆
c
x
os q
)

=
vi = 96.5 m/s
At the top of the arrow’s flight:
v = vx = vi(cos q ) = (96.5 m/s)(cos 45.0°) = 68.2 m/s
−(−9.81 m/s2)(9.50 × 102 m)

(2)(sin 45.0°)(cos 45.0°)
3. ∆x = 27.5 m
q = 50.0°
ay = −g = −9.81 m/s2
vi =

2(sin
−a
q
y
)(
∆
c
x
os q
)

=
vi = 16.6 m/s
−(−9.81 m/s2)(27.5 m)

(2)(sin 50.0°)(cos 50.0°)
8. ∆y = −1.95 m
vx = 3.0 m/s
ay = −g = −9.81 m/s2
vy
2
= 2ay ∆y
v =

vx
2
+
v
y
2
=

vx
2 + 2
ay∆y

v =

(3.0 m
/s)2 + (
2)(−9.8
1 m/s2
)(−1.95
m)

v =

9.
0
m
2/
s2
+
3
8.
3
m
2/
s2
=

47
.3
m
2
/
s2
=
q = tan−1

v
v
x
y

= tan−1
= tan−1

q = 64° below the horizontal

(2)(−9
.81 m/
s2
)(−1
.95 m)


3.0 m/s

2ay∆y


vx
6.88 m/s
4. ∆x = 44.0 m
q = 45.0°
ay = −g = −9.81 m/s2
a. vi =

2(sin
−a
q
y
)(
∆
c
x
os q
)

=
vi = 20.8 m/s
−(−9.81 m/s2)(44.0 m)

(2)(sin 45.0°)(cos 45.0°)

II Ch. 3–8
b. At maximum height, vy, f = 0 m/s
vy, f
2
= vy, i
2
+ 2ay∆ymax = 0
ymax = = 
−vi
2
(
2
s
a
in
y
q)2
 = = 11.0 m
c. ymax = 
−
2
v
a
y,
y
i
2
 = 
(2
−
)
(
(
2
−
0
9
.
.
8
81
m
m
/s
/
)
s
2
2
)
 = 22.1 m
The brick’s maximum height is 22.1 m.
The brick’s maximum height is 11.0 m.
−(20.8 m/s)2
(sin 45.0°)2

(2)(−9.81 m/s2
)
−vy, i
2

2ay
Givens Solutions
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
5. ∆x = 76.5 m
q = 12.0°
ay = −g = −9.81 m/s2
At maximum height, vy, f = 0 m/s.
vy, f
2
= vy, i
2
+ 2ay∆ymax = 0
ymax = 
−
2
v
a
y,
y
i
2
 = 
−vi
2
(
2
s
a
in
y
q)2

Using the derivation for vi
2
from problem 1,
∆ymax =

2(sin
−a
q
y
)(
∆
c
x
os q)


−(s
2
in
ay
q)2
 = 
∆
4
x
(c
(s
o
i
s
n
q
q
)
)
 = 
∆x(t
4
an q)

∆ymax = 
(76.5 m)(
4
tan 12.0°)
 = 4.07 m
6. vrunner = 5.82 m/s
vi,ball = 2vrunner
In x-direction,
vi,ball(cos q) = 2vrunner(cos q) = vrunner
2(cos q) = 1
q = cos−1

1
2

= 60°
7. vi = 8.42 m/s
q = 55.2°
∆t = 1.40 s
ay = −g = −9.81 m/s2
For first half of jump,
∆t1 = 
1.4
2
0 s
 = 0.700 s
∆y = vi(sin q)∆t1 + 
1
2
ay(∆t1)2
= (8.42 m/s)(sin 55.2°)(0.700 s) + 
1
2
(−9.81 m/s2
)(0.700 s)2
∆y = 4.84 m − 2.40 m = 2.44 m
∆x = vi(cos q)∆t
∆x = (8.42 m/s) (cos 55.2°)(1.40 s) = 6.73 m
The fence is 2.44 m high.
8. vi = 2.2 m/s
q = 21°
∆t = 0.16 s
ay = −g = −9.81 m/s2
∆x = vi(cos q)∆t = (2.2 m/s) (cos 21°)(0.16 s) =
Maximum height is reached in a time interval of 
∆
2
t

∆ymax = vi (sin q)

∆
2
t

+ 
1
2
ay
∆
2
t


2
∆ymax = (2.2 m/s)(sin 21°)

0.1
2
6 s

+ 
1
2
 (−9.81 m/s2
)

0.1
2
6 s


2
∆ymax = 6.3 × 10−2
m − 3.1 × 10−2
m = 3.2 × 10−2
m = 3.2 cm
The flea’s maximum height is 3.2 cm.
0.33 m

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Givens Solutions
1. vse = 126 km/h north
vgs = 40.0 km/h east
vge = vg
s
2
+
v
se
2
= (4
0.
0
km
/h
)2
+
(
12
6
km
/h
)2

vge = 1.
60
×
1
03
k
m
2
/
h
2
+
1
.5
9
×
1
04

k
m

2
/

h
2

vge = 1.
75
×
1
04
k
m
/h
=
q = tan−1

v
v
g
se
s

= tan−
1

4
1
0
2
.
6
0
k
k
m
m
/
/
h
h

132 km/h
2. vwe = −3.00 × 102
km/h
vpw = 4.50 × 102
km/h
∆x = 250 km
vpe = vpw + vwe = 4.50 × 102
km/h − 3.00 × 102
km/h = 1.50 × 102
km/h
∆t = 
v
∆
p
x
e
 = 
1.50
2
×
50
10
k
2
m
km/h
 = 1.7 h
3. vtw = 9.0 m/s north
vwb = 3.0 m/s east
∆t = 1.0 min
vtb = vtw + vwb
vtb =

vt
w
2
+
v
w
b
2
=

(9
.0
m
/s
)2
+
(
3.
0
m
/s
)2
=

81
m
2/
s2
+
9
.0
m
2/
s2

vtb =

9.
0
×
1
01
m
2
/
s2

vtb = 9.5 m/s
∆x = vtb∆t = (9.5 m/s)(1.0 min)

1
6
m
0
i
s
n

=
q = tan−1

v
v
w
tw
b

= tan−1

3
9
.
.
0
0
m
m
/
/
s
s

= 18° east of north
570 m
4. vsw = 40.0 km/h forward
vfw = 16.0 km/h forward
∆x = 60.0 m
vsf = vsw − vfw = 40.0 km/h − 16.0 km/h = 24.0 km/h toward fish
∆t = 
∆
vs
x
f
 = = 9.00 s
60.0 m

(24.0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m


5. v1E = 90.0 km/h
v2E = −90.0 km/h
∆t = 40.0 s
v12 = v1E − v2E
v12 = 90.0 km/h − (−90.0 km/h) = 1.80 × 102
km/h
∆x = v12∆t = (1.80 × 102
km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(40.0 s) = 2.00 × 103
m = 2.00 km
The two geese are initially 2.00 km apart
6. vme = 18.0 km/h forward
Vre = 0.333 Vme
= 6.00 km/h forward
∆x = 12.0 m
vmr = vme − vre
vmr = 18.0 km/h − 6.0 km/h = 12.0 km/h
∆t = 
v
∆
m
x
r
 = 
(12
1
.
2
0
.0
km
m
/h)


36
1
0
h
0 s


1
1
0
k
3
m
m


∆t = 3.60 s

Forces and the
Laws of Motion 4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
1. a. b.
FEarth-on diver
Fair resistance-on diver
FEarth-on diver
2.
Fchef-on-sack
Fscale-on-sack
FEarth-on-sack
3.
Ffloor-on-toy-vertical
Ffloor-on-toy-horizontal
Fhandlebars-on-toy
FEarth-on-toy
1. mw = 75 kg
mp = 275 kg
g = 9.81 m/s2
The normal force exerted by the platform on the weight lifter’s feet is equal to and
opposite of the combined weight of the weightlifter and the pumpkin.
Fnet = Fn − mwg − mpg = 0
Fn = (mw + mp)g = (75 kg + 275 kg) (9.81 m/s2
)
Fn = (3.50 × 102
kg)(9.81 m/s2
) = 3.43 × 103
N
Fn = 3.43 × 103
N upward against feet

II Ch. 4–2
Givens Solutions
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. mb = 253 kg
mw = 133 kg
g = 9.81 m/s2
Fnet = Fn,1 + Fn,2 − mbg − mwg = 0
The weight of the weightlifter and barbell is distributed equally on both feet, so the
normal force on the first foot (Fn,1) equals the normal force on the second foot (Fn,2).
2Fn,1 = (mb + mw)g = 2Fn,2
Fn,1 = Fn,2 = 
(mb +
2
mb)g
 =
Fn,1 = Fn,2 = = 1.89 × 103
N
Fn,1 = Fn,2 = 1.89 × 103
N upward on each foot
(386 kg)(9.81 m/s2
)

2
(253 kg + 33 kg)
9.81 
m
s2



2
3. Fdown = 1.70 N
Fnet = 4.90 N
Fnet
2
= Fforward
2
+ Fdown
2
Fforward =

F
ne
t
2
−
F
do
w
n
2
=

(4
.9
0
N
)2
−
(
1.
70
N
)2

Fforward =

21
.1
N
2
= 4.59 N
4. m = 3.10 × 102
kg
g = 9.81 m/s2
q1 = 30.0°
q2 = − 30.0°
Fx,net = ΣFx = FT,1(sin q1) + FT,2(sin q2) = 0
Fy,net = ΣFy = FT,1(cos q1) + FT,2(cos q2) + Fg = 0
FT,1(sin 30.0°) = −FT,2[sin (−30.0°)]
FT,1 = FT,2
FT,1(cos q1) + FT,1(cos q2) = −Fg = mg
FT,1(cos 30.0°) + FT,1[cos (−30.0°)] = (3.10 × 102
kg)(9.81 m/s2
)
FT,1 =
FT,1 = FT,2 =
As the angles q1 and q2 become larger, cos q1 and cos q2 become smaller. Therefore,
FT,1 and FT,2 must become larger in magnitude.
1.76 × 103
N
(3.10 × 102
kg)(9.81 m/s2
)

(2)(cos 30.0°)[cos(−30.0°)]

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
5. m = 155 kg
FT,1 = 2FT,2
g = 9.81 m/s2
q1 = 90° − q2
Fx,net = FT,1(cos q1) − FT,2(cos q2) = 0
Fy,net = FT,1(sin q1) + FT,2(sin q2) − mg = 0
FT,1[(cos q1) − 
1
2
(cos q2)] = 0
2 (cos q1) = cos q2 = cos(90° − q1) = sin q1
2 = tan q1
q1 = tan−1
(2) = 63°
q2 = 90° − 63° = 27°
FT,1(sin q1) + 
FT
2
,1
(sin q2) = mg
FT,1 =
FT,1 = = 
(155
0
k
.8
g
9
)(
+
9.
0
8
.
1
2
m
3
/s2
)
 = 
(155 kg
1
)
.1
(9
2
.81 m)

FT,1 =
FT,2 = 6.80 × 102
N
1.36 × 1.36 × 103
N
(155 kg)(9.81 m/s2
)

(sin 63°) + 
(sin
2
27°)

mg

(sin θ1) + 
1
2
 (sin θ2)
1. vi = 173 km/h
vf = 0 km/h
∆x = 0.660 m
m = 70.0 kg
g = 9.81 m/s2
a = 
vf
2
2∆
−
x
vi
2
 =
a = −1.75 × 103
m/s2
F = ma = (70.0 kg)(−1.75 × 103
m/s2
) =
Fg = mg = (70.0 kg)(9.81 m/s2
) =
The force of deceleration is nearly 178 times as large as David Purley’s weight.
6.87 × 102
N
−1.22° × 105
N
[(0 km/h)2
− (173 km/h)2
](103
m/km)2
(1 h/3600 s)2

(2)(0.660 m)
2. m = 2.232 × 106
kg
g = 9.81 m/s2
anet = 0 m/s2
a. Fnet = manet = Fup − mg
Fup = manet + mg = m(anet + g) = (2.232 × 106
kg)(0 m/s2
+ 9.81 m/s2
)
Fup = = mg
b. Fdown = mg(sin q)
anet = 
F
m
net
 = 
Fup −
m
Fdown
 = 
mg − m
m
g(sin q)

anet = g(1 − sin q) = (9.81 m/s2
)[1.00 − (sin 30.0°)] = 
9.81
2
m/s2
 = 4.90 m/s2
anet = 4.90 m/s2
up the incline
2.19 × 107
N
3. m = 40.00 mg
= 4.00 × 10−5
kg
g = 9.807 m/s2
anet = (400.0)g
Fnet = Fbeetle − Fg = manet = m(400.0) g
Fbeetle = Fnet + Fg = m(400.0 + 1)g = m(401)g
Fbeetle = (4.000 × 10−5
kg)(9.807 m/s2
)(401) =
Fnet = Fbeetle − Fg = m(400.0) g = (4.000 × 10−5
kg)(9.807 m/s2
)(400.0)
Fnet =
The effect of gravity is negligible.
1.569 × 10−1
N
1.573 × 10−1
N

II Ch. 4–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
4. ma = 54.0 kg
mw = 157.5 kg
anet = 1.00 m/s2
g = 9.81 m/s2
The net forces on the lifted weight is
Fw,net = mwanet = F′ − mwg
where F′ is the force exerted by the athlete on the weight.
The net force on the athlete is
Fa,net = Fn,1 + Fn,2 − F′ − mag = 0
where Fn,1 and Fn,2 are the normal forces exerted by the ground on each of the ath-
lete’s feet, and −F′ is the force exerted by the lifted weight on the athlete.
The normal force on each foot is the same, so
Fn,1 = Fn,2 = Fn and
F′ = 2Fn − mag
Using the expression for F′ in the equation for Fw,net yields the following:
mwanet = (2Fn − mag) − ma g
2Fn = mw(anet + g) + mag
Fn = 
mw(anet +
2
g) + mag
 =
Fn =
Fn = = 
223
2
2 N
 = 1116 N
Fn,1 − Fn,2 = Fn = 1116 N upward
1702 N + 5.30 × 102
N

2
(157.5 kg)(10.81 m/s2
) + (54.0 kg)(9.81 m/s2
)

2
(157.5 kg)(1.00 m/s2
+ 9.81 m/s2
) + (54.0 kg)

2
5. m = 2.20 × 102
kg
anet = 75.0 m/s2
g = 9.81 m/s2
Fnet = manet = Favg − mg
Favg = m(anet + g) = (2.20 × 102
kg)(75.0 m/s2
+ 9.81 m/s2
)
Favg = (2.20 × 102
kg)(84.8 m/s2
) = 1.87 × 104
N
Favg = 1.87 × 104
N upward
6. m = 2.00 × 104
kg
∆t = 2.5
vi = 0 m/s
vf = 1.0 m/s
g = 9.81 m/s2
anet = 
vf
∆
−
t
vi
 = 
(1.0 m/
2
s
.
−
5
0
s
.0 m/s)
 = 0.40 m/s2
Fnet = manet = FT − mg
FT = manet + mg = m(anet + g)
FT = (2.00 × 104
kg)(0.40 m/s2
+ 9.81 m/s2
)
FT = (2.00 × 104
kg)(10.21 m/s2
) = 2.04 × 105
N
FT = 2.04 × 105
N
7. m = 2.65 kg
q1 = q2 = 45.0°
anet = 2.55 m/s2
g = 9.81 m/s2
Fx,net = FT,1(cos q1) − FT,2(cos q2) = 0
FT,1(cos 45.0°) = FT,2(cos 45.0°)
FT,1 = FT,2
Fy,net = manet = FT,1(sin q1) + FT,2(sin q2) − mg
FT = FT,1 = FT,2
q = q1 = q2
FT(sin q) + FT(sin q) = m(anet + g)
2FT(sin q) = m(anet + g)

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
FT = 
m
2
(a
(s
n
i
e
n
t +
q)
g)
 =
FT = = 23.2 N
FT,1 = 23.2 N
FT,2 = 23.2 N
(2.65 kg)(12.36 m/s2
)

(2)(sin 45.0°)
(2.65 kg)(2.55 m/s2
= 9.81 m/s2
)

(2)(sin 45.0°)
Givens Solutions
8. m = 20.0 kg
∆x = 1.55 m
vi = 0 m/s
vf = 0.550 m/s
anet = 
vf
2
2∆
−
x
vi
2
 = = 9.76 × 10−2
m/s2
Fnet = manet = (20.0 kg)(9.76 × 10−2
m/s2
) = 1.95 N
(0.550 m/s)2
− (0.00 m/s)2

(2)(1.55 m)
9. mmax = 70.0 kg
m = 45.0 kg
g = 9.81 m/s2
Fmax = mmaxg = FT
Fmax = (70.0 kg)(9.81 m/s2
) = 687 N
Fnet = manet = FT − mg = Fmax − mg
anet = 
Fm
m
ax
 − g = 
4
6
5
8
.
7
0
N
kg
 − 9.81 m/s2
= 15.3 m/s2
− 9.81 m/s2
= 5.5 m/s2
anet = 5.5 m/s2
upward
10. m = 3.18 × 105
kg
Fapplied = 81.0 × 103
N
Ffriction = 62.0 × 103
N
Fnet = Fapplied − Ffriction = (81.0 × 103
− 62.0 × 103
N)
Fnet = 19.0 × 103
N
anet = 
F
m
net
 =

3
1
.
9
1
.
8
0
×
×
1
1
0
0
5
3
k
N
g

= 5.97 × 10−2
m/s2
11. m = 3.00 × 103
kg
Fapplied = 4.00 × 103
N
q = 20.0°
Fopposing = (0.120) mg
g = 9.81 m/s2
Fnet = manet = Fapplied(cos q) − Fopposing
anet =
anet =
anet = = 
3
2
.0
.3
0
×
×
1
1
0
0
2
3
N
kg

anet = 7.7 × 10−2
m/s2
3.76 × 103
N − 3.53 × 103
N

3.00 × 103
kg
(4.00 × 103
N)(cos 20.0°) − (0.120)(3.00 × 103
kg)(9.81 m/s2
)

3.00 × 103
kg
Fapplied(cos q) − (0.120) mg

m
12. mc = 1.600 × 103
kg
mw = 1.200 × 103
kg
vi = 0 m/s
g = 9.81 m/s2
∆y = 25.0 m
For the counterweight: The tension in the cable is FT.
Fnet = FT − mwg = mwanet
For the car:
Fnet = mcg − FT = mcanet
Adding the two equations yields the following:
mcg − mwg = (mw + mc)anet
anet = 
(m
m
c
c
−
+
m
m
w
w
)g
 =
anet = = 1.40 m/s2
(4.00 × 102
kg)(9.81 m/s2
)

2.800 × 103
kg
(1.600 × 103
kg − 1.200 × 103
kg)(9.81 m/s2
)

1.600 × 103
kg + 1.200 × 103
kg

II Ch. 4–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
13. m = 409 kg
d = 6.00 m
q = 30.0°
g = 9.81 m/s2
Fapplied = 2080 N
vi = 0 m/s
a. Fnet = Fapplied − mg(sin q) = 2080 N − (409 kg)(9.81 m/s2
)(sin 30.0°)
Fnet = 2080 N − 2010 N = 70 N
Fnet =
b. anet = 
F
m
net
 = 
4
7
0
0
9
N
kg
 = 0.2 m/s2
anet =
c. d = vi∆t + 
1
2
anet ∆t2
= (0 m/s)∆t + 
1
2
(0.2 m/s2
)∆t2
∆t = 
(
(
2
0
)
.
(
2
6
.
m
0
0
/s
m
2
)
)

= 8 s
0.2 m/s2
at 30.0° above the horizontal
70 N at 30.0° above the horizontal
vf =

2a
ne
t∆
y
+
v
i
2
=

(2
)(
1.
40
m
/s
2
)
(2
5.
0
m
)
+
(
0
m
/s
)2

vf = 8.37 m/s
Givens Solutions
14. amax = 0.25 m/s2
Fmax = 57 N
Fapp = 24 N
a. m = 
F
am
m
a
a
x
x
 = 
0.2
5
5
7
m
N
/s2
 =
b. Fnet = Fmax − Fapp = 57 N − 24 N = 33 N
anet = 
F
m
net
 = 
2.3
3
×
3
1
N
02
kg
 = 0.14 m/s2
2.3 × 102
kg
15. m = 2.55 × 103
kg
FT = 7.56 × 103
N
qT = −72.3°
Fbuoyant = 3.10 × 104
N
Fwind = −920 N
g = 9.81 m/s2
∆y = −45.0 m
vi = 0 m/s
a. Fx,net = ΣFx = max,net = FT(cos qT) + Fwind
Fx,net = (7.56 × 103
N)[cos(−72.3°)] − 920 N = 2.30 × 103
N − 920 N = 1.38 × 103
N
Fy,net = ΣFy = may,net = FT(sin qT) + Fbuoyant + Fg = FT(sin qT) + Fbuoyant − mg
Fy,net = (7.56 × 103
N)[sin(−72.3°)] = 3.10 × 104
N − (2.55 × 103
kg)(9.81 m/s2
)
Fy,net = −7.20 × 103
N + 3.10 × 104
N − 2.50 × 104
= −1.2 × 103
N
Fnet =

(F
x,
ne
t)
2
+
(
F
y,n
et
)2
=

(1
.3
8
×
1
03
N
)2
+
(
−
1.
2
×
1
03
N
)2

Fnet =

1.
90
×
1
06
N
2
+
1
.4
×
1
06
N
2

Fnet =

3.
3
×
1
06
N
2
= 1.8 × 103
N
q = tan−1

F
F
x
y,
,
n
n
e
e
t
t

= tan−1

−
1.
1
3
.
8
2
×
×
1
1
0
0
3
3
N
N


q = −41°
Fnet =
b. anet = 
F
m
net
 = 
2
1
.5
.8
5
×
×
1
1
0
0
3
3
N
kg

anet =
c. Because vi = 0
∆y = 
1
2
 ay,net ∆t2
∆x = 
1
2
 ax,net ∆t2
∆x = 
a
a
x
y,
,
n
n
e
e
t
t
 ∆y = ∆y = 
ta
∆
n
y
q

∆x = 
ta
−
n
4
(
5
−
.0
41
m
°)
 = 52 m
anet(cos q)

anet(sin q)
0.71 m/s2
1.8 × 103
N at 41° below the horizontal

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. m = 11.0 kg
mk = 0.39
g = 9.81 m/s2
Givens Solutions
2. m = 2.20 × 105
kg
ms = 0.220
g = 9.81 m/s2
Fs,max = msFn = msmg
Fs,max = (0.220)(2.20 × 105
kg)(9.91 m/s2
) = 4.75 × 105
N
3. m = 25.0 kg
Fapplied = 59.0 N
q = 38.0°
ms = 0.599
g = 9.81 m/s2
Fs,max = msFm
Fn = mg(cos q) + Fapplied
Fs,max = ms[mg(cos q) = Fapplied] = (0.599)[(25.0 kg)(9.81 m/s2
)(cos 38.0° + 59.0 N]
Fs,max = (0.599)(193 N + 59 N) = (0.599)(252 N) =
Alternatively,
Fnet = mg(sin q) − Fs,max = 0
Fs,max = mg(sin q) = (25.0 kg)(9.81 m/s2
)(sin 38.0°) = 151 N
151 N
Fk = mkFn = mkmg
Fk = (0.39) (11.0 kg)(9.81 m/s2
) = 42.1 N
4. q = 38.0°
g = 9.81 m/s2
Fnet = mg(sin q) − Fk = 0
Fk = mkFn = mkmg(cos q)
mkmg(cos q) = mg(sin q)
mk = 
c
si
o
n
s
q
q
 = tan q = tan 38.0°
mk = 0.781
5. q = 5.2°
g = 9.81 m/s2
mk = 
c
si
o
n
s
q
q
 = tan q = tan 5.2°
mk = 0.091

II Ch. 4–8
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
10. m = 3.00 × 103
kg
q = 31.0°
g = 9.81 m/s2
mk = 
c
si
o
n
s
q
q
 = tan q = tan 31.0°
mk =
Fk = mkmg(cos q) = (0.601)(3.00 × 103
kg)(9.81 m/s2
)(cos 31.0°)
Fk =
Alternatively,
Fk = mg(sin q) = (3.00 × 103
kg)(9.81 m/s2
)(sin 31.0°) = 1.52 × 104
N
1.52 × 104
N
0.601
6. m = 281.5 kg
q = 30.0°
Fnet = 3mg(sin q) − ms(3mg)(cos q) − Fapplied = 0
Fapplied = mg
ms = = =
ms = 
(3
1
)
.
(
5
c
0
o
−
s 3
1
0
.0
.0
0
°)
 = 
(3)(c
0
o
.
s
5
3
0
0.0°)

ms = 0.19
(3)(sin 30.0°) − 1.00

(3)(cos 30.0°)
3(sin q) − 1.00

3(cos q)
3mg(sin q) − mg

3mg(cos q)
Givens Solutions
7. m = 1.90 × 105
kg
ms = 0.460
g = 9.81 m/s2
Fnet = Fapplied − Fk = 0
Fk = mkFn = mkmg
Fapplied = mkmg = (0.460)(1.90 × 105
kg)(9.81 m/s2
)
Fapplied = 8.57 × 105
N
8. Fapplied = 6.0 × 103
N
mk = 0.77
g = 9.81 m/s2
Fnet = Fapplied − Fk = 0
Fk = mkFn
Fn = 
Fap
m
p
k
lied
 = 
6.0
0
×
.7
1
7
03
N
 =
Fn = mg
m = 
F
g
n
 = 
7
9
.8
.8
×
1
1
m
0
/
3
s
N
2
 = 8.0 × 102
kg
7.8 × 103
N
9. Fapplied = 1.13 × 108
N
ms = 0.741
Fnet = Fapplied − Fs,max = 0
Fs,max = msFn = msmg
m = 
Fa
m
pp
sg
lied
 = 
(0.
1
7
.
4
1
1
3
)(
×
9
1
.8
0
1
8
m
N
/s2
 = 1.55 × 102
kg

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. Fapplied = 130 N
anet = 1.00 m/s2
mk = 0.158
g = 9.81 m/s2
Fk = mkFn = mkmg
manet + mkmg = Fapplied
m(anet + mkg) = Fapplied
m = 
an
F
e
a
t
p
+
pli
m
ed
kg
 =
m = = = 51 kg
130 N

2.55 m/s2
130 N

1.00 m/s2
+ 1.55 m/s2
130 N

1.00 m/s2
+ (0.158)(9.81 m/s2
)
2. Fnet = −2.00 × 104
N
q = 10.0°
mk = 0.797
g = 9.81 m/s2
Fnet = manet = mg(sin q) − Fk
m[g(sin q) − mkg(cos q)] = Fnet
m = 
g[sin q −
Fn
m
e
k
t
(cos q)]
 =
m = = 
(9.8
−
1
2.
m
00
/s
×
2
)
1
(−
04
0.
N
611)

m =
Fn = mg(cos q) = (3.34 × 103
kg)(9.81 m/s2
)(cos 10.0°) = 3.23 × 104
N
3.34 × 103
kg
−2.00 × 104
N

(9.81 m/s2
)(0.174 − 0.785)
−2.00 × 104
N

(9.81 m/s2
)[(sin 10.0°) − (0.797)(cos 10.0°)]
3. Fnet = 6.99 × 103
N
q = 45.0°
mk = 0.597
m[g(sin q) − mkg(cos q)] = Fnet
m = 
g[sin q −
Fn
m
e
k
t
(cos q)]
 =
m = = 
(9.8
6
1
.9
m
9
/
×
s2
1
)
0
(
3
0.
N
285)

m =
Fn = mg(cos q) = (2.50 × 103
kg)(9.81 m/s2
)(cos 45.0°) = 1.73 × 104
N
2.50 × 103
kg
6.99 × 103
N

(9.81 m/s2
)(0.707 − 0.422)
6.99 × 103
N

(9.81 m/s2
)[(sin 45.0°) − (0.597)(cos 45.0°)]
4. m = 9.50 kg
q = 30.0 °
Fapplied = 80.0 N
anet = 1.64 m/s2
g = 9.81 m/s2
Fnet = manet = Fapplied − Fk − mg(sin q)
mkmg(cos q) = Fapplied − manet − mg(sin q)
mk =
mk =
80.0 N − (9.50 kg)[1.64 m/s2
+ (9.81 m/s2
)(sin 30.0°)]

(9.50 kg)(9.81 m/s2
)(cos 30.0°)
Fapplied − m[anet + g (sin q)]

mg(cos q)
Givens Solutions

II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 4–10
6. q = 38.0°
mk = 0.100
g = 9.81 m/s2
manet = mg[sin q − mk(cos q)]
anet = g[sin q − mk(cos q)] = (9.81 m/s2
)[(sin 38.0°) − (0.100)(cos 38.0°)]
anet = (9.81 m/s2
)(0.616 − 7.88 × 10−2
) = (9.81 m/s2
)(0.537)
anet =
Acceleration is independent of the rider’s and sled’s masses. (Masses cancel.)
5.27 m/s2
mk = =
mk = =
mk = 0.222
17.9 N

(9.50 kg)(9.81 m/s2
)(cos 30.0°)
80.0 N − 62.1 N

(9.50 kg)(9.81 m/s2
)(cos 30.0°)
80.0 N − (9.50 kg)(6.54 m/s2
)

(9.50 kg)(9.81 m/s2
)(cos 30.0°)
80.0 N − (9.50 kg)[1.64 m/s2
+ 4.90 m/s2
)

(9.50 kg)(9.81 m/s2
)(cos 30.0°)
5. m = 1.89 × 105
kg
Fapplied = 7.6 × 105
N
anet = 0.11 m/s2
Fk = Fapplied − manet = 7.6 × 105
N − (1.89 × 105
)(0.11 m/s2
) = 7.6 × 105
N − 2.1 × 104
N
Fk = 7.4 × 105
N
7. ∆t = 6.60 s
q = 34.0°
mk = 0.198
g = 9.81 m/s2
vi = 0 m/s
manet = mg[sin q − mk(cos q)]
anet = g[sin q − mk(cos q)] = (9.81 m/s2
)[(sin 34.0°) − (0.198)(cos 34.0°)]
anet = (9.81 m/s2
)(0.559 − 0.164) = (9.81 m/s2
)(0.395)
anet =
vf = vi + anet∆t = 0 m/s + (3.87 m/s2
)(6.60 s)
vf = 25.5 m/s2
= 92.0 km/h
3.87 m/s2

Work and Energy
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. W = 1.15 × 103
J
m = 60.0 kg
g = 9.81 m/s2
q = 0°
W = Fd(cos q) = mgd(cos q)
d = 
mg(
W
cos q)
 =
d = 195 m
1.15 × 105
J

(60.0 kg)(9.81 m/s2
)(cos 0°)
Givens Solutions
2. m = 1.45 × 106
kg
g = 9.81 m/s2
q = 0°
W = 1.00 × 102
MJ
F = (2.00 × 10−2
) mg
W = Fd(cos q)
d = 
F(c
W
os q)
 =
d = 352 m
1.00 × 108
J

(2.00 × 10−2
)(1.45 × 106
kg)(9.81 m/s2
)(cos 0.00°)
3. m = 1.7 g
W = 0.15 J
anet = 1.2 m/s2
q = 0°
g = 9.81 m/s2
4. m = 5.40 × 102
kg
W = 5.30 × 104
J
g = 9.81 m/s2
q = 30.0°
q′ = 0°
W = Fd(cos q′) = Fd
F = mg(sin q)
W = mg(sin q)d
d = 
mg(
W
sin q)
 =
d = 20.0 m
5.30 × 104
J

(5.40 × 102
kg)(9.81 m/s3
)(sin 30.0°)
Fnet = manet = F − mg
F = manet + mg
W = Fd(cos q) = m(anet + g)d(cos q)
d = 
m(anet +
W
g)(cos q)
 =
d =
d = 8.0 m
0.15 J

(1.7 × 10−3
kg)(11.0 m/s2
)
0.15 J

(1.7 × 10−3
kg)(1.2 m/s2
+ 9.81 m/s2
)(cos 0°)

II Ch. 5–2
II
5. d = 5.45 m
W = 4.60 × 104
J
q = 0°
Fnet = Flift − Fg = 0
F = Flift = Fg
W = Fd(cos q) = Fgd(cos q)
Fg = 
d(c
W
os q)
 = 
(5.
4
4
.
5
60
m
×
)(
1
c
0
o
4
s
J
0°)
 = 8.44 ⫻ 103
N
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. d = 52.0 m
m = 40.0 kg
W = 2.04 × 104
J
q = 0°
F = 
d(c
W
os q)
 = 
(5
2
2
.
.
0
0
4
m
×
)
1
(c
0
o
4
s
J
0°)
 = 392 N
7. d = 646 m
W = 2.15 × 105
J
q = 0°
F = 
d(c
W
os q)
 = 
(64
2
6
.1
m
5 ×
)(
1
co
0
s
5
0
J
°)
 = 333 N
8. m = 1.02 × 103
kg
d = 18.0 m
angle of incline = q = 10.0°
q′ = 0°
g = 9.81 m/s2
mk = 0.13
Fnet = Fg − Fk = mg (sin q) − mkmg(cos q)
Wnet = Fnetd(cos q′) = mgd(cos q′)[(sin q) − mk(cos q)]
Wnet = (1.02 × 103
kg)(9.81 m/s2
)(18.0 m)(cos 0°)[(sin 10.0°) − (0.13)(cos 10.0°)]
Wnet = (1.02 × 103
kg)(9.81 m/s2
)(18.0 m)(0.174 − 0.128)
Wnet = (1.02 × 103
kg)(9.81 m/s2
)(18.0 m)(0.046)
Wnet = 8.3 × 103
J
9. d = 881.0 m
Fapplied = 40.00 N
q = 45.00°
Fk = 28.00 N
q′ = 0°
Wnet = Fnetd(cos q′)
Fnet = Fapplied(cos q) − Fk
Wnet = [Fapplied(cos q) − Fk]d(cos q′)
Wnet = [40.00 N(cos 45.00°) − 28.00° N](881.0 m)(cos q)
Wnet = (28.28 N − 28.00 N)(881.0 m) = (0.28 N)(881.0 m)
Wnet = 246.7 J
10. m = 9.7 × 103
kg
q = 45°
F = F1 = F2 = 1.2 × 103
N
d = 12 m
Wnet = Fnetd(cos q) = (F1 + F2)d(cos q) = 2Fd(cos q)
Wnet = (2)(1.2 × 103
N)(12 m)(cos 45°) = 2.0 × 104
J
11. m = 1.24 × 103
kg
F1 = 8.00 × 103
N east
F2 = 5.00 × 103
N 30.0°
south of east
d = 20.0 m south
Only F2 contributes to the work done in moving the flag south.
q = 90.0° − 30.0° = 60.0°
Wnet = Fnetd(cos q) = F2d(cos q) = (5.00 × 103
N)(20.0 m)(cos 60.0°)
Wnet = 5.00 × 104
J

II
1. ∆x = 1.00 × 102
m
∆t = 9.85 s
KE = 3.40 × 103
J
v = 
∆
∆t
x

KE = 
1
2
mv2
= 
1
2
m

∆
∆
x
t


2
m = 
2K
∆
E
x
∆
2
t2
 = = 66.0 kg
(2)(3.40 × 103
J)(9.85 s)2

(1.00 × 102
m)2
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. v = 4.00 × 102
km/h
KE = 2.10 × 107
J
m = 
2
v
K
2
E
 = = 3.40 × 103
kg
(2)(2.10 × 107
J)

(4.00 × 102
km/h)2
(103
m km)2
(1 h/3600 s)2
3. v = 50.3 km/h
KE = 6.54 × 103
J
m = 
2
v
K
2
E
 = = 67.0 kg
(2)(6.54 × 103
J)

(50.3 km/h)2
(103
m/km)2
(1 h/3600 s)
4. v = 318 km/h
KE = 3.80 MJ
m = 
2
v
K
2
E
 = = 974 kg
(2)(3.80 × 106
J)

(318 km/h)2
(103
m/km)2
(1 h/3600 s)
5. m = 51.0 kg
KE = 9.96 × 104
J
v = 
2
m
K
E

= 
(2
)(
9
5
.
9
1
6
.
0
×
kg
10

4
J)

= 62.5 m/s = 225 km/h
6. ∆x = 93.625 km
∆t = 24.00 h
m = 55 kg
a. vavg = 
∆
∆
x
t
 = 
(24
9
.
.
0
3
0
62
h
5
)(
×
3
1
6
0
0
4
0
m
s/h)
 =
b. KE = 
1
2
mv2
= 
1
2
(55 kg)(1.084 m/s)2
= 32 J
1.084 m/s
7. m = 3.38 × 1031
kg
KE = 1.10 × 1042
J
v = 
2
m
K
E

= 
(2
3
)
.
(
3
1
8
.1
×
0
1
×
0
1
3
1
0

4
k
2
g
J
)

= 2.55 × 105
m/s = 255 km/s
8. m = 680 kg
v = 56.0 km/h
KELB = 3.40 × 103
J
a. KE = 
1
2
mv2
= 
1
2
(680 kg)[(56.0 km/h)(103
m/km)(1 h/3600 s)]2
= 8.23 × 104
J
b. 
K
K
E
E
L
p
B
b
 = 
3
8
.
.
4
2
0
×
×
1
1
0
0
4
3
J
J
 = 
2
1
4

9. v = 11.2 km/s
m = 2.3 × 105
kg
KE = 
1
2
mv2
= 
1
2
(2.3 × 105
kg)(11.2 × 103
m/s)2
= 1.4 × 1013
J

II Ch. 5–4
II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. d = 227 m
m = 655 g
g = 9.81 m/s2
Fresistance = (0.0220)mg
q = 0°
KEi = 0 J
Wnet = ∆KE = KEf − KEi = KEf
Wnet = Fnetd(cos q)
Fnet = Fg − Fresistance = mg − (0.0220)mg = mg(1 − 0.0220)
KEf = mg(1 − 0.0220)d(cos q) = (655 × 10−3
kg)(9.81 m/s2
)(1 − 0.0220)(227 m)(cos 0°)
KEf = (0.655 kg)(9.81 m/s2
)(0.9780)(227 m)
KEf = 1.43 × 103
J
2. vi = 12.92 m/s
Wnet = −2830 J
m = 55.0 kg
Wnet is the work done by friction.
Wnet = ∆KE = KEf − KEi = KEf − 
1
2
mvi
2
KEf = Wnet + 
1
2
mvi
2
= − 2830 J + 
1
2
(55.0 kg)(12.92 m/s)2
= −2830 J + 4590 J
KEf = 1.76 × 103
J
3. m = 25.0 g
hi = 553 m
hf = 353 m
vi = 0 m/s
vf = 30.0 m/s
g = 9.81 m/s2
q = 0°
Wnet = ∆KE = KEf − KEi = 
1
2
 mvf
2
− 
1
2
mvi
2
Wnet = Fnetd(cos q)
Fnet = Fg − Fr = mg − Fr
d = hi − hf
Wnet = (mg − Fr)(hi − hf)(cos q)
mg − Fr =

1
2
 m (vf
2
− vi
2
)
(hi – hf)(cos q)
Fr = m
g − 
2(h
(
i
v
−
f
2
h
−
f)(
v
c
i
2
o
)
s q)

= (25.0 × 10−3
kg)
9.81 m/s2
−

Fr = (25.0 × 10−3
kg)
9.81 m/s2
− 
(
9
2
.
)
0
(
0
2.
×
00
10
×
2
1
m
02
2
/
m
s2
)


Fr = (25.0 × 10−3
kg)(9.81 m/s2
− 2.25 m/s2
) = (25.0 × 10−3
kg)(7.56 m/s2
)
Fr = 0.189 N
(30.0 m/s)2
− (0 m/s)2

(2)(553 m − 353 m)(cos 0°)
4. vi = 404 km/h
Wnet = −3.00 MJ
m = 1.00 × 103
kg
1
2
mvf
2
− 
1
2
mvi
2

1
2
mvf
2
= 
1
2
mvi
2
+ Wnet
vf = vi
2
+

2
W
m
ne
t

= [(
40
4
km
/h
)(
10
3
m
/k
m
)(
1
h
/3
60
0
s)
]2
+


(
2)
1
(
.
−
0
0
3.
0
×
0
1
×
0
3
1
k
0
g

6
J)


vf =

1.
26
×
1
04
m
2
/
s2
−
6
.0
0
×
1
03
m
2
/
s2
=

6.
6
×
1
03
m
2
/
s2

vf = 81 m/s = 290 km/h
5. m = 45.0 g
hi = 8848.0 m
hf = 8806.0 m
vi = 0 m/s
vf = 27.0 m/s
g = 9.81 m/s2
q = 0°
1
2
mvf
2
− 
1
2
mvi
2
Wnet = Fnetd(cos q)
Fnet = Fg − Fr = mg − Fr
d = hi − hf
Wnet = mg(hi − hf)(cos q) − Fr(hi − hf)(cos q)
− Fr(hi − hf)(cos q) = Fr(hi − hf)(cos 180° + q) = Wr

1
2
m(vf
2
− vi
2
) = mg(hi − hf)(cos q) + Wr

II
6. vf = 35.0 m/s
vi = 25.0 m/s
Wnet = 21 kJ
1
2
mvf
2
− 
1
2
mvi
2
m = 
v
2
f
2
W
−
n
v
et
i
2
 = =
m = 
6.0
4
×
2
1
×
0
1
2
0
m
3
J
2/s2
 = 7.0 × 101
kg
42 × 103
J

1220 m2/s2 − 625 m2/s2
(2)(21 × 103
J)

(35.0 m/s)2 − (25.0 m/s)2
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
7. vi = 104.5 km/h
vf = 
1
2
vi
mk = 0.120
g = 9.81 m/s2
q = 180°
1
2
mvf
2
− 
1
2
mvi
2
Wnet = Wkd(cos q) = Fkd(cos q) = mkmgd(cos q)

1
2
m(vf
2
− vi
2
) = mkmgd(cos q)
d = 
2m
v
k
f
g
2
(
−
co
v
s
i
2
q)
 =
d = =
d = 268 m
−(3)

1
3
0
.6
4
0
.5
0
 m/s

2

−(8)(0.120)(9.81 m/s2
)

1
3
0
.6
4
0
.5
0
 m/s

2

1
4
 − 1

−(2)(0.120)(9.81 m/s2
)

(2)(0.120)(9.81 m/s2
)(cos 180°)
Wr = m[
1
2
(vf
2
− vi
2
) − g(hi − hf)(cos q)] = (45.0 × 10−3
kg)
1
2
(27.0 m/s)2
− 
1
2
(0 m/s)2
−(9.81 m/s2
)(8848.0 m − 8806.0 m)(cos 0°)
Wr = (45.0 × 10−3
kg)[364 m2
/s2
− (9.81 m/s2
)(42.0 m)]
Wr = (45.0 × 10−3
kg)(364 m2
/s2
− 412 m2
/s2
)
Wr = (45.0 × 10−3
kg)(−48 m2
/s2
) = −2.16 J
1. h = 6.13/2 m = 3.07 m
PEg = 4.80 kJ
g = 9.81 m/s2
m = 
P
g
E
h
g
 = 
(9.81
4.
m
80
/s
×
2)
1
(
0
3
3
.0
J
7 m)
 = 1.59 × 102
kg
2. h = 1.70 m
PEg = 3.04 × 103
J
g = 9.81 m/s2
m = 
P
g
E
h
g
 = 
(9.81
3.
m
04
/s
×
2
)
1
(
0
1
3
.7
J
0 m)
 = 182 kg
3. PEg = 1.48 × 107
J
h = (0.100)(180 km)
g = 9.81 m/s2
m = 
P
g
E
h
g
 = = 83.8 kg
1.48 × 107
J

(9.81 m/s2
)(0.100)(180 × 103
m)
4. m = 3.6 × 104
kg
PEg = 8.88 × 108
J
g = 9.81 m/s2
h = 
P
m
E
g
g
 = = 2.5 × 103
m = 2.5 km
8.88 × 108
J

(3.6 × 104
kg)(9.81 m/s2
)
[(104.5 km/h)(103
m/km)(1 h/3600 s)]2
[
1
2


2
− (1)2
]

II Ch. 5–6
II
5. 
P
m
Eg
 = 20.482 m2
/s2
g = 9.81 m/s2

P
m
Eg
 = gh = 20.482 m2
/s2
h = 
20.482
g
m2
/s2
 = 
20
9
.
.
4
8
8
1
2
m
m
/
2
s
/
2
s2
 = 2.09 m
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. k = 3.0 × 104
N/m
PEelastic = 1.4 × 102
J
x = ± 
2P
E
k
el
as
tic

= ± 
(
3
2
.
)
0
(1
×
.4
1
0
×
4
1
N
0
/
2
m
J)

= +9.7 × 10−2
m = 9.7 cm
7. m = 51 kg
g = 9.81 m/s2
h = 321 m − 179 m = 142 m
k = 32 N/m
x = 179 m − 104 m = 75 m
PEtot = PEg + PEelastic
Set PEg = 0 J at the river level.
PEg = mgh = (51 kg)(9.81 m/s2
)(142 m) = 7.1 × 104
J
PEelastic = 
1
2
kx2
= 
1
2
(32 N/m)(75 m)2
= 9.0 × 104
J
PEtot = (7.1 × 104
J) + (9.0 × 104
J) = 1.6 × 105
J
8. h2 = 4080 m
h1 = 1860 m
m = 905 kg
g = 9.81 m/s2
∆PEg = PEg,2 − PEg,1 = mg(h2 − h1) = (905 kg)(9.81 m/s2
)(4080 m − 1860 m)
∆PEg = (905 kg)(9.81 m/s2
)(2220 m) = 1.97 × 107
J
9. m = 286 kg
k = 9.50 × 103
N/m
g = 9.81 m/s2
x = 59.0 cm
h1 = 1.70 m
h2 = h1 − x
a. PEelastic = 
1
2
kx2
= 
1
2
(9.50 × 103
N/m)(0.590 m)2
=
b. PEg,1 = mgh1 = (286 kg)(9.81 m/s2
)(1.70 m) =
c. h2 = 1.70 m − 0.590 m = 1.11 m
PEg,2 = mgh2 = (286 kg)(9.81 m/s2
)(1.11 m) =
d. ∆PEg = PEg,2 − PEg,1 = (3.11 × 103
J) − (4.77 × 103
J) =
The answer in part (d) is approximately equal in magnitude to that in (a); the
slight difference arises from rounding. The increase in elastic potential energy
corresponds to a decrease in gravitational potential energy; hence the difference
in signs for the two answers.
−1.66 × 103
J
3.11 × 103
J
4.77 × 103
J
1.65 × 103
J

II
10. ∆x = 9.50 × 102
m
q = 45.0°
m = 65.0 g
g = 9.81 m/s2
x = 55.0 cm
a. vx = vi(cos q) = 
∆
∆
x
t

∆t = 
vi(c
∆
o
x
s q)

vertical speed of the arrow for the first half of the flight = vi(sin q) = g

∆
2
t


vi(sin q) = 
2vi(
g
c
∆
o
x
s q)

vi = 
2(
si
n
g
q
∆
)
(
x
c
o
s
q
)

= = 96.5 m/s
KEi = 
1
2
mvi
2
= 
1
2
(65.0 × 10−3
kg)(96.5 m/s)2
=
b. From the conservation of energy,
PEelastic = KEi

1
2
kx2
= KEi
k = 
2K
x2
Ei
 = 
(55.
(
0
2)
×
(3
1
0
0
3
−2
J)
m)2
 =
c. KEi = PEg,max + KEf
KEf = 
1
2
mvx
2
= 
1
2
m[(vi(cos q)]2
= 
1
2
(65.0 × 10−3
kg)(96.5 m/s)2
(cos 45.0°)2
= 151 J
PEg,max = KEi − KEf = 303 J − 151 J = 152 J
hmax = 
PE
m
g,m
g
ax
 =
h = 238 m
152 J
 
(65.0 × 10−3 kg)(9.81 m/s2)
2.00 × 103
N/m
303 J
(9.81 m/s2
)(9.50 × 102
m)

(2)(sin 45.0°)(cos 45.0°)
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. m = 118 kg
hi = 5.00 m
g = 9.81 m/s2
vi = 0 m/s
KEf = 4.61 kJ
mghi + 
1
2
mvi
2
= mghf + KEf
mghf = mghi + 
1
2
mvi
2
− KEf
hf = hi + 
v
2
i
g
2
 − 
K
m
E
g
f
 = 5.00 m + 
(2)
(
(
0
9.
m
81
/s
m
)2
/s2)
 − 
(118
4
k
.6
g
1
)(
×
9.
1
8
0
1
3
m
J
/s2)

hf = 5.00 m − 3.98 m = 1.02 m above the ground
2. vf = 42.7 m/s
hf = 50.0 m
vi = 0 m
g = 9.81 m/s2
mghi + 
1
2
mvi
2
= mghf + 
1
2
mvf
2
hi = hf + 
vf
2
2
−
g
vi
2
 = 50.0 m + = 50.0 m + 92.9 m
hi =
The mass of the nut is not needed for the calculation.
143 m
(42.7 m/s)2
− (0 m/s)2

(2)(9.81 m/s2
)

II Ch. 5–8
II
3. hi = 3150 m
vf = 60.0 m/s
KEi = 0 J
g = 9.81 m/s2
mghi = mghf + 
1
2
mvf
2
hf = hi − 
v
2
f
g
2
 = 3150 m − 
(2
(
)
6
(
0
9
.
.
0
81
m
m
/s
/
)
s
2
2
)
 = 3150 m − 183 m
hf = 2970 m
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. hi = 1.20 × 102
m
hf = 30.0 m
m = 72.0 kg
g = 9.81 m/s2
KEi = 0 J
5. hf = 250.0 m
∆ME = −2.55 × 105
J
m = 250.0 kg
g = 9.81 m/s2
∆ME = PEf − KEi = mghf − 
1
2
mvi
2
vi = 2g
h
f
−

2
∆
m
M
E

= (2
)(
9.
81
m
/s
2
)
(2
50
.0
m
)
−

(
2)
(−
2
2
5
.
0
5
.
5
0
×
k
g
1
05
J
)


vi =

4.
90
×
1
03
m
2
/
s2
+
2
.0
4
×
1
03
m
2
/
s2
=

6.
94
×
1
03
m
2
/
s2

vi = 83.3 m/s = 3.00 × 102
km/h
6. hi = 12.3 km
m = 120.0 g
g = 9.81 m/s2
KEi = 0 J
∆h = hi − hf = 3.2 km
PEi − PEf = KEf
KEf = PEi − PEf = mghi − mghf = mg∆h
KEf = mg∆h = (0.1200 kg)(9.81 m/s2
)(3.2 × 103
m) =
PEf = mghf = mg(hi − ∆h) = (0.1200 kg)(9.81 m/s2
)(12.3 × 103
m − 3.2 × 103
m)
PEf = (0.1200 kg)(9.81 m/s2
)(9.1 × 103
m) =
Alternatively,
PEf = PEi − KEf = mghi − KEf
PEf = (0.1200 kg)(9.81 m/s2
)(12.3 × 103
m) − 3.8 × 103
J = 1.45 × 104
J − 3.8 × 103
J
PEf = 1.07 × 104
J
1.1 × 104
J
3.8 × 103
J
7. h = 68.6 m
v = 35.6 m/s
g = 9.81 m/s2
PEf = 0 J
KEi = 0 J
MEi = PEi = mgh
MEf = KEf = 
1
2
mv2
percent of energy dissipated = 
(MEi −
M
M
E
E
i
f)(100)
 =
(100)
percent of energy dissipated =
(100)
percent of energy dissipated = (100)
percent of energy dissipated = 
(673 J −
6
6
7
3
3
4
J
J)(100)
 = 
(39
6
J
7
)
3
(1
J
00)
 = 5.8 percent
(9.81 m/s2
)(68.6 m) − 
1
2
(35.6 m/s)2

(9.81 m/s2)(68.6 m)
gh − 
1
2
v2

gh
mgh − 
1
2
mv2
)

mgh
PEi − PEf = KEf
KEf = ∆PE = mg(hi − hf)
KEf = (72.0 kg)(9.81 m/s2
)(1.20 × 102
m − 30.0 m) = (72.0 kg)(9.81 m/s2
)(9.0 × 101
m)
KEf =
vf = 
2K
m
E
f

= 
(2
)(
6
7
.
2
4
.0
×
k
1
g
04
J
)


vf = 42 m/s
6.4 × 104
J

II
1. P = 56 MW
∆t = 1.0 h
W = P∆t = (56 × 106
W)(1.0 h)(3600 s/h) = 2.0 × 1011
J
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. ∆t = 62.25 min
P = 585.0 W
W = P∆t = (585.0 W)(62.25 min)(60 s/min) = 2.185 × 106
J
3. h = 106 m
m = 14.0 kg
g = 9.81 m/s2
P = 3.00 × 102
W
q = 0°
W = Fgd(cos q) = Fgd = mgh
∆t = 
W
P
 = 
m
P
gh
 = = 48.5 s
(14.0 kg)(9.81 m/s2
)(106 m)

3.00 × 102
W
4. P = 2984 W
W = 3.60 × 104
J
∆t = 
W
P
 = 
3.6
2
0
98
×
4
1
W
04
J
 = 12.1 s
5. ∆t = 3.0 min
W = 54 kJ
P = 
∆
W
t
 = = 3.0 × 102
W
54 × 103
J

(3.0 min)(60 s/min)
6. ∆t = 16.7 s
h = 18.4 m
m = 72.0 kg
g = 9.81 m/s2
q = 0°
W = Fgd (cos q) = mgh
P = 
∆
W
t
 = 
m
∆
g
t
h
 =
P = 778 W
(72.0 kg)(9.81 m/s2
)(18.4 m)

16.7 s

Section Two—Problem Workbook Solutions II Ch. 6–1
II
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
Momentum
and Collisions
Givens Solutions
1. v = 40.3 km/h
p = 6.60 × 102
kg•m/s
m = 
v
p
 = = 59.0 kg
6.60 × 102
kg•m/s

(40.3 × 103 m/h)(1 h/3600 s)
2. mh = 53 kg
v = 60.0 m/s to the east
ptot = 7.20 × 103
kg•m/s to
the east
ptot = mhv + mpv
mp = 
ptot −
v
mhv
 =
mp = = = 67 kg
4.0 × 103
kg•m/s

60.0 m/s
7.20 × 103
kg•m/s − 3.2 × 103
kg•m/s

60.0 m/s
7.20 × 103
kg•m/s − (53 kg)(60.0 m/s)

60.0 m/s
3. m1 = 1.80 × 102
kg
m2 = 7.0 × 101
kg
ptot = 2.08 × 104
kg•m/s to
the west
= −2.08 × 104
kg•m/s
v = 
m1
p
+
tot
m2
 = =
v = −83.2 m/s = 83.2 m/s to the west
−2.08 × 104
kg•m/s

2.50 × 102
kg
−2.08 × 104
kg•m/s

1.80 × 102
kg + 7.0 × 101
kg
4. m = 83.6 kg
p = 6.63 × 105
kg•m/s
v = 
m
p
 = 
6.63 ×
83
1
.
0
6
5
k
k
g
g•m/s
 = 7.93 × 103
m/s = 7.93 km/s
1. m = 9.0 × 104
kg
vi = 0 m/s
vf = 12 cm/s upward
F = 6.0 × 103
N
∆t = =
∆t = = 1.8 s
(9.0 × 104
kg)(0.12 m/s)

6.0 × 103
N
(9.0 × 104
kg)(0.12 m/s) − (9.0 × 104
kg)(0 m/s)

6.0 × 103
N
mvf − mvi

F
5. m = 6.9 × 107
kg
v = 33 km/h
6. h = 22.13 m
m = 2.00 g
g = 9.81 m/s2
p = mv = (6.9 × 107
kg)(33 × 103
m/h)(1 h/3600 s) = 6.3 × 108
kg•m/s
mgh = 
1
2
mvf
2
vf =

2g
h

p = mvf = m

2g
h
= (2.00 × 10−3
kg)

(2
)(
9.
81
m
/s
2)
(2
2.
13
m
)

p = 4.17 × 10−2
kg•m/s downward

II Ch. 6–2
II
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
2. m = 1.00 × 106
kg
vi = 0 m/s
vf = 0.20 m/s
F = 12.5 kN
∆p = mvf − mvi = (1.00 × 106
kg)(0.20 m/s) − (1.00 × 106
kg)(0 m/s)
∆p =
∆t = 
∆
F
p
 = = 16 s
2.0 × 105
kg•m/s

12.5 × 103 N
2.0 × 105
kg•m/s
Givens Solutions
3. h = 12.0 cm
F = 330 N, upward
m = 65 kg
g = 9.81 m/s2
The speed of the pogo stick before and after it presses against the ground can be de-
termined from the conservation of energy.
PEg = KE
mgh = 
1
2
mv2
v = ±

2g
h

For the pogo stick’s downward motion,
vi = −

2g
h

For the pogo stick’s upward motion,
vf = +

2g
h

∆p = mvf − mvi = m

2g
h
− m −

2g
h

∆p = 2m

2g
h

∆t = 
∆
F
p
 = 
2m

F
2g
h

 =
∆t = 0.60 s
(2)(65 kg)

(2
)(
9.
81
m
/s
2
)
(0
.1
20
m
)


330 N
4. m = 6.0 × 103
kg
F = 8.0 kN to the east
∆t = 8.0 s
vi = 0 m/s
vf = =
vf = 11 m/s, east
(8.0 × 103
N)(8.0 s) + (6.0 × 103
kg)(0 m/s)

6.0 × 103 kg
F∆t + mvi

m
5. vi = 125.5 km/h
m = 2.00 × 102
kg
F = −3.60 × 102
N
∆t = 10.0 s
vf =
vf =
vf = = =
or vf = (16.8 × 10−3
km/s)(3600 s/h) = 60.5 km/h
16.8 m/s
3.37 ⫻ 103
kg•m/s

2.00 ⫻ 102
kg
−3.60 × 103
N•s + 6.97 × 103
kg•m/s

2.00 × 102 kg
(−3.60 × 102
N)(10.0 s) + (2.00 × 102
kg)(125.5 × 103
m/h)(1 h/3600 s)

2.00 × 102 kg
F∆t + mvi

m
6. m = 45 kg
F = 1.6 × 103
N
∆t = 0.68 s
vi = 0 m/s
vf = 
F∆t
m
+ mvi
 =
vf = = 24 m/s
(1.6 × 103
N)(0.68 s)

45 kg
(1.6 × 103
N)(0.68 s) + (45 kg)(0 m/s)

45 kg

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 7. m = 4.85 × 105
kg
vi = 20.0 m/s northwest
vf = 25.0 m/s northwest
∆t = 5.00 s
F = =
F = =
F = 4.8 × 105
N northwest
2.4 × 106
kg•m/s

5.00 s
1.21 × 107
kg•m/s − 9.70 × 106
kg•m/s

5.00 s
(4.85 × 105
kg)(25.0 m/s) − (4.85 × 105
kg)(20.0 m/s)

5.00 s
mvf − mvi

∆t
Givens Solutions
8. vf = 12.5 m/s upward
m = 70.0 kg
∆t = 4.00 s
vi = 0 m/s
F = = = 219 N
F = 219 N upward
(70.0 kg)(12.5 m/s) − (70.0 kg)(0 m/s)

4.00 s
mvf − mvi

∆t
9. m = 12.0 kg
h = 40.0 m
∆t = 0.250 s
vf = 0 m/s
g = 9.81 m/s2
From conservation of energy, vi = −

2g
h

∆p = mvf − mvi = mvf − m–

2g
h

∆p = (12.0 kg)(0 m/s) + (12.0 kg)

(2
)(
9.
81
m
/s
2)
(4
0.
0
m
)
= 336 kg•m/s
F = 
∆
∆
t
p
 = = 1340 N = 1340 N upward
336 kg•m/s

0.250 s
1. F = 2.85 × 106
N backward
= −2.85 × 106
N
m = 2.0 × 107
kg
vi = 3.0 m/s forward
= +3.0 m/s
vf = 0 m/s
∆t = 21 s
∆p = F∆t = (−2.85 × 106
N)(21 s)
∆p =
∆x = 
1
2
(vi + vf)∆t = 
1
2
(3.0 m/s + 0 m/s)(21 s) = 32 m forward
−6.0 × 107
kg•m/s forward or 6.0 × 107
kg•m/s backward
2. m = 6.5 × 104
kg
F = −1.7 × 106
N
vi = 1.0 km/s
∆t = 30.0 s
∆p = F∆t = (−1.7 × 106
N)(30.0 s) =
vf = 
∆p +
m
mvi
 =
vf = = = 220 m/s
∆x = 
1
2
(vi + vf)∆t = 
1
2
(1.0 × 103
m/s + 220 m/s)(30.0 s) = 
1
2
(1.2 × 103
m/s)(30.0 s)
∆x = 1.8 × 104
m = 18 km
1.4 × 107
kg•m/s

6.5 × 104
kg
−5.1 × 107
kg•m/s + 6.5 × 107
kg•m/s

6.5 × 104
kg
−5.1 × 107
kg•m/s + (6.5 × 104
kg)(1.0 × 103
m/s)

6.5 × 104
kg
−5.1 × 107
kg•m/s

Givens Solutions
II Ch. 6–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. m = 2.03 × 104
kg
vi = 5.00 m/s to the east
= 5.00 m/s
∆t = 20.3 s
F = 1.20 × 103
N to the west
∆p = F∆t = (−1.20 × 103
N)(20.3 s) =
vf = 
∆p +
m
mvi
 =
vf = =
vf = 3.73 m/s
∆x = 
1
2
(vi + vf)∆t = 
1
2
[5.00 m/s + (3.73 m/s)](20.3 s) = 
1
2
(8.73 m/s)(20.3 s)
∆x = 88.6 m = 88.6 m to the east
7.58 × 104
kg•m/s

2.03 × 104
kg
−2.44 × 104
kg•m/s + 1.02 × 105
kg•m/s

2.03 × 104
kg
−2.44 × 104
kg•m/s + (2.03 × 104
kg)(5.00 m/s)

2.3 × 104
kg
2.44 × 104
kg•m/s to the west
4. m = 113 g
vi = 2.00 m/s to the right
vf = 0 m/s
∆t = 0.80 s
F = 
mvf
∆
−
t
mvi
 = =
F = −0.28 N =
∆x = 
1
2
(vi + vf)∆t = 
1
2
(2.00 m/s + 0 m/s)(0.80 s)
∆x = 0.80 m to the right
0.28 N to the left
−(0.113 kg)(2.00 m/s)

0.80 s
(0.113 kg)(0 m/s) − (0.113 kg)(2.00 m/s)

0.80 s
6. h = 68.6 m
m = 1.00 × 103
kg
F = −2.24 × 104
N
g = 9.81 m/s2
vf = 0 m/s
From conservation of energy,
vi =

2g
h

∆p = mvf − mvi = mvf − m

2g
h

∆t = 
∆
F
p
 = 
mvf −
F
m

2g
h

 =
∆t = =
∆x = 
1
2
(vi + vf)∆t = 
1
2
(

2g
h
+ vf)∆t
∆x = 
1
2


(2
)(
9.
81
m
/s
2
)
(6
8.
6
m
)
+ 0 m/s(1.64 s) = 30.1 m
1.64 s
−(1.00 × 103
kg)

(2
)(
9.
81
m
/s
2
)
(6
8.
6
m
)


−2.24 × 104
N
(1.00 × 103
kg)(0 m/s) − (1.00 × 103
kg)

(2
)(
9.
81
. m
/s
2
)
(6
8.
6
m
)


−2.24 × 104
N
5. m = 4.90 × 106
kg
vi = 0.200 m/s
vf = 0 m/s
∆t = 10.0 s
F = 
∆
∆
p
t
 = 
mvf
∆
−
t
mvi
 =
F = ⫽ –9.80 ⫻ 104
N
F =
∆x = 
1
2
(vi + vf)∆t = 
1
2
(0.200 m/s + 0 m/s)(10.0 s)
∆x = 1.00 m
9.80 × 104
N opposite the palace’s direction of motion
–(4.90 ⫻ 106
kg)(0.200 m/s)

10.0 s
(4.90 × 106
kg)(0 m/s) − (4.90 × 106
kg)(0.200 m/s)

10.0 s

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 7. m = 100.0 kg
vi = 4.5 × 102
m/s
vf = 0 m/s
F = −188 N
∆t = 
mvf
F
− mvi
 =
∆t = =
∆x = 
1
2
(vi + vf)∆t = 
1
2
(4.5 × 102
m/s + 0 m/s)(240 s) = 5.4 × 104
m = 54 km
The tunnel is long.
54 km
240 s
−(100.0 kg)(4.5 × 102
m/s)

−188 N
(100.0 kg)(0 m/s) − (100.0 kg)(4.5 × 102
m/s)

−188 N
Givens Solutions
1. m1 = 3.3 × 103
kg
v1,i = 0 m/s
v2,i = 0 m/s
v2,f = 2.5 m/s to the right
= ⫹2.5 m/s
v1,f = 0.050 m/s to the left
= –0.050 m/s
Because the initial momentum is zero, the final momentum is also zero, and so
m2 = 
−m
v2
1v
,f
1,f
 = = 66 kg
−(3.3 × 103
kg)(−0.050 m/s)

2.5 m/s
2. m1 = 1.25 × 103
kg
v1,i = 0 m/s
v2,i = 0 m/s
v2,f = 1.40 m/s backward
= –1.40 m/s
∆t1 = 4.0 s
∆x1 = 24 cm forward
= ⫹24 cm
Because the initial momentum is zero, the final momentum is also zero, and so
v1,f = 
∆
∆
x
t1
1
 = 
0
4
.2
.0
4
s
m
 = 0.060 m/s forward
m2 = 
−m
v2
1v
,f
1,f
 = = 54 kg
−(1.25 × 103
kg)(0.060 m/s)

−1.40 m/s
3. m1 = 114 kg
v2, f = 5.32 m/s backward
= −5.32 m/s
v1, f = 3.41 m/s forward
= +3.41 m/s
m2 = 60.0 kg
m1vi + m2vi = m1v1, f + m2v2, f
vi = 
m1v
m
1,
1
f
+
+
m
m
2
2v2, f
 =
vi = = 
7.0 ×
1
1
7
0
4
1
k
k
g
g•m/s
 = 0.40 m/s
vi = 0.40 m/s forward
389 kg•m/s − 319 kg•m/s

174 kg
(114 kg)(3.41 m/s) + (60.0 kg)(−5.32 m/s)

114 kg + 60.0 kg
4. m1 = 5.4 kg
v1, f = 7.4 m/s forward
= +7.4 m/s
v2, f = 1.4 m/s backward
= −1.4 m/s
m2 = 50.0 kg
m1vi + m2vi = m1v1, f + m2v2, f
vi = =
vi = = 
−3.0 ×
55
1
.
0
4
1
k
k
g
g•m/s
 = –0.54 m/s
vi = 0.54 m/s backward
4.0 × 101
kg•m/s − 7.0 × 101
kg•m/s

55.4 kg
(5.4 kg)(7.4 m/s) + (50.0 kg)(−1.4 m/s)

5.4 kg + 50.0 kg
m1v1, f + m2v2, f

m1 + m2

5. m1 = 3.4 × 102
kg
v2, f = 9.0 km/h northwest
= −9.0 km/h
v1, f = 28 km/h southeast
= +28 km/h
m2 = 2.6 × 102
kg
m1vi + m2vi = m1v1, f + m2v2, f
vi = =
vi = =
vi = 12 km/h to the southeast
7.2 × 103
kg•km/h

6.0 × 102
kg
9.5 × 103
kg•km/h − 2.3 × 103
kg•km/h

6.0 × 102
kg
(3.4 × 102
kg)(28 km/h) + (2.6 × 102
kg)(−9.0 km/h)

3.4 × 102
kg + 2.6 × 102
kg
m1v1, f + m2v2, f

m1 + m2
Givens Solutions
6. mi = 3.6 kg
m2 = 3.0 kg
v1,i = 0 m/s
v2,i = 0 m/s
v2,f = 2.0 m/s to the left
= –2.0 m/s
Because the initial momentum is zero, the final momentum must also equal zero.
miv1,f = −m2v2,f
v1,f = 
−m
m
2v
1
2,f
 = = 1.7 m/s = 1.7 m/s to the right
−(3.0 kg)(−2.0 m/s)

3.6 kg
7. m1 = 449 kg
v1,i = 0 m/s
v2,i = 0 m/s
v2,f = 4.0 m/s backward
= –4.0 m/s
m2 = 60.0 kg
∆t = 3.0 s
Because the initial momentum is zero, the final momentum must also equal zero.
v1,f = 
−m
m
2
1
v2,f
 = = 0.53 m/s = 0.53 m/s forward
∆x = v1,f∆t = (0.53 m/s)(3.0 s) = 1.6 m forward
−(60.0 kg)(−4.0 m/s)

449 kg
1. m1 = 155 kg
v1,i = 6.0 m/s forward
v2,i = 0 m/s
vf = 2.2 m/s forward
m2 = =
m2 = =
m2 = 270 kg
590 kg•m/s

2.2 m/s
930 kg•m/s –340 kg•m/s

2.2 m/s
(155 kg)(6.0 m/s) − (155 kg)(2.2 m/s)

2.2 m/s − 0 m/s
m1v1,i − m1vf

vf − v2,i
II Ch. 6–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. v1,i = 10.8 m/s
v2,i = 0 m/s
vf = 10.1 m/s
m1 = 63.0 kg
m2 = =
m2 = = = 4.4 kg
44 kg•m/s

10.1 m/s
6.80 × 102
kg•m/s − 6.36 × 102
kg•m/s

10.1 m/s
(63.0 kg)(10.8 m/s) − (63.0 kg)(10.1 m/s)

10.1 m/s − 0 m/s
m1v1,i − m1vf

vf − v2,i
3. v1, i = 4.48 m/s to the right
v2, i = 0 m/s
vf = 4.00 m/s to the right
m2 = 54 kg
m1 = = 
(54 k
0
g
.
)
4
(
8
4
m
.00
/s
m/s)

m1 = 450 kg
(54 kg)(4.00 m/s) − (54 kg)(0 m/s)

4.48 m/s − 4.00 m/s

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. m1 = 9.50 kg
v1, i = 24.0 km/h to the north
m2 = 32.0 kg
vf = 11.0 km/h to the north
v2, i =
v2, i =
v2, i = =
= 
228
32
k
.
g
0
•k
k
m
g
/h

v2, i = 7.12 km/h to the north
456 kg•km/h − 228 kg•km/h

32.0 kg
(41.5 kg)(11.0 km/h) − 228 kg•km/h

32.0 kg
(9.5 kg + 32.0 kg)(11.0 km/h) − (9.50 kg)(24.0 km/h)

32.0 kg
(m1 + m2)vf − m1v,1

m2
7. m1 = m2
v1,i = 89 km/h
v2,i = 69 km/h
Because m1 = m2, vf = 
v1,i +
2
v2,i
 = = 
158 k
2
m/h
 = 79 km/h
vf = 79 km/h
89 km/h + 69 km/h

2
8. m1 = 3.0 × 103
kg
m2 = 2.5 × 102
kg
v2,i = 3.0 m/s down
= –3.0 m/s
v1,i = 1.0 m/s up = +1.0 m/s
vf = =
vf = =
vf = 0.69 m/s = 0.69 m/s upward
2.2 ⫻ 103
kg•m/s

3.2 ⫻ 103
kg
3.0 ⫻103
kg•m/s –7.5 ⫻ 102
kg•m/s

3.2 ⫻ 103
kg
(3.0 × 103
kg)(1.0 m/s) + (2.5 × 102
kg)(−3.0 m/s)

(3.0 × 103 kg) + (2.5 × 102 kg)
m1v1,i + m2v2,i

m1 + m2
9. m1 = (2.267 × 103
kg) +
(5.00 × 102
kg) = 2.767 ×
103
kg
m2 = (1.800 × 103
kg) +
(5.00 × 102
kg) = 2.300 ×
103
kg
v1,i = 2.00 m/s to the left
= –2.00 m/s
v2,i = 1.40 m/s to the right
= +1.40 m/s
vf = =
vf = = 
–23
5
1
0
0
67
kg
k
•
g
m/s
 = –0.456 m/s
vf = 0.456 m/s to the left
–5.53 ⫻103
kg•m/s + 3220 kg•m/s

5.067 × 103 kg
(2.767 × 103
kg)(−2.00 m/s) + (2.300 × 103
kg)(1.40 m/s)

2.767 × 103 kg + 2.300 × 103 kg
m1v1,i + m2v2,i

m1 + m2
4. m1 = 28 × 103
kg
m2 = 12 × 103
kg
v1,i = 0 m/s
vf = 3.0 m/s forward
v2,i =
v2,i =
v2,i =
v2,i = 1.0 × 101
m/s forward
(4.0 ⫻ 104
kg)(3.0 m/s)

12 ⫻ 103
kg
(28 × 103
kg + 12 × 103
kg)(3.0 m/s) − (28 × 103
kg)(0 m/s)

12 × 103 kg
(m1 + m2)vf − m1v1,i

m2
5. m1 = 227 kg
m2 = 267 kg
v1,i = 4.00 m/s to the left
= –4.00 m/s
vf = 0 m/s
v2,i =
v2,i = = 3.40 m/s
v2,i = 3.40 m/s to the right
(227 kg + 267 kg)(0 m/s) − (227 kg)(–4.00 m/s)

267 kg
(m1 + m2)vf − m1v1,i

m2
Givens Solutions

Givens Solutions
1. m1 = 2.0 g
v1,i = 2.0 m/s forward
= +2.0 m/s
m2 = 0.20 g
v2,i = 8.0 m/s backward
= −8.0 m/s forward
vf =
vf =
vf =
vf = 
2.4
2
⫻
.2 ⫻
10
–
1
3
0
k
–3
g•
k
m
g
/s
 = 1.1 m/s forward
KEi = 
1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
KEi = 
2
1
(2.0 × 10−3
kg)(2.0 m/s)2
+ 
2
1
(0.20 × 10−3
kg)(−8.0 m/s)2
KEi = 4.0 × 10−3
J + 6.4 × 10−3
J = 1.04 × 10−3
J
KEf = 
2
1
(m1 + m2)vf
2
= 
2
1
(2.0 × 10−3
kg + 0.20 × 10−3
kg)(1.1 m/s)2
KEf = 
2
1
(2.2 × 10−3
kg)(1.1 m/s)2
∆KE = KEf − KEi = 1.3 × 10−3
J − 1.04 × 10−2
J = −9.1 × 10−3
J
fraction of total KE dissipated = 
∆
K
K
E
E
i
 = = 0.88
9.1 × 10−3
J

1.04 × 10−2 J
4.0 ⫻ 10–3
kg•m/s − 1.6 ⫻ 10–3
kg•m/s

2.2 ⫻ 10–3
kg
(2.0 ⫻ 10–3
kg)(2.0 m/s) + (0.20 ⫻ 10–3
kg)(−8.0 m/s)

2.0 ⫻ 10–3
kg + 0.20 ⫻ 10–3
kg
m1v1,i + m2v2,i

m1 + m2
II Ch. 6–8
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. m1 = 313 kg
v1,i = 6.00 m/s away from
shore
v2,i = 0 m/s
vf = 2.50 m/s away from
shore
m2 = =
m2 = = = 4.4 × 102
kg
KEi = 
2
1
m1v1,i
2
+ 
2
1
m2v2,i
2
KEi = 
2
1
(313 kg)(6.00 m/s)2
+ 
2
1
(4.40 × 102
kg)(0 m/s)2
= 5630 J
KEf = 
2
1
(m1 + m2)vf
2
KEf = 

2
1
(313 kg + 4.40 × 102
kg)(2.50 m/s)2
= 
2
1
(753 kg)(2.50 m/s)2
= 2350 J
∆KE = KEf − KEi = 2350 J − 5630 J = −3280 J
1.10 × 103
kg•m/s

2.50 m/s
1880 kg•m/s − 782 kg•m/s

2.50 m/s
(313 kg)(6.00 m/s) − (313 kg)(2.50 m/s)

2.50 m/s − 0 m/s
m1v1,i − m1vf

vf − v2,i
3. m1 = m2 = 111 kg
v1, i = 9.00 m/s to the right
= +9.00 m/s
v2, i = 5.00 m/s to the left
= −5.00 m/s
vf = 
m1v
m
1,
1
i +
+
m
m
2
2
v2, i
 =
vf = = 
44
2
4
2
k
2
g
k
•m
g
/s
 = 2.00 m/s to the right
KEi = 
2
1
m1v1,i
2
+ 
2
1
m2v2,i
2
= 
2
1
(111 kg)(9.00 m/s)2
+ 
2
1
(111 kg)(–5.00 m/s)2
KEi = 4.50 × 103
J + 1.39 × 103
J = 5.89 × 103
J
KEf = 

1
2
(m1 + m2)vf
2
= 
2
1
(111 kg ⫹ 111 kg)(2.00 m/s)2
= 
2
1
(222 kg)(2.00 m/s)
KEf = 444 J
∆KE = KEf − KEi = 444 J − 5.89 × 103
J = −5450 J
999 kg•m/s − 555 kg•m/s

222 kg
(111 kg)(9.00 m/s) + (111 kg)(−5.00 m/s)

111 kg + 111 kg

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
5. m1 = 4.00 × 105
kg
v1, i = 32.0 km/h
m2 = 1.60 × 105
kg
v2, i = 45.0 km/h
vf = 
m1v
m
1,
1
i +
+
m
m2
2v2,i
 =
vf = =
vf = 35.7 km/h
KEi = 
1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
KEi = 
1
2
(4.00 × 105
kg)(32.0 × 103
m/h)(1 h/3600 s)2
+ 
1
2
(1.60 × 105
kg)
(45.0 × 103
m/h)2
(1 h/3600 s)2
KEi = 1.58 × 107
J + 1.25 × 107
J = 2.83 × 107
J
KEf = 
1
2
(m1 + m2)vf
2
KEf = 
1
2
(4.00 × 105
kg + 1.60 × 105
kg)(35.7 × 103
m/h)2
(1 h/3600 s)2
= 
1
2
(5.60 × 105
kg)(35.7 × 103
m/h)2
(1 h/3600 s)2
KEf = 2.75 × 107
J
∆KE = KEf − KEi = 2.75 × 107
J − 2.83 × 107
J = −8 × 105
J
2.00 × 107
kg•km/h

5.60 × 105
kg
1.28 × 107
kg•km/h + 7.20 × 106
kg•km/h

5.60 × 105
kg
(4.00 × 105
kg)(32.0 km/h) + (1.60 × 105
kg)(45.0 km/h)

4.00 × 105
kg + 1.60 × 105
kg
4. m1 = m2 = 60.0 kg + 50.0 kg
= 110.0 kg
v1, i = 106.0 km/h to the east
= +106.0 km/h
v2, i = 75.0 km/h to the west
= −75.0 km/h
vf = =
vf = = 
3.41 ×
22
1
0
0
.
3
0
k
k
g
g
•km/h

vf = 15.5 km/h to the east
KEi = 
1
2
m1v1, i
2
+ 
1
2
m2v2, i
2
KEi = 
1
2
(110.0 kg)(106.0 × 103
m/h)2
(1 h/3600 s)2
+ 
1
2
(110.0 kg)(−75.0 × 103
m/h)2
(1 h/3600 s)2
KEi = 4.768 × 104
J + 2.39 × 104
J = 7.16 × 104
J
KEf = 
1
2
(m1 + m2)vf
2
KEf = 
1
2
(110.0 kg + 110.0 kg)(15.5 × 103
m/h)2
(1 h/3600 s)2
= 
1
2
(220.0 kg)(15.5 × 103
m/h)2
(1 h/3600 s)2
KEf = 2.04 × 103
J
∆KE = KEf − KEi = 2.04 × 103
J − 7.16 × 104
J = −6.96 × 104
J
1.166 × 104
kg•km/h − 8.25 × 103
kg•km/h

220.0 kg
(110.0 kg)(106.0 km/h) + (110.0 kg)(−75.0 km/h)

110.0 kg + 110.0 kg
m1v1,i + m2v2,i

m1 + m2

Givens Solutions
II Ch. 6–10
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. m1 = 21.3 kg
v1,i = 0 m/s
m2 = 1.80 × 10−1
kg
vf = 6.00 × 10−2
m/s
v2,i = 
(m1 + m
m
2)
2
vf –m1v1,i

v2,i =
v2,i = ⫽ 7.17 m/s
KEi = 
1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
KEi = 
1
2
(21.3 kg)(0 m/s)2
+ 
1
2
(1.80 × 10−1
kg)(7.17 m/s)2
KEi = 0 J⫹ 4.63 J = 4.63 J
KEf = 
1
2
(m1 + m2)vf
2
KEf = 
1
2
(21.3 kg ⫹ 0.180 kg)(6.00 × 10−2
m/s)2
= 
1
2
(21.5 kg)(6.00 × 10−2
m/s)2
KEf = 3.87 × 10−2
J
∆KE = KEf − KEi = 3.87 × 10−2
J − 4.63 J = −4.59 J
(21.5 kg)(6.00 ⫻ 10−2
m/s)

1.80 ⫻ 10–1
kg
(21.3 kg + 1.80 × 10−1
kg)(6.00 × 10−2
m/s) – (21.3 kg)(0 m/s)

1.80 × 10−1 kg
7. m1 = 122 g
m2 = 96.0 g
v2,i = 0 m/s
Because v2,i = 0 m/s, m1v1,i = (m1 + m2)vf
v1,i =
fraction of KE dissipated = 
∆
K
K
E
E
i
 = 
KEf
K
−
Ei
KEi
 =
fraction of KE dissipated =
m1vf
2
+ m2vf
2
−

(m1vf )2
+ 2m1m2vf
2
+ (m2vf )2

m1
(m1 + m2)vf
2
− m1
(m1 +
m
m
1
2)vf


2

m1
(m1 +
m
m
1
2)vf


2

1
2

m1 + m2vf
2
− 
1
2
m1v1,i
2


1
2
m1v1,i
2
(m1 + m2)vf

m1

(m1vf )2
+ 2m1m2vf
2
+ (m2vf )2

m1
fraction of KE dissipated = =
fraction of KE dissipated = = =
The fraction of kinetic energy dissipated can be determined without the initial veloc-
ity because this value cancels, as shown above. The initial velocity is needed to find
the decrease in kinetic energy.
−0.440
−171.5 g

3.90 × 102 g
−96.0 g − 75.5 g

122 g + 192 g + 75.5 g
−96.0 g −

(9
1
6
2
.0
2
g
g
)2



122 g + (2)(96.0 g) +

(9
1
6
2
.0
2
g
g
)2


−m2 − 
m
m
2
1
2


m1 + 2m2 + 
m
m
2
1
2

vf
2
m1 + m2 − m1 − 2m2 − 
m
m
2
1
2



vf
2
m1 + 2m2 + 
m
m
2
1
2


II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Additional Practice G
Givens Solutions
2. m1 = 18.40 kg
m2 = 56.20 kg
= −5.000 m/s
v2, f = 6.600 × 10−2
m/s to
the left
= − 6.600 × 10−2
m/s
v1, f = 10.07 m/s to the left
= −10.07 m/s
Momentum conservation
m1v1, i + m2v2, i = m1v1, f + m2v2, f
v1, i =
v1, i =
v1, i = = 
92
1
.
8
0
.4
k
0
g•
k
m
g
/s
 = 5.00 m/s
v1, i =
Conservation of kinetic energy (check)

1
2
m1v1, i
2
+ 
1
2
m2v2, i
2
= 
1
2
m1v1, f
2
+ 
1
2
m2v2, f
2

1
2
(18.40 kg)(5.00 m/s)2
+ 
1
2
(56.20)(−5.000 m/s)2
= 
1
2
(18.40 kg)(−10.07 ms)2
+ 
1
2
(56.20 kg)(−6.600 × 10−2
m/s)2
2.30 × 102
J + 702.5 J = 932.9 J + 0.1224 J
932 J = 933 J
The slight difference arises from rounding.
−185.3 kg•m/s − 3.709 kg•m/s + 281.0 kg•m/s

18.40 kg
(18.40 kg)(−10.07 m/s) + (56.20 kg)(−6.600 × 10−2
m/s) − (56.20 kg)(−5.000 m/s)

18.40 kg
m1v1, f + m2v2, f − m2v2, i

m1
1. m2 = 0.500 m1
v1, i = 3.680 × 103
km/h
v1, f = −4.40 × 102
km/h
v2, f = 5.740 × 103
km/h
m1v1, i + m2v2, i = m1v1, f + m2v2, f
v2, i = =
v2, i = (2.00)v1, f + v2, f − (2.00)v1, i = (2.00)(−4.40 × 102
km/h) + 5.740 × 103
km/h
− (2.00)(3.680 × 103
km/h) = −8.80 × 102
km/h + 5.740 × 103
km/h
− 7.36 × 103
km/h
v2, i =

1
2
m1v1, i
2
+ 
1
2
m2v2, i
2
= 
1
2
m1v1, f
2
+ 
1
2
m2v2, f
2

1
2
m1v1, i
2
+ 
1
2
(0.500)m1v2, i
2
= 
1
2
m1v1, f
2
+ 
1
2
(0.500)m1v2, f
2
v1, i
2
+ (0.500)v2, i
2
= v1, f
2
+ (0.500)v2, f
2
(3.680 × 103
km/h)2
+ (0.500)(−2.50 × 103
km/h)2
= (−4.40 × 102
km/h)2
+ (0.500)
(5.740 × 103
km/h)2
1.354 × 107
km2
/h2
+ 3.12 × 106
km2
/h2
= 1.94 × 105
km2
/h2
+ 1.647 × 107
km2
/h2
1.666 × 107
km2
/h2
= 1.666 × 107
km2
/h2
−2.50 × 103
km/h
m1v1, f + (0.500)m1v2, f − m1v1, i

(0.500)m1
m1v1, f + m2v2, f − m1v1, i

m2

Givens Solutions
II Ch. 6–12
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. m1 = m2
= +5.0 m/s
v1, f = 2.0 m/s to the left
= −2.0 m/s
v2, f = 5.0 m/s to the right
= +5.0 m/s
m1v1, i + m2v2, i = m1v1, f + m2v2, f
v2, i = = v1, f + v2, f − v1, i
v2, i = −2.0 m/s + 5.0 m/s − 5.0 m/s = −2.0 m/s
v2, i =

1
2
miv1, i
2
+ 
1
2
m2v2, i
2
= 
1
2
m1v1, f
2
+ 
1
2
m2v2, f
2
v1,i
2
+ v2,i
2
= v1,f
2
+ v2,f
2
(5.0 m/s)2
+ (−2.0 m/s)2
= (−2.0 m/s)2
+ (5.0 m/s)2
25 m2
/s2
+ 4.0 m2
/s2
= 4.0 m2
/s2
+ 25 m2
/s2
29 m2
/s2
= 29 m2
/s2
2.0 m/s to the left
m1v1, f + m2v2, f − m1v1, i

m2
4. m1 = 45.0 g
v1, i = 273 km/h to the right
= +273 km/h
v2, i = 0 km/h
v1, f = 91 km/h to the left
= −91 km/h
v2, f = 182 km/h to the right
= +182 km/h
m1v1, i + m2v2, i = m1v1, f + m2v2, f
m2 = 
m1v
v
1
2
,
,
f
i −
−
v
m
2
1
,
v
f
1, i
 =
m2 = =
m2 =

1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
= 
1
2
m1v1, f
2
+ 
1
2
m2v2, f

1
2
(45.0 g)(273 ⫻ 103
m/h)2
(1 h/3600 s)2
+ 
1
2
(90.1 g)(0 m/s)2
= 
1
2
(45.0 g)(−91 × 103
m/h)2
(1 h/3600 s)2
+ 
1
2
(90.1 g)(182 × 103
m/h)2
(1 h/3600 s)2
129 J + 0 J = 14 J + 115 J
129 J = 129 J
90.1 g
−16.4 ⫻ 103
g •km/h

−182 km/h
−4.1 ⫻ 103
g •km/h − 12.3 ⫻ 103
g •km/h

−182 km/h
(45.0 g)(−91 km/h) − (45.0 g)(273 km/h)

0 km/h − 182 km/h
5. v1,i = 185 km/h to the right
⫽ ⫹185 km/h
v2,i = 0 km/h
vi,f = 80.0 km/h to the left
= −80.0 km/h
m1 = 5.70 ⫻ 10–2
kg
m1v1, i + m2v2,i = m1v1,f + m2v2,f

m
m
1
2

v1,i −

m
m
1
2

v1,f = v2,f –v2,i

m
m
1
2

[185 km/h − (−80.0 km/h)] = v2,f − 0 km/h
v2,f =

m
m
1
2

(265 km/h) to the right
Conservation of kinetic energy
KEi = 
1
2
m1v1,i
2
+ 
1
2
m2v2,i
2
= 
1
2
m1v1,i
2
KEf = 
1
2
m1v1,f
2
+ 
1
2
m2v2,f
2

1
2
m1v1,i
2
= 
1
2
m1v1,f
2
+ 
1
2
m2v2,f
2

m
m
1
2

(v1,i)2
=

m
m
1
2

(v1,f)2
+ v2,f
2

m
m
1
2

(185 km/h)2
=

m
m
1
2

(−80.0 km/h)2
+ v2,f
2

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions

m
m
1
2


(3
.4
2
×
1
04
k
m
2
/
h
2
)
−


m
m
1
2


(6
.4
0
×
1
03
k
m
2
/
h
2
)
= v2,f
v2,f = 
m
m
1
2


(2
.7
8
×
1
04
k
m2

/h
2
) = 
m
m
1
2

167 km/h

Equating the two results for v2,f yields the ratio of m1 to m2.

m
m
1
2

(265 km/h) = 
m
m
1
2

(167 km/h)
265 km/h = 
m
m
2
1

(167 km/h)

m
m
2
1
 =

2
1
6
6
5
7
k
k
m
m
/
/
h
h


2
= 2.52
m2 = (2.52) m1 ⫽ (2.52)(5.70 ⫻ 10–2
kg)
m2 = 0.144 kg
6. m1 = 4.00 × 105
kg
m2 = 1.60 × 105
kg
v1, i = 32.0 km/h to the right
v2, i = 36.0 km/h to the right
v1, f = 35.5 km/h to the right
m1v1, i + m2v2, i = m1v1, f + m2v2, f
v2, f =
v2, f =
v2, f =
v2, f = 
4.4
1
×
.6
1
0
0
×
6
1
k
0
g
5
•k
k
m
g
/h

v2, f =

1
2
m1v1, i
2
+ 
1
2
m2v2, i
2
= 
1
2
m1v1, f
2
+ 
1
2
m2v2, f
2

1
2
(4.00 × 105
kg)(32.0 × 103
m/h)2
(1 h/3600 s)2
+ 
1
2
(1.60 × 105
kg)(36.0 × 103
m/h)2
(1 h/3600 s)2
= 
1
2
(4.00 × 105
kg)(35.5 × 103
m/h)2
(1 h/3600 s)2
+ 
1
2
(1.60 × 105
kg)
(28 ⫻ 103
m/h)2
(1 h/3600 s)2
1.58 × 107
J + 8.00 × 106
J = 1.94 × 107
J + 4.8 × 106
J
2.38 × 107
J = 2.42 × 107
J
28 km/h to the right
1.28 × 107
kg•km/h + 5.76 × 106
kg•km/h − 1.42 × 107
kg•km/h

1.60 × 105
kg
(4.00 × 105
kg)(32.0 km/h) + (1.60 × 105
kg)(36.0 km/h) − (4.00 × 105
kg)(35.5 km/h)

1.60 × 105
kg
m1v1, i + m2v2, i − m1v1, f

m2

7. m1 = 5.50 × 105
kg
m2 = 2.30 × 105
kg
= +5.00 m/s
= −5.00 m/s
v2, f = 9.10 m/s to the right
= +9.10 m/s
m1v1,i + m2v2,i = m1v1,f + m2v2,f
v1,f =
v1,f =
v1,f = = −0.89 m/s right
v1,f =

1
2
m1v1, i
2
+ 
1
2
m2v2, i
2
= 
1
2
 m1v1, f
2
+ 
1
2
m2v2, f
2

1
2
(5.50 × 105
kg)(5.00 m/s)2
+ 
1
2
(2.30 × 105
kg)(−5.00 m/s)2
= 
1
2
(5.50 × 105
kg)
(−0.89 m/s)2
+ 
1
2
(2.30 × 105
kg)(9.10 × m/s)2
6.88 × 106
J + 2.88 × 106
J = 2.2 × 105
J + 9.52 × 106
J
9.76 × 106
J = 9.74 × 106
J
0.89 m/s left
2.75 ⫻ 106
kg•m/s – 1.15 ⫻106
kg•m/s –2.09 × 106
kg•m/s

5.50 × 105
kg
(5.50 × 105
kg)(5.00 m/s) + (2.30 × 105
kg)(−5.00 m/s) − (9.10 m/s)

5.50 × 105 kg
m1v1,i + m2v2,i − m2v2,f

m1
Givens Solutions
II Ch. 6–14
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

Circular Motion
and Gravitation
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
1. vt = 0.17 m/s
ac = 0.29 m/s2
r = 
v
a
t
c
2
 = 
(0
0
.
.
1
2
7
9
m
m
/
/
s
s
)
2
2
 = 0.10 m
2. vt = 465 m/s
ac = 3.4 × 10−2
m/s2
r = 

v
a
t
c
2
 = 
3.4
(4
×
6
1
5
0
m
−2
/s
m
)2
/s2
 = 6.4 × 106
m
3. r = 
58.4
2
cm
 = 29.2 cm
ac = 8.50 × 10−2
m/s2
vt =

ra
c
=

(2
9.
2
×
1
0−
2
m
)(
8.
50
×
1
0−
2
m
/s
2

vt = 0.158 m/s
4. r = 
12
2
cm
 = 6.0 cm
ac = 0.28 m/s2
vt =

ra
c
=

(6
.0
×
1
0−
2
m
)(
0.
28
m
/s
2
)
= 0.13 m/s
5. vt = 7.85 m/s
r = 20.0 m
ac = 
v
r
t
2
 = 
(7.
2
8
0
5
.0
m
m
/s)2
 = 3.08 m/s2
6. ∆t = 1.000 h
∆s = 47.112 km
r = 6.37 × 103
km
ac = 
v
r
t
2
 = = 
r
∆
∆
s
t
2
2

ac = = 2.69 × 10−5
m/s2
(47 112 m)2

(6.37 × 106 m)[(1.000 h)(3600 s/h)]2

∆
∆
s
t


2

r
1. m1 = 235 kg
m2 = 72 kg
r = 25.0 m
Fc = 1850 N
mtot = m1 + m2 = 235 kg + 72 kg = 307 kg
Fc = mtot ac = mtot 
v
r
t
2

vt =

m
r

F
to
c
t

=

(2

5.

0
3
m
0

)
7
(

1
k

8
g
5

0

N

)

= 12.3 m/s
2. m = 30.0 g
r = 2.4 m
FT = 0.393 N
g = 9.81 m/s2
FT = Fg + Fc = mg + m
v
r
t
2

vt = 
r(
F
T
m
−
m
g)

=
vt = =
vt = 2.8 m/s
(2.4 m)(0.099 N)

30.0 × 10−3
kg
(2.4 m)(0.393 N − 0.294 N)

30.0 × 10−3
kg
(2.4 m)[0.393 N − (30.0 × 10−3
kg)(9.81 m/s2
)]

30.0 × 10−3
kg

II Ch. 7–2
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
2. m1 = 3.08 × 104
kg
r = 1.27 × 107
m
Fg = 2.88 × 10−16
N
G = 6.673 × 10−11
N•m2

kg2
m2 = =
m2 = 2.26 × 104
kg
(2.88 × 10−16
N)(1.27 × 107
m)2

6.673 × 10−11

N
k
•
g
m
2
2

(3.08 × 104
kg)
Fgr2

Gm1
3. vt = 8.1 m/s
r = 4.23 m
m1 = 25 g
g = 9.81 m/s2
Fg = Fc
m1g = 
m2
r
vt
2

m2 = 
m
v
1
t
2
gr

m2 = = 1.6 × 10−2
kg
(25 × 10−3
kg)(9.81 m/s2
)(4.23 m)

(8.1 m/s)2
4. vt = 75.57 km/h
m = 92.0 kg
Fc = 12.8 N
Fc = m 
v
r
t
2

r = 
m
F
v
c
t
2
 =
r = 3.17 × 103
m = 3.17 km
(92.0 kg)[(75.57 km/h)(103
m/km)(1 h/3600 s)]2

12.8 N
5. m = 75.0 kg
r = 446 m
vt = 12 m/s
g = 9.81 m/s2
Fc = 
m
r
vt
2
 = =
FT = Fc + mg = 24 N + (75.0 kg)(9.81 m/s2
)
FT = 24 N + 736 N = 7.60 × 102
N
24 N
(75.0 kg)(12 m/s)2

446 m
1. r = 6.3 km
Fg = 2.5 × 10−2
N
m1 = 3.0 kg
G = 6.673 × 10−11
N•m2

kg2
m2 = =
m2 = 5.0 × 1015
kg
(2.5 × 10−2
N)(6.3 × 103
m)2

6.673 × 10−11

N
k
•
g
m
2
2

(3.0 kg)
Fgr2

Gm1
3. m1 = 5.81 × 104
kg
r = 25.0 m
Fg = 5.00 × 10−7
N
G = 6.673 × 10−11
N•m2

kg2
m2 = =
m2 = 80.6 kg
(5.00 × 10−7
N)(25.0 m)2

6.673 ×10−11

N
k
•
g
m
2
2

(5.81 × 104
kg)
Fgr2

Gm1

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
7. m1 = 318mE
m2 = 50.0 kg
VJ = 1323VE
mE = 5.98 × 1024
kg
rE = 6.37 × 106
m
G = 6.673 × 10−11
N•m2

kg2
If VJ = 1323 VE, then rJ =

3
13
23
rE.
Fg = 
Gm
rJ
1
2
m2
 =
Fg = 1.30 × 103
N
(6.673 × 10−11
N•m2
/kg2
)(318)(5.98 × 1024
kg)(50.0 kg)

[(

3
13
23
)(6.37 × 106 m)]2
4. m1 = 621 g
m2 = 65.0 kg
Fg = 1.0 × 10−12
N
G = 6.673 × 10−11
N•m2

kg2
r = 
G

m
F
1
g
m
2


r = = 52 m
(6.673 × 10−11 N•m2/kg2)(0.621 kg)(65.0 kg)

1.0 × 10−12 N
5. m1 = m2 = 1.0 × 108
kg
Fg = 1.0 × 10−3
N
G = 6.673 × 10−11
N•m2

kg2
r = 
G

m
F
1
g
m
2


r =
r = 2.6 × 104
m = 26 km
(6.673 × 10−11 N•m2/kg2)(1.0 × 108
kg)2

1.0 × 10−3 N
6. ms = 25 × 109
kg
m1 = m2 = 
1
2
ms
r = 1.0 × 103
km
G = 6.673 × 10−11
N•m2

kg2
Fg = 
Gm
r
1
2
m2
 = = 1.0 × 10−2
N
6.673 × 10−11 
N
k
•
g
m
2
2


1
2
(25 × 109
kg)2

(1.0 × 106 m)2
1. T = 88 643 s
m = 6.42 × 1023
kg
rm = 3.40 × 106
m
r =
3
=
3

r = 2.04 × 107
m
rs = r − rm = 2.04 × 107
m − 3.40 × 106
m = 1.70 × 107
m
6.673 × 10−11

N
k
•
g
m
2
2

(6.42 × 1023
kg)(88 643 s)2

4p2
GmT2

4p2
2. T = 5.51 × 105
s
m = 1.25 × 1022
kg
r =
3
=
3

r = 1.86 × 107
m
6.673 × 10−11

N
k
•
g
m
2
2

(1.25 × 1022
kg)(5.51 × 105
s)2

4p2
GmT2

4p2

6.673
× 10−1
1
N
k
•
g
m
2
2


5
6
.9
.7
7
4
×
×
1
1
0
0
2
6
4
m
kg


6.673
× 10−1
1
N
k
•
g
m
2
2


5
6
.9
.7
7
4
×
×
1
1
0
0
2
6
4
m
kg


II Ch. 7–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
3. r = 4.22 × 107
m
m = 5.97 × 1024
kg
vt = G
m
r

=
6.673 × 10−11

N
k
•
g
m
2
2

= 3.07 × 103
m/s
(5.97 × 1024
kg)

(4.22 × 107
m)
4. r = 3.84 × 108
m
m = 5.97 × 1024
kg
vt = G
m
r

=
6.673 × 10−11

N
k
•
g
m
2
2

= 1.02 × 103
m/s
(5.97 × 1024
kg)

(3.84 × 108
m)
5. r = 3.84 × 108
m
m = 5.97 × 1024
kg
T = 2p
G
r
m
3

= 2p

= 2.37 × 106
s = 27.4 d
(3.84 × 108
m)3


6.673 × 10−11

N
k
•
g
m
2
2

(5.97 × 1024
kg)
6. r = 4.50 × 1012
m
m = 1.99 × 1030
kg
T = 2p 
G
r
m
3

= 2p

= 5.20 × 109
s = 165 years
(4.50 × 1012
m)3


6.673 × 10−11

N
k
•
g
m
2
2

(1.99 × 1030
kg)
7. r = 1.19 × 106
m
T = 4.06 × 105
s
m = 4p2

G
r
T
3
2
 = 4p2
= 6.05 × 1018
kg
(1.19 × 106
m)3


6.673 × 10−11

N
k
•
g
m
2
2

(4.06 × 105
s)2
8. r = 2.30 × 1010
m
T = 5.59 × 105
s
ms = 1.99 × 1030
kg
m = 4p2

G
r
T
3
2
 = 4p2
=

m
m
s
 = 
2
1
.
.
3
9
0
9
×
×
1
1
0
0
3
3
1
0
k
k
g
g
 = 11.6
2.30 × 1031
kg
(2.30 × 1010
m)3


6.673 × 10−11

N
k
•
g
m
2
2

(5.59 × 105
s)2
1. m = 3.00 × 105
kg
q = 90.0° − 45.0° = 45.0°
t = 3.20 × 107
N•m
g = 9.81 m/s2
t = Fd(sin q) = mgl (sin q)
l = 
mg(s
t
in q)

l =
l = 15.4 m
3.20 × 107
N•m

(3.00 × 105 kg)(9.81 m/s2)(sin 45.0°)

II
2. tnet = 9.4 kN•m
m1 = 80.0 kg
m2 = 120.0 kg
g = 9.81 m/s2
tnet = t1 + t2 = F1d1(sin q1) + F2d2(sin q2)
q1 = q2 = 90°, so
tnet = F1d1 + F2d2 = m1g
+ m2gl
l =
l =
9.4 × 103
N•m

+ (120.0 kg)(9.81 m/s2)
=
l = = 6.0 m
9.4 × 103
N•m

1.57 × 103
N
9.4 × 103
N•m

392 N + 1.18 × 103
N
(80.0 kg)(9.81 m/s2)

2
tnet


m
2
1g
 + m2g
l

2
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. tnet = 56.0 N•m
m1 = 3.9 kg
m2 = 9.1 kg
d1 = 1.000 m − 0.700 m =
0.300 m
g = 9.81 m/s2
q1 = q2 = 90°, so
tnet = F1d1 + F2d2 = m1gd1 + m2g(1.000 m − x)
x = 1.000 m − 
tnet
m
−
2
m
g
1gd1

x = 1.000 m −
x = = = 1.000 m − 0.50 m
x = 0.50 m = 5.0 × 101
cm
45 N•m

(9.1 kg)(9.81 m/s2
)
56.0 N•m − 11 N•m

(9.1 kg)(9.81 m/s2
)
56.0 N•m − (3.9 kg)(9.81 m/s2
)(0.300 m)

(9.1 kg)(9.81 m/s2)
4. t = −1.3 × 104
N•m
l = 6.0 m
d = 1.0 m
q = 90.0° − 30.0° = 60.0°
t = Fd(sin q) = −Fg(l − d)(sin q)
Fg = = =
Fg = 3.0 × 103
N
1.3 × 104
N•m

(5.0 m)(sin 60.0°)
−(−1.3 × 104
N•m)

(6.0 m − 1.0 m)(sin 60.0°)
−t

(l − d)(sin q)
5. R = 
76
2
m
 = 38 m
q = 60.0°
t = −1.45 × 106
N•m
t = Fd(sin q) = −FgR(sin q)
Fg = 
R(s
−
in
t
q)
 =
Fg = 4.4 × 104
N
−(−1.45 × 106
N•m)

(38 m)(sin 60.0°)

II
6. m1 = 102 kg
m2 = 109 kg
l = 3.00 m
l1 = 0.80 m
l2 = 1.80 m
g = 9.81 m/s2
q1 = q2 = 90°, so
tnet = F1d1 + F2d2 = m1g
− l1+ m2g
− l2
tnet = (102 kg)(9.81 m/s2
)

3.0
2
0 m
 − 0.80 m
+ (109 kg)(9.81 m/s2
)

3.0
2
0 m
 − 1.80 m

tnet = (102 kg)(9.81 m/s2
)(1.50 m − 0.80 m) + (109 kg)(9.81 m/s2
)(1.50 m − 1.80 m)
tnet = (102 kg)(9.81 m/s2
)(0.70 m) + (109 kg)(9.81 m/s2
)(−0.30 m)
tnet = 7.0 × 102
N•m − 3.2 × 102
N•m
tnet = 3.8 × 102
N•m
l

2
l

2
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 7–6
7. m = 5.00 × 102
kg
d1 = 5.00 m
t = 6.25 × 105
N•m
g = 9.81 m/s2
q1 = 90.0° − 10.0° = 80.0°
d2 = 4.00 m
q2 = 90°
a. t⬘ = Fd(sin q) = mgd1(sin q1)
t ⬘ = (5.00 × 102
kg)(9.81 m/s2
)(5.00 m)(sin 80.0°)
t⬘ =
b. tnet = Fd2(sin q2) − t⬘ = Fd2(sin q2) − mgd1(sin q1)
F =
F = =
F = 1.62 × 105
N
6.49 × 105
N•m

4.00 m
6.25 × 105
N•m + 2.42 × 104
N•m

4.00 m (sin 90°)
tnet + mgd1(sin q1)

d2(sin q2)
2.42 × 104
N•m

Fluid Mechanics
II
1. mp = 1158 kg
V = 3.40 m3
ρ = 1.00 × 103
kg/m3
g = 9.81 m/s2
FB = Fg
ρVg = (mp + mr)g
mr = ρV − mp = (1.00 × 103
kg/m3
)(3.40 m3
) − 1158 kg = 3.40 × 103
kg − 1158 kg
mr = 2.24 × 103
kg
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. V = 4.14 × 10−2
m3
apparent weight =
3.115 × 103
N
ρsw = 1.025 × 103
kg/m3
g = 9.81 m/s2
FB = Fg − apparent weight
ρswVg = mg − apparent weight
m = ρswV + 
apparen
g
t weight
 = (1.025 × 103
kg/m3
)(4.14 × 10−2
m3
) + 
3.1
9
1
.8
5
1
×
m
1
/
0
s
3
2
N

m = 42.4 kg + 318 kg = 3.60 × 102
kg
3. l = 3.00 m
A = 0.500 m2
rfw = 1.000 × 103
kg/m3
rsw = 1.025 × 103
kg/m3
Fnet,1 = Fnet,2 = 0
FB,1 − Fg,1 = FB,2 − Fg,2
rfwVg − mg = rswVg − (m + mballast)g
mballastg = (rsw − rfw)Vg
mballast = (rsw − rfw)Al
m0 = (1.025 × 103
kg/m3
− 1.000 × 103
kg/m3
)(0.500 m2
)(3.00 m)
m0 = (25 kg/m3
)(0.500 m2
)(3.00 m) = 38 kg
4. A = 3.10 × 104
km2
h = 0.84 km
r = 1.025 × 103
kg/m3
g = 9.81 m/s2
FB = rVg = rAhg
FB = (1.025 × 103
kg/m3
)(3.10 × 1010
m2
)(840 m)(9.81 m/s2
) = 2.6 × 1017
N
5. m = 4.80 × 102
kg
g = 9.81 m/s2
apparent weight = 4.07 × 103
N
FB = Fg − apparent weight = mg − apparent weight
FB = (4.80 × 102
kg)(9.81 m/s2
) − 4.07 × 103
N = 4.71 × 103
N − 4.07 × 103
N
FB = 640 N

II Ch. 8–2
II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. h = 167 m
H = 1.50 km
rsw = 1.025 × 103
kg/m3
Fg,i = FB
riVig = rswVswg
ri(h + H)Ag = rswHAg
ri = 
h
rs
+
wH
H

ri = = = 921 kg/m3
(1.025 × 103
kg/m3
)(1.50 × 103
m)

1670 m
(1.025 × 103
kg/m3
)(1.50 × 103
m)

167 m + 1.50 × 103
m
7. l = 1.70 × 102
m
r = 
13.
2
9 m
 = 6.95 m
msw = 2.65 × 107
kg
a = 2.00 m/s2
g = 9.81 m/s2
Fnet = Fg − FB
msuba = msubg − mswg
ρsubVa = ρsubVg − mswg
ρsub(g − a)V = mswg
ρsub = 
(g
m
−
sw
a
g
)V
 = 
(g −
m
a)
s
(
w
π
g
r2
l )

ρsub =
ρsub =
ρsub = 1.29 × 103
kg/m3
(2.65 × 107
kg)(9.81 m/s2
)

(9.81 m/s2
)(π)(6.95 m)2
(1.70 × 102
m)
(2.65 × 107
kg)(9.81 m/s2
)

(9.81 m/s2
− 2.00 m/s2
)(π)(6.95 m)2
(1.70 × 102
m)
8. V = 6.00 m3
∆ apparent weight = 800 N
ρwater = 1.00 × 103
kg/m3
g = 9.81 m/s2
Fg,1 = Fg,2
FB,1 + apparent weight in water = FB,2 + apparent weight in PEG solution
ρwaterVg + apparent weight in water − apparent weight in PEG solution = ρsolnVg
ρsoln =
ρsoln =
ρsoln = =
ρsoln = 1.01 × 103
kg/m3
5.97 × 104
N

(6.00 m3
)(9.81 m/s2
)
5.89 × 104
N + 800 N

(6.00 m3
)(9.81 m/s2
)
(1.00 × 103
kg/m3
)(6.00 m3
)(9.81 m/s2
) + 800 N

(6.00 m3
)(9.81 m/s2
)
ρwaterVg + ∆ apparent weight

Vg
1. P = 1.01 × 105
Pa
A = 3.3 m2
F = PA (1.01 × 105
Pa)(3.3 m2
) = 3.3 × 105
N

II
2. P = 4.0 × 1011
Pa
r = 50.0 m
F = PA = P(πr2
)
F = (4.0 × 1011
Pa)(π)(50.0 m)2
F = 3.1 × 1015
N
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. m1 = 181 kg
m2 = 16.0 kg
A1 = 1.8 m2
g = 9.81 m/s2
P1 = P2

A
F1
1
 = 
A
F2
2

A2 = 
F2
F
A
1
1
 = 
3m
m
2
1
g
g
A1
 = 
3m
m
2
1
A1

A2 = = 0.48 m2
(3)(16.0 kg)(1.8 m2
)

181 kg
4. m = 4.0 × 107
kg
F2 = 1.2 × 104
N
A2 = 5.0 m2
g = 9.81 m/s2
P1 = P2

A
F1
1
 = 
A
F2
2

A1 = 
A
F
2F
2
1
 = 
A
F
2m
2
g

A1 = = 1.6 × 105
m2
(5.0 m2
)(4.0 × 107
kg)(9.81 m/s2
)

1.2 × 104
N
5. P = 2.0 × 1016
Pa
F = 1.02 × 1031
N
A = 
P
F
 = 
1
2
.
.
0
0
2
×
×
1
1
0
0
1
3
6
1
P
N
a
 =
A = 4πr2
r = =
r = 6.4 × 106
m
5.1 × 1014
m2

4π
A

4π
5.1 × 1014
m2
6. F = 4.6 × 106
N
r = 
38
2
cm
 = 19 cm
P = 
A
F

Assuming the squid’s eye is a sphere, its total surface area is 4πr2
. The outer half of
the eye has an area of
A = 2πr2
P = 
2π
F
r2
 = 
(2
4
π
.6
)(
×
0.
1
1
0
9
6
m
N
)2
 = 2.0 × 107
Pa
7. A = 26.3 m2
F = 1.58 × 107
N
Po = 1.01 × 105
Pa
P = 
A
F
 = 
1.5
2
8
6.
×
3
1
m
07
2
N
 =
Pgauge = P − Po = 6.01 × 105
Pa − 1.01 × 105
Pa = 5.00 × 105
Pa
6.01 × 105
Pa

II
1. h = (0.800)(16.8 m)
P = 2.22 × 105
Pa
Po = 1.01 × 105
Pa
g = 9.81 m/s2
P = Po + ρgh
ρ = 
P
g
−
h
Po
 = =
ρ = 918 kg/m3
1.21 × 105
Pa

(9.81 m/s2
)(0.800)(16.8 m)
2.22 × 105
Pa − 1.01 × 105
Pa

(9.81 m/s2
)(0.800)(16.8 m)
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. h = −950 m
P = 8.88 × 104
Pa
Po = 1.01 × 105
Pa
g = 9.81 m/s2
P = Po + ρgh
ρ = = =
ρ = 1.3 kg/m3
−1.2 × 104
Pa

(9.81 m/s2
)(−950 m)
8.88 × 104
Pa − 1.01 × 105
Pa

(9.81 m/s2
)(−950 m)
P − Po


g
1
h

3. P = 13.6P0
P0 = 1.01 × 105
Pa
r = 1.025 × 103
kg/m3
g = 9.81 m/s2
P = P0 + rgh
h = 
13.6P
r
0
g
− P0
 = 
12
r
.6
g
P0

h = = 127 m
(12.6)(1.01 × 105
Pa)

(1.025 × 103 kg/m3)(9.81 m/s2)
4. P = 4.90 × 106
Pa
P0 = 1.01 × 105
Pa
r = 1.025 × 103
kg/m3
g = 9.81 m/s2
P = P0 + rgh
h = 
P
r
−
g
P0
 =
h = = 477 m
4.80 × 106
Pa

(1.025 × 103 kg/m3)(9.81 m/s2)
4.90 × 106
Pa − 1.01 × 105
Pa

(1.025 × 103 kg/m3)(9.81 m/s2)
6. h = 10 916 m
P0 = 1.01 × 105
Pa
r = 1.025 × 103
kg/m3
g = 9.81 m/s2
P = P0 + rgh = 1.01 × 105
Pa + (1.025 × 103
kg/m3
)(9.81 m/s2
)(10 916 m)
P = 1.01 × 105
Pa + 1.10 × 108
Pa = 1.10 × 108
Pa
5. h = 245 m
Po = 1.01 × 105
Pa
ρ = 1.025 × 103
kg/m3
g = 9.81 m/s2
P = Po + ρgh
P = 1.01 × 105
Pa + (1.025 × 103
kg/m3
)(9.81 m/s2
)(245 m)
P = 1.01 × 105
Pa + 2.46 × 106
Pa
P = 2.56 × 106
Pa
II Ch. 8–4

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. TC = 14°C T = TC + 273.15
T = (14 + 273.15) K
T =
TF = 
9
5
TC + 32.0
TF = 
9
5
(14) + 32.0°F = (25 + 32.0)°F
TF = 57°F
287 K
Givens Solutions
2. TF = (4.00 × 102
)°F TC = 
5
9
(TF − 32.0)
TC = 
5
9
[(4.00 × 102
) − 32.0]°C = 
5
9
(368)°C
TC =
T = TC + 273.15
T = (204 + 273.15) K
T = 477 K
204°C
3. TC,1 = 117°C
TC,2 = −163°C
∆TC = TC,1 − TC,2 = 117°C − (−163°C)
∆TC = (2.80 × 102
)°C
∆TF = 
5
9
∆TC
∆TF = 
5
9
(2.80 × 102
)°F
∆TF = 504°F
Heat
4. TF = 860.0°F TC = 
5
9
(TF − 32.0)
TC = 
9
5
(860.0 − 32.0)°C = 
9
5
(828.0)°C
TC = 460.0°C

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 9–2
5. ∆TF = 49.0°F
TC,2 = 7.00°C
TF = 
9
5
TC + 32.0
TF,2 = 
9
5
(7.00) + 32.0°F = (12.6 + 32.0)°F
TF,2 =
TF,1 = TF,2 − ∆TF = 44.6°F − 49.0°F
TF,1 =
TC,1 = 
5
9
(TF,1 − 32.0)
TC,1 = 
5
9
(−4.4 − 32.0)°C = 
5
9
(−36.4)°C
TC,1 = −20.2°C
−4.4°F
44.6°F
Givens Solutions
6. ∆TC = 56°C
TC,2 = −49°C
TC,1 = TC,2 + ∆TC
TC,1 = −49°C + 56°C
TC,1 = 7°C
T1 = TC,1 + 273.15
T1 = (7 + 273.15) K
T1 =
T2 = TC,2 + 273.15
T2 = (−49 + 273.15) K
T2 = 2.24 × 102
K
2.80 × 102
K
1. mH = 3.05 × 105
kg
vi = 120.0 km/h
vf = 90.0 km/h
∆T = 10.0°C
k = 
m
∆
w
U
∆T
 =

(1.00 k
4
g
1
)
8
(
6
1.
J
00°C)

∆PE + ∆KE + ∆U = 0 ∆PE = 0
∆KE = 
1
2
mHvf
2
− 
1
2
mHvi
2
= 
m
2
H
(vf
2
− vi
2
)
∆U = −∆KE = 
m
2
H
(vi
2
− vf
2
)
mw =

m
∆
w
U
∆T


∆
∆
U
T

=

1
k


∆
∆
U
T

= 
2
m
k∆
H
T
(vi
2
− vf
2
)
mw =

120.
h
0 km


2
−

90.0
h
km


2

36
1
0
h
0 s


1
1
0
k
3
m
m


2
mw = (3.64 kg•s2
/m2
)(1110 m2
/s2
− 625 m2
/s2
)
mw = (3.64 kg•s2
/m2
)(480 m2
/s2
)
mw = 1.7 × 103
kg
3.05 × 105
kg


(2
(1
)(
.0
4
0
18
k
6
g)
J
(
)
1
(1
.0
0
0
.0
°C
°C
)
)


7. TF = 116 °F T = TC + 273.15 = 
5
9
(TF − 32.0) + 273.15
T = 
5
9
(116 − 32.0) + 273.15 K = 
5
9
(84) + 273.15 K = (47 + 273.15) K
T = 3.20 × 102
K

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 2. h = 228 m
Ti = 0.0°C
g = 9.81 m/s2
fraction of MEf converted
to U = 0.500
k = (∆U/m) = energy
needed to melt ice =
3.33 × 105
J/1.00 kg
∆PE = −mgh
When the ice lands, its kinetic energy is tranferred to the internal energy of the
ground and the ice. Therefore, ∆KE = 0 J.
∆U = (0.500)(MEf ) = −(0.500)(∆PE) = (0.500)(mgh)

∆
m
U
 = (0.500)(gh)
f = 
∆
km
U
 = 
(0.500
k
)(gh)

f =
f = 3.36 × 10−3
(0.500)(9.81 m/s2
)(228 m)

(3.33 × 105 J/1.00 kg)
Givens Solutions
3. vi = 2.333 × 103
km/h
h = 4.000 × 103
m
g = 9.81 m/s2
fraction of ME converted
to U = 0.0100
k = 
m
∆
∆
U
T
 =

(1.00 k
(3
g
5
)(
5
1
J
.
)
00°C)

4. h = 8848 m
g = 9.81 m/s2
to U = 0.200
Ti = −18.0°C

∆U
∆T
/m
 = 
4
1
4
.
8
00
J
°
/k
C
g

∆PE = −mgh
MEf = −∆PE
When the hook lands, its kinetic energy is transferred to the internal energy of the
hook and the ground. Therefore, ∆KE = 0 J.
∆U = (0.200)(MEf) = (−0.200)(∆PE) = (0.200)(mgh)
∆U/m = (0.200)(gh)
∆T =

∆U
∆T
/m


∆
m
U

=

4
1
4
.
8
00
J
°
/k
C
g

[(0.200)(gh)]
∆T =

4
1
4
.
8
00
J
°
/k
C
g

(0.200)(9.81 m/s2
)(8848 m) = 38.7°C
Tf = Ti + ∆T = −18.0°C + 38.7°C
Tf = 20.7°C
(0.0100)(∆PE + ∆KE) + ∆U = 0
∆PE = PEf − PEi = 0 − mgh = −mgh
∆KE = KEf − KEi = 0 − 
1
2
mvi
2
= −
1
2
mvi
2
∆U = −(0.0100)(∆PE + ∆KE) = −(0.0100)(m)−gh − 
1
2
v2
= (0.0100)(m)gh + 
1
2
v2

∆T = =
∆T =
∆T =
∆T = 7.02°C
(0.0100)[(3.92 × 104
m2
/s2
) + (2.100 × 105
m2
/s2
)]

355 m2/s2•°C
(0.0100)
(9.81 m/s2)(4.000 × 103
m) + 
1
2


2.33
3
3
6
×
00
10
s/
6
h
m/h


2


355 m2/s2•°C
(0.0100)gh + 
1
2
v2



(1.00 k
3
g
5
)
5
(1
J
.00°C)


∆
m
U



k

II Ch. 9–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
7. ∆T = 0.230°C
g = 9.81 m/s2
to U = 0.100

∆
∆
U
T
/m
 = 
41
1
8
.0
6
0
J
°
/
C
kg


∆
m
U
 = ∆T

∆
∆
U
T
/m

= 
(0.100
m
)(MEf )
 = 
(0.100
m
)(∆PE)
 = (0.100)(gh)
Because the kinetic energy at the bottom of the falls is converted to the internal en-
ergy of the water and the ground, ∆KE = 0 J.
h =
h =

41
1
8
.0
6
0
J
°
/
C
kg


h = 981 m
0.230°C

(0.100)(9.81 m/s2)
∆T

∆
∆
U
T
/m



(0.100)(g)
5. hi = 629 m
g = 9.81 m/s2
vf = 42 m/s
to U = 0.050
m = 3.00 g
Because hf = 0 m, PEf = 0 J. Further, vi = 0 m/s, so KEi = 0 J.
∆U = −(0.050)(∆ME) = −(0.050)(∆PE + ∆KE)
∆PE = PEf − PEi = 0 J − PEi = −mgh
∆KE = KEf − KEi = KEf − 0 J = 
1
2
mvf
2
∆U = (0.050)(−∆PE − ∆KE) = (0.050)(mgh − 
1
2
mvf
2
) = (0.050)(m)(gh − 
1
2
vf
2
)
∆U = (0.050)(3.00 × 10−3
kg)[(9.81 m/s2
)(629 m) − (0.5)(42 m/s)2
]
∆U = (0.050)(3.00 × 10−3
kg)(6170 m2
/s2
− 880 m2
/s2
)
∆U = (0.050)(3.00 × 10−3
kg)(5290 m2
/s2
)
∆U = 0.79 J
Givens Solutions
6. h = 2.49 m
g = 9.81 m/s2
m = 312 kg
v = 0.50 m/s
to U = 0.500
(0.500)(∆PE + ∆KE) + ∆U = 0
∆PE = PEf − PEi = 0 − mgh = −mgh
∆KE = KEf − KEi = 0 − 
2
1
mv2
= 
−m
2
v2

∆U = −(0.500)(∆PE + ∆KE) = −(0.500)
−mgh − 
m
2
v2

= (0.500)
mgh + 
m
2
v2


∆U = (0.500)[(312 kg)(9.81 m/s2)(2.49 m) + (0.5)(312 kg)(0.50 m/s)2
]
∆U = (0.500)[(7.62 × 103
J) + 39 J]
∆U = 3.83 × 103
J

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. Q = (2.8 × 109
W)(1.2 s)
cp,c = 387 J/kg•°C
Tc = 26.0°C
Tf = 21.0°C
Q = −mccp,c(Tf − Tc) = mccp,c(Tc − Tf )
mc = 
cp,c(T
Q
c − Tf )

mc =
mc = = 1.7 × 106
kg
(2.8 × 109
W)(1.2 s)

(387 J/kg•°C)(5.0°C)
(2.8 × 109
W)(1.2 s)

(387 J/kg•°C)(26.0°C − 21.0°C)
2. mw = 143 × 103
kg
Tw = 20.0°C
Tx = temperature of
burning wood = 280.0°C
Tf = 100.0°C
cp,x = specific heat
capacity of wood =
1.700 × 103
J/kg•°C
cp,w = 4186 J/kg•°C
− cp,xmx (Tf − Tx) = cp,wmw(Tf − Tw)
mx =
mx =
mx =
mx = 1.56 × 105
kg
(4186 J/kg•°C)(143 × 103
kg)(80.0°C)

(1.700 × 103 J/kg•°C)(180.0°C)
(4186 J/kg•°C)(143 × 103
kg)(100.0°C − 20.0°C)

(1.700 × 103 J/kg•°C)(280.0°C − 100.0°C)
cp,wmw(Tf − Tw)

cp,x(Tx − Tf )
Givens Solutions
3. ∆U = Q = (0.0100)
(1.450 GW)(1.00 year)
cp,x = specific heat capacity
of iron = 448 J/kg•°C
mx = mass of steel =
25.1 × 109
kg
Q = cp,x mx ∆T
∆T = 
cp,x
Q
mx

∆T =

365
1
.2
y
5
ea
d
r
ays


1
2
d
4
a
h
y


36
1
0
h
0 s


∆T = 40.7°C
(0.0100)(1.450 × 109
W)(1.00 year)

(448 J/kg•°C)(25.1 × 109
kg)
4. ml = 2.25 × 103
kg
Tl,i = 28.0°C
cp,l = cp,w = 4186 J/kg•°C
mi = 9.00 × 102
kg
Ti,i = −18.0°C
cp,i = 2090 J/kg•°C
Ti,f = 0.0°C
−mlcp,l (Tl,f − Tl,i) = micp,i(Ti,f − Ti,i)
Tl,f = Tl,i −

m
m
l
i


c
c
p
p
,
,
l
i

(Ti,f − Ti,i)
Tl,f = (28.0°C) −

2
9
.
.
2
0
5
0
×
×
1
1
0
0
3
2
k
k
g
g

[(0.0°C) − (−18.0°C)]
Tl,f = 28.0°C − 3.59°C = 24.4°C
2090 J/kg•°C

4186 J/kg•°C
5. mw = 1.33 × 1019
kg
Tw = 4.000°C
cp,w = 4186 J/kg•°C
P = 1.33 × 1010
W
∆t = 1.000 × 103
years
P∆t = Q = mwcp,w(Tf − Tw)
Tf =

m
P
w
∆
cp
t
,w

+ Tw
Tf = + 4.000°C
Tf = (7.54 × 10−3
)°C + 4.000°C
Tf = 4.008°C
(1.33 × 1010
W)(1.000 × 103
years)

36
1
5.
y
2
e
5
a
d
r
ay


1
2
d
4
a
h
y


36
1
0
h
0 s



(1.33 × 1019 kg)(4186 J/kg•°C)

II Ch. 9–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
7. Tm = −62.0°C
Tw = 38.0°C
mm = 180 g
mw = 0.500 kg
Tf = 36.9°C
cp,w = 4186 J/kg•°C
mmcp,m(Tf − Tm) = −mwcp,w(Tf − Tw)
cp,m =

m
m
m
w

(cp,w)

T
T
f
w
−
−
T
T
m
f


cp,m =

0
0
.5
.1
0
8
0
k
k
g
g

(4186 J/kg•°C)

cp,m =
The metal could be gold (cp = 129 J/kg•°C) or lead (cp = 128 J/kg•°C).
1.3 × 102
J/kg•°C
(38.0°C) − (36.9°C)

(36.9°C) − (−62.0°C)
Givens Solutions
6. Ti = 18.0°C
Tf = 32.0°C
Q = 20.8 kJ
mx = 0.355 kg
Q = mxcp,x∆T
cp,x = 
mx
Q
∆T
 = 
mx(T
Q
f − Ti)

cp,x =
cp,x = 4190 J/kg•°C
20.8 × 103
J

(0.355 kg)(32.0°C − 18.0°C)
1. mw,S = 1.20 × 1016
kg
mw,E = 4.8 × 1014
kg
TE = 0.0°C
TS = 100.0°C
cp,w = 4186 J/kg•°C
Lf of ice = 3.33 × 105
J/kg
QS = energy transferred by heat from Lake Superior = cp,wmw,S(TS − Tf)
QE = energy transferred by heat to Lake Erie = mw,ELf + mw,Ecp,w(Tf − TE)
From the conservation of energy,
QS = QE
cp,wmw,S(TS − Tf ) = mw,ELf + mw,Ecp,w(Tf − TE)
(mw,Ecp,w + cp,wmw,S)Tf = cp,wmw,STS + mw,Ecp,wTE − mw,ELf
Tf = , where TE = 0.0°C
Tf =
Tf =
Tf =
Tf = 92.9°C
(5.02 × 1021
J) − (1.6 × 1020
J)

(4186 J/kg•°C)(1.25 × 1016 kg)
(4186 J/kg•°C)(1.20 × 1016
kg)(100.0°C) − (4.8 × 1014
kg)(3.33 × 105
J/kg)

(4186 J/kg•°C)[(4.8 × 1014
kg) + (1.20 × 1016
kg)]
cp,wmw,STS − mw,ELf

cp,w (mw,E + mw,S)
cp,w(mw,STS + mw,ETE) − mw,ELf

cp,w (mw,E + mw,S)
2. Tf = −235°C
Tfreezing = 0.0°
mw = 0.500 kg
cp,w = 4186 J/kg•°C
cp,ice = cp,i = 2090 J/kg•°C
Lf of ice = 3.33 × 105
J/kg
Qtot = 471 kJ
Qtot = cp,wmw(Ti − 0.0°) + Lf mw + mwcp,i(0.0°− Tf) = cp,wmwTi + Lf mw − cp,imwTf
Ti =
Ti =
Ti =
Ti = 28°C
(4.71 × 105
J) − (1.66 × 105
J) − (2.46 × 105
J)

2093 J/°C
(4.71 × 105
J) − (3.33 × 105
J/kg)(0.500 kg) + (−235°C)(2090 J/kg•°C)(0.500 kg)

(4186 J/kg•°C)(0.500 kg)
Qtot − Lf mw + cp,imwTf

cp,wmw

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 3. Ti = 0.0°C
mi = 4.90 × 106
kg
Lf of ice = 3.33 × 105
J/kg
Ts = 100.0°C
Lv of steam = 2.26 × 106
J/kg
msLv = miLf
ms = 
m
L
i
v
Lf

ms =
ms = 7.22 × 105
kg
(4.90 × 106
kg)(3.33 × 105
J/kg)

2.26 × 106
J/kg
Givens Solutions
4. ms = 1.804 × 106
kg
Lf of silver = Lf,s =
8.82 × 104
J/kg
Lf of ice = Lf,i =
3.33 × 105
J/kg
msLf,s = miLf,i
mi = 
m
L
sL
f,i
f,s

mi =
mi = 4.78 × 105
kg
(1.804 × 106
kg)(8.82 × 104
J/kg)

3.33 × 105 J/kg
5. mg = 12.4414 kg
Tg,i = 5.0°C
Q = 2.50 MJ
cp,g = 129 J/kg•°C
Tg,f = 1063°C
Q = mgcp,g(Tg,f − Tg,i) + mgLf
Lf =
Lf =
Lf =
Lf = 6.4 × 104
J/kg
(2.50 × 106
J) − (1.70 × 106
J)

12.4414 kg
(2.50 × 106
J) − (12.4414 kg)(129 J/kg•°C)(1063°C − 5.0°C)

12.4414 kg
Q − mgcp,g(Tg,f − Tg,i)

mg
6. Vp = 7.20 m3
Vc = (0.800)(Vp)
rc = 8.92 × 103
kg/m3
Lf = 1.34 × 105
J/kg
a. mc = rcVc
mc = (8.92 × 103
kg/m3
)(0.800)(7.20 m3
)
mc =
b. fraction of melted coins = 
m
Q
cLf
 = 
1
1
0
5
0

Q = 
1
1
0
5
0
 mcLf =
Q = 1.03 × 109
J
15(5.14 × 104
kg)(1.34 × 105 J/kg)

100
5.14 × 104
kg

II Ch. 9–8
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
7. mw = 3.5 × 1019
kg
Ti = 10.0°C
Tf = 100.0°C
cp,w = 4186 J/kg•°C
Lv of water = 2.26 × 106
J/kg
P = 4.0 × 1026
J/s
a. Q = mwcp,w(Tf − Ti) + mwLv
Q = (3.5 × 1019
kg)(4186 J/kg•°C)(100.0°C − 10.0°C)
+ (3.5 × 1019
kg)(2.26 × 106
J/kg)
Q = 1.3 × 1025
+ 7.9 × 1025
J =
b. Q = P∆t
∆t = 
Q
P
 = 
4
9
.0
.2
×
×
1
1
0
0
2
2
6
5
J/
J
s
 = 0.23 s
9.2 × 1025
J

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. P = 5.1 kPa
W = 3.6 × 103
J
Vi = 0.0 m3
W = P∆V
∆V = 
W
P
 = 
5
3
.1
.6
×
×
1
1
0
0
3
3
P
J
a
 = 7.1 × 10−1
m3
V = Vi + ∆V = 0.0 m3
+ 7.1 × 10−1
m3
= 7.1 × 10−1
m3
Givens Solutions
2. m = 207 kg
g = 9.81 m/s2
h = 3.65 m
P = 1.8 × 106
Pa
W = mgh = −P∆V
∆V = 
m
−
g
P
h

∆V = = −4.1 × 10−3
m3
(207 kg)(9.81 m/s2
)(3.65 m)

−(1.8 × 106 Pa)
3. rf = 1.22 m
ri = 0.0 m
W = 642 kJ
W = P∆V
P = 
∆
W
V

∆V = 
3
4
p(rf
3
− ri
3
)
P = = = 8.44 × 104
Pa
642 × 103
J


3
4
p (1.22 m)3 − (0.0 m)3

W


3
4
p(rf
3 − ri
3)
4. rf = 7.0 × 105
km
rf = 7.0 × 108
m
ri = 0.0 m
W = 3.6 × 1034
J
W = P∆V
V = 
3
4
pr3
∆V = Vf − Vi = 
3
4
p(rf
3
− ri
3
)
W = (P)(
3
4
p)(rf
3
− ri
3
)
P = W

(
3
4
p)(rf
3 − ri
3)
5. P = 87 kPa
∆V = −25.0 × 10−3
m3
W = P∆V
W = (87 × 103
Pa)(−25.0 × 10−3
m3
) = −2.2 × 103
J
Thermodynamics
P = = 2.5 × 107
Pa
(3.6 × 1034
J)

(
3
4
p )[(7.0 × 108
m)3
− (0.0 m)3
]

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 10–2
6. rf = 29.2 cm
ri = 0.0 m
P = 25.0 kPa
m = 160.0 g
W = P∆V
∆V = 
3
4
p(rf
3
− ri
3
)
W = 
1
2
mv2

1
2
mv2
= (P)
4
3
p(rf
3
− ri
3
)
v = 
8
3
p
m
P

(rf
3
− ri
3
)
v = (
29
.2
×
1
0−
2
m
)3
−
(
0.
0
m
)3

v = 181 m/s
(8p)(25.0 × 103
Pa)

(3)(160.0 × 10−3 kg)
Givens Solutions
1. m = 227 kg
h = 8.45 m
g = 9.81 m/s2
Ui = 42.0 kJ
Q = 4.00 kJ
∆U = Uf − Ui = Q − W
W = mgh
Uf = Ui + Q − W = Ui + Q − mgh
Uf = (42.0 × 103
J) + (4.00 × 103
J) − (227 kg)(9.81 m/s2
)(8.45 m)
Uf = (42.0 × 103
J) + (4.00 × 103
J) − (18.8 × 103
J)
Uf = 27.2 × 103
J = 27.2 kJ
2. m = 4.80 × 102
kg
Q = 0 J
v = 2.00 × 102
m/s
Uf = 12.0 MJ
a. Assume that all work is transformed to the kinetic energy of the cannonball.
W = 
1
2
mv2
W = 
1
2
(4.80 × 102
kg)(2.00 × 102
m/s)2
W =
b. ∆U = Q − W = −W
Uf − Ui = −W
Ui = Uf + W
Ui = (12.0 × 106
J) + (9.60 × 106
J)
Ui = 21.6 × 106
J = 21.6 MJ
9.60 × 106
J = 9.60 MJ
3. m = 4.00 × 104
kg
cp = 4186 J/kg•°C
∆T = −20.0°C
W = 1.64 × 109
J
a. Q = mcp∆T
Q = (4.00 × 104
kg)(4186 J/kg•°C)(−20.0°C)
Q =
b. Q of gas = −Q of jelly = −(−3.35 × 109
J) = 3.35 × 109
J
∆U = Q − W
∆U = (3.35 × 109
J) − (1.64 × 109
J)
∆U = 1.71 × 109
J
−3.35 × 109
J

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. P = 
∆
Q
t
 = 5.9 × 109
J/s
∆t = 1.0 s
∆U = 2.6 × 109
J
∆U = Q − W = P∆t − W
W = P∆t − ∆U
W = (5.9 × 109
J/s)(1.0 s) − (2.6 × 109
J)
W = 3.3 × 109
J
Givens Solutions
5. m = 5.00 × 103
kg
v = 40.0 km/h
Ui = 2.50 × 105
J
Uf = 2Ui
W = 
1
2
mv2
∆U = Uf − Ui = Q − W
Uf = 2Ui
∆U = 2Ui − Ui = Ui
Q = ∆U + W = Ui + 
1
2
mv2
Q = (2.50 × 105
J) + 
1
2
(5.00 × 103
kg)

40.0
h
km


36
1
0
h
0 s


1
1
0
k
3
m
m


2
Q = (2.50 × 105
J) + (3.09 × 105
J)
Q = 5.59 × 105
J
4. m = 1.64 × 1015
kg
h = 75.0 m
g = 9.81 m/s2
Ti = 6.0°C
Tf = 100.0°C
cp,w = 4186 J/kg•°C
Lv of water = 2.26 × 106
J/kg
∆U = (−0.900)(Ui)
W = mgh = (1.64 × 1015
kg)(9.81 m/s2
)(75.0 m)
W = 1.21 × 1018
J
Q = −mcp,w(Tf − Ti) − mLv = −m[cp,w(Tf − Ti) + Lv]
Tf − Ti = 100.0°C − 6.0°C = 94.0°C
Q = −(1.64 × 1015
kg)[(4186 J/kg•°C)(94.0°C) + (2.26 × 106
J/kg)]
Q = −4.35 × 1021
J
∆U = Uf − Ui = (−0.900)(Ui) = Q − W
Uf = (1 − 0.900)Ui = (0.100)(Ui)
−∆U = Ui − Uf = 
0.
U
10
f
0
 − Uf = (0.900)

0.
U
10
f
0

= W − Q
Uf =

0
0
.
.
1
9
0
0
0
0

(W − Q)
Uf =

0
0
.
.
1
9
0
0
0
0

[(1.21 × 1018
J) − (−4.35 × 1021
J)]
Uf =
(Note: Nearly all of the energy is used to increase the temperature of the water
and to vaporize the water.)
4.83 × 1020
J

II Ch. 10–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
7. h = 1.00 × 102
m
v = 141 km/h
Ui = 40.0 ΜJ
m = 76.0 kg
a. ∆U = Q − W
All energy is transferred by heat, so W =
b. ∆U = Q = 
1
2
mv2

∆
U
U
i
 × 100
=

m
2U
v2
i

(100)

∆
U
U
i
 × 100
=

∆
U
U
i
 × 100
= 0.146 percent
(76.0 kg)

141
h
km


2

36
1
0
h
0 s


2

1
1
0
k
3
m
m


2
(100)

(2)(40.0 × 106 J)
0 J
Givens Solutions
1. eff = 8 percent = 0.080
Qh = 2.50 kJ
eff = 
Qh
Q
−
h
Qc
 = 1 − 
Q
Q
h
c

−Qc = Qh(eff − 1)
Qc = Qh(1 − eff )
Qc = (2.50 kJ)(1 − 0.08) = (2.50 kJ)(0.92)
Qc =
W = Qh − Qc
W = 2.50 kJ − 2.3 kJ
W = 0.2 kJ
2.3 kJ
2. Pnet = 1.5 MW
eff = 16 percent = 0.16
Qh = 2.0 × 109
J
eff = 
W
Q
n
h
et
 = 
Pn
Q
et
h
∆t

∆t = 
(eff
P
)
n
(
e
Q
t
h)

∆t =
∆t = 2.1 × 102
s
(0.16)(2.0 × 109
J)

1.5 × 106 W
3. Pnet = 19 kW
eff = 6.0 percent = 0.060
∆t = 1.00 h
Wnet = Pnet∆t
eff = 
W
Q
n
h
et

Qh = 
W
ef
n
f
et
 = 
Pn
e
e
f
t
f
∆t

Qh =
Qh = 1.1 × 106
kJ = 1.1 × 109
J
(19 kW)(1.00 h)

3.6 ×
1 h
103
s



(0.060)

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. Pnet = 370 W
∆t = 1.00 min = 60.0 s
eff = 0.19
eff = 
W
Q
n
h
et
 = 
Pn
Q
et
h
∆t

Qh = 
Pn
e
e
f
t
f
∆t

Qh =
Qh = 1.2 × 105
J = 120 kJ
(370 W)(60.0 s)

0.19
Givens Solutions
5. Wnet = 2.6 MJ
Qh/m = 32.6 
M
kg
J

m = 0.80 kg
eff = 
W
Q
n
h
et
 =
eff =
eff = 0.10 = 10 percent
2.6 MJ

32.6 
M
kg
J

(0.80 kg)
Wnet


Q
m
h

(m)
6. m = 3.00 × 104
kg
g = 9.81 m/s2
h = 1.60 × 102
m
Qc = 3.60 × 108
J
Wnet = mgh = Qh − Qc
Qh = Wnet + Qc
eff = 
W
Q
n
h
et
 = 
Wn
W
et
n
+
et
Qc
 = 
mg
m
h
g
+
h
Qc

eff =
eff = 0.12
(3.00 ⫻ 104
kg)(9.81 m/s2
)(1.60 ⫻ 102
m)

(3.00 ⫻ 104
kg)(9.81 m/s2
)(1.60 ⫻ 102
m) + 3.60 ⫻ 108
J

Vibrations and Waves
II
1. m = 0.019 kg
g = 9.81 m/s2
k = 83 N/m
k = 
x
F
 = 
m
x
g

x =
x = 2.25 × 10−3
m
(0.019 kg)(9.81 m/s2
)

83 N/m
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. m = 187 kg
k = 1.53 × 104
N/m
g = 9.81 m/s2
k = 
x
F
 = 
m
x
g

x = 
(18
1
7
.5
k
3
g
×
)(
1
9
0
.8
4
1
N
m
/m
/s2
)
 = 0.120 m
3. m1 = 389 kg
x2 = 1.2 × 10−3
m
m2 = 1.5 kg

x
F
1
1
 = 
F
x2
2

x1 = 
F
F
1
2
x2
 = 
m
m
1g
2
x
g
2

x1 = = 0.31 m
(389 kg)(1.2 × 10−3
m)

(1.5 kg)
4. m = 18.6 kg
x = 3.7 m
g = 9.81 m/s2
k = 
x
F
 = 
m
x
g
 =
k = 49 N/m
(18.6 kg)(9.81 m/s2
)

(3.7 m)
5. h = 533 m
x1 = 
1
3
h
m = 70.0 kg
x2 = 
2
3
h
g = 9.81 m/s2
k = 
x
F
 = 
(x2
m
−
g
x1)
 = 
3m
h
g

k = = 3.87 N/m
3(70.0 kg)(9.81 m/s2
)

(533 m)
6. k = 2.00 × 102
N/m
x = 0.158 m
g = 9.81 m/s2
a. F = kx = (2.00 × 102
N/m)(0.158 m) =
b. m = 
F
g
 = 
k
g
x

m =
m = 3.22 kg
(2.00 × 102
N/m)(0.158 m)

(9.81 m/s2)
31.6 N

II Ch. 11–2
II
7. h = 1.02 × 104
m
L = 4.20 × 103
m
k = 3.20 × 10−2
N/m
F = kx = k(h − L)
F = (3.20 × 10−2
N/m)(6.0 × 103
m) = 190 N
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. L = 6.7 m
ag = g = 9.81 m/s2
T = 2π 
a
L
g

= 2π 
(9
(
.8
6
1
.7
m
m
/
)
s
2
)

= 5.2 s
2. L = 0.150 m
ag = g = 9.81 m/s2
T = 2p
a
L
g

= 2p = 0.777 s
(0.150 m)

(9.81 m/s2)
3. x = 0.88 m
ag = g = 9.81 m/s2
T = 2p
4
a
x
g

= 2p
T = 3.8 s
4(0.88 m)

(9.81 m/s2)
4. f = 6.4 × 10−2
Hz
ag = g = 9.81 m/s2
T = 
1
f
 = 2p
a
L
g


L = 
4p
a
2
g
f 2
 =
L = 61 m
(9.81 m/s2
)

4π2(6.4 × 10−2 Hz)2
5. t = 3.6 × 103
s
N = 48 oscillations
ag = g = 9.81 m/s2
T = 2p
a
L
g

= 
N
t

L = =
L = 1.4 × 103
m
(3.6 × 103
s)2
(9.81 m/s2
)

4p2 (48)2

N
t


2
ag

4p2
8. h = 348 m
L = 2.00 × 102
m
k = 25.0 N/m
g = 9.81 m/s2
F = kx = k(h − L) = mg
m = = 377 kg
(25.0 N/m)(148 m)

(9.81 m/s2)
6. L = 1.00 m
T = 10.5 s
ag = 
4p
T
2
2
L
 = = 0.358 m/s2
4p2
(1.00 m)

(10.5 s)2

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. f1 = 90.0 Hz
k = 2.50 × 102
N/m
T = 2p
m
k

= 
3.00 ×
1
10−2f1

m = =
m = 0.869 kg
(2.50 × 102
N/m)

4p2(3.00 × 10−2)2(90.0 Hz)2
k

4p2(3.00 × 10−2)2f1
2
Givens Solutions
2. m1 = 3.5 × 106
kg
f = 0.71 Hz
k = 1.0 × 106
N/m
T = 
1
f
 = 2p
m
1
k
+

m
2


m2 = 
4p
k
2f 2
 − m1
m2 = − 3.5 × 104
kg = 1.5 × 104
kg
(1.0 × 106
N/m)

4p2(0.71 Hz)2
3. m = 20.0 kg
f = 
4
6
2
0
.7
s
 = 0.712 Hz
k = 
4p
T
2
2
m
 = 4p2
mf 2
k = 4p2
(20.0 kg)(0.712 Hz)2
k = 4.00 × 102
N/m
4. m = 2.00 × 105
kg
T = 1.6 s
T = 2p
m
k


k = 
4p
T
2
2
m
 = = 3.1 × 106
N/m
4p2
(2.00 × 105
kg)

(1.6 s)2
5. m = 2662 kg
x = 0.200 m
g = 9.81 m/s2
T = 2p
m
k

= 2p
m
m

x
g


T = 2p
(
(
9
0
.8
.
2
1
0
m
0
m
/
s2
)
)

= 0.897 s
1. f = 2.50 × 102
Hz
v = 1530 m/s
l = 
v
f
 = 
2.5
1
0
53
×
0
1
m
02
/s
Hz
 = 6.12 m
6. m = 10.2 kg
k = 2.60 × 102
N/m
T = 2p
m
k

= 2p = 1.24 s
(10.2 kg)

(2.60 × 102 N/m)

II Ch. 11–4
II
2. f = 123 Hz
v = 334 m/s
l = 
v
f
 = 
(
(
3
1
3
2
4
3
m
H
/
z
s
)
)
 = 2.72 m
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. l = 2.0 × 10−2
m
v = 334 m/s
f = 
l
v
 = 
(2.
(
0
33
×
4
1
m
0−
/
2
s)
m)
 = 1.7 × 104
Hz
4. l = 2.54 m
v = 334 m/s
f = 
l
v
 = 
(
(
3
2
3
.5
4
4
m
m
/s
)
)
 = 131 Hz
5. f = 73.4 Hz
l = 4.50 m
v = fl = (73.4 Hz)(4.50 m) = 3.30 × 102
m/s
6. f = 2.80 × 105
Hz
l = 5.10 × 10−3
m
∆x = 3.00 × 103
m
v = fl = (2.80 × 105
Hz)(5.10 × 10−3
m)
v =
∆t = 
∆
v
x
 = 
(
(
1
3
.4
.0
3
0
×
×
1
1
0
0
3
3
m
m
/s
)
)

∆t = 2.10 s
1.43 × 103
m/s

Sound
II
1. Intensity = 3.0 × 10−3
W/m2
r = 4.0 m
Intensity = 
4p
P
r2

P = 4pr2
(Intensity) = 4p(4.0 m)2
(3.0 × 10−3
W/m2
)
P = 0.60 W
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. r = 8.0 × 103
m
Intensity = 1.0 × 10−12
W/m2
Intensity = 
4p
P
r2

P = 4pr2
(Intensity)
P = 4p(8.0 × 103
m)2
(1.0 × 10−12
W/m2
) = 8.0 × 10−4
W
3. Intensity = 1.0 × 10−12
W/m2
P = 2.0 × 10−6
W
Intensity = 
4p
P
r2

r = 
4p
(I
n
P
te
n
si
ty
)


r = = 4.0 × 102
m
2.0 × 10−6
W

4p(1.0 × 10−12 W/m2)
4. Intensity = 1.1 × 10−13
W/m2
P = 3.0 × 10−4
W
r 2 = 
4p In
P
tensity

r = = = 1.5 × 104
m
(3.0 × 10−4
W)

4p(1.1 × 10−13
W/m2)
P

4p Intensity
5. P = 1.0 × 10−4
W
r = 2.5 m
Intensity = 
4p
P
r2

Intensity = = 1.3 × 10−6
W/m2
(1.0 × 10−4
W)

4p(2.5 m)2
6. Intensity = 2.5 × 10−6
W/m2
r = 2.5 m
P = 4pr2
(Intensity)
P = 4p(2.5 m)2
(2.5 × 10−6
W/m2
)
P = 2.0 × 10−4
W

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. f15 = 26.7 Hz
v = 334 m/s
n = 15
L = 
4
15
f1
v
5
 =
L = 46.9 m
15(334 m/s)

4(26.7 Hz)
Givens Solutions
2. l = 3.47 m
vs = 5.00 × 102
m/s
n = 3
va = 334 m/s
L = 
l
2
v
v
s
a
n
 =
L = 7.79 m
(3.47 m)(5.00 × 102 m/s)(3)

2(334 m/s)
3. n = 19
L = 86 m
v = 334 m/s
f19 = 
2
n
L
v
 = 
19
2
(
(
3
8
3
6
4
m
m
)
/s)

f19 = 37 Hz
4. L = 3.50 × 102
m
f75 = 35.5 Hz
n = 75
f75 = 
7
2
5
L
v

v = 
2L
7
f
5
75
 =
v = 331 m/s
2(3.50 × 102
m)(35.5 Hz)

75
5. L = 4.7 × 10−3
m
l = 3.76 × 10−3
m
ln = 
4
n
L

n = 
l
4L
n
 = = 5
4(4.7 × 10−3
m)

(3.76 × 10−3 m)
II Ch. 12–2

II
1. f = 9.00 × 108
Hz
d = 60.0 m
c = 3.00 × 108
m/s
c = fl

l
d
 = = 
d
c
f


l
d
 =

l
d
 = 1.80 × 102
wavelengths
(60.0 m)(9.00 × 108
Hz)

(3.00 × 108 m/s)
d


f
c


Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. f = 5.20 × 1014
Hz
d = 2.00 × 10−4
m
c = 3.00 × 108
m/s
c = fl

l
d
 = = 
d
c
f


l
d
 =

l
d
 = 347 wavelengths
(2.00 × 10−4
m)(5.20 × 1014
Hz)

(3.00 × 108 m/s)
d


f
c


3. f = 2.40 × 1010
Hz
c = 3.00 × 108
m/s
c = fl
l = 
c
f

l =
l = 1.25 × 10−2
m = 1.25 cm
(3.00 × 108
m/s)

(2.40 × 1010 Hz)
4. l = 1.2 × 10−6
m
c = 3.00 × 108
m/s
c = fl
f = 
l
c

f =
f = 2.5 × 1014
Hz = 250 TH
(3.00 × 108
m/s)

(1.2 × 10−6 m)

II Ch. 13–2
II
5. l1 = 2.0 × 10−3
m
l2 = 5.0 × 10−3
m
c = 3.00 × 108
m/s
c = fl
f1 = 
l
c
1
 =
f1 = 1.5 × 1011
Hz = 15 × 1010
Hz
f2 = 
l
c
2
 =
f2 = 6.0 × 1010
Hz
6.0 × 1010
Hz f 15 × 1010
Hz
(3.00 × 108
m/s)

(5.0 × 10−3 m)
(3.00 × 108
m/s)

(2.0 × 10−3 m)
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. f = 10.0 Hz
c = 3.00 × 108
m/s
c = fl
l = 
c
f

l =
l = 3.00 × 107
m = 3.00 × 104
km
(3.00 × 108
m/s)

(10.0 Hz)
1. p = 3.70 × 105
m
f = 2.50 × 105
m

q
1
 = 
1
f
 − 
p
1


q
1
 = 
(2.50 ×
1
105 m)
 − 
(3.70 ×
1
105 m)
 = 
(4.00
1
×
m
10−6
)
 − 
(2.70
1
×
m
10−6
)

q =

1.30
1
×
m
10−6


−1
= 7.69 × 105
m =
M = −
p
q
 = 
−
3
7
.7
.6
0
9
×
×
1
1
0
0
5
5
m
m

M = −2.08
769 km
2. h = 8.00 × 10−5
m
f = 2.50 × 10−2
m
q = −5.9 × 10−1
m

p
1
 + 
1
q
 = 
1
f



p
1
 = 
1
f
 − 
1
q


p
1
 = 
(2.50 ×
1
10−2 m)
 − 
(−5.9 ×
1
10−1 m)
 = 
4
1
0
m
.0
 − 
1
1
.6
m
9
 = 
4
1
1
m
.7

p =
M = 
h
h
⬘
 = −
p
q
 = −
(
(
−
2.
5
4
.
0
9
×
×
1
1
0
0
−
−
2
1
m
m
)
)
 = 24.6
2.40 × 10−2
m

II
3. h⬘ = −28.0 m
h = 7.00 m
f = 30.0 m
Image is real, so q 0 and
h⬘ 0.
M = −
p
q
 = 
h
h
⬘

q = −
p
h
h⬘


p
1
 + 
q
1
 = 
1
f


p
1
 + = 
1
f


p
1

1 − 
h
h
⬘

= 
1
f

p = f
1 − 
h
h
⬘


p = (30.0 m)
1 + 
7
2
.
8
0
.
0
0
m
m


p = 37.5 m
1


−p
h
h⬘


Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. h⬘ = 67.4 m
h = 1.69 m
R = 12.0 m
(h⬘ 0, q 0)
M = − 
p
q
 = 
h
h
⬘

q = −
p
h
h⬘


p
1
 + 
q
1
 = 
R
2


p
1
 + = 
R
2


p
1

1 − 
h
h
⬘

= 
R
2

p =

R
2

1 − 
h
h
⬘


p = 
(12.
2
0 m)

1 − 
1
6
.
7
6
.
9
4
m
m

= (6.00 m)(0.975)
p =
Image is virtual and therefore upright.
5.85 m
1


−p
h
h⬘


II
5. h = 32 m
f = 120 m
p = 180 m

p
1
 + 
q
1
 = 
1
f


q
1
 = 
1
f
 − 
p
1


q
1
 = 
(120
1
m)
 − 
(180
1
m)
 = 
0.
1
00
m
83
 − 
0.
1
00
m
56
 = 
0.
1
00
m
27

q =
M = 
h
h
⬘
 = −
p
q

h⬘= −
q
p
h

h⬘= 
−(37
(
0
18
m
0
)
m
(3
)
2 m)

h⬘ =
The image is inverted (h⬘ 1)
and real (q 0)
−66 m
3.7 × 102
m
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 13–4
6. h = 0.500 m
R = 0.500 m
p = 1.000 m

q
1
 = 
R
2
 − 
p
1


q
1
 = 
(0.50
2
0 m)
 − 
(1.00
1
0 m)
 = 
4
1
.0
m
0
 − 
1
1
.0
m
00
 = 
3
1
.0
m
0

q =
M = −
p
q
 = 
h
h
⬘

h⬘ = −
q
p
h
 =
h⬘ =
The image is real (q 0).
−0.166 m = −166 mm
−(0.333 m)(0.500 m)

(1.000 m)
0.333 m = 333 mm

II
7. p = 1.00 × 105
m
h = 1.00 m
h⬘ = −4.00 × 10−6 m
(h⬘ 0 because image is
inverted)
M = −
p
q
 = 
h
h
⬘

q = −
p
h
h⬘


p
1
 + 
q
1
 = 
R
2

R = =
R = = 
(
(
1
2.
+
00
2.
×
50
10
×
5
1
m
05
)
)

R = 0.800 m = 80.0 cm
2(1.00 × 105
m)

1 + 
(4.0
(
0
1.
×
00
10
m
−6
)
m)


2p

1 − 
h
h
⬘


2


p
1
 − 
p
h
h⬘


Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
8. h = 10.0 m
p = 18.0 m
h⬘ = −24.0 m
Image is real, so q 0, and
h⬘ must be negative.
M = − 
p
q
 = 
h
h
⬘

q = −
h
h
⬘p


p
1
 + 
q
1
 = 
R
2

R = =
R = = 
(1
3
+
6.
0
0
.4
m
17)
 = 
(
(
3
1
6
.
.
4
0
1
m
7)
)

R = 25.4 m
2(18.0 m)

1 + 
1
2
0
4
.
.
0
0
m
m


2p

1 − 
h
h
⬘


2


p
1
 − 
p
h
h⬘


II Ch. 13–6
2. p = 553 m
R = −1.20 × 102
m

p
1
 + 
q
1
 = 
R
2


q
1
 = 
R
2
 − 
p
1


q
1
 = 
(−1.20 ×
2
102 m)
 − 
(553
1
m)
 = − 
0.
1
01
m
67
 − 
0.0
1
0
m
181
 = − 
0.
1
01
m
85

q = −54.1 m
M = − 
p
q
 = 
−(
(
−
5
5
5
4
3
.1
m
m
)
)

M = 9.78 × 10−2
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. R = −6.40 × 106
m
p = 3.84 × 108
m
h = 3.475 × 106
m

p
1
 + 
q
1
 = 
R
2


q
1
 = 
R
2
 − 
p
1


q
1
 = 
(−6.40 ×
2
106 m)
 − 
(3.84 ×
1
108 m)
 = − 
(3.13
1
×
m
10−7
)
 − 
(2.60
1
×
m
10−9
)

q = −

3.16
1
×
m
10−7


−1
= −3.16 × 106
m = −3.16 × 103
km
M = −
p
q
 = 
h
h
⬘

h⬘ = − 
q
p
h

h⬘ =
h⬘ = 2.86 × 104
m = 28.6 km
−(−3.16 × 106
m)(3.475 × 106
m)

(3.84 × 108 m)
Givens Solutions
3. R = −35.0 × 103
m
p = 1.00 × 105
m

p
1
 + 
q
1
 = 
R
2


q
1
 = 
R
2
 − 
p
1


q
1
 = 
(−35.0 ×
2
103 m)
 − 
(1.00 ×
1
105 m)
 = − 
(5.71
1
×
m
10−5
)
 − 
(1.00
1
×
m
10−5
)

q = −

6.71
1
×
m
10−5


−1
= −1.49 × 104
m = −14.9 km

II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 4. h = 1.4 × 106
m
h⬘ = 11.0 m
R = −5.50 m
M = 
h
h
⬘

M = 
(1.4
11
×
.0
10
m
6
m)

M =
q = −pM

p
1
 + 
q
1
 = 
R
2


p
1

1 − 
M
1

= 
R
2

p = 
R
2

1 − 
M
1


p =

−5.5
2
0 m


7.9
1
×
−
1
1
0−6


p = 3.5 × 105
m = 3.5 × 102
km
Scale is 7.9 × 10−6
:1
7.9 × 10−6
5. scale factor = 1:1400
f = −20.0 × 10−3
m
M = 
14
1
00

M = − 
p
q

q = −Mp

p
1
 + 
q
1
 = 
1
f


p
1

1 − 
M
1

= 
1
f

p = f
1 − 
M
1


p = (−20.0 × 10−3
m)(1 − 1400)
p = 28 m

II Ch. 13–8
7. h⬘ = 4.78 × 10−3
m
h = 12.8 × 10−2
m
f = −64.0 × 10−2
m
M = − 
p
q
 = 
h
h
⬘

p = − 
q
h
h
⬘


p
1
 + 
q
1
 = 
1
f

+ 
q
1
 = 
1
f


q
1


−
h
h⬘
 + 1
= 
1
f

q = f
1 − 
h
h
⬘


q = (−64.0 × 10−2
m)
1 − 
4
1
.
2
7
.
8
8
×
×
1
1
0
0
−
−
3
2
m
m

= (−64.0 × 10−2
m)(0.963)
q = −61.6 × 10−2
m = −61.6 cm
1


−
h
q
⬘
h


II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. h = 1.38 m
p = 6.00 m
h⬘ = 9.00 × 10−3
m
M = − 
p
q
 = 
h
h
⬘

q = − 
p
h
h⬘


p
1
 + 
q
1
 = 
R
2


p
1
 − 
p
h
h⬘
 = 
R
2

R =
R = = 
(1
12
−
.0
15
m
3)

R = −7.89 × 10−2
m = −7.89 cm
2(6.00 m)

1 − 
9.00
1.
×
38
10
m
−3 m


2p

1 − 
h
h
⬘


II
8. h = 0.280 m
h⬘ = 2.00 × 10−3
m
q = −50.0 × 10−2
m
M = 
h
h
⬘
 = − 
p
q

p = −
q
h
h
⬘


p
1
 + 
q
1
 = 
1
f

+ 
q
1
 = 
1
f


q
1


−
h
h⬘
 + 1
= 
1
f

f =
f = = 
(−50.
(
0
0.
×
99
1
3
0
)
−2
m)

f = −50.4 × 10−2
m = −50.4 cm
(−50.0 × 10−2
m)

1 − 
(2.0
(0
0
.2
×
8
1
0
0
m
−3
)
m)


q

1 − 
h
h
⬘


1


−
h
q
⬘
h


Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. qi = 72°
θr = 34°
ni = 1.00
nr = ni 
s
s
i
i
n
n
θ
θ
r
i
 = (1.00) 
(
(
s
s
i
i
n
n
7
3
2
4
°
°
)
)
 = 1.7
Givens Solutions
2. θi = 47.9°
θr = 29.0°
ni = 1.00
nr = ni 
s
s
i
i
n
n
θ
θ
r
i
 = (1.00) 
(
(
s
s
i
i
n
n
4
2
7
9
.
.
9
0
°
°
)
)
 = 1.53
3. θr = 17°
ni = 1.5
nr = 1.33
θr = 15°
nr = 1.5
ni = 1.00
glass to water:
θi = sin−1

n
n
r
i
(sin θr)
= sin−1

1
1
.3
.5
3
(sin 17°)
=
air to glass:
θi = sin−1

n
n
r
i
(sin θr)
= sin−1

1
1
.
.
0
5
0
(sin 15°)
= 23°
15°
4. θi = 55.0°
θr = 53.8°
nr = 1.33
ni = nr 
(
(
s
s
i
i
n
n
θ
θ
r
i)
)
 = 1.33 
(
(
s
s
i
i
n
n
5
5
3
5
.
.
8
0
°
°
)
)
 = 1.31
5. θi = 48°
ni = 1.00
nr = 1.5
θi = 3.0 × 101
°
ni = 1.5
nr = 1.6
θi = 28°
ni = 1.6
nr = 1.7
air to glass 1:
θr = sin−1

n
n
r
i
(sin θi)
= sin−1

1
1
.0
.5
0
(sin 48°)
=
glass 1 to glass 2:
θr = sin−1

n
n
r
i
(sin θi)
= sin−1

1
1
.
.
5
6
(sin 3.0°)
=
glass 2 to glass 3:
θr = sin−1

n
n
r
i
(sin θi)
= sin−1

1
1
.
.
6
7
(sin 28°)
= 26°
28°
3.0 × 101
°
Refraction

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 14–2
1. f = 8.45 m
q = −25 m
Givens Solutions
2. h⬘ = 1.50 m
q = −6.00 m
f = −8.58 m

p
1
 = 
1
f
 − 
1
q
 = 
−8.5
1
8 m
 − 
−6.0
1
0 m


p
1
 = 
−0
1
.1
m
17
 + 
0
1
.1
m
67
 = 
0
1
.0
m
50

p =
h = 
−h
q
′p
 = − 
(1.5
(
0
−
m
6.0
)(
0
2
m
0.0
)
m)
 = 5.00 m
20.0 m
3. h = 7.60 × 10−2
m
h⬘ = 4.00 × 10−2
m
f = −14.0 × 10−2
m
M = 
h
h
⬘
 = − 
p
q

q = − 
p
h
h⬘


p
1
 + 
q
1
 = 
1
f


p
1
 + = 
−
f
1


p
1

1 − 
h
h
⬘

= 
1
f

p = f
1 − 
h
h
⬘


p = (−14.0 × 10−2
m)
1 − 
7
4
.
.
6
0
0
0
×
×
1
1
0
0
−
−
2
2
m
m

= (−14.0 × 10−2
m)(0.90)
p =
q = − 
p
h
h⬘
 = −
q = −6.84 × 10−2
m = −6.84 cm
(1.3 × 10−1
m)(4.00 × 10−2
m)

(7.60 × 10−2 m)
1.30 × 10−1
m = 13.0 cm
1


−p
h
h′



p
1
 + 
q
1
 = 
1
f


p
1
 = 
1
f
 − 
q
1


p
1
 = 
(8.4
1
5 m)
 − 
(−
1
25)
 = 
0
1
.1
m
18
 + 
0
1
.0
m
40
 = 
0
1
.1
m
58

p = 6.3 m
M = − 
p
q
 = 
−(
6
−
.
2
3
5
m
m)

M = 4.0

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. h = 28.0 m
h⬘ = 3.50 m
f = −10.0 m
M = 
h
h
⬘
 = − 
p
q

q = − 
h
h
⬘p


p
1
 + 
q
1
 = 
1
f


p
1
 + = 
1
f


p
1

1 − 
h
h
⬘

= 
1
f

p = f
1 − 
h
h
⬘


p = (−10.0 m)
1 − 
2
3
8
.5
.0
0
m
m


p = 70.0 m
1


−h
h
⬘p


Givens Solutions
5. h⬘ = 1.40 cm
q = −19.0 cm
f = 20.0 cm

p
1
 = 
1
f
 − 
q
1
 = 
−20.
1
0 cm
 − 
−19.
1
0 cm


p
1
 = 
−0
1
.0
cm
500
 + 
0
1
.0
c
5
m
26
 = 
2.6
1
0
c
×
m
103

p = 385 cm =
h = − 
p
q
h⬘
 = − 
(385
(−
cm
19
)
.
(
0
1
c
.4
m
0
)
cm)
 = 28.4 cm
3.85 m
6. h = 1.3 × 10−3
m
h⬘ = 5.2 × 10−3
m
f = 6.0 × 10−2
m
M = 
h
h
⬘
 = − 
p
q

q = − 
p
h
h⬘


p
1
 + 
q
1
 = 
1
f


p
1
 + = 
1
f


p
1

1 − 
h
h
⬘

= 
1
f

p = f
1 − 
h
h
⬘


p = (6.0 × 10−2
m)
1 − 
(
(
1
5
.
.
3
2
×
×
1
1
0
0
−
−
3
3
m
m
)
)


p =
q = − 
p
h
h⬘
 =
q = −0.18 m = −18 cm
−(4.5 × 10−2
m)(5.2 × 10−3
m)

(1.3 × 10−3 m)
4.5 × 10−2
m = 4.5 cm
1

− 
p
h
h⬘


II Ch. 14–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
7. f = 26.7 × 10−2
m
p = 3.00 m
Image is real, so h⬘ 0.

p
1
 + 
q
1
 = 
1
f


q
1
 = 
1
f
 − 
p
1


q
1
 = 
(26.7 ×
1
10−2 m)
 − 
(3.0
1
0 m)
 = 
3
1
.7
m
5
 − 
0
1
3
m
33
 = 
3
1
.4
m
2

q =
M = − 
p
q

M = − 
(
(
0
3
.2
.0
9
0
2
m
m
)
)

M = −9.73 × 10−2
0.292 m = 29.2 cm
Givens Solutions
8. h⬘ = 2.25 m
p = 12.0 m
f = −5.68 m
9. h = 0.108 m
p = 4h = 0.432 m
f = −0.216 m

p
1
 + 
q
1
 = 
1
f


1
q
 = 
1
f
 − 
p
1


q
1
 = 
(−0.2
1
16 m)
 − 
(0.43
1
2 m)
 = − 
4
1
.6
m
3
 − 
2
1
.3
m
1
 = − 
6
1
.9
m
4

q =

h
h
⬘
 = − 
p
q

h⬘ = − 
q
p
h

h⬘ =
h⬘ = 0.0360 m = 36.0 mm
− (−0.144 m)(0.108 m)

(0.432 m)
− 0.144 m = −144 mm

1
q
 = 
1
f
 − 
p
1
 = 
−5.6
1
8 m
 − 
12.
1
0 m


1
q
 = 
−0
1
.1
m
76
 − 
0
1
.0
m
83
 = 
−0
1
.2
m
59

q =
h = − 
h
q
′p
 = − 
(2.25
−
m
3.8
)(
6
1
m
2.0 m)
 = 6.99 m
−3.86 m

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 10. p = 117 × 10−3
m
M = 2.4
M = − 
p
q

q = −pM = −(117 × 10−3
m)(2.4)
q = − 0.28 m

p
1
 + 
q
1
 = 
1
f


1
f
 = 
(117 ×
1
10−3 m)
 − 
(0.2
1
8 m)
 = 
8
1
.5
m
5
 − 
1
3.
m
6
 = 
1
5.
m
0

f = 0.20 m = 2.0 × 102
mm
Givens Solutions
11. Image is real, and therefore
inverted.

h
h
⬘
 = M = −64
q = 12 m
p = − 
M
q


p
1
 + 
q
1
 = 
1
f

− 
M
q
 + 
q
1
 = 
1
f

f = 
(1 −
q
M)

f = 
[1
(
−
12
(−
m
6
)
4)]

f = Image is inverted
0.18 m = 18 cm
12. h⬘ = −0.55 m
h = 2.72 m
p = 5.0 m
−
p
q
 = 
h
h
⬘

q = − 
p
h
h⬘


p
1
 + 
q
1
 = 
1
f


1
f
 = 
p
1
 − 
p
h
h⬘


1
f
 = 
p
1

1 − 
h
h
⬘


f =
f = = 
5.
5
0
.9
m

f = 0.85 m
5.0 m

1 − 
(
(
−
2
0
.7
.5
2
5
m
m
)
)


p

1 − 
h
h
⬘


II Ch. 14–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
13. p = 12.0 × 10−2
m
M = 3.0
M = − 
p
q

q = − Mp

p
1
 + 
q
1
 = 
1
f


p
1
 − 
M
1
p
 = 
1
f


p
1

1 − 
M
1

= 
1
f

f =
f =
f = 1.8 × 10−1
m = 18 cm
(12.0 × 10−2
m)

1 − 
3
1
.0


p

1 − 
M
1


14. h = 7.60 × 10−2
m
p = 16.0 × 10−2
m
f = −12.0 × 10−2
m

p
1
 + 
q
1
 = 
1
f

M = − 
p
q
 = 
h
h
⬘

q = − 
p
h
h⬘


p
1
 + = 
1
f


p
1

1 − 
h
h
⬘

= 
1
f

1 − 
h
h
⬘
 = 
p
f


h
h
⬘
 = 1 − 
p
f

h⬘ =
h⬘ = = 
(7.60
(
×
2.3
1
3
0
)
−2
m)

h⬘ = 3.26 × 10−2
m = 3.26 cm
(7.60 × 10−2
m)

1 − 
(
(
−
1
1
6
2
.0
.0
×
×
1
1
0
0
−
−
2
2
m
m
)
)


h

1 − 
p
f


1


−p
h
h⬘


II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 15. h = 48 m
f = 1.1 × 10−1
m
p = 120 m

p
1
 + 
q
1
 = 
1
f


q
1
 = 
1
f
 − 
p
1


q
1
 = 
(1.1 × 1
1
0−1 m)
 − 
(120
1
m)
 = 
1
9.
m
1
 − 
(8.3
1
×
m
10−3
)
 = 
1
9.
m
1

q = 1.1 × 10−1
m
M = 
h
h
⬘
 = − 
p
q

h⬘ = − 
q
p
h

h⬘ =
h⬘ = 4.4 × 10−2
m = − 4.4 cm
−(1.1 × 10−1
m)(48 m)

(120 m)
Givens Solutions
16. f = −0.80 m
h⬘ = 0.50 × 10−3
m
h = 0.280 m
M = 
h
h
⬘
 = − 
p
q

q = − 
p
h
h⬘


p
1
 + 
q
1
 = 
1
f


p
1
 + = 
1
f


p
1

1 − 
h
h
⬘

= 
1
f

p = f
1 − 
h
h
⬘


p = (− 0.80 m)
1 − 
(0.5
(0
0
.2
×
8
1
0
0
m
−3
)
m)


p =
q = − 
p
h
h⬘
 =
q = −0.80 m
−(4.5 × 102
m)(0.50 × 10−3
m)

(0.280 m)
4.5 × 102
m
1


−p
h
h⬘


1. θc = 46°
ni = 1.5
nr = nisinθc = (1.5)(sin 46°) = 1.1

II Ch. 14–8
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. ni = 1.00
qi = 75.0°
qr = 23.3°
ni = 2.44
nr = 1.00
nr = ni 
(
(
s
s
i
i
n
n
θ
θ
r
i)
)
 = (1.00) 
(
(
s
s
i
i
n
n
7
2
5
3
.
.
0
3
°
°
)
)
 = 2.44
θc = sin = −1

n
n
r
i


θc = sin−1

1
2
.
.
0
4
0
4

= 24.2°
Givens Solutions
3. θc = 42.1°
nr = 1.00
ni = 
sin
nr
θc
 = 
sin
1.
4
0
2
0
.1°
 = 1.49
4. ni = 1.56
nr = 1.333
sin qc = 
n
n
i
r

θc = sin−1

n
n
r
i

= sin−1

1
1
.3
.5
3
6
3

= 58.7°
5. ni = 1.52
h = 0.025 mm
nr = 1.00
θc = sin−1

n
n
r
i

= sin−1

1
1
.
.
0
5
0
2

=
∆x = h(tan qc) where tan qc = 
n
n
r
i

∆x = h

n
n
r
i

= (0.025 mm)

1
1
.
.
0
5
0
2

= 0.0160 mm
d = 2∆x = 2(0.0160 mm) = 0.0320 mm
41.1°

Interference and
Diffraction
II
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
Givens Solutions
1. d = 1.20 × 10−6
m
l = 156.1 × 10−9
m
m = 5; constructive
interference
For constructive interference,
dsin q = ml
sin q = 
m
d
l

q = sin−1

m
d
l


q = sin−1

(5
(
)
1
(1
.2
5
0
6.
×
1
1
×
0
1
−
0
6
−
m
9
)
m)


q = 40.6°
2. d = 6.00 × 10−6
m
l = 6.33 × 10−7
m
m = 0; destructive
interference
For destructive interference,
dsin q = m + 
1
2

l
sin q =
q = sin−1

q = sin−1

q = 3.02°
0 + 
1
2

(6.33 × 10−7
m)

(6.00 × 10−6
m
m + 
1
2

l

d
m + 
1
2

l

d
3. d = 0.80 × 10−3
m
m = 3; destructive
interference
q = 1.6°
dsin q = m + 
1
2

l
l =
l =
l = 6.4 × 10−6
m = 6.4 mm
(0.80 × 10−3
m)(sin 1.6°)

3 + 
1
2


dsin q

m + 
1
2


II Ch. 15–2
4. d = 15.0 × 10−6
m
m = 2; constructive
interference
q = 19.5°
dsin q = ml
l = 
ds
m
in q

l =
l = 2.50 × 10−6
m = 2.50 mm
(15.0 × 10−6
m)[sin(19.5°)]

2
6. f = 60.0 × 103
Hz
c = 3.00 × 108
m/s
m = 4; constructive
interference
q = 52.0°
dsin q = ml = 
m
f
c

d = 
f s
m
in
c
q

d =
d = 2.54 × 104
m = 25.4 km
(4)(3.00 × 108
m/s)

(60.0 × 103 Hz)(sin 52.0°)
7. f = 137 × 106
Hz
c = 3.00 × 108
m/s
m = 2; constructive
interference
q = 60.0°
dsin q = ml = 
m
f
c

d = 
f s
m
in
c
q

d =
d = 5.06 m
(2)(3.00 × 108
m/s)

(137 × 106 Hz)(sin 60.0°)
mmax = 
d(sin
l
90.0°)
 = 
l
d
 = 
d
c
f

mmax = = 2.31
The second-order maximum (m = 2) is the highest observable with this apparatus.
(5.06 m)(137 × 106
Hz)

(3.00 × 108 m/s)
Givens Solutions
5. l = 443 × 10−9
m
m = 4; destructive
interference
q = 2.27°
dsin q = m + 
1
2

l
d =
d =
d = 5.03 × 10−5
m
4 + 
1
2

(443 × 10−9
m)

(sin 2.27°)
m + 
1
2

l

sin q
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. l = 40.0 × 10−9
m
d = 150.0 × 10−9
m
m = 2
d(sin q) = ml
q = sin−1

m
d
l


q = sin−1

q = 32.2°
2(40.0 × 10−9
m)

(150.0 × 10−9 m)
Givens Solutions
1. d = 
1.00 × 10
1
2
lines/m

m = 1
q = 30.0°
c = 3.00 × 108
m/s
d(sin q) = ml
l = 
d(si
m
n q)

l =
l =
f = 
l
c
 = 
(
(
3
5
.
.
0
0
0
0
×
×
1
1
0
0
8
−3
m
m
/s
)
)

f = 6.00 × 1010
Hz = 60.0 Ghz
5.00 × 10−3
m = 5.00 mm
[sin(30.0°)]

(1.00 × 102
lines/m)(1)
3. l = 714 × 10−9
m
m = 3
q = 12.0°
d(sin q) = ml
d = 
(s
m
in
l
q)

d = 
(3)
[
(
s
7
i
1
n
4
(
×
12
1
.0
0
°
−
)
9
]
m)

d =
or
9.71 × 104
lines/m
1.03 × 10−5
m between lines
2. d = 2.0 × 10−8
m
m = 3
q = 12°
d(sin q) = ml
l = 
d(si
m
n q)

l =
l = 1.4 × 10−9
m = 1.4 nm
(2.0 × 10−8
m)[sin(12°)]

3

II Ch. 15–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. l = 2.2 × 10−6
m
d = 
6.4 × 10
1
4 lines/m

q = 34.0°
d(sin q) = ml
m = 
d(si
l
n q)

m = = 4.0
m = 4.0
[sin (34.0°)]

(6.4 × 104 lines/m)(2.2 × 10−6 m)
5. f = 1.612 × 109
Hz
c = 3.00 × 108
m/s
d = 45.0 × 10−2
m
m = 1
d(sin q) = ml = 
m
f
c

q = sin−1

m
df
c


q = sin−1

q = 24.4°
(1)(3.00 × 108
m/s)

(45.0 × 10−2 m)(1.612 × 109 Hz)
Givens Solutions
7. d = 
25 × 104
1
lines/m

l = 7.5 × 10−7
m
q = 48.6°
d(sin q) = ml
m = 
d(si
l
n q)

m = = 4.0
m = 4.0
[sin(48.6°)]

(25 × 104 lines/m)(7.5 × 10−7 m)

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. q1 = 0.085 C
r = 2.00 × 103
m
Felectric = 8.64 × 10−8
N
kC = 8.99 × 109
N•m2
/C2
Felectric = kC 
q
r
1q
2
2

q2 = 
Fel
k
e
C
ctr
q
ic
1
r2

q2 = = 4.5 × 10−10
C
(8.64 × 10−8
N)(2.00 × 103
m)2

(8.99 × 109
N•m2/C2)(0.085 C)
Givens Solutions
2. q1 = q
q2 = 3q
Felectric = 2.4 × 10−6
N
r = 3.39 m
kC = 8.99 × 109
N•m2
/C2
F = kC 
q
r
1q
2
2
 = kC 
3
r
q
2
2

q = 
3
F
k
r
C
2

=
q = 3.2 × 10−8
C
(2.4 × 10−6 N)(3.39 m)2

(3)(8.99 × 109 N•m2/C2)
3. Felectric = 1.0 N
r = 2.4 × 1022
m
kC = 8.99 × 109
N•m2
/C2
F = kC 
N2
r
(q
2
e)2

qe = 
F
k
r
C
2

= r
k
F
C


qe = (2.4 × 1022
m)

qe = 2.5 × 1017
C
1.0 N

8.99 × 109 N•m2/C2
4. r = 1034 m
q1 = 2.0 × 10−9
C
q2 = −2.8 × 10−9
C
kC = 8.99 × 109
N•m2
/C2
r2 = 2r
Felectric = kC 
q
r
1q
2
2
 =
Felectric =
r2 = 2r = (2)(1034 m) = 2068 m
q = 
F
el
ec
k
t
C
ri
cr
2
2

=
q = 4.7 × 10−9
C
(4.7 × 10−14 N)(2068 m)2

8.99 × 109 N•m2/C2
4.7 × 10−14
N
(8.99 × 109
N•m2
/C2
)(2.0 × 10−9
C)(2.8 × 10−9
C)

(1034 m)2
5. q1 = 1.0 × 105
C
q2 = −1.0 × 105
C
r = 7.0 × 1011
m
kC = 8.99 × 109
N•m2
/C2
F = kC 
q
r
1q
2
2

F = (8.99 × 109
N•m2
/C2
)

(
(
7
1
.0
.0
×
×
1
1
0
0
1
5
1
C
m
)
)
2
2


F = 1.8 × 10−4
N
Electric Forces
and Fields

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 16–2
6. N = 2 000 744
qp = 1.60 × 10−19
C
r = 1.00 × 103
m
kC = 8.99 × 109
N•m2
/C2
q = 
N
2
qp
 = =
Felectric = kC 
q
r2
2

Felectric = (8.99 × 109
N•m2
/C2
)

(
(
1
1
.6
.0
0
0
×
×
1
1
0
0
−
3
13
m
C
)
)
2
2


Felectric = 2.30 × 10−22
N
1.60 × 10−13
C
(2 000 744)(1.60 × 10−19
C)

2
Givens Solutions
7. N1 = 4.00 × 103
N2 = 3.20 × 105
q = 1.60 × 10−19
C
r = 1.00 × 103
m
kC = 8.99 × 109
N•m2
/C2
8. Felectric = 2.0 × 10−28
N
N = 111
qp = 1.60 × 10−19
C
kC = 8.99 × 109
N•m2
/C2
9. q = 1.00 C
Felectric = 4.48 m × 104
N
kC = 8.99 × 109
N•m2
/C2
r = kC

F
el
q
ec
2
tr
ic

= = 448 m
(8.99 × 109
N•m2
/C2
)(1.0 C)2

4.48 × 104
N
10. Felectric = 1.18 × 10−11
N
q1 = 5.00 × 10−9
C
q2 = −2.50 × 10−9
C
kC = 8.99 × 109
N•m2
/C2
Felectric = kC 
q
r
1q
2
2

r = 
F
k
el
C
ec
q
t
2
r
ic

=
r =
L = r cos q = (97.6 m)cos 45° = 69.0 m
97.6 m
(8.99 × 109
N•m2
/C2
)(5.00 × 10−9
C)(2.50 × 10−9
C)

1.18 × 10−11
N
Felectric = 
kC
r
q
2
1q2
 = 
kCN
r
1N
2
2q2

Felectric =
Felectric =
Felectric = kC 
N2
r
2
2
q2
 =
Felectric = 2.36 × 10−23
N
(8.99 × 109
N•m2
/C2
)(3.20 × 105
)2
(1.60 × 10−19
C)2

(1.00 × 103 m)2
2.95 × 10−25
N
(8.99 × 109
N•m2
/C2
)(4.00 × 103
)(3.20 × 105
)(1.60 × 10−19
C)2

(1.00 × 103 m)2
Felectric = kC 
q
r2
2
 = kC 
N
r
2
q
2
p
2

r = 
k
F
C
e
N
le
c
2
t
q
ri
p
c
2

=
r = 1.2 × 102
m
(8.99 × 109 N•m2/C2)(111)2(1.60 × 10−19 C)2

2.0 × 10−28 N

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. q1 = 2.0 × 10−9
C
q2 = 3.0 × 10−9
C
q3 = 4.0 × 10−9
C
q4 = 5.5 × 10−9
C
r1,2 = 5.00 × 102
m
r1,3 = 1.00 × 103
m
r1,4 = 1.747 × 103
m
kC = 8.99 × 109
N•m2
/C2
3. w = 7.00 × 10−2
m
L = 2.48 × 10−1
m
q = 1.0 × 10−9
C
kC = 8.99 × 109
N•m2
/C2
F = kC 
q
r
1q
2
2

Fx = F1 + F2(cos q) = F1 + F2

Fx = kCq2

L
1
2
 + 
(w2 +
L
L2)3/2


Fx = kCq2

(2.48 × 1
1
0−1 m)2
 +

Fx = (8.99 × 109
N•m2
/C2
)(1.0 × 10−9
C)2
(30.8/m2
) = 2.8 × 10−7
N
Fy = F3 + F2(sin q) = F3 + F2

Fy = kCq2

w
1
2
 + 
(w2 +
w
L2)3/2


Fy = kCq2

(7.00 × 1
1
0−2 m)2
 +

Fy = (8.99 × 109
N•m2
/C2
)(1.0 × 10−9
C)2
(2.00 × 102
/m2
) = 1.8 × 10−6
N
Fnet =

F
x
2
+
F
y
2
=

(2
.8
×
1
0−
7
N
)2
+
(
1.
8
×
1
0−
6
N
)2

Fnet = 1.8 × 10−6
N
q⬘ = tan−1

F
F
x
y

= tan−1

1
2
.
.
8
8
×
×
1
1
0
0
−
−
6
7
N
N

= 81°
Fnet = 1.8 × 10−6
N, 81° above the positive x-axis
7.00 × 10−2 m

[(7.00 × 10−2 m)2 + (2.48 × 10−1 m)2]3/2
w


w
2
+
L
2

2.48 × 10−1 m

[(7.00 × 10−2 m)2 + (2.48 × 10−1 m)2]3/2
L


w
2
+
L
2

1. q1 = 2.80 × 10−3
C
q2 = −6.40 × 10−3
C
q3 = 4.80 × 10−2
C
r1,3 = 9740 m
r1,2 = 892 m
kC = 8.99 × 109
N•m2
/C2
F = kC 
q
r
1q
2
2

F1,2 = = 2.02 × 10−1
N
F1,3 = = 1.27 × 10−2
N
F1,tot = F1,2 + F1,3 = −(2.02 × 10−1
N) + (1.27 × 10−2
N) = −0.189 N
F1,tot = 0.189 N downward
(8.99 × 109
N•m2
/C2
)(2.80 × 10−3
C)(4.80 × 10−2
C)

(9740 m)2
(8.99 × 109
N•m2
/C2
)(2.80 × 10−3
C)(6.40 × 10−3
C)

(892 m)2
Givens Solutions
F = kC 
q
r
1q
2
2

F1,2 = = 2.2 × 10−13
N
F1,3 = = 7.2 × 10−14
N
F1,4 = = 3.2 × 10−14
N
F1,tot = F1,2 + F1,3 + F1,4 = (2.2 × 10−13
N) + (7.2 × 10−14
N) + (3.2 × 10−14
N)
F1,tot = 3.2 × 10−13
N down the rope
(8.99 × 109
N•m2
/C2
)(2.0 × 10−9
C)(5.5 × 10−9
C)

(1.747 × 103 m)2
(8.99 × 109
N•m2
/C2
)(2.0 × 10−9
C)(4.0 × 10−9
C)

(1.00 × 103 m)2
(8.99 × 109
N•m2
/C2
)(2.0 × 10−9
C)(3.0 × 10−9
C)

(5.00 × 102 m)2

II Ch. 16–4
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. L = 10.7 m
w = 8.7 m
q1 = −1.2 × 10−8
C
q2 = 5.6 × 10−9
C
q3 = 2.8 × 10−9
C
q4 = 8.4 × 10−9
C
kC = 8.99 × 109
N•m2
/C2
5. d = 1.2 × 103
m
q1 = 1.6 × 10−2
C
q2 = 2.4 × 10−3
C
q3 = −3.2 × 10−3
C
q4 = −4.0 × 10−3
C
kC = 8.99 × 109
N•m2
/C2
∆x = ∆y = = = 8.5 × 102
m
F = 
kC
r
q
2
1q2

Fx = −F2 + F3(cos 45°) = kCq1− 
∆
q
x
2
2
 + 
q3(co
d
s
2
45°)


Fx = (8.99 × 109
N•m2
/C2
)(1.6 × 10−2
C)
− 
(8
2
.
.
5
4
×
×
1
1
0
0
2
−3
m
C
)2
 +

Fx = −0.24 N
Fy = −F4 − F3(sin 45°) = kCq1
∆
q
y
4
2
 + 
q3(si
d
n
2
45°)


Fy = −(8.99 × 109
N•m2
/C2
)(1.60 × 10−2
C)

(8
4
.
.
5
0
×
×
1
1
0
0
2
−3
m
C
)2
 +

Fy = −1.0 N
Fnet =

F
x
2
+
F
y
2
=

(0
.2
4
N
)2
+
(
1.
0
N
)2
= 1.0 N
q⬘ = tan−1

F
F
x
y

= tan−1

(
(
0
1
.
.
2
0
4
N
N
)
)

= 77°
Fnet = 1.0 N, 77° below the negative x-axis
(3.2 × 10−3
C)(sin 45°)

(1.2 × 103 m)2
(3.2 × 10−3
C)(cos 45°)

(1.2 × 103 m)2
1.2 × 103
m


2

d


2

Givens Solutions
F = kC 
q
r
1q
2
2

Fx = F4 + F3(cos q)
Fy = F2 + F3(sin q)
Fx = kCq1
L
q4
2
 + 
(L2 +
q3
w
L
2)3/2


Fx = (8.99 × 109
N•m2
/C2
)(1.2 × 10−8
C)

(8.
(
4
10
×
.7
10
m
−9
)2
C)
 +

Fx = 9.1 × 10−9
N
Fy = kCq1
w
q2
2
 + 
(L2 +
q3
w
w
2)3/2


Fy = (8.99 × 109
N•m2
/C2
)(1.2 × 10−8
C)

(5.6
(8
×
.7
1
m
0−
)
9
2
C)
 +

Fy = 9.0 × 10−9
N
Fnet =

F
x
2
+
F
y
2
=

(9
.1
×
1
0−
9
N
)2
+
(
9.
0
×
1
0−
9
N
)2
= 1.28 × 10−8
N
q⬘ = tan−1

F
F
x
y

= tan−1

9
9
.
.
1
0
×
×
1
1
0
0
−
−
9
9
N
N
)

= 45°
Fnet = 1.28 × 10−8
N, 45° above the positive x-axis
(2.8 × 10−9
C)(8.7 m)

[(10.7 m)2 + (8.7 m)2]3/2
(2.8 × 10−9
C)(10.7 m)

[(10.7 m)2 + (8.7 m)2]3/2

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
1. q1 = 2.5 × 10−9
C
q3 = 1.0 × 10−9
C
r2,1 = 5.33 m
r3,1 = 1.90 m
r3,2 = r2,1 − r3,1 = 5.33 m − 1.90 m = 3.43 m
F3,1 = F3,2 = kC
(
q
r3
3
,
q
1)
1
2

= kC
(
q
r3
3
,
q
2)
2
2


q2 = q1
r
r
3
3
,
,
1
2


2
q2 = (2.50 × 10−9
C)

3
1
.
.
4
9
3
0
m
m


2
= 8.15 × 10−9
C
6. d = 
228.930
3
× 103
m
 =
7.631 × 104
m
q1 = 8.8 × 10−9
C
q2 = −2.4 × 10−9
C
q3 = 4.0 × 10−9
C
kC = 8.99 × 109
N•m2
/C2
q = 60.0°
F = 
kC
r
q
2
1q2

Fx = F2 − F3(cos 60.0°)
Fy = F3(sin 60.0°)
Fx = kCq1
d
q2
2
 − 
q3(co
d
s
2
60.0°)


Fx = (8.99 × 109
N•m2
/C2
)(8.8 × 10−9
C)

(7.
2
6
.
3
4
1
×
×
1
1
0
0
−
4
9
m
C
)2
 −

Fx = 5.5 × 10−18
N
Fy = − 
kCq1q3(
r
si
2
n 60.0°)

Fy = −
Fy = −4.7 × 10−17
N
Fnet =

F
x
2
+
F
y
2
=

(5
.5
×
1
0−
18
N
)2
+
(
4.
7
×
1
0−
17
N
)2
= 4.7 × 10−17
N
q⬘ = tan−1

F
F
x
y

= tan−1

4
5
.
.
7
5
×
×
1
1
0
0
−
−
1
1
7
8
N
N

= 83°
Fnet = 4.7 × 10−18
N, 83° below the positive x-axis
(8.99 × 109
N•m2
/C2
)(8.8 × 10−9
C)(4.0 × 10−9
C)(sin 60.0°)

(7.631 × 104 m)2
(4.0 × 10−9
C)(cos 60.0°)

(7.631 × 104 m)2
2. q1 = 7.5 × 10−2
C
q3 = 1.0 × 10−4
C
r2,1 = 6.00 × 102
km
r3,1 = 24 km
r3,2 = r2,1 − r3,1 = 6.00 × 102
km − 24 km = 576 km
F3,1 = F3,2 = kC
(
q
r3
3
,
q
1)
1
2

= kC
(
q
r3
3
,
q
2)
2
2


q2 = q1 =

r
r
3
3
,
,
1
2


2
q2 = (7.5 × 10−2
C)

5
2
7
4
6
k
k
m
m


2
= 43 C

II Ch. 16–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. mE = 6.0 × 1024
kg
mm = 7.3 × 1022
kg
G = 6.673 × 10−11
N•m2
/kg2
kC = 8.99 × 109
N•m2
/C2
Fg = Felectric

Gm
r
E
2
mm
 = 
kC
r2
q2

q = 
G
m
k
E
C
m
m

=
q = 5.7 × 1013
C
(6.673 × 10−11
N•m2
/kg2
)(6.0 × 1024
kg)(7.3 × 1022
kg)

8.99 × 109 N•m2/C2
4. m = 17.23 kg
r = 0.800 m
Fnet = 167.6 N
g = 9.81 m/s2
kC = 8.99 × 109
N•m2
/C2
Fnet = Fg − Felectric
Fnet = mg − 
kC
r2
q2

q =

q =
q = 1.0 × 10−5
C
(0.800 m)2[(17.23 kg)(9.81 m/s2) − (167.6 N)]

8.99 × 109 N•m2/C2
r2
(mg − Fnet)

kC
5. m1 = 9.00 kg
m2 = 8.00 kg
r = 1.00 m
kC = 8.99 × 109
N•m2
/C2
g = 9.81 m/s2
Fg,1 = Fg,2 + Felectric
g(m1 − m2) = 
kC
r2
q2

q = 
gr

2
(
m
k
1
C
−
m
2)

=
q = 3.30 × 10−5
C
(9.81 m/s2)(1.00 m)2(9.00 kg − 8.00 kg)

8.99 × 109
N•m2
/C2
6. m = 9.2 × 104
kg
l1 = 1.00 m
g = 9.81 m/s2
l2 = 8.00 m
r = 2.5 m
kC = 8.99 × 109
N•m2
/C2
t1 = t2
mgl1 = 
kC
r
q
2
2
l2

q = 
r2
k
m
C
l
g
2
l1


q = = 8.9 × 10−3
C
(2.5 m)2
(9.2 × 104
kg)(9.81 m/s2
)(1.00 m)

(8.99 × 109 N•m2/C2)(8.00 m)
Givens Solutions
7. q1 = 2.0 C
q2 = 6.0 C
q3 = 4.0 C
L = 2.5 × 109
m
Fnet = 0 = F1 + F2 kC 
q
x
1q
2
3
 = 
(
k
L
C
−
q2
x
q
)
3
2


x
q
2
1
 = 
(L
q
−
2
x)2
 (L − x)

q1
= x

q2


L
x
 − 
x
x
 = 
q
q
2
1


L
x
 = 
q
q
2
1

+ 1
x = = = 9.3 × 108
m
2.5 × 109
m


6
2
.
.

0
0

C
C

+ 1
L


q
q
2
1

+ 1

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
8. q1 = 55 × 10−6
C
q2 = 137 × 10−6
C
q3 = 14 × 10−6
C
L = 87 m
Fnet = 0 = F1 + F2
kC 
q
x
1q
2
3
 = 
(
k
L
C
−
q2
x
q
)
3
2


x
q
2
1
 = 
(L
q
−
2
x)2

(L − x)

q1
= x

q2


L
x
 − 
x
x
 = 
q
q
2
1



L
x
 = 
q
q
2
1

+ 1
x = = = 34 m
87 m


1
5
3
5
7
×
×
1
1
0
0
−

−
6
6
C
C

+ 1
L


q
q
2
1

+ 1
9. F = 1.00 × 108
N
q1 = 1.80 × 104
C
q2 = 6.25 × 104
C
kC = 8.99 × 109
N•m2
/C2
F = 
kC
r
q
2
1q2

r = 
kC

q
F
1

q2


r =
r = 3.18 × 105
m
(8.99 × 109 N•m2/C2)(1.80 × 104 C)(6.25 × 104 C)

1.00 × 108 N
10. m = 5.00 kg
q = 4.00 × 10−2
C
kC = 8.99 × 109
N•m2
/C2
g = 9.81 m/s2
Fg = Felectric
mg = 
kC
h
q
2
2

h = 
k
m
Cq
g
2

h = = 542 m
(8.99 × 109 N•m2/C2)(4.00 × 10−2 C)2

(5.00 kg)(9.81 m/s2)
11. m = 1.0 × 10−19
kg
r = 1.0 m
q = 1.60 × 10−19
C
kC = 8.99 × 109
N•m2
/C2
Fres = Felectric = 
kC
r
q
2
2

Fres =
Fres = 2.3 × 10−28
N
(8.99 × 109
N•m2
/C2
)(1.60 × 10−19
C)2

(1.0 m)2
12. m = 5.0 × 10−6
kg
q = 2.0 × 10−15
C
r = 1.00 m
kC = 8.99 × 109
N•m2
/C2
G = 6.673 × 10−11
N•m2
/kg2
Fnet = Felectric + Fg
Felectric = 
kC
r
q
2
2
 =
Fg = 
G
r
m
2
2
 =
Fnet = 3.6 × 10−20
N + 1.7 × 10−21
N = 3.8 × 10−20
N
(6.673 × 10−11
N•m2
/kg2
)(5.0 × 10−6
kg)2

(1.00 m)2
(8.99 × 109
N•m2
/C2
)(2.0 × 10−15
C)2

(1.00 m)2

II Ch. 16–8
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
13. m = 2.00 × 10−2
kg
q1 = 2.0 × 10−6
C
q2 = −8.0 × 10−6
C
r = 1.7 m
kC = 8.99 × 109
N•m2
/C2
g = 9.81 m/s2
Felectric = Ffriction

kC
r
q
2
1q2
 = mkmg
mk = 
k
m
Cq
g
1
r
q
2
2

mk = = 0.25
(8.99 × 109
N•m2
/C2
)(2.0 × 10−6
C)(8.0 × 10−6
C)

(2.00 × 10−2 kg)(9.81 m/s2)(1.7 m)2
1. r = 3.72 m
E = 0.145 N/C
kC = 8.99 × 109
N•m2
/C2
q = 60.0°
2. ∆y = 190 m
q1 = 1.2 × 10−8
C
∆x = 120 m
Ex = 1.60 × 10−2
N/C
kC = 8.99 × 109
N•m2
/C2
E = 
k
r
C
2
q

Ex = E1 + E2(cos q) = 
k
∆
C
x
q
2
1
 +
q2 =
Ex − 
k
∆
C
x
q
2
1


(∆x2
k
+
C∆
∆
x
y2
)3/2


Ex − 
k
∆
C
x
q
2
1
 =
1.60 × 10−2
N/C −

= 8.5 × 10−3
N/C

(∆x2
k
+
C∆
∆
x
y2
)3/2
 =

= 1.0 × 10−5
C2
/N
q2 = (8.5 × 10−3
N/C)(1.0 × 10−5
C2
/N) = 8.5 × 10−8
C
[(120 m)2
+ (190 m)2
]3/2

(8.99 × 109 N•m2/C2)(120 m)
(8.99 × 109
N•m2
/C2
)(1.2 × 10−8
C)

(120 m)2
kCq2(∆x)

(∆x
2
+ ∆y2)

∆
x
2
+
∆
y
2

E = 
k
r
C
2
q

Ex =

k
r
C
2
q

(cos 60.0°) −

k
r
C
2
q

(cos 60.0°) = 0 N/C
Because Ex = 0 N/C, the electric field points directly upward.
Ey = 
2kCq(s
r
in
2
60.0°)

q = 
2kC(s
E
in
yr
6
2
0.0°)
 = = 1.29 × 10−10
C
(0.145 N/C)(3.72 m)2

(2)(8.99 × 109 N•m2/C2)(sin 60.0°)
3. q1 = 1.80 × 10−5
C
q2 = −1.20 × 10−5
C
Enet = 22.3 N/C toward q2
kC = 8.99 × 109
N•m2
/C2
Enet = 
k
r
C
2
(q1 + q2) r2
= 
E
k
n
C
et
(q1 + q2)
r = 
kC
(q
E
1
n
e
+
t
q
2)


r =
r = 1.10 × 102
m
(8.99 × 109
N•m2
/C2
)[(1.80 × 10−5
C) + (1.20 × 10−5
C)]

22.3 N/C toward q2

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
4. d = 86.5 m
q1 = 4.8 × 10−9
C
q2 = 1.6 × 10−8
C
5. q = 3.6 × 10−6
C
L = 960 m
w = 750 m
kC = 8.99 × 109
N•m2
/C2
E = 
k
r
C
2
q

Ey = E1 + E2(sin q) = 
k
w
C
2
q
 +
Ey = kCq

w
1
2
 + 
(w2 +
w
L2)3/2


Ey = (8.99 × 109
N•m2
/C2
)(3.6 × 10−6
C)

(750
1
m)2
 +

Ey = 7.1 × 10−2
N/C
Ex = E3 + E2(cos q) = 
k
L
C
2
q
 +
Ex = kCq

L
1
2
 + 
(w2 +
L
L2)3/2


Ex = (8.99 × 109
N•m2
/C2
)(3.6 × 10−6
C)

(960
1
m)2
 +

Ex = 5.2 × 10−2
N/C
Enet =

E
y
2
+
E
x
2
=

(7
.1
×
1
0−
2
N
/C
)2
+
(
5.
2
×
1
0−
2
N
/C
)2
= 8.8 × 10−2
N/C
q⬘ = tan−1

E
E
y
x

= tan−1

7
5
.
.
1
2
×
×
1
1
0
0
−
−
2
2
N
N
/
/
C
C

= 54°
Enet = 8.8 × 10−2
N/C, 54° above the horizontal
960 m

[(750 m)2 + (960 m)2]3/2
kCqL


w
2
+
L
2
(w2 + L2)
750 m

[(750 m)2 + (960 m)2]3/2
kCqw


w
2
+
L
2
(w2 + L2)
Enet = E1 + E2 = 0
E1 = E2

x
q1
2
 = 
(d −
q2
x)2

(d − x)

q1
= x

q
2

x

q1
+

q2
= d

q1

x = =
x = 3.0 × 101
m
(86.5 m)

4.
8
×
1
0−
9
C



(4
.8
×
1
0−
9
C
)
+

(1
.6
×
1
0−
8
C
)

d

q1



q1
+

q2

II Ch. 16–10
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. w = 218 m
h = 50.0 m
q = 6.4 × 10−9
C
kC = 8.99 × 109
N•m2
/C2
q1 = q2 = q
q3 = 3q
q4 = 2q
r = = = 112 m
q = tan−1

w
h

= tan−1

5
2
0
1
.
8
0
m
m

= 12.9°
The electric fields of charges on opposite corners of the rectangle cancel to give 2q
on the lower left corner and q on the lower right corner.
E = 
k
r
C
2
q

Ex =

kC
r2
2q
 − 
k
r
C
2
q

(cos q) = 
kCq(
r
c
2
os q)

Ex = = 4.5 × 10−3
N/C
Ey =

kC
r2
2q
 + 
k
r
C
2
q

(sin q) = 
3kCq
r
(
2
sin q)

Ey = = 3.1 × 10−3
N/C
Enet =

E
x
2
+
E
y
2
=

(4
.5
×
1
0−
3
N
/C
)2
+
(
3.
1
×
1
0−
3
N
/C
)2

Enet = 5.5 × 10−3
N/C
q⬘ = tan−1

E
E
x
y

= tan−1

3
4
.
.
1
5
×
×
1
1
0
0
−
−
3
3
N
N
/
/
C
C

= 35°
Enet = 5.5 × 10−3
N/C, 35° above the positive x-axis
(3)(8.99 × 109
N•m2
/C2
)(6.4 × 10−9
C)(sin 12.9°)

(112 m)2
(8.99 × 109
N•m2
/C2
)(6.4 × 10−9
C)(cos 12.9°)

(112 m)2

(5
0.
0
m
)2
+
(
21
8
m
)2


2

h
2
+
w
2


2
Givens Solutions

II
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
1. r = 4.8 × 10−4
m
q = 2.9 × 10−9
C
∆V = kC 
q
r
 = (8.99 × 109
N•m2
/C2
)

2
2
.
.
8
9
×
×
1
1
0
0
−
−
4
9
m
C

= 5.4 × 104
V
Givens Solutions
2. q = −1.6 × 10−19
C
∆PEelectric = 3.3 × 10−15
J
d = 3.5 cm
∆PEelectric = −qEd
Rearrange to solve for E.
E = 
∆PE
−
e
q
l
d
ectric
 = = 5.9 × 105

N
C

3.3 × 10−15
J

−(−1.6 × 10−19
C)(0.035 m)
3. ∆PEelectric = 3.1 × 10−12
J
d = 4.7 cm
∆V = −73 V
∆PEelectric = 3.1 × 10−12
J
d = 4.7 cm
∆V = −73 V
a. ∆V = −Ed
Rearrange to solve for E.
E = −
∆
d
V
 = 
4.7
−
×
7
1
3
0
V
−2
m
 =
b. ∆V = 
∆PE
q
electric

Rearrange to solve for q.
q = 
∆PE
∆
e
V
lectric
 = 
3.1
−
×
7
1
3
0
V
−12
J
 = −4.2 × 10−14
C
1.6 × 103

N
C

4. d = 9.35 m
∆PEelectric = 3.17 × 10−10
J
E = 1.25 × 105
N/C
d = 9.35 m
∆PEelectric = 3.17 × 10−10
J
E = 1.25 × 105
N/C
a. ∆PEelectric = −qEd
q = − 
∆PE
E
e
d
lectric
 = −
q =
b. ∆PEelectric = −qEd
q = − 
∆PE
E
e
d
lectric
 = −
q = −2.71 × 10−16
C
∆V = 
∆PE
q
electric
 = 
−
3
2
.
.
1
7
7
1
×
×
1
1
0
0
−
−
1
1
0
6
J
C
 = −1.17 × 106
V
3.17 × 10−10
J

(1.25 × 105
N/C)(9.35 m)
−2.71 × 10−16
C
3.17 × 10−10
J

(1.25 × 105
N/C)(9.35 m)
Electrical Energy
and Current

II Ch. 17–2
II
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
5. E = 1.5 × 102
N/C
d = 439 m
∆PEelectric = −3.7 × 10−8
J
E = 1.5 × 102
N/C
d = 439 m
J
E = 1.5 × 102
N/C
d = 439 m
J
a. q = − 
∆PE
E
e
d
lectric
 = −
q =
b. ∆V = −Ed = −(1.5 × 102
N/C)(439 m)
∆V =
c. Use the value for q found in part a.
V = 
∆PE
q
electric
 = 
5
−
.
3
6
.7
×
×
10
1
−
0
1
−
3
8
C
J
 = −6.6 × 104
V
−6.6 × 104
V
5.6 × 10−13
C
–3.7 × 10−8
J

(1.5 × 102
N/C)(439 m)
Givens Solutions
6. E = 6.5 × 102
N/C
d = 0.077 cm
∆V = −Ed = −(6.5 × 102
N/C)(7.7 × 10−4
m) = −5.0 × 10−1
V
The absolute value gives the magnitude of the potential difference.
−5.0 × 10−1
V = 5.0 × 10−1
V
7. q = 1.6 × 10−19
C
E = 383 N/C
d = 3.75 m
q = 1.6 × 10−19
C
E = 383 N/C
d = 3.75 m
a. ∆V = −Ed = −(383 N/C)(3.75 m) = −1.44 × 103
V
−1.44 × 103
V =
b. ∆V = −Ed = −(383 N/C)(3.75 m) = −1.44 × 103
V
∆V = 
∆PE
q
electric

Rearrange to solve for ∆PEelectric .
∆PEelectric = ∆Vq = (−1.44 × 103
V) × (1.6 × 10−19
C)
∆PEelectric = −2.3 × 10−16
J
1.44 × 103
V
8. q = −4.8 × 10−19
C
d = −0.63 cm
E = 279 V/m
q = −4.8 × 10−19
C
d = −0.63 cm
E = 279 V/m
a. V = 

N
C
•m
; Rearrange to get 
m
V
 = 
N
C

279 V/m = 279 N/C
∆PEelectric = −qEd = (−4.8 × 10−19
C)(279 N/C)(−6.3 × 10−3
m)
∆PEelectric =
b. V = 
N
C
•m
; Rearrange to get 
m
V
 = 
N
C

279 V/m = 279 N/C
∆PEelectric = −qEd = (−4.8 × 10−19
C)(279 N/C)(−6.3 × 10−3
m)
∆PEelectric = −8.4 × 10−19
J
Find the electric potential associated with a charged particle.
V = 
PEe
q
lectric
 = 
−
−
4
8
.
.
8
4
×
×
1
1
0
0
−
−
1
1
9
9
C
J
 = 1.8 V
−8.4 × 10−19
J

II
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
Givens Solutions
1. ∆V = 3.00 × 102
V
PEelectric = 17.1 kJ
PEelectric = 
1
2
C(∆V)2
C = 
2P
(∆
E
V
ele
)
ct
2
ric

C = 
(
2
3
(
.
1
0
7
0
.1
×
×
10
1
2
03
V
J
)
)
2

C = 3.80 × 10−1
F
2. PEelectric = 1450 J
∆V = 1.0 × 104
V
PEelectric = 
1
2
C(∆V)2
C = 
2P
(∆
E
V
ele
)
ct
2
ric

C = 
(1.
2
0
(
×
14
1
5
0
0
4
J
V
)
)2

C = 2.9 × 10−5
F
3. Emax = 3.0 × 106
V/m
d = 0.2 × 10−3
m
A = 6.7 × 103
m2
e0 = 8.85 × 10−12
C2
/N•m2
∆Vmax = Emaxd
∆Vmax = 
Q
C
max
 =
Emaxd =
Qmax = Emaxe0A
Qmax = (3.0 × 106
V/m)(8.85 × 10−12
C2
/N•m2
)(6.7 × 103
m2
)
Qmax = 0.18 C
Qmax


e0
d
A


Qmax


e0
d
A


4. r = 3.1 m
d = 1.0 × 10−3
m
Emax = 3.0 × 106
V/m
e0 = 8.85 × 10−12
C2
/N•m2
Qmax = C∆Vmax = CEmaxd
C = 
e0
d
A

Qmax = e0AEmax = e0pr2
Emax
Qmax = (8.85 × 10−12
C2
/N•m2
)(p)(3.1 m)2
(3.0 × 106
V/m)
Qmax = 8.0 × 10−4
C = 0.80 mC
5. P = 5.0 × 1015
W
∆t = 1.0 × 10−12
s
C = 0.22 F
PEelectric = 
1
2
C(∆V)2
PEelectric = P∆t
P∆t = 
1
2
C(∆V)2
∆V = 
2P
C
∆

t


∆V =
∆V = 210 V
2(5.0 × 1015 W)(1.0 × 10−12 s)

(0.22 F)

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 17–4
6. A = 2.32 × 105
m2
d = 1.5 × 10−2
m
Q = 0.64 × 10−3
C
e0 = 8.85 × 10−12
C2
/N•m2
PEelectric = 
1
2
 
Q
C
2

C = 
e0
d
A

PEelectric = 
1
2
 
Q
e0
2
A
d

PEelectric =
PEelectric = 1.5 × 10−3
J
(0.64 × 10−3
C)2
(1.5 × 10−2
m)

(8.85 × 10−12 C2/N•m2)(2.32 × 105 m2)
1

2
Givens Solutions
7. r = 18.0 m
∆V = 575 V
PEelectric = 3.31 J
PEelectric = 
1
2
C(∆V)2
C = 
2 P
(∆
E
V
ele
)
c
2
tric
 = 
(
2
5
(
7
3
5
.3
V
1
)
J
2
)

C =
d = 
e0
C
A
 = 
e0
C
πr2

d =
d = 4.5 × 10−4
m = 0.45 mm
(8.85 × 10−12
C2/N•m2)(π)(18.0 m)2

(2.00 × 10−5
F)
2.00 × 10−5
F
8. di = 5.00 × 10−3
m
df = 0.30 × 10−3
m
e0 = 8.85 × 10−12
C2
/N•m2
A = 1.20 × 10−4
m2
∆C = Cf − Ci = 
e
d
0A
f
 − 
e
d
0A
i

∆C = e0A

d
1
f
 − 
d
1
i


∆C =
8.85 × 10−12

N
C
•m
2
2

(1.20 × 10−4
m2
)

0.30 ×
1
10−3 m
 − 
5.00 ×
1
10−3 m


∆C = 3.3 × 10−12
F = −3.3 pF
9. A = 98 × 106
m2
C = 0.20 F
e0 = 8.85 × 10−12
C2
/N•m2
C = 
e0
d
A

d = 
e0
C
A

d =
d = 4.3 × 10−3
m = 4.3 mm
(8.85 × 10−12
C2
/N•m2
)(98 × 106
m2
)

(0.20 F)

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
11. A = 44 m2
e0 = 8.85 × 10−12
C2
/N•m2
Q = 2.5 × 10−6
C
∆V = 30.0 V
a. C = 
∆
Q
V

C = 
(2.5
(3
×
0.
1
0
0
V
−6
)
C)

C =
b. C = 
e0
d
A

d = 
e0
C
A

d =
d =
c. PEelectric = 
1
2
Q∆V
PEelectric = 
1
2
(2.5 × 10−6
C)(30.0 V)
PEelectric = 3.8 × 10−5
J
4.7 × 10−3
m
(8.85 × 10−12
C2
/N•m2
)(44 m2
)

(8.3 × 10−8 F)
8.3 × 10−8
F = 83 nF
10. A = 7.0 m × 12.0 m
d = 1.0 × 10−3
m
e0 = 8.85 × 10−12
C2
/N•m2
PEelectric = 1.0 J
a. C = 
e0
d
A

C =
C =
b. PEelectric = 
1
2
C(∆V)2
∆V = 
2P

E
C
el
ec
tr
ic


∆V = 
(7
.4
2
(
×
1.
1
0
0
J
−
)
7
F
)


∆V = 1.6 × 103
V = 1.6 kV
7.4 × 10−7
F = 0.74 mF
(8.85 × 10−12
C2
/N•m2
)(7.0 m)(12.0 m)

(1.0 × 10−3 m)
1. I = 3.00 × 102
A
∆t = 2.4 min
∆Q = I∆t
∆Q = (3.00 × 102
A)(2.4 min)

1
6
m
0
i
s
n


∆Q = 4.3 × 104
C

II Ch. 17–6
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. ∆t = 7 min, 29 s
I = 0.22 A
∆Q = I∆t
∆Q = (0.22 A)
(7 min)

1
6
m
0
i
s
n

+ 29 s
= (0.22 A)(449 s)
∆Q = 99 C
3. ∆t = 3.3 × 10−6
s
I = 0.88 A
q = e = 1.60 × 10−19

elec
C
tron

∆Q = I∆t = nq
n = 
I∆
q
t

n =
n = 1.8 × 1013
electrons
(0.88 A)(3.3 × 10−6 s)

(1.60 × 10−19 C/electron)
4. ∆t = 3.00 h
∆Q = 1.51 × 104
C
I = 
∆
∆
Q
t

I =
I = 1.40 A
(1.51 × 104
C)

(3.00 h)

3.60
1
×
h
103 s


5. ∆Q = 1.8 × 105
C
∆t = 6.0 min
I = 
∆
∆
Q
t

I =
I = 5.0 × 102
A
(1.8 × 105
C)

(6.0 min)

1
6
m
0
i
s
n


Givens Solutions
6. I = 13.6 A
Q = 4.40 × 105
C
∆t = 
∆
I
Q

∆t = 
(4.4
(1
0
3
×
.6
1
A
05
)
C)

∆t = 3.24 × 104
s = 9.00 h
1. ∆V = 440 V
I = 0.80 A
R = 
∆
I
V

R = 
(
(
0
4
.
4
8
0
0
V
A
)
)

R = 5.5 × 102
Ω

II
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book. 2. ∆V = 9.60 V
I = 1.50 A
R = 
∆
I
V

R = 
(
(
9
1
.
.
6
5
0
0
V
A)
)

R = 6.40 Ω
3. ∆V = 312 V
∆Q = 2.8 × 105
C
∆t = 1.00 h
I = 
∆
∆
Q
t

R = 
∆
I
V
 = = 
∆
∆
V
Q
∆t

R =
R = 4.0 Ω
(312 V)(1.00 h)

3.60
1
×
h
103
s



(2.8 × 105 C)
∆V


∆
∆
Q
t


4. I = 3.8 A
R = 0.64 Ω
∆V = IR
∆V = (3.8 A)(0.64 Ω)
∆V = 2.4 V
5. R = 0.30 Ω
I = 2.4 × 103
A
∆V = IR = (2.4 × 103
A)(0.30 Ω) = 7.2 × 102
V
6. ∆V = 3.0 V
R = 16 Ω
I = 
∆
R
V

I = 
(
(
3
1
.
6
0
Ω
V
)
)

I = 0.19 A
7. ∆V = 6.00 × 102
V
R = 4.4 Ω
I = 
∆
R
V
 = = 1.4 × 102
A
(6.00 × 102
V)

(4.4 Ω)
1. P = 12 × 103
W
R = 2.5 × 102
Ω
P = I2
R
I = 
R
P


I = 
(
(
2
1
.
2
5
×
×
1
1
0
0
3
2
W
Ω
)
)


I = 6.9 A

II Ch. 17–8
II
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
2. P = 33.6 × 103
W
∆V = 4.40 × 102
V
P = I∆V
I = 
∆
P
V

I = 
(
(
3
4
3
.4
.6
0
×
×
1
1
0
0
3
2
W
V)
)

I = 76.4 A
3. P = 850 W
V = 12.0 V
P = I∆V
I = 
∆
P
V

I = 
8
1
5
2
0
.0
W
V

I = 70.8 A
4. P =

4
1
.
.
2
1
×
×
1
1
0
0
1
3
0
h
J


R = 40.0 Ω
P = 
(∆V
R
)2

∆V =

P
R

∆V = 
4
1
.
.
2
1
×
×
1
1
0
0
1
3
0
h
J



36
1
0
h
0
s

(
40
.0
Ω
)

∆V = 6.5 × 102
V
5. P = 6.0 × 1013
W
∆V = 8.0 × 106
V
P = 
(∆
R
V)

2
R = 
(∆
P
V)

2
R = 
(
(
6
8
.
.
0
0
×
×
1
1
0
0
1
6
3
V
W
)2
)

R = 1.1 Ω
6. I = 6.40 × 103
A
∆V = 4.70 × 103
V
P = I∆V
P = (6.40 × 103
A)(4.70 × 103
V)
P = 3.01 × 107
W = 30.1 MW

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
1. q1 = −12.0 × 10−9
C
q2 = −68.0 × 10−9
C
V = −25.3 V
r1 = 16.0 m
r2 = d − r1
kC = 8.99 × 109

N
C
•m
2
2

V = kC
q
r1
1
 + 
q
r2
2

= kC
q
r1
1
 + 
(d
q
−
2
r1)



k
V
C
 − 
q
r1
1
 + 
(d
q
−
2
r1)

d = + r1
d = +16.0 m
d = 33.0 m + 16.0 m = 49.0 m
−68.0 × 10−9
C


8.99 ×
−
1
2
0
5
9
.3
N
V
•m2
/C2
 − 
(−12.
1
0
6
×
.0
1
m
0−9
C)


q2


k
V
C
 − 
q
r1
1


2. q1 = 18.0 × 10−9
C
q2 = 92.0 × 10−9
C
V = 53.3 V
r1 = d − r2
d = 97.5 m
kC = 8.99 × 109

N
C
•m
2
2

V = kC 
q
r
 = kC
q
r1
1
 + 
q
r2
2


V = kC
d −
q1
r2
 + 
q
r2
2



k
V
C

= 
(q1r
(
2
d
+
−
q
r
2
2
d
)(
−
r2
q
)
2r2)

−

k
V
C

r2
2
+

k
V
C

dr2 = (q1 − q2)r2 + q2d

k
V
C

r2
2
+
q1 − q2 − 
V
kC
d

r2 + q2d = 0
Solve using the quadratic formula:
r2 =
q1 − q2 − 
V
kC
d

= 18.0 × 10−9
C − 92.0 × 10−9
C −

q1 − q2 − 
V
kC
d

= −652 × 10−9
C

4V
k
q
C
2d
 = = 2.13 × 10−13
C2

2
k
V
C
 = = 11.9 × 10−9

m
C

r2 =
r2 = 
652
11
±
.9
460
 m
−(−652 × 10−9
C) ±

(−
65
2
×
1
0−
9
C
)2
−
(
2.
13
×
1
0−
13
C
2)


(11.9 × 10−9 C/m)
2(53.3 V )

(8.99 × 109 N•m2/C2)
4(53.3 V)(92.0 × 10−9
C)(97.5 m)

(8.99 × 109 N•m2/C2)
(53.3 V)(97.5 m)

8.99 × 109

N
C
•m
2
2


−
q1 − q2 − 
V
kC
d

± q
1
−
q
2
−

V
k
C
d


2
−


4V
k
q
C
2d




2
k
V
C


II Ch. 17–10
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. V = 1.0 × 106
V
r = 12 × 10−2
m
kC = 8.99 × 109

N
C
•m
2
2

V = kC 
q
r

q = 
V
kC
r

q =
q = 1.3 × 10−5
C
(1.0 × 106
V)(12 × 10−2
m)

8.99 × 109

N
C
•m
2
2


4. ME = 5.98 × 1024
kg
G = 6.673 × 10−11

N
k
•
g
m
2
2

kC = 8.99 × 109

N
C
•m
2
2

m = 1.0 kg
q = 1.0 C
mVgravity = qVelectric

mM
r
EG
 = 
qQ
r
EkC

QE = 
m
q
M
kC
EG

QE =
QE = 4.44 × 104
C
(1.0 kg)(5.98 × 1024
kg)
6.673 × 10−11

N
k
•
g
m
2
2



(1.0 C)
8.99 × 109

N
C
•m
2
2


Givens Solutions
Of the two roots, the one that yields the correct answer is
r2 = 
(652
11
−
.9
460)
 m
r2 = 16.1 m
5. msun = 1.97 × 1030
kg
mH = mass of hydrogen
atom = 1.67 × 10−27 kg
q1 = charge of proton
= +1.60 × 10−19
C
q2 = charge of electron
= −1.60 × 10−19 C
r1 = 1.1 × 1011
m
r2 = 1.5 × 1011
m − 1.1 ×
1011
m = 4.0 × 1010
m
kC = 8.99 × 109

N
C
•m
2
2

a. Q+ = charge of proton cloud = (number of protons)q1 = 
m
m
su
H
nq1

Q+ =
Q+ =
Q− = charge of electron cloud = 
m
m
sun
H
q2

Q− =
b. V = kC 
q
r
 = kC 
Q
r1
+
 + 
Q
r2
−


V =
8.99 × 109

N
C
•m
2
2


1
1
.
.
8
1
9
×
×
1
1
0
0
1
3
1
8
m
C
 − 
1
4
.
.
8
0
9
×
×
1
1
0
0
1
3
0
8
m
C


V = −2.7 × 1037
V
−1.89 × 1038
C
1.89 × 1038
C
(1.97 × 1030
kg)(1.60 × 10−19
C)

(1.67 × 10−27 kg)

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Givens Solutions
Givens Solutions
6. r = r1 = r2 = r3 = r4 =

2
x


2
+


2
y


2

x = 292 m
y = 276 m
q = 64 × 10−9
C
q1 = 1.0q
q2 = −3.0q
q3 = 2.5q
q4 = 4.0q
kC = 8.99 × 109

N
C
•m
2
2

V = kC 
q
r
 = kC 
q
r1
1
 + 
q
r2
2
 + 
q
r3
3
 + 
q
r4
4


V =
V =
V = 13 V
8.99 × 109

N
C
•m
2
2

(64 × 10−9
C)(4.5)


2
92
2
m


2
+


27
6
2
m


2

kC q(1.0 − 3.0 + 2.5 + 4.0)


2
x



2

+


2
y


2

7. q1 = q2 = q3 = q
= 7.2 × 10−2 C
l = 1.6 × 107
m
r1 = r2 = 
2
l
r3 =
l 2
−

2
l

2
kC = 8.99 × 109

N
C
•m
2
2

V = kC 
q
r
 = kC 
q
r1
1
 + 
q
r2
2
 + 
q
r3
3


V = kC

+ +

=
2 + 2 +

V = 4 +

V = 2.1 × 102
V
1


3
4


8.99 × 109

N
C
•m
2
2

(0.072 C)

(1.6 × 107 m)
1

1
−

1
2


2

kCq

l
q


l 2
−

2
l

2
q


2
l

q


2
l

8. q1 = q2 = q3 = q
= 25.0 × 10−9
C
r1 = r2 = l
r3 =

l 2 + l 2
l = 184 m
kC = 8.99 × 109

N
C
•m
2
2

V = kC 
q
r
 = kC 
q
r1
1
 + 
q
r2
2
 + 
q
r3
3


V = kCq
+ +
=
1 + 1 +

V = (2.707)
V = 3.31 V
8.99 × 109

N
C
•m
2
2

(25.0 × 10−9
C)

(184 m)
1


2

kCq

l
1


l 2 + l 2
1

l
1

l

4. ∆V = 110 V
R = 80.0 Ω (for maximum
power)
∆t = 24 h
cost of energy =
$0.086/kW•h
P = 
(∆
R
V)2

total cost of electricity = P∆t(cost of energy)
total cost = 
(∆V
R
)2
(∆t)
 (cost of energy)
total cost = 
(11
(
0
8
V
0.
)
0
2
(
Ω
2
)
4 h)


1
$0
k
.
W
08
•
6
h


1
1
00
k
0
W
W


total cost = $0.31
5. 15.5 percent of solar energy
converted to electricity
cost of energy =
$0.080/kW•h
purchase power = $1000.00
(0.155)Esolar = 
p
c
u
o
r
s
c
t
h
o
a
f
se
en
p
e
o
r
w
gy
er

Esolar =
Esolar = 8.1 × 104
kW•h = 2.9 × 1011
J
($1000.00)

(0.155)($0.080/kW•h)
II Ch. 17–12
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. P = 8.8 × 106
kW
total cost = $1.0 × 106
cost of energy =
$0.081/kW•h
∆t =
∆t =
∆t = 1.4 h
$1.0 × 106

(8.8 × 106
kW)($0.081/kW•h)
total cost of electricity

P(cost of energy)
2. P = 104 kW
cost of energy =
$0.120/kW•h
purchase power = $18 000
energy that can be purchased = 
p
c
u
o
r
s
c
t
h
o
a
f
se
en
p
e
o
r
w
gy
er
 = P∆t
∆t = 
(c
p
o
u
st
rc
o
h
f
a
e
s
n
e
e
p
rg
o
y
w
)
e
(
r
P)

∆t =
∆t = 1.4 × 103
h = 6.0 × 101
days
$18 000

($0.120/kW•h)(104 kW)
3. ∆t = 1.0 × 104
h
cost of energy =
$0.086/kW•h
total cost = $23
P =
P =
P = 2.7 × 10−2
kW
$23

(1.0 × 104
h)($0.086 kW•h)
total cost of electricity

∆t(cost of energy)
Givens Solutions

Circuits and
Circuit Elements
II
1. R = 160 kΩ
R1 = 2.0R
R2 = 3.0R
R3 = 7.5R
Req = R1 + R2 + R3 = 2.0R + 3.0R + 7.5R = 12.5R
Req = (12.5)(160 kΩ) = 2.0 × 103
kΩ
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. R = 5.0 × 108
Ω
R1 = 
1
3
R
R2 = 
2
7
R
R3 = 
1
5
R
Req = R1 + R2 + R3 = 
1
3
R + 
2
7
R + 
1
5
R
Req = 
35 +
1
3
0
0
5
+ 21
 R = 
1
8
0
6
5
R = 
1
8
0
6
5
(5.0 × 108
Ω) = 4.1 × 108
Ω
3. R1 = 16 kΩ
R2 = 22 kΩ
R3 = 32 kΩ
Req = 82 kΩ
R4 = Req − R1 − R2 − R3 = 82 kΩ − 16 kΩ − 22 kΩ − 32 kΩ = 12 kΩ
4. R1 = 3.0 kΩ
R2 = 4.0 kΩ
R3 = 5.0 kΩ
P = (0.0100)(3.2 MW) =
0.032 MW
Req = R1 + R2 + R3 = 3.0 kΩ + 4.0 kΩ + 5.0 kΩ = 12.0 kΩ
P = 
(∆V
R
)2

∆V =

P
R
eq
=

(3
.2
×
1
04
W
)(
1.
20
×
1
04
Ω
)
= 2.0 × 104
V
5. R1 = 4.5 Ω
R2 = 4.0 Ω
R3 = 16.0 Ω
R12 = R1 + R2 = 4.5 Ω + 4.0 Ω =
R13 = R1 + R3 = 4.5 Ω + 16.0 Ω =
R23 = R2 + R3 = 4.0 Ω + 16.0 Ω = 20.0 Ω
20.5 Ω
8.5 Ω
6. R1 = 2.20 × 102
Ω
∆Vi = 1.20 × 102
V
∆Vf = 138 V
Because the current is unchanged, the following relationship can be written.
R
V
1
i
 = 
R1
V
+
f
R2

R2 = 
Vf R1
V
−
i
Vi R1
 =
R2 = = 
40
1
0
2
0
0
V
V
•Ω
 = 33 Ω
30 400 V•Ω − 26 400 V•Ω

120 V
(138 V)(220 Ω) − (120 V)(220 Ω)

120 V

II
7. R1 = 3.6 × 10−5
Ω
R2 = 8.4 × 10−6
Ω
I = 280 A
Req = R1 + R2 = 3.6 × 10−5
Ω + 8.4 × 10−6
Ω = 4.4 × 10−5
Ω
P = I2
Req = (280 A)2
(4.4 × 10−5
Ω) = 3.4 W
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 18–2
1. R1 = 1.8 Ω
R2 = 5.0 Ω
R3 = 32 Ω
Req =

R
1
1
 + 
R
1
2
 + 
R
1
3


−1
=

1.8
1
Ω
 + 
5.0
1
Ω
 + 
32
1
Ω


−1
Req =
0.55 
Ω
1
 + 0.20 
Ω
1
 + 0.031 
Ω
1


−1
=
0.78 
Ω
1


−1
= 1.3 Ω
2. R = 450 Ω
R1 = R
R2 = 2.0R
R3 = 0.50R
Req =

R
1
1
 + 
R
1
2
 + 
R
1
3


−1
=

450
1
Ω
 + 
900
1
Ω
 + 
220
1
Ω


−1
Req =
0.0022 
Ω
1
 + 0.0011 
Ω
1
 + 0.0045 
Ω
1


−1
=
0.0078 
Ω
1


−1
= 1.3 × 102
Ω
3. R1 = 2.48 × 10−2
Ω
Req = 6.00 × 10−3
Ω
R2 =

R
1
eq
 − 
R
2
1


−1
=

6.00 ×
1
10−3
Ω
 − 
2.48 ×
2
10−2
Ω


−1
R2 =
167 
Ω
1
 − 80.6 
Ω
1


−1
=
86 
Ω
1


−1
= 0.012 Ω
4. R1 = R
R2 = 3R
R3 = 7R
R4 = 11R
Req = 6.38 × 10−2
Ω
Req =

R
1
1
 + 
R
1
2
 + 
R
1
3
 + 
R
1
4


−1
=

R
1
 + 
3
1
R
 + 
7
1
R
 + 
11
1
R


−1
Req =

231 + 7
2
7
31
+
R
33 + 21


−1
=

2
3
3
6
1
2
R


−1
=

1.
R
57


−1
R = 1.57Req = 1.57(6.38 × 10−2
Ω) = 0.100 Ω
5. ratio = 1.22 × 10−2
Ω/m
l = 1813 km
R1 = 
1
2
R
R2 = 
1
4
R
R3 = 
1
5
R
R4 = 
2
1
0
R
a. R = (ratio)(l) = (1.22 × 10−2
Ω/m)(1.813 × 106
m) =
b. Req =

R
1
1
 + 
R
1
2
 + 
R
1
3
 + 
R
1
4


−1
=

R
2
 + 
R
4
 + 
R
5
 + 
2
R
0


−1
Req =

3
R
1


−1
=

1.00 ×
3
1
1
010 Ω


−1
= 3.23 × 108
Ω
2.21 × 104
Ω
6. ∆V = 14.4 V
P = 225 W
P = 
(∆
R
V)2

R = 
(∆
P
V)2
 = 
(1
2
4
2
.
5
4
W
V)2
 =
Req =

R
4


−1
= 
R
4
 = 
0.92
4
2 Ω
 = 0.230 Ω
I = 
R
∆
e
V
q
 = 
0
1
.2
4
3
.4
0
V
Ω
 = 62.6 A
0.922 Ω

II
7. L = 3.22 × 105
km
l = 1.00 × 103
km
ratio = 1.0 × 10−2
Ω/m
∆V = 1.50 V
Req = N

R
1

where N = and R = (ratio)l
Req =

−1
=

−1
= 31 Ω
I = 
R
∆
e
V
q
 = 
1
3
.5
1
0
Ω
V
 = 0.048 A
3.22 × 108
m

(1.0 × 10−2 Ω/m)(1.00 × 106 m)2
L

(ratio)l 2
L

l
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. R1 = 6.60 × 102
Ω
R2 = 2.40 × 102
Ω
R3 = 2.00 × 102
Ω
R4 = 2.00 × 102
Ω
R12 = R1 + R2 = 660 Ω + 240 Ω = 900 Ω
R123 =

R
1
12
 + 
R
1
3


−1
=

900
1
Ω
 + 
200
1
Ω


−1
R123 =
0.00111 
Ω
1
 + 0.00500 
Ω
1


−1
=
0.00611 
Ω
1


−1
= 164 Ω
Req = R123 + R4 = 164 Ω + 200 Ω = 364 Ω
3. R1 = 2.5 Ω
R2 = 3.5 Ω
R3 = 3.0 Ω
R4 = 4.0 Ω
R5 = 1.0 Ω
∆V = 12 V
R12 = R1 + R2 = 2.5 Ω + 3.5 Ω = 6.0 Ω
R123 =

R
1
12
 + 
R
1
3


−1
=

6.0
1
Ω
 + 
3.0
1
Ω


−1
R123 =
0.17 
Ω
1
 + 0.33 
Ω
1


−1
=
0.50 
Ω
1


−1
= 2.0 Ω
R45 =

R
1
4
 + 
R
1
5


−1
=

4.0
1
Ω
 + 
1.0
1
Ω


−1
R45 =
0.25 
Ω
1
 + 1.0 
Ω
1


−1
=
1.2 
Ω
1


−1
= 0.83 Ω
Req = R123 + R45 = 2.0 Ω + 0.83 Ω =
I = 
∆
R
V
 = 
2
1
.
2
8
V
Ω
 = 4.3 A
2.8 Ω
2. ∆V = 24 V
R1 = 2.0 Ω
R2 = 4.0 Ω
R3 = 6.0 Ω
R4 = 3.0 Ω
R12 = R1 + R2 = 2.0 Ω + 4.0 Ω = 6.0 Ω
R34 =

R
1
3
 + 
R
1
4


−1
=

6.0
1
Ω
 + 
3.0
1
Ω


−1
R34 =
0.17 
Ω
1
 + 0.33 
Ω
1


−1
=
0.50 
Ω
1


−1
= 2.0 Ω
Req =

R
1
12
 + 
R
1
34


−1
=

6.0
1
Ω
 + 
2.0
1
Ω


−1
Req =
0.17 
Ω
1
 + 0.50 
Ω
1


−1
=
0.67 
Ω
1


−1
= 1.5 Ω
I = 
R
∆
e
V
q
 = 
1
2
.
4
5
V
V
 = 16 A

Holt Physics Solutions Manual
II Ch. 18–4
II
4. ∆V = 1.00 × 103
V
R1 = 1.5 Ω
R2 = 3.0 Ω
R3 = 1.0 Ω
R12 =

R
1
1
 + 
R
1
2


−1
=

1.5
1
Ω
 + 
3.0
1
Ω


−1
R12 =
0.67 
Ω
1
 + 0.33 
Ω
1


−1
=
1.00 
Ω
1


−1
= 1.00 Ω
Req = R12 + R3 = 1.00 Ω + 1.0 Ω =
P = 
(∆
R
V
eq
)2
 = 
(1.00
2
×
.0
1
Ω
03
V)2
 = 5.0 × 105
W
2.0 Ω
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
5. ∆V = 2.00 × 103
V
I = 1.0 × 10−8
A
R1 = r
R2 = 3r
R3 = 2r
R4 = 4r
Req = 
∆
I
V
 = 
2
1
.
.
0
0
0
×
×
1
1
0
0
−
3
8 A
V
 =
R12 = R1 + R2 = r + 3r = 4r
R34 = R3 + R4 = 2r + 4r = 6r
Req =

R
1
12
 + 
R
1
34


−1
=

4
1
r
 + 
6
1
r


−1
Req =

3
1
+
2r
2


−1
=

1
5
2r


−1
= 
1
5
2
r
r = 
1
5
2
Req = 
1
5
2
(2.0 × 1011
Ω) = 8.3 × 1010
Ω
2.0 × 1011
Ω
1. R = 8.1 × 10−2
Ω
Req = 0.123 Ω
∆V = 220 V
R12 = R45 = 0.16 Ω
R12345 = 0.042 Ω
a. I = 
R
∆
e
V
q
 = 
0
2
.1
2
2
0
3
V
Ω
 = 1800 A
∆V12345 = IR12345 = (1800 A)(0.042 Ω) = 76 V
∆V3 = ∆V12345 =
I3 = 
∆
R
V
3
3
 = 
8.1 ×
76
10
V
−2 Ω
 = 9.4 × 102
A
76 V
6. P = 6.0 × 105
W
∆V = 220 V
R = 
(∆
P
V)2
 = 
6.
(
0
22
×
0
1
V
05
)2
W
 =
R12 = R45 = 2R = 2(0.081 Ω) = 0.16 Ω
R12345 =

R
1
12
 + 
R
1
3
 + 
R
1
45


−1
=

0.1
1
6 Ω
 + 
0.08
1
1 Ω
 + 
0.1
1
6 Ω


−1
R12345 =
6.2 
Ω
1
 + 12 
Ω
1
 + 6.2 
Ω
1


−1
=
24 
Ω
1


−1
= 0.042 Ω
Req = R12345 + R6 = 0.042 Ω + 0.081 Ω = 0.123 Ω
P = 
(∆
R
V
eq
)2
 = 
(
0
2
.
2
1
0
23
V
Ω
)2
 = 3.9 × 105
W
8.1 × 10−2
Ω

II
b. ∆V12 = ∆V12345 = 76 V
I12 = 
∆
R
V
12
12
 = 
0
7
.1
6
6
V
Ω
 = 4.8 × 102
A
I2 = I12 =
∆V2 = I2R2 = (4.8 × 102
A)(8.1 × 10−2
Ω) =
c. Same as part b:
I4 =
∆V4 = 39 V
4.8 × 102
A
39 V
4.8 × 102
A
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. ∆V = 12 V
R1 = 2.5 Ω
R3 = 3.0 Ω
R4 = 4.0 Ω
R5 = 1.0 Ω
R12 = 6.0 Ω
R123 = 2.0 Ω
R45 = 0.83 Ω
Req = 2.8 Ω
I = 4.3 A
a. ∆V45 = IR45 = (4.3 A)(0.83 Ω) = 3.6 V
∆V5 = ∆V45 =
I5 = 
∆
R
V
5
5
 = 
1
3
.
.
0
6
Ω
V
 =
b. ∆V123 = IR123 = (4.3 A)(2.0 Ω) = 8.6 V
∆V12 = ∆V123 = 8.6 V
I1 = I12 = 
∆
R
V
1
1
2
2
 = 
6
8
.
.
0
6
Ω
V
 =
∆V1 = I1R1 = (1.4 A)(2.5 Ω) =
c. I45 = I = 4.3 A
∆V45 = I45R45 = (4.3 A)(0.83 Ω) = 3.6 V
V4 = ∆V45 =
I4 = 
∆
R
V
4
4
 = 
4
3
.
.
0
6
Ω
V
 =
d. ∆V3 = ∆V123 =
I3 = 
∆
R
V
3
3
 = 
3
8
.
.
0
6
Ω
V
 = 2.9 A
8.6 V
0.90 V
3.6 V
3.5 V
1.4 A
3.1 A
3.6 V

II
3. R1 = 15 Ω
R2 = 3.0 Ω
R3 = 2.0 Ω
R4 = 5.0 Ω
R5 = 7.0 Ω
R6 = 3.0 Ω
R7 = 3.0 × 101
Ω
∆V = 2.00 × 103
V
R23 = R2 + R3 = 3.0 Ω + 2.0 Ω = 5.0 Ω
R234 =

R
1
23
 + 
R
1
4


−1
=

5.0
1
Ω
 + 
5.0
1
Ω


−1
R234 =
0.40
Ω
1


−1
= 2.5 Ω
R56 = R5 + R6 = 7.0 Ω + 3.0 Ω = 10.0 Ω
R567 =

R
1
56
 + 
R
1
7


−1
=

10.
1
0 Ω
 + 
30
1
Ω


−1
R567 =
0.100 
Ω
1
 + 0.033 
Ω
1


−1
=
0.133 
Ω
1


−1
= 7.52 Ω
Req = R1 + R234 + R567 = 15 Ω + 2.5 Ω + 7.52 Ω = 25 Ω
a. I = 
R
∆
e
V
q
 = 
2.00
2
×
5 Ω
103
V
 = 80 A
∆V234 = IR234 = (80 A)(2.5 Ω) = 2.0 × 102
V
∆V4 = ∆V234 =
I4 = 
∆
R
V
4
4
 = 
2
5
0
.0
0
Ω
V
 =
b. ∆V23 = ∆V234 = 200 V
I23 = 
∆
R
V
23
23
 = 
2
5
0
.0
0
Ω
V
 = 40 A
I3 = I23 =
∆V3 = I3R3 = (40 A)(2.0 Ω) =
c. I567 = I = 80 A
V567 = I567R567 = (80 A)(7.52 Ω) = 600 V
∆V56 = ∆V567 = 600 V
I56 = 
∆
R
V
56
56
 = 
1
6
0
0
.
0
0
V
Ω
 = 60 A
I5 = I56 =
∆V5 = I5R5 = (60 A)(7.0 Ω) =
d. ∆V7 = ∆V567 =
I7 = 
∆
R
V
7
7
 = 
6
3
0
0
0
Ω
V
 = 2.0 × 101
A
6.0 × 102
V
4.2 × 102
V
6.0 × 101
A
8.0 × 101
V
4.0 × 101
A
4.0 × 101
A
2.0 × 102
V
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Holt Physics Solutions Manual
II Ch. 18–6

Magnetism
II
1. B = 45 T
v = 7.5 × 106
m/s
q = e = 1.60 × 10−19
C
me = 9.109 × 10−31
kg
Fmagnetic = qvB
Fmagnetic = (1.60 × 10−19
C)(7.5 × 106
m/s)(45 T)
Fmagnetic = 5.4 × 10−11
N
Givens Solutions
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. q = 12 × 10−9
C
v = 450 km/h
B = 2.4 T
Fmagnetic = qvB
Fmagnetic = (12 × 10−9
C)(450 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(2.4 T)
Fmagnetic = 3.6 × 10−6
N
3. v = 350 km/h
q = 3.6 × 10−8
C
B = 7.0 × 10−5
T
q = 30.0°
Fmagnetic = qvB = q[v (sin q)]B
Fmagnetic = (3.6 × 10−8
C)(350 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m

(sin 30.0°)(7.0 × 10−5
T)
Fmagnetic = 1.2 × 10−10
N
4. v = 2.60 × 102
km/h
Fmagnetic = 3.0 × 10−17
N
q = 1.60 × 10−19
C
Fmagnetic = qvB
B = 
Fma
q
g
v
netic

B =
B = 2.6 T
(3.0 × 10−17
N)

(1.60 × 10−19 C)(2.60 × 102 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m



II
5. q = 1.60 × 10−19
C
v = 60.0 km/h
Fmagnetic = 2.0 × 10−22
N
Fmagnetic = qvB
B = 
Fma
q
g
v
netic

B =
B = 7.5 × 10−5
T
(2.0 × 10−22
N)

(1.60 × 10−19 C)(60.0 km/h)

36
1
0
h
0 s


1
1
0
k
3
m
m


Givens Solutions
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 19–2
6. q = 88 × 10−9
C
B = 0.32 T
Fmagnetic = 1.25 × 10−6
N
Fmagnetic = qvB
v = 
Fm
q
ag
B
netic

v =
v = 44 m/s = 160 km/h
(1.25 × 10−6
N)

(88 × 10−9 C)(0.32 T)
7. q = 1.60 × 10−19
C
B = 6.4 T
Fmagnetic = 2.76 × 10−16
N
∆x = 4.0 × 103
m
vi = 0 m/s
vf = 270 m/s
a. Fmagnetic = qvB
v = 
Fm
q
ag
B
netic

v =
v =
b. ∆x = 
(vf
2
+ vi)
 ∆t
∆t = 
(vf
2∆
+
x
vi)

∆t = 
(2
2
7
(
0
4.
m
0
/
×
s
1
+
0
0
3
m
m
/
)
s)

∆t = 3.0 × 101
s
2.7 × 102
m/s = 9.7 × 102
km/h
(2.76 × 10−16
N)

(1.60 × 10−19 C)(6.4 T)
8. B = 0.600 T
q = 1.60 × 10−19
C
v = 2.00 × 105
m/s
m1 = 9.98 × 10−27
kg
m2 = 11.6 × 10−27
kg
a. Fmagnetic = qvB
Fmagnetic = (1.60 × 10−19
C)(2.00 × 105
m/s)(0.600 T)
Fmagnetic =
b. Fc,1 = 
m
r
1
1
v2
 = Fmagnetic
Fc,2 = 
m
r
2
2
v2
 = Fmagnetic
r1 = 
Fm
m
a
1
g
v
ne
2
tic

r2 = 
Fm
m
a
2
g
v
ne
2
tic

1.92 × 10−14
N

II
r1 =
r1 = 2.08 × 10−2
m
r2 =
r2 = 2.42 × 10−2
m
r2 − r1 = 3.40 × 10−3
m = 3.4 mm
(11.6 × 10−27
kg)(2.00 × 105
m/s)2

(1.92 × 10−14 N)
(9.98 × 10−27
kg)(2.00 × 105
m/s)2

(1.92 × 10−14 N)
Givens Solutions
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. B = 22.5 T
l = 12 × 10−2
m
I = 8.4 × 10−2
A
Fmagnetic = BIl
Fmagnetic = (22.5 T)(8.4 × 10−2
A)(12 × 10−2
m)
Fmagnetic = 0.23 N
2. l = 1066 m
N
I = 0.80 A
Fmagnetic = BIl
B =
B = 
(0
(
.
6
8
.
0
3
A
×
)
1
(1
0
0
−
6
2
6
N
m
)
)

B = 7.4 × 10−5
T
Fmagnetic

Il
3. l = 5376 m
Fmagnetic = 3.1 N
I = 12 A
q = 38°
Fmagnetic = BIl = [B(sin q)]Il
B =
B =
B = 7.8 × 10−5
T
(3.1 N)

(12 A)(5376 m)(sin 38.0°)
Fmagnetic

Il(sin q)
4. l = 21.0 × 103
m
B = 6.40 × 10−7
T
Fmagnetic = 1.80 × 10−2
N
Fmagnetic = BIl
I =
I =
I = 1.34 A
(1.80 × 10−2
N)

(6.40 × 10−7 T)(21.0 × 103 m)
Fmagnetic

Bl

II Ch. 19–4
II
5. B = 2.5 × 10−4
T
l = 4.5 × 10−2
m
N
Fmagnetic = BIl
I =
I =
I = 3.2 ⫻ 10–2
A
(3.6 × 10−7
N)

(2.5 × 10−4 T)(4.5 × 10−2 m)
Fmagnetic

Bl
Givens Solutions
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. Fmagnetic = 5.0 × 105
N
B = 3.8 T
I = 2.00 × 102
A
Fmagnetic = BIl
l = 
Fma
B
g
I
netic

l =
l = 6.6 × 102
m
(5.0 × 105
N)

(3.8 T)(2.00 × 102 A)
7. Fmagnetic = 16.1 N
B = 6.4 × 10−5
T
I = 2.8 A
Fmagnetic = BIl
l = 
Fma
B
g
I
netic

l =
l = 9.0 × 104
m
(16.1 N)

(6.4 × 10−5 T)(2.8 A)
8. B = 0.040 T
I = 0.10 A
q = 45°
l = 55 cm ⫽ 0.55 m
Fmagnetic = BIl = [B(sin q)]Il
Fmagnetic = (0.040 T)(sin 45°)(0.10 A)(0.55 m)
Ν
9. B = 38 T
l = 2.0 m
m = 75 kg
g = 9.81 m/s2
Fmagnetic = BIl
Fg = mg
Fmagnetic = Fg
BIl = mg
I =
I = 
(75
(3
k
8
g
T
)(
)
9
(
.
2
8
.
1
0
m
m
/
)
s2
)

I = 9.7 A
mg

Bl

II
10. l = 478 × 103
m
Fmagnetic = 0.40 N
B = 7.50 × 10−5
T
Fmagnetic = BIl
I =
I =
I = 1.1 × 10−2
A
(0.40 N)

(7.50 × 10−5 T)(478 × 103 m)
Fmagnetic

Bl
Givens Solutions
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. Ai = 6.04 × 105
m2
Af = 
1
2
(6.04 × 105
m2
)
B = 6.0 × 10−5
T
emf = 0.80 V
N = 1 turn
q = 0.0°
emf = −N =
∆t = ∆A
∆t = (Af − Ai)
∆t = (6.04 × 105
m2
)
1
2
 − 1
∆t = 23 s
−(1)(6.0 × 10−5
T)(cos 0.0°)

(0.80 V)
−NB cos q

emf
−NB cos q

emf
−N∆[AB cos q]

∆t
∆ΦM

∆t
Givens Solutions
4. Af = 3.2 × 104
m2
Ai = 0.0 m2
∆t = 20.0 min
B = 4.0 × 10−2
T
N = 300 turns
q = 0.0°
emf = −N = = −NB cos q = (Af − Ai)
emf = [(3.2 × 104
m2
) − (0.0 m2
)]
emf = −3.2 × 102
V
−(300)(4.0 × 10−2
T)(cos 0.0°)

(20.0 min)

1
6
m
0
i
s
n


−NB cos q

∆t
∆A

∆t
−N∆[AB cos q]

∆t
∆ΦM

∆t
2. r = 
100
2
.0 m
 = 50.0 m
Bi = 0.800 T
Bf = 0.000 T
q = 0.00°
emf = 46.7 V
N = 1 turn
emf = −N =
∆t = −NA cos q =
∆t =
∆t = 135 s
−(1)(p)(50.0 m)2
(cos 0.0°)(0.000 T − 0.800 T)

(46.7 V)
−N(pr2
)(cos q)(Bf − Bi)

emf
∆B

emf
−N∆[AB cos q]

∆t
∆ΦM

∆t
Electromagnetic
Induction
3. emf = 32.0 × 106
V
Bi = 1.00 × 103
T
Bf = 0.00 T
A = 4.00 × 10−2
m2
N = 50 turns
q = 0.00°
emf = −N =
∆t = −NA cos q =
∆t =
∆t = 6.3 × 10−5
s
−(50)(4.00 × 10−2
m2
)(cos 0.00°)[(0.00 T) − (1.00 × 103
T)]

(32.0 × 106 V)
−NAcos q(Bf − Bi)

emf
∆B

emf
−N∆[AB cos q]

∆t
∆ΦM

∆t

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 20–2
5. Bi = 8.0 × 10−15
T
Bf = 10 Bi = 8.0 × 10−14
T
∆t = 3.0 × 10−2
s
A = 1.00 m2
emf = −1.92 × 10−11
V
q = 0.0°
emf = −N =
N = =
N =
N = 8 turns
−(−1.92 × 10−11
V)(3.0 × 10−2
s)

(1.00 m2)(cos 0.0°)[(8.0 × 10−14 T) − (8.0 × 10−15 T)]
−(emf)(∆t)

A cos q(Bf − Bi)
−(emf)(∆t)

A cos q ∆B
−N∆[AB cos q]

∆t
∆ΦM

∆t
6. Bi = 0.50 T
Bf = 0.00 T
N = 880 turns
∆t = 12 s
emf = 147 V
q = 0.0°
emf = −N = = −NA cos q 
∆
∆
B
t

A = =
A =
A = 4.0 m2
−(147 V)(12 s)

(880)(cos 0.0°)(0.00 T − 0.50 T)
−(emf)(∆t)

N cos q (Bf − Bi)
−(emf)(∆t)

N cos q ∆B
−N∆[AB cos q]

∆t
ΦM

∆t
Givens Solutions
1. ∆Vrms = 120 V
R = 6.0 × 10−2
Ω
= 0.707
1


2

a. Irms = 
∆V
R
rms

Irms = 
(6.0
(1
×
2
1
0
0
V
−2
)
Ω)

Irms =
b. Imax = (Irms)

2

Imax = 
(2.0
(0
×
.7
1
0
0
7
3
)
A)

Imax =
c. P = (Irms)(∆Vrms)
P = (2.0 × 103
A)(120 V)
P = 2.4 × 105
W
2.8 × 103
A
2.0 × 103
A

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. 2. P = 10.0(Acoustic power)
Acoustic power =
30.8 × 103 W
∆Vrms = 120.0 V
= 0.707
1


2

P = ∆Vrms Irms
Irms = 
∆V
P
rms

Irms = 
I

ma
2

x


I

ma
2

x
 = 
∆V
P
rms

Imax = 
∆
P
V

rm
2

s

Imax =
Imax = 3.63 × 103
A
(10.0)(30.8 × 103
W)

(120.0 V)(0.707)
Givens Solutions
3. P = 1.325 × 108
W
∆Vrms = 5.4 × 104
V
= 0.707
1


2

P = ∆VrmsIrms = (Irms)2
R = 
(∆V
R
rms)2

Irms = 
I

ma
2

x

Imax =

2
Irms = 
∆

V
2

rm
P
s

Imax =
Imax =
R = 
(∆V
P
rms)2

R = 
(1
(5
.3
.4
25
×
×
10
1
4
08
V
W
)2
)

R = 22 Ω
3.5 × 103
A
1.325 × 108
W

(5.4 × 104 V)(0.707)
4. ∆Vrms = 1.024 × 106
V
Irms = 2.9 × 10−2
A
= 0.707
1


2

∆Vmax = ∆Vrms

2

∆Vmax = 
(1.02
(0
4
.7
×
0
1
7
0
)
6
V)

∆Vmax =
Imax = Irms

2

Imax = 
(2.9
(0
×
.7
1
0
0
7
−
)
2
A)

Imax = 4.1 × 10−2
A
1.45 × 106
V = 1.45 MV

II Ch. 20–4
II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
R = 
∆
I
V
m
m
ax
ax
 = 
∆
I
V
rm
rm
s
s

R = 
(
(
0
3
.
2
8
0
0
V
A
)
)
 = 
(
(
0
2
.
3
5
0
7
V
A
)
)

R = 4.0 × 102
Ω
Givens Solutions
6. Imax = 75 A
R = 480 Ω
= 0.707
1


2

∆Vrms = 
∆V
m
2

ax

∆Vmax = (Imax)(R)
∆Vrms = 
Im

a
2

xR

∆Vrms = (75 A)(480 Ω)(0.707)
∆Vrms = 2.5 × 104
V = 25 kV
7. Ptot = 6.2 × 107
W
Ptot = 24 P
R = 1.2 × 105
Ω
= 0.707
1


2

P = (Irms)2
R = 
P
2
t
4
ot

P = 
6.2 ×
2
1
4
07
W

P =
Irms = 
R
P


Irms = 
(
(
2
1
.
.
6
2
×
×
1
1
0
0
6
5
W
Ω
)
)


Irms =
Imax =

2
Irms
Imax = 
0
4
.
.
7
7
0
A
7

Imax = 6.6 A
4.7 A
2.6 × 106
W = 2.6 MW
5. ∆Vmax = 320 V
Imax = 0.80 A
= 0.707
1


2

∆Vrms = 
∆V
m
2

ax

∆Vrms = (320 V)(0.707)
∆Vrms =
Irms = 
I

ma
2

x

Irms = (0.80 A)(0.707)
Irms = 0.57 A
2.3 × 102
V

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. N1 = 5600 turns
N2 = 240 turns
∆V2 = 4.1 × 102
V
∆V1 = ∆V2 
N
N
1
2


∆V1 = (4.1 × 103
V) ⫽

5
2
6
4
0
0
0


∆V1 = 9.6 × 104
V = 96 kV
Givens Solutions
2. N1 = 74 turns
N2 = 403 turns
∆V2 = 650 V
∆V1 = ∆V2 
N
N
1
2


∆V1 = (650 V)

4
7
0
4
3


∆V1 = 120 V
4. ∆V1 = 765 × 103
V
∆V2 = 540 × 103
V
N1 = 2.8 × 103
turns

∆
∆
V
V
1
2
 = 
N
N
2
1

N2 =

∆
∆
V
V
1
2

N1
N2 =

5
7
4
6
0
5
×
×
1
1
0
0
3
3
V
V

(2.8 × 103
)
N2 = 2.0 × 103
turns
3. ∆V1 = 2.0 × 10−2
V
N1 = 400 turns
N2 = 3600 turns
∆V2 = 2.0 × 10−2
V
∆V2 = ∆V1 
N
N
2
1


∆V2 = (2.0 × 10−2
V)

3
4
6
0
0
0
0


∆V2 =
∆V1 = ∆V2 
N
N
1
2


∆V1 = (2.0 × 10−2
V)

3
4
6
0
0
0
0


∆V1 = 2.2 × 10−3
V
0.18 V

II Ch. 20–6
II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.

N
N
1
2
 = 
∆
∆
V
V
2
1

N1 = N2
∆
∆
V
V
1
2


N1 = (660)

1
2
2
2
0
0
V
V


N1 = 360 turns
Givens Solutions
6. P = 20.0 W
∆V1 = 120 V

N
N
1
2
 = 0.36
a. P = (∆V1)(I1)
I1 = 
∆
P
V1
 = 
(
(
2
1
0
2
.0
0
W
V)
)

I1 =
b. 
∆
∆
V
V
1
2
 = 
N
N
2
1

∆V2 =

N
N
2
1

∆V1
∆V2 =

0.
1
36

(120 V)
∆V2 = 3.3 × 102
V
0.17 A
5. ∆V1 = 230 × 103
V
∆V2 = 345 × 103
V
N1 = 1.2 × 104
turns

N
N
1
2
 = 
∆
∆
V
V
2
1

N2 = N1 
∆
∆
V
V
2
1


N2 = (1.2 × 104
)

3
2
4
3
5
0
×
×
1
1
0
0
3
3
V
V


N2 = 1.8 × 104
turns
7. ∆V1 = 120 V
∆V2 = 220 V
I2 = 30.0 A
N2 = 660 turns
P1 = P2
∆V1I1 = ∆V2I2
I1 =

∆
∆
V
V
2
1

I2
I1 =

2
1
2
2
0
0
V
V

(30.0 A)
I1 = 55 A

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. E = 1.29 × 10−15
J
C = 3.00 × 108
m/s
h = 6.63 × 10−34
J•s
l = 
h
E
c
 =
l = 1.54 × 10−10
m = 0.154 nm
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

1.29 × 10−15
J
Givens Solutions
2. E = 6.6 × 10−19
J
C = 3.00 × 108
m/s
h = 6.63 × 10−34
J•s
l = 
h
E
c
 =
l = 3.0 × 10−7
m
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

6.6 × 10−19
J
3. E = 5.92 × 10−6
eV
C = 3.00 × 108
m/s
h = 6.63 × 10−34
J•s
l = 
h
E
c
 =
l = 0.210 m
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

(5.92 × 10−6
eV)(1.60 × 10−19
J/eV)
Atomic Physics
4. E = 2.18 × 10−23
J
h = 6.63 × 10−34
J•s
E = hf
f = 
E
h

f = 
6
2
.6
.1
3
8
×
×
1
1
0
0
−
−
34
23
J
J
•s

f = 3.29 × 1010
Hz
5. E = 1.85 × 10−23
J
h = 6.63 × 10−34
J•s
f = 
E
h
 = 
6
1
.6
.8
3
5
×
×
1
1
0
0
−
−
3
2
4
3
J/
J
s
 = 2.79 × 1010
Hz
6. f = 9 192 631 770 s−1
h = 6.626 0755 × 10−34
J•s
1 eV = 1.602 117 33 × 10−19
J
E = hf
E =
E = 3.801 9108 × 10−5
eV
(6.626 0755 × 10−34
J•s)(9 192 631 770 s−1
)

1.602 117 33 × 10−19 J/eV
7. l = 92 cm = 92 × 10−2
m
c = 3.00 × 108
m/s
h = 6.63 × 10−34
J•s
h = 4.14 × 10−15
eV•s
f = 
l
c

f = 
3.
9
0
2
0
×
×
1
1
0
0
−
8
2
m
m
/s

f =
E = hf
3.3 × 108
Hz = 330 MHz

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
II Ch. 21–2
Givens Solutions
8. v = 1.80 × 10−17
m/s
∆t = 1.00 year
l = ∆x
c = 3.00 × 108
m/s
h = 6.63 × 10−34
J•s
∆x = v∆t
∆x = (1.80 × 10−17
m/s)(1.00 year)

365
1
.2
y
5
ea
d
r
ays


1
24
da
h
y


36
1
0
h
0 s


∆x =
E = hf = 
h
l
c
 = 
∆
h
x
c

E =
E = 3.50 × 10−16
J
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

5.68 × 10−10
m
5.68 × 10−10
m
E = (6.63 × 10−34
J•s)(3.3 × 108
Hz)
E =
E = (4.14 × 10−15
eV•s)(3.3 × 108
Hz)
E = 1.4 × 10−6
eV
2.2 × 10−25
J
1. hft = 4.5 eV
KEmax = 3.8 eV
h = 4.14 × 10−15
eV•s
f = ᎏ
[KEma
h
x + hft]
ᎏ = 
4
[3
.1
.8
4
e
×
V
10
+
−
4
1
.
5
5
e
e
V
V
•
]
s
 = 2.0 × 1015
Hz
2. hft = 4.3 eV
KEmax = 3.2 eV
h = 4.14 × 10−15
eV•s
KEmax = hf − hft
f = 
KEma
h
x + hft

f = 
4.
3
1
.
4
2
×
eV
10
+
−
4
15
.3
e
e
V
V
•s

f = 1.8 × 1015
Hz
3. hft,Cs = 2.14 eV
hft,Se = 5.9 eV
h = 4.14 × 10−15
eV•s
c = 3.00 × 108
m/s
KEmax = 0.0 eV for both
cases
a. KEmax = hf − hft = 0.0 eV = 
h
l
c
 − hft
l = 
h
h
f
c
t

lCs = 
hf
h
t,
c
Cs
 =
lCs =
b. lSe = 
hf
h
t,
c
Se
 =
lSe = 2.1 × 10−7
m = 2.1 × 102
nm
(4.14 × 10−15
eV•s)(3.00 × 108
m/s)

5.9 eV
5.80 × 10−7
m = 5.80 × 102
nm
(4.14 × 10−15
eV•s)(3.00 × 108
m/s)

2.14 eV

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved. 4. l = 2.00 × 102
nm =
2.00 × 10−7
m
v = 6.50 × 105
m/s
me = 9.109 × 10−31
kg
c = 3.00 × 108
m/s
h = 4.14 × 10−15
eV•s
KEmax = 
1
2
mev2
= hf − hft

1
2
mev2
= 
h
l
c
 − hft
hft = 
h
l
c
 − 
1
2
mev2
hft = −
hft = 6.21 eV − 1.20 eV
hft =
ft = 
4.14 ×
5.0
1
1
0−
e
1
V
5
eV•s
 = 1.21 × 1015
Hz
5.01 eV
(0.5)(9.109 × 10−31
kg)(6.50 × 105
m/s)2

1.60 × 10−19
J/eV
(4.14 × 10−15
eV•s)(3.00 × 108
m/s)

2.00 × 10−7
m
6. l = 2.00 × 102
nm =
2.00 × 10−7
m
KEmax = 0.46 eV
h = 4.14 × 10−15
eV•s
c = 3.00 × 108
m/s
KEmax = hf − hft
hft = hf − KEmax = 
h
l
c
 − KEmax
hft = − 0.46 eV
hft = 6.21 eV − 0.46 eV
hft =
ft = 
4.14 ×
5.
1
8
0
e
−
V
15
eV•s
 = 1.4 × 1015
Hz
5.8 eV
(4.14 × 10−15
eV•s)(3.00 × 108
m/s)

2.00 × 10−7
m
7. l = 589 nm = 589 × 10−9
m
hft = 2.3 eV
c = 3.00 × 108
m/s
h = 4.14 × 10−15
eV•s
KEmax = hf − hft = 
h
l
c
 − hft
KEmax = − 2.3 eV
KEmax = 2.11 eV − 2.3 eV
KEmax =
No. The photons in the light produced by sodium vapor need 0.2 eV more energy
to liberate photoelectrons from the solid sodium.
−0.2 eV
(4.14 × 10−15
eV•s)(3.00 × 108
m/s)

589 × 10−9 m
5. f = 2.2 × 1015
Hz
KEmax = 4.4 eV
h = 4.14 × 10−15
eV•s
KEmax = hf − hft
hft = hf − KEmax
hft = (4.14 × 10−15
eV•s)(2.2 × 1015
Hz) − 4.4 eV
hft = 9.1 eV − 4.4 eV =
ft = 
4.14 ×
4
1
.7
0−
e
1
V
5
eV•s
 = 1.1 × 1015
Hz
4.7 eV
Givens Solutions

II Ch. 21–4
II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
8. hft = 2.3 eV
l = 410 nm = 4.1 × 10−7
m
h = 4.14 × 10−15
eV•s
c = 3.00 × 108
m/s
Givens Solutions
9. hft,Zn = 4.3 eV
hft,Pb = 4.1 eV
KEmax,Zn = 0.0 eV
me = 9.109 × 10−31
kg
KEmax = hf − hft
KEmax,Pb = hf − hft,Pb = (KEmax,Zn + hft,Zn) − hft,Pb
KEmax,Pb = 
1
2
mev2

1
2
mev2
= (KEmax,Zn + hft,Zn) − hft,Pb
v =
v =

v = 
9
.1
(
0
2
9
)
(
×
0
.
1
2
0
e
−
V
31
)
k
g



1
.6
0
1
×
e
1
V
0−

19
J

= 3 × 105
m/s
1.60 × 10−19 J

1 eV
(2)(0.0 eV + 4.3 eV − 4.1 eV)

9.109 × 10−31 kg
2(KEmax,Zn + hft,Zn − hft,Pb)

me
KEmax = 
h
l
c
 − hft
KE = − 2.3 eV
KE = 3.03 eV − 2.3 eV = 0.7 eV
(4.14 × 10−15
eV•s)(3.00 × 108
m/s)

4.1 × 10−7 m
1. l = 671.9 nm
Efinal = E1 = 0 eV
E = Einitial − Efinal = Einitial − E1
E = 
h
l
c

Einitial =
+ 0 eV
Einitial = 1.85 eV + 0 eV =
The photon is produced by the transition of the electron from the E2 energy level
to E1.
1.85 eV
1 eV

1.60 × 10−19
J
109
nm

1 m
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

671.9 nm
2. Einitial = E4 = 5.24 eV
Efinal = E1 = 0 eV
E = Einitial − Efinal = E4 − E1
E = 
h
l
c

l = 
h
E
c
 =
l =

l = 2.37 × 10−7
m = 237 nm
1 eV

1.60 × 10−19
J
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

5.24 eV − 0 eV
hc

E4 − E1

II
Efinal = E1 = 0 eV
E = 
h
l
c

l = 
h
E
c
 =
l =

l = 2.65 × 10−7
m = 265 nm
1 eV

1.60 × 10−19
J
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

4.69 eV − 0 eV
hc

E3 − E1
Givens Solutions
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Efinal = E1 = 0 eV
E = 
h
l
c

l = 
h
E
c
 =
l =

l = 3.95 × 10−7
m = 395 nm
1 eV

1.60 × 10−19
J
(6.63 × 10−34
J•s)(3.00 × 108
m/s)

3.15 eV − 0 eV
hc

E2 − E1

II Ch. 21–6
II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.

1
)
−



1. v = 3.2 m/s
l = 3.0 × 10−32
m
h = 6.63 × 10−34
J•s
m = 
l
h
v
 = =
2. l = 6.4 × 10−11
m
6.9 × 10−3
kg
6.63 × 10−34
J•s

(3.0 × 10−32
m)(3.2 m/s)
v = 64 m/s
h = 6.63 × 10−34
J•s
mv = 
l
h

m = 
l
h
v

m =
m = 1.6 × 10−25
kg
6.63 × 10−34
J•s

(6.4 × 10−11 m)(64 m/s)
l
c
t

3. q = (2)(1.60 × 10−19
C) =
3.20 × 10−19
C
∆V = 240 V
h = 6.63 × 10−34
J•s
l = 4.4 × 10−13
m
KE = q∆V = 
1
2
mv2
m = 
2q
V
∆
2
V

v = 
l
h
m
 = = 1.0 × 105
m/s
m =
m = 1.5 × 10−26
kg
2(3.20 × 10−19
C)(240 V)

(1.0 × 105
m/s)2
6.63 × 10−34
J•s

(4.4 × 10−13
m)(1.5 × 10−26
kg)

II
Copyright
©
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. l = 2.5 nm = 2.5 × 10−9
m
mn = 1.675 × 10−27
kg
h = 6.63 × 10−34
J•s
mv = 
l
h

v = 
lm
h
n

v =
v = 1.6 × 102
m/s
6.63 × 10−34
J•s

(2.5 × 10−9 m)(1.675 × 10−27 kg)
Givens Solutions
5. m = 7.65 × 10−70
kg
l = 5.0 × 1032
m
h = 6.63 × 10−34
J•s
mv = 
l
h

v = 
l
h
m

v =
v = 1.7 × 103
m/s
6.63 × 10−34
J•s

(5.0 × 1032 m)(7.65 × 10−70 kg)
6. m = 1.6 g = 1.6 × 10−3
kg
v = 3.8 m/s
h = 6.63 × 10−34
J•s
mv = 
l
h

l = 
m
h
v

l =
l = 1.1 × 10−31
m
6.63 × 10−34
J•s

(1.6 × 10−3 kg)(3.8 m/s)
7. ∆x = 42 195 m
∆t = 3 h 47 min = 227 min
m = 0.080 kg
h = 6.63 × 10−34
J•s
v = 
∆
∆
x
t
 = =

l
h
 = mv
l = 
m
h
v

l =
l = 2.7 × 10−33
m
6.63 × 10−34
J•s

(0.080 kg)(3.10 m/s)
3.10 m/s
42 195 m

(227 min)

1
6
m
0
i
s
n


Subatomic Physics
II
1. E = 610 TW•h
atomic mass of 1
2
H =
2.014 102 u
atomic mass of 26
56
Fe =
55.934 940 u
atomic mass of 226
88Ra =
226.025 402 u
a. ∆m = 
c
E
2
 =
∆m =
b. n = 
atomic
∆
m
m
ass of 1
2
H
 =
n =
c. n = =
n =
d. n = =
n = 6.4 × 1025 226
88Ra nuclei
24 kg

(1.66 × 10−27 kg/u)(226.025 402 u)
∆m

atomic mass of 226
88Ra
2.6 × 1026
26
56
Fe nuclei
24 kg

(1.66 × 10−27 kg/u)(55.934 940 u)
∆m

atomic mass of 26
56
Fe
7.2 × 1027
1
2
H nuclei
24 kg

(1.66 × 10−27 kg/u)(2.014 102 u)
24 kg
(610 × 109
kW•h)(3.6 × 106
J/kW•h)

(3.00 × 108 m/s)2
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
2. m = 4.1 × 107
kg
h = 10.0 cm
Z = 26
N = 56 − 26 = 30
mH = 1.007 825 u
mn = 1.008 665 u
atomic mass of 26
56
Fe =
55.934 940 u
a. E = mgh = (4.1 × 107
kg)(9.81 m/s2
)(0.100 m)
E =
b. Etot = = 2.5 × 1020
MeV
∆mtot = = 2.7 × 1017
u
∆m = Z(atomic mass of H) + Nmn − atomic mass of 26
56
Fe
∆m = 26(1.007 825 u) + 30(1.008 665 u) − 55.934 940 u
∆m = 0.528 460 u
Ebind = (0.528 460 u)
931.49 
M
u
eV


Ebind = 492.26 MeV
n = 
E
E
b
t
i
o
n
t
d
 = = 5.1 × 1017
reactions
mtot = (5.1 × 1017
)(55.934 940 u)
1.66 × 10−27

k
u
g

= 4.7 × 10−8
kg
2.5 × 1020
MeV

492.26 MeV
2.5 × 1020
MeV

931.49 MeV/u
(4.0 × 107
J)(1 × 10−6
MeV/eV)

(1.60 × 10−19 J/eV)
4.0 × 107
J

6. P = 42 MW = 42 × 106
W
atomic mass of 14
7N =
14.003 074 u
atomic mass of H =
1.007 825 u
mn = 1.008 665 u
Z = 7
N = 14 − 7 = 7
∆t = 24 h
II
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
3. E = 2.0 × 103
TW•h =
2.0 × 1015
W•h
atomic mass of 235
92U =
235.043 924 u
atomic mass of H =
1.007 825 u
mn = 1.008 665 u
Z = 92
N = 235 − 92 = 143
92U
∆m = 92(1.007 825 u) + 143(1.008 665 u) − 235.043 924 u = 1.915 071 u
Ebind = (1.915 071 u)
931.49 
M
u
eV

= 1.7839 × 103
MeV = 1.7839 × 109
eV
Ebind = (1.7839 × 109
eV)
1.60 × 10−19

e
J
V

= 2.85 × 10−10
J
E = (2.0 × 1015
W•h)

3.60 ×
h
103
s

= 7.2 × 1018
J
n = 
Eb
E
ind
 = 
2
7
.8
.2
5
×
×
1
1
0
0
1
−
8
10
J
J
 = 2.5 × 1028
reactions
mtot = (2.5 × 1028
)(235.043 924 u)
1.66 × 10−27

k
u
g

= 9.8 × 103
kg
4. E = 2.1 × 1019
J
atomic mass of 12
6C =
12.000 000 u
atomic mass of H =
1.007 825 u
mn = 1.008 665 u
Z = 6
N = 12 − 6 = 6
6C
∆m = 6(1.007 825 u) + 6(1.008 665 u) − 12.000 000 u
∆m = 9.8940 × 10−2
u
Ebind = (9.8940 × 10−2
u)
931.49 
M
u
eV

= 92.162 MeV
Ebind = (92.162 × 106
eV)
1.60 × 10−19

e
J
V

= 1.47 × 10−11
J
n = 
Eb
E
ind
 = 
1
2
.4
.1
7
×
×
1
1
0
0
1
−
9
11
J
J
 = 1.4 × 1030
reactions
mtot = (1.4 × 1030
)(12.000 000 u)
1.66 × 10−27

k
u
g

= 2.8 × 104
kg
7N
∆m = 7(1.007 825 u) + 7(1.008 665 u) − 14.003 074 u
∆m = 0.112 356 u
Ebind = (0.112 356 u)
931.49 
M
u
eV

= 104.66 MeV
Ebind = (104.66 × 106
eV)
1.60 × 10−19

e
J
V

= 1.67 × 10−11
J
n = 
E
P
b
∆
in
t
d
 = = 2.2 × 1023
reactions
mtot = (2.2 × 1023
)(14.003 074 u)
1.66 × 10−27

k
u
g

= 5.1 × 10−3
kg = 5.1 g
(42 × 106
W)(24 h)(3600 s/h)

1.67 × 10−11 J
5. Ptot = 3.9 × 1026
J/s
Z = 2
N = 4 − 2 = 2
atomic mass of 4
2He =
4.002 602 u
atomic mass of H =
1.007 825 u
mn =1.008 665 u
2He
∆m = (2)(1.007 825 u) + (2)(1.008 665 u) − 4.002 602 u
∆m = 0.030 378 u
E = (0.030 378 u)
931.49 
M
u
eV


E = 28.297 MeV

∆
n
t
 = 
P
E
tot
 =

∆
n
t
 = 8.6 × 1037
reactions/s
(3.9 × 1026
J/s)(1 × 10−6
MeV/eV)

(1.60 × 10−19 J/eV)(28.297 MeV)
II Ch. 22–2

II
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book. 7. P = 3.84 × 107
W
atomic mass of 12
6C =
12.000 000 u
atomic mass of H =
1.007 825 u
mn = 1.008 665 u
Z = 6
N = 12 − 6 = 6
6C
∆m = 6(1.007 825 u) + 6(1.008 665 u) − 12.000 000 u
∆m = 9.8940 × 10−2
u
Ebind = (9.8940 × 10−2
u)
931.49 × 106

e
u
V

1.60 × 10−19

e
J
V


Ebind = 1.47 × 10−11
J

∆
n
t
 = 
Eb
P
ind
 = 
1
3
.
.
4
8
7
4
×
×
1
1
0
0
−
7
1
W
1 J
 = 2.61 × 1018
reactions/s

m
∆
t
t
ot
 = (2.61 × 1018
s−1
)(12.000 000 u)
1.66 × 10−27

k
u
g

= 5.20 × 10−8
kg/s
1. 238
92U + 0
1
n → X
X → 939
93Np + −1
0
e + v

239
93Np → 239
94Pu + −1
0
e + v

mass number of X = 238 + 1 = 239
atomic number of X = 92 + 0 = 92 (uranium)
X = 239
92U
The equations are as follows:
238
92U + 0
1
n → 239
92U
239
92U → 939
93Np + −1
0
e + v

239
93Np → 239
94Pu + −1
0
e + v

3. X → 135
56Ba + −1
0
e + v

atomic number of X = 56 + (−1) = 55 (cesium)
X = 135
55 Cs
135
55 Cs →
135
56Ba + −1
0
e + v

2. X → Y + 4
2He
Y → Z + 4
2He
Z → 212
83Bi + −1
0
e + v

mass number of Z = 212 + 0 = 212
atomic number of Z = 83 − 1 = 82 (lead)
Z = 212
82Pb
mass number of Y = 212 + 4 = 216
atomic number of Y = 82 + 2 = 84 (polonium)
Y = 216
84Po
atomic number of X = 84 + 2 = 86 (radon)
X = 220
86Rn
The equations are as follows:
220
86Rn → 216
84Po + 4
2He
216
84Po → 212
82Pb + 4
2He
212
82Pb → 212
83Bi + −1
0
e + v


II
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book.
5. 228
90Th → X + 4
2He + g mass number of X = 228 − 4 = 224
atomic number X = 90 − 2 = 88 (radium)
X = 224
88Ra
228
90Th → 224
88Ra + 4
2He + g
6. 1
1
p + 7
3Li → X + 4
2He mass number of X = 1 + 7 − 4 = 4
atomic number of X = 1 + 3 − 2 = 2 (helium)
X = 4
2He
1
1
p + 7
3Li → 4
2He + 4
2He
7. 217
85At → X + 4
2He mass number of X = 217 − 4 = 213
atomic number of X = 85 − 2 = 83 (bismuth)
X = 213
83Bi
217
85At → 213
83Bi + 4
2He
1. T1/2 = 26 min, 43.53 s
l = 
0
T
.6
1
9
/2
3
 =
l =
5 times the run time = 5 half-lives
percent of sample remaining = (0.5)5
(100)
percent decayed = 100 − percent remaining = 100 − (0.5)5
(100) = 96.875 percent
4.32 × 10−4
s−1
0.693

(26 min)(60 s/min) + 43.53 s
4. 235
92U + 1
0n → 144
56 Ba +
89
36Kr + X
mass number of X = 235 + 1 − 144 − 89 = 3
atomic number of X = 92 + 0 − 56 − 36 = 0 (neutron)
X = 3 1
0n
235
92U + 1
0n → 144
56Ba + 89
36Kr + 31
0n
235
92U + 1
0n → 140
54Xe + Y +
2 1
0n
mass number of Y = 235 + 1 − 140 − 2 = 94
atomic number of Y = 92 + 0 − 54 − 0 = 38 (strontium)
Y = 94
38Sr
235
92U + 1
0n → 140
54Xe + 94
38Sr + 2 1
0n
II Ch. 22–4

II
Givens Solutions
HRW
material
copyrighted
under
notice
appearing
earlier
in
this
book. 2. T1/2 = 1.91 years
decrease = 93.75 percent =
0.9375
If 0.9375 of the sample has decayed, 1.0000 − 0.9375 = 0.0625 of the sample remains.
0.0625 = (0.5)4
, so 4 half-lives have passed.
∆t = 4T1/2 = (4)(1.91 years) = 7.64 years
3. T1/2 = 11.9 s
Ni = 1.00 × 1013
atoms
Nf = 1.25 × 1012
atoms

∆
N
N
i
 = = 0.875
If 0.875 of the sample has decayed, 1.000 − 0.875 = 0.125 of the sample remains.
0.125 = (0.5)3
∆t = 3T1/2 = (3)(11.9 s) = 35.7 s
1.00 × 1013
− 1.25 × 1012

1.00 × 1013
4. ∆t = 4800 years
T1/2 = 1600 years

T
∆
1
t
/2
 = 
4
1
8
6
0
0
0
0
y
y
e
e
a
a
r
r
s
s
 = 3 half-lives
amount remaining after 3T1/2 = (0.5)3
= 0.125 = 12.5 percent
7. T = 4.4 × 10−22
s 
T
1
 = l = 
0
T
.6
1
9
/2
3

T = 
0
T
.6
1
9
/2
3

T1/2 = (0.693)(T) = (0.693)(4.4 × 10−22
s) = 3.0 × 10−22
s
5. ∆t = 88 years
amount of sample
remaining = 
1
1
6
 = 0.0625
0.0625 = (0.5)4
T1/2 = 
1
4
∆t = 
88 y
4
ears
 = 22 years
l = 
0
T
.6
1
9
/2
3
 = 
22
0.
y
6
e
9
a
3
rs

l = 3.2 × 10−2
years−1
6. ∆t = 34 days, 6 h, 26 min
amount of sample
remaining = 
5
1
12
 = 1.95 × 10−3
∆t = (34 days)

2
d
4
ay
h


60
h
min

+ (6 h)

60
h
min

+ 26 min
∆t = 4.9346 × 104
min
1.95 × 10−3
= (0.5)9
T1/2 = 
1
9
∆t = 
4.9346 ×
9
104
min
 = 5482.9 min
l = 
0
T
.6
1
9
/2
3
 = 
548
0
2
.6
.9
93
min

l = 1.26 × 10−4
min−1
= 0.182 days−1

Section Two—Problem Workbook Solutions Appendix J–1
Appendix J
Advanced Topics
II
1. r = 10.0 km
∆q = +15.0 rad
∆s = r∆q = (10.0 km)(15.0 rad) =
The particle moves in the positive, or , direction around the
neutron star’s “north” pole.
counterclockwise
1.50 × 102
km
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
2. ∆q = 3(2p rad)
r = 6560 km
∆s = r∆q = (6560 km)[(3)(2p rad)] = 1.24 × 105
km
3. r = 
1.40 ×
2
105
km

= 7.00 × 104
km
∆q = 1.72 rad
rE = 6.37 × 103
km
a. ∆s = r∆q = (7.00 × 104
km)(1.72 rad) =
b. ∆qE = 
∆
rE
s
 = = 3.00 rev, or 3.00 orbits
(1.20 × 105
km)(1 rev/2p rad)

6.37 × 103
km
1.20 × 105
km
4. ∆q = 225 rad
∆s = 1.50 × 106
km
r = 
∆
∆
q
s
 = 
1.50
22
×
5
1
r
0
a
6
d
km
 = 6.67 × 103
km
5. r = 5.8 × 107
km
∆s = 1.5 × 108
km
∆q = 
∆
r
s
 = 
1
5
.
.
5
8
×
×
1
1
0
0
8
7
k
k
m
m
 = 2.6 rad
6. ∆s = −1.79 × 104
km
r = 6.37 × 103
km
∆q = 
∆
r
s
 = 
−
6
1
.3
.7
7
9
×
×
1
1
0
0
3
4
k
k
m
m
 = −2.81 rad
1. r = 1.82 m
wavg = 1.00 × 10−1
rad/s
∆t = 60.0 s
∆q = wavg∆t = (1.00 × 10−1
rad/s)(60.0 s) =
∆s = r∆q = (1.82 m)(6.00 rad) = 10.9 m
6.00 rad
2. ∆t = 120 s
wavg = 0.40 rad/s
∆q = wavg∆t = (0.40 rad/s)(120 s) = 48 rad
3. r = 30.0 m
∆s = 5.0 × 102
m
∆t = 120 s
wavg = 
∆
∆
q
t

 = 
r
∆
∆
s
t
 = 
(3
5
0
.
.
0
0
×
m
1
)(
0
1
2
2
m
0 s)
 = 0.14 rad/s

Appendix J–2
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
4. ∆q = 16 rev
∆t = 4.5 min
wavg = 
∆
∆
q
t
 = = 0.37 s
(16 rev)(2p rad/rev)

(4.5 min)(60 s/min)
Givens Solutions
5. wavg = 2p rad/24 h
∆q = 0.262 rad
∆t = 
w
∆
a
q
vg
 = = 1.00 h
0.262 rad


2
2
p
4
r
h
ad


6. r = 2.00 m
∆s = 1.70 × 102
km
wavg = 5.90 rad/s
∆t = 
w
∆
a
q
vg
 = 
rw
∆
a
s
vg
 = = 1.44 × 104
s = 4.00 h
1.70 × 105
m

(2.00 m)(5.90 rad/s)
1. aavg = 2.0 rad/s2
w1 = 0 rad/s
w2 = 9.4 rad/s
∆t = 
w2
a
−
avg
w1

∆t =
∆t = 4.7 s
9.4 rad/s − 0.0 rad/s

2.0 rad/s2
2. ∆tJ = 9.83 h
aavg = −3.0 × 10−8
rad/s2
w2 = 0 rad/s
w1 = 
∆
∆
t
q
J

 = 
(9.83 h
2p
)(3
ra
6
d
00 s/h)
 = 1.78 × 10−4
rad/s
∆t = 
w2
a
−
avg
w1
 =
∆t = 5.9 × 103
s
0.00 rad/s − 1.78 × 10−4
rad/s

−3.0 × 10−8 rad/s2
3. w1 = 2.00 rad/s
w2 = 3.15 rad/s
∆t = 3.6 s
aavg = 
w2
∆
−
t
w1
 = = 
1.1
3
5
.6
ra
s
d/s

aavg = 0.32 rad/s2
3.15 rad/s − 2.00 rad/s

3.6 s
4. w1 = 8.0 rad/s
w2 = 3w1 = 24 rad/s
∆t = 25 s
aavg = 
w2
∆
−
t
w1
 = 
24 rad/s
2
−
5
8
s
.0 rad/s
 = 
16
2
r
5
ad
s
/s

aavg = 0.64 rad/s2
5. ∆t1 = 365 days
∆q1 = 2p rad
aavg = 6.05 × 10−13
rad/s2
∆t2 = 12.0 days
w1 = 
∆
∆
q
t2
1
 = = 1.99 × 10−7
rad/s
w2 = w1 + aavg∆t2 = 1.99 × 10−7
rad/s + (6.05 × 10−13
rad/s2
)(12.0 days)
(24 h/day)(3600 s/h)
w2 = 1.99 × 10−7
rad/s + 6.27 × 10−7
rad/s = 8.26 × 10−7
rad/s
2p rad

(365 days)(24 h/day)(3600 s/h)
6. w1 = 0 rad/s
aavg = 0.800 rad/s2
∆t = 8.40 s
aavg = 
w2
∆
−
t
w1

w2 = w1 + aavg∆t
w2 = 0 rad/s + (0.800 rad/s2
)(8.40 s)
w2 = 6.72 rad/s

II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. wi = 5.0 rad/s
a = 0.60 rad/s2
∆t = 0.50 min
wf = wi + a∆t
wf = 5.0 rad/s + (0.60 rad/s2
)(0.50 min)(60.0 s/min)
wf = 5.0 rad/s + 18 rad/s
wf = 23 rad/s
2. a = 1.0 × 10−10
rad/s2
∆t = 12 h
wi = 
27
2
.
p
3
r
d
a
a
d
ys

wi =

27
2
.
p
3
r
d
a
a
d
ys


1
24
da
h
y


36
1
0
h
0 s

= 2.66 × 10−6
rad/s
wf = wi + a∆t = 2.66 × 10−6
rad/s + (1.0 × 10−10
rad/s2
)(12 h)(3600 s/h)
wf = 2.66 × 10−6
rad/s + 4.3 × 10−6
rad/s = 7.0 × 10−6
rad/s
3. r = 
2
4
p
3
r
m
ad

wi = 0 rad/s
∆s = 160 m
a = 5.00 × 10−2
rad/s2
∆q = 
∆
r
s

wf
2
= wi
2
+ 2a∆q = wi
2
+ 
2a
r
∆s

wf = w
i
2
+

2
a
r
∆
s

=
(0 rad/s)2
+
wf = 1.5 rad/s
(2)(5.00 × 10−2
rad/s2
)(160 m)


2
4
p
3
r
m
ad


4. ∆s = 52.5 m
a = −3.2 × 10−5
rad/s2
wf = 0.080 rad/s
r = 8.0 cm
∆q = 
∆
r
s

wf
2
= wi
2
+ 2a∆q = wi
2
+ 
2a
r
∆s

wi = w
f
2
−

2
a
r
∆
s

= (0
.0
80
r
ad
/s
)2
−

wi =

6.
4
×
1
0−
3
ra
d
2
/
s2
+
4
.2
×
1
0−
2
ra
d
2
/
s2
=

4.
8
×
1
0−
2
ra
d
2
/
s2

wi = 0.22 rad/s
(2)(−3.2 × 10−5
rad/s2
)(52.5 m)

8.0 × 10−2
m
5. r = 3.0 m
wi = 0.820 rad/s
wf = 0.360 rad/s
∆s = 20.0 m
∆q = 
∆
r
s

a = 
wf
2
2
∆
−
q
wi
2
 = =
a = =
a = −4.1 × 10−2
rad/s2
−0.542 rad2
/s2

(2)

2
3
0
.
.
0
0
m
m


0.130 rad2
/s2
− 0.672 rad2
/s2

(2)

2
3
0
.
.
0
0
m
m


(0.360 rad/s)2
− (0.820 rad/s)2

(2)

2
3
0
.
.
0
0
m
m


wf
2
− wi
2

2

∆
r
s



II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
6. r = 1.0 km
wi = 5.0 × 10−3
rad/s
∆t = 14.0 min
∆q = 2p rad
∆q = wi∆t + 
1
2
a∆t2
a = 
2(∆q
∆
−
t2
wi∆t)
 =
a = = = 6.0 × 10−6
rad/s2
(2)(2.1 rad)

[(14.0 min)(60 s/min)]2
(2)(6.3 rad − 4.2 rad)

[(14.0 min)(60 s/min)]2
(2)[2p rad − (5.0 × 10−3
rad/s)(14.0 min)(60 s/min)]

[(14.0 min)(60 s/min)]2
7. wi = 7.20 × 10−2
rad/s
∆q = 12.6 rad
∆t = 4 min, 22 s
∆t = (4 min)(60 s/min) + 22 s = 262 s
∆q = wi∆t + 
1
2
a∆t2
a = 
2(∆q
∆
−
t2
wi∆t)
 =
a = = 
(2)(
(
−
2
6
6
.
2
3
s
r
)
a
2
d/s)
 = −1.8 × 10−4
rad/s2
(2)(12.6 rad − 18.9 rad)

(262 s)2
(2)[12.6 rad − (7.20 × 10−2
rad/s)(262 s)]

(262 s)2
8. wi = 27.0 rad/s
wf = 32.0 rad/s
∆t = 6.83 s
aavg = 
wf
∆
−
t
wi
 = = 
5.
6
0
.8
r
3
ad
s
/s

aavg = 0.73 rad/s2
32.0 rad/s − 27.0 rad/s

6.83 s
9. a = 2.68 × 10−5
rad/s2
∆t = 120.0 s
wi = 
2p
1
r
2
ad

∆q = wi∆t + 
1
2
a∆t2
∆q =

2
1
p
2
r
h
ad

(1 h/3600 s)(120.0 s) + 
1
2
(2.68 × 10−5
rad/s2
)(120.0 s)2
∆q = 1.7 × 10−2
rad + 1.93 × 10−1
rad = 0.210 rad
10. wi = 6.0 × 10−3
rad/s
wf = 3wi = 18 × 10−3
rad/s
a = 2.5 × 10−4
rad/s2
∆q = 
wf
2
2
−
a
wi
2

∆q = =
∆q = = 0.56 rad
2.8 × 10−4
rad2
/s2

5.0 × 10−4
rad/s2
3.2 × 10−4
rad2
/s2
− 3.6 × 10−5
rad2
/s2

(2)(2.5 × 10−4
rad/s2
)
(18 × 10−3
rad/s)2
− (6.0 × 10−3
rad/s)2

(2)(2.5 × 10−4
rad/s2
)
11. wi = 9.0 × 10−7
rad/s
wf = 5.0 × 10−6
rad/s
a = 7.5 × 10−10
rad/s2
∆t = 
wf
a
− wi

∆t = =
∆t = 5.5 × 103
s = 1.5 h
4.1 × 10−6
rad/s

7.5 × 10−10 rad/s2
5.0 × 10−6
rad/s − 9.0 × 10−7
rad/s

7.5 × 10−10 rad/s2
Appendix J–4

II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
12. r = 7.1 m
∆s = 500.0 m
wi = 0.40 rad/s
a = 4.0 × 10−3
rad/s2
∆q = 
∆
r
s
 = wi∆t + 
1
2
a∆t2

1
2
a∆t2
+ wi∆t − 
∆
r
s
 = 0
Using the quadratic equation:
∆t =
∆t =
∆t = =
Choose the positive value:
∆t = = 
0.4
ra
5
d
r
/
a
s
d
2
/s
 = 1.1 × 102
s
−0.40 rad/s + 0.85 rad/s

4.0 × 10−3
rad/s2
– 0.40 rad/s ±

0.
72
r
ad
2
/
s2


4.0 × 10−3
rad/s2
−0.40 rad/s ±

0.
16
r
ad
2
/
s2
+
0
.5
6
ra
d
2
/
s2


4.0 × 10−3
rad/s2
−0.40 rad/s ± (0
.4
0
ra
d
/s
)2
+
(
4)

1
2

(
4.
0
×
1
0−
3
ra
d
/s
2
)

5
0
7
0
.
1
.0
m
m



(2)
1
2

(4.0 × 10−3
rad/s2
)
−wi ± w
i
2
−
4

1
2

a


−
∆
r
s



2
1
2
a
1. w = 4.44 rad/s
vt = 4.44 m/s
r = 
w
vt
 = 
4
4
.4
.4
4
4
r
m
ad
/
/
s
s
 = 1.00 m
2. vt = 16.0 m/s
w = 1.82 × 10−5
rad/s
r = 
w
vt
 = 
1.82
1
×
6.
1
0
0
m
−5
/
r
s
ad/s
 =
circumference = 2pr = (2p)(879 km) = 5.52 × 103
km
8.79 × 105
m = 879 km
3. w = 5.24 × 103
rad/s
vt = 131 m/s
r = 
w
vt
 = 
5.24
1
×
31
10
m
3
/
r
s
ad/s
 = 2.50 × 10−2
m = 2.50 cm
4. vt = 29.7 km/s
r = 1.50 × 108
km
w = 
v
r
t
 = 
1.5
2
0
9.
×
7
1
k
0
m
8
/
k
s
m
 = 1.98 × 10−7
rad/s
5. r = 
19.0
2
mm
 = 9.50 mm
w = 25.6 rad/s
vt = rw = (9.50 × 10−3
m)(25.6 rad/s) = 0.243 m/s

II
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. r = 32 m
at = 0.20 m/s2
a = 
a
r
t
 = 
0.2
3
0
2
m
m
/s2

a = 6.2 × 10−3
rad/s2
2. r = 8.0 m
at = −1.44 m/s2
a = 
a
r
t
 = 
−1.
8
4
.
4
0
m
m
/s2
 = −0.18 rad/s2
3. ∆w = −2.4 × 10−2
rad/s
∆t = 6.0 s
at = − 0.16 m/s2
a = 
∆
∆
w
t
 = 
−2.4 ×
6
1
.0
0−
s
2
rad/s
 = −4.0 × 10−3
rad/s2
r = 
a
a
t
 = 
−4.0
−0
×
.1
1
6
0−
m
3
/
r
s
a
2
d/s2
 = 4.0 × 101
m
4. ∆q′ = 14 628 turns
∆t′ = 1.000 h
at = 33.0 m/s2
wi = 0 rad/s
∆q = 2p rad
r = 

a
a
t

a = 
wf
2
2∆
−
q
wi
2

wf =
r = =
r =

2
− (0 rad/s)2
= 0.636 m
(14 628 turns)(2p rad/turn)

(1.000 h)(3600 s/h)
2at∆q


∆
∆
q
t′
′


2
− wi
2

∆
∆
q
t′
′


2
− wi
2

2∆q
∆q′

∆t′
5. r = 56.24 m
wi = 6.00 rad/s
wf = 6.30 rad/s
∆t = 0.60 s
at = ra
a = 
wf
∆
−
t
wi

at = r

wf
∆
−
t
wi

= (56.24 m)
=
at = 28 m/s2
(56.24 m)(0.30 rad/s)

0.60 s
6.30 rad/s − 6.00 rad/s

0.60 s
at
(2)(33.0 m/s2
)(2p rad)
6. r = 1.3 m
∆q = 2p rad
∆t = 1.8 s
wi = 0 rad/s
at = ra
α = 
2(∆q
∆
−
t2
wi∆t)

at = r

2(∆q
∆
−
t2
wi∆t)

= (1.3 m)

at = 5.0 m/s2
(2)[2p rad − (0 rad/s)(1.8 s)]

(1.8 s)2
Appendix J–6

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. t1 = 2.00 × 105
N•m
t2 = 1.20 × 105
N•m
h = 24 m
Apply the second condition of equilibrium, choosing the base of the cactus as the
pivot point.
tnet = t1 − t2 − Fd(sin q) = 0
Fd(sin q) = t1 − t2
For F to be minimum, d and sin q must be maximum. This occurs when the force is
perpendicular to the cactus (q = 90°) and is applied to the top of the cactus (d = h =
24 m).
Fmin = 
t1 −
h
t2
 =
Fmin = = 3.3 × 103
N applied to the top of the cactus
8.0 × 104
N•m

24 m
2.00 × 105
N•m − 1.20 × 105
N•m

24 m
Givens Solutions
2. m1 = 40.0 kg
m2 = 5.4 kg
d1 = 70.0 cm
d2 = 100.0 cm − 70.0 cm
= 30.0 cm
g = 9.81 m/s2
Apply the first condition of equilibrium.
Fn − m1g − m2g − Fapplied = 0
Fn = m1g + m2g + Fapplied = (40.0 kg)(9.81 m/s2
) + (5.4 kg)(9.81 m/s2
) + Fapplied
Fn = 392 N + 53 N + Fapplied = 455 N + Fapplied
Apply the second condition of equilibrium, using the fulcrum as the location for the
axis of rotation.
Fappliedd2 + m2gd2 − m1gd1 = 0
Fapplied = 
m1gd1
d
−
2
m2gd2
 =
Fapplied = =
Fapplied =
Substitute the value for Fapplied into the first-condition equation to solve for Fn.
Fn = 455 N + 863 N = 1318 N
863 N
259 N•m

0.300 m
275 N•m − 16 N•m

0.300 m
(40.0 kg)(9.81 m/s2
)(0.700 m) − (5.4 kg)(9.81 m/s2
)(0.300 m)

0.300 m
3. m = 134 kg
d1 = 2.00 m
d2 = 7.00 m − 2.00 m = 5.00 m
q = 60.0°
g = 9.81 m/s2
Apply the first condition of equilibrium in the x and y directions.
Fx = Fapplied (cos q) − Ff = 0
Fy = Fn − Fapplied (sin q) − mg = 0
To solve for Fapplied, apply the second condition of equilibrium, using the fulcrum as
the pivot point.
Fapplied (sin q)d2 − mgd1 = 0
Fapplied = 
d2
m
(s
g
in
d1
q)
 =
Fapplied =
Substitute the value for Fapplied into the first-condition equations to solve for Fn and
Ff.
Fn = Fapplied(sin q) + mg = (607 N)(sin 60.0°) + (134 kg)(9.81 m/s2
)
Fn = 526 N + 1.31 × 103
N =
Ff = Fapplied(cos q) = (607 N)(cos 60.0°) = 304 N
1.84 × 103
N
607 N
(134 kg)(9.81 m/s2
)(2.00 m)

(5.00 m)(sin 60.0°)

II
4. m = 8.8 × 103
kg
d1 = 3.0 m
d2 = 15 m − 3.0 m = 12 m
q = 20.0°
g = 9.81 m/s2
Apply the first condition of equilibrium in the x and y directions.
Fx = Ffulcrum,x − F (sin q) = 0
FyFfulcrum,y − F (cos q) − mg = 0
To solve for F, apply the second condition of equilibrium •, using the fulcrum as the
pivot point.
Fd2 − mg d1 (cos q) = 0
F = 
mg d1
d
(
2
cos q)
 =
F =
Substitute the value for F into the first-condition equations to solve for the compo-
nents of Ffulcrum.
Ffulcrum,x = F (sin q) = (2.0 × 104
N)(sin 20.0°)
Ffulcrum,x =
Ffulcrum,y = F (cos q) + mg = (2.0 × 104
N)(cos 20.0°) + (8.8 × 104
kg)(9.81 m/s2
)
Ffulcrum,y = 1.9 × 104
N + 8.6 × 105
N = 8.8 × 105
N
6.8 × 103
N
2.0 × 104
N
(8.8 × 103
kg)(9.81 m/s2
)(3.0 m)(cos 20.0°)

12 m
Givens Solutions
6. m1 = 3.6 × 102
kg
m2 = 6.0 × 102
kg
l = 15 m
l1 = 5.0 m
g = 9.81 m/s2
Apply the second condition of equilibrium, using the pool’s edge as the pivot point.
Assume the total mass of the board is concentrated at its center.
m1 g d − m2 g
− l1= 0
d = =
d = =
d = = 4.2 m from the pool’s edge
(6.0 × 102
kg)(2.5 m)

3.6 × 102
kg
(6.0 × 102
kg)(7.5 m − 5.0 m)

3.6 × 102
kg
(6.0 × 102
kg)

15
2
m
 − 5.0 m


3.6 × 102
kg
m2
2
l − l1


m1
m2 g

2
l − l1


m1 g
l

2
5. m1 = 64 kg
m2 = 27 kg
d1 = d2 = 
3.0
2
0 m
 = 1.50 m
Fn = 1.50 × 103
N
g = 9.81 m/s2
Apply the first condition of equilibrium to solve for Fapplied.
Fn − m1 g − m2 g − Fapplied = 0
Fapplied = Fn − m1 g − m2 g = 1.50 × 103
N − (64 kg)(9.81 m/s2
) − (27 kg)(9.81 m/s2
)
Fapplied = 1.50 × 103
N − 6.3 × 102
N − 2.6 × 103
N = 6.1 × 102
N
To solve for the lever arm for Fapplied, apply the second condition of equilibrium,
using the fulcrum as the pivot point.
Fapplied d + m2 g d2 − m1 g d1 = 0
d = 
m1 g d
F
1
ap
−
pl
m
ied
2 g d2
 =
d = =
d = 0.89 m from the fulcrum, on the same side as the less massive seal
5.4 × 102
N•m

6.1 × 102
N
9.4 × 102
N•m − 4.0 × 102
N•m

6.1 × 102
N
(64 kg)(9.81 m/s2
)(1.50 m) − (27 kg)(9.81 m/s2
)(1.50 m)

6.1 × 102
N
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Appendix J–8

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 7. m = 449 kg
l = 5.0 m
F1 = 2.70 × 103
N
g = 9.81 m/s2
Apply the first condition of equilibrium to solve for F2.
F1 + F2 − mg = 0
F2 = mg − F1
F2 = (449 kg)(9.81 m/s2
) − 2.70 × 103
N = 4.40 × 103
N − 2.70 × 103
N = 1.70 × 103
N
Apply the second condition of equilibrium, using the left end of the platform as the
pivot point.
F2 l − m g d = 0
d = =
d = 1.9 m from the platform’s left end
(1.70 × 103
N)(5.0 m)

(449 kg)(9.81 m/s2
)
F2 l

m g
Givens Solutions
8. m1 = 414 kg
l = 5.00 m
m2 = 40.0 kg
F1 = 50.0 N
g = 9.81 m/s2
Apply the first condition of equilibrium to solve for F2.
F1 + F2 − m1 g − m2 g = 0
F2 = m1 g + m2 g − F1 = (m1 + m2) g − F1
F2 = (414 kg + 40.0 kg)(9.81 m/s2
) − 50.0 N = (454 kg)(9.81 m/s2
) − 50.0 N = 4.45 ×
103
N − 50.0 N
F2 = 4.40 × 103
N
Apply the second condition of equilibrium, using the supported end (F1) of the stick
as the rotation axis.
F2 d − m1 g
− m2 g l = 0
d = =
d = =
d = 2.75 m from the supported end
(247 kg)(9.81 m/s2
)(5.00 m)

4.40 × 103
N
(207 kg + 40.0 kg)(9.81 m/s2
)(5.00 m)

4.40 × 103
N

414
2
kg
 + 40.0 kg
(9.81 m/s2
)(5.0 m)

4.40 × 103
N

m
2
1
 + m2g l

F2
l

2
1. R = 50.0 m
M = 1.20 × 106
kg
t = 1.0 × 109
N•m
a = 
t
I
 = 
M
t
R2
 =
a = 0.33 rad/s2
1.0 × 109
N•m

(1.20 × 106
kg)(50.02
)
Additional Practice H
2. M = 22 kg
R = 0.36 m
t = 5.7 N•m
a = 
t
I
 = 
M
t
R2
 =
a = 2.0 rad/s2
5.7 N•m

(22 kg)(0.36 m)2

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
3. M = 24 kg
l = 2.74 m
F = 1.8 N
The force is applied perpendicular to the lever arm, which is half the pencil’s length.
Therefore,
t = F d (sin q) = F

a = 
t
I
 = =
a = 0.16 rad/s2
(1.8 N)

2.7
2
4 m




1
1
2
 (24 kg)(2.74 m)2
F 
l
2



1
1
2
 M l 2
l

2
Givens Solutions
4. M = 4.07 × 105
kg
R = 5.0 m
t = 5.0 × 104
N•m
a = 
t
I
 =
a =
a = 9.8 × 10−3
rad/s2
(5.0 × 104
N•m)


1
2
(4.07 × 105 kg)(5.0 m)2
t


1
2
MR2
5. R = 2.00 m
F = 208 N
a = 3.20 × 10−2
rad/s2
The force is applied perpendicular to the lever arm, which is the ball’s radius.
Therefore,
t = F d (sin q) = F R
T = 
a
t
 = 
F
a
R
 =
I = 1.30 × 104
kg•m2
(208 N)(2.00 m)

3.20 × 10−2
rad/s2
6. r = 8.0 m
t = 7.3 × 103
N•m
a = 0.60 rad/s2
I = 
a
t
 = mr2
I = =
m = 
r
I
2
 = = 1.9 × 102
kg
1.2 × 104
kg•m2

(8.0 m)2
1.2 × 104
kg•m2
7.3 × 103
N•m

0.60 rad/s2
7. vt,i = 2.0 km/s
l = 15.0 cm
∆t = 80.0 s
t = −0.20 N•m
vt,f = 0 m/s
I = 
a
t
 = =

−0.20 N•m
I =

=
I = 6.0 × 10−4
kg•m2
0 m/s − 2.0 × 103
m/s


0.15
2
0 m

(80.0 s)
vt,f − vt,i


l
d
2
∆t
t


wf
∆
−
t
wi


t
−0.20 N•m

(0
−
.0
2
7
.0
5
×
m
1
)
0
(
3
80
m
.0
/s
s)


Appendix J–10

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
8. R = 
1.7
2
0 m
 = 0.85 m
t = 125 N•m
∆t = 2.0 s
wi = 0 rad/s
wf = 12 rad/s
I = 
a
t
 = MR2
I = 
a
t
 = = =
I =
M = 
R
I
2
 = = 29 kg
21 kg•m2

(0.85 m)2
21 kg•m2
125 N•m

6.0 rad/s2
125 N•m


12 rad/
2
s
.0
−
s
0 rad/s


t


wf
∆
−
t
wi


Givens Solutions
9. R = 3.00 m
M = 17 × 103
kg
wi = 0 rad/s
wf = 3.46 rad/s
∆t = 12 s
t = I a = 
1
2
 MR2

wf
∆
−
t
wi


t = = 2.2 × 104
N•m
(17 × 103
kg)(3.00 m)2
(3.46 rad/s − 0 rad/s)

(2)(12 s)
10. R = 4.0 m
M = 1.0 × 108
kg
wi = 0 rad/s
wf = 0.080 rad/s
∆t = 60.0 s
t = Ia = 
1
2
 MR2

wf
∆
−
t
wi


t = = 1.1 × 106
N•m
(1.0 × 108
kg)(4.0 m)2
(0.080 rad/s − 0 rad/s)

(2)(60.0 s)
11. I = 2.40 × 103
kg•m2
∆q = 2(2p rad) = 4p rad
∆t = 6.00 s
wi = 0 rad/s
∆q = wi ∆t + 
1
2
 a ∆t2
Because wi = 0,
∆q = 
1
2
 a∆t2
a = 
2
∆
∆
t2
q

t = Ia = 
2
∆
I
t
∆
2
q
 =
t = 1.68 × 103
N•m
(2)(2.40 × 103
kg•m2
)(4p rad)

(6.00 s)2
12. m = 7.0 × 103
kg
r = 18.3 m
at = 25 m/s2
t = Ia = (mr2
)
a
r
t
 = mrat
t = (7.0 × 103
kg)(18.3 m)(25 m/s2
)
t = 3.2 × 106
N•m

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. ri = 4.95 × 107
km
vi = 2.54 × 105
Km/h
vf = 1.81 × 105
km/h
Li = Lf
Iiwi = If wf
mri
2

v
ri
i

= mrf
2

v
rf
f


ri vi = rf vf
rf = 
ri
v
v
f
i
 =
rf = 6.95 × 107
km
(4.95 × 107
km)(2.54 × 105
km/h)

1.81 × 105
km/h
Additional Practice I
Givens Solutions
2. vi = 399 km/h
vf = 456 km/h
R = 0.20 m
∆q = 20 rev
Li = Lf
Ii wi = If wf
m ri
2

v
ri
i

= mrf
2

v
rf
f


ri vi = rf vf
rf = ri − ∆s = ri − R ∆q
ri vi = (ri − R ∆q) vf
ri (vf − vi) = (R ∆q) vf
ri = 
v
v
f
f
R
−
∆
v
q
i
 =
=
ri = 2.0 × 102
m
(456 km/h)(0.20 m)(20 rev)(2p rad/rev)

57 km/h
(456 km/h)(0.20 m)(20 rev)(2p rad/rev)

456 km/h − 399 km/h
3. M = 25.0 kg
R = 15.0 cm
wi = 4.70 × 10−3
rad/s
wf = 4.74 × 10−3
rad/s
Li = Lf
Ii wi = If wf
If = =

2
5
MR2
wi
If = = 0.223 kg•m2
Ii = 
2
5
 MR2
= 
2
5
 (25.0 kg)(0.150 m)2
= 0.225 kg•m2
∆I = If − Ii = 0.223 kg•m2
− 0.225 kg•m2
= −0.002 kg•m2
The moment of inertia decreases by 0.002 kg•m2
.
(2)(25.0 kg)(0.150 m)2
(4.70 × 10−3
rad/s)

(5)(4.74 × 10−3
rad/s)
wf
Ii wi

wf
Appendix J–12

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 4. vi = 395 km/h
ri = 1.20 × 102
m

∆
∆
r
t
 = 0.79 m/s
∆t = 33 s
rf = ri −

∆
∆
r
t

∆t
Li = Lf
Ii wi = Lf wf
mri
2

v
ri
i

= mrf
2

v
rf
f


ri vi = rf vf =
ri −

∆
∆
r
t

∆t
vf
vf = =
vf = =
vf = 5.0 × 102
km/h
(1.20 × 102
m)(395 km/h)

94 m
(1.20 × 102
m)(395 km/h)

1.20 × 102
m − 26 m
(1.20 × 102
m)(395 km/h)

1.20 × 102
− (0.79 m/s)(33 s)
ri vi

[ri −

∆
∆
r
t

∆t]
Givens Solutions
5. ri = 
10.
2
0 m
 = 5.00 m
rf = 
4.0
2
0 m
 = 2.00 m
wi = 1.26 rad/s
Li = Lf
Iiwi = Ifwf
mri
2
wi = mrf
2
wf
wf = 
ri
r
2
f
w
2
i
 =
wf = 7.88 rad/s
(5.00 m)2
(1.26 rad/s)

(2.00 m)2
6. R = 3.00 m
M = 1.68 × 104
kg
ri = 2.50 m
rf = 3.00 m
m = 2.00 × 102
kg
wi = 3.46 rad/s
Li = Lf
Iiwi = Ifwf

2
1
MR2
+ mri
2
wi = 
1
2
MR2
+ mrf
2
wf
wf =
wf =

2
1
(1.68 × 104
kg)(3.00 m)2
+ (2.00 × 102
kg)(2.50 m)2
(3.46 rad/s)

2

1
(1.68 × 104
kg)(3.00 m)2 + (2.00 × 102 kg)(3.00 m)2

wf =
wf =
wf = 3.43 rad/s
∆w = wf − wi = 3.43 rad/s − 3.46 rad/s = −0.03 rad/s
The angular speed decreases by 0.03 rad/s.
(7.68 × 104
kg•m2
)(3.46 rad/s)

7.74 × 104
kg•m2
(7.56 × 104
kg•m2
+ 1.25 × 103
kg•m2
)(3.46 rad/s)

7.56 × 104
kg•m2
+ 1.80 × 103
kg•m2

2
1
MR2
+ mri
2
wi


1
2
MR2
+ mrf
2


1. m = 407 kg
h = 57.0 m
vf = 12.4 m/s
wf = 28.0 rad/s
g = 9.81 m/s2
MEi = MEf
mgh = 
1
2
 mvf
2
+ 
1
2
 I wf
2

1
2
 I wf
2
= mgh − 
1
2
 mvf
2
I = 
2mgh
w
−
f
2
mvf
2
 = 
m(2g
w
h
f
2
− vf
2
)

I =
I = =
I = 5.0 × 102
kg•m2
(407 kg)(9.7 × 102
m2
/s2
)

(28.0 rad/s)2
(407 kg)(1.12 × 103
m2
/s2
− 154 m2
/s2
)

(28.0 rad/s)2
(407 kg)[(2)(9.81 m/s2
)(57.0 m) − (12.4 m/s)2
]

(28.0 rad/s)2
Givens Solutions
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Additonal Practice J
2. h = 5.0 m
g = 9.81 m/s2
MEi = MEf
mgh = 
1
2
mvf
2
+ 
2
1
Iwf
2
mgh = 
1
2
mvf
2
+ 
1
2
(mr2
)

v
r
f
2
2


mgh = mvf
2

1
2
 + 
1
2
 = mvf
2
vf =

gh
=

(9
.8
1
m
/s
2)
(5
.0
m
)

vf = the mass is not required
7.0 m/s
3. h = 1.2 m
g = 9.81 m/s2
MEi = MEf

1
2
mvi
2
+ 
1
2
Iwi
2
= mgh

2
1
mvi
2
+ 
1
2

1
2
mr2

v
r
i
2
2

= mgh
mvi
2

1
2
 + 
1
4
 = 
3
4
 mvi
2
= mgh
vi = 
4
3
g
h

= = 4.0 m/s
(4)(9.81 m/s2
)(1.2 m)

3
4. vf = 12.0 m/s
I = 0.80mr2
g = 9.81 m/s2
MEi = MEf
mgh = 
2
1
mvf
2
+ 
2
1
Iwf
2
= 
2
1
mvf
2
+ 
2
1
(0.80 mr2
)

v
r
f


2
mgh = mvf
2

2
1
 + 
0.
2
80

= 0.90 mvf
2
h = 
0.90
g
vf
2
 = 
(0.9
9
0
.
)
8
(
1
12
m
.0
/s
m
2
/s)2

h = 13 m
Appendix J–14

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 5. vi = 5.4 m/s
g = 9.81 m/s2
q = 30.0°
MEi = MEf

2
1
mvi
2
+ 
2
1
Iwi
2
= mgh = mgd(sin q)
mgd(sin q) = 
2
1
mvi
2
+ 
2
1


2
5
 mr2

v
r
i
2
2


mgd(sin q) = mvi
2

2
1
 +
1
5

= 
1
7
0
 mvi
2
d = 
10 g
7
(
v
si
i
n
2
q)
 = = 4.2 m
(7)(5.4 m/s)2

(10)(9.81 m/s2)(sin 30.0°)
Givens Solutions
6. r = 2.0 m
wf = 5.0 rad/s
g = 9.81 m/s2
m = 4.8 × 103
kg
MEi = MEf
mgh = 
2
1
mvf
2
+ 
2
1
Iwf
2
mgh = 
2
1
mr2
wf
2
+ 
2
1


2
5
 mr2
wf
2
mgh = mr2
wf
2

2
1
 +
1
5

= 
1
7
0
 mr2
wf
2
h = =
h =
KEtrans = 
2
1
mvf
2
= 
2
1
mr2
wf
2
KEtrans = 
2
1
(4.8 × 103
kg)(2.0 m)2
(5.0 rad/s)2
KEtrans = 2.4 × 105
J
7.1 m
(7)(2.0 m)2
(5.0 rad/s)2

(10)(9.81 m/s2)

1
7
0
r2
wf
2

g
7. m = 5.55 kg
h = 1.40 m
g = 9.81 m/s2
MEi = MEf
mgh = 
2
1
mvf
2
+ 
2
1
Iwf
2
mgh = 
2
1
mvf
2
+ 
2
1


2
5
 mr2

v
r
f
2
2


mgh = mvf
2

2
1
 +
1
5

= 
1
7
0
 mvf
2
vf = 
10
7
g
h

= = 4.43 m/s
KErot = 
2
1
Iwf
2
= 
5
1
mvf
2
KErot = = 21.8 J
(5.55 kg)(4.43 m/s)2

5
(10)(9.81 m/s2)(1.40 m)

7

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
1. P1 = (1 + 0.12)P2 = 1.12 P2
v1 = 0.60 m/s
v2 = 4.80 m/s
ρ = 1.00 × 103
kg/m3
h1 = h2
P1 + 
1
2
ρv1
2
+ ρgh1 = P2 + 
1
2
ρv2
2
+ ρgh2
h1 = h2, and P2 = 
1
P
.1
1
2
, so the equation simplifies to
P1 + 
1
2
ρv1
2
= 
1
P
.1
1
2
 + 
1
2
ρv2
2
P11 − 
1.
1
12

= 
1
2
ρ(v2
2
− v1
2
)
P1 = =
P1 =
P1 = = 1.06 × 105
Pa
(1.00 × 103
kg/m3
)(22.6 m2
/s2
)

(2)(0.107)
(1.00 × 103
kg/m3
)(23.0 m2
/s2
− 0.36 m2
/s2
)

(2)(1 − 0.893)
(1.00 × 103
kg/m3
)[(4.80 m/s)2
− (0.60 m/s)2
]
(2)
1 − 
1.
1
12


ρ(v2
2
− v1
2
)
(2)
1 − 
1.
1
12


Additional Practice K
Givens Solutions
2. r1 = 
4.1
2
0 m
 = 2.05 m
v1 = 3.0 m/s
r2 = 
2.7
2
0 m
 = 1.35 m
P2 = 82 kPa
ρ = 1.00 × 103
kg/m3
h1 = h2
A1v1 = A2v2
v2 = 
A
A
1v
2
1
 = 
π
π
r1
r
2
2
v
2
1
 = 
r1
r2
2
2
v1

v2 = = 6.9 m/s
P1 + 
1
2
rv1
2
+ ρgh1 = P2 + 
1
2
rv2
2
+ ρgh2
h1 = h2, so the equation simplifies to
P1 + 
2
1
rv1
2
= P2 + 
2
1
rv2
2
P1 = P2 + 
2
1
r(v2
2
− v1
2
)
P1 = 82 × 103
Pa + 
2
1
(1.00 × 103
kg/m3
)[(6.9 m/s)2
− (3.0 m/s)2
]
P1 = 82 × 103
Pa + 
2
1
(1.00 × 103
kg/m3
)(48 m2
/s2
− 9.0 m2
s2
)
P1 = 82 × 103
Pa + 
2
1
(1.00 × 103
kg/m3
)(39 m2
/s2
)
P1 = 82 × 103
Pa + 2.0 × 104
Pa = 10.2 × 104
Pa = 102 kPa
(2.05 m)2
(3.0 m/s)

(1.35 m)2
3. h2 − h1 = 
1
2
 h
∆x = 19.7 m
To find the horizontal speed of the cider, recall that for a projectile with no initial
vertical speed,
∆x = v∆t
∆y = − 
1
2
g ∆t2
= − 
1
2
h
∆t = 
h
g


v = 
∆
∆
x
t
 = = 
g
∆
h
x2


P1 + 
1
2
 ρv1
2
+ ρgh1 = P2 + 
1
2
 ρv2
2
+ ρgh2
∆x


h
g


Appendix J–16

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. Assuming the vat is open to the atmosphere, P1 = P2.
Also assume v2 ≈ 0. Therefore, the equation simplifies to

1
2
 ρv1
2
+ ρgh1 = ρgh2

1
2
 v1
2
= 
1
2


g
∆
h
x2


2
= g(h2 − h1) = g
1
2
 h

g ∆
h
x2
 = gh
h2
= ∆x2
h = ∆x = 19.7 m
Givens Solutions
4. v1 = 59 m/s
g = 9.81 m/s2
P1 + 
2
1
rv1
2
+ rgh1 = P2 + 
2
1
rv2
2
+ rgh2
Assume v2 ≈ 0 and P1 = P2 = P0.

2
1
rv1
2
+ rgh1 = rgh2
h2 − h1 = 
v
2
1
g
2
 = 
(2)
(
(
5
9
9
.8
m
1
/
m
s)
/
2
s2)
 = 1.8 × 102
m
5. h2 − h1 = 66.0 m
g = 9.81 m/s2
P1 + 
2
1
rv1
2
+ rgh1 = P2 + 
2
1
rv2
2
+ rgh2

2
1
rv1
2
+ rgh1 = rgh2
v1 =

2g
(h
2
−
h
1)
=

(2
)(
9.
81
m
/s
2)
(6
6.
0
m
)
= 36.0 m/s
6. h2 − h1 = 3.00 × 102
m
g = 9.81 m/s2
P1 + 
2
1
rv1
2
+ rgh1 = P2 + 
2
1
rv2
2
+ rgh2

2
1
rv1
2
+ rgh1 = rgh2
v1 =

2g
(h
2
−
h
1)
=

(2
)(
9.
81
m
/s
2)
(3
.0
0
×
1
02
m
)
= 76.7 m/s
7. h2 − h1 = 6.0 m
g = 9.81 m/s2
P1 + 
2
1
rv1
2
+ rgh1 = P2 + 
2
1
rv2
2
+ rgh2

2
1
rv1
2
+ rgh1 = rgh2
v1 =

2g
(h
2
−
h
1)
=

(2
)(
9.
81
m
/s
2)
(6
.0
m
)
= 11 m/s

1. V = 3.4 × 105
m3
T = 280 K
N = 1.4 × 1030
atoms
kB = 1.38 × 10−23
J/K
PV = NkBT
P = 
Nk
V
BT
 =
P = 1.6 × 104
Pa
(1.4 × 1030
atoms)(1.38 × 10−23
J/K)(280 K)

3.4 × 105 m3
Additional Practice L
Givens Solutions
2. V = 1.0 × 10−3
m3
N = 1.2 × 1013
molecules
T = 300.0 K
kB = 1.38 × 10−23
J/K
PV = NkBT
P = 
Nk
V
BT
 =
P = 5.0 × 10−5
Pa
(1.2 × 1013
molecules)(1.38 × 10−23
J/K)(300.0 K)

1.0 × 10−3 m3
3. V = 3.3 × 106
m3
N = 1.5 × 1032
molecules
T = 360 K
kB = 1.38 × 10−23
J/K
P V = NkB T
P = 
Nk
V
B T
 =
P = 2.3 × 105
Pa
(1.5 × 1032
molecules)(1.38 × 10−23
J/K)(360 K)

3.3 × 106
m3
4. N = 1.00 × 1027
molecules
T = 2.70 × 102
K
P = 36.2 Pa
kB = 1.38 × 10−23
J/K
P V = NkB T
V = 
Nk
P
B T
 =
V = 1.03 × 105
m3
(1.00 × 1027
molecules)(1.38 × 10−23
J/K)(2.70 × 102
K)

36.2 Pa
5. V1 = 3.4 × 105
m2
T1 = 280 K
P1 = 1.6 × 104
Pa
T2 = 240 K
P2 = 1.7 × 104
Pa

P1
T
V
1
1
 = 
P
T
2 V
2
2

V2 = 
P1
P
V
2 T
1
1
T2
 =
V2 = 2.7 × 105
m3
(1.6 × 104
Pa)(3.4 × 105
m3
)(240 K)

(1.7 × 104
Pa)(280 K)
6. A = 2.50 × 102
m2
T = 3.00 × 102
K
P = 101 kPa
N = 4.34 × 1031
molecules
kB = 1.38 × 10−23
J/K
P V = NkB T
V = 
Nk
P
B T
 =
V =
V = lA
l = 
V
A
 = 
1
2
.
.
7
5
8
0
×
×
1
1
0
0
6
2
m
m
3
2
 = 7.12 × 103
m
1.78 × 106
m3
(4.34 × 1031
molecules)(1.38 × 10−23
J/K)(3.00 × 102
K)

101 × 103
Pa
II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Appendix J–18

II
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved. 7. V = 7.36 × 104
m3
P = 1.00 × 105
Pa
N = 1.63 × 1030
particles
kB = 1.38 × 10−23
J/K
PV = NkBT
T = 
N
P
k
V
B
 =
T = 327 K
(1.00 × 105
Pa)(7.36 × 104
m3
)

(1.63 × 1030
particles)(1.38 × 10−23
J/K)
Givens Solutions
8. l = 3053 m
A = 0.040 m2
N = 3.6 × 1027
molecules
P = 105 kPa
kB = 1.38 × 10−23
J/K
P V = NkBT
T = P 
N
V
kB
 = 
P
N
A
kB
l

T = = 260 K
(105 × 103
Pa)(0.040 m2
)(3053 m)

(3.6 × 1027
molecules)(1.38 × 10−23
J/K)
9. P1 = 2.50 × 106
Pa
T1 = 495 K
V1 = 3.00 m3
V2 = 57.0 m3
P2 = 1.01 × 105
Pa


P1
T
V
1
1
 = 
P
T
2 V
2
2

T2 = 
P2
P
V
1 V
2 T
1
1
 =
T2 =

P1
T
V
1
1
 = 
P
T
2 V
2
2
T2 = 
P2
P
V
1 V
2 T
1
1
 =
(1.01 × 105
Pa)(57.0 m3
)(495 K)

(2.50 × 106
Pa)(3.00 m3
)
3.80 × 102
K
(1.01 × 105
Pa)(57.0 m3
)(495 K)

(2.50 × 106
Pa)(3.00 m3
)
1. f = 833 Hz
D = 5.0 cm ⫽ 0.050 m
B = 8.0 × 10−2
T
maximum emf ⫽ 330 V
maximum emf = NABw = NAB(2pf )
A ⫽ pr2
⫽ p

D
2


2
⫽ p

0.05
2
m


2
⫽ 2.0 ⫻ 10⫺3
m2
N ⫽ 
ma
A
xi
B
m
(
u
2p
m
f)
emf
 ⫽
N = 4.0 × 102
turns
330 V

(2.0 ⫻ 10–3
m2
)(2p)(833 Hz)(8.0 ⫻ 10–2
T)
Additional Practice M
3. r = 
19.
2
3 m
 = 9.65 m
w = 0.52 rad/s
maximum emf = 2.5 V
N = 40 turns
maximum emf = NABw
B = 
ma
N
xi
(
m
p
u
r2
m
)w
emf

B =
B = 4.1 × 10−4
T
2.5 V

(40)(p)(9.65 m)2(0.52 rad/s)
2. w = 335 rad/s
maximum emf = 214 V
B = 8.00 × 10−2
T
A = 0.400 m2
maximum emf = NABw
N = 
maxim
AB
u
w
m emf

N =
N = 20.0 turns
214 V

(0.400 m2)(0.0800 T)(335 rad/s)

II
4. maximum emf =
8.00 × 103
V
N = 236
A = (6.90 m)2
w = 57.1 rad/s
maximum emf = NABw
B = 
maxi
N
m
A
u
w
m emf

B =
B = 1.25 × 10−2
T
8.00 × 103
V

(236)(6.90 m)2(57.1 rad/s)
Givens Solutions
Copyright
©
by
Holt,
Rinehart
and
Winston.
All
rights
reserved.
Appendix J–20
5. N = 1000 turns
A = 8.0 × 10−4
m2
B = 2.4 × 10−3
T
maximum emf = 3.0 V
maximum emf = NABw
w = 
maxim
NA
um
B
emf

w =
w = 1.6 × 103
rad/s
3.0 V

(1000)(8.0 × 10−4 m2)(2.4 × 10−3 T)
6. N = 640 turns
A = 0.127 m2
maximum emf =
24.6 × 103
V
B = 8.00 × 10−2
T
maximum emf = NABw
w = 
maxim
NA
um
B
emf

w =
w = 3.78 × 103
rad/s
24.6 × 103
V

(640)(0.127 m2)(8.00 × 10−2 T)
7. f = 1.0 × 103
Hz
B = 0.22 T
N = 250 turns
r = 12 × 10−2
m
maximum emf = NABw = NAB(2pf ) = N(pr3
)Bw = N(pr2
)B(2pf )
maximum emf = (250)(p)(12 × 10−2
m)2
(0.22 T)(2p)(1.0 × 103
Hz)
maximum emf = 1.6 × 104
V = 16 kV

physics_problem_workbooks.pdf.pdf

More Related Content

What's hot

Similar to physics_problem_workbooks.pdf.pdf

More from MervatMarji2

Recently uploaded

physics_problem_workbooks.pdf.pdf