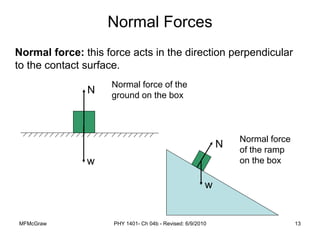
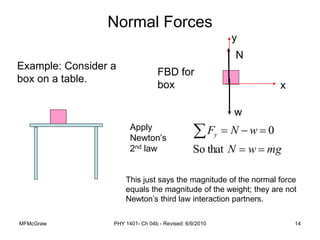
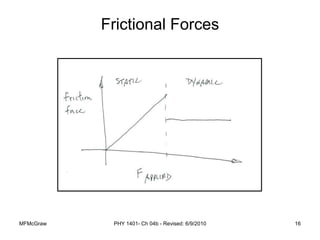
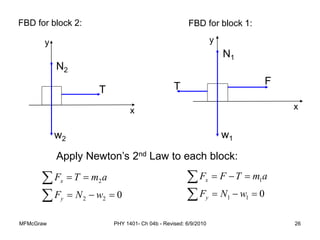
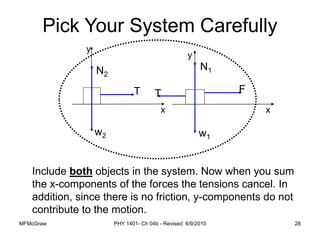
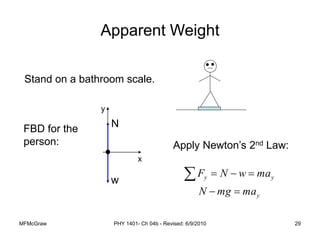
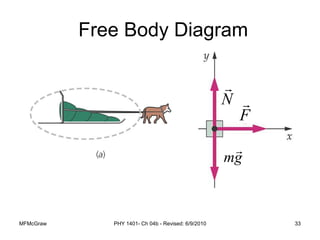
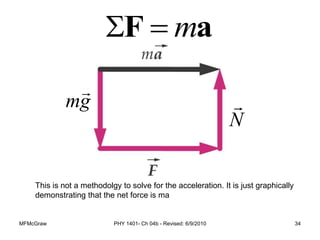
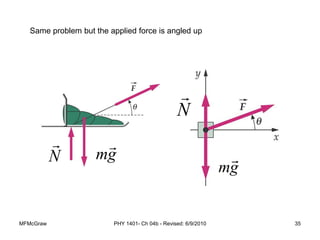
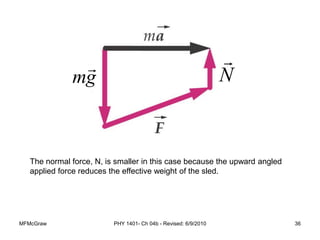
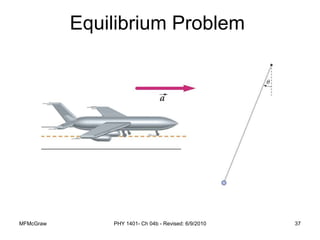
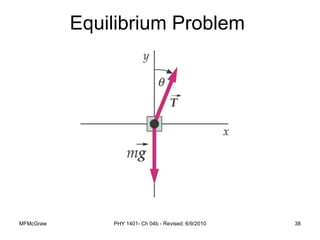
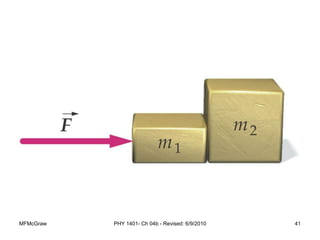
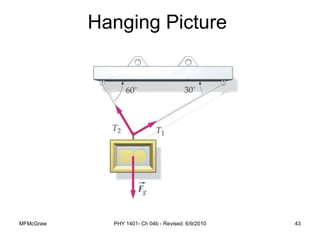
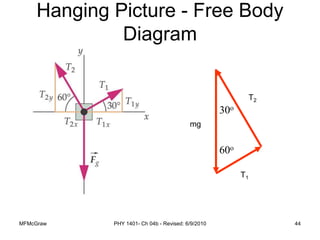
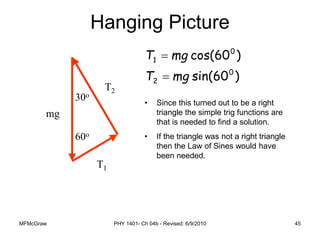
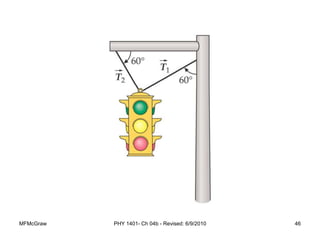
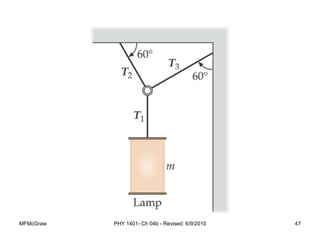
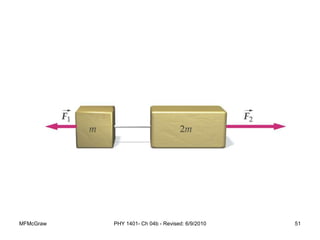
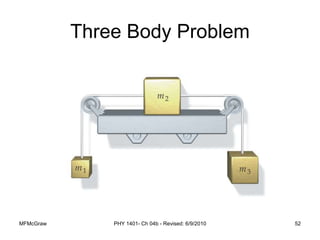
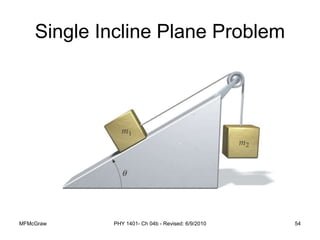
This document summarizes Newton's laws of motion and the different types of forces. It introduces Newton's three laws, including inertia, action-reaction pairs, and F=ma. Forces discussed include normal forces, friction, tension, and gravitational forces. It provides examples of applying free body diagrams and Newton's second law to solve mechanics problems. Key concepts are forces and Newton's laws, types of contact and other forces, and using physics equations to analyze motion.

1. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 1
Chapter 4
Forces and Newton’s Laws of Motion

2. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 2
Forces and Newton’s Laws of
Motion
• Forces
• Newton’s Three Laws of Motion
• The Gravitational Force
• Contact Forces (normal, friction, tension)
• Application of Newton’s Second Law
• Apparent Weight

3. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 3
The net force is the vector sum of all the forces acting
on a body.






 3
2
1
net F
F
F
F
F
Net Force
The net force is the resultant of this vector addition.
Bold letters represent vectors. The units of Force are Newtons, or
the abbreviation N, which represent the SI units: kg-m/s2

4. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 4
Free Body Diagrams
The free body diagram (FBD) is a simplified representation of an object, and the
forces acting on it. It is called free because the diagram will show the object without
its surroundings; i.e. the body is “free” of its environment.
We will consider only the forces acting on our object of interest. The object is
depicted as not connected to any other object – it is “free”. Label the forces
appropriately. Do not include the forces that this body exerts on any other body.
The best way to explain the free body diagram is to describe the steps required to
construct one. Follow the procedure given below.
(1) Isolate the body of interest. Draw a dotted circle around the object that
separates our object from its surroundings.
(2) Draw all external force vectors acting on that body.
(3) You may indicate the body’s assumed direction of motion. This does not
represent a separate force acting on the body.
(4) Choose a convenient coordinate system.

5. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 5
Free Body Diagram
T F
w1
N1
x
y
The force directions are as
indicated in the diagram.
The magnitudes should be
in proportion if possible.

6. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 6
Newton’s First Law of Motion:
Inertia and Equilibrium
Newton’s 1st Law (The Law of Inertia):
If no force acts on an object, then the speed and
direction of itsmotion do not change.
Inertia is a measure of an object’s resistance to
changes in its motion.
It is represented by the inertial mass.

7. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 7
If the object is at rest, it remains at rest (velocity = 0).
If the object is in motion, it continues to move in a
straight line with the same velocity.
No force is required to keep a body in straight line
motion when effects such as friction are negligible.
An object is in translational equilibrium if the net
force on it is zero and vice versa.
Newton’s First Law of Motion
Translational Equilibrium

8. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 8
Newton’s Second Law of Motion
Net Force, Mass, and Acceleration
Newton’s 2nd Law:
The acceleration of a body is directly proportional to
the net force acting on the body and inversely
proportional to the body’s mass.
Mathematically: a
F
F
a m
m

 net
net
or
This is the workhorse of mechanics

9. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 9
An object’s mass is a measure of its inertia. The
more mass, the more force is required to obtain a
given acceleration.
The net force is just the vector sum of all of the
forces acting on the body, often written as F.
Newton’s Second Law of Motion
If a = 0, then F = 0. This body can have:
Velocity = 0 which is called static equilibrium, or
Velocity  0, but constant, which is called dynamic
equilibrium.

10. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 10
Newton’s Third Law of Motion
Interaction Pairs
Newton’s 3rd Law:
When 2 bodies interact, the forces on the bodies,
due to each other, are always equal in magnitude
and opposite in direction.
In other words, forces come in pairs.
Mathematically: .
12
21 F
F 

designates the force on object 2 due to object 1.

11. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 11
Types of Forces
Contact forces: Normal Force & Friction
Tension
Gravitational Force

12. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 12
Contact Forces
Contact forces: these are forces that arise due
to of an interaction between the atoms in the
surfaces of the bodies in contact.

13. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 13
Normal force: this force acts in the direction perpendicular
to the contact surface.
Normal force
of the ramp
on the box
N
w
Normal force of the
ground on the box
N
w
Normal Forces

14. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 14
Example: Consider a
box on a table.
FBD for
box
mg
w
N
w
N
Fy






that
So
0
This just says the magnitude of the normal force
equals the magnitude of the weight; they are not
Newton’s third law interaction partners.
Apply
Newton’s
2nd law
N
w
x
y
Normal Forces

15. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 15
Friction: a contact force parallel to the contact surfaces.
Static friction acts to prevent objects from sliding.
Kinetic friction acts to make sliding objects slow down. Sometimes
called Dynamic friction.
Frictional Forces
max
s s
f = μ N
d d
f = μ N

16. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 16
Frictional Forces

17. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 17
Tension
An ideal cord has zero mass, does not stretch,
and the tension is the same throughout the cord.
This is the force transmitted through a “rope”
from one end to the other.

18. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 18
Example (text problem 4.77): A pulley is hung from the ceiling by a rope.
A block of mass M is suspended by another rope that passes over the
pulley and is attached to the wall. The rope fastened to the wall makes a
right angle with the wall. Neglect the masses of the rope and the pulley.
Find the tension in the rope from which the pulley hangs and the angle .
FBD for the
mass M
w
T
x
y
Mg
w
T
w
T
Fy





 0
Apply Newton’s 2nd
Law to the mass M.

19. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 19
FBD for the pulley:
0
sin
0
cos








T
F
F
T
F
F
y
x


Apply Newton’s 2nd Law:

 sin
cos F
F
T 

This statement is true
only when  = 45 and
Mg
T
F 2
2 

Example continued:
x
y
T
F

T

20. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 20
Gravitational Forces
2
2
1
r
M
GM
F 
Gravity is the force between two masses. Gravity is a
long-range force. No contact is needed between the
bodies. The force of gravity is always attractive!
r is the distance between the two masses
M1 and M2 and G = 6.671011 Nm2/kg2.
M2
r
M1
F21 F12
.
12
21 F
F 


21. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 21
Let M1 = ME = mass of the Earth. 2
2
M
r
GM
F E







Here F = the force the Earth exerts on mass M2. This is the
force known as weight, w.
.
2
2
2
gM
M
r
GM
w
E
E










2
2
m/s
8
.
9
N/kg
8
.
9
where 


E
E
r
GM
g
Near the surface of
the Earth
km
6400
kg
10
98
.
5
E
24
E



r
M
Gravitational Forces

22. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 22
What is the direction of g?
Note that
m
F
g 
is the gravitational force per unit mass. This is called
the gravitational field strength. It is also referred to as
the acceleration due to gravity.
What is the direction of w?
Gravitational Forces

23. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 23
Example: What is the weight of a 100 kg astronaut on the
surface of the Earth (force of the Earth on the astronaut)?
How about in low Earth orbit? This is an orbit about 300
km above the surface of the Earth.
On Earth: N
980

 mg
w
In low Earth orbit:
 
N
890
)
( 2












h
R
GM
m
r
mg
w
E
E
o
The weight is reduced by about 10%.
The astronaut is NOT weightless!
Gravitational Forces

24. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 24
Applying Newton’s Second Law
a
F m


The one equation everyone remembers!
This equation is just the tip of the “iceberg” of the mechanics
problem. The student will need to anlyze the forces in the
problem and sum the force vector components to build the
left hand side of the equation.
Sumof the forces
acting on the objects
in the system
“m” is the
System
Mass
“a” is the
System
Response

25. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 25
Example: A force of 10.0 N is applied to the right on block 1.
Assume a frictionless surface. The masses are m1 = 3.00 kg
and m2 = 1.00 kg.
Find the tension in the cord connecting the two blocks as
shown.
F
block 2 block 1
Assume that the rope stays taut so that both blocks
have the same acceleration.
Applying Newton’s Second Law

26. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 26
FBD for block 2:
T F
w1
N1
x
y
x
T
w2
N2
y
FBD for block 1:
0
1
1
1








w
N
F
a
m
T
F
F
y
x
0
2
2
2







w
N
F
a
m
T
F
y
x
Apply Newton’s 2nd Law to each block:

27. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 27
a
m
T
F 1


a
m
T 2

To solve for T, a must be eliminated. Solve for a in (2)
and substitute in (1).
(1)
(2)
Example continued:
These two equations contain
the unknowns: a and T.
N
5
.
2
kg
1
kg
3
1
N
10
1
1
2
1
2
1
2
1
2
1
1




















































m
m
F
T
T
m
m
T
m
T
m
F
m
T
m
a
m
T
F

28. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 28
Pick Your System Carefully
x
T
w2
N2
y
T F
w1
N1
x
y
Include both objects in the system. Now when you sum
the x-components of the forces the tensions cancel. In
addition, since there is no friction, y-components do not
contribute to the motion.

29. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 29
Apparent Weight
Stand on a bathroom scale.
FBD for the
person: Apply Newton’s 2nd Law:
y
y
y
ma
mg
N
ma
w
N
F






w
N
x
y

30. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 30
The normal force is the force the scale exerts on you. By
Newton’s 3rd Law this is also the force (magnitude only)
you exert on the scale. A scale will read the normal force.
 
y
a
g
m
N 
 is what the scale reads.
When ay = 0, N = mg. The scale reads your true weight.
When ay  0, N > mg or N < mg.
Apparent Weight
In free fall ay = -g and N = 0. The person is weightless.

31. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 31
Example (text problem 4.128):
A woman of mass 51 kg is standing in an elevator. The elevator
pushes up on her feet with 408 newtons of force.
What is the acceleration of the elevator?
FBD for
woman:
y
y
y
ma
mg
N
ma
w
N
F






Apply Newton’s 2nd Law: (1)
w
N
x
y
Apparent Weight

32. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 32
Solving (1) for ay:
2
m/s
8
.
1




m
mg
N
ay
The elevator could be (1) traveling upward with decreasing
speed, or (2) traveling downward with increasing speed.
The change in velocity is DOWNWARD.
Given: N = 408 newtons, m = 51 kg, g = 9.8 m/s2
Unknown: ay
Example continued:
Apparent Weight

33. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 33
N
mg
F
Free Body Diagram

34. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 34
N
mg
a
F m


This is not a methodolgy to solve for the acceleration. It is just graphically
demonstrating that the net force is ma

35. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 35
N mg
mg
N
Same problem but the applied force is angled up

36. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 36
mg N
The normal force, N, is smaller in this case because the upward angled
applied force reduces the effective weight of the sled.

37. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 37
Equilibrium Problem

38. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 38
Equilibrium Problem

39. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 39
Equilibrium Problem
This is an example of three-vector equilibrium problem. It lends itself
to a simple solution because the vector sum of the three vectors
closes on itself (equilibrium) and forms a triangle

40. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 40
Milk Carton
Max static friction force
Non-slip limit on applied force

41. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 41

42. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 42
Hanging Problems

43. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 43
Hanging Picture

44. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 44
Hanging Picture - Free Body
Diagram
T1
mg
60o
30o
T2

45. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 45
Hanging Picture
T1
mg
60o
30o
T2
0
1
0
2
cos(60 )
sin(60 )
T mg
T mg


• Since this turned out to be a right
triangle the simple trig functions are
that is needed to find a solution.
• If the triangle was not a right triangle
then the Law of Sines would have
been needed.

46. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 46

47. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 47

48. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 48
Atwood Machine and
Variations

49. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 49
Atwood’s Machine

50. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 50
A 2-Pulley Atwood Machine

51. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 51

52. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 52
Three Body Problem

53. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 53
Incline Plane Problems

54. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 54
Single Incline Plane Problem

55. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 55
Double Incline Plane Problem

56. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 56
Force Summary
Friction
Opposes motion
Proportional to normal
force
Non-conservative
Static & dynamic
Normal Forces
Perpendicular to surface
at point of contact.
Magnitude needed to
maintain equilibrium
Tension
No mass
No stretching
Pulleys
Massless
No friction (bearing)
Tension in rope
continuously changes
direction

57. MFMcGraw PHY 1401- Ch 04b - Revised: 6/9/2010 57
Summary
• Newton’s Three Laws of Motion
• Drawing free body diagrams
• Contact forces versus long-range forces
• Different forces (gravity, friction, normal, tension,
air resistance)
• Application of Newton’s Second Law