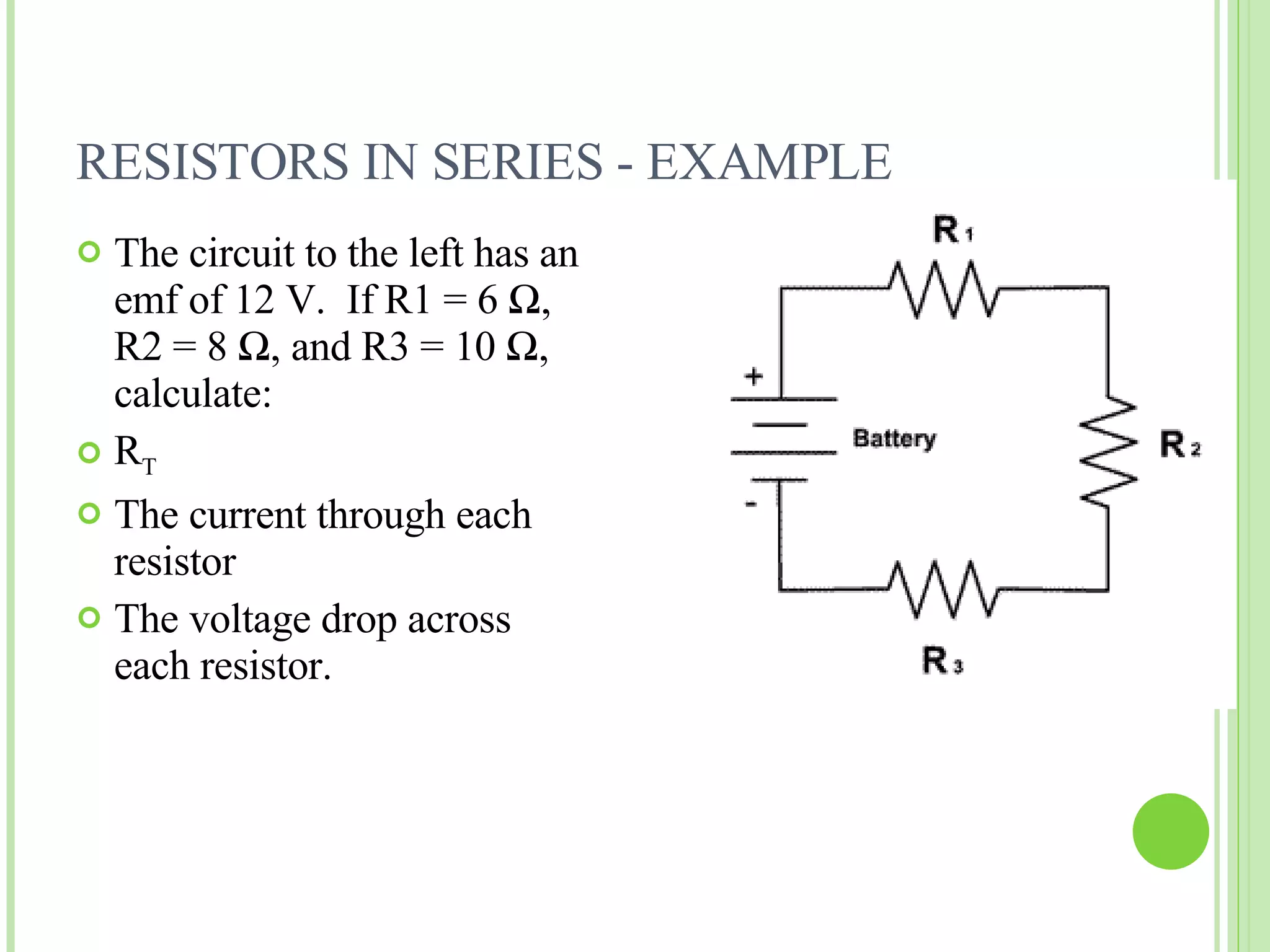
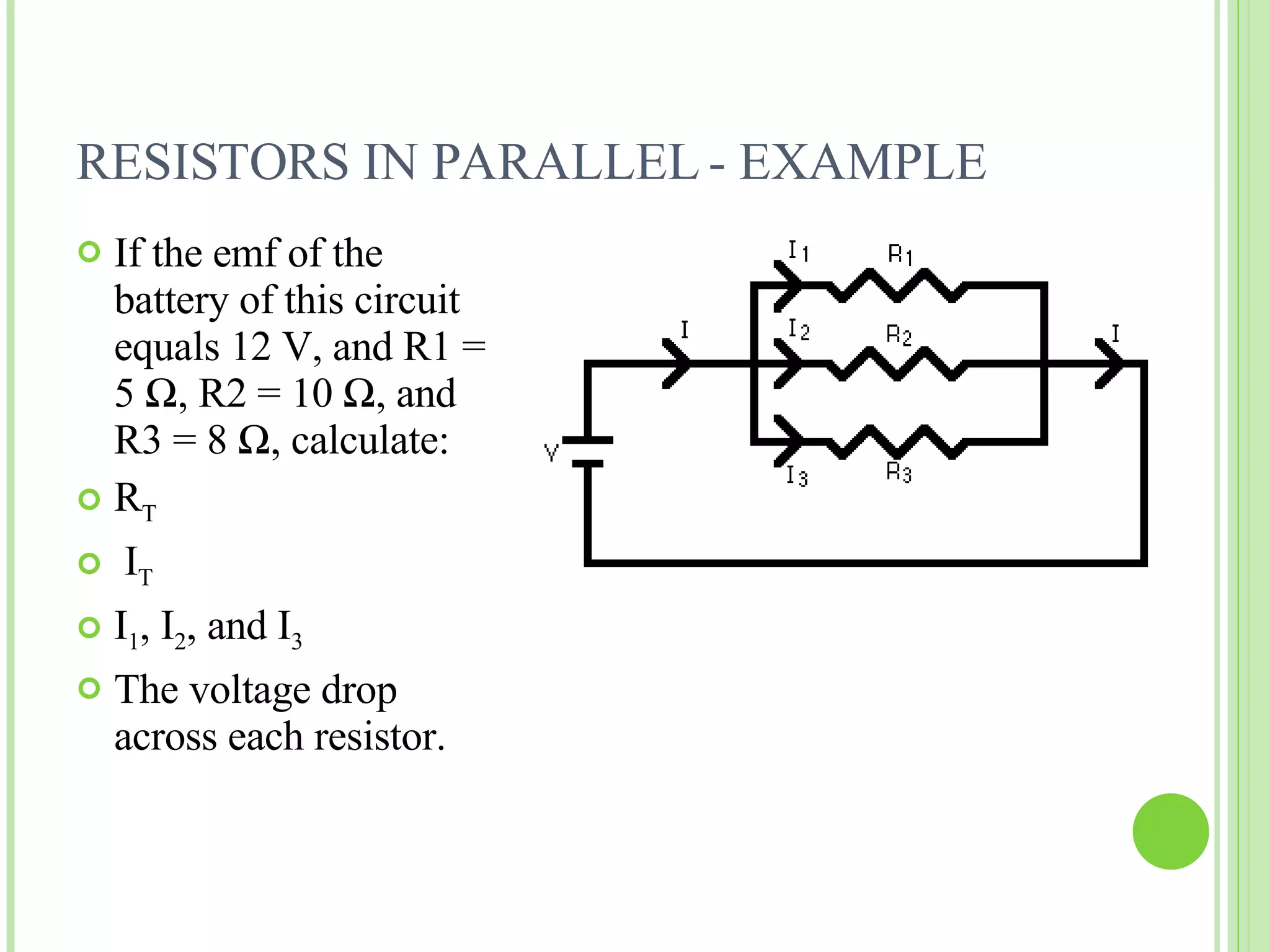
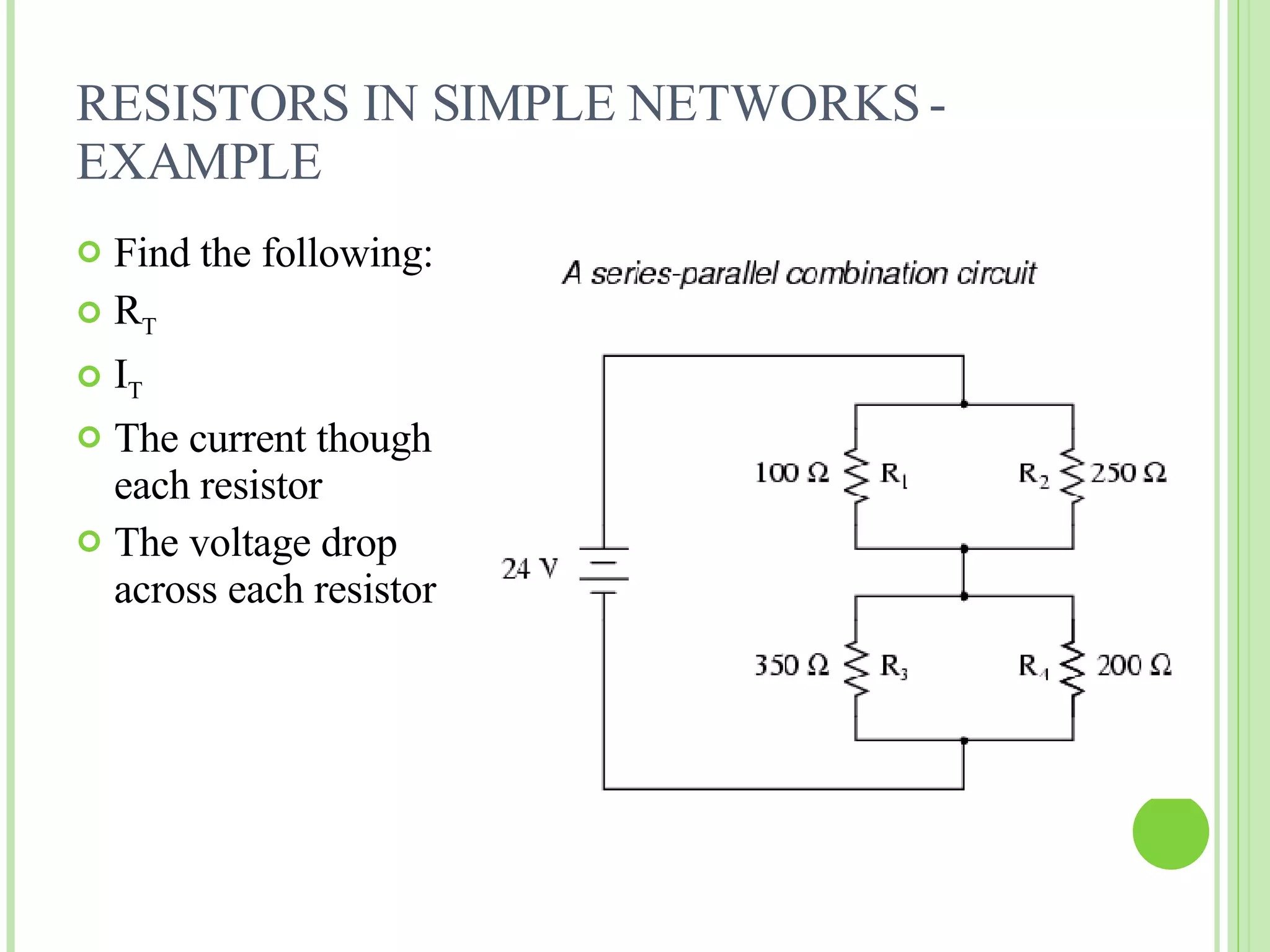
The document discusses resistors in series, parallel, and simple networks. It provides the cardinal rules for series and parallel circuits, including that the total resistance in a series circuit equals the sum of individual resistances, and the total current in a parallel circuit equals the sum of branch currents. Examples are given of calculating total resistance, current, and voltage drops in series and parallel circuits. Kirchhoff's laws of voltage and current are also summarized.

1. RESISTORS IN SERIES, PARALLEL, AND SIMPLE NETWORKS Physics II

2. RESISTORS IN SERIES Series – components arranged to provide a single conducting path for current Cardinal Rules for a Series Circuit: The current in all parts of a series circuit has the same magnitude. The sum of all the separate drops in potential around a series circuit is equal to the applied emf. The total resistance in a series circuit is equal to the sum of all the separate resistances.

3. RESISTORS IN SERIES - EXAMPLE The circuit to the left has an emf of 12 V. If R1 = 6 Ω , R2 = 8 Ω , and R3 = 10 Ω , calculate: R T The current through each resistor The voltage drop across each resistor.

4. RESISTORS IN SERIES Notice again, the sum of the voltage drops across the circuit is equal to the emf of the circuit. In other words, there is 12 V of potential, and that drops to zero when you reach the battery again. Gustav Kirchhoff stated this in another way in his 2 nd Law – the algebraic sum of all the changes in potential occurring around the complete circuit is equal to zero . In other words, Energy is conserved!

5. RESISTANCES IN PARALLEL Parallel – a circuit in which two or more components are connected across two common points in the circuit to provide separate conducing paths. Cardinal Rules of Parallel Circuits: The total current in a parallel circuit is equal to the sum of the currents in the separate branches. The potential difference across all branches of a parallel circuit must have the same magnitude The reciprocal of the total resistance is equal to the sum of the reciprocals of the separate resistances in parallel.

6. RESISTORS IN PARALLEL - EXAMPLE If the emf of the battery of this circuit equals 12 V, and R1 = 5 Ω , R2 = 10 Ω , and R3 = 8 Ω , calculate: R T I T I 1 , I 2 , and I 3 The voltage drop across each resistor.

7. RESISTANCES IN PARALLEL Notice again that the current into the juncture is equal to the currents in each branch. In other words, Kirchhoff’s 1 st Law applies to parallel circuits: the algebraic sum of the currents at any circuit juncture is equal to zero. In other words, charge is conserved!

8. RESISTORS IN SIMPLE NETWORKS Practical circuits are more complicated than these simple examples – you have combinations of series and parallel resistors, and might have different sources of emfs. A complex network needs to be reduced stepwise to a simple equivalent resistance. To do this, you want to separate different parts of the circuit!

9. RESISTORS IN SIMPLE NETWORKS - EXAMPLE Find the following: R T I T The current though each resistor The voltage drop across each resistor

10. THE LAWS OF RESISTANCE In the case of pure metals and most metallic alloys, the resistance of the material is proportional to the temperature. The resistance of a uniform conductor is proportional to the length of the conductor. (in cm) The resistance of a uniform conductor is inversely proportional to its cross-sectional area. (usually in square cm) The resistance of a given conductor depends on the material of which it is made. A given material has a constant associated with its resistance – the constant is called resistivity constant ,  and usually has the units of Ω -cm.