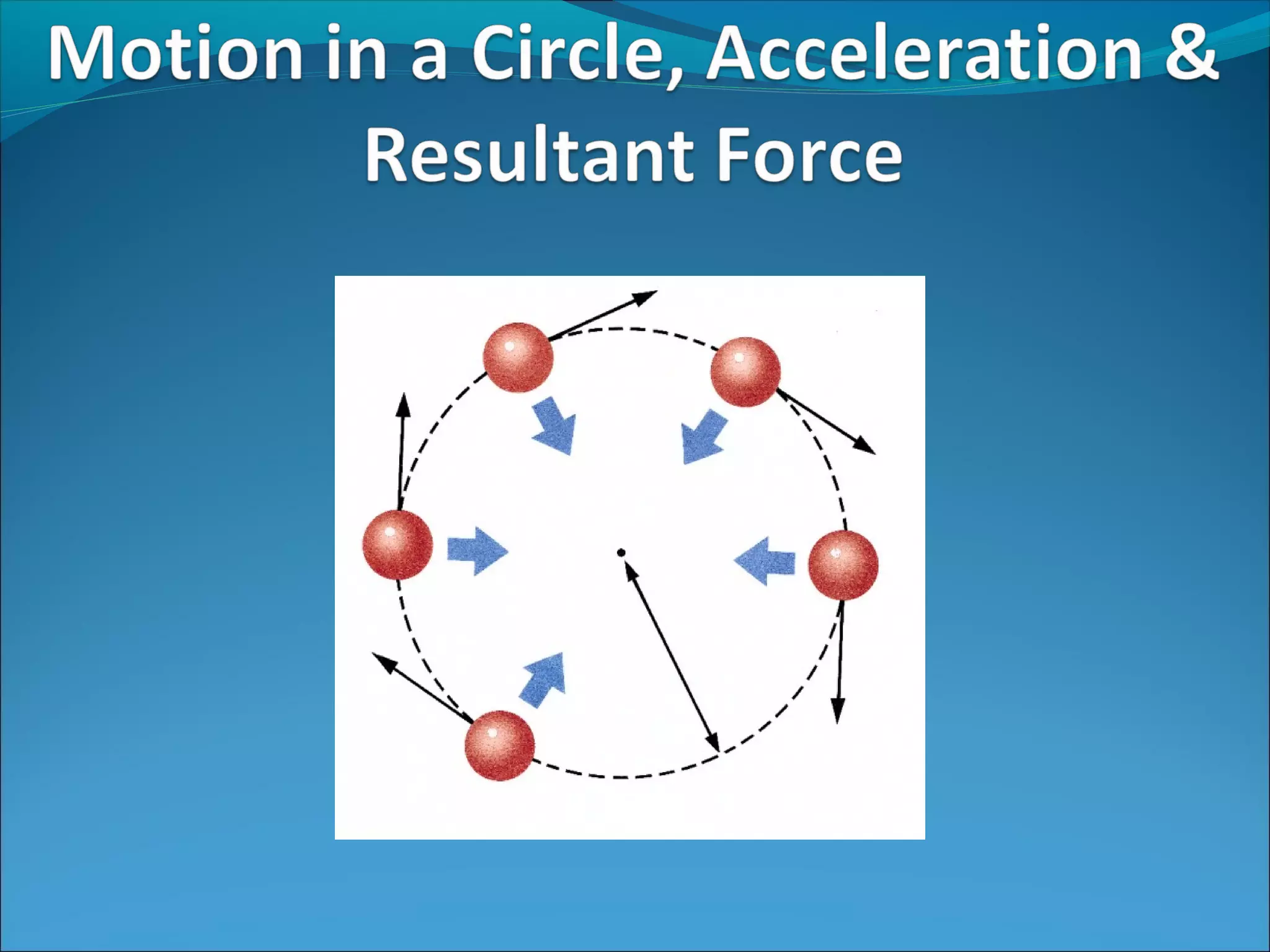
1. The document defines key terms related to circular motion such as speed, velocity, acceleration, and resultant force. 2. It derives equations for acceleration (a = v2/r and a = rω2) and resultant force (ΣF = mv2/r or ΣF = mω2r) for an object moving in circular motion with constant speed. 3. Examples are provided to demonstrate how to use the equations to calculate speed, acceleration, and force for real-world circular motion scenarios.

2. 1.
To consider speed & velocity around a circle
2.
To consider acceleration as a change in
velocity
3.
To define an equation for acceleration when
an object moves in a circular path
4.
To define an equation for resultant force
when an object moves in a circular path

3. Velocity v
n
atio
er
cel
ac
If an object is moving in a circle
with a constant linear speed, its
velocity is constantly changing....
Because the direction is
constantly changing....
If the velocity is constantly
changing then by definition the
object is accelerating
If the object is accelerating, then
an unbalanced force must exist

4. Velocity vB
B
δθ
C
δv
Velocity vB δθ
Consider an object moving
in circular motion with a
speed v which moves from
Velocity v
point A to point B in δ t
A
seconds
(From speed=distance / time),
the distance moved along the arc
AB, δ s is vδ t
Velocity vA
A
The vector diagram shows
the change in velocity δ v :
(vB – vA)

5. The triangles ABC & the
vector diagram are similar
Velocity vB
B
δθ
C
Velocity vA
A
Substituting for δs = vδt
δv
Velocity vB δθ
If δθ is small, then δv / v = δs / r
δv / v = vδt / r
Velocity vA
(a = change in velocity / time)
a = δ v / δ t = v2 / r

6. We can substitute for angular velocity....
a = v2 / r
From the last lesson we saw that:
v = rω
a = (rω)2 / r (substituting for v into above)
a = rω 2

7. Velocity v
n
atio
er
cel
ac
We have seen already that
any object travelling in a
circular path is accelerating
towards the centre of this
circular path.
This means that the
resultant force is also
pointing to the centre!
(ΣF = ma)

8. Velocity v
But we know more….
We have learnt two things
about the acceleration
n
atio
er
cel
ac
a = v2 / r
(1)
and
a = rω 2
(2)
YOUR TASK: Substitute the two equations (1) and (2)
in Newton’s second law (ΣF = ma) and find the
magnitude

9. You should have found out
that the magnitude of the
resultant force is:
Velocity v
n
atio
er
cel
ac
ΣF = mv2 / r
or
ΣF = mω 2r

10. So, for any object of
•mass m that travels at
•linear speed v, moving in a circle of
•Radius r,
We know the following about the
resultant force ΣF acting on it:
•Direction: pointing towards the centre
•Magnitude: ΣF = mv2 / r = mω 2r

11. satellite
Gravity
Planet

12. String
∑F = FT
The point
of support

13. ∑F= F
friction

14. The wheel of the London Eye has a diameter of
130 m and takes 30 min for 1 revolution.
Calculate:
a. The linear speed of the capsule
b. The linear acceleration
c. The resultant force acting on a person with a
mass of 65 kg

15. The linear speed of the capsule :
Using v = rω
we know that we do a full revolution (2π rad)
in 30mins (1800s)
v = (130/2) x (2π / 1800)
v = 0.23 ms-1

16. The linear acceleration:
Using a = v2 / r
a = (0.23)2 / (130/2)
a = 7.92 x 10-4 ms-2
The resultant force:
Using ΣF = ma
ΣF = 65 x 7.92 x 10-4
ΣF = 0.051 N

17. An object of mass 0.150 kg moves around a
circular path which has a radius of 0.420 m once
every 5.00 s at a steady rate. Calculate:
a. The speed and acceleration of the object
b. The resultant force on the object
[.528 ms-1, 0.663ms-2, 0.100N]