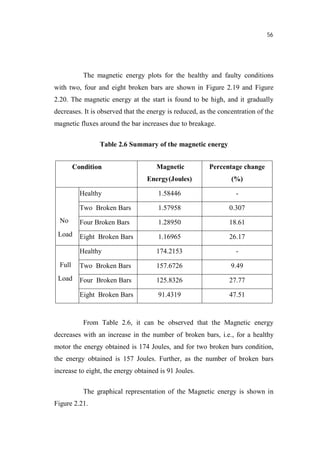
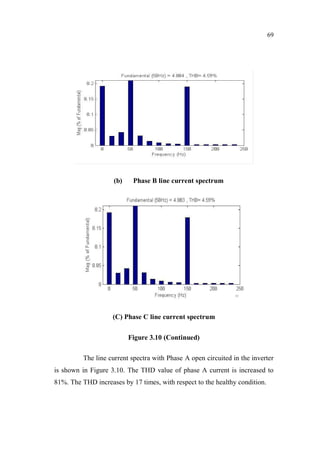
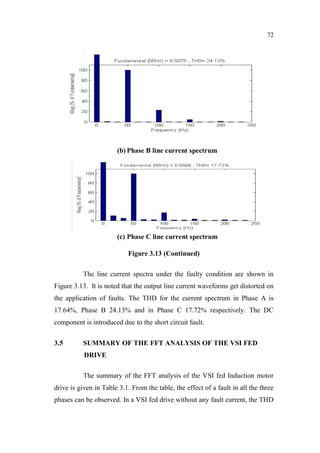
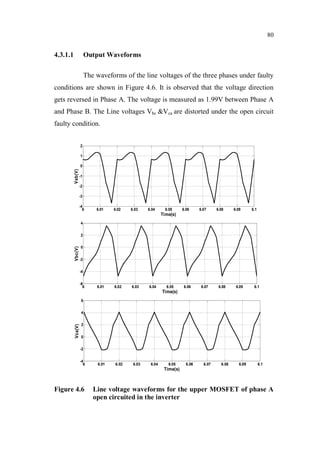
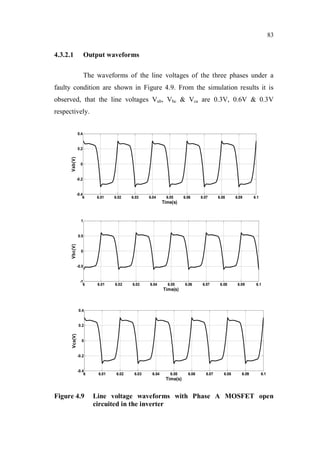
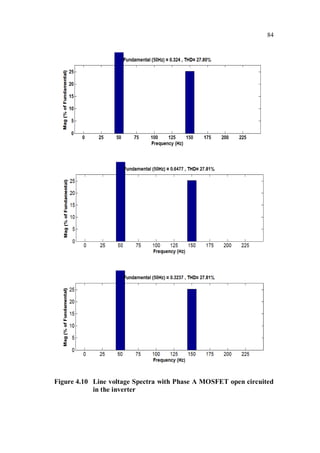
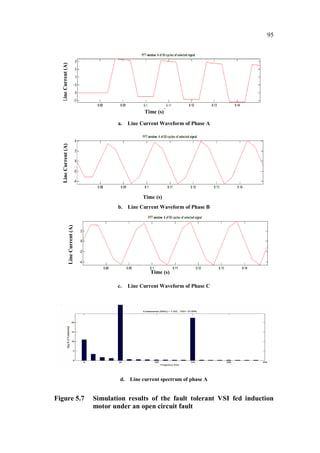
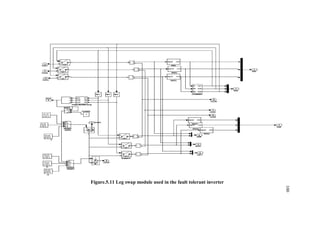
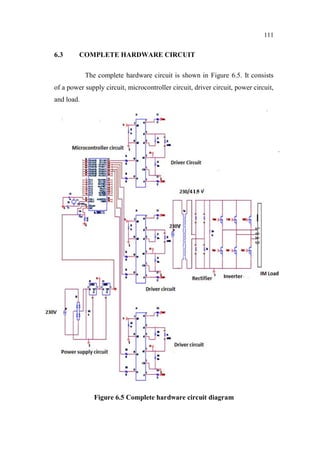
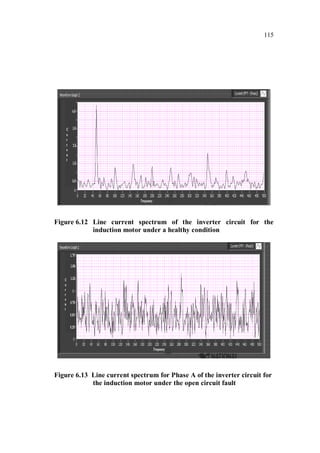
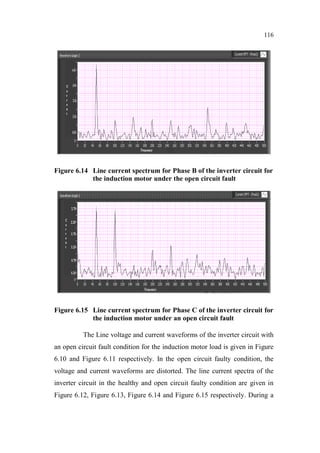
This document is a thesis submitted by Nagarajan S. for the degree of Doctor of Philosophy at Anna University, Chennai, India in November 2013. The thesis investigates fault detection of inverter-fed three-phase squirrel cage induction motors using finite element analysis. It models an induction motor using finite element software and analyzes parameters like flux density and magnetic energy under healthy and faulty rotor bar conditions. It also analyzes faults in voltage source inverters and current source inverters feeding induction motor drives. Finally, it proposes a fault tolerant voltage source inverter to overcome inverter faults.

1. INVESTIGATIONS ON FAULT DETECTION OF
INVERTER FED THREE PHASE SQUIRREL
CAGE INDUCTION MOTOR
A THESIS
Submitted by
NAGARAJAN S
in partial fulfilment for the requirement of award of the degree
of
DOCTOR OF PHILOSOPHY
FACULTY OF ELECTRICAL ENGINEERING
ANNA UNIVERSITY
CHENNAI 600 025
NOVEMBER 2013

2. ii
ANNA UNIVERSITY
CHENNAI 600 025
BONA FIDE CERTIFICATE
Certified that this Thesis titled “INVESTIGATIONS ON FAULT
DETECTION OF INVERTER FED THREE PHASE SQUIRREL CAGE
INDUCTION MOTOR” is the bona fide work of Mr.NAGARAJAN. S.
who carried out the research under my supervision. Certified Further, that to
the best of my knowledge the work reported herein does not form part of any
other thesis or dissertation on the basis of which a degree or award was
conferred on an earlier occasion on this or any other scholar.
Place : Chennai Dr. S. RAMAREDDY
Date: SUPERVISOR
Professor,
Department of Electrical and Electronics
Engineering,
Jerusalem college of engineering,
Pallikaranai,
Chennai-600100.
27-11-2013

3. iii
ABSTRACT
The induction Motor has been regarded as a workhorse in industrial
applications for many years. In the last few decades, the induction motor has
evolved from being a constant speed motor to a variable speed and variable
torque machine. When the application requires large power and torque
specifications, the usage of the induction motor comes into demand. This
results in the requirement of an efficient machine, which is stable during fault
conditions. The various faults that occur in induction motors are, rotor broken
bar, stator inter-turn fault, bearing fault and eccentricity fault. Out of these,
the rotor broken bar fault is very specific in squirrel cage induction machines.
The interior faults of the induction motor account for more than 70% of the
induction motor failures. Conventional methods make use of the test
machines; however, the machine has to be damaged to complete the
experiments of interior faults. Interior faults include the stator and rotor faults
of induction motors. Rotor faults are related to broken bars. Rotor failures are
caused by a combination of various stresses that act on the rotor. These
stresses are identified as electromagnetic, thermal, dynamic, environmental,
and mechanical. These lead to low frequency torque harmonics, which
increase noise and vibration. Hence, the detection of a broken bar fault is
essential for the protection of the induction motor against failures and
permanent damages.

4. iv
The Finite Element Method (FEM) is a general technique, for
numerical solution of the integral or differential equations governing the
behavior of systems. The finite element software accurately calculates
magnetic fields and related motor design parameters, for motors of
complicated geometry with saturation and/or permanent magnets, with
significant armature reaction and with or without eddy currents. The finite
element method saves the cost of the machines and the possibility of
improving the design during the planning stage. The finite element method is
distinguished from finite difference equations in determining the shapes that
the discrete steps can take. The magnet is the most advanced package
currently available for modeling electromagnetic devices.
This work deals with the detection of broken bars in a three phase
squirrel cage induction motor, using the finite element model of the induction
machine. FEM is more precise than the winding function approach method, as
it is based on the actual geometry of the machine. The machine model can be
easily modified to study the effects of faults on the machine’s performance.
The CAD package called “Magnet 6.26.6” is used for the Static 2D and
Transient 2D analysis. The various machine parameters like flux density, flux
function, magnetic energy and current are calculated, using this CAD
package, and their values are compared under healthy and faulty conditions.A
three phase squirrel cage induction motor is modeled on the basis of the finite
element method. The simulation results are obtained for the broken bar fault.
It is found that the faults due to broken bars saturate the magnetic force

5. v
distribution on the rotor tooth, adjacent to the bars that are broken. In the
static analysis, the stored magnetic energy is decreased when the number of
broken bars is increased. The flux function and flux density are increased,
when the number of broken bars is increased. In the transient analysis, it is
found that the flow of current in the stator phases, and the flux linkage
produced in the motor are increased, whereas, the stored magnetic energy is
decreased, when the number of bars broken is increased. The simulated
results are compared with the theoretical results for parameters like the flux
function and flux density.
Simulation studies are also carried out for different fault conditions
in the Voltage Source Inverter (VSI), Current Source Inverter (CSI) and fault
tolerant inverter systems. The Total Harmonic Distortion (THD) of the VSI
fed drive is evaluated under healthy conditions and various faults in the
inverter circuit. From the simulation results, it is seen that there is an increase
in the harmonic distortion due to faults. The current harmonics get introduced
upon the introduction of faults in the inverter module. The THDs of the
normal VSI fed drive and fault tolerant VSI fed drive are evaluated, under the
open leg fault condition. From the simulation results it is seen, that there is a
decrease in the harmonic distortion by using a fault tolerant VSI fed drive
with Stator Phase Connection (SPC). However, the fault tolerant inverter with
a leg swap module replicates the performance of a healthy VSI. The hardware
is implemented in the VSI fed drive, and comparisons are made between the
healthy and faulty conditions. In a healthy condition, the motor runs at a

6. vi
speed of 1430 rpm. In the open leg faulty condition, the voltage waveforms
are distorted, and the motor fails to run.
Using FEM the fault can be easily detected and analyzed for the
three phase squirrel cage induction motor, without damaging the parts of the
machine. On the converter side, the THD analysis helps to find out the
various faults that occur in the VSI & CSI. A fault tolerant inverter, with a leg
swap module, was also developed for the VSI fed induction motor drive, to
overcome the effect of the fault in the inverter.

7. vii
ACKNOWLEDGEMENT
I express my deep sense of gratitude to Dr. S. Rama Reddy,
Professor, Department of Electrical and Electronics Engineering, Jerusalem
College of Engineering, Chennai, Tamilnadu, India, for his wholehearted and
constant encouragement in the conception, execution and completion of this
research work. I also thank him for giving me an opportunity to work under
his guidance.
I express my sincere thanks to Dr.M.A.Pannerselvam, Professor,
TEC, Dr. T. Thyagarajan, Professor, MIT, Chennai, and Dr.Krishna
Vasudevan, Professor, IIT, Chennai, for their valuable suggestions towards
the improvement of the research work.
I express my thanks to Dr.D. Padma Subramanian, Principal,
Jerusalem College of Engineering, and the management, for their kind support
and the facilities provided to complete my work in time.
I also extend my thanks to my colleagues and friends, for their
support and suggestions during the course of the research work.
S. NAGARAJAN

8. viii
TABLE OF CONTENTS
CHAPTER NO. TITLE PAGE NO.
ABSTRACT iii
LIST OF TABLES xiii
LIST OF FIGURES xiv
LIST OF SYMBOLS AND ABBREVIATIONS xx
1. INTRODUCTION 1
1.1 GENERAL 1
1.2 LITERATURE SURVEY 2
1.3 OBJECTIVES OF THE THESIS 17
1.4 TREE DIAGRAM OF THE PRESENT WORK 18
1.5 ORGANISATION OF THE THESIS 19
1.6 CONCLUSION 20
2. ANALYSIS OF A ROTOR BROKEN BAR FAULT 21
2.1 GENERAL 21
2.2 FINITE ELEMENT METHOD 21
2.2.1 Steps Involved in FEM 22
2.2.1.1 Discretisation 22
2.2.1.2 Shaping function 22
2.2.1.3 Stiffness matrix 23
2.2.1.4 Solution technique 23
2.3 MAGNET PACKAGE 24
2.3.1 Organization of the Package 24
2.3.1.1 Pre processing 24
2.3.1.2 Solver 27
2.3.1.3 Post processing 27

9. ix
CHAPTER NO. TITLE PAGE NO.
2.4 DESIGN OF AN INDUCTION MOTOR 28
2.4.1 Machine Data for the 3 Induction Motor 28
2.4.2 Assumptions 29
2.4.3 Main Dimensions 29
2.5 DISCRETISATION OF THE INDUCTION
MOTOR 31
2.6 STATIC ANALYSIS - DISTRIBUTION OF
THE MAGNETIC FIELD 31
2.6.1 Field and Flux Profile 37
2.7 TRANSIENT ANALYSIS 46
2.8 MODEL OF INDUCTION MOTOR FOR
TRANSIENT ANALYSIS 46
2.9 ANALYSIS OF AN INDUCTION MOTOR
DURING THE TRANSIENT PERIOD 48
2.10 CONCLUSION 57
3. FAULT ANALYSIS OF THE VSI FED
INDUCTION MOTOR DRIVE 59
3.1 GENERAL 59
3.2 VSI FED DRIVE 60
3.2.1 Open Circuiting of one of the MOSFETs
In the Inverter 61
3.2.2 Open Circuiting of Phase A in the Inverter 61
3.2.3 Short Circuiting of one of MOSFETs in the
Inverter 61
3.3 SIMULINK MODEL OF THE VSI FED DRIVE 61
3.3.1 Output Waveforms 63

10. x
CHAPTER NO. TITLE PAGE NO.
3.4 FAULT ANALYSIS OF INVERTER MODULE 64
3.4.1 Open Circuit of one of the MOSFETs in
the Inverter Module 64
3.4.1.1 Output waveforms 65
3.4.2 Open Circuiting of Phase A
in the Inverter 67
3.4.2.1 Output waveforms 67
3.4.3 Short Circuit fault in the Upper leg of
Phase A of the Inverter 70
3.4.3.1 Output waveforms 70
3.5 SUMMARY OF THE FFT ANALYSIS OF
THE VSI FED DRIVE 72
3.6 CONCLUSION 74
4. FAULT ANALYSIS OF THE CSI FED INDUCTION
MOTOR DRIVE 75
4.1 GENERAL 75
4.2 CIRCUIT MODEL OF THE CSI FED DRIVE 76
4.2.1 Output Waveforms 77
4.3 FAULT ANALYSIS OF THE INVERTER
MODULE 79
4.3.1 Open Circuiting of one of the Six MOSFETs 79
In the Inverter
4.3.1.1 Output waveforms 80
4.3.2 Open Circuiting of Phase A leg in the
Inverter 82
4.3.2.1 Output waveforms 83

11. xi
CHAPTER NO. TITLE PAGE NO.
4.3.3 Short Circuit Fault in the Upper MOSFET
of the Phase A Leg of the Inverter 85
4.3.3.1 Output waveforms 86
4.4 SUMMARY OF THE FFT ANALYSIS OF THE
CSI FED DRIVE 88
4.5 CONCLUSION 89
5. FAULT TOLERANT VOLTAGE SOURCE
INVERTER FED INDUCTION MOTOR 90
5.1 GENERAL 90
5.2 FAULT TOLERANT INVERTER FED DRIVE
WITH SPC 92
5.2.1 Output Waveforms 92
5.3 FAULT TOLERANT VSI FED FED DRIVE
WITH OPEN CIRCUIT FAULT 94
5.3.1 Output Waveforms 94
5.4 THREE PHASE FOUR SWITCH INVERTER
FED INDUCTION MOTOR 96
5.4.1 Output Waveforms 97
5.5 SUMMARY OF FFT ANALYSIS OF
FAULT TOLERANT VOLTAGE
SOURCE INVERTER FED DRIVE WITH SPC 98
5.6 FAULT TOLERANT VSI FED INDUCTION
MOTOR DRIVE WITH LEG SWAP MODULE 99
5.6.1 Logical Operator System 101
5.6.2 Phase Identifier 102
5.6.3 Line Current Waveforms 102

12. xii
CHAPTER NO. TITLE PAGE NO.
5.7 SUMMARY OF FFT ANALYSIS OF
FAULT TOLERANT VOLTAGE SOURCE
INVERTER FED DRIVE WITH LEG SWAP
MODULE 104
5.8 CONCLUSION 105
6. HARDWARE IMPLEMENTATION 106
6.1 GENERAL 106
6.2 HARDWARE DESCRIPTION 106
6.2.1 Power Supply Circuit 107
6.2.2 Driver Circuit 108
6.2.3 Controller Circuit 108
6.2.4 Power Circuit 109
6.3 COMPLETE HARDWARE CIRCUIT 111
6.4 TESTING 112
6.5 VALIDATION OF THE RESULTS 117
6.6 CONCLUSION 117
7. CONCLUSION 118
7.1 GENERAL 118
7.2 SCOPE FOR FUTURE WORK 119
REFERENCES 120
LIST OF PUBLICATIONS 127

13. xiii
LIST OF TABLES
TABLE NO. TITLE PAGE NO.
2.1 Current at no load Simulation 26
2.2 Flux Function 44
2.3 Flux Density under different load conditions 45
2.4 Summary of the Stator Current 50
2.5 Summary of the Flux Linkage 53
2.6 Summary of the Magnetic Energy 56
2.7 Comparison of the Simulation Results with
the theoretical values 58
3.1 Summary of the FFT Analysis 73
4.1 Summary of the FFT Analysis of the CSI Fed
Drive 88
5.1 FFT analysis of the Fault Tolerant VSI Fed
Drive 98
5.2 Output of the Logical operator 101
5.3 Phase Identifier multiplier table 102
5.4 A Comparison of the Fault operation of the
VSI and Fault Tolerant VSI 104
6.1 Switching Sequence of the driving signals for
the Healthy Condition 110
6.2 Switching Sequence of the driving signals for
the open circuit Fault Condition 110
6.3 Summary of the hardware and simulation
results for the IM load 117

14. xiv
LIST OF FIGURES
FIGURE NO. TITLE PAGE NO.
2.1 Excitation sequence 26
2.2 Discretization of the model for the
induction motor 31
2.3 Magnetic Field and Flux Distribution
under Healthy Condition 32
2.4 Magnetic Field and Flux Distribution
under two broken bars Condition 33
2.5 Magnetic Field and Flux Distribution
under four broken bars Condition 34
2.6 Magnetic Field and Flux Distribution
under six broken bars Condition 35
2.7 Magnetic Field and Flux Distribution
under eight broken bars Condition 36
2.8 Field and Flux Distribution under Healthy
Condition 39
2.9 Field and Flux Distribution under two
broken bars Condition 40
2.10 Field and Flux Distribution under four
broken bars Condition 41
2.11 Field and Flux Distribution under six
broken bars Condition 42
2.12 Field and Flux Distribution under eight
broken bars Condition
43

15. xv
FIGURE NO. TITLE PAGE NO.
2.13 Model of the Three phase squirrel cage
Induction Motor 47
2.14 Equivalent Circuit of the three phase
squirrel cage Induction Motor 47
2.15 Stator Current Plots under no load
condition 48
2.16 Stator Current Plots under full load
condition 49
2.17 Flux linkage plots under no load
condition 51
2.18 Flux Linkage plots under full load
condition 52
2.19 Magnetic Energy Plots under no load
condition 54
2.20 Magnetic Energy Plots under full load
condition 55
2.21 Graphical Representation of Magnetic
Energy 57
3.1 VSI fed Drive 60
3.2 Simulation circuit of the VSI fed drive 62
3.3 Line Current waveforms of the VSI fed
Drive under a Healthy Condition 63
3.4 Line Current spectrum of VSI fed Drive
under the Healthy Condition 64
3.5 Simulation circuit for the open circuit of
the upper leg of Phase A MOSFET in the
inverter 65

16. xvi
FIGURE NO. TITLE PAGE NO.
3.6 Line Current waveforms for the open
circuit of the upper leg of Phase A
MOSFET in the inverter 65
3.7 Line Current spectra for the open circuit
of the upper leg of Phase A MOSFET in
the inverter 66
3.8 Simulation Circuit for the open circuiting
of Phase A 67
3.9
3.10
Line Current waveforms for the open
circuiting of Phase A
Line Current spectra for open circuiting
of Phase A
68
68
3.11 Simulation Circuit for the Short
Circuiting of the Upper leg MOSFETs in
Phase A 70
3.12 Line Current for the Short Circuiting of
the Upper leg MOSFETs in Phase A 71
3.13 Line Current spectra for Short Circuiting
of the Upper leg MOSFETs in Phase A 71
4.1 CSI fed Induction Motor Drive 75
4.2 Simulation circuit of the CSI fed drive 76
4.3 Line voltage waveforms of the CSI fed
drive under a healthy condition 77
4.4 Line voltage spectra of the CSI fed drive
under a healthy condition 78

17. xvii
FIGURE NO. TITLE PAGE NO.
4.5 Simulation circuit for the upper MOSFET
of Phase A open circuited in the inverter 79
4.6 Line voltage waveforms for the upper
MOSFET of Phase A open circuited in
the inverter 80
4.7 Line voltage spectra for the upper
MOSFET of Phase A open circuited in
the inverter 81
4.8 Simulation circuit with phase A
MOSFET open circuited in the inverter 82
4.9 Line voltage waveforms with phase A
MOSFET open circuited in the inverter 83
4.10 Line voltage spectra with phase A
MOSFET open circuited in the inverter 84
4.11 Simulation circuit for short circuiting of
the upper MOSFETs in phase A leg 85
4.12 Line voltage waveforms of the upper
MOSFET of phase A leg short circuited 86
4.13 Line voltage spectra of the upper
MOSFET of phase A leg short circuited 87
5.1 Typical VSI Fed Drive with SPC 90
5.2 Induction motor drive structure for a
reconfiguration based on SPC 91
5.3 Induction motor drive with SPC drive
reconfiguration for an inverter leg
fault(leg A) 91

18. xviii
FIGURE NO. TITLE PAGE NO.
5.4 Simulation circuit of the VSI fed
induction motor drive with SPC 92
5.5 Simulation results of the VSI fed
induction motor drive with SPC 92
5.6 Simulation circuit of a fault tolerant VSI
fed three phase induction motor with
open circuit fault 94
5.7 Simulation results of the fault tolerant
VSI fed induction motor under an open
circuit fault 95
5.8 Simulation circuit of the three phase four
switch inverter fed induction motor 96
5.9 Simulation results of the three phase four
switch inverter fed induction motor 97
5.10 Simulink model of a fault tolerant VSI
fed induction motor drive 99
5.11 Leg swap module used in the fault
tolerant inverter 100
5.12 Logical operator system 101
5.13 Phase identifier 102
5.14 Simulation results of a Fault tolerant
inverter fed induction motor with the leg
swap module 103
6.1 Block Diagram of the hardware design 107
6.2 Driver Circuit 108
6.3 Controller Circuit 109
6.4 Power Circuit 109

19. xix
FIGURE NO. TITLE PAGE NO.
6.5 Complete Hardware Circuit Diagram 111
6.6 Complete Hardware Setup 112
6.7 Driving Pulses 112
6.8 Output of the Driver Circuit 113
6.9 Line Voltage and Current of the Inverter
for the Induction Motor Load 113
6.1 Line Voltage of the Inverter circuit for
the Induction Motor Load with an open
circuit fault 114
6.11 Line Current of the Inverter circuit for the
Induction Motor Load with an open
circuit fault 114
6.12 Line current spectrum of the inverter
circuit for the Induction Motor Load
under a healthy condition 115
6.13 Line current spectrum for Phase A of the
inverter circuit for the Induction Motor
Load under the open circuit fault 115
6.14 Line current spectrum for Phase B of the
inverter circuit for the Induction Motor
Load under the open circuit fault 116
6.15 Line current spectrum for Phase C of the
inverter circuit for the IM- Load under an
open circuit fault 116

20. xx
LIST OF SYMBOLS AND ABBREVIATIONS
AC - Alternating Current
A - Ampere
Ar - Area of Rotor Core
As - Area of Stator Core
CAD - Computer Aided Design
Iz - Current Through A Conductor
dcs - Depth of Stator Core
dss - Depth of Stator Slot
D - Diameter of stator bore
Dr - Diameter of The Rotor
e.m.f. - Electromagnetic Force
R - Equivalent Resistance
FFT - Fast Fourier Transform
FEA - Finite element analysis
FEM - Finite element method
B - Flux Density
H - Flux Intensity
FrFT - Fractional Fourier transform
f - Frequency
L - Gross iron length
Hz - Hertz
hp - Horse power
kW - Kilo watt
Lmts - Length of Mean Turn
lg - Length of The Airgap
MATLAB - Matrix Laboratory

21. xxi
m - Maximum Flux In The Core
mm - Millimeters
ms - Milliseconds
Li - Net iron length
NR - Newton Raphson algorithm
Nm - Newton-Meter
nd - Number of Ducts
npp - Number of Parallel Paths
p - Number of Poles
D0 - Outer Diameter of The Stator Core
- Pole pitch
- Resistivity of Material
rpm - Revolutions per minute
rps - Revolutions per second
Lr - Rotor Inductance
rb - Rotor Resistance
SF - Shaping Function
qs - Slots per pole per phase
ac - Specific Electric loading
Bav - Specific Magnetic loading
Zss - Stator Conductors Per Slot
Is - Stator Current
Ls - Stator Inductance
Es - Stator Phase Voltage
rs - Stator Resistance
yss - Stator Slot Pitch
Ts - Stator Turns Per Phase
Kws - Stator Winding Factor
Wm - Stored Energy

22. xxii
L - Total Inductance
Ss - Total Stator Slots
2D - Two dimension
V - Volt
Wb/m2
- Weber per meter squared
wd - Width of Ventilating Ducts

23. 1
CHAPTER 1
INTRODUCTION
1.1 GENERAL
An induction motor is a type of asynchronous Alternating Current
(AC) motor, in which power is supplied to the rotating device by means of
electromagnetic induction. The induction motor is definitely one of the most
used electric machines in the world. When supplied by a symmetrical and
balanced sinusoidal three phase voltage, and operating according to the
manufacturer’s instructions, namely, regarding the environment and load
type, the induction motor is a very robust machine. However, faults can
always occur.
The main causes of the three phase induction motor failures are
related to the bearing damages and stator faults, particularly, the rotor broken
bar fault. The growing popularity of the AC drive is chiefly due to its ability
to control the speed of the induction motor, which is most commonly used in
industry. The induction motor is the most cost effective motor. It is
considerably smaller, lighter and more readily available. It is a very rugged
and virtually maintenance free motor.
The induction motor has acquired an essential place in industrial
applications due to its increased advantages and steady responses. With
growing demands, an efficient machine is the need of the hour. So fault
detection in the machine, and the advantages of a fault tolerant voltage source
inverter, become more prominent and necessary, to enhance operations.

24. 2
1.2 LITERATURE SURVEY
Elkasabgy & Eastham (1992) dealt with the broken bar and its
detection technique. Computations were done using non-linear complex
steady state technique. Burnett et al (1995) used a signal processing technique
which obtains the time frequency representation of multicomponent non-
stationary signals, to detect the presence of the non stationary components
within the transient line current of a 3 phase induction motor supply which is
indicative of rotor faults such as broken rotor bars.
Bentounsi & Nicolas (1998) proposed a local approach to tackle the
problem of breaking bars and end rings, by using a finite element formulation
of the coupled problem implemented in a CAD software, Flux 2D. Bangura &
Demerdash (1999) computed the characteristic frequency components, which
are indicative of rotor bar and connector breakages in the armature current
waveforms and developed torque profiles. They used the MCSA technique for
the diagnosis of rotor breakages in an induction motor and the finite element
method to calculate the parameters, and modeled them using State Space
Modeling approach.
Watson et al (1999) described how commercial finite element
packages may be used to simulate rotor faults, and thus, enhance the
capability of practical condition monitoring schemes. Accurate models of the
machine under faulted conditions were developed, using both the fixed mesh
and time stepping finite element packages. Bianchi et al (1999) presented a
comparison between two different finite element analyses of three phase
induction motors. The first method is based on the equivalent circuit of the
motor, and the second method is based on the field solution. Both approaches
worked with the 2D discretized domain, and implemented in Ansoft Maxwell
and in Cedrat Flux 2D.

25. 3
Subhasis et al (2001) presented the effect of pole pair and rotor slot
numbers on the presence of different harmonics under healthy and eccentric
conditions. Other harmonics due to slotting, saturation and asymmetry can
also be predicted. But this simulation technique was not as accurate as finite
element method. Mirafzal & Demerdash (2004) presented new technique
based on rotor magnetic field space vector orientation which is used to
diagnose broken-bar faults in induction machines operating at steady state.
Jung & Kwan (2006) proposed a corrosion rotor bar model derived
from electromagnetic field theory and simulated using Matlab Simulink.
Weili et al (2007) developed the foundations of a technique for diagnosis and
characterization of effects of broken bars in squirrel cage induction motors
based on the time-stepping coupled finite-element approach .
Sizov et al (2009) described the effect of adjacent and nonadjacent
bar breakages on rotor fault diagnostics in squirrel-cage induction machines.
They have also described how nonadjacent bar breakages result in the
masking of the commonly used fault indices and other problems and the
solution to overcome these problems. Sanchez et al (2010) proposed the
optimization of the FrFT to generate a spectrum where the frequency-varying
fault harmonics appears as a single spectral lines and therefore facilitate the
diagnostic process.
Llinares et al (2011) presented a new induction motor diagnosis
based on a Transient current analytic wavelet transform via frequency B-
splines. The technique was applied to the experimental start up current of
motors in a healthy and faulty state. Here the diagnosis is performed only for
rotor broken bar fault condition.
Cardoso & Mendes (1997) presented the on-line detection and
location of inter-turn short circuits in the stator windings of three-phase

26. 4
induction motors using a noninvasive approach, based on the computer-aided
monitoring of the stator current Park’s vector approach. Preston et al (1988)
conveyed that the equivalent circuit approach usually gives adequate
predictions of torque and current but gives no information on flux
distribution. This deficiency was overcome by numerical approach which uses
2D, nonlinear, time-stepping finite element method for excitation from a
constant voltage source. Comparison of stator current for no load and other
load conditions show good agreement with test values on a large induction
motor.
Balamurugan et al (2004) dealt with the analysis of induction motor
behavior during transient periods using coupled electric circuit with 2D finite
element electromagnetic field analysis. The designed geometric dimension of
induction motor is modeled in the finite element domain and the transient
performance are found at the starting of motor with no load, the operation of
asymmetrical excitation of the stator and turn to turn fault condition .
Dai et al (2005) this paper presented three phase trapezoidal back-
emf permanent magnet machines were used in many applications were the
reliability and fault tolerance were important requirements. Knowledge of the
machine transient processed under various fault conditions is the key issue in
evaluating the impact of machine fault on the entire electromechanical
system.
Yilamaz & Krein (2008) reviewed the literature concerned with
capabilities and limitations of finite element analysis and Magnetic
Equivalent Circuit(MEC) analysis for electrical machine design. The most
common known models were based on equivalent circuits and related
analytical models or on FEA. Analytical models use highly simplified
magnetics, and have difficulty extending into saturation. FEA typically uses
magnetic vector potential representations that model additional effects such as

27. 5
eddy currents, but requires detailed nonlinear models for saturation and
hysteresis. MEC methods represent a third possibility for electrical machine
analysis, based on permeance network models comprising reluctances and
mmf sources. Advantages of the MEC method include reduced model
complexity compared to FEA, enhanced accuracy compared to analytical
approaches, ease of parameterization, methods for extension to 3-D
capability, and fast computation time.
Zouzou ( 2010) proposed the use of Partial Relative Indexes (PRI)
as a new fault indicators to ameliorate the reliability of fault detection task
and uses MCSA method.
Das et al (2011) presented about the detection of stator winding
inter-turn insulation failure at early stages using advanced signal and data
processing tool. It presented the experimental results of minor faults due to
failure of insulation between the stator windings. Results of this method under
different loading conditions was not that much accurate.
Ceban et al (2012) presented a new signature for detection of rotor
faults in induction motors, such as eccentricity and broken rotor bars, that
uses the external magnetic field analysis. The Proposed method is based on
the variations of axial flux density in the presence of these faults. The low
frequency part of the magnetic field spectrum is particularly analyzed. The
analysis is realized through a machine modeling based on permeance circuit
under eccentricity fault and also by machine modeling based on coupled
magnetic circuit theory under broken rotor bars fault. In particular, an inverse
stator cage induction machine have been used to measure the bar currents
under healthy and faulty cases.
Boqiang et al (2012) presented a novel detection method for broken
rotor bar fault (BRB) in induction motors based on the estimation of signal

28. 6
parameters via rotational invariance technique (ESPRIT) and simulated
annealing algorithm (SAA). The performance of ESPRIT is tested with the
simulated stator current signal of an induction motor with BRB. It shows that
even with short time measurement data, the technique is capable of correctly
identifying the frequencies of the BRB characteristic components but with a
low accuracy on the amplitudes and initial phases of those components.
Ebrahimi et al (2013) proposed new analytical method for the
calculation ohmic and core losses in induction motors under broken bar fault.
In this method, new coefficients are introduced to consider non-sinusoidal
distribution effects of flux density due to bar breakage. Then, core losses of
induction motors in this condition are estimated. In order to calculate ohmic
losses in faulty induction motors, impacts of the bar breakage on the harmonic
components of the stator currents are taken into account. In this modeling
approach, the effects of the nonlinear characteristics of the core materials,
stator, and rotor slots are taken into account. The simulation results are
verified by the 2-D time stepping finite-element method and experimental
results.
Kim et al (2013) proposed a new frequency analysis of stator
current to estimate fault-sensitive frequencies and their amplitudes for broken
rotor bars (BRBs). The proposed method employs a frequency estimator, an
amplitude estimator, and a fault decision module. The frequency estimator is
implemented by a zoom technique and a high-resolution analysis technique
known as the estimation of signal parameters via rotational invariance
techniques, which can extract frequencies accurately. For the amplitude
estimator, a least squares estimator is derived to obtain amplitudes of fault
harmonics, without frequency leakage. Experimental results obtained from
induction motors show that the proposed diagnosis algorithm is capable of

29. 7
detecting BRB faults with an accuracy that is superior to the zoom-based
MUSIC algorithm.
Williamson & Robinson (1991) described about the conventional
equivalent circuit model to determine the equivalent circuit components for a
three phase squirrel cage induction motor using finite element model. The use
of minimal models leads to a fast execution time. The method used separate
finite element models for rotor and stator.
Thomson & Fenger (2001) focused on the industrial application of
motor current signature analysis (MCSA) to diagnose the faults in the three-
phase induction motor drives.
Bangura et al (2003) developed the foundations of a technique for
detection and categorization of dynamic, static eccentricities and bar, end ring
connector breakages in squirrel cage induction motors using time Stepping
coupled finite element state space method to generate fault case performance
data, which contain phase current waveforms and time domain torque profiles.
A new artificial immune based support vector machine algorithm
for fault diagnosis of induction motor was proposed by J.Aydin et al (2007).
Mohammed et al (2006) examines the behavior of three phase induction
motors with internal fault conditions under sinusoidal supply voltages.
Discrete wavelet transform is used to extract the different harmonic
components of stator currents.
Mir et al (1998) presented direct torque control (DTC) of induction
machines used the stator resistance of the machine for estimation of the stator
flux. Variations of stator resistance due to changes in temperature or
frequency make the operation of DTC difficult at low speeds. A method for
the estimation of changes in stator resistance during the operation of the

30. 8
machine is presented. The estimation method is implemented using
proportional-integral (PI) control and fuzzy logic control schemes. The
estimators observe the machine stator current vector to detect the changes in
stator resistance. The performances of the two methods are compared using
simulation and experimental results. Results obtained have shown
improvement in DTC at low speeds.
Chan et al (1999) described a generalized model of the three-phase
induction motor and its computer simulation using MATLAB/SIMULINK.
Constructional details of various sub-models for the induction motor were
given and their implementation in SIMULINK is outlined.
Benbouzid (2000) introduced a concise manner the fundamental
theory, main results, and practical applications of motor signature analysis for
the detection and the localization of abnormal electrical and mechanical
conditions that indicate, or may lead to, a failure of induction motors. The
paper is focused on the so called Motor Current Signature Analysis (MCSA)
which utilizes the results of spectral analysis of the stator current.
Huo & Trzynadlowske (2001) presented simple stator fault detector
for ac motors, based on the TMC320C243 DSP controller is presented. The
detector provides compensation of the constructional and supply voltage
imbalances, and senses the ripple of the compensated instantaneous power.
The power ripple is indicative of such stator faults as open and short circuits
in the stator winding.
Llinares et at (2011), proposed a new induction motor diagnosis
methodology. The approach is based on obtaining a 2-D time frequency plot
representing the time frequency evolution of the main components in an
electrical machine transient current. The identification of characteristic
patterns in the time frequency plane caused by many of the fault-related

31. 9
components enables a reliable machine diagnosis. Unlike other continuous
wavelet transform based methods, this work uses frequency B-spline (FBS)
wavelets. It is shown that these wavelets enable an efficient filtering in the
region neighboring the main frequency, as well as enable a high level of detail
in the time frequency maps. As a consequence, the evolution of the most
important current components is precisely traced. These characteristics make
it easy to identify the patterns related to the fault components. The technique
is applied to the experimental no load start up current of motors in a healthy
state and with broken bars, the FBS capabilities are revealed.
Hwang et al (2003) described the distribution characteristics of
switching the surge voltage in the stator windings of an induction motor
driven by IGBT PWM inverter. To analyze the voltage distribution between
turns and coils of the stator winding, an equivalent circuit model of the
induction motor including feeder cable is proposed and high frequency
parameters are computed by finite element analysis.
Mendes et al (2003) presented comparative analysis involving
several fault tolerant operating strategies applied to three phase induction
motor drives. The paper exploits the advantages and the inconveniences of
using remedial operating strategies under different control techniques, such as
the field oriented control and the direct torque control.
Ribeiro & Jacobina (2003) investigated the use of different
techniques for fault detection in voltage-fed asynchronous drive systems.
Such detection requires measurement of voltages which is based on analytical
model of voltage source inverter. Fault detection is based on voltages which
require more voltage sensors to be installed in the drive system.
Tusof & Yatin (2003) presented accurate stator flux estimation for
high performance induction motor drives are very important to ensure proper

32. 10
drive operation and stability. Unfortunately, there is some problems occurred
when estimating stator flux especially at zero speed and at low frequency.
Hence a simple open loop controller of pulse width modulation voltage source
inverter (PWM-VSI) fed induction motor configuration is presented. By a
selection of voltage model-based of stator flux estimation, a simple method
Using artificial neural network (ANN) technique is proposed to estimate
stator flux by means of feed forward back propagation algorithm. In motor
drives applications, artificial neural network has several advantages such as
faster execution speed, harmonic ripple immunity and fault tolerance
characteristics that will result in a significant improvement in the steady state
performances. Thus, to simulate and model stator flux estimator,
Matlab/Simulink software package particularly power system cblock set and
neural network toolbox is implemented. A structure of three-layered artificial
neural network technique has been applied to the proposed stator flux
estimator. As a result, this technique gives good improvement in estimating
stator flux which the estimated stator flux is very similar in terms of
magnitude and phase angle if compared to the real stator flux.
Kou & Corzine (2004) presented a unique design for flying
capacitor type multilevel inverters with fault tolerant features. They have also
discussed the capacitor balancing approaches under fault conditions.
welchko & Lipo (2004) compared the many fault tolerant three
phase ac motor drive topologies for inverter faults of switch short or open
circuits, phase leg short circuits and single phase open circuits.
Zhou & Smedley (2005) presented fault tolerant control method for
hexagram inverter motor drive. This proposed method consists of fault
detection, fault isolation and post fault control method.

33. 11
Pereira et al (2005) presented the development and the practical
implementation of a system for detection and diagnosis of inter turn short
circuits in the stator windings of induction motors. Motor Current Signature
Analysis (MCSA) and Fuzzy Logic techniques are utilized in order to achieve
that. After a brief description of the MCSA, the causes of short circuits are
discussed and characterized with frequency relationships and frequency
spectra.
Sun et at (2005), investigated stator-rotor-hybrid fault in squirrel
cage induction motors, which means that rotor bar breaking fault and stator
winding inter-turn short circuit fault based on the motor multi-loop model.
The results indicate that the features of rotor bar breaking fault and stator
winding inter-turn short circuit fault always interlace and interact to some
extent. The detection method, which is only suitable for single fault, may lead
to a misinterpretation. In this work, the stator rotor-hybrid fault feature of
rotor bar breaking and stator winding inter turn short circuit has been
summarized and the mutual relationship of the two types of fault has been
disclosed by thoroughly analyzing the simulation and experiment results. As
establishes an important theoretical foundation for joint detection of rotor bar
breaking and stator winding inter turn short circuit fault.
Shengming & Longya (2006) proposed fault tolerant operation
strategies for three level neutral point clamped pulse width modulation
inverters in high power safety critical applications.
Corres et al (2006) proposed a new method to detect the negative
effects of a particular unbalanced voltage and inverter harmonics on the
performance of an induction motor using fiber sensors. A new in-line fiber
etalon accelerometer has been designed.

34. 12
Blodt et al (2006) presented the detection of small torque
oscillations in induction motor drives during speed transients by stator current
analysis. The proposed solution is time-frequency signal analysis. This work
particularly deals with the extraction of fault indicators that could be used in a
permanent and automatic condition monitoring system.
Jung et al (2006) described, an online induction motor diagnosis
system using motor current signature analysis (MCSA) with advanced signal-
and-data-processing algorithms is proposed. MCSA is a method for motor
diagnosis with stator-current signals. The proposed system diagnoses
induction motors having four types of faults such as breakage of rotor bars
and end rings, short-circuit of stator windings, bearing cracks, and air gap
eccentricity. Therefore, advanced signal-and-data-processing algorithms are
proposed.
Jung & Kwon (2006) proposed a corrosion model of a rotor bar
under fault progress in induction motors for simulations of induction
machines with a rotor bar fault. A rotor-bar model is derived from the
electromagnetic theory. A leakage inductance of the corrosion model of a
rotor bar is calculated from the relations of magnetic energy, inductance,
current, and magnetic field intensity by Ampere’s law. The leakage
inductance and resistance of a rotor bar varies when the rotor bar rusts. In
addition, the skin effect is considered to establish the practical model of a
rotor bar. Consequently, the variation of resistance and leakage inductance
has an effect on the results of motor dynamic simulations and experiments,
since a corrosive rotor bar is one model of a rotor bar in fault progress. The
results of simulations and experiments are shown to be in good agreement
with the spectral analysis of stator current harmonics. From the proposed

35. 13
corrosion model, motor current signature analysis can detect the fault of a
corrosive rotor bar as the progress of a rotor-bar fault.
Mendes et al (2007) presented the results of an investigation
regarding the thermal behavior of a three-phase induction motor when
supplied by a reconfigured three-phase voltage source inverter with fault-
tolerant capabilities. For this purpose, a fault tolerant operating strategy based
on the connection of the faulty inverter leg to the dc link middle point was
considered. The experimentally obtained results show that, as far as the motor
thermal characteristics are concerned, it is not necessary to reinforce the
motor insulation properties since it is already prepared for such an operation.
Mingyao et at (2007), focused on the fault-tolerance potential of
multilevel inverters with redundant switching states such as the cascaded
multilevel inverters and capacitor self-voltage balancing inverters. The gate
signals can be reconfigured according to the failure modes when some of the
power devices fail. Balanced line-to-line voltage will be achieved with the
proposed method when device failure occurs. Furthermore, the circuit
structures can be the same as the general ones and the voltage stress of the
devices does not increase. Simulation and experimental results are included in
the paper to verify the proposed method.
Mendes et al (2008), presented the thermal behavior of a three
phase induction motor under direct torque control, when supplied by a three
phase voltage source inverter with fault tolerant capabilities. The motor
thermal profile is obtained through the use of nine thermocouples positioned
in both stator and rotor circuits. The experimental results obtained under fault
compensated operation show that, as far as the motor thermal characteristics

36. 14
are concerned, it is not necessary to reinforce the motor insulation properties
since it is already prepared for such an operation.
Biswas et al (2009) dealt with harmonic analysis of motor current
signatures under different fault conditions of medium and high power
Variable Frequency Drive (VFD) systems. Computer simulation of a VSI fed
induction motor based on constant voltage/frequency (V/f) operation is
implemented using Powersim (PSIM) simulation software. Frequency
response characteristics of motor currents are compared to analyze fault
conditions in motor drive system.
Banerjee & Ranganathan (2009) proposed a CSI-fed induction
motor drive scheme where GTOs are replaced by thyristors in the CSI without
any external circuit to assist the turning off of the thyristors. Here, the current-
controlled VSI, connected in shunt, is designed to supply the volt ampere
reactive requirement of the induction motor, and the CSI is made to operate in
leading power factor mode such that the thyristors in the CSI are auto
sequentially turned off. The resulting drive will be able to feed medium-
voltage, high-power induction motors directly.
Rodriguez et al (2009) proposed a fault tolerant strategy wherein a
damaged inverter leg is replaced by an auxiliary leg. Current signature
analysis is not performed in this paper.
Julian et al (2010) presented a digital control architecture that
demonstrates operating standby redundancy for a voltage source inverter
(VSI) controller.
Salmasi et al (2010) proposed an adaptive flux observer for
concurrent estimation of rotor fluxes, unknown dc-link voltage, and rotor

37. 15
resistance of induction motor with voltage source inverters is presented in this
paper. Estima & Cardoso (2011) presented a new method for real-time
diagnostics of multiple open-circuit faults in VSI feeding ac machines.
Salmasi et al (2011), proposed a sensor fault detection and isolation
unit for induction-motor drives based on an adaptive observer with rotor-
resistance estimation. In the proposed fault-detection and isolation unit, the
estimated phase currents and rotor resistance are sent to a decision-making
unit, which identifies the faulty sensor type based on a deterministic rule base.
In the case of a current-sensor failure, it also detects the phase with erroneous
sensor output. The accuracy of the proposed approach is analytically proved.
Furthermore, extensive simulation and experimental tests verify the
effectiveness of the proposed method at different operating conditions.
Alberti & Bianchi et al (2011) described a set of experimental tests
on a dual three-phase induction machine for fault-tolerant applications.
Different winding configurations are investigated and compared in case of
both open-circuit and short-circuit faults. Experimental tests for each
configuration are reported at no-load and under load operating conditions.
Blanco et al (2011) proposed a novel failure-detection technique
and its analog circuit for insulated gate bipolar transistors (IGBTs), under
open- and short-circuit failures. This technique is applied to a three-phase
induction motor (IM) drive system. However, this technique required addition
of extra voltage sensor in the drive.
Kim et al (2011), proposed online basis fault-detecting scheme
during motor operation to detect faults in an inverter-fed permanent magnet
synchronous motor drive under faults in a stator winding and inverter switch.

38. 16
The proposed scheme is achieved by monitoring the second-order harmonic
component in q-axis current and the fault is detected by comparing these
components with those in normal conditions.
Espinoza et al (2012), explained a robust model-based fault
detection and isolation (FDI) scheme for open-circuit faults for voltage source
inverters (VSI) feeding induction motor drives. The actuator faults are
modelled with an additive perspective in the non-linear dynamics of the
induction motor. The ideas presented in the study are verified experimentally
in a test-bench of 3/4 HP induction motor under variable operating conditions
(reference frequency and unknown load torque), and parameter uncertainty
induced by a continuous operation of the induction motor.
The above mentioned literature used vibration monitoring
techniques, like the MCSA, Thermal Monitoring etc, for the detection of
faults and modeling purposes. In the present work, the “Finite Element
Method” is adopted to detect the faults in the three phase induction motor,
and to perform the static transient 2D analysis for healthy and faulty
conditions. The analysis is carried out with a CAD package, called the
Magnet. The fault analysis of the VSI&CSI fed induction motor drives using
matlab simulation is not present in the literature. This work proposes circuit
models for VSI fed induction motor drives with various faults. It also
proposes a fault tolerant voltage source inverter for the control of the
induction motor. The fault analysis of the fault tolerant voltage source inverter
fed induction motor drive is also presented. A leg swap module is proposed
for the induction motor drive.

39. 17
1.3 OBJECTIVES OF THE THESIS
The objectives of the present work are summarized as follows:
To detect the rotor broken bars in a three phase squirrel cage
induction motor, using the finite element model of the
induction machine.
To model and simulate the VSI fed induction motor drive of
the three phase squirrel cage induction motor and to analyze
the various faults, using the FFT analysis.
To model and simulate the CSI fed induction motor drive of
the three phase squirrel cage induction motor, and to analyze
the various faults, using the FFT analysis.
To model and simulate the fault tolerant voltage source
inverter under faulty conditions.
To implement the Hardware of the VSI fed induction motor to
analyze the faulty and healthy conditions.
In order to study the fault analysis of the three phase squirrel cage
induction motor, MAGNET 6.26.6 software is used. For the fault analysis of
the VSI&CSI fed drive, MATLAB R2007b/ SIMULINK software is used.

40. 18
1.4 TREE DIAGRAM OF THE PRESENT WORK
Fault detection of the inverter fed squirrel cage induction motor
Real time experimental studies
Modeling of squirrel
cage induction motor
Fault detection of squirrel
cage induction motor
VSI fed IM inverter fault
Rotor broken bar
fault
VSI fed IM
inverter fault
CSI fed IM
inverter fault
Fault tolerant
VSI fed IM
Simulation studies

41. 19
1.5 ORGANISATION OF THE THESIS
The thesis is divided into seven chapters. The organization of the
thesis is as follows:
The first chapter presents the general introduction to the problem,
and the previous investigations reported in the literature. The objectives of the
present work, scope and organization are also presented in this chapter.
The simulation results of the rotor broken bar faults of a three phase
squirrel cage induction motor, using the static & transient 2D analysis are
provided in the second chapter. The simulation models and results for a
healthy and faulty motor are also presented.
The fault analysis of the VSI fed induction motor drive is explained
in chapter three. The simulation results, output waveforms and total harmonic
distortion measurements of the VSI fed induction motor drives are recorded.
The results of the various faults in an inverter and rectifier are also presented.
Chapter four describes the fault analysis of CSI fed induction motor
drive. The simulation results, output waveforms and total harmonic distortion
measurements of the CSI fed induction motor drives, for various inverter and
rectifier fault conditions are also presented.
The results of the investigations on the fault analysis, of a three
phase induction motor powered by a reconfigured three phase voltage source
inverter with fault tolerant capabilities, is explained in chapter five. The
simulation study of a three phase induction motor fed by a fault tolerant
voltage source inverter, with open leg fault is given in this chapter.

42. 20
Chapter six presents the hardware results of the VSI fed induction
motor drive for healthy and faulty conditions. Voltage waveforms are
obtained and comparisons are made between the healthy and faulty
conditions.
A comprehensive summary and concrete conclusions drawn for
fault detection using Magnet 6.26.2 and Mat Lab R2007b, are given in
chapter seven. The scope for further research work is also presented.
1.6 CONCLUSION
The literature review, objectives and organization of the thesis are
presented in this chapter.

43. 21
CHAPTER 2
ANALYSIS OF A ROTOR BROKEN BAR FAULT
2.1 GENERAL
The interior faults of induction motor account for more than 70% of
the induction motor failures. Conventional methods make use of test
machines; however, the machine has to be damaged to complete the
experiments of interior faults. Interior faults include stator and rotor faults of
induction motors. Rotor faults are related to broken bars. Rotor failures are
caused by a combination of various stresses that act on the rotor. These
stresses are identified as electromagnetic, thermal, dynamic, environmental
and mechanical. These leads to low frequency torque harmonics, which
increases noise and vibration. The stator faults are related to inter-turn or turn-
to-turn faults. This occurs due to the failure of the insulation in the windings.
The stator impedance decreases, and this value increases with the augment of
the shorted turn ratio.
2.2 FINITE ELEMENT METHOD
The finite element method is a general technique for the numerical
solution of the integral or differential equations governing the behavior of
systems. The finite element software accurately calculates magnetic fields and
related motor design parameters, for motors of complicated geometry with
saturation and/or permanent magnets, with significant armature reaction, and
with or without eddy currents. This saves the cost of the device and the

44. 22
possibility of improving the design during the planning stage. It also increases
the rating of electromagnetic devices that were significantly designed and
built many decades ago. This method is distinguished from the finite
difference equations in determining the shapes that the discrete steps can take.
A magnet is the most advanced package currently available for modeling
electromagnetic devices.
2.2.1 Steps Involved in FEM
The various steps involved in FEM are as follows:
Discretisation
Shaping Function
Stiffness Matrix
Solution Technique
2.2.1.1 Discretisation
In the finite element method, the original field problem domain is
divided into a number of sub domains or elements of triangular shapes. The
entire field problem region is subdivided into triangles in any desired manner,
ensuring only that all types of material interfaces coincide with the triangle
sides. It is observed that the number, shape and size of the triangles are not
restricted in anyway. Any shapes other than triangular, such as quadrilateral
or curvilinear, can also be used
2.2.1.2 Shaping function
The function used to represent the behavior of the solution within
an element is called the shaping function. The shape functions constitute a
convenient local system of coordinates, called area coordinates, because each

45. 23
represents the ratio of the area of the sub triangle defined by each side, and
the point to the total area of the triangle element.
The shape function is defined as,
(SF)N = 1 at node N
0 at other nodes.
The properties, together with the linearity of the shape functions,
assure the convergence of the solution to the correct values of the function, as
the area of the element becomes infinitely small.
2.2.1.3 Stiffness matrix
To achieve minimization, the global energy is separated into its
element components, by minimizing one triangle at a time. The nonlinearity
of the problem is preserved, since the stiffness matrix [S] depends not only on
the shape and size of each triangle, but also on the reluctivity. The matrix [S]
is equal to the number of node potentials. [S] is also symmetrical, i.e., [S] =
[S]T
. Therefore, only half the bandwidth will be stored; then the matrix is
bounded and positive definite.
2.2.1.4 Solution technique
The most common method for solving the equations is the Newton
Raphson (NR) algorithm. Nowadays, a fast, powerful and general purpose
software is used as part of the finite element technique for solving
electromagnetic field equations. The CAD packages are used as the
simulation tool for the finite element analysis. There are various CAD
packages like Flux 2D, Ansoft, EMTDC, Femta fe, etc. The newly adopted
efficient CAD package used for the finite element analysis is “Magnet”.

46. 24
2.3 MAGNET PACKAGE
“Magnet” is the most advanced package currently available for
modeling electromagnetic devices. It provides a virtual laboratory, in which
the user can create models from magnetic materials and coils, view the
displays of field plots and graphs, and get the numerical values for quantities
such as flux linkage, force, torque, etc. This package is designed as a full 3D
modeling tool for solving static magnetic field and eddy current problems.
With 2D models, the magnet can also handle problems where currents are
induced by the motion of part of the system.
2.3.1 Organization of the Package
The software package has three modules:
Pre Processing
Solver
Post Processing
2.3.1.1 Pre processing
A pre processing module enables the user to define the problem’s
geometry and specify the boundary conditions, and excitation sources. The
objective of the pre processing phase is to build a complete and detailed
model of the physical system. In addition to the CAD task of specifying the
geometry of each object in the model, the user must assign the necessary
physical attributes to each object, and carefully direct the process of breaking
up the model into a sufficiently refined mesh of finite elements.

47. 25
The pre processing involves the following tasks:
Modeling
Mesh Generation
Material Properties Specification
Boundary Condition Application
Excitation
Model Validation
Modeling: This defines precisely the geometry of the model, by building the
outline of each object, using the CAD features of the FEA system.
Mesh Generation: Once an object is created it must be discretised; this is
achieved by this module. Most FEA systems provide a variety of mesh
generation options, ranging from totally automatic to totally user controlled.
Material Specification: Once the geometry of the objects has been defined,
the material properties of each must be specified.
Boundary Condition Application: FEA systems provide options for
applying the boundary conditions to the specified geometry of the object.
Excitation: It provides excitation at each winding of the system. The
excitation for a 4 pole machine is illustrated below. Because of the star
connection, the phase current is Io=ILO where ILO is the no load line current.
The current flowing in each coil is given by Ic =Io/2.The current at no load
simulation is given in Table 2.1, and its excitation sequence is given in Figure
2.1.

48. 26
Table 2.1 Current at no load simulation
Phase Current
A +(2)½
Ic
B -(2)½
Ic/2
C -(2)½
Ic/2
Figure 2.1 Excitation sequence

49. 27
Model Validation: Building a complex FEA model requires considerable
effort on the part of the analyst, and the solutions of complex models requires
significant computing resources. Hence, it is important to verify that the
model is correct.
2.3.1.2 Solver
Once the model has been completed, the analysis package is
invoked. At this point, the program takes over and automatically assembles
the stiffness matrix, modifies it to include the boundary condition, and solves
the system of N equations in the N unknown potential values. This is the
computer bound phase analysis. The numerical analysis is performed and the
graphical outputs obtained.
2.3.1.3 Post processing
The purpose of post processing is to provide the user with the
clearest visualization of the solution and its implications. Machine
parameters, such as flux linkages, inductances, induced voltage, current,
power loss, etc., are extracted during this process.
Several visualization modes are offered in this package. They are
Flux Plots
Numerical values
Animation
Flux Plots: The primary purpose of electromagnetic FEA is generally to
identify regions of intense saturation, since they indicate the points through
which the flux flows inside the device, when the excitation is applied.

50. 28
Numerical Values: Flux density plots generally include a colour code key
with which the user can interpret the flux density values numerically.
Animation: Animation sequences may be generated, by constructing a series
of frames connecting the initial position to the final position of the moving
geometry.
2.4 DESIGN OF AN INDUCTION MOTOR
Each component of the field quantities is assumed to vary
sinusoidally with time. The approach is based on the field solution. The stator
winding is a double layer winding. A double cage rotor is used. The star
connection is adopted. Detailed design calculations are given below.
2.4.1 Machine Data for the 3 induction motor
Rated Power - 22 kW
Rated Voltage - 415 V
Rated Frequency - 50Hz
Rated Speed - 1458 rpm
Number of Poles - 4
Number of Stator Slots - 36
Number of Rotor Slots - 28
Slip - 0.028
Efficiency - 0.85
Power factor - 0.88

51. 29
2.4.2 Assumptions
For 50Hz machines of normal design, the value of the average flux
density (Bav) lies between 0.3 to 0.6 Wb/m². Therefore Bav is assumed as
0.45Wb/m².
For a good overall design and simulation, the following values are
assumed L/ =1.
Winding Factor Kws = 0.955.
Slot pitch yss = 25mm.
Slots per pole per phase qs = 3.
2.4.3 Main Dimensions
The stator bore diameter and core length of the machines are the
main dimensions. The design calculations for main dimensions are given
below, they are used in the magnet to develop a machine model for
simulation.
Synchronous speed Ns = speed in rpm/60 =1500/60=25rps.
Slot pitch yss = D/Ss = 25mm
Ss=No of stator slots = 36.
So, Stator diameter D = (yss*Ss)/ = 286mm.
Since L/ = 1
Pole pitch , = D/p = 224mm.
Therefore Gross iron length, L = 224mm.
Net iron length Li = (L- nd wd )Ki

52. 30
As the length of the core is 0.224, there is no necessity to provide
any radial ventilating duct. So neglecting nd and wd, Li=201.6mm.
The machine is designed for a star connection.
Stator voltage per phase (Eph) = EL/(3)½
= 239.6V
Stator current (Is)=IL = 40.91A
Flux per pole ( m) = 0.0225 Wb
Stator turns per phase = 50 turns/phase
Stator conductors = 300
Stator conductors per slot = 6 conductors
No of turns/slot = 4
Ampere conductors (ac) = 23674A/m
Flux density in stator teeth = 0.885 Wb/m²
Depth of the slot = h+dos+d1s = 28mm
Depth of stator core = 46.5mm
Outside diameter (D0) = D+dss+dcs = 436mm
Shaft diameter = 53.4mm
Air gap length (lg) = 0.2+2(DL) ½
= 0.7mm
Rotor diameter (Dr) = D-2lg = 284.6m

53. 31
2.5 DISCRETISATION OF THE INDUCTION MOTOR
In the finite element method, the original field problem domain is
divided into a number of sub domains or elements. The several element
shapes in use are triangular, quadrilateral and curvilinear. Figure 2.2 shows
one possible subdivision (discretization) of a problem region. The entire field
problem region is subdivided into triangles in any desired manner, ensuring
only that all types of material interfaces coincide with the triangle sides. It can
be seen that the number, shape and size of the triangles is not restricted in
anyway. The model is developed using a magnet simulation tool.
Figure 2.2 Discretization of the model for the induction motor
2.6 STATIC ANALYSIS - DISTRIBUTION OF THE MAGNETIC
FIELD
Under normal load conditions, the distribution of the magnetic field
for the case of no broken bars is symmetrical, while the magnetic field

54. 32
distribution is unsymmetrical in the case of broken bars, and a higher degree
of magnetic saturation can be observed around the broken bars.
Figure 2.3 Magnetic field and flux distribution under healthy
condition; field distribution at: (a) no load (b) half load (c)
full load; flux distribution at: (d) no load (e) half load (f) full
load
(c) (f)
(a) (d)
(b) (e)

55. 33
Figure 2.4 Magnetic field and flux distribution under two broken bars
condition; field distribution at (a) no load (b) half load (c)
full load; flux distribution at (d) no load (e) half load (f) full
load
(a)
(b)
(c)
(d)
(e)
(f)
Broken Bars

56. 34
Figure 2.5 Magnetic field and flux distribution under four broken bars
condition; field distribution at (a) no load (b) half load
(c) full load; flux distribution at (d) no load; (e) half load
(f) full load
(a) (d)
(b) (e)
(c) (f)
Broken Bars

57. 35
Figure 2.6 Magnetic field and flux distribution under 6 broken bars
condition; field distribution at (a) no load (b) half load (c)
full load; flux distribution at (d) no load (e) half load (f) full
load
(a) (d)
(b) (e)
(c) (f)
Broken Bars

58. 36
Figure 2.7 Magnetic field and flux distribution under eight broken bars
condition; field distribution at (a) no load (b) half load (c)
full load; flux distribution at (d) no load (e) half load (f) full
load
(c) (f)
(b) (e)
(a) (d)
Broken Bars

59. 37
The field and flux distribution plots under different load conditions
of a healthy motor are shown in Figure 2.3. The Flux distribution plots of a
faulty motor with no load, half load and full load conditions with two broken
bars, are shown in Figure 2.4. The flux distribution plots for four, six and
eight-broken bars are shown in Figure2.5, Figure2.6 and Figure2.7
respectively. It can be seen that the plots drastically change their symmetry,
when the number of broken bars in the rotor increases.
2.6.1 Field and Flux Profile
The field and flux distribution is evaluated, with respect to the
circumference (which is calculated as the distance in mm). The plots for no
load, half load and full load conditions of a healthy motor are shown in Figure
2.8. The field and flux distribution for a faulty motor with two, four, six and
eight-broken bars are shown in Figure2.9, Figure2.10, Figure2.11 and
Figure2.12 respectively.
It can be seen that the amplitude of the flux function under no load
in a healthy condition is 0.0023 Wb, and under faulty condition with two,
four, six and eight broken bars are 0.0025 Wb, 0.0032 Wb, 0.0034 Wb and
0.0035 Wb respectively. Similarly, the amplitude for flux density under no
load with healthy condition is 0.1229 Wb/m2
and under faulty condition with
two, four, six, and eight broken bars are 0.1250 Wb/m2
, 0.1298 Wb/m2
,
0.1363 Wb/m2
and 0.1401 Wb/m2
respectively.
The amplitude of the flux function under half load in a healthy
condition is 0.0115 Wb, and under faulty condition with two, four, six and
eight broken bars are 0.0131 Wb, 0.0141 Wb, 0.0157 Wb and 0.0191Wb

60. 38
respectively. Similarly, the amplitude of the flux density under no load in a
healthy condition is 0.085332 Wb/m2
, and under faulty condition with two
four, six and eight broken bars are 0.9061 Wb/m2
, 0.9548 Wb/m2
, 1.0043
Wb/m2
and 1.0425 Wb/m2
respectively.
Under full load in a healthy condition, the amplitude of the flux
function is 0.0229 Wb, and under faulty condition with two, four, six and
eight broken bars are 0.0348 Wb, 0.0432 Wb, 0.0428 Wb and 0.0435 Wb
respectively. Similarly, the amplitude of the flux density under no load in a
healthy condition is 1.2278 Wb/m2
, and under faulty condition with two, four,
six and eight broken bars are 1.3745 Wb/m2
, 1.4861 Wb/m2
, 1.4830 Wb/m2
and 1.5032 Wb/m2
respectively.

61. 39
Figure 2.8 Field and flux distribution under healthy condition;
field distribution at: (a) no load (b) half load (c) full load
flux distribution at: (d) no load (e) half load (f) full load
(a) (d)
(b) (e)
(c) (f)

62. 40
Figure 2.9 Field and flux distribution under two broken bar condition;
field distribution at: (a) no load (b) half load (c) full load
flux distribution at: (d) no load (e) half load (f) full load
(a)
(b) (e)
(c)
(d)
(f)

63. 41
Figure 2.10 Field and flux distribution under four broken bars condition;
field distribution at: (a) no load (b) half load (c) full load
flux distribution at: (d) no load (e) half load (f) full load
(c) (f)
(b) (e)
(a) (d)

64. 42
Figure 2.11 Field and flux distribution under six broken bars condition;
field distribution at: (a) no load (b) half load (c) full load
flux distribution at: (d) no load (e) half load (f) full load
(c)
(b) (e)
(f)
(a) (d)

65. 43
Figure 2.12 Field and flux distribution under eight broken bars condition;
field distribution at: (a) no load; (b) half load; (c) full load
flux distribution at: (d) no load; (e) half load; (f) full load
(a) (d)
(b) (e)
(c) (f)

66. 44
From the above analysis, it is clear that the amplitude of the flux
function and flux density increases when the number of broken bars is
increased. The values of the flux function under different load conditions are
summarized in Table 2.2. There is a drastic increase in the flux function when
the load increases from no load to full load. It is also observed that the flux
function increases, when the number of broken bars increases from two to
eight.
Table 2.2 Flux Function
Condition
Flux function
(Wb)
Percentage change
(%)
No Load
Condition
Healthy 0.0023 -
Two Broken Bars 0.0025 8.69
Four Broken Bars 0.0032 39.13
Six Broken Bars 0.0034 47.82
Eight Broken Bars 0.0035 52.17
Half Load
Condition
Healthy 0.0115 -
Two Broken Bars 0.0131 13.91
Four Broken Bars 0.0141 22.60
Six Broken Bars 0.0157 36.52
Eight Broken Bars 0.0191 66.08
Full Load
Condition
Healthy 0.0229 -
Two Broken Bars 0.0348 51.96
Four Broken Bars 0.0432 88.64
Six Broken Bars 0.0428 86.89
Eight Broken Bars 0.0435 89.95

67. 45
The flux function increases to 8.69% for two broken bars, 39.13%
for four broken bars, 47.82% for six broken bars and 52.17% for eight broken
bars. The respective percentage change in the flux function is also tabulated.
Table 2.3 Flux Density under different load conditions
Condition
Flux density
B
(Wb/m2
)
Percentage change
(%)
No Load
Condition
Healthy 0.1229 -
Two Broken
Bars
0.1250 1.70
Four Broken
Bars
0.1298 5.61
Six Broken
Bars
0.1363 10.90
Eight
Broken Bars
0.1401 13.99
Half Load
Condition
Healthy 0.8532 -
Two Broken
Bars
0.9061 6.20
Four Broken
Bars
0.9548 11.90
Six Broken
Bars
1.0043 12.89
Eight
Broken Bars
1.0425 22.18
Full Load
Condition
Healthy 1.2278 -
Two Broken
Bars
1.3745 11.94
Four Broken
Bars
1.4861 21.03
Six Broken
Bars
1.4830 20.78
Eight
Broken Bars
1.5032 22.43

68. 46
The values of flux density under different load conditions are
presented in Table 2.3. The flux density increases by 1.70% for two broken
bars, 5.61% for four broken bars, 10.90% for six broken bars and 13.99% for
eight broken bars respectively. The percentage changes in the flux function
and flux density are calculated for no load, half load and full load conditions,
and shown in the Table 2.2 and Table 2.3.
2.7 TRANSIENT ANALYSIS
Analyzing the performance of the motor during transient periods is
difficult under real time operating conditions. Hence, simulation methods are
used for the predication of the transient performance of the Induction Motor.
The magnet package allows modeling the dynamics of motion, if there is a
moving component in the device. To model the effects of motion, the eddy
currents that are induced due to motion, are taken into account. The transient
2D analysis is performed in a healthy condition, and various faulty conditions,
for various loads, and the parameters like instantaneous magnetic energy, and
the current and flux linkages are compared.
2.8 MODEL OF INDUCTION MOTOR FOR TRANSIENT
ANALYSIS
The electrical model of a three phase squirrel cage star connected
induction motor is shown in Figure 2.13. The power source is considered as a
voltage source connected with the series resistance and inductance of the
stator winding in each phase. The rotor is made of short-circuited bar
conductors. The equivalent circuit of the three phase squirrel cage induction
motor is shown in Figure 2.14.

69. 47
Figure 2.13 Model of the three phase squirrel cage induction motor
Figure 2.14 Equivalent circuit of the three phase squirrel cage induction
motor

70. 48
2.9 ANALYSIS OF AN INDUCTION MOTOR DURING THE
TRANSIENT PERIOD
The stator is excited by a three phase AC supply, and the rotor
rotates due to the torque developed. The induced emf circulates the current in
the rotor, and the motor is operated in the full load condition. The self and
mutual inductances are calculated from the flux linkages of the coil and the
current passing through it. The relative speed at the time of starting is the
maximum, and hence, a large emf is induced in the rotor conductors. Due to
this very high current in the rotor which is generally five to seven times the
full load current flows. The starting current in the stator is eight to ten times
the rated current. When a bar is broken, the current through the broken bar is
zero.
Figure 2.15 Stator current plots under no load condition (a) healthy condition
(b) two broken bars (c) four broken bars (d) eight broken bars
(c) (d)
(a) (b)

71. 49
The stator current for the healthy and faulty conditions with two,
four and eight broken bars is shown in Figure 2.15 and Figure 2.16
respectively.
Figure 2.16 Stator current plots under full load condition
(a) healthy condition (b) two broken bars (c) four broken
bars (d) eight broken bars
From the simulation results, it is observed that the currents are high
at the start and vary with time in an oscillatory manner, when the time is
increased.
(a)
(b)
(d)
(c)

72. 50
Table 2.4 Summary of the stator current
Condition Current (A) Percentage change
(%)
No Load
Healthy 7.35 -
Two Broken
Bars
9.99 35.86
Four Broken
Bars
10.50 42.88
Eight Broken
Bars
11.15 51.79
Full Load
Healthy 40.46 -
Two Broken
Bars
49.47 22.25
Four Broken
Bars
52.53 29.82
Eight Broken
Bars
61.44 51.84
From Table 2.4, it can be observed that the value of the current
increases, with the increase in the number of broken bars. For a healthy
motor, the current obtained is 40 A, and under two broken bars condition, the
current obtained is 49 A. Further, as the broken bars increase to eight, the
current obtained is 61 A. The percentage change in current for two broken
bars is 22%, for four broken bars 29% and for eight broken bars 51%.This
indicates an increase in the percentage change, with the increase in the
broken bars.

73. 51
Figure 2.17 Flux linkage plots under no load condition (a) healthy
condition (b) two broken bars (c) four broken bars (d) eight
broken bars
(a) (b)
(c) (d)

74. 52
Figure 2.18 Flux Linkage plots under full load condition (a) healthy
condition (b) two broken bars (c) four broken bars (d) eight
broken bars
The flux linkage plots for the healthy and faulty conditions with
two, four and eight broken bars are shown in Figure 2.17 and Figure2.18. The
flux linkages for different load conditions are given in Table 2.5.
(a) (b)
(c) (d)

75. 53
Table 2.5 Summary of the flux linkage
Condition Flux linkage
(Wb)
Percentage change
(%)
No Load
Healthy 0.01104 -
Two Broken Bars 0.01327 20.19
Four Broken Bars 0.01791 62.22
Eight Broken Bars 0.02205 99.72
Full Load
Healthy 0.16668 -
Two Broken Bars 0.19386 16.30
Four Broken Bars 0.22034 32.19
Eight Broken Bars 0.31012 86.05
From Table 2.5, it can be observed that the flux linkage increases
with the increase in the number of broken bars, i.e., in the healthy motor
condition, the flux linkage obtained is 0.16668 Wb and under two broken bars
condition, it is 0.19386 Wb. Further, as the broken bars increase to eight, the
flux linkage obtained is 0.3102 Wb. The percentage change in torque for two
broken bars is 16%, for four broken bars 32% and for eight broken bars 86%.
This indicates an increase in the percentage change with the increase in the
number of broken bars.

76. 54
Figure 2.19 Magnetic energy plots under no load condition
(a) healthy condition (b) two broken bars (c) four broken
bars (d) eight broken bars
(b)
(a)
(c)
(d)

77. 55
Figure 2.20 Magnetic energy plots under full load condition (a) healthy
(b) two broken bars (c) four broken bars (d) six broken bars
(e) eight broken bars
(a) (b)
(c) (d)

78. 56
The magnetic energy plots for the healthy and faulty conditions
with two, four and eight broken bars are shown in Figure 2.19 and Figure
2.20. The magnetic energy at the start is found to be high, and it gradually
decreases. It is observed that the energy is reduced, as the concentration of the
magnetic fluxes around the bar increases due to breakage.
Table 2.6 Summary of the magnetic energy
Condition Magnetic
Energy(Joules)
Percentage change
(%)
No
Load
Healthy 1.58446 -
Two Broken Bars 1.57958 0.307
Four Broken Bars 1.28950 18.61
Eight Broken Bars 1.16965 26.17
Full
Load
Healthy 174.2153 -
Two Broken Bars 157.6726 9.49
Four Broken Bars 125.8326 27.77
Eight Broken Bars 91.4319 47.51
From Table 2.6, it can be observed that the Magnetic energy
decreases with an increase in the number of broken bars, i.e., for a healthy
motor the energy obtained is 174 Joules, and for two broken bars condition,
the energy obtained is 157 Joules. Further, as the number of broken bars
increase to eight, the energy obtained is 91 Joules.
The graphical representation of the Magnetic energy is shown in
Figure 2.21.

79. 57
0
5
10
15
20
25
30
35
40
45
50
Healthy 2 broken bar 4 broken bar 8 broken bar
Noload
Full load
percentage
change
in
energy
Figure 2.21 Graphical representation of magnetic energy
The percentage change in energy for two broken bars is 9%, for
four broken bars 27% and for eight broken bars 47%. This shows a decrease
in the percentage change with the increase in the number of broken bars.
2.10 CONCLUSION
Broken bars saturate the magnetic force distribution on the rotor
tooth adjacent to the bars that are broken. Hence, the bars adjacent to broken
bars become more susceptible to additional wear and eventual breaking.
The simulation results for the static and transient 2D analysis for
the rotor broken bar condition are presented in this chapter. From the
summary, it can be observed that during the static analysis, the flux function
and flux density increase as the number of broken bars increases. The
simulated values of the average flux density and flux function correlate with
the theoretical values. Similarly, during the transient analysis, the stator phase
current, flux linkage and magnetic energy decrease when the number of

80. 58
broken bars increases. The comparison of the simulation results with the
theoretical values is shown in Table 2.7.
Table 2.7 Comparison of the simulation results with the theoretical values
Parameters under
Healthy condition
Theoretical value Simulation value
Flux Function 0.02257 Wb 0.0225 Wb
Flux Density 1.187 Wb/m² 1.227 Wb/m²

81. 59
CHAPTER 3
FAULT ANALYSIS OF THE VSI FED INDUCTION
MOTOR DRIVE
3.1 GENERAL
The induction motor has acquired an essential place in industrial
applications, with its increased advantages and steady responses. With
growing demands, an efficient machine is the need of the hour. So the fault
detection in the machine becomes more prominent and necessary to enhance
its operations. The growing popularity of AC drives is chiefly due to their
ability to control the speed of the induction motor, which is most commonly
used in industry. This Chapter deals with the harmonic analysis of the motor
current signatures for the following types of faults in the converter.
1. open circuit of one of the MOSFETs in the inverter
2. open circuit fault in phase A
3. short circuit in one of the MOSFETs in the inverter
The faults are introduced in the inverter modules of the VSI fed
induction motor drive.

82. 60
3.2 VSI FED DRIVE
The circuit for the VSI fed drive is shown in Figure 3.1. In the
variable frequency drives, a three phase AC voltage is converted to DC, using
a rectifier. The DC bus contains capacitors to accept power from the rectifier,
store it and deliver that power to the induction motor through the inverter
section.
Figure 3.1 VSI fed drive
The inverter contains transistors that deliver power to the motor.
The MOSFET can switch on and off several thousand times per second and
precisely control the power delivered to the motor. The MOSFET uses the
Pulse Width Modulation (PWM) technique to simulate a sine wave current at
the desired frequency to the motor. A variable output voltage can be obtained
by varying the input DC voltage, and maintaining the gain of the inverter
constant. On the other hand, if the DC input voltage is constant and not
controllable, a variable voltage can be obtained, by varying the gain of the
inverter by the PWM control within the inverter.

83. 61
3.2.1 Open Circuiting of one of the MOSFETs in the Inverter
In this case, one of the six MOSFETs is replaced by the very high
resistance of one mega ohm. The motor current and FFT are recorded and
compared with the waveforms of a healthy motor drive system.
3.2.2 Open Circuiting of phase A in Inverter
To simulate this condition, MOSFETs in the phase A leg have been
replaced by the high resistance of one Mega ohm.
3.2.3 Short Circuiting of one of MOSFETs in the Inverter
To simulate the short circuit condition, one of MOSFETs in phase
A has been replaced by a low resistance of one micro ohm.
3.3 SIMULINK MODEL OF THE VSI FED DRIVE
The circuit for the detection of faults for the three phase induction
motor is simulated by using MATLAB. The simulation circuit for the VSI fed
drive is shown in Figure3.2. The 415v AC voltage is applied to the 5HP, 3
squirrel cage induction motor.
The circuit involves a rectifier and inverter circuit, connected
through a DC link. The inverter operates in the 180 degree mode.

84. 62
Figure 3.2 Simulation circuit of the VSI fed drive

85. 63
3.3.1 Output Waveforms
The waveforms of the line current for phases A, B and C under a
healthy condition are shown in Figure 3.3. It is observed that the current is
4.6A under a healthy condition.
Figure 3.3 Line current waveforms of the VSI fed drive under a
healthy condition

86. 64
Figure 3.4 Line current spectrum of the VSI fed drive under the
healthy condition
The line current spectrum under the healthy condition is shown in
Figure 3.4. The THD value is 4.70%.
3.4 FAULT ANALYSIS OF INVERTER MODULE
In this section, various faults are introduced in the inverter of the
VSI-fed drive. The simulation results are given as follows.
3.4.1 Open Circuit of one of the MOSFETs in the Inverter Module
To simulate this condition, the upper MOSFET in phase A has been
replaced by a high resistance of one Mega ohm. The introduction of the high
resistance with one of the six MOSFETs is equivalent to the open circuiting
of one of the six MOSFETs. The simulation circuit of the open circuit of the
upper leg of phase A MOSFET in the inverter is shown in Figure 3.5.

87. 65
Figure 3.5 Simulation circuit for the open circuit of the upper leg of
Phase A MOSFET in the inverter
3.4.1.1 Output waveforms
The waveforms of the line currents of the three phases under the
open circuit of the upper leg of phase A MOSFET in the inverter are shown in
Figure 3.6. It is observed that the current direction gets reversed in Phase A.
The current is measured as 3.83A. The Phase currents Ib&Ic are distorted
under the open circuit faulty condition.
Figure 3.6 Line current wave forms for the open circuit of the upper
leg of Phase A MOSFET in the inverter

88. 66
(a) Phase A line current Spectrum
(b) Phase B line current Spectrum
(c) Phase C line current Spectrum
Figure 3.7 Line current spectra for open circuit of upper leg of Phase A
MOSFET in the inverter

89. 67
The line current spectra with Phase A MOSFET open circuited in
the inverter is shown in Figure 3.7. The THD in Phase A is 69.24%. It is
observed that the THD increases by 11 times with respect to the healthy
condition.
3.4.2 Open Circuiting of Phase A in the Inverter
To simulate this condition, the MOSFET in the phase A leg has
been replaced by a high resistance of one Mega ohm. The introduction of the
high resistance in phase A is equivalent to the open circuiting of phase A. The
Simulink circuit is shown in Figure.3.8.
Figure 3.8 Simulation circuit for the open circuiting of phase A
3.4.2.1 Output waveforms
The waveforms of the line current of the three phases under a faulty
condition are shown in Figure.3.9. From the simulation results it is observed
that Phase A current becomes zero. The line currents Ia & Ic are distorted
under a faulty condition.

90. 68
Figure 3.9 Line current waveforms for the open circuiting of Phase A
(a) Phase A Line current Spectrum
Figure 3.10 Line current spectra for the open circuiting of Phase A

91. 69
(b) Phase B line current spectrum
(C) Phase C line current spectrum
Figure 3.10 (Continued)
The line current spectra with Phase A open circuited in the inverter
is shown in Figure 3.10. The THD value of phase A current is increased to
81%. The THD increases by 17 times, with respect to the healthy condition.

92. 70
3.4.3 Short Circuit Fault in the Upper leg of Phase A of the Inverter
To simulate this faulty condition, the upper leg MOSFET in phase
A is replaced by a low resistance of one micro ohm, which is equivalent to the
short circuiting of the upper leg in phase A. The simulink circuit is shown in
Figure 3.11.
Figure 3.11 Simulation circuit for the short circuiting of the upper leg
MOSFETs in Phase A
3.4.3.1 Output waveforms
The waveform of the line current and voltage of the three phases A,
B & C respectively, due to short circuiting the upper leg of Phase A faulty
condition is shown in Figure 3.12. On introducing the fault, the fundamental
line current is reduced to 0.3A in phase A.

93. 71
Figure 3.12 Line current for the short circuiting of the upper leg
MOSFETS in phase A
(a) Phase A line current spectrum
Figure 3.13 Line current spectra for short circuiting of upper leg
MOSFETS in phase A

94. 72
(b) Phase B line current spectrum
(c) Phase C line current spectrum
Figure 3.13 (Continued)
The line current spectra under the faulty condition are shown in
Figure 3.13. It is noted that the output line current waveforms get distorted on
the application of faults. The THD for the current spectrum in Phase A is
17.64%, Phase B 24.13% and in Phase C 17.72% respectively. The DC
component is introduced due to the short circuit fault.
3.5 SUMMARY OF THE FFT ANALYSIS OF THE VSI FED
DRIVE
The summary of the FFT analysis of the VSI fed Induction motor
drive is given in Table 3.1. From the table, the effect of a fault in all the three
phases can be observed. In a VSI fed drive without any fault current, the THD

95. 73
is 4.7%. The current spectrum is within the IEEE standard of 5%. On
introducing an open circuit fault in upper leg MOSFET of phase A, the THD
in the line current is 69.24%. Due to short circuiting of upper MOSFET in
phase A, the THD in the line current is 17.64%. Similarly, due to the
complete open circuit fault in Phase A, the THD in the line current is 81%. In
general, due to a fault, the THD increases. This leads to excess heating and
reduction of the efficiency of the motor.
Table 3.1 Summary of the FFT analysis
Conditions Parameters
VSI
Phase A Phase B Phase C
Healthy
Circuit
Line current (A) 4.676 4.676 4.718
Current THD
(%)
4.7 4.7 4.54
Open circuit
fault
in phase A
MOSFET
Line current (A) 3.831 5.582 2.687
Current THD
(%)
69.24 23.48 50.83
Phase A open
circuited
Line current (A) 0 4.084 4.083
Current THD
(%)
81.01 4.59 4.59
Short circuit
fault
in phase A
MOSFET
Line current (A) 0.356 0.507 0.656
Current THD
(%)
17.64 24.13 17.72

96. 74
3.6 CONCLUSION
In this Chapter, the THDs of the VSI fed drive are evaluated under
various faults in the inverter circuit. The output waveforms are obtained and
THD values tabulated. From the simulation, it is seen that the current
harmonics are increased for both the open and short circuit faulty conditions.
The current direction in phase A is reversed, due to the open circuit of one of
the MOSFETs in phase A. But for the phase A open circuit fault, the current
in phase A becomes zero. In a short circuit fault, the fundamental components
are almost zero, but the DC components are introduced. The line current
spectra under four different faulty conditions are distinctly different.

97. 75
CHAPTER 4
FAULT ANALYSIS OF THE CSI FED INDUCTION
MOTOR DRIVE
4.1 GENERAL
This chapter deals with the fault analysis of the CSI fed induction
motor drive. An inverter, in which the input current is maintained constant, is
called the current fed inverter. The circuit of a CSI fed induction motor drive
is shown in Figure 4.1. In the current source inverter, the input behaves as a
current source. This can be incorporated by connecting a high inductance in
series to the voltage source.
Figure 4.1 CSI fed Induction motor Drive
Induction

98. 76
The inverter contains transistors that deliver power to the motor.
The MOSFET can switch on and off several thousand times per second and
precisely control the power delivered to the motor. The MOSFET uses the
PWM technique to supply sinusoidal current at the desired frequency to the
motor.
The CSI fed drive provides controlled input DC current. Hence the
problem of a short circuit and misfiring of the switching devices would not be
serious. It has the enhanced ability to handle reactive or regenerative loads
without freewheeling diodes.
4.2 CIRCUIT MODEL OF THE CSI FED DRIVE
The circuit for the detection of faults of the CSI fed three phase
induction motor is simulated by using MATLAB. The simulation circuit of
the CSI fed drive is shown in Figure 4.2. The 415V AC voltage of variable
frequency is applied to the induction motor.
Figure 4.2 Simulation circuit of the CSI fed drive

99. 77
4.2.1 Output Waveforms
The simulation results of the CSI fed drive under healthy conditions
are shown in Figure 4.3 and Figure 4.4. It is observed that the Line voltage is
590.4V (peak) and the THD of voltage is 4.56% under healthy conditions.
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-1000
-500
0
500
1000
Time(s)
Vab(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-1000
-500
0
500
1000
Time(s)
Vbc(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-1000
-500
0
500
1000
Time(s)
Vca(V)
Figure 4.3 Line voltage waveforms of the CSI fed drive under a
healthy condition

100. 78
Figure 4.4 Line voltage spectra of the CSI fed drive under healthy
conditions

101. 79
4.3 FAULT ANALYSIS OF THE INVERTER MODULE
Simulation studies are done for various faults in the inverter of the
CSI fed drive. The simulation results are given in the following sections.
4.3.1 Open Circuiting of one of the Six MOSFETs in the Inverter
To simulate this condition, the upper MOSFET in phase A has been
replaced by a high resistance of one Mega ohm. The introduction of the high
resistance with one of the six MOSFETs is equivalent to the open circuiting
of one of the six MOSFETs. The simulation circuit for the upper MOSFET in
Phase A open circuited in the inverter is shown in Figure 4.5.
Figure 4.5 Simulation circuit for the upper MOSFET of Phase A open
circuited in the inverter

102. 80
4.3.1.1 Output Waveforms
The waveforms of the line voltages of the three phases under faulty
conditions are shown in Figure 4.6. It is observed that the voltage direction
gets reversed in Phase A. The voltage is measured as 1.99V between Phase A
and Phase B. The Line voltages Vbc &Vca are distorted under the open circuit
faulty condition.
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-4
-3
-2
-1
0
1
2
Time(s)
Vab(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-6
-4
-2
0
2
4
Time(s)
Vbc(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-4
-2
0
2
4
6
Time(s)
Vca(V)
Figure 4.6 Line voltage waveforms for the upper MOSFET of phase A
open circuited in the inverter

103. 81
Figure 4.7 Line voltage Spectra for the upper MOSFET of Phase A
open circuited in the inverter

104. 82
The line voltage spectra with the upper MOSFET of Phase A open
circuited in the inverter is shown in Figure 4.7. The THD value of Vab is
47.12%. The THD increases by 10 times, with respect to a healthy condition.
4.3.2 Open Circuiting of the Phase A leg in the Inverter
To simulate this condition, the upper and lower MOSFETs in
phase A are replaced by a high resistance of one Mega Ohm. The Simulation
circuit with the phase A MOSFET open circuited in the inverter is shown in
Figure 4.8.
Figure 4.8 Simulation circuit with Phase A MOSFET open circuited in
the inverter

105. 83
4.3.2.1 Output waveforms
The waveforms of the line voltages of the three phases under a
faulty condition are shown in Figure 4.9. From the simulation results it is
observed, that the line voltages Vab, Vbc & Vca are 0.3V, 0.6V & 0.3V
respectively.
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-0.4
-0.2
0
0.2
0.4
Time(s)
Vab(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-1
-0.5
0
0.5
1
Time(s)
Vbc(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-0.4
-0.2
0
0.2
0.4
Time(s)
Vca(V)
Figure 4.9 Line voltage waveforms with Phase A MOSFET open
circuited in the inverter

106. 84
Figure 4.10 Line voltage Spectra with Phase A MOSFET open circuited
in the inverter

107. 85
The line voltage spectra with Phase A MOSFET open circuited in
the inverter are shown in Figure 4.10. The THD value of Vab is 27.8 %. The
THD increases by 7 times, with respect to a healthy condition.
4.3.3 Short Circuit Fault in the Upper MOSFET of Phase A Leg of
the Inverter
To simulate this condition, the upper MOSFET in phase A has been
replaced by a low resistance of one micro ohm. The replacement of the
MOSFET with low resistance is equivalent to the short circuiting of one of
the six MOSFETs. The simulation circuit for this fault is shown in
Figure 4.11.
Figure 4.11 Simulation Circuit for Short Circuiting of the Upper
MOSFETs in Phase A Leg

108. 86
4.3.3.1 Output waveforms
The waveforms of the line voltage for the three phases A, B & C
respectively, due to Short Circuiting of the Upper leg MOSFET of Phase A
under faulty conditions are shown in Figure 4.12. On introducing the fault, the
line Voltage of Vab is reduced to 111.1V.
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-100
-50
0
50
100
150
200
Time(s)
Vab(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-200
-150
-100
-50
0
50
100
150
Time(s)
Vbc(V)
6 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.1
-150
-100
-50
0
50
Time(s)
Vca(V)
Figure 4.12 Line voltage waveforms of the upper MOSFET of phase A
Leg short circuited

109. 87
Figure 4.13 Line voltage spectrums of the upper MOSFET of phase A
Leg short circuited

110. 88
The line voltage spectra under the short circuit faulty condition are
shown in Figure 4.13. It is noted that the line voltage waveforms get distorted
on the application of faults. The THD for the line voltage spectrum of Vab is
52.69%. The THD increases by 12 times, with respect to a healthy condition.
4.4 SUMMARY OF THE FFT ANALYSIS OF THE CSI FED
DRIVE
The summary of the FFT analysis of the CSI fed Induction motor
drive is given in Table 4.1. In a CSI fed drive without any fault, the THD in
line voltage is 4.56%. On introducing an open circuit fault in the upper leg
MOSFET of phase A, the THD in the line voltage is 47.12%. Due to short
circuiting of the upper MOSFET in phase A, the THD in line Voltage is
52.69%, and in an open circuit fault in Phase A, the THD in line voltage is
60.48%. In general the THD in CSI fed drive is higher than that of VSI fed
drive.
Table 4.1 Summary of the FFT analysis of the CSI fed drive
Conditions Parameters CSI
Vab(peak) Vbc(peak) Vca(peak)
Healthy Circuit Line Voltage (v) 590.4 590.4 590.2
Voltage THD (%) 4.56 4.56 4.56
Open circuit
fault
In ph-A
MOSFET
Line Voltage (v) 1.99 2.33
2.7 9
Voltage THD (%) 47.12 35.58 19.59
Phase A open
circuited
Line Voltage (v) 0.15 0.21 0.12
Voltage THD (%) 60.48 33.75 48.04
Short circuit
fault
In ph-A
MOSFET
Line Voltage (v) 111.1 124.7
61.58
Voltage THD (%) 52.69 45.84 52.23

111. 89
4.5 CONCLUSION
In this Chapter, the THDs of the CSI fed drive are evaluated under
various faulty conditions of the inverter circuit. The output waveforms are
obtained and the THD values tabulated. From the simulation results it is seen,
that the voltage harmonics increase with faults in the inverter module. The
THD value increases when fault occurs in the inverter. The CSI fed drive
provides controlled input DC current. Hence, the problem of a short circuit
and misfiring of the switching devices would not be a serious problem.

112. 90
CHAPTER 5
FAULT TOLERENT VOLTAGE SOURCE INVERTER FED
INDUCTION MOTOR
5.1 GENERAL
A standard three-phase voltage source inverter is used in AC drives.
This type of inverter creates a relatively well-defined switched voltage
waveform at the induction motor (I.M) terminals. If one of its power switches
fails, this voltage waveform will change, and critical damage can occur either
in the inverter or in the motor connected to it. For that purpose, a voltage
source inverter reconfiguration strategy is used, based on a stator phase
connection (SPC), as illustrated in Figure 5.1.
Figure 5.1 Typical VSI fed drive with SPC
C
C

113. 91
To implement the SPC hardware drive reconfiguration, three
controlled power switches are essential, represented by the switches Su, Sv,
and Sw in Figure 5.2.
Figure 5.2 Induction motor drive structure for a reconfiguration based
on SPC
After the fault detection, the inverter control system also isolates
the faulty leg, and connects it directly to the midpoint of the DC link. Figure
5.3 illustrates, as an example, the required SPC voltage source inverter
reconfiguration for an open-circuit fault in the inverter leg A.
Figure 5.3 Induction motor drive with SPC drive reconfiguration for
an inverter leg fault (leg A)

114. 92
Time (s)
5.2 FAULT TOLERENT INVERTER FED DRIVE WITH SPC
The circuit for the fault tolerant voltage source inverter fed three
phase induction motor under stator phase configuration is simulated, by using
MATLAB. The simulation circuit of the VSI fed induction motor drive with
SPC is shown in Figure 5.4.
Figure 5.4 Simulation circuit of the VSI fed induction motor drive with SPC
5.2.1 Output Waveforms
The line current Vs time waveforms for the three phases A, B& C
on the motor side under the SPC configuration are shown in Figure 5.5.
a. Line Current Waveform of Phase A
Figure 5.5 Simulation results of the VSI fed induction motor drive with SPC
Line
Current
(A)

115. 93
b. Line Current Waveform of Phase B
c. Line Current Waveform of Phase C
d. Line current spectrum of phase A
Figure 5.5(Continued)
Line
Current
(A)
Time (s)
Time (s)
Line
Current
(A)

116. 94
5.3 FAULT TOLERANT VSI FED DRIVE WITH OPEN
CIRCUIT FAULT
The circuit for the fault tolerant voltage source inverter fed three phase
induction motor, under open circuit fault (leg A) is shown in Figure 5.6.
Figure 5.6 Simulation circuit of a fault tolerant VSI fed three phase
induction motor with open circuit fault
In this case, during the fault, the breaker connected to the faulty leg
is closed. It works like a three phase induction motor working with a four
switch inverter.
5.3.1 Output Waveforms
The waveforms of the line current Vs time of the three phases A, B
& C respectively, under the faulty conditions are shown in Figure 5.7.

117. 95
a. Line Current Waveform of Phase A
b. Line Current Waveform of Phase B
c. Line Current Waveform of Phase C
d. Line current spectrum of phase A
Figure 5.7 Simulation results of the fault tolerant VSI fed induction
motor under an open circuit fault
Line
Current
(A)
Time (s)
Line
Current
(A)
Time (s)
Line
Current
(A)
Time (s)

118. 96
It is observed that for Phase A, the current is improved. The FFT
spectrum under the open circuit condition in a fault tolerant VSI fed inverter,
is shown in Figure 5.7(d). The Total Harmonic distortion is 23%.
5.4 THREE PHASE FOUR SWITCH INVERTER FED
INDUCTION MOTOR
The circuit of a three phase four switch inverter fed induction motor
shown in Figure 5.8.
Figure 5.8 Simulation circuit of the three phase four switch inverter fed
induction motor
The circuit for the fault tolerant voltage source inverter fed three
phase induction motor, under open circuit fault(leg A) is shown in Figure 5.8.
To verify the operation, the three phase four switch inverter fed induction
motor is simulated.

119. 97
5.4.1 Output Wave Forms
The waveforms of the line current Vs time of the three phases A, B
& C respectively, under the three phase four switch inverter fed induction
motor are shown in Figure 5.9.
a. Line Current Waveform of Phase A
b. Line Current Waveform of Phase B
c. Line Current Waveform of Phase C
Figure 5.9 Simulation results of the three phase four switch inverter
fed induction motor

120. 98
d. Line spectrum of phase A
Figure 5.9 (Continued)
5.5 SUMMARY OF THE FFT ANALYSIS OF A FAULT
TOLERANT VOLTAGE SOURCE INVERTER FED
DRIVE WITH SPC
The summary of the THD for faults in a normal VSI fed inverter,
and the fault tolerant VSI fed inverter is given in Table 5.1. It can be observed
that the total harmonic distortion is decreased, when the fault tolerant VSI is
introduced. For the normal inverter fed drive due to an open circuit fault, the
THD value is 81%, whereas for the fault tolerant inverter fed drive, it is 23%.
Table 5.1 FFT analysis of the fault tolerant VSI fed drive
VSI fed induction motor with Phase A open circuit
fault
Line current(A) THD
0.0007 81
Fault tolerant VSI fed induction motor with SPC for
Phase A open circuit fault
Line current(A) THD
1.5 23

121. 99
5.6 FAULT TOLERANT VSI FED INDUCTION MOTOR DRIVE
WITH LEG SWAP MODULE
A Fault tolerant design is proposed which is capable of operating
even after the occurrence of a fault during runtime. The Simulink model of
the fault tolerant VSI fed induction motor drive is shown in Figure 5.10.
Figure 5.10 Simulink model of a fault tolerant VSI fed induction motor
drive
The above Simulink model includes a leg swap module which
contains an auxiliary leg. The logical operator in the leg swap module senses
the fault current. The corresponding fault phase is identified by the Phase
identifier. The fault Phase is isolated and replaced by auxiliary leg. The
swapping is done by means of a breaker. The leg swap module is presented in
Figure5.11.

122. 100
Figure.5.11 Leg swap module used in the fault tolerant inverter

123. 101
The proposed Leg Swap module comprises of two important
blocks. They are as follows:
Logical Operator: The operation of the logical operator is based
on the logic given in Table 5.2.
Table 5.2 Output of the logical operator
Current OUTPUT
Ia or Ib or Ic ~0 0
For other values Output is the current value itself
Phase Identifier: Tags the signal with appropriate phase signal.
5.6.1 Logical Operator System
The Simulink model of the logical operator system is given in
Figure 5.12. In the figure, Path 1 is closed when the condition is true. Path 2
is closed when the condition is false. When the Control signal >=0, a negative
step signal is applied. This signal becomes negative in 0.5 seconds. Hence,
path 2 is closed for 0.5 second. This time can be varied by varying the step
time. Till 0.5second, the output is 1. During a fault, the fault phase current is
of the order of mA. Hence, the output is rounded to zero, by means of the
rounding function.
Figure.5.12 Logical operator system

124. 102
5.6.2 Phase Identifier
If a fault occurs in the phase, the input signal to the phase identifier
becomes one. The input is converted from the Boolean to a single. It is
multiplied based on the value given in table 5.3. The output of the phase
identifier is an equivalent number of the fault phase such as 1 for Phase A
failure.
Table 5.3 Phase Identifier multiplier table
Phase Multiplier
A 1
B 2
C 3
The Simulink model of the phase identifier is given in Figure 5.13
Figure 5.13 Phase identifier
5.6.3 Line Current Waveforms
415V AC voltage is applied to the induction motor. In a healthy
condition, the performance of the fault tolerant inverter was similar to that of
the healthy VSI, as shown in Figure 3.5. The waveform of the line current
versus time during the single phase open circuit fault in phase A, is presented

125. 103
in Figure 5.14.a. The magnitude of the current in Phase A is 4.71 A, in phase
B is 4.66 A and in phase C 4.54 A respectively.
(a) Line current wave forms during the single phase open circuit fault
(b) Line Current spectra of phases A, B & C
Figure 5.14 Simulation results of a Fault tolerant inverter fed induction
motor with the leg swap module

126. 104
The line current spectrum under the faulty condition is shown in
Figure 5.14.b. The total harmonic distortion of the phases is observed. The
THD values in Phase A, Phase B, and Phase C is 4.7%.
5.7 SUMMARY OF THE FFT ANALYSIS OF THE FAULT
TOLERANT VOLTAGE SOURCE INVERTER FED DRIVE
WITH THE LEG SWAP MODULE
The comparison of fault operation of the VSI and Fault tolerant
VSI, is given in Table.3.4. From the tabulations, it is inferred that during the
single phase open circuit fault, the fault tolerant inverter was able to replicate
the performance of a healthy VSI system. The performance of the fault
tolerant inverter was similar even when the single phase open circuit fault
occurs either in phase B or phase C.
Table 5.4 A Comparison of the Fault operation of the VSI and Fault
Tolerant VSI
Phase Healthy VSI
During fault operation
Voltage source
inverter
Fault tolerant voltage
source inverter
Current
(A)
THD
(%)
Current
(A)
THD
(%)
Current
(A)
THD
(%)
A 4.67 4.71 0.038 80.4 4.82 4.71
B 4.67 4.71 4.08 4.59 4.84 4.66
C 4.67 4.52 4.08 4.59 4.87 4.54

127. 105
5.8 CONCLUSION
In this chapter, the fault tolerant VSI fed drive is developed to work
under an open circuit faulty condition. the output waveforms are obtained and
the THD values tabulated. From the simulation it is seen that there is a 30%
decrease in the harmonic distortion, by using the fault tolerant VSI fed drive
with SPC configuration. But the fault tolerant inverter with the leg swap
module replicates the performance of a healthy VSI. The Leg swap module
requires three more bidirectional switches for controlling the auxiliary leg.

128. 106
CHAPTER 6
HARDWARE IMPLEMENTATION
6.1 GENERAL
This Chapter deals with the hardware circuit implementation of the
voltage control of the three phase induction motor with a healthy and an open
leg faulty condition. The whole circuit can be brought down with a power
supply circuit, the control circuit and the power circuit. The performance of
this circuit is evaluated on the basis of the low voltage laboratory scaled down
prototype.
6.2 HARDWARE DESCRIPTION
The hardware design involves the following sections
i. Power Supply Circuit.
ii. Driver Circuit
iii. Controller Circuit
iv. Power Circuit
An AC voltage of 230V is fed to the power supply circuit
comprising of ICs 7805 and 7812 to obtain the required DC output voltages.
The 5V DC output voltage obtained from the regulator IC 7805 is given to the
controller circuit, and the 12V DC output voltage obtained from the regulator
IC 7812 is given to the driver circuit. The control circuit comprising of the

129. 107
microcontroller AT89C51and IR2110 decides the sequence of pulses to be
given to the switches in the power circuit. The driver circuit amplifies the
pulses to the required level. The power circuit is an arrangement of six
MOSFET switches (IRF840) with an input AC supply. The gate terminals of
the switches are triggered, according to the output frequency requirements.
The block diagram of the hardware design is shown in Figure 6.1.
Figure 6.1 Block diagram of the hardware design
6.2.1 Power Supply Circuit
The circuit consists of the following components:
i. Transformer
ii. Bridge rectifier
iii. Filter
iv. IC Regulator

130. 108
6.2.2 Driver Circuit
The driver circuit is used for the purpose of the isolation of the
negative current to the microcontroller, amplification of the voltage and to
create a constant voltage source. The driver circuit diagram is shown in
Figure 6.2. The square pulse should have a constant voltage of 5V. This
voltage is connected to the isolator for isolation purposes. Isolation refers to
the separation of the power circuit from the microcontroller. The output
voltage from the microcontroller is given to the IR2110 driver IC. The output
voltage will have an increased magnitude that will be sufficient for driving the
MOSFET IRF840.
Figure 6.2 Driver circuit
6.2.3 Controller Circuit
The main part of the hardware circuit is the Micro controller
AT89C51. A suitable program is written in the controller to generate a train
of pulses. In the control circuit, a Microcontroller is used. The driving pulse
required for the MOSFETs IRF840 is obtained from this controller. For this
the AT89C51 IC is used.

131. 109
The circuit diagram of the micro-controller is shown in Figure 6.3.
Figure 6.3 Controller circuit
6.2.4 Power Circuit
The power circuit of the three phase inverter is shown in Figure 6.4.
The MOSFETs (IRF530) are connected in the required fashion, and the gate
pulses are given by the driver circuit. The inverter switching sequences for the
healthy and faulty conditions are given in Table 6.1 & Table 6.2 respectively.
Figure 6.4 Power circuit

132. 110
Table 6.1 Switching sequence of the driving signals for the healthy
condition
Sequence 6 5 4 3 2 1 Hex Code
I 1 1 0 0 0 1 31H
II 0 0 0 0 0 0 00H
III 1 0 0 0 1 1 23H
IV 0 0 0 0 0 0 00H
V 0 0 0 1 1 1 07H
VI 0 0 0 0 0 0 00H
VII 0 0 1 1 1 0 0EH
VIII 0 0 0 0 0 0 00H
IX 0 1 1 1 0 0 1CH
X 0 0 0 0 0 0 00H
XI 1 1 1 0 0 0 38H
XII 0 0 0 0 0 0 00H
Table 6.2 Switching sequence of the driving signals for the open
circuit faulty Condition
Sequence 6 5 4 3 2 1 Hex Code
I 1 1 0 0 0 0 30H
II 0 0 0 0 0 0 00H
III 1 0 0 0 1 0 22H
IV 0 0 0 0 0 0 00H
V 0 0 0 1 1 0 06H
VI 0 0 0 0 0 0 00H
VII 0 0 0 1 1 0 06H
VIII 0 0 0 0 0 0 00H
IX 0 1 0 1 0 0 14H
X 0 0 0 0 0 0 00H
XI 1 1 0 0 0 0 30H
XII 0 0 0 0 0 0 00H

133. 111
6.3 COMPLETE HARDWARE CIRCUIT
The complete hardware circuit is shown in Figure 6.5. It consists
of a power supply circuit, microcontroller circuit, driver circuit, power circuit,
and load.
Figure 6.5 Complete hardware circuit diagram

134. 112
The driver circuit generates the gate pulses, which are responsible
for the turn on and turn off of the MOSFET switches in the power circuit. The
output of the power circuit drives the induction motor.
6.4 TESTING
The complete hardware setup is given in Figure 6.6.The hardware
setup comprises of a power circuit, controller, and driver circuit. MOSFET
switches are used in the Inverter Power circuit.
Figure 6.6 Complete Hardware Setup
The output waveforms of the hardware setup for the healthy
condition are as follows. The driving pulses are shown in Figure 6.7.
Figure 6.7 Driving pulses
Voltage(V)
Time(S)
Inverter
Induction
motor
microcontroller
x-axis 1cm=2ms
y-axis 1cm=5v

135. 113
The output of the driver circuit is given in Figure 6.8.
Figure 6.8 Output of the Driver circuit
The line voltage and current of the inverter circuit in the healthy
condition for the induction motor load, is given in Figure 6.9. In the healthy
condition, the motor runs at a speed of 1430 rpm.
Figure 6.9 Line voltage and Current of the Inverter for the induction
motor load
Time(S)
Voltage(V)
Time (ms) Time (ms)
Current
(A)
Voltage
(V)
Y axis 1unit=200v
X axis 1 unit=2ms
Y axis 1unit=2A
X axis 1 unit=2ms
x-axis 1cm=2ms
y-axis 1cm=5v

136. 114
(a) Vab (b) Vbc (c) Vac
Figure 6.10 Line Voltage of the Inverter circuit for the induction motor
Load with an open circuit fault
(a) Phase A (b) Phase B (c) Phase C
Figure 6.11 Line Current of the Inverter circuit for the induction motor
Load with an open circuit fault
Time(ms)
Voltage
(V)
Y axis 1unit=200v
X axis 1 unit=2ms
Y axis 1unit=2A
X axis 1 unit=2ms
Time(ms)
Current
(A)

137. 115
Figure 6.12 Line current spectrum of the inverter circuit for the
induction motor under a healthy condition
Figure 6.13 Line current spectrum for Phase A of the inverter circuit for
the induction motor under the open circuit fault

138. 116
Figure 6.14 Line current spectrum for Phase B of the inverter circuit for
the induction motor under the open circuit fault
Figure 6.15 Line current spectrum for Phase C of the inverter circuit for
the induction motor under an open circuit fault
The Line voltage and current waveforms of the inverter circuit with
an open circuit fault condition for the induction motor load is given in Figure
6.10 and Figure 6.11 respectively. In the open circuit faulty condition, the
voltage and current waveforms are distorted. The line current spectra of the
inverter circuit in the healthy and open circuit faulty condition are given in
Figure 6.12, Figure 6.13, Figure 6.14 and Figure 6.15 respectively. During a

139. 117
faulty condition more harmonics are introduced, and the motor will not run.
From Figure.3.6 and Figure 6.11, it is observed that the hardware results are
similar to the simulation results. The summary of the simulation and hardware
results are given in Table.6.3.
6.5 VALIDATION OF THE RESULTS
For the induction motor load in a healthy condition the motor runs
at a speed of 1420 rpm. In the open circuit faulty condition, the voltage and
current waveforms are distorted, and the motor fails to run.
Table 6.3 Summary of the hardware and simulation results for the IM
load
Parameters Healthy Open circuit fault
Simulation Hardware Simulation Hardware
Current THD Current THD Current THD Current THD
Ia 4.83A 4.71 4.81A 5.1 0.003A 80.4 0.004A 85.2
Ia 4.83A 4.71 4.78A 5.3 4.23A 4.57 4.24A 5.1
Ia 4.88A 4.52 4.82A 5.5 4.25A 4.58 4.51A 5.4
speed 1430 1420 0 0
6.6 CONCLUSION
The hardware is implemented using the micro controller AT89C51,
which generates the triggering pulses. The experimentally generated phase
voltage waveforms for the three phase inverter with an induction motor load
in the healthy condition and open circuit the faulty condition are presented.
From the voltage and current waveforms it is seen, that the waveforms are
distorted during faulty condition, and the induction motor fails to run during
that period.

140. 118
CHAPTER 7
CONCLUSION
7.1 GENERAL
A three phase squirrel cage induction motor is modeled on the basis
of the finite element method. The simulation results are obtained for the
broken bar and stator inter-turn faults. It is found that the faults due to the
broken bars saturate the magnetic force distribution, on the rotor tooth
adjacent to the bars that are broken. In the static analysis, the flux function
and flux density are increased, when the number of broken bars is increased.
In the transient analysis, it is found that the flow of current in the stator phases
and the flux linkage produced in the motor are increased, whereas, the stored
magnetic energy is decreased when the number of bars broken is increased.
The simulated results are verified theoretically for parameters like the flux
function and flux density.
The THD of the VSI fed drive is evaluated, under healthy and
various faulty conditions of the inverter circuits. From the simulation it is
seen, that there is an increase in the harmonic distortions due to faults. The
current harmonics get introduced upon the introduction of faults in the
inverter module. The THDs of the normal VSI fed drive and fault tolerant VSI
fed drive are evaluated under an open circuit faulty condition. From the
simulation results it is seen, that there is a decrease in the harmonic distortion
by using the fault tolerant VSI fed drive with Stator Phase Connection.
However, the fault tolerant inverter with the leg swap module replicates the
performance of a healthy VSI. The hardware is implemented for the VSI fed
drive and comparisons are made between healthy and faulty conditions. In the

141. 119
healthy condition, the motor runs at a speed of 1430 rpm. In the open circuit
faulty condition voltage waveforms are distorted and the motor fails to run.
The leg swap module requires three more bidirectional switches for
controlling the auxiliary leg.
Using FEM, the fault can be easily detected and analyzed for the
three phase squirrel cage induction motor, without damaging the parts of the
machine. On the drive side, the THD analysis helps to find out various faults
that occur in inverter of the VSI & CSI. The fault tolerant inverter with the leg
swap module was also developed for the VSI fed induction motor drive, to
overcome the effect of the inverter fault.
7.2 SCOPE FOR FUTURE WORK
This work can be further extended to bearings and eccentricity
faults. Hardware can be implemented using the current signature analysis for
the condition monitoring set up. The induction motor drive system is
simulated using the VSI and fault tolerant VSI. There is scope for simulating
the faults in the induction motor drive fed from ZSI and three Phase AC
Chopper circuits. The analysis can be further done using artificial intelligence
techniques like neural networks and fuzzy logic. The control logic for five leg
topology may be developed for the induction motor drive using two inverters.

142. 120
REFERENCES
1. Alberti, L & Bianchi, N 2011, ‘Experimental tests of dual three phase
induction motor’, IEEE transactions on industrial electronics, vol. 59,
no. 5, pp. 2041-2048.
2. Aydin, I, Karakose, M & Akin, E 2007, ‘Artificial Immune Based
Support Vector Machine Algorithm for fault diagnosis of Induction
motors’, Proceedings of Aegean conference on Electrical Machines
and Power electronics, pp. 217-221.
3. Balamurugan, S, Arumugam, R, Paramasivam, S & Malaiappan, M
2004, ‘Transient Analysis of induction Motor Using Finite Element
Analysis’, Proceedings of IEEE Industrial Electronics Society, 30th
annual conference, pp. 1526-1529.
4. Banerjee, D & Ranganathan, VT 2009, ‘Load-Commutated SCR
Current-Source-Inverter-Fed Induction Motor Drive With Sinusoidal
Motor Voltage and Current’ IEEE Transactions on Power Electronics,
vol. 24, no. 4, pp. 1048-1061.
5. Bangura, JF & Demerdash, NA 1999, ‘Diagnosis and Characterization
of Effects of Broken Bars and Connectors in Squirrel-Cage Induction
Motor by Time-Stepping Coupled Finite Element State Space
Modeling Approach’, IEEE Transactions on Electromagnetic.
Compatibility, vol. 14, no. 4, pp. 1167-1176.
6. Bangura, JF, Povinelli, RJ, Demerdash, NAO & Brown, RH 2003,
‘Diagnostics of Eccentricities and Bar/End-Ring Connector Breakages
in Polyphase Induction Motors through a combination of Time-Series
Data Mining and Time Stepping Coupled FE – State Space
Technique’, IEEE Transactions on Industrial Applications, vol. 39,
no. 4, pp. 1005-1013.
7. Benbouzid, MEH 2000, ‘A Review of Induction Motors Signature
Analysis as a Medium for Faults Detection’, IEEE Transactions on
Industrial Electronics, vol. 47, no. 5, pp. 984- 993.

143. 121
8. Bentounsi, A & Nicolas, A 1998, ‘On Line Diagnosis of Defaults on
Squirrel Cage Motor Using FEM’, IEEE Transactions on Magnetics,
vol. 34, no. 5, pp. 3511-3574.
9. Bianchi, N, Bolognani, S & Comelato, G 1999, ‘Finite Element
Analysis of Three Phase Induction Motors: Comparison of Two
Different Approaches’, IEEE Transactions On Energy Conversion,
vol. 14, no. 4, pp. 1523-1528.
10. Biswas, B & Das S 2009, ‘Current Harmonics Analysis of Inverter-Fed
Induction Motor Drive System under Fault Conditions,’ in Proceedings
of the International Multi Conference of Engineers and Computer,
pp. 978-988.
11. Blanco, MAR, Sánchez, AC, Theilliol, D, Valdés, LGV, Terán, PS,
González, LH , & Alquicira, JA 2011, ‘A failure detection strategy for
IGBT – based On-Gate Voltage behavior applied to a Motor Drive
System’ IEEE transactions on Industrial Electronics, vol. 58, no. 5,
pp.1625-1633.
12. Blodt, M, Chaber, MRJ & Faucher, J 2006, ‘Fault Indicators for
Stator Current Based Detection of Torque Oscillations in Induction
Motors at Variable Speed Using Time-Frequency Analysis’, in
Proceedings of 3rd IET International Conference on Power
Electronics, Machines and Drives, pp. 56-60.
13. Boqiang, Xu, Liling, Sun, Lie, Xu & Guoyi, Xu 2012, ‘An ESPRIT-
SAA-Based Detection Method for Broken Rotor Bar Fault in Induction
Motors’, IEEE Transactions on energy conversion, vol. 27, no. 3,
pp. 654-660.
14. Burnett, R, Watson, JF & Elder, S 1995, ‘The Application of Modern
Signal Processing Technique to Rotor Fault Detection and location
within three phase induction motor’, Proceedings of IEEE
Instrumentation and Measurement Technology conference-IMTC ’95,
pp.110-120.
15. Cardoso, AJM & Mendes, AMS 1997, ‘Converter Fault Diagnosis in
Variable Speed DC Drives, by Park’s Vector Approach’, Proceedings
of international on Industrial Electronics, pp. 497-500.
16. Ceban, A, Pusca, R & Romary, R 2012, ‘Study of Rotor Faults in
Induction Motors Using External Magnetic Field Analysis’, IEEE
Transactions on Industrial Electronics, vol. 59, no. 5, pp. 2082-2092.

144. 122
17. Corres, JM, Bravo, J Arregui, FJ & Matias, IR 2006, ‘Unbalance &
Harmonics Detection in Induction motors using an Optical Fiber
Sensor’, IEEE sensors Journal, vol. 6, no. 3, pp. 605-612.
18. Dai, M, Keyhani, A & Sebastion, T 2005, ‘Fault Analysis of a PM
Brushless DC Motor Using Finite Element Method’, IEEE
Transactions on Energy conversion, vol. 20, no. 1, pp. 1-6.
19. Das, S, Purkait, P, Dey, D & Chakravorti, S 2011, ‘Monitoring of
Inter-turn Insulation Failure in Induction Motor using Advanced Signal
and Data Processing Tools’, IEEE Transactions on Dielectrics and
Electrical Insulation Vol. 18, No. 5, , pp. 1599-1608
20. Ebrahimi, BM, Takbash, AM & Faiz, J 2013, ‘Losses Calculation in
Line-Start and Inverter-Fed Induction Motors Under Broken Bar
Fault’, IEEE Transactions on instrumentation and measurement,
vol. 62, no. 1, pp. 140-152 .
21. Elkasabgy, NM & Eastham, AR 1992, ‘Detection of Broken Bars in
the Cage Rotor on an Induction Machine’, IEEE Transactions on
Industrial Applications, vol. 28, no. 1, pp. 165-171.
22. Espinoza, TDR, Campos, DU, Ba´rcenas, E & Mart nez, LFZ 2012,
‘Robust fault diagnosis scheme for open-circuit faults in voltage source
inverters feeding induction motors by using non-linear proportional-
integral observers’, IET Power Electronics, vol. 5, no. 7,
pp. 1204-1216.
23. Estima, JO & Cardoso, AJM 2011, ‘A new approach for real time
multiple open-circuit fault diagnosis’ IEEE transactions on Industry
Applications, vol. 47, no. 6, pp. 2487-2491.
24. Huo, B & Trzynadlowski, AM 2001, ‘Simple Stator Fault Detector for
AC Motors’, IEEE Transactions on Industry Applications, vol. 39,
no. 1, pp. 192-194.
25. Julian, AL, Oriti, G & Stephen, T 2010, ‘Operating standby redundant
controller to improve Voltage source inverter reliability’ on IEEE
Transactions on Industry Applications, vol. 46, no. 5, pp. 3145-3164.
26. Jung, JH & Kwon, BH 2006, ‘Corrosion Model of a Rotor Bar Under
Fault Progress in Induction Motors’, IEEE Transactions on Industrial
Electronics, vol. 53, no. 6, pp. 1829-1841.

145. 123
27. Jung, JH, Lee, JJ & Kwon, BH 2006, ‘Online Diagnosis of Induction
Motors Using MCSA’, IEEE Transactions on Industrial Electronics,
vol. 53, no. 6, pp. 1842-1852.
28. Kim, KH , Gu, BH & Jung, IS 2011, ‘Online fault-detecting scheme of
an inverter-fed permanent magnet synchronous motor under stator
winding shorted turn and inverter switch open’, IET Electric Power
Applications, Vol. 5, no. 6, pp. 529-539.
29. Kim, YH , Youn, YW, Hwang, DH, Sun, JH & Kang, DS 2013,
‘High-Resolution Parameter Estimation Method to Identify Broken
Rotor Bar Faults in Induction Motors’, IEEE Transactions on industrial
electronics, vol. 60, no. 9, pp. 4103-4177.
30. Kou, X & Corzine, KA, 2004, ‘A Unique Fault-Tolerant Design for
Flying Capacitor Multilevel Inverter’, IEEE transactions on power
electronics, vol. 19, no. 4, pp. 979-987.
31. Llinares, JP, Daviu, JAA & Gausp, MR 2011, ‘Induction Motor
diagnosis based on a transient current analytic wavelet transform via
Frequency B-Splines’, IEEE Transactions on Industrial Electronics,
vol. 58, no. 5, pp. 1530-1544.
32. Mendes, AMS & Marques Cardoso AJ 2003 ‘Continuous operation
performance of faulty induction motor drives,’ Proceedings of Electric
Machines and Drives, pp. 547-553.
33. Mendes, AMS & Cardoso, AJM 2003, ‘Performance analysis of three-
phase induction motor drives under inverter fault conditions’,
Proceedings of Diagnostics for Electric Machines, Power Electronics
and Drives, pp. 205-210.
34. Mendes, AMS, Fernandez, XML & Cardoso, AJM 2007 ‘Thermal
Behavior of a Three-Phase Induction Motor Fed by a Fault-Tolerant
Voltage Source Inverter’, IEEE transactions on Industry Applications,
vol. 43, no. 3, pp. 724-730
35. Mendes, AMS, Fernandez, XML, & Cardoso, AJM 2008, ‘Thermal
Performance of a Three-Phase Induction Motor Under Fault Tolerant
Operating Strategies’, Proceedings of Power Electronics Specialist
Conference, vol. 23, pp. 1537-1544.

146. 124
36. Mingyao, MA, Hu, L, Chen, A & Xiangning, H 2007,
‘Reconfiguration of Carrier-Based Modulation Strategy for Fault
Tolerant Multilevel Inverters’, IEEE Transactions on power
electronics, vol. 22, no. 5, pp. 2050-2060.
37. Mir, S, Elbuluk, ME & Zinger, DS 1998, ‘PI and Fuzzy Estimators for
Tuning the Stator Resistance in Direct Torque Control of Induction
Machines’, IEEE Transactions on power electronics, vol. 13, no. 2,
pp. 279-287.
38. Mirafzal, B & Demerdash, NAO 2004, ‘Induction Machine Broken-
Bar Fault Diagnosis Using the Rotor Magnetic Field Space-Vector
Orientation’, IEEE Transactions on Industrial Applications, vol. 40,
no. 2, pp. 534-542.
39. Mohammed, OA, Abed NY & Ganu, S, 2006, ‘Modeling and
Characterization of induction motor internal faults using Finite
Element and Discrete Wavelet Transforms’, IEEE Transactions on
Magnetics, vol. 42, no. 10, pp. 3434-3436.
40. Pereira, LA, Da Zana, SGG & Pereira, LF 2005, ‘Motor current
signature analysis and fuzzy logic applied to the diagnosis of short-
circuit faults in induction motors’, Proceedings of 32nd Annual
Conference of IEEE Industrial Electronics Society IECON,
pp. 275-280.
41. Preston, TW, Reece, ABJ & Sangha, PS 1988 ‘Induction Motor
Analysis by Time-Stepping Techniques’, IEEE Transactions on
Magnetics, vol. 24, no. 1, pp. 471-474.
42. Ribeiro, RLDA & Jacobina, CB 2003, ‘Fault Detection of open switch
damage in voltage fed PWM motor drive systems’, IEEE transactions
on power electronics, vol. 18, no. 2, pp. 587-593.
43. Rodriguez, AM, Claudio, A, Theilliol, D, Vela, LG & Hernandez, L
2009, ‘Strategy to replace the Damaged Power Device for Fault
Tolerant Induction Motor Drive’ Proceedings of Applied Power
Electronics conference and Exposition, pp. 343-346.
44. Salmasi, FR, Najafabadi, TA & Maralani, PJ 2010, ‘An adaptive flux
observer with on-line estimation of dc-link voltage and rotor resistance
for VSI based induction motors’, on IEEE Transactions on Power
Electronics, vol. 25, no. 5, pp. 1310-1319.

147. 125
45. Salmasi, FR, Najafabadi, TA & Maralani, PJ 2011, ‘Detection and
Isolation of Speed, DC-Link Voltage, and Current-Sensor Faults Based
on an Adaptive Observer in Induction-Motor Drives’, on IEEE
Transactions on Industrial Electronics, vol. 58, no. 5, pp. 1662-1671.
46. Sanchez, MP, Guasp, MR, Daviu JAA, Folch, JR, Cruz, JP &
Panadero, RP 2010, ‘Diagnosis of Induction motor faults in the
Fractional Fouries Domain’, IEEE Transactions on Instrumentation
and Measurement, vol. 59, no. 8, pp. 2065-2075.
47. Sawhney, AK 2005, ‘A Course in Electrical Machine Design’,
Dhanpat Rai and Sons.
48. Shengming Li, & Longya, Xu 2006, ‘Strategies of Fault Tolerant
Operation for Three-Level PWM Inverters’, IEEE transactions on
power electronics, vol. 21, no. 4, pp. 933-940.
49. Shi, KL, Chan, TF & Wong, YK 1999, ‘Modelling And Simulation Of
The Three-Phase Induction Motor Using Simulink’, Proceedings of
International Journal of Electrical Engineering and Education, vol. 36,
no. 1, pp. 163–172.
50. Sizov, GY, Ahmed, AS, Nabeel 2009, ‘Analysis and Diagnostics of
Adjacent and Nonadjacent Broken-Rotor-Bar Faults in Squirrel-Cage
Induction Machines’, IEEE Transactions on Industrial Electronics,
vol. 56, no. 11, pp. 4627-4641.
51. Subhasis, N, Shehab, A & Toliyat, HA 2001, ‘Detection of Rotor Slot
and other Eccentricity Related Harmonics in a Three Phase Induction
Motor with different rotor cages’, IEEE Transactions on Energy
Conversion, vol. 16, no. 3, pp. 253-260.
52. Sun, L, Heming, LH & Xu, B 2005, ‘Analysis on the transient of
stator-rotor-hybrid fault in squirrel cage induction motors’, in
Proceedings of Eighth International Conference on Electrical Machines
and Systems, vol. 3, pp. 1939-1944.
53. Thomson, WT & Fenger, M 2001, ‘Current Signature Analysis to
detect Induction Motor Faults’, IEEE Industry Application Magazine,
pp. 26-34.
54. Watson, JF, Paterson, NC & Dorrell, DG 1999, ‘The Use of Finite
Element Methods to Improve Techniques for the Early Detection of
Faults in 3-Phase Induction Motors’, IEEE Transactions on Energy
Conversion, vol. 14, no. 3, pp. 655-660.

148. 126
55. Weili, Li, Ying, X, Jiafeng, S & Yingli, L 2007, ‘Finite Element
Analysis of Field Distribution and Characteristic Performance of
Squirrel-Cage Induction Motor with Broken Bars’, IEEE Transactions
on Magnetics, vol. 43, no. 4, pp. 1537-1540.
56. Welchko, BA & Lipo, TA , 2004, ‘Fault Tolerant Three Phase AC
Motor Drive Topologies : A comparison of Features , Cost, and
Limitation’, IEEE transactions on power electronics, vol. 19, no. 4,
pp. 1108-1116.
57. Williamson, S & Robinson, MJ 1991, ‘Calculation of Cage Induction
Motor Equivalent Circuit Parameters using Finite Elements’, IEE
Proceedings B of Electric Power Applications, vol. 138, no. 5,
pp. 264-276.
58. Yilmaz, M & Krein, PT 2008, ‘Capabilities of Finite Element Analysis
and Magnetic Equivalent Circuits for Electrical Machine Analysis and
Design’, Proceedins of IEEE Power Electronics Specialists conference,
pp. 4027-4033.
59. Yusof, Y & Yatim, AHM 2003, ‘Simulation and Modeling of Stator
Flux Estimator for Induction Motor using Artificial Neural Network
Technique’, Proceedings of National Power and Energy Conference
(PECon) Bangi, Malaysia, pp. 11-15.
60. Zhou, L & Smedley, K 2010, ‘A Fault Tolerant Control System for
Hexagram Inverter Motor Drive’, Proceedings of Applied Power
Electronics conference and Exposition(APEC), pp. 264-270.
61. ZouZou, SE 2010, ‘Detection of Inter-Turn Short-Circuit and broken
Rotor Bars in Induction Motors Using the Partial Relative Indexes:
Application on the MCSA’, International Conference on Electrical
Machines, pp. 1-6 .

149. 127
LIST OF PUBLICATIONS
International Journals
1. Nagarajan, S & Rama Reddy, S 2010, ‘Modeling and Simulation of
Faulty Squirrel Cage Induction Motor using magnet’, International
Journal of Computer and Electrical Engineering (IJCEE), vol. 2, no. 5,
pp.867-869, Singapore.
2. Nagarajan, S & Rama Reddy, S 2011, ‘Simulation of fault detection
in AC to AC converter fed induction motor’, International Journal of
Electrical Engineering, vol.4, no.6, pp.711-732, Egypt.
3. Nagarajan, S & Rama Reddy, S 2012, ‘Diagnosis and characterization
of effects of broken bars in three phase squirrel cage induction motor
using finite element method’, ARPN Journal of Engineering and
applied sciences, vol.7, no.9, pp.1170-1179.
4. Nagarajan, S & Rama Reddy, S 2012, ‘Detection of inter-turn fault in
three phase squirrel cage induction motor using magnet’, Journal of
Electrical Engineering, vol.58, no.3, pp.384-391.
5. Nagarajan, S & Rama Reddy, S 2013, ‘Fault analysis on VSI fed
induction motor drive with fault tolerant strategy’, Research Journal of
Applied sciences, Engineering and Technology, (Accepted).
6. Nagarajan, S & Rama Reddy, S 2013, ‘Detection of Broken bars in
Three phase Squirrel Cage Induction Motor using Finite Element
Method’ International Journal of Electrical Engineering (IJEE),
(Accepted)
International Conferences
1. Nagarajan, S & Rama Reddy, S 2009, ‘Online condition monitoring
of Squirrel cage Induction Motor using Electrical signature analysis’,
International conference on Electrical Energy System and Power
Electronics in Emerging Economics, organized by SRM University,
vol.1, pp.329-333.

150. 128
2. Nagarajan, S & Rama Reddy, S 2010, ‘Detection of Faults in AC to
AC converter fed induction motor using Matlab’, International
Conference on Swarm, Evolutionary and Memetic Computing
organized by SRM University, vol.1, pp.379-391.
3. Sudarvizhi,A, Nagarajan, S & Ramareddy, S 2012, ‘Detection and
Analysis of Broken Bar in Three Phase Squirrel Cage Induction Motor
using FEM’, 2012 International Conference on Computing, Electronics
and Electrical Technologies (ICCEET) 978-1-4673-0210-4/12/IEEE,
pp.40-50, 2012.
4. Dhanya, B, Nagarajan, S, & Ramareddy, S 2012, ‘Fault Analysis of
Induction Motor Fed by a Fault Tolerant Voltage Source Inverter’,
2012 International Conference on Computing, Electronics and
Electrical Technologies (ICCEET) 978-1-4673-0210-4/12/ IEEE,
pp.51-58, 2012.
5. Nagarajan, S. & Rama Reddy, S 2012, ‘Embedded Controlled Fault
Tolerant Inverter with A Leg Swap Module For Induction Motor
Drive’, IEEE International conference on Power Electronics, Drives
and Energy systems (PEDES 2012). 978-1-4673-4508-8/12/IEEE-
2012.