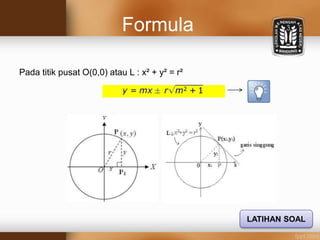
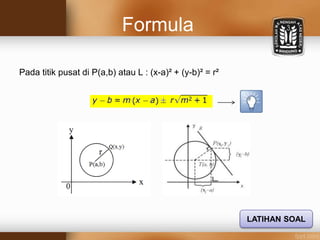
Dokumen tersebut memberikan penjelasan tentang persamaan garis singgung lingkaran dengan gradien yang diketahui. Terdapat formula umum persamaan lingkaran dan cara mendapatkan persamaan garis singgung lingkaran dengan menggunakan substitusi nilai gradien ke dalam persamaan lingkaran. Kemudian diikuti oleh beberapa soal latihan untuk mendapatkan persamaan garis singgung lingkaran berdasarkan informasi yang diberikan.

1. Persamaan Garis Singgung Lingkaran
dengan Gradien Diketahui
Sebayang, Lovanda C. A.
XI IPA 4

2. Formula
Pada titik pusat O(0,0) atau L : x² + y² = r²
LATIHAN SOAL

3. Formula
Pada titik pusat di P(a,b) atau L : (x-a)² + (y-b)² = r²
LATIHAN SOAL

4. How To Get The Formula
1. Substitusi y = mx + n ke  L : x²+y² = r²
x² + (mx + n) ² = r²
x² + m²x² + 2mnx + n² = r²
(1+ m²)x² + 2mnx + (n² – r²) = 0
2. Nilai D = 0
(2mn) ² – 4(1+ m²) (n² – r²) = 0
4 m²n² – 4(m²n² – m²r² + n² – r²) = 0
4 m²n² – 4 m²n² + 4m²r² – 4n² + 4r² = 0
4 (m²r² – n² + r²) = 0
m²r² – n² + r² = 0
n² = r² (1 + m²)
n = ± r

5. How To Get The Formula
3. Substitusi n = ± r √1 + m²  y = mx + n
SO,
BACK LATIHAN SOAL

6. How To Get The Formula
1. Substitusi y = mx + n  L ≡ (x – a) ² + (y – b) ² = r²
(x – a) ² + (mx + n – b) ² = r²
x² – 2ax + a² + m²x² + n² + b² + 2mnx – 2bmx – 2bn – r² = 0
x²(1 + m²) – 2(a – mn + bm)x + (a² + n² + b² – 2bn – r²) = 0

7. How To Get The Formula
2. Nilai D = 0 adalah
4(a – mn + bm) ² – 4(1 + m²)(a² + n² + b² – 2bn – r²) = 0
(a – mn + bm) ² – (1 + m²)(a² + n² + b² – 2bn – r²) = 0
– 2amn + 2abm – n² – b² + 2bn + r² – a²m² + m²r² = 0
2amn – 2abm + n² + b² – 2bn – r² + a²m² – m²r² = 0
(n² + a²m² + b² + 2amn –2bn – 2abm) – r²(1+ m²) = 0
(n + am – b) ² = r² (1+ m²)
(n + am – b) = r √1 + m²
n = (–am + b) ± r√1 + m²
3. Substitusi n = (–am + b) ± r√1 + m² ke persamaan garis y = mx + n
SO,
BACK LATIHAN SOAL

8. LATIHAN SOAL
1. Tentukan persamaan garis singgung pada lingkaran L : x² + y² = 16,
jika diketahui mempunyai gradien 3!
2. Tentukan persamaan garis singgung lingkaran L : (x – 1)² + (y + 2)² =
9 yang mempunyai gradien m = 5/12
3. Persamaan garis singgung lingkaran (x-2)² + (y+4)² = 100 yang
tegak lurus dengan 4x – 3y + 25 = 0 adalah
4. Persamaan garis singgung lingkaran yang berpusat di (-2,4) dan
melalui titik (4,1) serta sejajar garis 2x – y + 3 = 0 adalah
KLIK!

9. KLIK!
1.
2.
3. m2 = -1/m1
4. R² = (x₁ - x₂)² + (Y₁ - y₂),

10. T H A N K . Y O U . 