Downloaded 13 times
Uploaded byTenia Wahyuningrum
Pengujian hipotesis
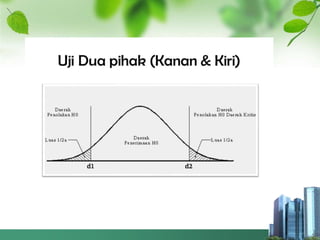
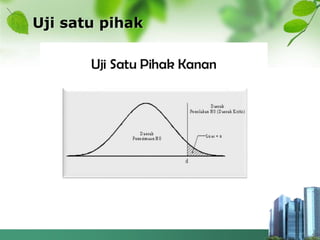
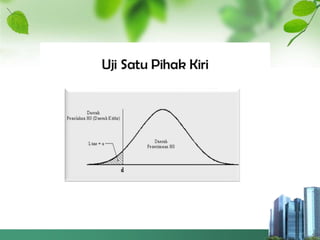
Dokumen ini membahas tentang pengujian hipotesis, menjelaskan definisi hipotesis, jenis-jenis kesalahan dalam pengujian, serta langkah-langkah yang diperlukan dalam merencanakan penelitian. Ditekankan pentingnya memahami peluang kekeliruan dan penggunaan uji satu pihak atau dua pihak tergantung pada adanya informasi mengenai arah kecenderungan. Penelitian diilustrasikan dengan dua contoh kasus yang menunjukkan perbedaan metode pengujian berdasarkan informasi yang tersedia.
More Related Content
More from Tenia Wahyuningrum
Pengujian hipotesis
- 1. L/O/G/O BY TENIA WAHYUNINGRUM,MT TATAPMUKA KE 8 PENGUJIAN HIPOTESIS
- 2. HIPOTESIS HIPO : LEMAH TESIS: SUATU PERNYATAAN KEBENARAN YANG DIDUKUNG FAKTA HIPOTESIS : PERNYATAAN KEBENARAN YANG MASIH LEMAH KARENA BELUM TERBUKTI (Armien, 2008)
- 3. HIPOTESIS Adalah asumsi ataudugaan mengenai suatu hal yang dibuat untuk menjelaskan hal tersebut (Sudjana, 1995) Contoh : Peluang lahirnya bayi laki-laki 0,5 30% masyarakat termasuk golongan A Rata-rata pendapatan keluarga suatu daerah Rp. 35.000,-
- 4. Setiap hipotesis dapatbernilai benar atau salah dan karenanya perlu diadakan penelitian sebelum hipotesis itu diterima atau ditolak Jika hasil yang didapat dari penelitian jauh berbeda dari hasil yang diharapkan terjadi berdasarkan hipotesis, maka hipotesis ditolak. Jika sebaliknya, hipotesis diterima.
- 5. DUA MACAM KEKELIRUAN Dalammelakukan pengujian hipotesis, ada dua macam kekeliruan yang dapat terjadi, dikenal dengan nama Kekeliruan tipe I : ialah menolak hipotesis yang seharusnya diterima Kekeliruan tipe II : ialah menerima hipotesis yang seharusnya ditolak
- 6. KESIMPULAN KEADAAN SEBENARNYA HIPOTESIS BENAR HIPOTESIS SALAH TERIMA HIPOTESIS BENARKELIRU (TIPE I) TOLAK HIPOTESIS KELIRU (TIPE II) BENAR
- 7. Ketika merencanakan suatupenelitian dalam rangka pengujian hipotesis, jelas kiranya bahwa kedua tipe kekeliruan itu harus dibuat sekecil mungkin. Agar penelitian dapat dilakukan, maka kedua tipe kekeliruan itu kita nyatakan dalam peluang. Peluang membuat kekeliruan tipe I biasa dinyatakan dengan α (baca : alpha)
- 8. Peluang membuat kekeliruantipe II dinyatakan dengan β (baca : beta). Dalam penggunaannya, α disebut juga taraf signifikan atau taraf arti atau taraf nyata. Besar kecilnya α dan β yang dapat diterima dalam pengambilan kesimpulan bergantung pada akibat- akibat atas diperbuatnya kekeliruan- kekeliruan tsb.
- 9. Untuk keperluan praktis,α akan diambil lebih dulu dengan harga yang biasa digunakan, yaitu α = 0,01 atau α = 0,05. Besarnya α ditentukan oleh penguji sendiri. Biasanya untuk penelitian bidang teknik, digunakan ketelitian α = 0,01, dan untuk bidang sosial α = 0,05
- 10. Dengan α =0,05, misalnya atau sering disebut taraf nyata 5%, berarti kira- kira 5 dari setiap 100 kesimpulan bahwa kita menolak hipotesis yang seharusnya diterima. Dengan kata lain, 95% yakin bahwa kita telah membuat kesimpulan yang benar.
- 11. LANGKAH PENGUJIAN Tuliskan hipotesisdalam bentuk kalimat Tuliskan hipotesis dalam simbol Tentukan statistik hitung Tentukan daerah penerimaan/penolakan hipotesis Buatlah kesimpulan
- 12. Uji dua pihak/arah Jikah0 mengandung pembanding = Dan h1 mengandung pembanding ≠
- 13. Uji satu pihak/arah JikaH0 mengandung pembanding = Dan H1 mengandung pembanding > atau <
- 14. KAPAN MEMAKAI UJISATU PIHAK(ARAH) /DUA PIHAK(ARAH)? Uji t 2-arah digunakan apabila peneliti tidak memiliki informasi mengenai arah kecenderungan dari karakteristik populasi yang sedang diamati. Sedangkan uji t 1-arah digunakan apabila peneliti memiliki informasi mengenai arah kecenderungan dari karakteristik populasi yang sedang diamati.
- 15. Uji satu pihak(ada info kecenderungan lebih besar dari ) Kasus 1: Seorang peneliti ingin mengetahui rata-rata uang saku mahasiswa Univ X perbulan. Menurut isu yang berkembang, rata-rata uang saku yang dimiliki mahasiwa univ X LEBIH BESAR DARI Rp. 500 ribu/bulan. Untuk itu dilakukan penelitian dengan mengambil 50 sampel mahasiswa secara acak.
- 16. Uji dua pihak(tidak ada info kecenderungan lebih besar/kurang dari) kasus 2: Seorang peneliti ingin mengetahui rata-rata uang saku mahasiswa Univ X perbulan. Menurut isu yang berkembang, rata-rata uang saku mahasiswa univ X adalah SEKITAR Rp.500 ribu /bulan. Untuk itu dilakukan penelitian dengan mengambil 50 sampel mahasiswa secara acak.
- 17. Yang akan dipelajari Hipotesisnol dengan lambang H0 melawan Hipotesis tandingannya dengan lambang H1. Hipotesis mengandung pengertian tidak sama, lebih besar, atau lebih kecil. H1 harus ditentukan peneliti sesuai dengan persoalan yang dihadapi.
- 18. Bentuk pasangan H0dan H1 H0 : ϴ= ϴ 0 H1 : ϴ≠ ϴ 0 atau H0 : ϴ= ϴ 0 H1 : ϴ> ϴ 0 atau H0 : ϴ= ϴ 0 H1 : ϴ< ϴ 0
- 19. Menguji rata-rata µ: uji dua pihak dan satu pihak Jika rata-rata µ dan simpang baku δ Akan diuji mengenai parameter rata-rata µ Maka, ambil sampel acak berukuran n, lalu hitung x dan s. Jika δ diketahui, gunakan uji z Jika δ tidak diketahui, gunakan uji t
- 20.
- 21.
- 23.
- 25.