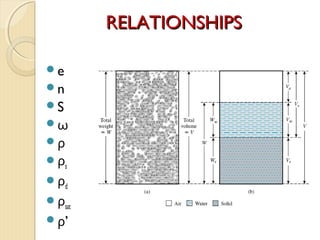
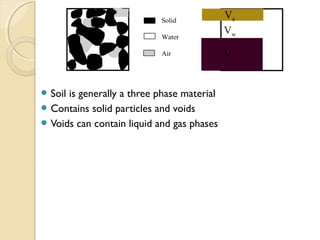
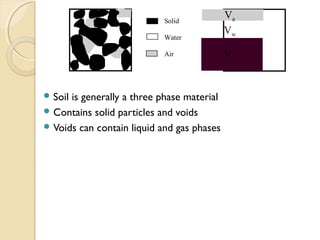
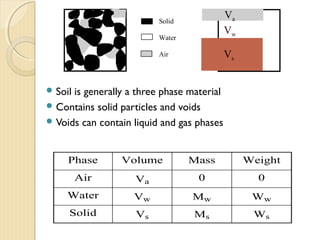
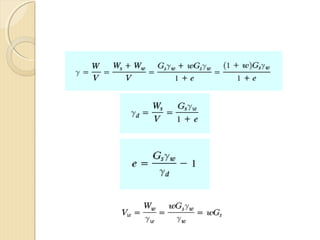
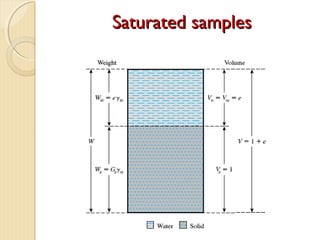
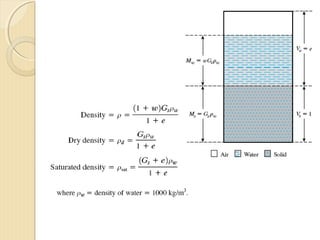
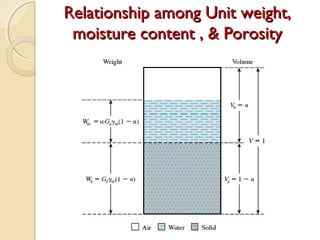
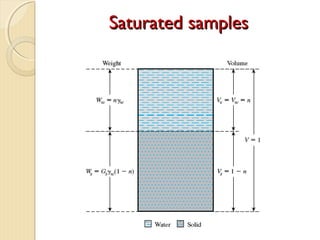
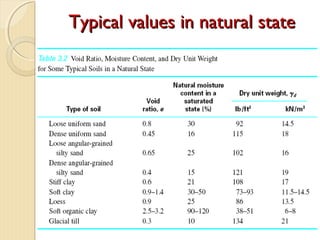
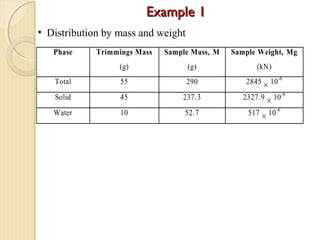
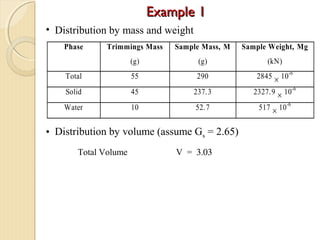
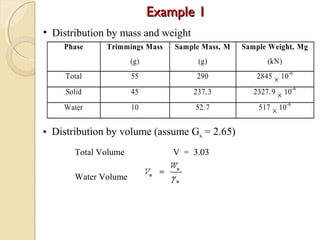
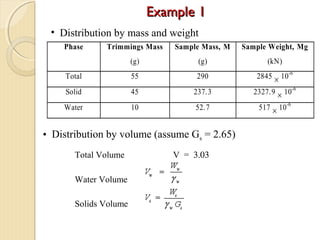
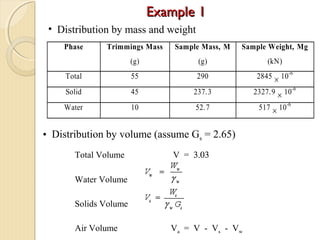
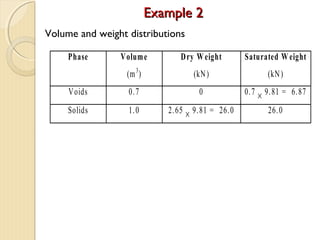
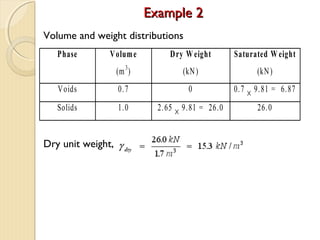
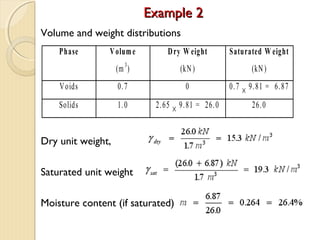
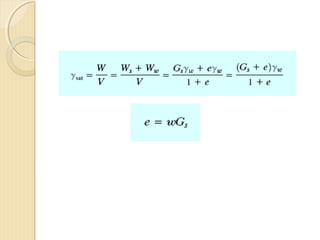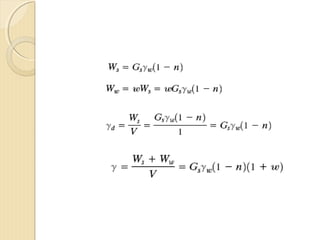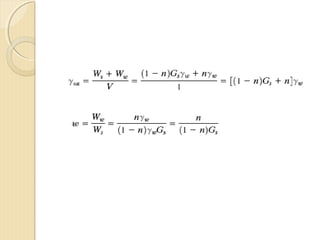This document provides information about pavement materials engineering. It discusses the relationships between different phases in soil, including solid particles, water, and air. Key terms discussed include density, unit weight, specific gravity, voids ratio, porosity, degree of saturation, bulk unit weight, dry unit weight, and saturated unit weight. Examples are provided to demonstrate how to calculate volumes, weights, moisture content, and other properties for soil samples. Relationships between these various properties are also examined.

2. PAVEMENT MATERIALSPAVEMENT MATERIALS
ENGINEERINGENGINEERING
(CE-862)(CE-862)
Lec-02
Fall Semester 2016
Dr. Arshad Hussain
arshad_nit@yahoo.com , Office Room#111, Tel: 05190854163,
Cell: 03419756251
National Institute of Transportation (NIT)
National University of Science and Technology (NUST)
NUST Campus, Sector H-12, Islamabad

3. ROADBED SOILS -B
Phase Relationship,
Shear Strength & Soil
Structure

4. PHASE RELATIONSHIPPHASE RELATIONSHIP

5. Density and Unit WeightDensity and Unit Weight
 Mass is a measure of a body's
inertia, or its "quantity of
matter". Mass is not changed
at different places.
 Weight is force, the force of
gravity acting on a body. The
value is different at various
places (Newton's second law F
= ma) (Giancoli, 1998)
 The unit weight is frequently
used than the density is (e.g. in
calculating the overburden
pressure).
w
s
w
s
w
s
s
3
2
g
g
G
m
kN8.9,Water
sec
m8.9g
gravitytodueonaccelerati:g
Volume
gMass
Volume
Weight
,weightUnit
Volume
Mass
,Density
γ
γ
=
⋅ρ
⋅ρ
=
ρ
ρ
=
=γ
⋅ρ=⋅ρ=γ
⋅
==γ
=ρ

6. RELATIONSHIPSRELATIONSHIPS
e
n
S
ω
ρ
ρs
ρd
ρsat
ρ’

7.  Soil is generally a three phase material
 Contains solid particles and voids
 Voids can contain liquid and gas phases
Solid
Water
Air Vs
Vw
Va

8.  Soil is generally a three phase material
 Contains solid particles and voids
 Voids can contain liquid and gas phases
Solid
Water
Air Vs
Vw
Va

9.  Soil is generally a three phase material
 Contains solid particles and voids
 Voids can contain liquid and gas phases
Solid
Water
Air
Phase Volume Mass Weight
Air Va 0 0
Water Vw Mw Ww
Solid Vs Ms Ws
Vs
Vw
Va

10. UnitsUnits
Length metres
Mass tonnes (1 tonne = 103
kg)
Density t/m3
Weight kilonewtons (kN)
Stress kilopascals (kPa) 1 kPa= 1 kN/m2
Unit weight kN/m3
Accuracy Density of water, ρw = 1 t/m3

11. Weight and Unit weightWeight and Unit weight
 Force due to mass (weight) more important than mass
 W = M g
 Unit weight

12. Weight and Unit weightWeight and Unit weight
 Force due to mass (weight) more important than mass
 W = M g
 Unit weight
γ = ρ g

13. Weight and Unit weightWeight and Unit weight
 Force due to mass (weight) more important than mass
 W = M g
 Unit weight
γ = ρ g
σv
z σv = ρ g z
σv = γ z

14. Unit weight

15. Specific GravitySpecific Gravity
 Gs ≅ 2.65 for most soils
 Gs is useful because it enables the volume of solid
particles to be calculated from mass or weight
G
Density of Material
Densityof Water w
= =
ρ
ρ
G
UnitWeight of Material
UnitWeight of Water w
= =
γ
γ
This is defined by

16. Specific GravitySpecific Gravity
 Gs ≅ 2.65 for most soils
 Gs is useful because it enables the volume of solid
particles to be calculated from mass or weight
G
Density of Material
Densityof Water w
= =
ρ
ρ
G
UnitWeight of Material
UnitWeight of Water w
= =
γ
γ
This is defined by
V
M M
G
W W
G
s
s
s
s
s w
s
s
s
s w
= = = =
ρ ρ γ γ

17. Voids ratioVoids ratio
 It is not the actual volumes that are important but rather
the ratios between the volumes of the different phases.
This is described by the voids ratio, e, or porosity, n, and
the degree of saturation, S.

18. Voids ratioVoids ratio
 It is not the actual volumes that are important but rather
the ratios between the volumes of the different phases.
This is described by the voids ratio, e, or porosity, n, and
the degree of saturation, S.
 The voids ratio is defined as

19. Voids ratioVoids ratio
 It is not the actual volumes that are important but rather
the ratios between the volumes of the different phases.
This is described by the voids ratio, e, or porosity, n, and
the degree of saturation, S.
 The voids ratio is defined as
 and the porosity as

20. Voids ratioVoids ratio
 It is not the actual volumes that are important but rather
the ratios between the volumes of the different phases.
This is described by the voids ratio, e, or porosity, n, and
the degree of saturation, S.
 The voids ratio is defined as
 and the porosity as
The relation between these quantities can be simply
determined as follows
Vs = V - Vv = (1 - n) V

21. Voids ratioVoids ratio
 It is not the actual volumes that are important but rather
the ratios between the volumes of the different phases.
This is described by the voids ratio, e, or porosity, n, and
the degree of saturation, S.
 The voids ratio is defined as
 and the porosity as
The relation between these quantities can be simply
determined as follows
Vs = V - Vv = (1 - n) V
Hence

22. Relationship among Unit weight,Relationship among Unit weight,
moisture content , & Sp. gravitymoisture content , & Sp. gravity

24. Degree of SaturationDegree of Saturation

25. Saturated samplesSaturated samples

28. Relationship among Unit weight,Relationship among Unit weight,
moisture content , & Porositymoisture content , & Porosity

30. Saturated samplesSaturated samples

32. Various Forms of relationshipsVarious Forms of relationships

33. Typical values in natural stateTypical values in natural state

34. Example 1Example 1
Phase Trimmings Mass
(g)
Sample Mass, M
(g)
Sample Weight, Mg
(kN)
Total 55 290 2845 × 10-6
Solid 45 237.3 2327.9 × 10-6
Water 10 52.7 517 × 10-6
• Distribution by mass and weight

35. Phase Trimmings Mass
(g)
Sample Mass, M
(g)
Sample Weight, Mg
(kN)
Total 55 290 2845 × 10-6
Solid 45 237.3 2327.9 × 10-6
Water 10 52.7 517 × 10-6
• Distribution by mass and weight
• Distribution by volume (assume Gs = 2.65)
Total Volume V = 3.03
Example 1Example 1

36. Phase Trimmings Mass
(g)
Sample Mass, M
(g)
Sample Weight, Mg
(kN)
Total 55 290 2845 × 10-6
Solid 45 237.3 2327.9 × 10-6
Water 10 52.7 517 × 10-6
• Distribution by mass and weight
• Distribution by volume (assume Gs = 2.65)
Total Volume V = 3.03
Water Volume
Example 1Example 1

37. Phase Trimmings Mass
(g)
Sample Mass, M
(g)
Sample Weight, Mg
(kN)
Total 55 290 2845 × 10-6
Solid 45 237.3 2327.9 × 10-6
Water 10 52.7 517 × 10-6
• Distribution by mass and weight
• Distribution by volume (assume Gs = 2.65)
Total Volume V = 3.03
Water Volume
Solids Volume
Example 1Example 1

38. Phase Trimmings Mass
(g)
Sample Mass, M
(g)
Sample Weight, Mg
(kN)
Total 55 290 2845 × 10-6
Solid 45 237.3 2327.9 × 10-6
Water 10 52.7 517 × 10-6
• Distribution by mass and weight
• Distribution by volume (assume Gs = 2.65)
Total Volume V = 3.03
Water Volume
Solids Volume
Air Volume Va = V - Vs - Vw
Example 1Example 1

39. Moisture content

40. Moisture content
Voids ratio

41. Moisture content
Voids ratio
Degree of Saturation

42. Moisture content
Voids ratio
Degree of Saturation
Bulk unit weight

43. Moisture content
Voids ratio
Degree of Saturation
Bulk unit weight
Dry unit weight

44. Moisture content
Voids ratio
Degree of Saturation
Bulk unit weight
Dry unit weight
Saturated unit weight
Note that γdry < γbulk < γsat

45. Example 2Example 2
Volume and weight distributions
Phase Volume
(m3
)
Dry Weight
(kN)
Saturated W eight
(kN)
Voids 0.7 0 0.7 × 9.81 = 6.87
Solids 1.0 2.65 × 9.81 = 26.0 26.0

46. Volume and weight distributions
Dry unit weight,
Phase Volume
(m3
)
Dry Weight
(kN)
Saturated Weight
(kN)
Voids 0.7 0 0.7 × 9.81 = 6.87
Solids 1.0 2.65 × 9.81 = 26.0 26.0
Example 2Example 2

47. Volume and weight distributions
Dry unit weight,
Saturated unit weight
Phase Volume
(m3
)
Dry Weight
(kN)
Saturated Weight
(kN)
Voids 0.7 0 0.7 × 9.81 = 6.87
Solids 1.0 2.65 × 9.81 = 26.0 26.0
Example 2Example 2

48. Volume and weight distributions
Dry unit weight,
Saturated unit weight
Moisture content (if saturated)
Phase Volume
(m3
)
Dry W eight
(kN)
Saturated W eight
(kN)
Voids 0.7 0 0.7 × 9.81 = 6.87
Solids 1.0 2.65 × 9.81 = 26.0 26.0
Example 2Example 2

49. RelationshipsRelationships
(1)Water Content w (100%)

 For some organic soils w>100%, up
to 500 %
 For quick clays, w>100%
(2)Density of water (slightly varied
with temperatures)
(3) Density of soil
a. Dry density
b. Total, Wet, or Moist density
(0%<S<100%, Unsaturated)
c. Saturated density (S=100%, Va =0)
d. Submerged density (Buoyant density)
%100
)(
)(
⋅=
s
w
MsolidssoilofMass
MwaterofMass
w )V(samplesoilofvolumeTotal
)M(solidssoilofMass
t
s
d =ρ
)V(samplesoilofvolumeTotal
)MM(samplesoilofMass
t
ws +
=ρ
)V(samplesoilofvolumeTotal
)MM(watersolidssoilofMass
t
ws
sat
++
=ρ
wsat
'
ρ−ρ=ρ
333
w m/Mg1m/kg1000cm/g1 ===ρ

50. ThanksThanks