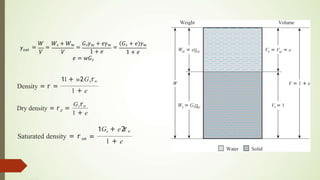
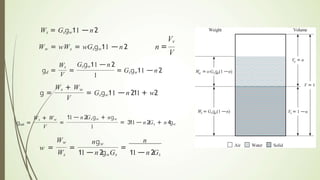
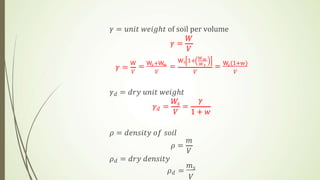The document discusses weight-volume relationships in soil, detailing calculations for various parameters, including unit weight, void ratio, porosity, and moisture content. It provides equations and examples for determining properties of soil samples, including determining density, dry density, and degree of saturation based on moisture content and specific gravity. The information serves as a guide for understanding soil behavior in relation to its physical properties.

1. Weight-Volume Relationships
and Plasticity

2. Weight-Volume Relationships
- relationships between
a.Unit weight
b.Void ratio
c.Porosity
d.Moisture content
e.Specific gravity

3. Volume and Weight Relationships
V=𝑉𝑠 + 𝑉𝑣 = 𝑉𝑠 + 𝑉w + 𝑉𝑎
Where :
V=total volume of the soil
sample
𝑉
𝑠=volume of soil soil solids
𝑉
𝑣=volume of voids
𝑉
w=volume of water
𝑉
𝑎=volume of air
𝑊 = 𝑊w + 𝑊𝑠
Where:
W =total weight of soil sample
𝑊
w=weight of water
𝑊𝑠=weight of soil
e=void ratio
𝑒 =
𝑉𝑣
𝑉𝑠
n=porosity
𝑛 =
𝑉𝑣
𝑉
S=degree of saturation
𝑉w
S =
𝑉𝑣
w=moisture content or water
content
𝑤 =
𝑊w
𝑊𝑠

4. 𝛾 = 𝑢𝑛𝑖𝑡 𝑤𝑒𝑖𝑔ℎ𝑡 of soil per volume
𝛾 =
𝑊
𝑉
𝛾 =
𝖶
𝑉
𝖶 +𝖶
𝑉
= 𝑠 w
=
𝖶𝑠 1+ Ww
W𝑠
𝑉
= 𝑠
𝖶 1+w
𝑉
𝛾𝑑 = 𝑑𝑟𝑦 𝑢𝑛𝑖𝑡 𝑤𝑒𝑖𝑔ℎ𝑡
𝑑
𝛾 =
𝑊𝑠
=
𝛾
𝑉 1 + 𝑤
𝜌 = 𝑑𝑒𝑛𝑠𝑖𝑡𝑦 𝑜𝑓 𝑠𝑜𝑖𝑙
𝜌 =
𝑚
𝑉
𝜌𝑑 = 𝑑𝑟𝑦 𝑑𝑒𝑛𝑠𝑖𝑡𝑦
𝑚
𝜌𝑑 = 𝑠
𝑉

5. 𝑊𝑠 = 𝐺𝑠𝛾w
𝑊w = 𝑤𝑊𝑠 = 𝑤𝐺𝑠𝛾w
𝐺𝑠 = speciEic gravity of soil solids
𝛾 = 𝑉
= = =
𝖶 𝖶𝑠+𝖶w 𝐺𝑠𝛾w+w𝐺𝑠𝛾w 1+w 𝐺𝑠𝛾w
𝑉 1+𝑒 1+𝑒
𝛾𝑑 =
𝑊𝑠
=
𝐺𝑠𝛾w
𝑉 1 + 𝑒
Ws
Total
weight
= W
Total
volume
= V
W
Vs
Va
V
(a) (b)
Air Water Solid
W
V
V
𝑉w =
𝛾w
=
𝑊w 𝑤𝐺𝑠𝛾w
𝛾w
+ 𝑤𝐺𝑠
𝑉 𝑤𝐺
𝑆 = w
= 𝑠
𝑉
𝑣 𝑒
𝑆𝑒 = 𝑤𝐺𝑠

6. V = V = e
Ws = Gsg
W
Vs = 1
V = 1 + e
Weight Volume
W = eg
Water Solid
11 + w2Gsrw
Density = r =
1 + e
d
Dry density = r =
Gsrw
1 + e
Saturated density = r sat
1Gs + e2rw
=
1 + e
𝛾𝑠𝑎𝑡
𝑉 𝑉
=
𝑊
=
𝑊𝑠 + 𝑊w
=
𝐺𝑠𝛾w + 𝑒𝛾w
=
𝐺𝑠 + 𝑒 𝛾w
1 + 𝑒
1 + 𝑒
𝑒 = 𝑤𝐺𝑠

7. Ww = wWs = wGsgw11 —n 2
Ws = Gsgw11 —n 2
W = Gsg (1 —n)
Ws = Gsg (1 —n) Vs = 1 —n
V = 1
V = n
Weight Volume
Air Water Solid
Ws
gd =
V
=
Gsgw11 —n 2
1
= Gsgw11 —n 2
g =
Ws + Ww
V
= Gsgw11 —n 211 + w2
gsat =
Ws + Ww
V
=
11 — n 2Gsgw + ngw
1
= 311 — n 2Gs + n 4
gw
Ww
w = =
ngw
Ws 11 —n 2gwGs
n
=
11 —n 2Gs
Vv
n =
V

8. Example
A moist soil has these values: V=7.08x10-3 m3, m=13.95 kg, w=9.8%and Gs=2.66
Determine the following:
a. Density
b. Dry density
c. Void ratio
d. Porosity
e. Degree of saturation (%)
f. Volume occupied by water

9. In the natural state, a moist soil has a volume of 0.30 m3 and weighs 5500 N. The oven dry
weight of the soil is 4911 N. If𝐺𝑠= 2.74, calculate the following:
a. moisture content
b. moist unit weight
c. dry unit weight
d. void ratio
e. Porosity
f. degree of saturation

10. A representative soil specimen collected from the field weighs 1.8 kN and has a volume of
0.1 m3. The moisture content as determined in the laboratory is 1.2%. Given Gs=2.71,
determine the following:
a. Moist unit weight
b. Dry unit weight
c. Void ratio
d. Porosity
e. Degree of saturation

11. A saturated soil has a dry unit weight of 16.2 kN/m3. Its moisture content is 20%. Determine:
a. Saturated unit weight
b. Specific gravity
c. Void ratio

12. The following data are given for a soil: porosity =0.45, specific gravity of the soil solids=2.68,
and moisture content =10%. Determine the mass of water to be added to 10 m3 of soil for
full saturation.