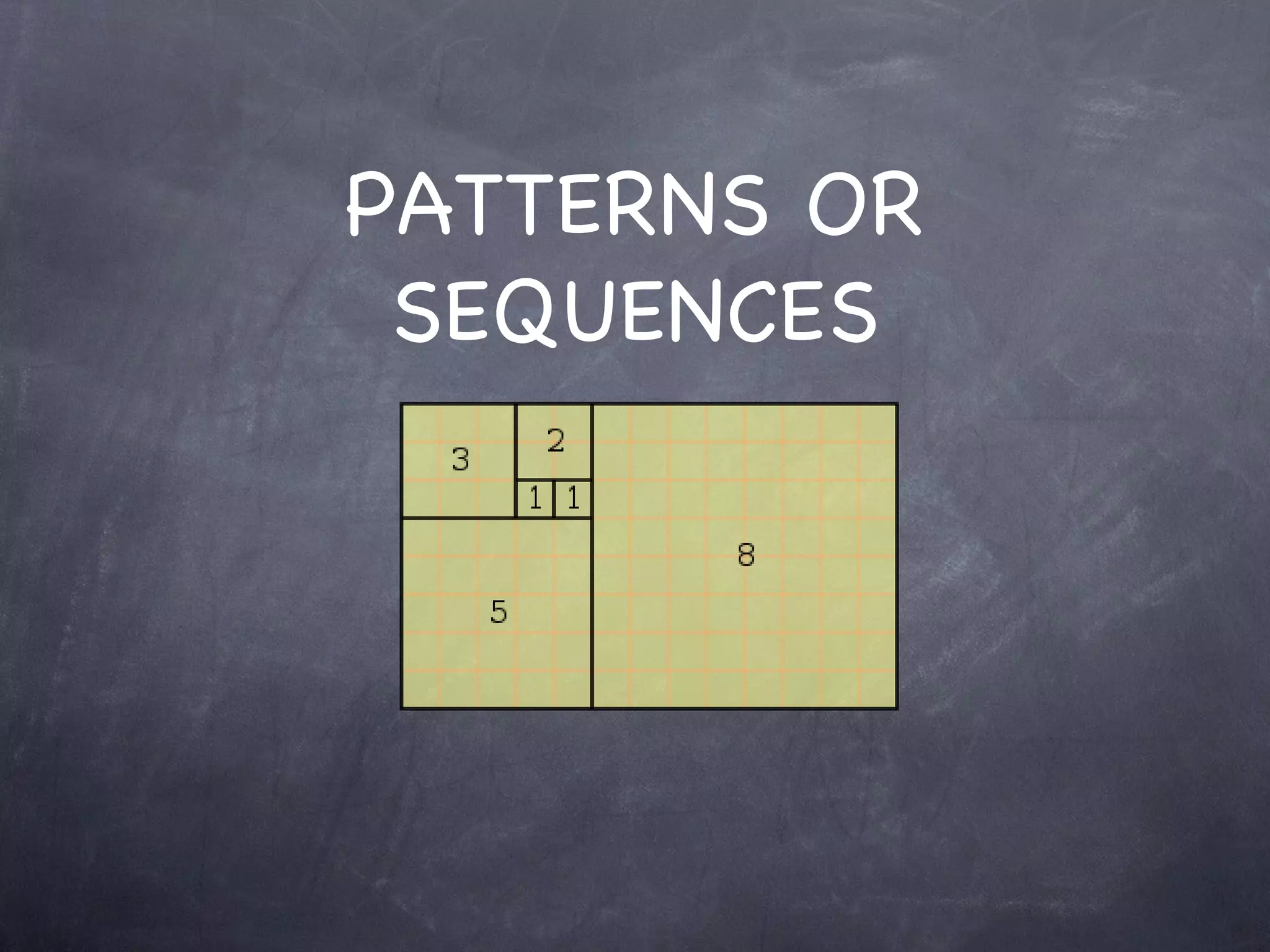
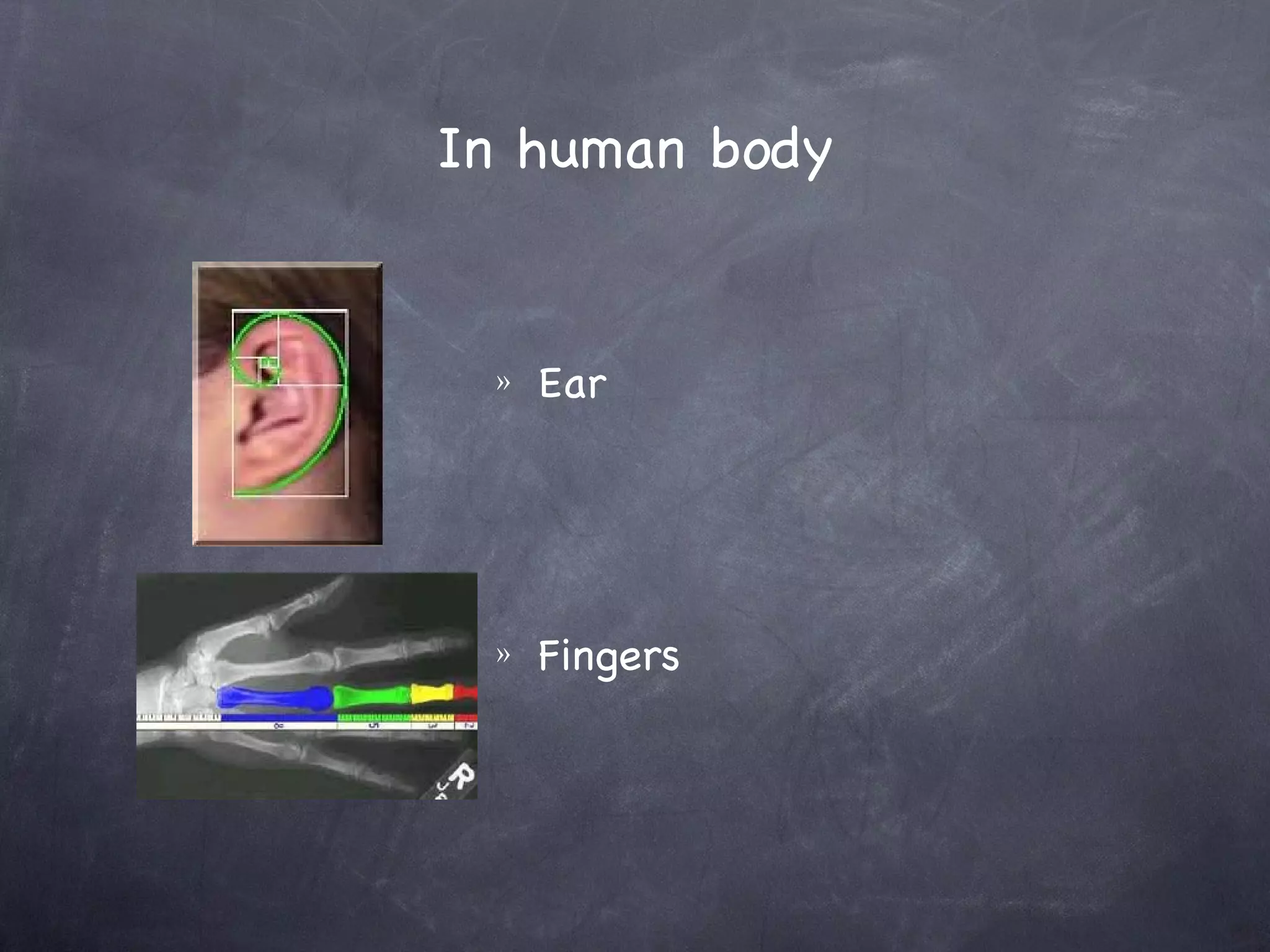
The document discusses patterns and sequences. It introduces the Fibonacci sequence as an example of a numerical pattern found in nature. The Fibonacci sequence begins with 1, 1, 2, 3, 5, 8, etc where each number is the sum of the previous two. Leonardo Fibonacci first introduced this sequence to Western mathematics to model the reproductive growth of rabbits. The ratio of consecutive Fibonacci numbers approaches the golden ratio of approximately 1.618, which appears throughout nature, art, architecture and design.

1. PATTERNS OR
SEQUENCES

2. PURPOSE
• To appreciate and investigate a numerical
pattern
• To look for evidence of mathematical
patterns in nature

3. Order is the key
• What do t hese sit uat ions have in common?
• 1 There are people wait ing for t heir t urn t o buy some fruit
.-
• 2.- You are looking for your name on a list because you want t o
know t he mark you got on your last exam
• 3.- You are t rying t o follow inst ruct ions, being careful t o do every
st ep of t he process in order

4. KEY WORDS
• The situations given before are related to a
concept known as SEQUENCE
• A sequence is an ordered list of things
(objects, events, numbers,...)
• Like a set it contains members (elements or
TERMS

5. GUESS THE NEXT TERM OR ELEMENT OF THE
SERIES GIVEN BELOW
• A) O, T, T, F,....?
• B) 1, 3, 6, 10,...? (HINT: TRIANGLE
NUMBERS)
• C) 1, 4, 9, 16,...?
• D) -5, 4, -3, 2,...?
• E) 1, 1, 2, 3, 5,... (FIBONACCI SEQUENCE)

6. WHO WAS FIBONACCI?
» The “Greatest European
mathematician” of the middle
ages, his full name was Leonardo
of Pisa

7. • He was born in Pisa about 1175 AD
• He was one of the first people to introduce
the Hindu-Arabic number system into Europe

8. • He discovered Fibonacci sequence after an
investigation on the reproduction of rabbits
• The number sequence was known to Indian
Mathematician as early as the 6th century,
but Fibonacci introduced it to the west

9. The rabbit problem
• Suppose a newly-born pair of rabbits, one male, one female, are
put in a field.
• Rabbits are abble to mate at the age of one month so that at the
end of its second month a female can produce another pair of
rabbits.
• Suppose that our rabbits never die and that the female always
produces a new pair (one male, one female) every month from the
second month on
• How many pairs will there be in one year?
• The numbers of pairs of rabbits in the field at the start of each
month is 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

10. Fibonacci pattern in nature
» In the head and petals of
sunflowers
» Pinecones show the Fibonacci
Spiral

11. In music
– A piano keyboard has 8 white keys, 5
black keys in groups of 2 and 3 these 13
keys comprise one octave

12. • The number of petals on a flower are often
Fibonacci numbers
• This important pattern can be found in
pineapples, bananas, cauliflowers

13. The Golden Ratio
• The Golden ratio is an irrational
mathematical constant, approximately equals
to 1.6180339887
• A golden rectangle is a rectangle where the
ratio of its length to width is the golden
number

14. Relation between Fibonacci Sequence
and the Golden ratio
• Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, 21, 34,
55, 89, 144, 233, 377, 610, 987, 1597,
2584,...
• If you calculate the ratios...
• 1/1 = 1, 2/1 = 2, 3/2 = 1.5, 5/3 =
1.6666...
• 8/5 = 1.6, 13/8 = 1.625, 21/13 =
1.615384..
• 34/21 = 1.61904... 55/34 = 1.617647...

15. • Aha! Notice that as we continue down the
sequence, the ratios seem to be converging
upon one number
• If we continue to look at the ratios as the
numbers in the sequence get larger and
larger the ratio will become the same
number, and this number is THE GOLDEN
RATIO 1.6180339887...

16. Golden ratio in nature
» Nautilus Shell
» Butterfly

17. In human body
» Ear
» Fingers

18. In art

19. In design, architecture, publicity,...