Downloaded 20 times
Uploaded byVarun Sharma
Fibonacci
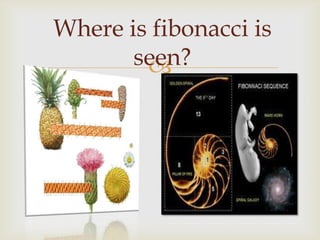
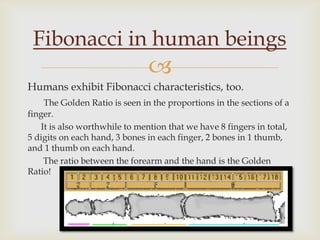
Leonardo of Pisa, also known as Fibonacci, was an Italian mathematician born in 1182 who is famous for introducing the Fibonacci sequence to Western European mathematics. The Fibonacci sequence appears frequently in nature, such as the spiral arrangement of leaves and petals in plants and the patterns of seed heads like pinecones and sunflowers. Many parts of the human body also exhibit proportions related to the Fibonacci sequence and the golden ratio.
Fibonacci
- 2. Introduction:- Fibonacci's full namewas Leonardo of Pisa, (or Leonardo Pisano in Italian). He was born in Pisa, Italy. He was born in the year 1182. He died in the year 1226. His name was short for Filius Bonacci, which means the son of Bonacci. He combined two of his names to get Fibonacci. He combined Filius and Bonacci. His nickname might mean "Lucky Son".
- 3. For Example:- A manputs a pair of rabbits in a place surrounded on all sides by a wall . How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?
- 4. Answer This produces 1 2 3 5 8 13 21 34 55 89 144 233 The answer is 233 pairs of rabbits. (It would be 4096 pairs if the number doubled every month for 12 months.) Let’s look carefully at fibonacci.m. It’s a good example of how to create a Matlab function.
- 5. Fibonacci in Nature Plants do not know about this sequence – They just grow in the most efficient ways. Many plants show the Fibonacci numbers in the arrangement of the leaves around the stem. Some pine cones and fir cones also show the numbers, as do daisies and sunflowers. Sunflowers can contain the number 89, or even 144.
- 6. Where is fibonacciis seen?
- 7. Fibonacci in Plants Phyllotaxis is the study of the ordered position of leaves on a stem. The leaves on this plant are staggered in a spiral pattern to permit optimum exposure to sunlight. If we apply the Golden Ratio to a circle we can see how it is that this plant exhibits Fibonacci qualities. Click on the picture to see a more detailed illustration of leaf arrangements.
- 8. Fibonacci Petals 3 petals lily, iris 5 petals buttercup, wild rose, larkspur, columbine 8 petals delphiniums 13 petals ragwort, corn marigold, cineraria 21 petals aster, black-eyed susan, chicory 34 petals plantain, pytethrum 55, 89 petals michelmas daisies, the asteraceae family The occurrence of Fibonacci Numbers in Nature is interesting but the ratio of consecutive Fibonacci Numbers is important.
- 9. Fibonacci In Fruits Example of pine-apple:- In the case of tapered pinecones or pineapples, we see a double set of spirals – one going in a clockwise direction and one in the opposite direction. When these spirals are counted, the two sets are found to be adjacent Fibonacci numbers.
- 10. Fibonacci in humanbeings Humans exhibit Fibonacci characteristics, too. The Golden Ratio is seen in the proportions in the sections of a finger. It is also worthwhile to mention that we have 8 fingers in total, 5 digits on each hand, 3 bones in each finger, 2 bones in 1 thumb, and 1 thumb on each hand. The ratio between the forearm and the hand is the Golden Ratio!
- 11. Conclusion The Fibonacci method should only be used in a combination with other methods, and the results derived should be considered just another point in favor of a decision if they coincide with the results produced by the other methods in the combination.
- 12.