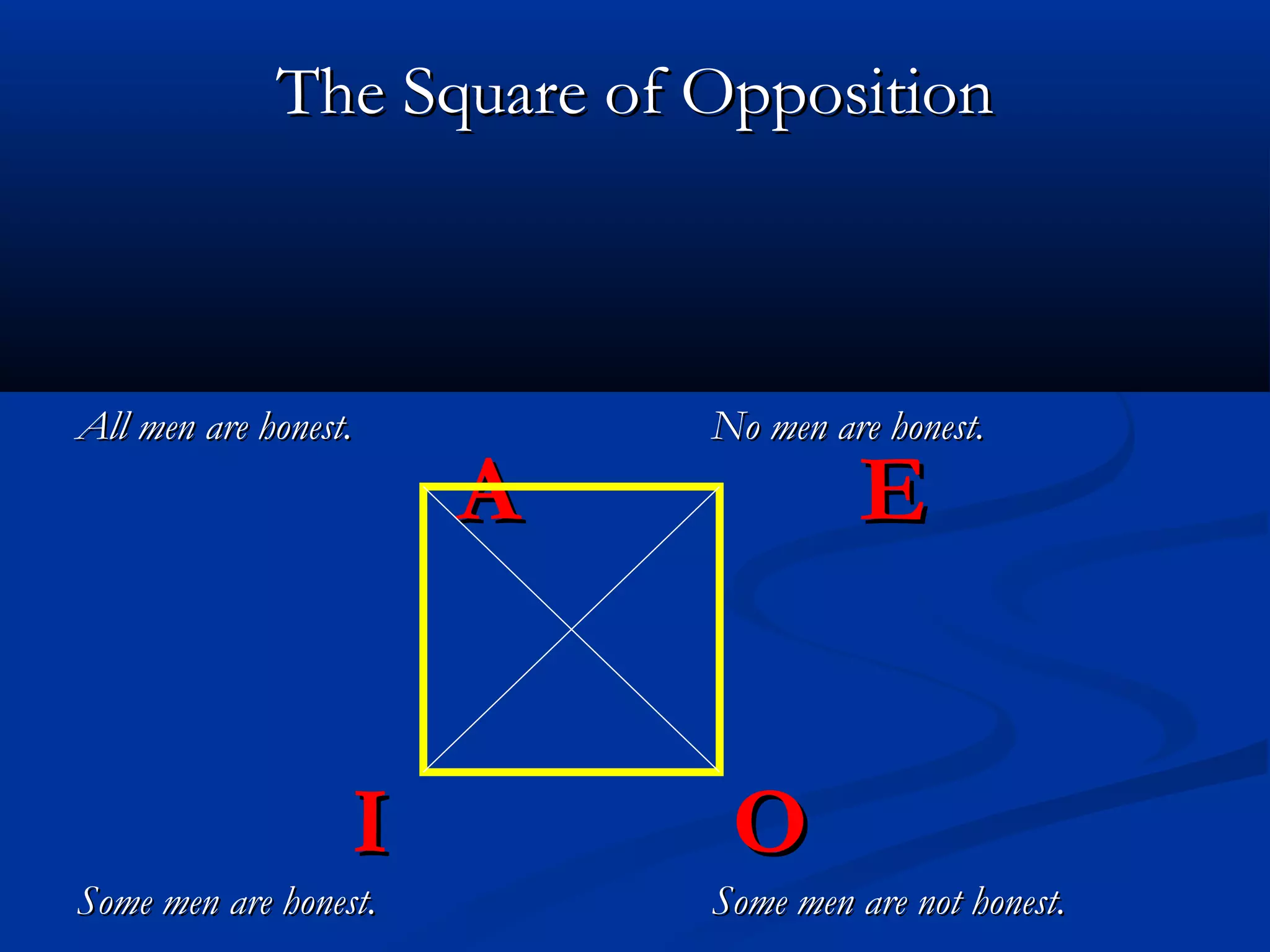
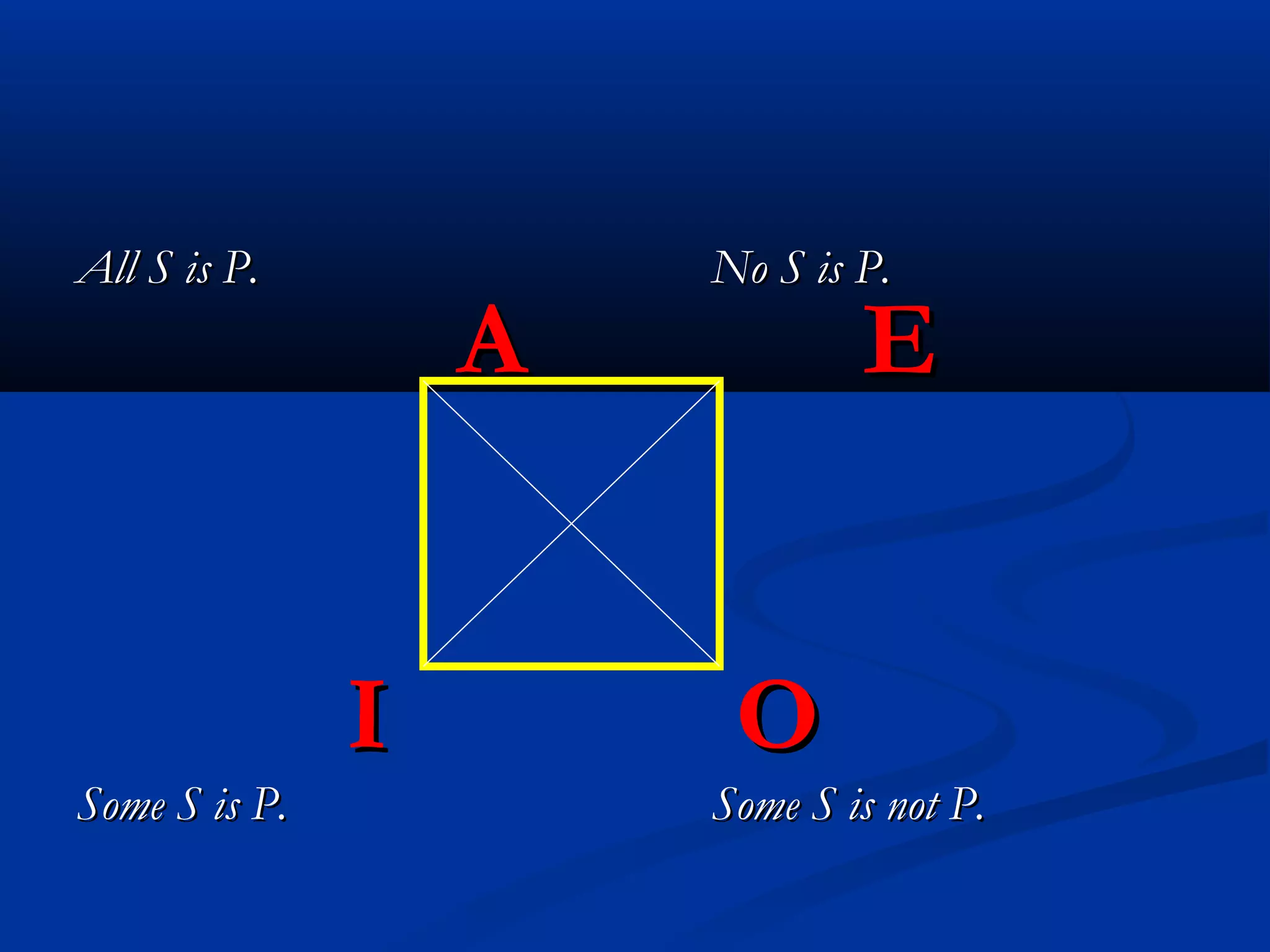
The document discusses the opposition and relation between propositions. It defines three types of opposition between propositions: contradictory, contrary, and sub-contrary. Contradictory propositions cannot both be true or false, contrary propositions cannot both be true, and sub-contrary propositions cannot both be false. It also discusses the relation of sub-alternation between propositions. The square of opposition is presented as a visual aid to understand these relationships between propositions.

1. Part II, Lesson FourPart II, Lesson Four
The Opposition of PropositionsThe Opposition of Propositions
The Rules of Truth and FalsityThe Rules of Truth and Falsity

2. IntroductionIntroduction
Opposition between propositions occurs when we
relate two propositions to each other.
We have already seen how to distinguish the parts
of a proposition (subject, predicate, and copula),
as well as the use of words within the
proposition (supposition and distribution).
Now we will consider the ways of relating one
proposition to another.

3. Opposition of PropositionsOpposition of Propositions
In general, opposition between two propositions
occurs when one affirms and the other denies
the same predicate of the same subject.
Example:
All dogs are cats.
No dogs are cats.
These two propositions are said to be opposed
because one affirms and the other denies “cats”
of “dogs”.

4. If a different predicate is used (or a different
subject), then there is no opposition between the
two propositions; they are merely different.
Example: All dogs are carnivorous.
No dogs are rational.
Because we are not affirming and denying the
same subject of the same predicate, these
propositions are not opposed to each other in
any way.

5. Furthermore, in order to have opposition between
two propositions, not only must the same
subject and same predicate be used in each, but
also they must have the same meaning and the
same supposition. Nor is it permissible to use
equivocal or analogous words.

6. Kinds of OppositionKinds of Opposition
There are different ways of affirming and denying
the same predicate of the same subject, which
gives rise to different kinds of opposition
between propositions.
The distinction of the kinds of opposition has to
do with both the quality (affirmative or
negative) and the quantity (universal, particular,
indefinite, or singular) of the two propositions.

7. 1. Contradictory Opposition1. Contradictory Opposition
When there is contradictory opposition between
two propositions, one denies absolutely
everything that the other affirms. They are as
opposed as can be.
Example: All men are honest.
Some men are not honest.

8. At first glance, we might be tempted to think that
the contradictory of “All men are honest” is
“No men are honest”, as it seems that they are
more opposed than the two mentioned
previously. Yet this is not so; in order to refute
the truth of the proposition “All men are
honest”, it would be enough to show that some
men are not honest, or even that one man is not
honest. One exception would disprove the truth
of the universal affirmative proposition.

9. Thus, in order to contradict the proposition,
“All apples are red”, all we need to show is that
“Some apples are not red”, or even “This apple
is not red”.
The contradictory proposition of a universal
affirmative proposition is a particular negative
proposition (using the same subject and the
same predicate, of course.)

10. The same applies in the case of a universal
negative proposition, whose contradictory will
be a particular (or singular) affirmative
proposition that uses the same subject and the
same predicate.
Example: No exam is difficult.
will be contradicted by
Some exams are difficult.
or even by
This exam is difficult.

11. Contradictory opposition is opposition in truth
and falsity.
This means that whenever we know that one of
the two propositions with this kind of
opposition is true, the other must necessarily be
false. It is impossible that both be true or that
both be false.

12. All men are honest.
Some men are not honest.
If the first proposition is false, the second must
necessarily be true.

13. All apples are red.
This apple is not red.

14. No exam is difficult.
Some exams are difficult.
This exam is difficult.

15. 2. Contrary Opposition2. Contrary Opposition
Contrary opposition exists between two
propositions when both have universal quantity
but one affirms and the other denies its
predicate of the subject.
Example: All men are honest.
No men are honest.

16. At first glance, it might appear that this is a more
radical type of opposition than contradictory
opposition because “all” and “none” are
extremes.
However, contrary opposition is in fact not as
great as contradictory opposition because the
contraries are opposed only in truth.
That is, it is impossible for both propositions to be
true, but both may be false.

17. To say that contrary opposition between
propositions is an opposition only in truth is to
say that when one of the contrary propositions
is true, its contrary must necessarily be false.
But if we only know that one of the two contrary
propositions is false, we cannot by that fact alone
know that its contrary is true; it could be true or it
might also be false.

18. Sometimes when one contrary is false, the other is
true.
Example:
No man is rational. (False)
All men are rational. (True)

19. But other times, the contrary of a false proposition
is also false.
Example:
All men are honest.
No man is honest.
(False)
(False)

20. In other words, when one of the contrary
propositions is false, the other may be true or it
may be false. In this case its truth is unknown.

21. Contrary propositions do not have as absolute an
opposition as is found between contradictory
propositions.
Contradictory propositions are opposed in truth
and in falsity, but contrary propositions are only
opposed in truth.
Also, contrary propositions are both universal.
With contradictory propositions, one is universal
and the other is particular or singular. Thus,
contradictory propositions differ in quality and
quantity, whereas contrary propositions only
differ in quality.

22. 3. Sub-contrary Opposition3. Sub-contrary Opposition
Two propositions are in sub-contrary opposition
when they differ in quality but are both
particular.
Example: Some dogs are black.
Some dogs are not black.

23. Propositions in sub-contrary opposition are
opposed in falsity only. That is, if one is false,
the other is necessarily true.
However, it may be that both are true, as in the
example just given.
Example: Some dog is black.
Some dog is not black.

24. Example:
Some dogs are cats. (False)
Some dogs are not cats. (True)

25. Summary of OppositionSummary of Opposition
1. Contradictory Opposition:
One proposition denies the other absolutely.
Opposition in truth and falsity.
The propositions differ in both quality and
quantity.
To have opposition between two propositions,
they must use the same subject and the same
predicate.

26. 2. Contrary Opposition
Opposition in truth only.
Both propositions are universal (one is
affirmative, the other negative.)

27. 3. Sub-contrary Opposition
Opposition in falsity only.
Both propositions are particular (one is
affirmative, the other is negative).

28. The Relation of Sub-alternationThe Relation of Sub-alternation
There is another possible relation between two
propositions that use the same subject and the
same predicate, but this is not a relation of
opposition.
This relation, called sub-alternation, occurs when
the propositions differ in quantity but not in
quality (which is why there is no opposition
between them.)

29. Example: All men are brave.
Some men are brave.

30. When the universal proposition is true, its
subalternate must also be true.
If all we know is that the particular is true, this tells
us nothing about the truth of the universal.
But if the particular is false, the universal must also
be false.

31. Since subalternation is not a kind of opposition,
there is no opposition in truth or falsity.
Yet we can conclude from the truth of the
universal to the truth of the particular, or from
the falsity of the particular to the falsity of the
universal.

32. Example:
All strawberries are sweet.
Some strawberries are sweet.
If the universal is true, the particular is necessarily
true as well.

33. And if it is false that
Some children are not human beings.
then it must necessarily be false that
No children are human beings.

34. The Square of OppositionThe Square of Opposition
The Square of Opposition is a very useful visual
aid to understanding the consequences of the
various relations of opposition and sub-
alternation of propositions using the same
subject and the same predicate.

35. It uses vowels to represent the main types of
propositions:
A stands for the universal affirmative.
E stands for the universal negative.
I stands for the particular affirmative.
O stands for the particular negative.

36. The Square of OppositionThe Square of Opposition
All men are honest.All men are honest. No men are honest.No men are honest.
AA EE
II OO
Some men are honest.Some men are honest. Some men are not honest.Some men are not honest.

37. The lines of the Square represent the three types
of opposition and the relation of subalternation.
AO and EI (the diagonals) represent the
propositions in contradictory opposition.
AE represents the propositions in contrary
opposition.
IO represents the propositions in sub-contrary
opposition.
AI and EO represent the relation of sub-
alternation.

38. The Rules of Truth and Falsity inThe Rules of Truth and Falsity in
the Square of Oppositionthe Square of Opposition
To use the Square of Opposition, the propositions
must use the same subject and the same
predicate with the same meaning, the same
supposition (personal or simple) and must
respect the difference between true universal
names and collective names.

39. 1. Two propositions in contradictory
opposition cannot simultaneously be true,
nor simultaneously false.
If one is true, the other will be false, and if one
is false, the other will be true.

40. 2. Two propositions in contrary opposition
cannot be simultaneously true.
When one is true, the other will be false, but if
one is false, the other will be unknown.

41. 3. Two propositions in sub-contrary
opposition cannot be simultaneously false.
If one is false, the other must be true, but if
one is true, the other is unknown.

42. 4. In the relation of subalternation, when the
universal is true, the particular must also
be true, and when the particular is false,
the universal must also be false.
If the particular is known to be true, this tells
us nothing about the truth of the universal (its
truth is unknown.)
Similarly, when the universal is known to be
false, the particular is unknown.
This is sometimes summarized by saying that we
can descend with truth and rise with
falsehood.

43. In this entire discussion, we have been examining
what can be concluded from the formal
relationship between propositions. To have a
starting point (to know that a proposition is true
or false), we need knowledge from some science
outside of Logic. Logic can help us arrive at
valuable consequences from the formal
relationship between propositions once we have
that starting point.
We can be quite sure that these consequences
follow from the mere fact that propositions are
related in this way, no matter what the subject
matter being discussed.

44. We are always forced to distinguish between the
matter and form of the propositions we use,
between the subject matter and the form we use
to express our knowledge of it. Elementary
Logic is necessarily a consideration of the form
of our expressions. Knowledge of the subject
matter comes from other branches of
knowledge.

45. Whenever we use words we are necessarily
considering the “subject matter” of the
proposition, that is, what the proposition means
as well as what form it is expressed in.
In order to avoid being distracted unnecessarily by
the content of propositions, we could merely use
letters in place of actual subjects and predicates,
to bring out more clearly the formal aspects of
the propositions.
For example, we could avoid considering the
specific subject matter by using expressions such
as “All S is P” or “Some S is not P.”

46. All S is P.All S is P. No S is P.No S is P.
AA EE
II OO
Some S is P.Some S is P. Some S is not P.Some S is not P.