Downloaded 78 times
Uploaded byManoj maurya
Numerical solution, couette flow using crank nicolson implicit method
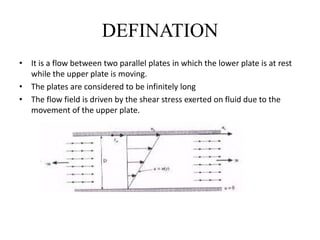
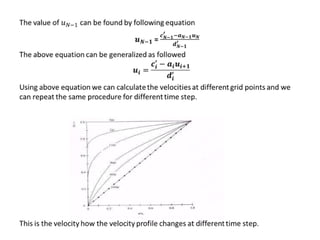
Couette flow is the flow of a fluid between two parallel plates, where the lower plate is stationary and the upper plate is moving, creating shear stresses that drive the fluid flow. The document describes numerically solving the governing equations for Couette flow using the Crank-Nicolson technique, which involves discretizing the equations on a grid and solving the resulting tridiagonal matrix using methods like Thomas algorithm.
Numerical solution, couette flow using crank nicolson implicit method
- 1. NUMERICAL SOLUTION OFCOUETTE FLOW USING CRANK NICOLSON TECHNIQUE MANOJKUMAR MAURYA M.E. 13906
- 2. DEFINATION • It isa flow between two parallel plates in which the lower plate is at rest while the upper plate is moving. • The plates are considered to be infinitely long • The flow field is driven by the shear stress exerted on fluid due to the movement of the upper plate.
- 3.
- 4.
- 5.
- 7. Crank Nicolson technique,the finite difference representation
- 8. • We getdifferent equations as we apply this equation at different grid points • The order of the matrix depends upon the number of grid points taken into consideration • The matrix thus obtained is tridiagonal matrix which is converted into bidiagonal form using Thomas algorithm or Gauss elimination method
- 9.
- 10.
- 11.