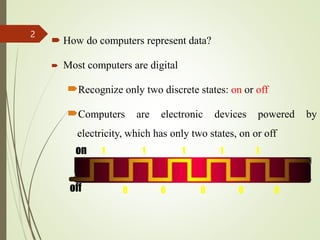
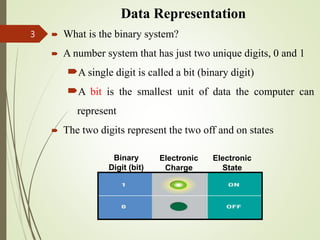
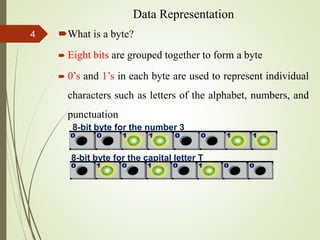
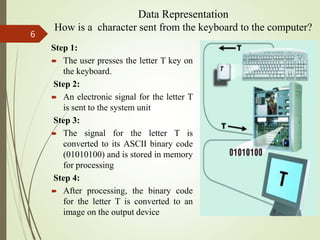
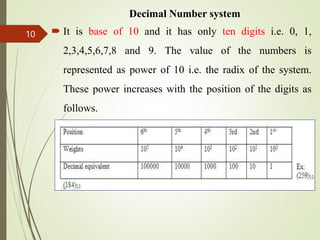
The document explains how computers represent data using different numbering systems, primarily focusing on the binary system which consists of two states: on (1) and off (0). It details various data representations such as bits, bytes, and character encoding systems like ASCII and EBCDIC, along with methods for converting between binary, decimal, octal, and hexadecimal systems. Additionally, it includes practical examples for conversions and shortcuts for translating between these systems.

1. CHAPTER THREE
DATA REPRESENTATION
1

2.  How do computers represent data?
 Most computers are digital
Recognize only two discrete states: on or off
Computers are electronic devices powered by
electricity, which has only two states, on or off
2
on
off 0 0 0 0 0
1 1 1 1 1

3. Data Representation
 What is the binary system?
 A number system that has just two unique digits, 0 and 1
A single digit is called a bit (binary digit)
A bit is the smallest unit of data the computer can
represent
 The two digits represent the two off and on states
3
Binary
Digit (bit)
Electronic
Charge
Electronic
State

4. Data Representation
What is a byte?
 Eight bits are grouped together to form a byte
 0’s and 1’s in each byte are used to represent individual
characters such as letters of the alphabet, numbers, and
punctuation
4
8-bit byte for the number 3
8-bit byte for the capital letter T

5. Data Representation
What are two popular coding systems to represent data?
5
 American Standard Code for
Information Interchange
(ASCII)
 Extended Binary Coded
Decimal Interchange Code
(EBCDIC)
• Sufficient for English and
Western European
languages
• Unicode often used for
others

6. Data Representation
How is a character sent from the keyboard to the computer?
Step 1:
 The user presses the letter T key on
the keyboard.
Step 2:
 An electronic signal for the letter T
is sent to the system unit
Step 3:
 The signal for the letter T is
converted to its ASCII binary code
(01010100) and is stored in memory
for processing
Step 4:
 After processing, the binary code
for the letter T is converted to an
image on the output device
6

7. Numbering Systems
 The data representation of computer consist alphabets,
numerals, and special symbols. Here we discuss about the
numerals (numbers). In our daily life we use decimal
system, where as computer use only binary system .
Basically Number system is divided in to four types
 Binary Numbering System
 Octal Numbering system
 Decimal Numbering system
 Hexa-decimal Numbering System
7

8. Binary Number System
Note:A number in base r contains r digits 0,1,2,...,r-1
 It is base (radix) of 2 and it has only two digits i.e. 0 and 1.
 The value of the numbers is represented as power of 2 i.e.
the radix of the system. These power increases with the
position of the digits as follows. Ex: (1011)2 (11010)2
8

9. Octal Number System
 It is base of 8 and it has only eight digits i.e. 0, 1, 2,
3,4,5,6 and 7. The value of the numbers is represented as
power of 8 i.e. the radix of the system.
 These power increases with the position of the digits as
follows.
9

10. Decimal Number system
 It is base of 10 and it has only ten digits i.e. 0, 1,
2,3,4,5,6,7,8 and 9. The value of the numbers is
represented as power of 10 i.e. the radix of the system.
These power increases with the position of the digits as
follows.
10

11. Hexa Decimal Number System
 It is base of 16 and it has only sixteen digits i.e.
0,1,2,3,4,5,6,7,8,9, A(10),B(11), C(12), D(13),E(14)
and F(15).
 The value of the numbers is represented as power of
16 i.e. the radix of the system. These power increases
with the position of the digits.
 Example:- (5D)16
11

12. Conversions
 We can convert from any system to any other system as
follows.
Decimal to Binary
 Divide the decimal number by 2 repeatedly and note the
remainders from bottom to top.
 Ex1: Convert (13)10 to (?)2
2 13 1
2 6 0
2 3 1
1
So, (13)10 = (1101)2
12

13. Cont...
 Ex2: Convert (37)10 to (?)2
2 37 1
2 18 0
2 9 1
2 4 0
2 2 0
1
(100101)2
13

14. Decimal to Octal:
 Divide the decimal number by 8 repeatedly and note
the remainders from bottom to top.
 Ex1: convert (50)10 to (?)8
8 50 2
6
(62)8
 Exercise: convert (124)10 to (?)8
14

15. Decimal to hexadecimal:
 Divide the decimal number by 16 repeatedly and note
the remainders from bottom to top.
 Ex1: Convert (50)10 to (?)16
16 50 2
3
(32)16
 Ex2: Convert (380)10 to (?)16
16 380 C
16 23 7
1
(17C) 16
15

16. Binary to Decimal
 Multiply the binary number with the weights of binary
system according to their position and note the sum.
 Ex1: Convert (11010)2 to (?)10
11010 = 1 x 2 4 +1 x 23 + 0 x 22 +1 x 21 + 0 x 20
= 1 x 16 + 1 x 8 + 0 x 4 + 1 x 2 + 0 x 1
(174)8
= 16 + 8 + 0 +2 + 0 = (26)10
 Ex2: Convert (1101)2 into (?)10
1101 = 1 x 23 + 1 x 22 +0 x 21 + 1 x 20
= 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1
= 8 + 4 + 0 +1 = (13)10
16

17. Octal to Decimal
 Multiply the Octal number with the weights of octal system
according to their position and note the sum.
 Ex1: Convert (62)8 into (?)10
(62)8 = 6 x 81 + 2 x 80
= 6 x 8 + 2 x 1
= 48 + 2 = (50)10
 Ex2: Convert (174)8 into (?)10
(174)8 = 1 x 82 + 7 x 81 + 4 x 80
= 1 x 64 + 7 x 8 + 4 x 1
= 64 + 56 + 4 = (124)10
17

18. Hexadecimal to Decimal
Multiply the hexadecimal number with the weights of
hexadecimal system according to their position and note
the sum.
 Ex1: Convert (5D) 16 into (?)10
(5D) 16 = 5 x 161 + D x 160
= 5 x 16 + 13 x 1
= 80 + 13 = (93)10
 Ex2: Convert (1A5)16 into (?)10
(1A5)16 = 1 x 162 + A x 161 + 5 x 160
= 1 x 256 + 10 x 16 + 5 x 1
= 256 + 160 + 5 = (421)10
18

19. Shortcut method - Binary to Octal
Step 1 - Divide the binary digits into groups of three (starting
from the right).
Step 2 - Convert each group of three binary digits to one
octal digit.
Example
Binary Number: 101012
Calculating Octal Equivalent: 101012=258
19
Step` Binary Number Octal Number
Step 1 101012 010 101
Step 2 101012 28 58
Step 3 101012 258

20. Shortcut method - Octal to Binary
Step1 - Convert each octal digit to a 3 digit binary number
(the octal digits may be treated as decimal for this
conversion).
Step 2 - Combine all the resulting binary groups (of 3 digits
each) into a single binary number.
Example: Octal Number: 258
Calculating Binary Equivalent: 258=101012
20
Step Octal Number Binary Number
Step 1 258 210 510
Step 2 258 0102 1012
Step 3 258 0101012

21. Shortcut method - Binary to Hexadecimal
Step 1 - Divide the binary digits into groups of four
(starting from the right).
Step 2 - Convert each group of four binary digits to one
hexadecimal symbol.
Example: Binary Number: 101012
Calculating hexadecimal Equivalent: 101012=1516
21
Step Binary Number Hexadecimal Number
Step 1 101012 0001 0101
Step 2 101012 110 510
Step 3 101012 1516

22. Shortcut method - Hexadecimal to Binary
Step1 - Convert each hexadecimal digit to a 4 digit binary
number (the hexadecimal digits may be treated as decimal for
this conversion).
Step 2 - Combine all the resulting binary groups (of 4 digits
each) into a single binary number.
Example: Hexadecimal Number: 1516
Calculating Binary Equivalent: 1516=101012
22
Step Hexadecimal Number Binary Number
Step 1 1516 110 510
Step 2 1516 00012 01012
Step 3 1516 000101012

23. Number Systems Summary
 Computers are binary devices
We’re forced to think in terms of base 2.
We learned how to convert numbers between binary,
decimal, octal and hexadecimal
 We’ve already seen some of the recurring themes of
architecture:
We showed how to represent numbers using just these
two signals. And
23

24. Home Activity
1. The equivalent of the decimal number 90 in hexadecimal numb. System
is
A) (5A) 16 B) (4A) 16 C) (5B) 16 D) (3B) 16
2. Convert
A.(BDC2)16 to binary number system AND to octal number system
B. (1000001101)2 to hexadecimal numb. System.
C. (129)10 to binary
D.(422)10 to octal
3.How would you represent the decimal value of 30 in Hexadecimal?
A. (1E)16 B) (1C )8 C) (30)16 D) (11010) 2
24

25. 25