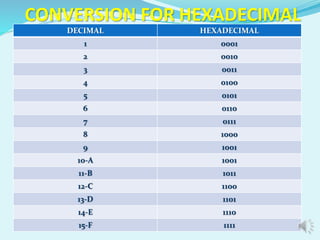
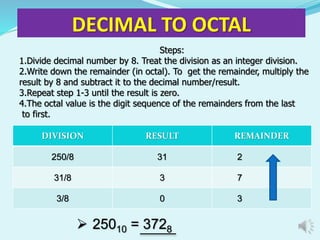
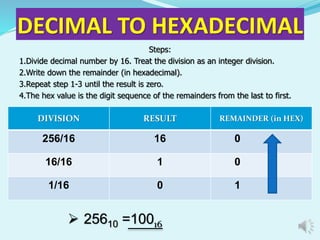
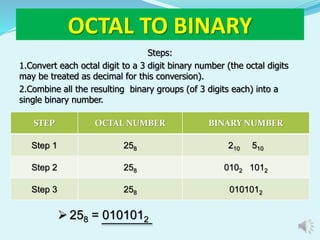
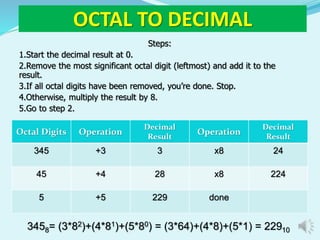
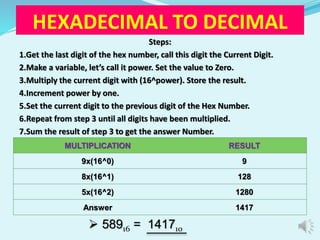
The document discusses different number systems including decimal, binary, octal, and hexadecimal. It provides examples and steps for converting between these number systems. The decimal system uses base 10, while binary uses base 2, octal uses base 8, and hexadecimal uses base 16. Computers commonly use binary, octal, and hexadecimal in addition to decimal. Conversion methods between the systems include division, multiplication, and treating digits as place values.

1. A set of values used to
represent different quantities.
Examples:
Number of students in a Class or number of
viewers watching a certain TV program.
It includes audio, graphics, video, text, and
numbers.
Base or Radix are the total number of digits
used in a number system.

2. Some important number systems
are as follows:
 DECIMAL number system
 BINARY number system
 OCTAL number system
 HEXADECIMAL number system
The decimal number system is used in general.
However, the computers use binary number , octal, and
hexadecimal number systems.

3. BINARY NUMBER SYSTEM

4. DECIMAL NUMBER SYSTEM
 It is the most widely used number system.
 It consists of ten numbers from 0 to 9.
 It’s base is 10.
Examples:
1. 145010
2. 24210
3. 1000002410

5. OCTAL NUMBER SYSTEM
 It is the shorthand representation of binary numbers.
 Any digit in this system is always less than 8.
 It consists of eight digits from 0 to 7.
 It’s base is 8.
Examples:
1. 56568
2. 1248
3. 3788

6. HEXADECIMAL NUMBER
SYSTEM
 It consists of 16 digits from 0 to 9 and A to F.
 The alphabets A to F represent decimal numbers 10 to
15.
 It’s base is 16.
Examples:
1. 29716
2. BA5916
3. BACA16

7. CONVERSION FOR HEXADECIMAL
DECIMAL HEXADECIMAL
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
10-A 1001
11-B 1011
12-C 1100
13-D 1101
14-E 1110
15-F 1111

9. STEP BINARY NUMBER DECIMAL NUMBER
Step 1 111012 ((1x24)+(1x23)+(1x22)+
(0x21)+(1x20)) 10
Step 2 111012 (16+8+4+0+1) 10
Step 3 111012 2910
1.Determine the column (positional) value of each digit (this depends
on the position of the digit and the base of the number system.)
2.Multiply the obtained column values (in step 1) by the digits in the
corresponding columns.
3.Sum the products calculated in step 2. The total is the equivalent
value in decimal.

10. BINARY TO OCTAL
STEPS:
1.Divide the binary digits into groups of three (starting left to
right).
2.Convert each group of three binary digits to one octal digit.
Add a (0) Zero digit to complete
the 3 digits group.
STEP BINARY NUMBER OCTAL NUMBER
Step 1 101012 010 101
Step 2 101012 28 58
Step 3 101012 258

11. BINARY TO HEXADECIMAL
STEPS:
1.Divide the binary digits into groups of four (starting from the
right).
2.Convert each group of four binary digits to one hexadecimal
symbol.
Add two(2) Zero(0) digits to complete the four
(4) digits group.
STEP BINARY NUMBER
H10101EXADECIMAL
NUMBER
Step 1 101012 0001 0101
Step 2 101012 110 510
Step 3 101012 1516

12. DECIMAL TO BINARY
STEP OPERATION RESULT REMAINDER
Step 1 29/2 14 1
Step 2 14/2 7 0
Step 3 7/2 3 1
Step 4 3/2 1 1
Step 5 1/2 0 1
1.Divide the decimal number to be converted by the value of the new base.
2.Get the remainder from step 1 as the rightmost digit (least significant digit) of
new base number.
3.Divide the quotient of the previous divide by the new base.
4.Record the remainder from step 3 as the next digit (to the left) of the new
base number.

13. DECIMAL TO OCTAL
Steps:
1.Divide decimal number by 8. Treat the division as an integer division.
2.Write down the remainder (in octal). To get the remainder, multiply the
result by 8 and subtract it to the decimal number/result.
3.Repeat step 1-3 until the result is zero.
4.The octal value is the digit sequence of the remainders from the last
to first.
DIVISION RESULT REMAINDER
250/8 31 2
31/8 3 7
3/8 0 3
 25010 = 3728

14. DECIMAL TO HEXADECIMAL
Steps:
1.Divide decimal number by 16. Treat the division as an integer division.
2.Write down the remainder (in hexadecimal).
3.Repeat step 1-3 until the result is zero.
4.The hex value is the digit sequence of the remainders from the last to first.
DIVISION RESULT REMAINDER (in HEX)
256/16 16 0
16/16 1 0
1/16 0 1
 25610 =10016

15. OCTAL TO BINARY
Steps:
1.Convert each octal digit to a 3 digit binary number (the octal digits
may be treated as decimal for this conversion).
2.Combine all the resulting binary groups (of 3 digits each) into a
single binary number.
STEP OCTAL NUMBER BINARY NUMBER
Step 1 258 210 510
Step 2 258 0102 1012
Step 3 258 0101012
 258 = 0101012

16. OCTAL TO DECIMAL
Steps:
1.Start the decimal result at 0.
2.Remove the most significant octal digit (leftmost) and add it to the
result.
3.If all octal digits have been removed, you’re done. Stop.
4.Otherwise, multiply the result by 8.
5.Go to step 2.
Octal Digits Operation
Decimal
Result
Operation
Decimal
Result
345 +3 3 x8 24
45 +4 28 x8 224
5 +5 229 done
3458= (3*82)+(4*81)+(5*80) = (3*64)+(4*8)+(5*1) = 22910

17. HEXADECIMAL TO BINARY
Steps:
1.Convert each hexadecimal digit to a 4 digit binary number (the
hexadecimal digits may be treated as decimal for this conversion).
2.Combine all the resulting binary groups (of 4 digits each) into a
single binary number.
STEP
HEXADECIMAL
NUMBER
BINARY NUMBER
Step 1 15 12 52
Step 2 15 00012 01012
Step 3 15 000101012
 1516 = 000101012

18. HEXADECIMAL TO DECIMAL
Steps:
1.Get the last digit of the hex number, call this digit the Current Digit.
2.Make a variable, let’s call it power. Set the value to Zero.
3.Multiply the current digit with (16^power). Store the result.
4.Increment power by one.
5.Set the current digit to the previous digit of the Hex Number.
6.Repeat from step 3 until all digits have been multiplied.
7.Sum the result of step 3 to get the answer Number.
MULTIPLICATION RESULT
9x(16^0) 9
8x(16^1) 128
5x(16^2) 1280
Answer 1417
 58916 = 141710

20. WORKING COMMITTEE
CHERRY MARIE GALAUS
ROSEANN FORONDA
CRISTINA FABROS
CRISTINA FABROS
MICAH HADASSAH GUILLERMO
DANILO PALTENG
JANUEL ANTONIO
MICAH HADASSAH GUILLERMO
DANILO PALTENG
JANUEL ANTONIO
BS ACCOUNTANCY 1-2