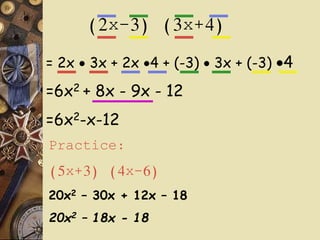The document discusses factoring polynomials and operations on polynomials. It explains that students will learn to factor polynomials using various methods, add, subtract, and multiply polynomials, and sketch rough graphs using key features like zeros. The document provides examples of factoring polynomials using the distributive property, FOIL method, and special products like the square of a binomial and difference of squares. It also gives rules and examples for performing operations on polynomials.

1. Multiplying
Polynomials

2. 4 3 2 1 0
In addition
to level 3,
students
make
connections
to other
content
areas and/or
contextual
situations
outside of
math.
Students will factor
polynomials using multiple
methods, perform operations
(excluding division) on
polynomials and sketch rough
graphs using key features.
- Factor using methods
including common factors,
grouping, difference of two
squares, sum and difference
of two cubes, and
combination of methods.
- Add, subtract, and multiply
polynomials,
- Explain how the
multiplicity of the zeros
provides clues as to how the
graph will behave.
- Sketch a rough graph using
the zeros and other easily
identifiable points.
Students will factor
polynomials using
limited methods,
perform operations
(excluding division)
on polynomials, and
identify key features
on a graph.
- Add and subtract
polynomials.
- Multiply
polynomials using an
area model.
- Factor polynomials
using an area model.
- Identify the zeros
when suitable
factorizations are
available.
- Identify key features
of a graph.
Students will
have partial
success at a 2
or 3, with
help.
Even with
help, the
student is not
successful at
the learning
goal.
Focus 9 Learning Goal – (HS.A-SSE.A.1, HS.A-SSE.A.2, HS.A-SEE.B., HS.A-
APR.A.1, HS.A-APR.B.3, HS.A-REI.B.4) = Students will factor polynomials using multiple
methods, perform operations (excluding division) on polynomials and sketch rough graphs
using key features.

3. 1. 5x(3x2-2x+1) (give the 5x to each term)
5x(3x2)+5x(-2x)+5x(1)
15x3-10x2+5x
2. 6x2(5x2+3x-9)
30x4+18x3-54x2
Simple multiplication:
Distribute monomial to all terms!

4. FOIL
F first terms
O outer terms
I inner terms
L last terms

5. (2x-3) (3x+4)
= 2x  3x + 2x 4 + (-3)  3x + (-3) 4
=6x2 + 8x - 9x - 12
=6x2-x-12
Practice:
(5x+3) (4x-6)
20x2 – 30x + 12x – 18
20x2 – 18x - 18

6. Distributive Property
(x-2)(5+3x-x2)
=x(5+3x-x2)+(-2)(5+3x-x2)
=5x + 3x2 - x3 – 10 - 6x + 2x2
=-x + 5x2 - x3 - 10 (put in order)
=-x3+5x2-x-10

7. Special Products:
Square of a binomial
(a+b)2 = a2+ab+ab+b2
= a2+2ab+b2
(a-b)2 =a2-ab-ab+b2
=a2-2ab+b2

8. RULE
: 2
2
2
2
)
( b
ab
a
b
a 



You can do this mentally when
you recognize the pattern!
(x+2)2
(x-6)2
x2 + 2x + 2x + 4
x2+4x+4
x2-12x+36

9. Product of the sum and
difference of two terms:
(a+b) (a-b)=a2+ab-ab-b2
=a2-b2
The middle terms cancel out and
you end up with the difference of
perfect squares.
(5x+2) (5x-2)= 25x2-4

10. PRACTICE :
(x+2) (x-2)
(b+6)2
(y-4)2
x2 - 4
b2 + 12b + 36
y2 - 8y + 16