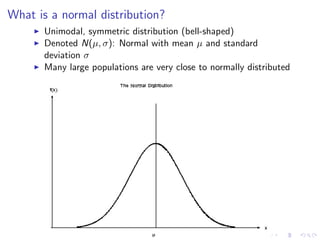
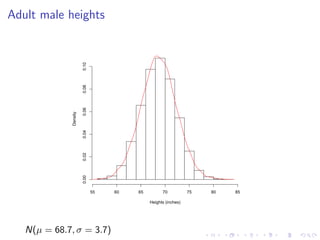
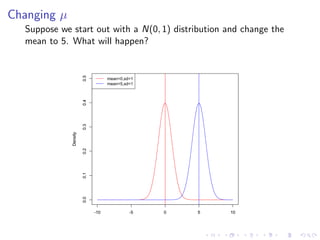
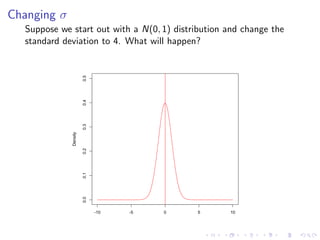
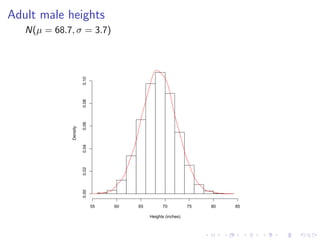
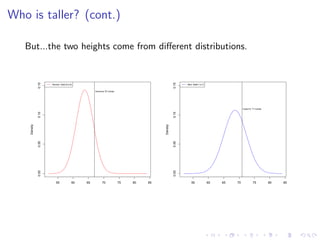
The document discusses the normal distribution and its properties. It summarizes data from a 2008 report on the heights of 4,482 adult males in the US. It finds the heights are normally distributed with a mean of 68.7 inches and standard deviation of 3.7 inches. It also discusses how changing the mean and standard deviation of a normal distribution affects its shape. Finally, it demonstrates how to standardize scores to compare values from different normal distributions.