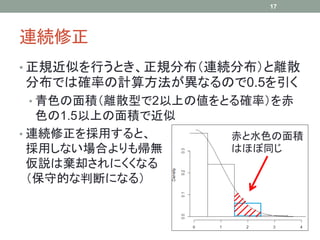
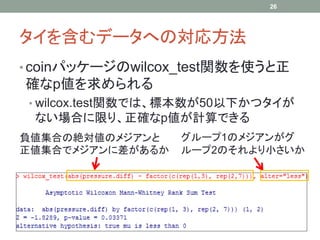
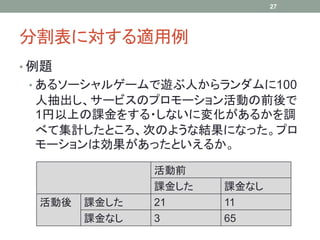
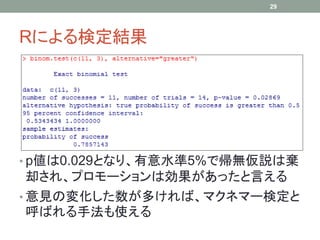
At Nagoya.R #10, I introduced basic nonparametric statistical methods, sign test and Wilcoxon signed-rank test. These slides show that they can also be used in some special cases such as test for contigency table.
Nagoya.R #10において、符号検定とウィルコクソンの符号付き順位和検定という、基本的なノンパラメトリックな統計手法について紹介した。スライドでは、これらの手法が例えば分割表に対する検定などのような、特別な場合においても利用することもできることを示した。


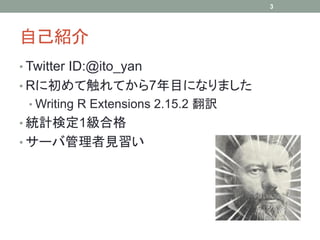






![メジアンの信頼区間の構成
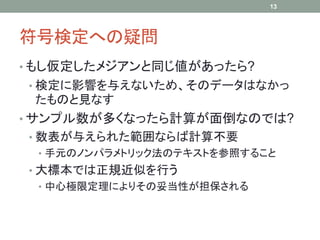
• p値が有意水準0.05を下回らない範囲にする
• +と-が1個以下ではp値は0.05を下回る
→+は2~8個になるような値が信頼区間に入る
→メジアンの名目上の95%信頼区間は[55, 78]
• 実際の信頼度は1-0.0215=97.9%
12](https://image.slidesharecdn.com/nonparametric1-130730074630-phpapp01/85/R-1-12-320.jpg)


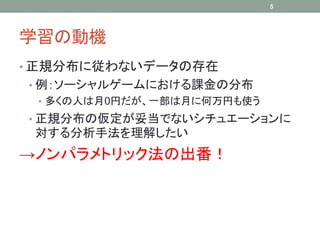
![符号検定の正規近似による解法
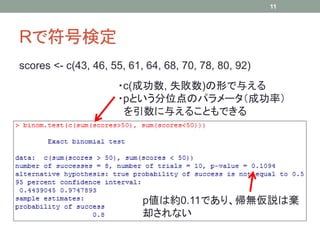
• 50点を超える人数を確率変数Xで表す。Xの期待
値と分散は の下で次のようになる
• E[X] = 50 * 0.5 = 25
• V[X] = 50 * 0.5 * (1 – 0.5 ) = 12.5
• 標本数が大きいので中心極限定理を用いて解く
• z = (34 – E[X]) / sqrt(V[X]) = 2.55 であり、
|z| > 1.96 (N(0, 1)の上側2.5%点)なので、メジアン
が50点という帰無仮説を有意水準5%で棄却
• メジアンは50点でないと言える
16
X~Bin(50, 0.5)
から計算する](https://image.slidesharecdn.com/nonparametric1-130730074630-phpapp01/85/R-1-16-320.jpg)