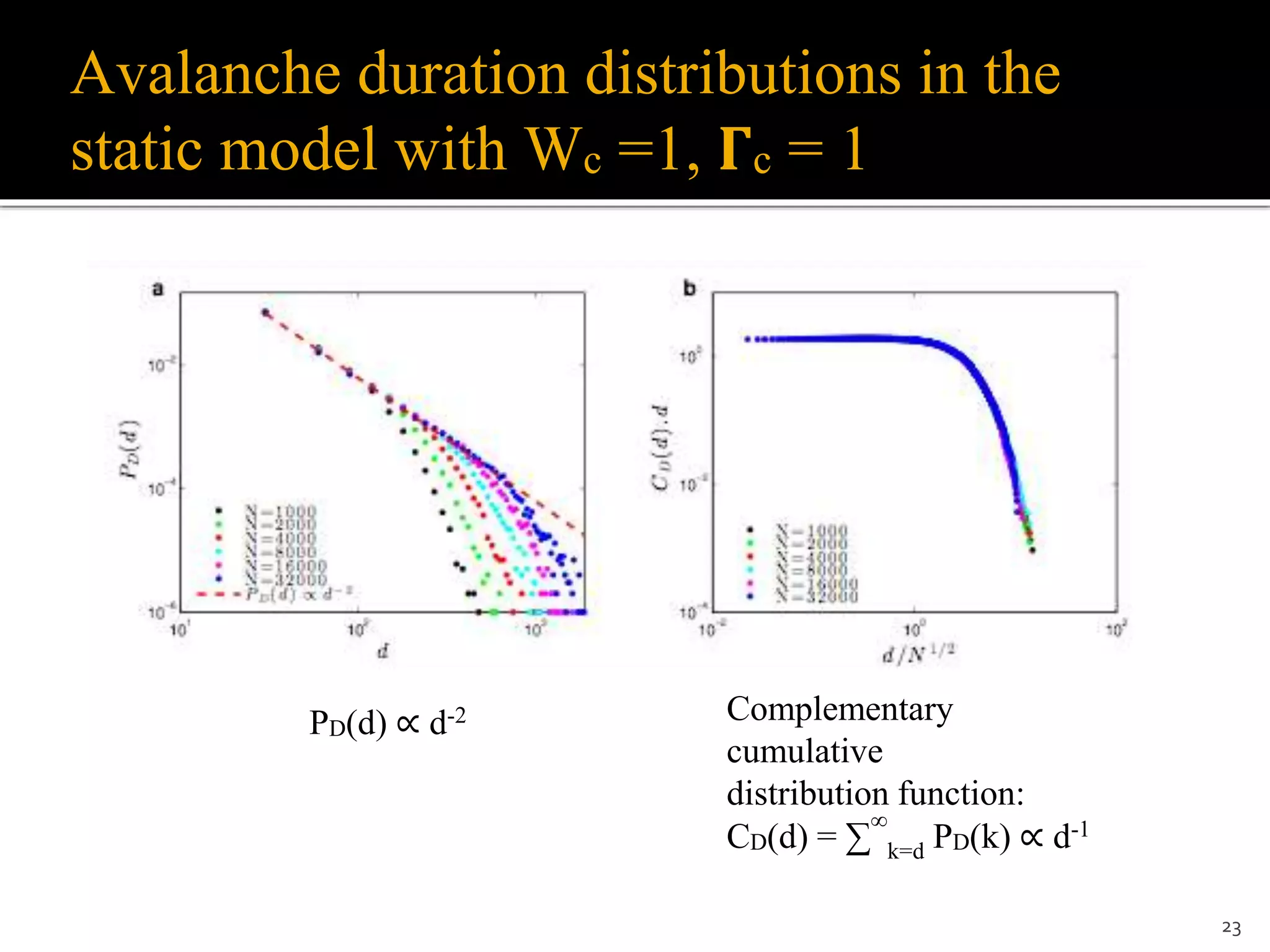
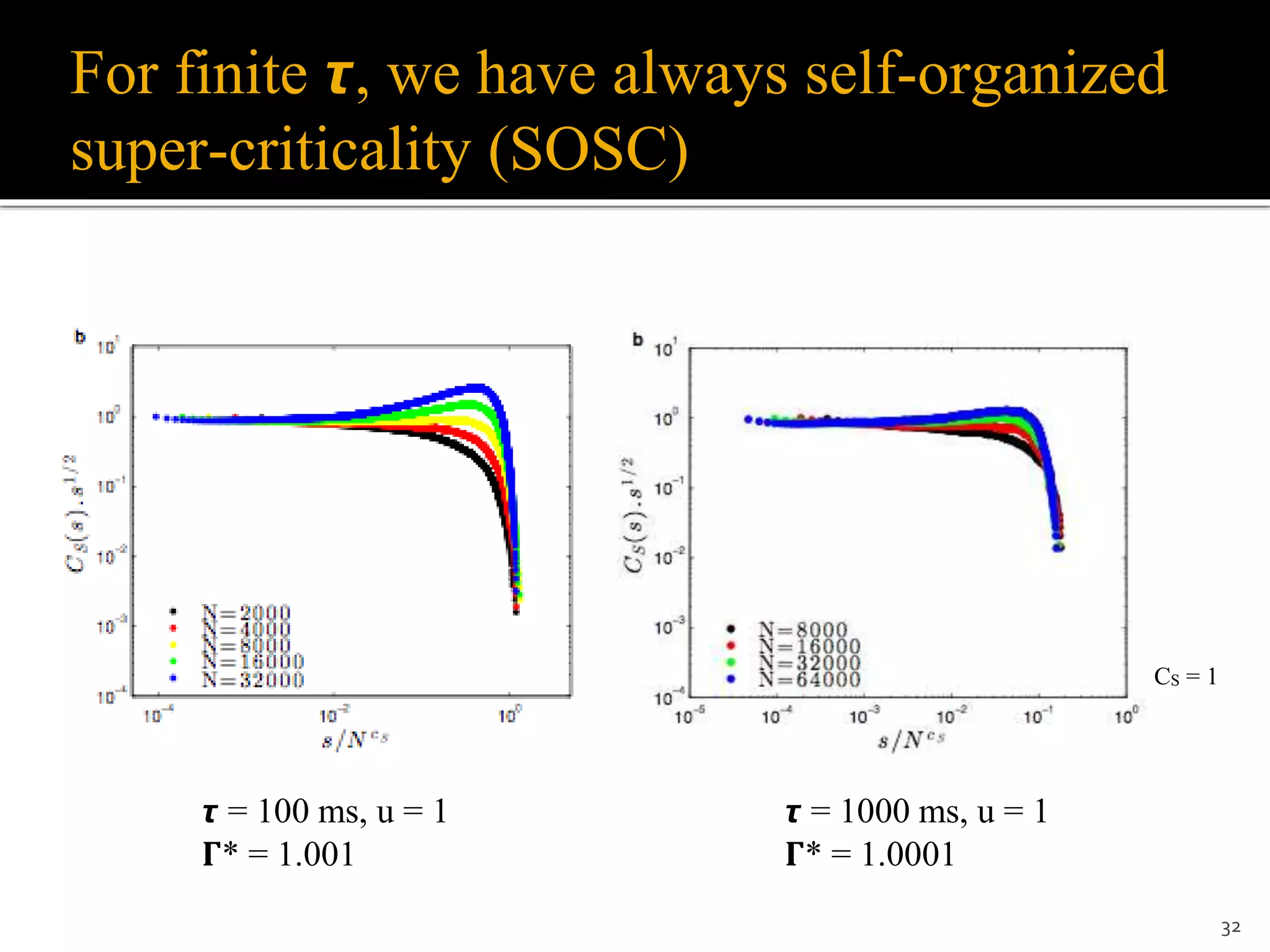
1) The document discusses a model of stochastic spiking neural networks where dynamical neuronal gains produce self-organized criticality. Introducing dynamic neuronal gains Γi[t] in addition to dynamic synaptic weights Wij[t] allows the system to self-organize toward a critical region without requiring divergent timescales. 2) For finite recovery timescales τ, the model exhibits self-organized supercriticality (SOSC) where the average neuronal gain Γ* is always slightly above critical. SOSC may help explain biological phenomena like large avalanches and epileptic activity. 3) The model provides a new framework to study self-organized phenomena in neuronal networks, including potential analytic solutions and

1. Dynamical neuronal gains produce self-
organized criticality in stochastic spiking
neural networks
Osame Kinouchi
Physics Department - FFCLRP - USP
Departamento de Física - UFSC, Florianópolis - SC, December 19 2016

2. Scientific Reports 6: 35831 (2016)
2

3. Collaborators at NEUROMAT
3
Ludmila Brochini
Jorge Stolfi
Ariadne A. Costa
Antônio C. Roque Mauro Copellihttp://neuromat.numec.prp.usp.br/team

4. Allan Turing (1950)
Computing machinery and intelligence. Mind, 59, 433-460.
Is there a corresponding phenomenon [criticality] for minds, and
is there one for machines? There does seem to be one for the
human mind. The majority of them seems to be subcritical, i.e., to
correspond in this analogy to piles of subcritical size. An idea
presented to such a mind will on average give rise to less than one
idea in reply.
A smallish proportion are supercritical. An idea presented to such
a mind may give rise to a whole "theory" consisting of secondary,
tertiary and more remote ideas. (...) Adhering to this analogy we
ask, "Can a machine be made to be supercritical?"
4

5. Motivation: Neuronal Avalanches
5
Avalanche Size
Distribution:
PS(s) ∝ s-3/2
Avalanche Duration
Distribution:
PD(d) ∝ d-2
Mean-field exponents
Beggs & Plenz, 2003

6. Our model: Stochastic discrete time spiking
neurons (Galves & Löcherbach, 2013)
i = 1, 2, …, N neurons Xi[t] = 1 (spike)
Vi[t+1] = 0 reset if Xi[t] = 1
Vi[t+1] = μVi[t] + I + N-1 ∑j Wij Xj[t] if Xi[t] = 0
Prob( Xi[t+1] = 1 ) = Φ(Vi[t])
Φ = firing probability function
0 ≤ Φ(V) ≤ 1
7
All-to-all network

7. Examples of firing functions
8
1
VT VS V
r = 1
r > 1
r < 1
Φ(V) For VT < V < VS: Φ(V) = [ 𝚪(V-VT) ]r
𝚪 = Neuronal Gain

8. Mean field approach
 Order parameter: ρ[t] = 1/N ∑i Xi[t]
 MF approximation:
1/N ∑i Wij Xi[t] = W ρ[t], where W = <Wij>
 Voltages evolve as:
Vi[t+1] = 0 if Xi[t] = 1
Vi[t+1] = μVi[t] + I + Wρ if Xi[t] = 0
 ρ[t] = ∫ Φ(V) pt(V) dV
 In the stationary state, the voltages assume a discrete stationary set of values Uk.
 The density of neurons with Uk is 𝛈k . Normalization: ∑ 𝛈k = 1
 So, in the stationary state, ρ = ∑k Φ(Uk) 𝛈k
9

9. Stationary distributions
pt(V) dV → P(V) with discrete peaks

10. Mean field stationary states
Uk = Voltage of the k-th stationary peak
𝛈k = peak height
μ > 0 case (several peaks, only numeric solutions):
ρ = ∑k=1 Φ(Uk) ηk
Uk = μ Uk-1 + I + W ρ
ηk = [1- Φ(Uk-1)] ηk-1
η0 = ρ = 1 - ∑k=1 ηk (Normalization)
11
Uk
η0 = ρ η1
η2
η3
η4
Φ
(1- Φ)η0
Φ
Φ
Φ
(1- Φ)η1
(1- Φ)η2
(1- Φ)η3
U1 U2 U3 U4U0 = 0

11. Example: μ > 0, r = 1, VT = 0, I = 0
12

12.  Due to the one step refractory period,
we cannot have ρ > 1/2.
 ρ(𝚪b,Wb) = 1/2 defines a bifurcation
line (𝚪b = 2/Wb for the μ = 0 case)
 Cycles-2 occur because there is only
two peaks, with U1 > VS
 Deterministic dynamics since now
Φ(U1 > VS) = 1
𝛈0[t+1] = 𝛈1[t] = 1 - ρ[t]
𝛈1[t+1] = 𝛈0[t] = ρ[t]
 Cycle dynamics:
ρ[t+1] = 1 - ρ[t]
 Solutions occur for any values inside
the region [VS/W, (W-VS)/W]
Observation: marginally stable cycles-2
13
VS
Φ(U1) = 1
V
1
VVS
1
Φ(U1) = 1
0
0
𝛈1[t]
𝛈1[t+1]
𝛈1[t+1]
𝛈1[t]
𝛈0[t+1]
𝛈0[t]
𝛈0[t]
𝛈0[t+1]

13. Case μ = 0
14
μ = 0 case (only two peaks, analytic solutions):
η0 = ρ = Φ(U1) η1 = Φ(I+Wρ) (1 - ρ)
η1 = 1 - ρ (Normalization)
With:
Φ(x) = 0 for x < VT
Φ(x) = [ 𝚪(x-VT) ]r for VT < x < VS = VT + 1/𝚪
Φ(x) = 1 for x > VS
Very easy Math! (polinomial equations). Solve for 0 < ρ <1/2:
ρ = [𝚪(I+Wρ-VT)]r (1-ρ)
ρ
η1 = 1- ρ
1-Φ
1
Φ
U1

14. Parameters of the firing function Φ
15
1
Threshold voltage VT Saturation voltage VS =VT + 1/𝚪 V
r = 1
r > 1
r < 1
Φ(V) For VT < V < VS: Φ(V) = [𝚪(V-VT)]r
𝚪 = Neuronal Gain

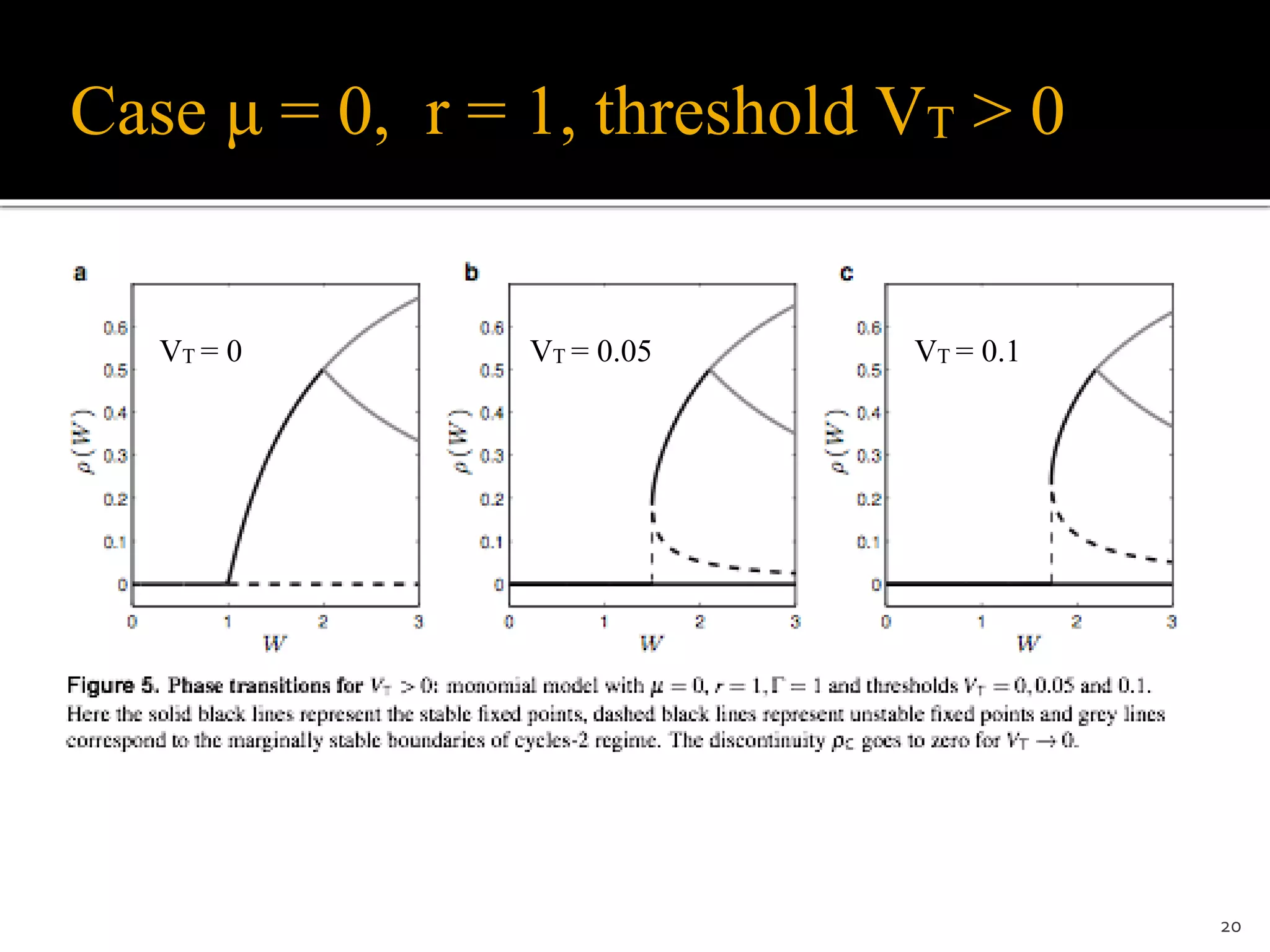
15. μ = 0, linear saturating case r = 1, VT = 0
(Larremore et al., PRL 2014) But they do not report phase transitions
16
• Case r = 1, solve for 0 < ρ <1/2:
ρ = [𝚪(I + Wρ − VT)] (1 − ρ) or:
𝚪W ρ2 + (1 − 𝚪W + 𝚪I − 𝚪VT) ρ + 𝚪VT − 𝚪I = 0
• Solutions:
• Continuous and discontinuous phase transitions here
Φ
V

16. Case μ = 0, VT = 0, r = 1
Linear saturating model without threshold
 Solutions:
ρ+ = (W - Wc)/ W with Wc = 1/ 𝚪
or
ρ+ = (𝚪 - 𝚪c) / 𝚪 with 𝚪c = 1/ W
ρ− = 0 for W < Wc or 𝚪 < 𝚪 c
Continuous transition with exponent
β = 1
17
ρ = 0
0 < ρ < 1/2
cycles-2

17. Case μ = 0, VT = 0, r = 1, I > 0
18
At the critical line 𝚪cWc = 1, for I → 0: ρ ∝ I1/2 χ = dρ/dI ∝ I-1/2
Mean field critical exponent δ = 2
Stevens network psychophysical exponent: m = 1/δ = 1/2
(Kinouchi and Copelli, Nat. Phys. 2006)

18. Case μ = 0, VT = 0, 0 < r < 2
19
r = 1
Continuous phase
transition
r = 1.2
Discontinuous phase
transition
r = 2
Transition only to
cycles-2
r < 1
Wc = 0
Φ(V)
𝚪 x W
phase diagram
r=1

19. Case μ = 0, r = 1, threshold VT > 0
20
VT = 0 VT = 0.1VT = 0.05

20. V
Summary
 Continuous absorbing state phase
transition only for linear-saturating
model without threshold: r =1, VT = 0
 r < 1: no transition, Wc = 0.
 r > 1: discontinuous transition
 VT > 0: discontinuous transition
 Is r =1, VT = 0 biological?
 Is r =1, VT = 0 a kind of fine-tuning?
21
Φ(V)

21. Avalanche size distributions in the static
model with Wc =1, 𝚪c = 1
22
Complementary
cumulative
distribution function:
CS(s) = ∑
∞
k=s
PS(k) ∝ s-1/2
Linear saturating model: r = 1, VT = 0
PS(s) ∝ s-3/2

22. Avalanche duration distributions in the
static model with Wc =1, 𝚪c = 1
23
PD(d) ∝ d-2 Complementary
cumulative
distribution function:
CD(d) = ∑
∞
k=d PD(k) ∝ d-1

23. Self-organization in a continuous phase
transition: dynamic synapses and dynamic gains
24
r =1, VT =0
Idea: not dissipation and
loading at the sites but
decreasing and increasing
the links Wij (or the gains 𝚪i)
NEW!
Can dynamical
synapses produce true self-
organized criticality?
Ariadne de Andrade Costa,
Mauro Copelli and Osame
Kinouchi
Journal of Statistical Mechanics:
Theory and Experiment, 2015(6),
P06004

24. Why to separate the average gain 𝚪 from the
average synaptic weight W?
 In a biological network, each
neuron i has a neuronal gain 𝚪i[t]
located at the Axonal Initial
Segment (AIS). Its dynamics is
linked to sodium channels.
 The synapses Wij[t] are located at
the dendrites, very far from the
axon. Its dynamics is due to
neurotransmitter vesicle
depletion.
 So, although in our model they
appear always together as 𝚪W,
this is due to the use of point like
neurons. A neuron with at least
two compartments (dendrite +
soma) would segregate these
variables.
25AIS, 𝚪i[t]
Wij[t]

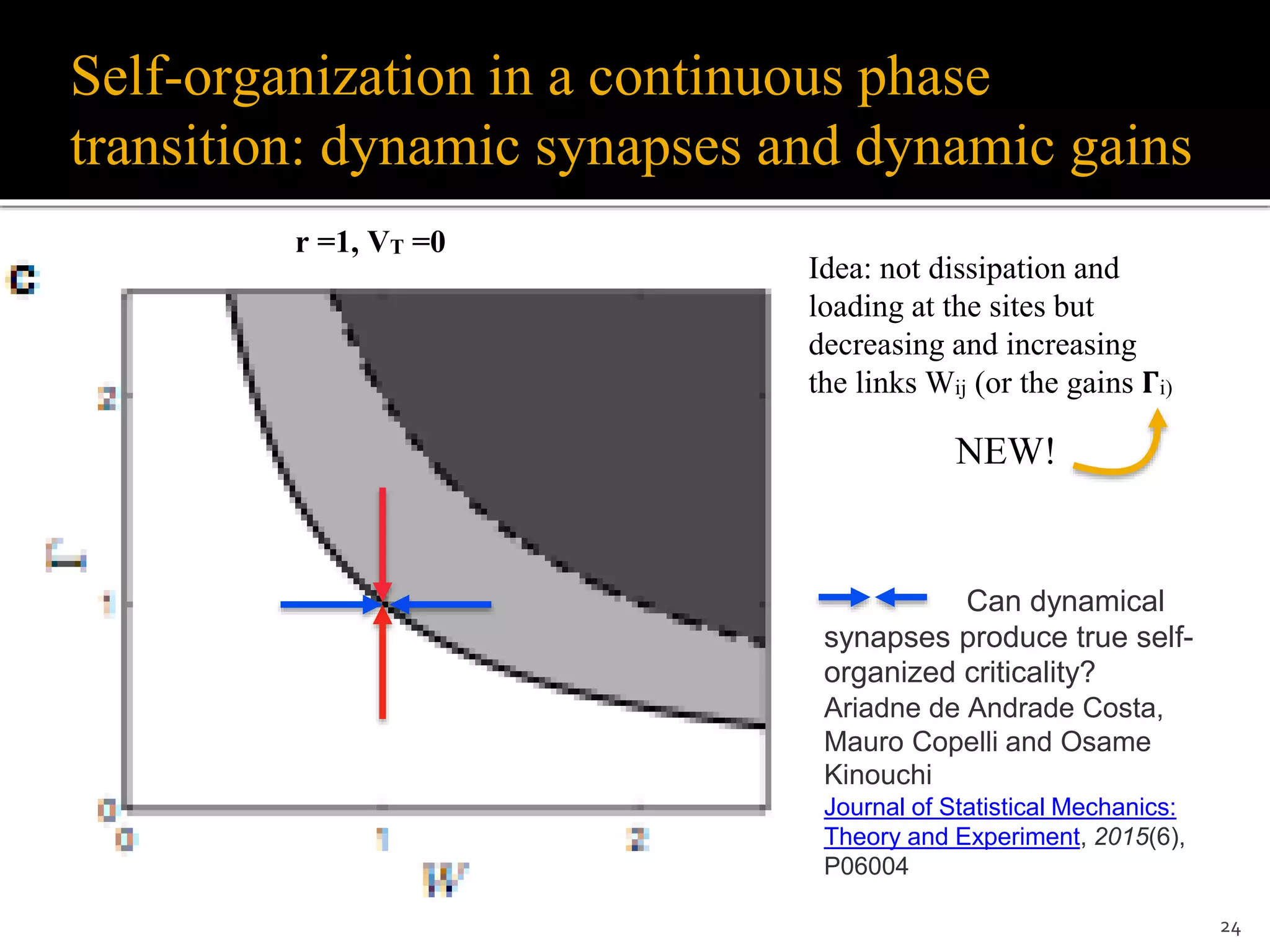
25. Dynamic synapses and dynamic gains
 Dynamic synapses (Levina et al., 2007; Levina et al.,
2009; Bonachela et al., 2010; Costa et al., 2015, Campos
et al., 2016):
Wij[t+1] = Wij[t] + 1/𝞽 (A − Wij[t]) − u Wij[t] Xj[t]
 Dynamic gains (Brochini et al., 2016):
𝚪i[t+1] = 𝚪i[t] + 1/𝞽 (A − 𝚪i[t]) − u 𝚪i[t] Xi[t]
 Parameters range:
0 < u < 1, A > Wc (or A > 𝚪c)
All works with dynamic synapses used
𝞽 = O(N)
26
Wc, 𝚪c
A, 𝞽 u
O(N2) equations
O(N) equations!

26. Problem 1: Same dynamics, different
universality classes?
27
Costa et al., 2015
Campos et al., 2016
Brochini et al. 2016
Levina et al., 2007
Bonachela et al., 2010
Dynamic PercolationDirected Percolation

27. Problem 2: scaling with N
 Up to now, models used 𝞽 =
O(N)
 When N → ∞, the dependence on
parameters (𝞽, A,u) vanishes,
with convergence to the critical
point Wc (good!)
 But this means a divergent
recovery time 𝞽 → ∞
(not biological, bad)
28

28. The same problem occurs with dynamic gains
 𝚪i[t+1] = 𝚪i[t] + 1/𝞽 (A - 𝚪i[t]) - u 𝚪i[t] Xi[t]
 Averaging + stationary state:
1/𝞽 (A - 𝚪*) = u 𝚪* ρ
 With ρ = ( 𝚪*- 𝚪c )/𝚪*, we get:
𝚪* = (𝚪c - Ax)/(1+x), with x = 1/(u𝞽)
We have 𝚪* → 𝚪c only for x → 0, that is, if 𝞽 → ∞ (not biological)
29

29. Self-organization of the average gain
toward the critical region
30
𝚪c

30. If we use 𝞽 = O(N), then x = O(N-1):
good power laws with scaling
31
cS = 2/3
𝚪* = (𝚪c - Ax)/(1+x)
x = 1/(u𝞽) ∝ 1/N

31. For finite 𝞽, we have always self-organized
super-criticality (SOSC)
32
𝞽 = 100 ms, u = 1
𝚪* = 1.001
𝞽 = 1000 ms, u = 1
𝚪* = 1.0001
CS = 1

32. Finite 𝞽: self-organized super-criticality
(SOSC) seems to be unavoidable
 But is this bad?
 Perhaps supercritical avalanches
exist but are being filtered away
in standard experiments
 Perhaps SOSC can explain
biological phenomena: large
avalanches (dragon kings),
epileptic activity etc.
 Perhaps only large avalanches
process informations and elicit
actions (who notice small
avalanches?)
 Perhaps, Turing was right…
34
Shaukat & Thivierge, 2016
Front. Comput. Neurosci. 10:29

33. 0
0
1 1 1 1 1 1 1 1 1 1 1
𝚪1 = 1, 𝚪2 = 1,2
Observation: We can study self-organized
bistability (SOB) in this formalism
35
di Santo, S., Burioni, R., Vezzani, A., &
Muñoz, M. A. (2016). Self-Organized
Bistability Associated with First-Order
Phase Transitions. Physical Review Letters,
116(24), 240601.
Φ(V) = 𝚪1 for V < V1
Φ(V) = 𝚪2 + (𝚪1 − 𝚪2) V1 for V1 < V < VS
Φ(V) = 1 for V > VS
W
𝚪1
𝚪2
Φ(V)
VV1 VS

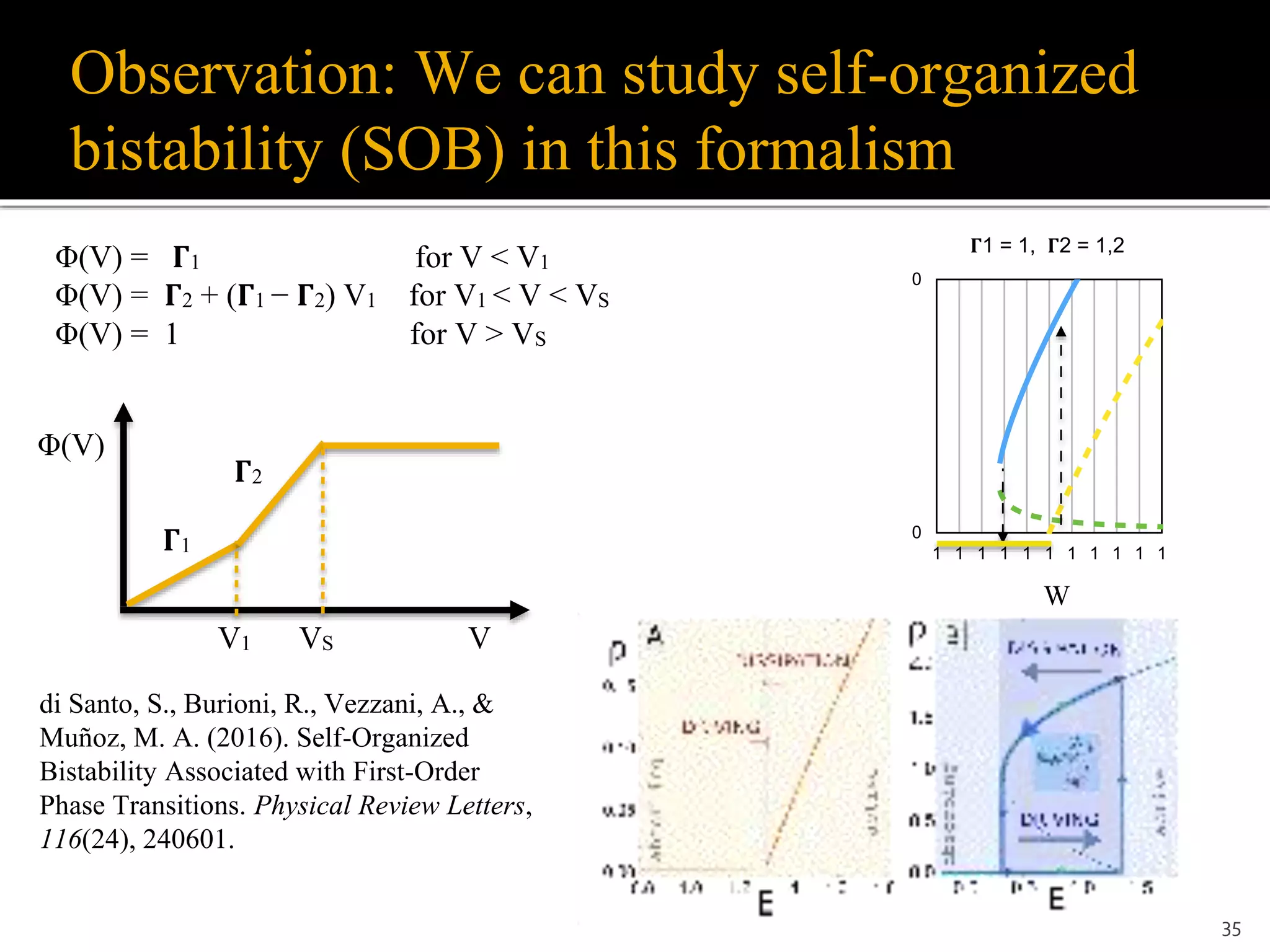
34. Perpectives: a new neuronal network
formalism to be explored
 More results, perhaps analytic, for the μ > 0 case.
 Better study of dynamic synapses and dynamic gains
 Other specific Φ functions (ex: Φ(V) = [𝚪(V-VT)]r/[1+[𝚪(V-VT)]r] = no 2-
cycles
 Theorems for general Φ functions (ex: all linear piecewise functions give
analytic solutions)
 Self-organized bistability (SOB)
 Other network topologies (scale free, small world etc.)
 Other kinds of couplings
 Inhibitory neurons (ex: Larremore et al., 2014)
 Very large networks: N > 106, synapses > 1010
 Realistic topologies (ex: cortical Potjans-Diesmann model with layers and
different neuron populations, N=8x104, synapses = 3x108, Cordeiro et al.,
2016)
 Etc., etc., etc…
36

35. Visit us at Ribeirão Preto!
(we also have research fellowships at Neuromat)
37
This paper results from research
activity on the
FAPESP Center for
Neuromathematics (FAPESP grant
2013/07699-0).
OK and AAC also received support
from Núcleo de Apoio à Pesquisa
CNAIPS-USP and FAPESP (grant
2016/00430-3).
LB, JS and ACR also received CNPq
support (grants 165828/2015-3,
310706/2015-7 and 306251/2014-0).