Download to read offline
Uploaded byOsame Kinouchi
SOC neunoral networks
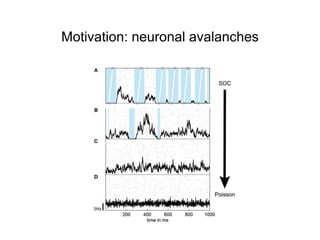
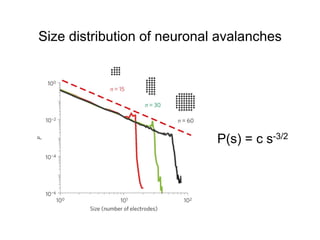
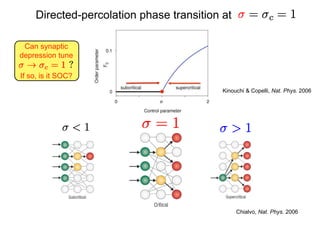
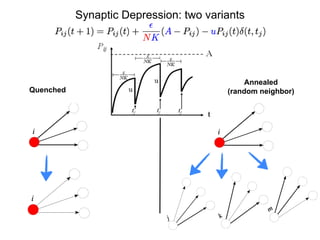
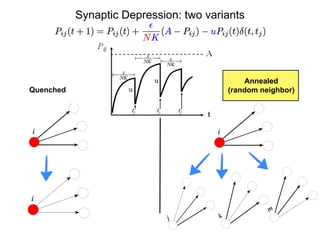
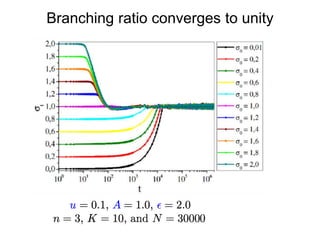
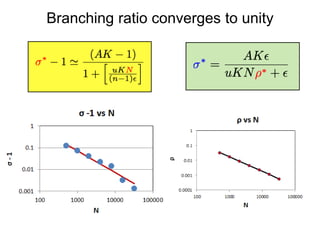
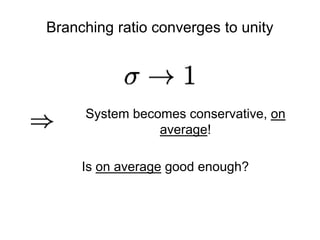
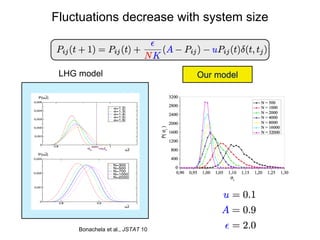
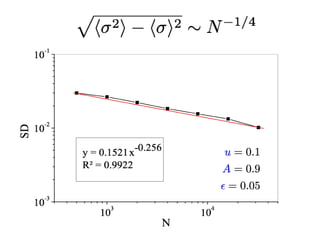
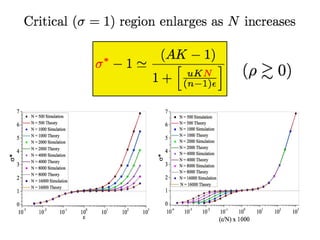
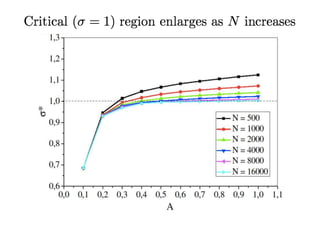
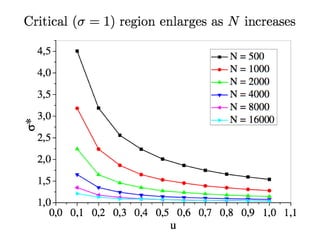
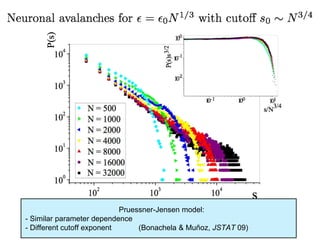
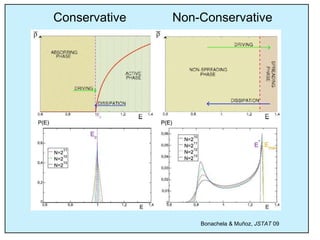
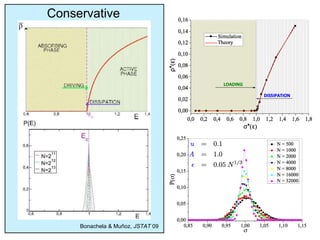
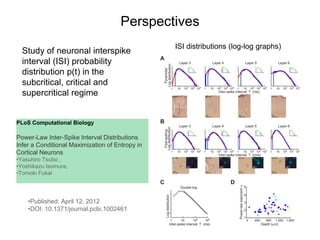
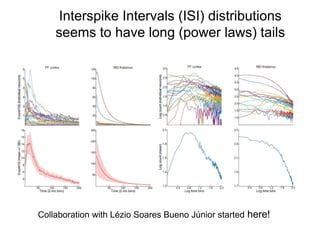
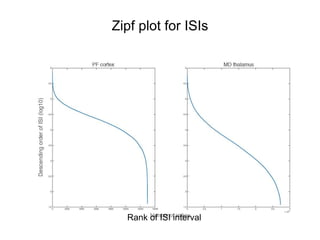
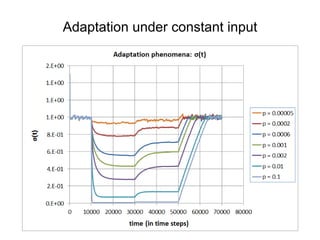
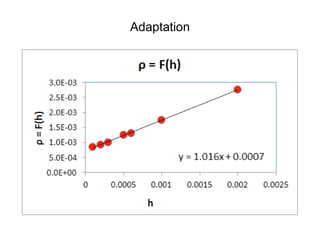
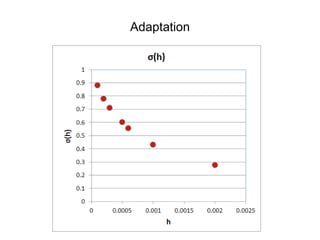
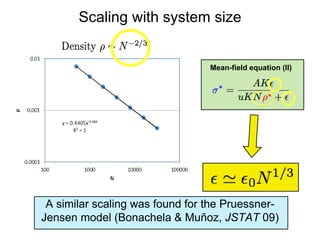
This document summarizes a presentation on self-organized criticality and neuronal avalanches in networks with dynamical synapses. It discusses how synaptic depression can tune networks to a critical state in a non-conservative model. The model uses a probabilistic cellular automata on a random graph with synaptic depression, which slowly loads the system. Mean-field theory and simulations show the branching ratio converges to unity, making the system conservative on average. Analysis of neuronal interspike interval distributions in different regimes is proposed to further understand the model's behavior.
SOC neunoral networks
- 1. Self-Organized Criticality andNeuronal Avalanches in Networks with Dynamical Synapses Ariadne Costa, Mauro Copelli, Osame Kinouchi First Workshop of Young Researchers of NeuroMat, São Paulo, May 2015 University of São Paulo (USP), Ribeirão Preto, Brazil Federal University of Pernambuco (UFPE), Recife, Brazil
- 2.
- 3. Size distribution ofneuronal avalanches P(s) = c s-3/2
- 4. Quick historical backgroundof SOC • Microscopically conservative models with true SOC (Bak, Tang & Wiesenfeld PRL 87, Jensen SOC 98) • Non-conservative models with after- avalanche (hard) loading, presenting pseudo-SOC (Drossel PRL 92, Kinouchi & Prado, PRE 99) • Non-conservative models with intra- avalanche (soft) loading, presenting SOqC (self-organized quase-criticality) (Levina, Herrmann & Geisel Nat Phys 07, Bonachela et al JSTAT 09, 10)
- 5. Self-Organized Criticality andNeuronal Avalanches in Networks with Dynamical Synapses • Microscopically non-conservative model with “soft” loading, but • Probabilistic cellular automata (larger system sizes & easier mean field) • Finite connectivity (random graph) • Stationary regime: conservative on average • Fluctuations vanish when N → ∞ Here:
- 6. Random network ofexcitable cellular automata Random graph with K outcoming synapses Kinouchi & Copelli, Nat. Phys. 06 Control parameter: Branching ratio: Order parameter: Mean firing rate: Mean-field equation: (I)
- 7. Directed-percolation phase transitionat Kinouchi & Copelli, Nat. Phys. 06 Chialvo, Nat. Phys. 06
- 8. Directed-percolation phase transitionat Kinouchi & Copelli, Nat. Phys. 2006 Chialvo, Nat. Phys. 2006 Can synaptic depression tune If so, is it SOC?
- 9. Synaptic Depression Levina etal, Nat. Phys. 07 (LHG) - Integrate and fire neurons (deterministic) - all-to-all coupling Synaptic depression: slow load Here - Cellular automata (probabilistic) - random graph Synaptic depression: slow load
- 10. Synaptic Depression: twovariants Quenched Annealed (random neighbor)
- 11. Synaptic Depression: twovariants Quenched Annealed (random neighbor)
- 12. Results • Analytical (mean-fieldtheory) • Simulations
- 13. Mean-field theory Mean-field equation(I) Mean-field equation (II) Kinouchi & Copelli, Nat. Phys. 06
- 14. Mean-field theory Mean-field equation(I) Mean-field equation (II)
- 15. Results • Analytical (mean-fieldtheory) • Simulations
- 16. Branching ratio convergesto unity
- 17. Branching ratio convergesto unity
- 18. Branching ratio convergesto unity System becomes conservative, on average! Is on average good enough?
- 19. Our model Fluctuations decreasewith system size Bonachela et al., JSTAT 10 LHG model
- 24. Pruessner-Jensen model: - Similarparameter dependence - Different cutoff exponent (Bonachela & Muñoz, JSTAT 09)
- 25. Conservative Bonachela & Muñoz,JSTAT 09 Non-Conservative
- 26. Bonachela & Muñoz,JSTAT 09 Conservative
- 27. Conclusions Costa, Copelli andKinouchi – Can dynamical synapses produce true Self-organized criticality? accepted for publication in Journal of Statistical Mechanics (2015)
- 28. Perspectives • Study ofneuronal interspike interval (ISI) probability distribution p(t) in the subcritical, critical and supercritical regime
- 29. PLoS Computational Biology Power-LawInter-Spike Interval Distributions Infer a Conditional Maximization of Entropy in Cortical Neurons •Yasuhiro Tsubo , •Yoshikazu Isomura, •Tomoki Fukai •Published: April 12, 2012 •DOI: 10.1371/journal.pcbi.1002461 Study of neuronal interspike interval (ISI) probability distribution p(t) in the subcritical, critical and supercritical regime Perspectives ISI distributions (log-log graphs)
- 30. Interspike Intervals (ISI)distributions seems to have long (power laws) tails Collaboration with Lézio Soares Bueno Júnior started here!
- 31. Zipf plot forISIs Rank of ISI interval
- 32. Thank you Come visitus in Ribeirão Preto!
- 33.
- 34.
- 35.
- 36. Scaling with systemsize Mean-field equation (II) A similar scaling was found for the Pruessner- Jensen model (Bonachela & Muñoz, JSTAT 09)
Editor's Notes
- #8 In 2006 Osame Kinouchi and I proposed a simple model an excitable network K random neighbors P_ij = probability that a spike in i causes a spike in j P_ij => control parameter sigma Order parameter F Self-consistent mean-field equation (I)
- #9 Phase transition from quiescent (subcritical) to active (supercritical)
- #12 - Cellular automata: allow larger system sizes [ up to O(10^5) ] - Ultra-slow load: dP/dt ~ O(1/N), but for FINITE CONNECTIVITY!
- #26 Bad side: for fixed epsilon, varying N can take from subcritical, critical and supercritical (sigma = 1 might not necessarily be the critical value for finite N)
- #48 Pruessner-Jensen model considered non-conservative by Bonachela & Muñoz 10