1) Dynamic neuronal gain models and other dissipative self-organized critical (SOC) systems exhibit puzzling stochastic oscillations hovering around the critical region. 2) Through analysis of a mean-field map, the authors find that these systems exhibit double criticality - the control parameter is very close to an absorbing state critical line, and the fixed point is near a Neimark-Sacker bifurcation. 3) As a result, the system is a stable spiral very close to becoming indifferent, and critical fluctuations from neuronal avalanches perturb and maintain the oscillations of the quasi-indifferent spiral, providing the origin of hovering oscillations in SOC systems.

1. Origin of hovering oscillations
in self-organized critical systems
Osame Kinouchi, Ludmila Brochini
and Ariadne A. da Costa
Neuromat Seminar
November 13, 2017 São Paulo - Brazil

2. Articles published with NEUROMAT/FAPESP
support
Today
Preliminary results
Origins of hovering oscillations in
self-organized critical systems

3. State of art of self-organized criticality
Conservative systems on the bulk (sandpiles
models): OK!
But needs strong separation between drive
time scale tD and avalanches time scale tA
such that R = tA/tD → 0. Also needs
conservation of sand grains, energy etc.
Extremal models (invasion percolation, Bak-
Sneppen coevolutionary model): OK!
But needs non-local information about the
extremal site, equivalent to R = tA/tD → 0. Also,
to define avalanches, the avalanche limiar LA
must be chosen as identical to the self-
organized limiar LC, that is, L = LA/LC

4. And about non-conservative systems in the
bulk?
Earthquake models are critical only in the conservative limit. Otherwise they are not critical (Kinouchi and
Prado, 2008; Brooker and Grassberger, 2008; Xavier and Prado, 2008) .
Forest-fire models are conservative in average, and thus critical, only with fine-tuning of model
parameters.
These models have been named self-organized quasi criticality (SOqC) because the oscillations do not
disappear in the thermodynamic limit, that is, the system do not settles at the critical point (Bonachela et
al. 2009).
All other dissipative models have been found to be examples of SOqC.
Neuronal networks models with dynamic synapses or dynamic gains are conservative in average only
with fine-tuning of a parameter (recovery time 𝞽 → ∞). (Levina et al., 2007 = LHG model; Bonachela et
al., 2010, Costa et al., 2015; Brochini et al., 2016; Campos et al., 2017; Costa et al., 2017).
The stationary state is not exactly critical but small super criticality can be achieved (SOSC), with good
power laws for the neuronal avalanches (Brochini et al., 2016; Costa et al., 2017).
All these dissipative models (in the bulk) show hovering stochastic oscillations around the critical point

5. Dissipative SOC models present oscillations hovering around the critical region
These oscillations are puzzling and of unknown origin
Levina-Herrmann-Geisel model - Nature Physics (2007)
Bonachela et al.- Journal of Statistical Mechanics (2010)
W = <Wij> =
Our model (Costa et al., 2017)
dynamic neuronal gains
𝚪i[t]
LHG model
dynamic synapses
Wij[t]
𝚪c

6. Models with
van Hemmen-Gestner-Galves-Löcherbach (HGGL)
escape rate discrete time stochastic neurons
Our discrete time integrate − stochastic fire model: Xi = 0 (rest) Xi = 1 (fire)
Vi[t+1] = μ Vi[t] + ∑ Wij Vj[t] if Xi[t] = 0 and Vi[t+1] = 0 (reset) if Xi[t] = 1
P(Xi[t+1] = 1| Vi[t]) = ɸ(Vi[t]) = 𝚪i[t] (Vi[t] − VT) / [1 + 𝚪i[t] (Vi[t] − VT)] Θ(Vi[t] − VT )
Firing function

7. Static model:
Order parameter ρ
Control parameters W and 𝚪
ρ = N−1 ∑ Xi = density of firing neurons
W = N−1 ∑ Wij = average synaptic weights
𝚪 = N−1 ∑ 𝚪i = average neuronal gains
Continuous
absorbing state
phase transitions
in the mean-field
Directed Percolation
(DP) universality class
Self-organization mechanism = Adaptive neuronal gains: 𝚪i[t+1] = 𝚪i[t] + 1/𝞽 𝚪i[t] − 𝚪i[t] Xj[t]

8. Phase transitions and phase diagram
Dynamic synapses: LHG model
Dynamic neuronal gains: 𝚪i[t+1] = 𝚪i[t] + 1/𝞽 𝚪i[t] − 𝚪i[t] Xj[t]

9. SOC models = slow drive + fast dissipation
Self-organization by using depressing and recovering dynamic neuronal gains
𝚪i[t+1] = 𝚪i[t] + 1/𝞽 𝚪i[t] − 𝚪i[t] Xj[t]
Recover = Slow Drive Depression = Fast Dissipation
Dynamic synapses
models
Wij[t]
Dynamic neuronal
gains models
𝚪i[t]

10. Self-organization towards the critical 𝚪c = 1 (W =1)
But what are these noisy oscillations hovering
around the critical point?

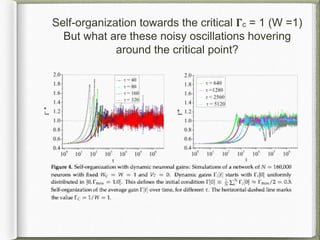
11. The mean-field bi-dimensional map
(predator-prey like, very nice mathematical connection!)
ρ[t+1] = 𝚪[t] ρ[t] ( 1 − ρ[t] ) / ( 1 + 𝚪[t] ρ[t] ) (predator)
𝚪[t+1] = 𝚪[t] + 1/𝞽 𝚪[t] − 𝚪[t] ρ[t] (prey)
Solution = stable spiral (infinite size system, no fluctuations) but with eigenvalue |ƛ| = 1 - O(1/𝞽)
Fixed point: 𝚪* = 𝚪c / (1 − 2/𝞽 ) , ρ* = 1/𝞽 (stable spiral)
Large 𝞽: 𝚪* ≈ 𝚪c + 2 𝚪c /𝞽 ➞ 𝚪c = 1, ρ* ➞ 0+ (W=1)

12. Critical fluctuations perturbs the almost indifferent spiral
and drive the stochastic oscillations
Spiral Eigenvalue |ƛ| = ( 1 − (𝞽+2)/[𝞽(𝞽-1)] )1/2 ≈ 1 − 1/(2𝞽)
(very close to a Neimark-Sacker critical point)
Map with white noise and 𝞽 = 320
|ƛ| = 0.9984 Simulations without external noise
but with avalanches:
N = 160,000
𝞽 = 320
|ƛ| ≃ 1 − 1/(2 x 320) ≈ 0.9984

13. Conclusions:
Double criticality and stochastic oscillations
SOqC systems (forest-fire models, earthquake models, LHG
dynamic synapses model (2007) , Costa et al. model (2017)
present puzzling “hovering" stochastic oscillations around
the critical region.
Here we have found, for the first time, the origin of these
oscillations.
This occurs because we have double criticality:
𝚪* is very close to an absorbing state critical line (usual
SOC) as 𝚪* = 𝚪c + O(1/𝞽).
(𝚪*, ρ*) is a stable spiral but very close a Neimark-Sacker
bifurcation (another critical point ƛc = 1) as ƛ = ƛc − O(1/𝞽)).
The avalanches and critical fluctuations make the role of
noise and excite/maintain the oscillations of the quasi-
indifferent spiral.

14. Collaborators:
Ludmila Brochini (IME-USP)
Ariadne A. da Costa (UNICAMP)
Mauro Copelli (DF-UFPE)
João Guilherme F. Campos (DF-UFPE)
Financial support from:
CEPID NEUROMAT
NAP CNAIPS
Discussions and ideas:
Jorge Stolfi (UNICAMP)
Marcelo Tragtenberg (DF-UFSC)