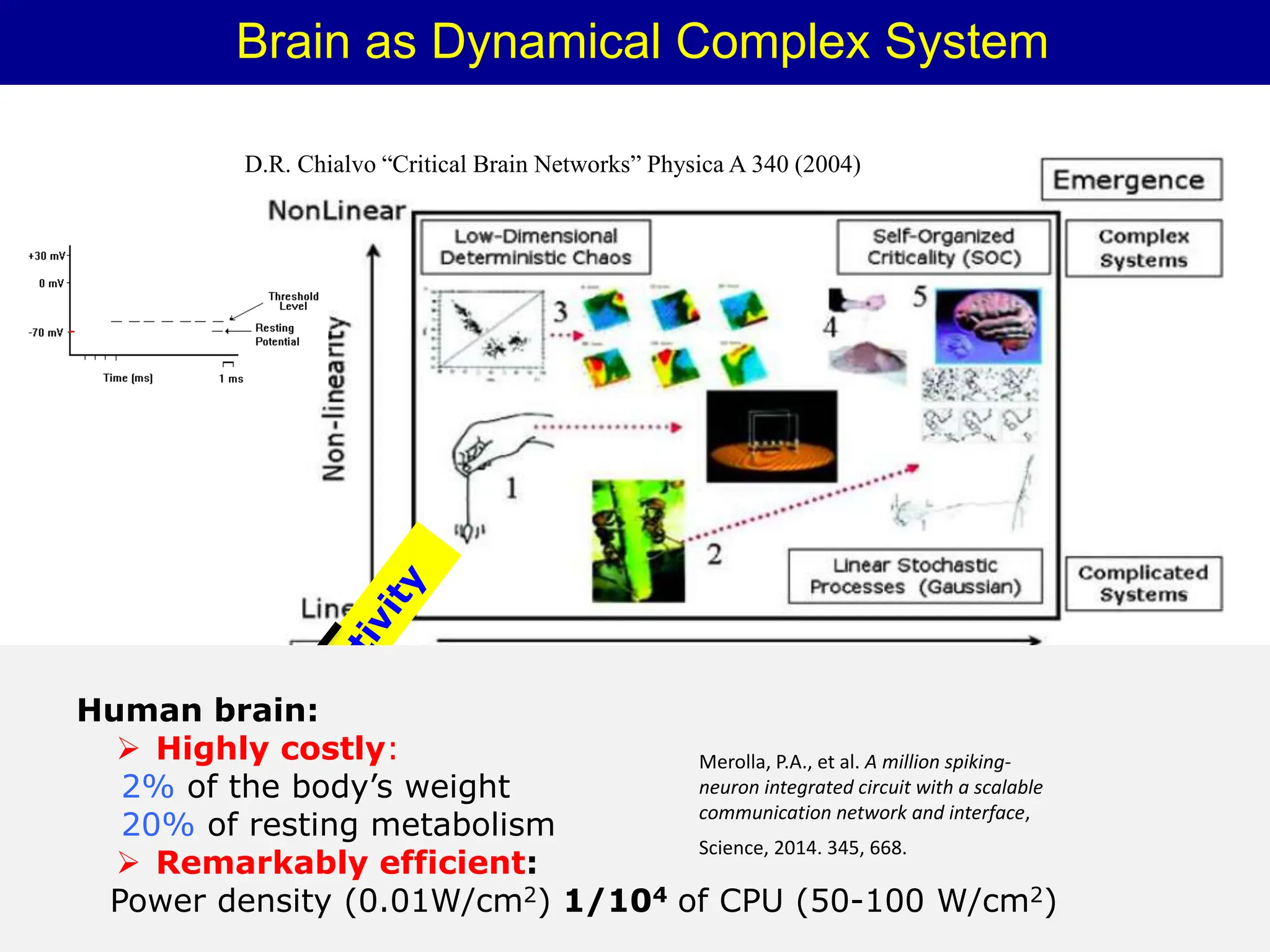
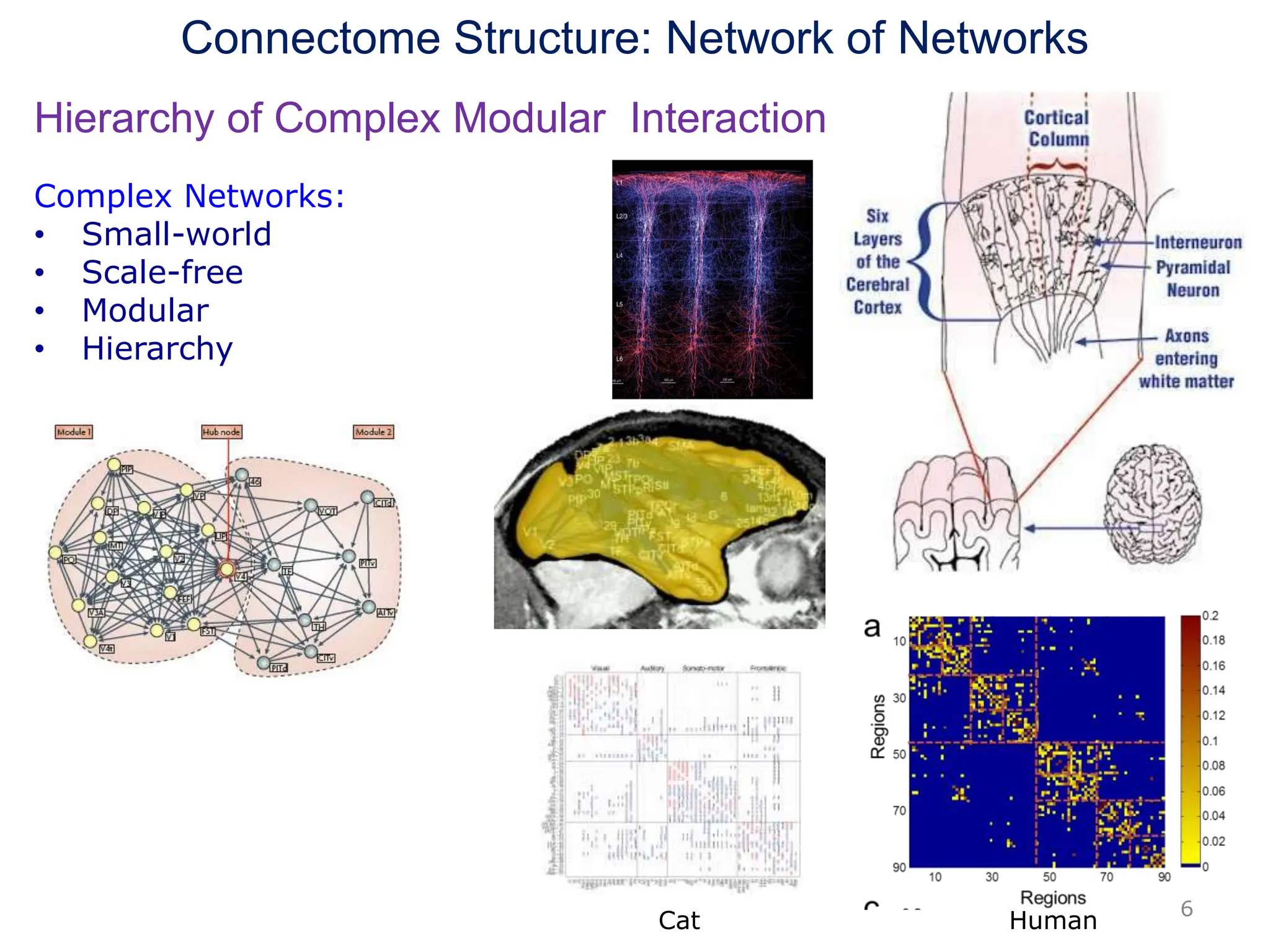
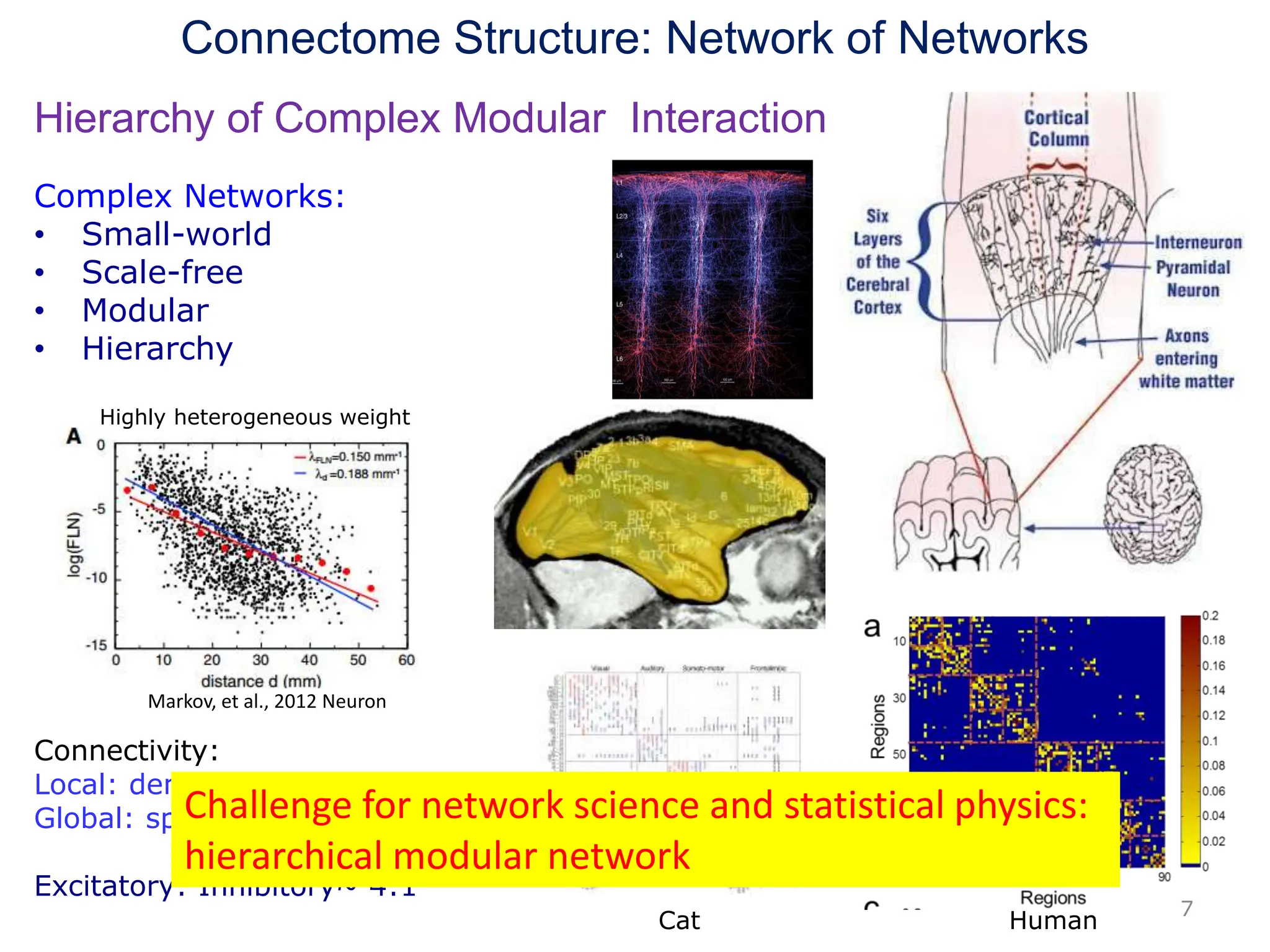
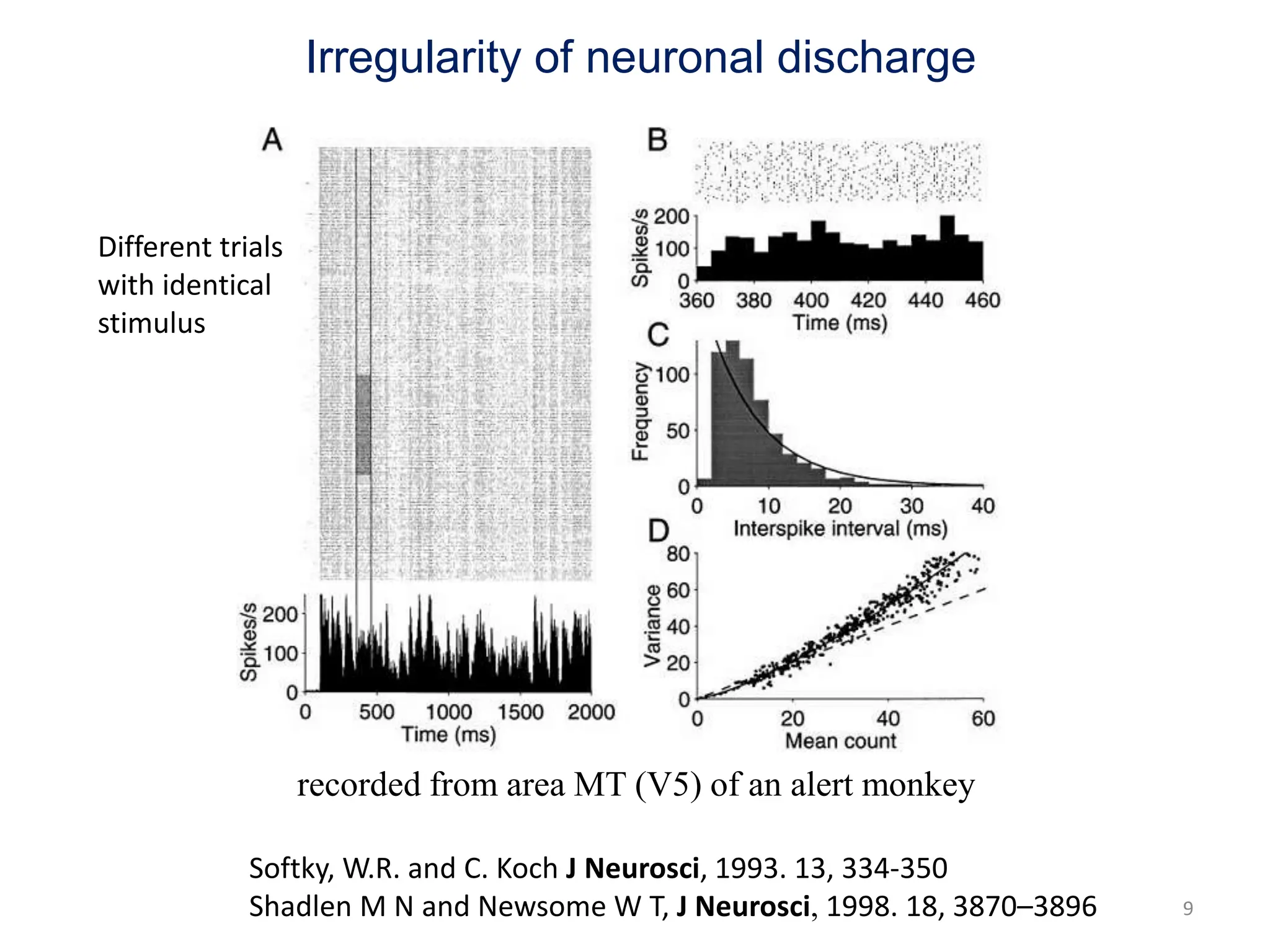
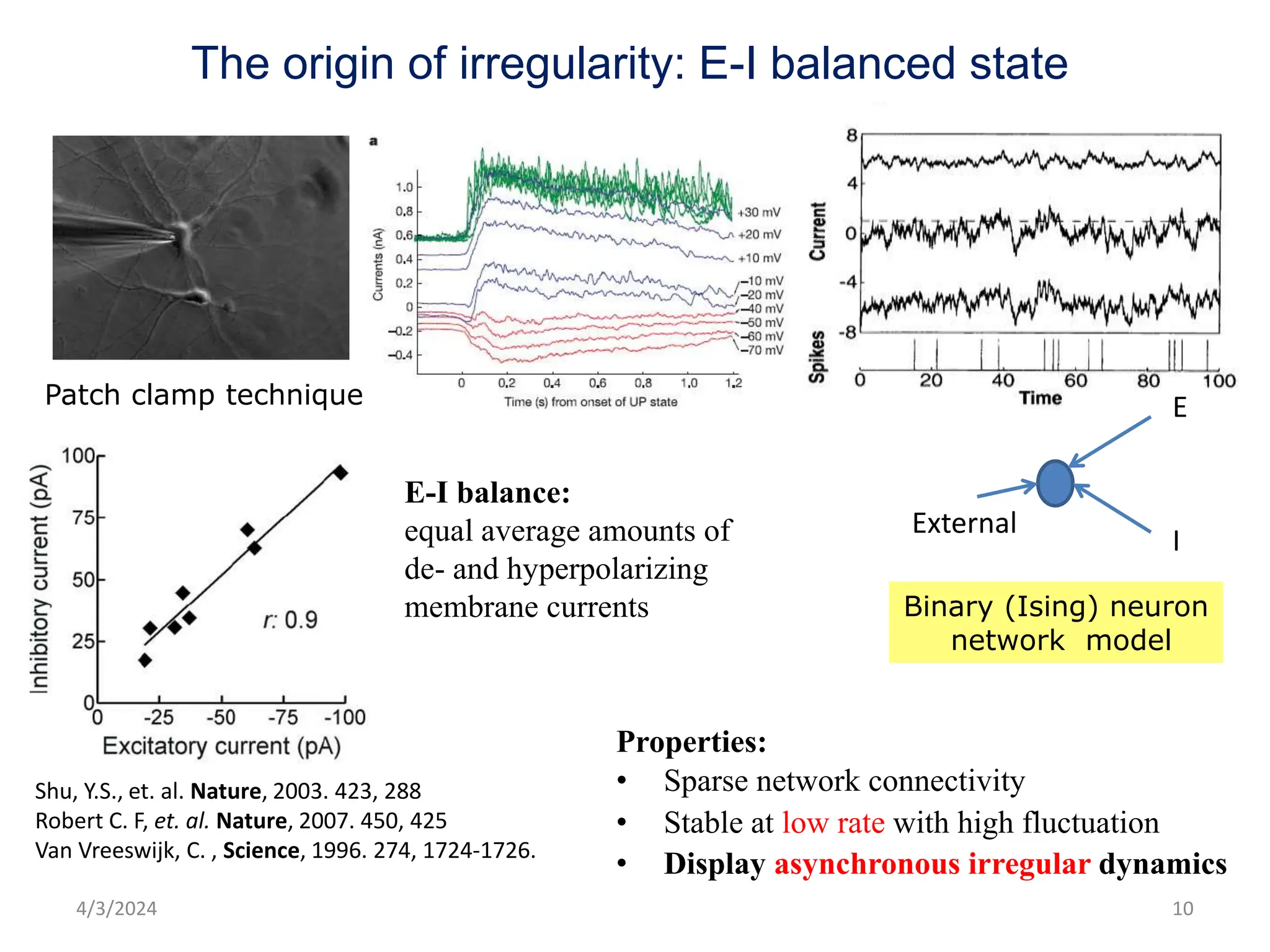
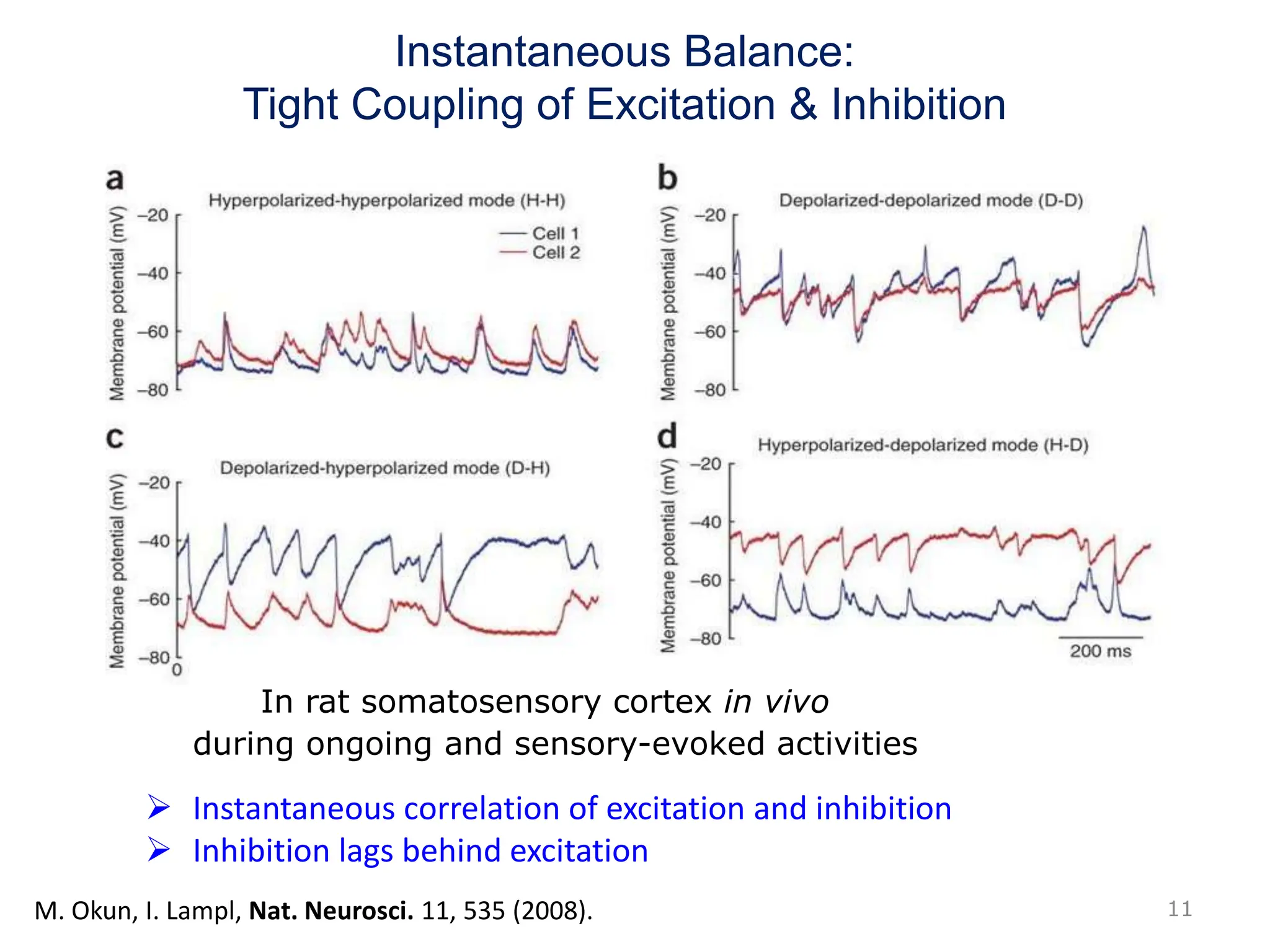
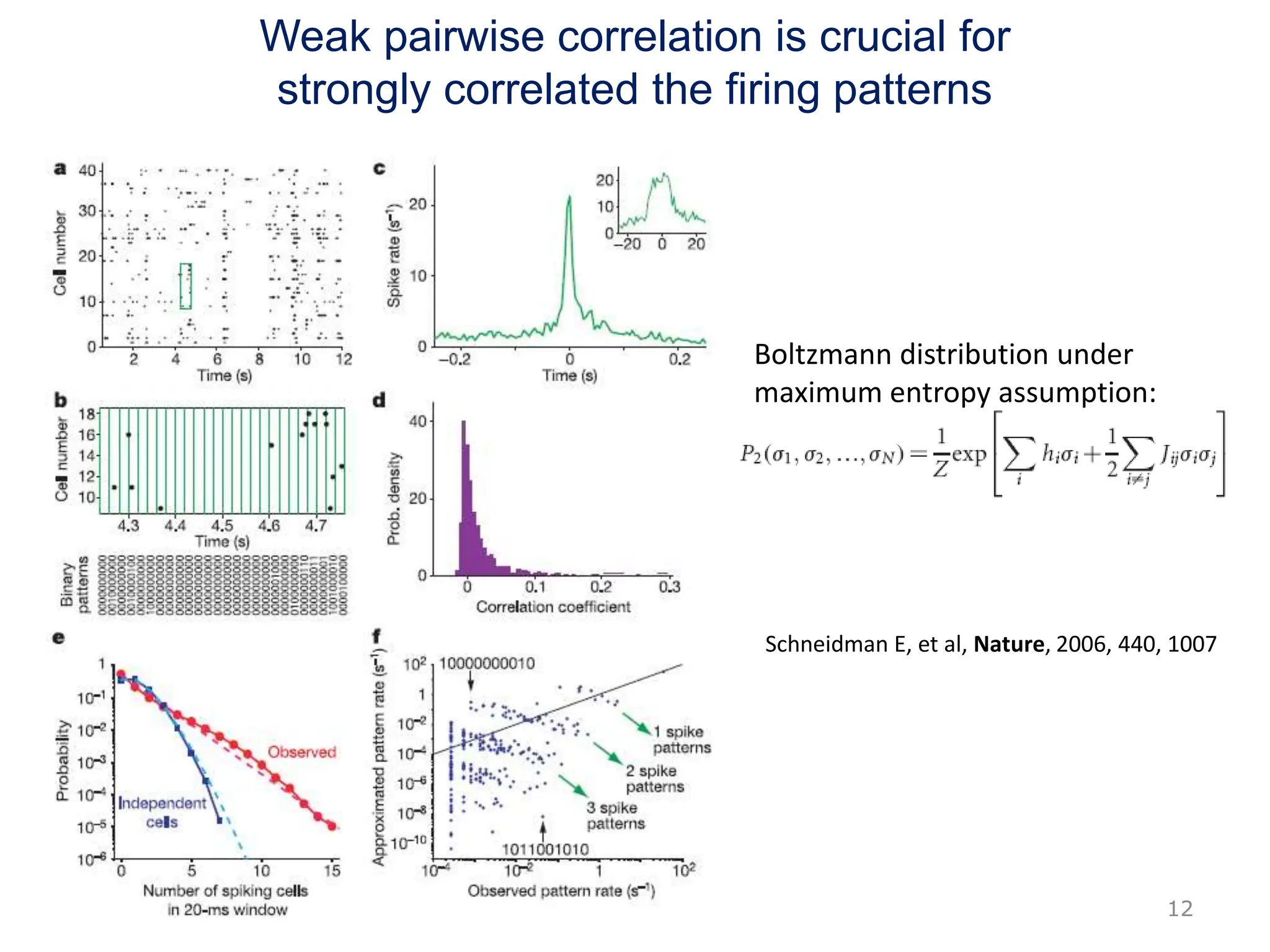
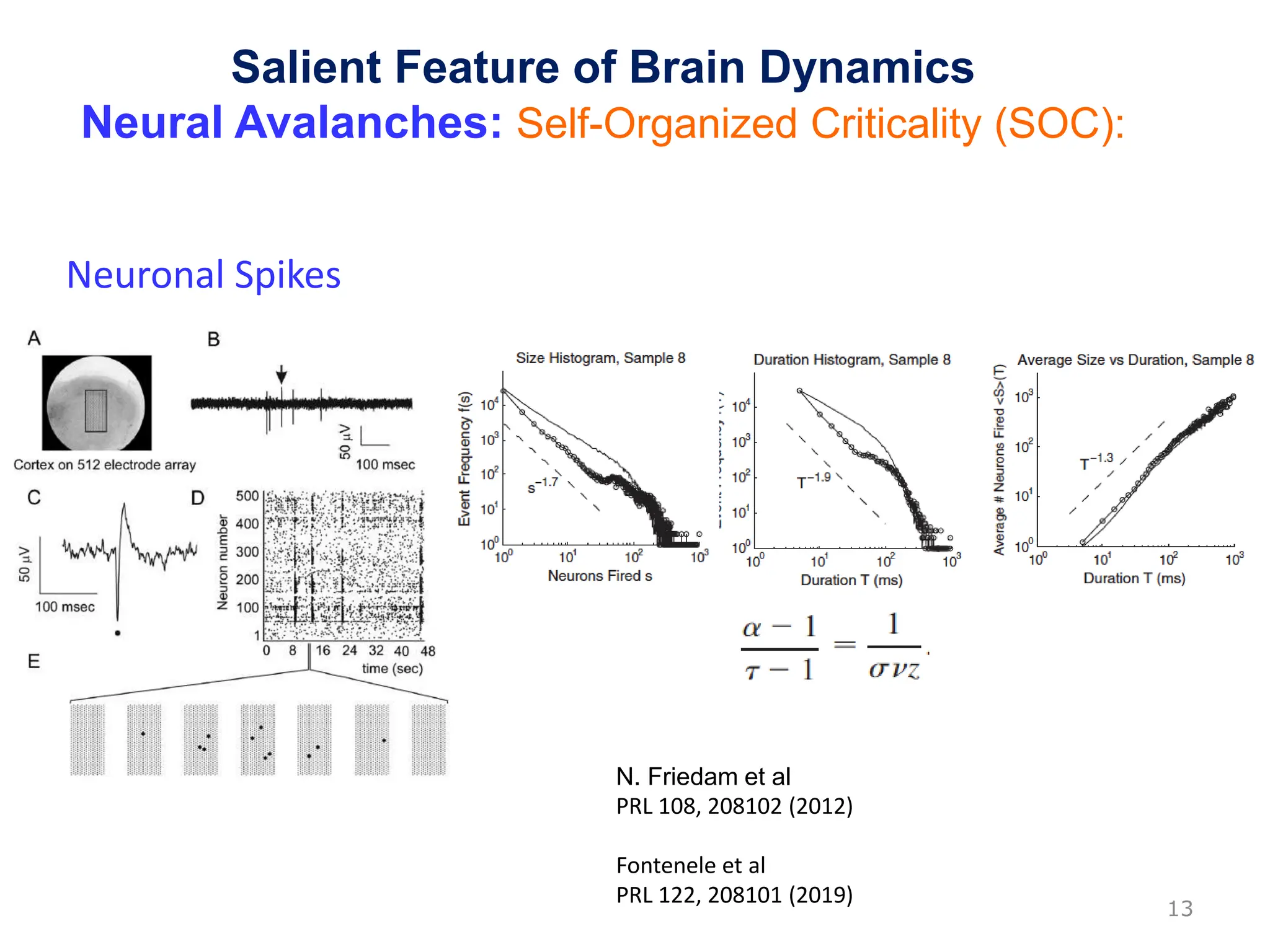
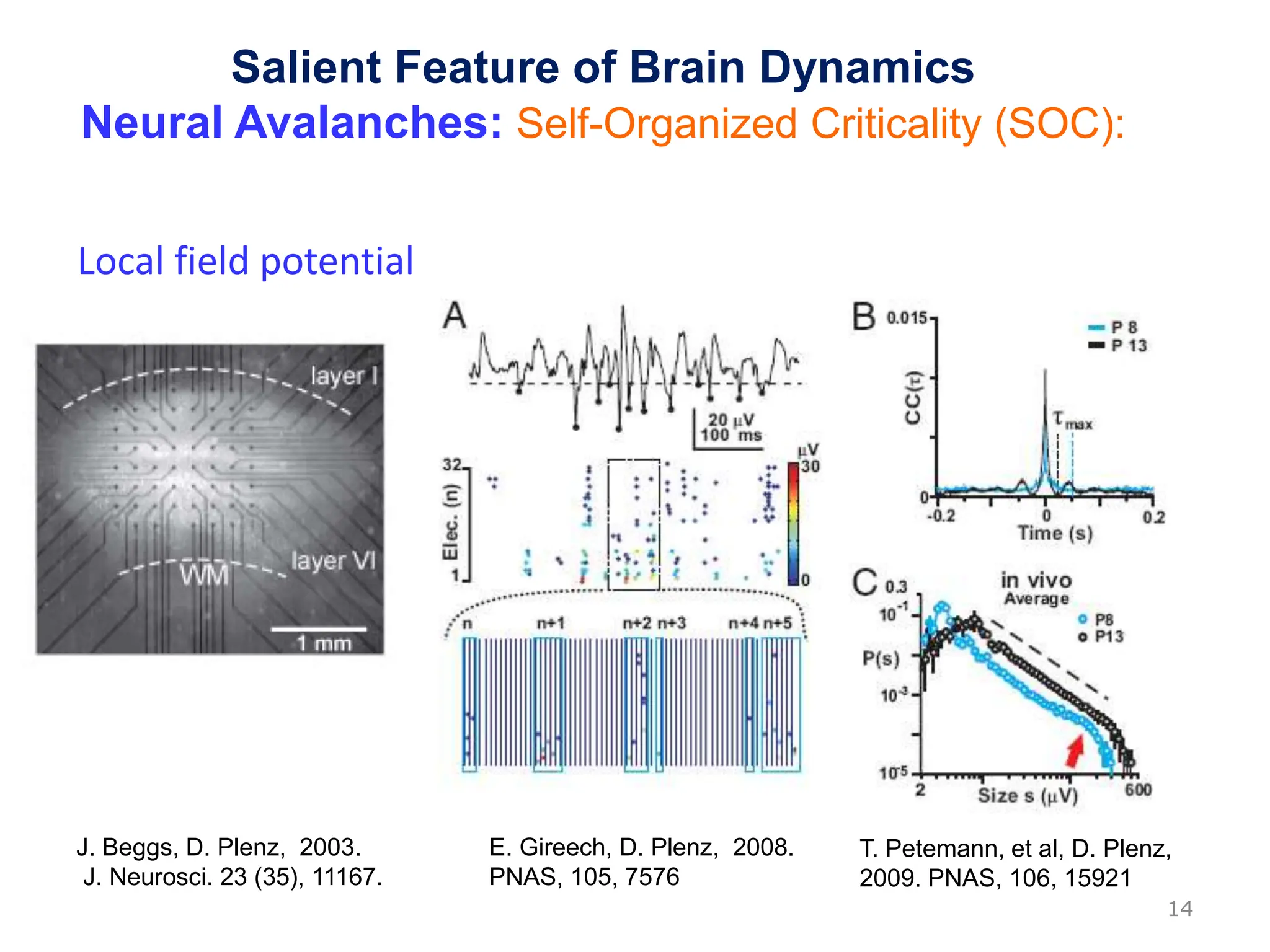
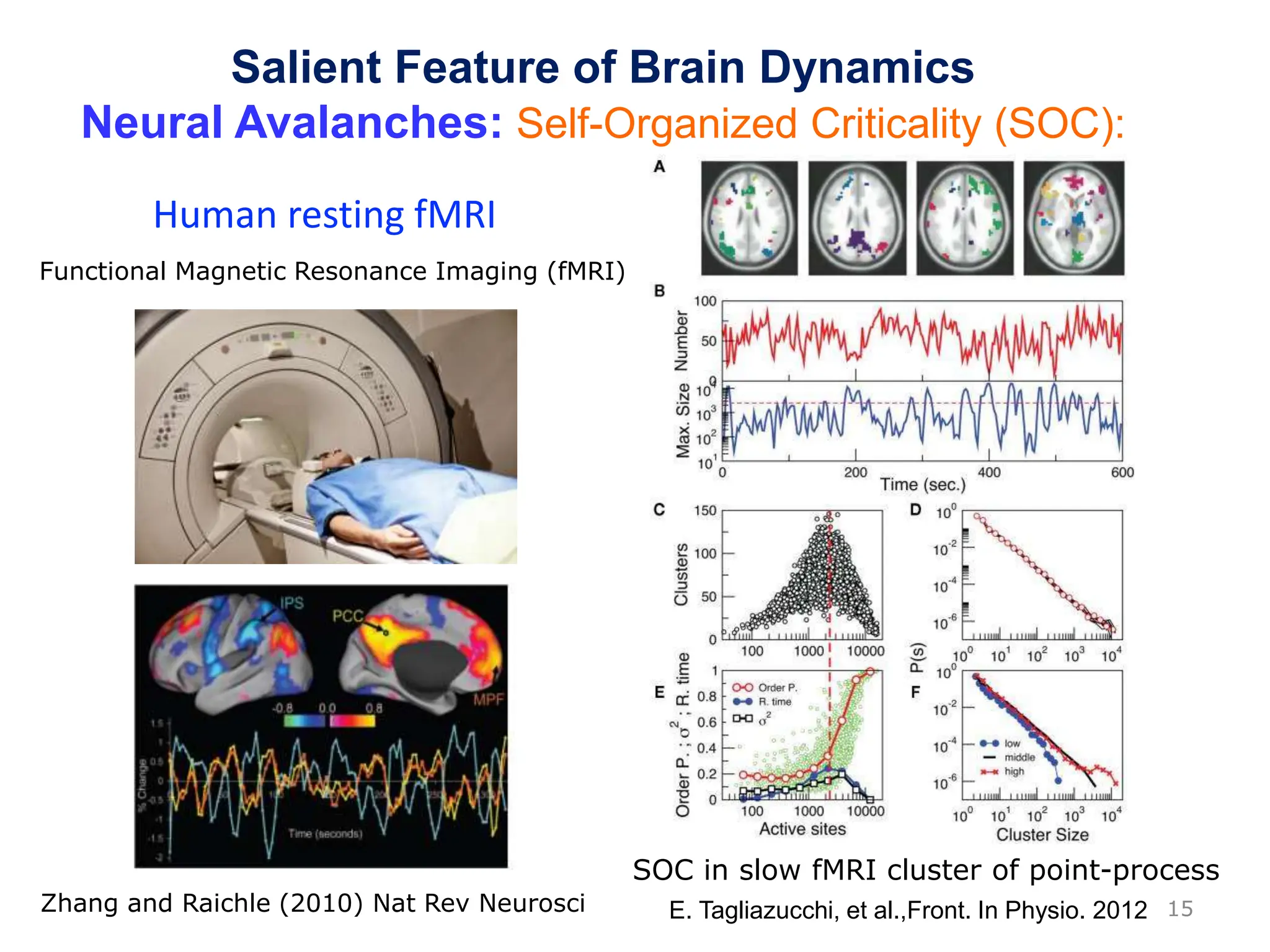
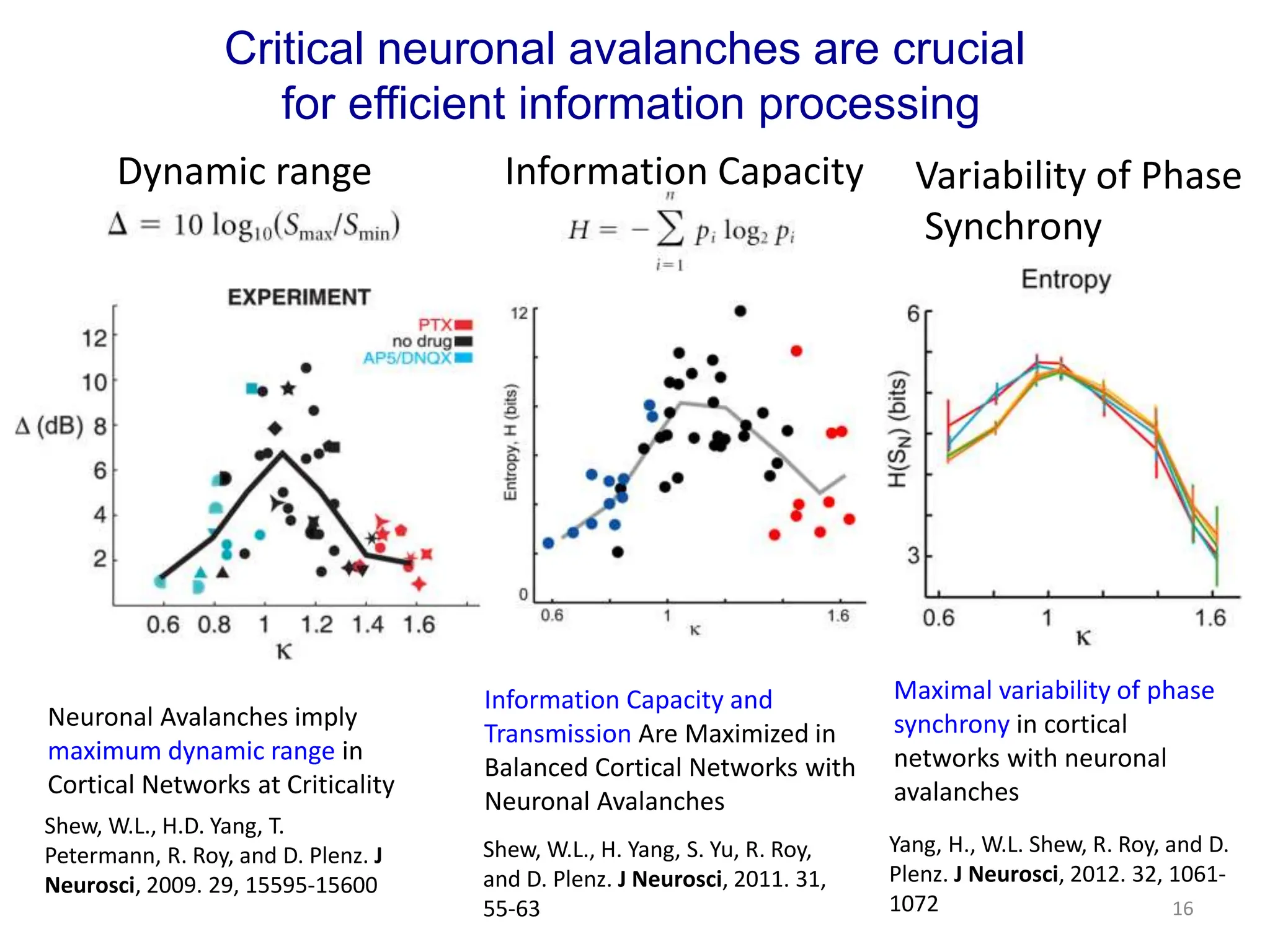
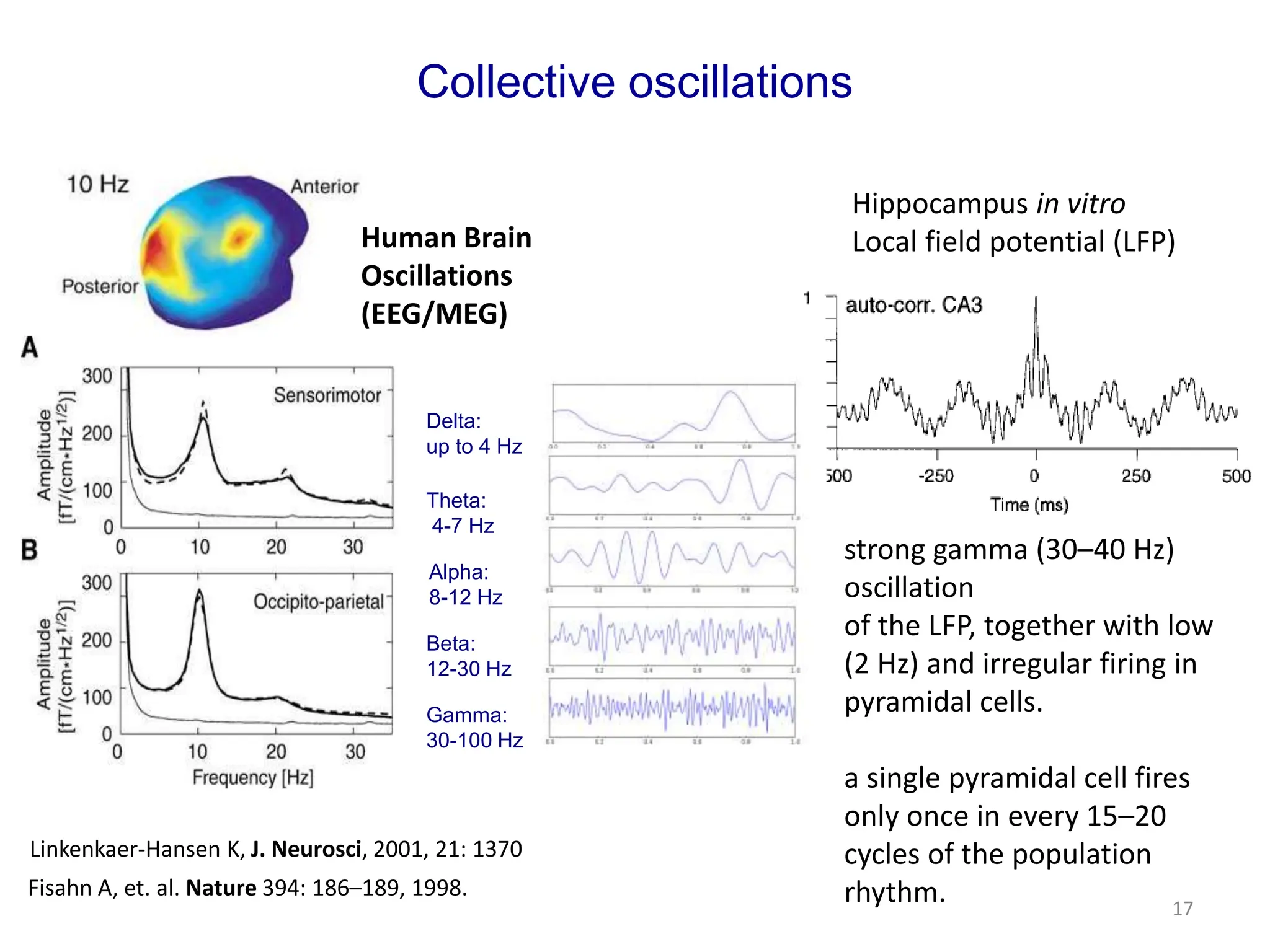
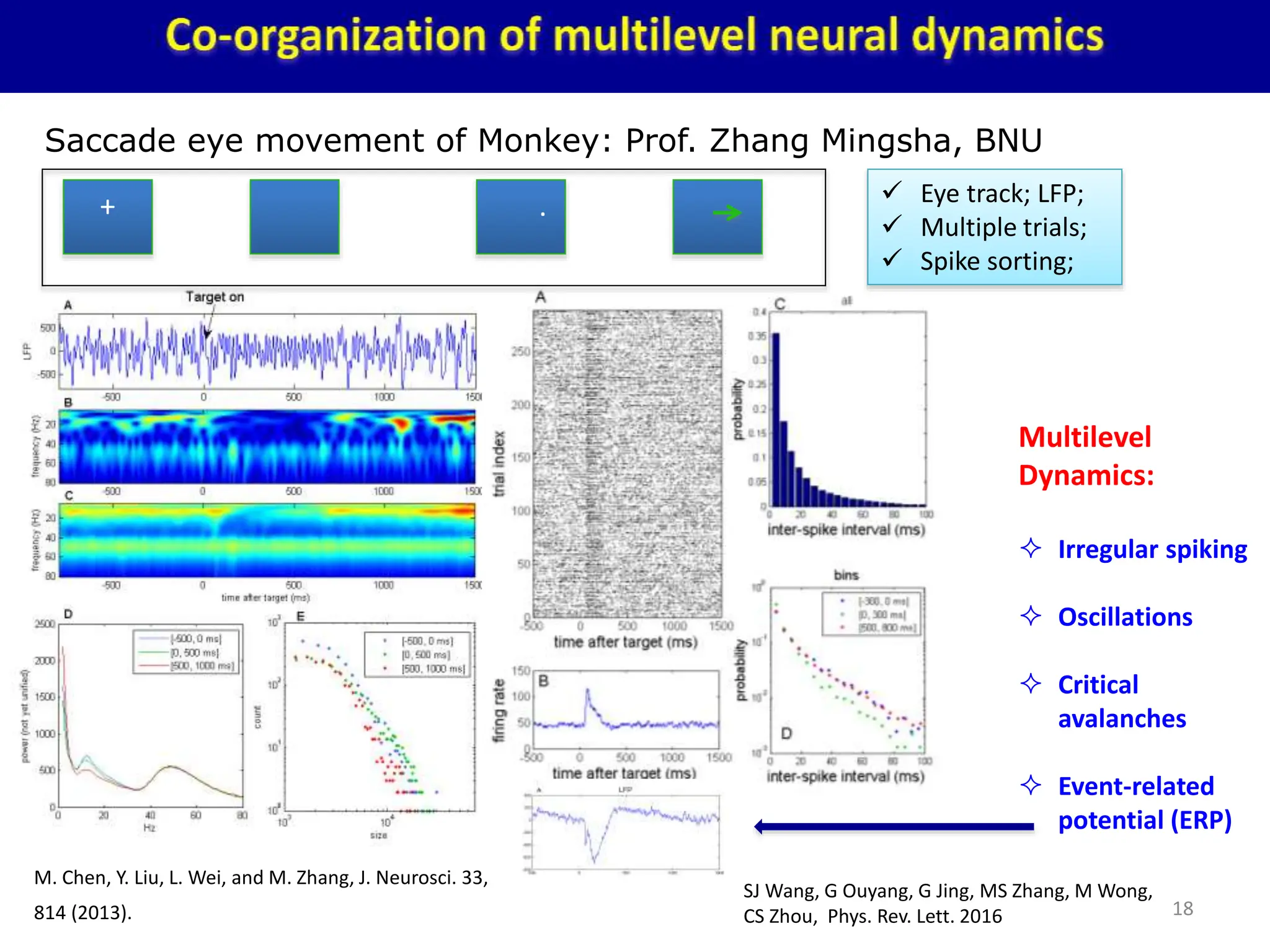
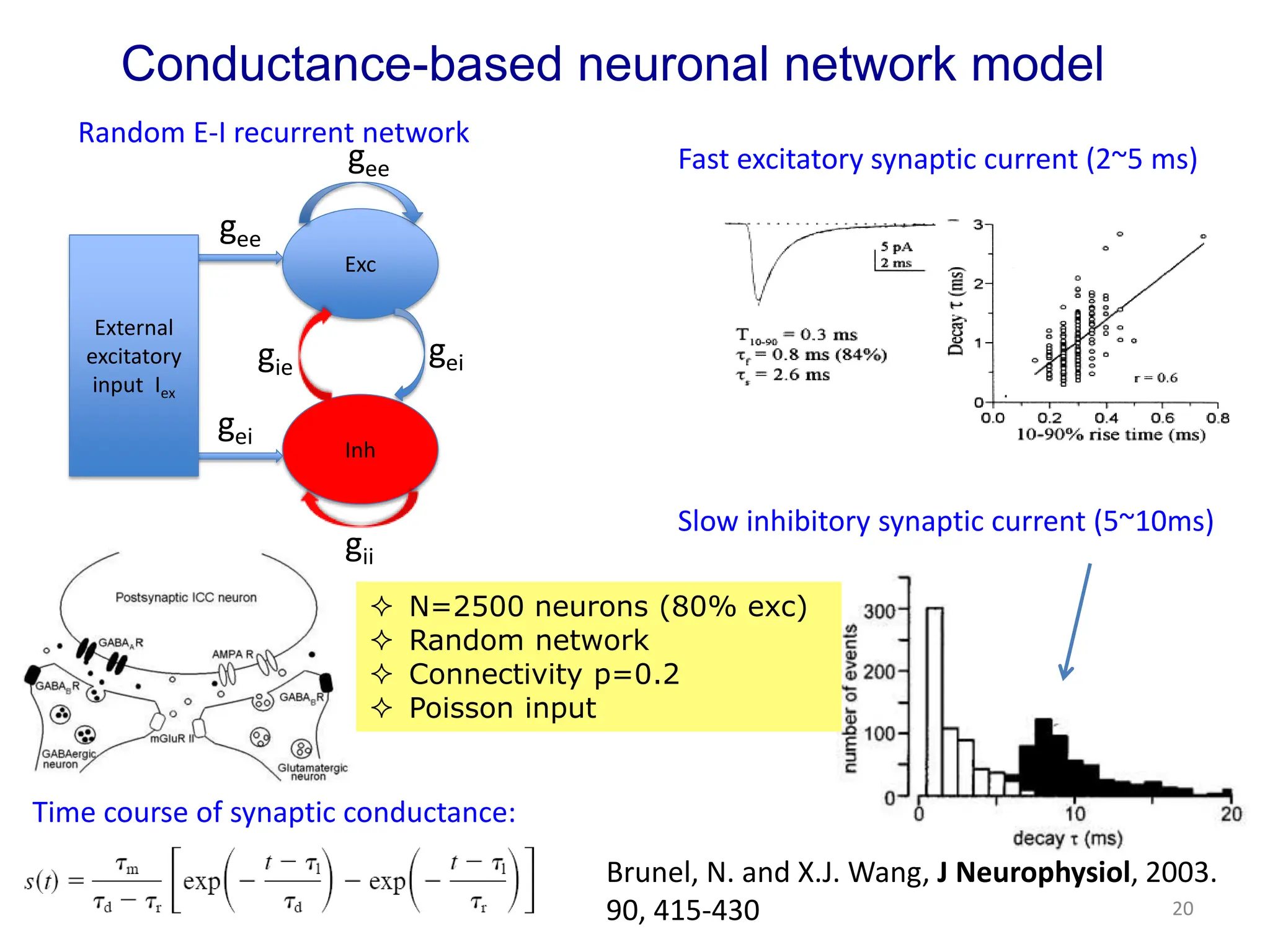
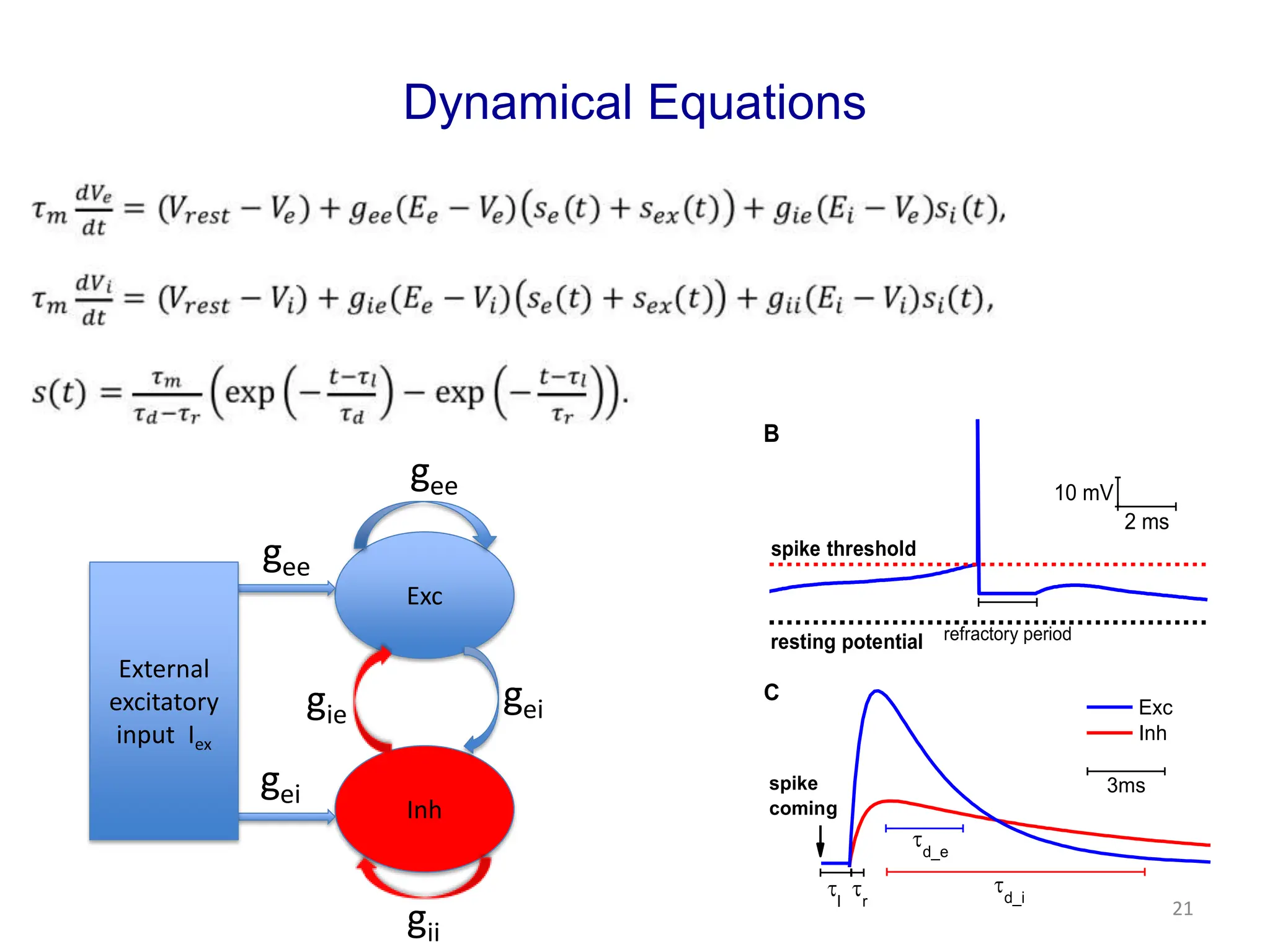
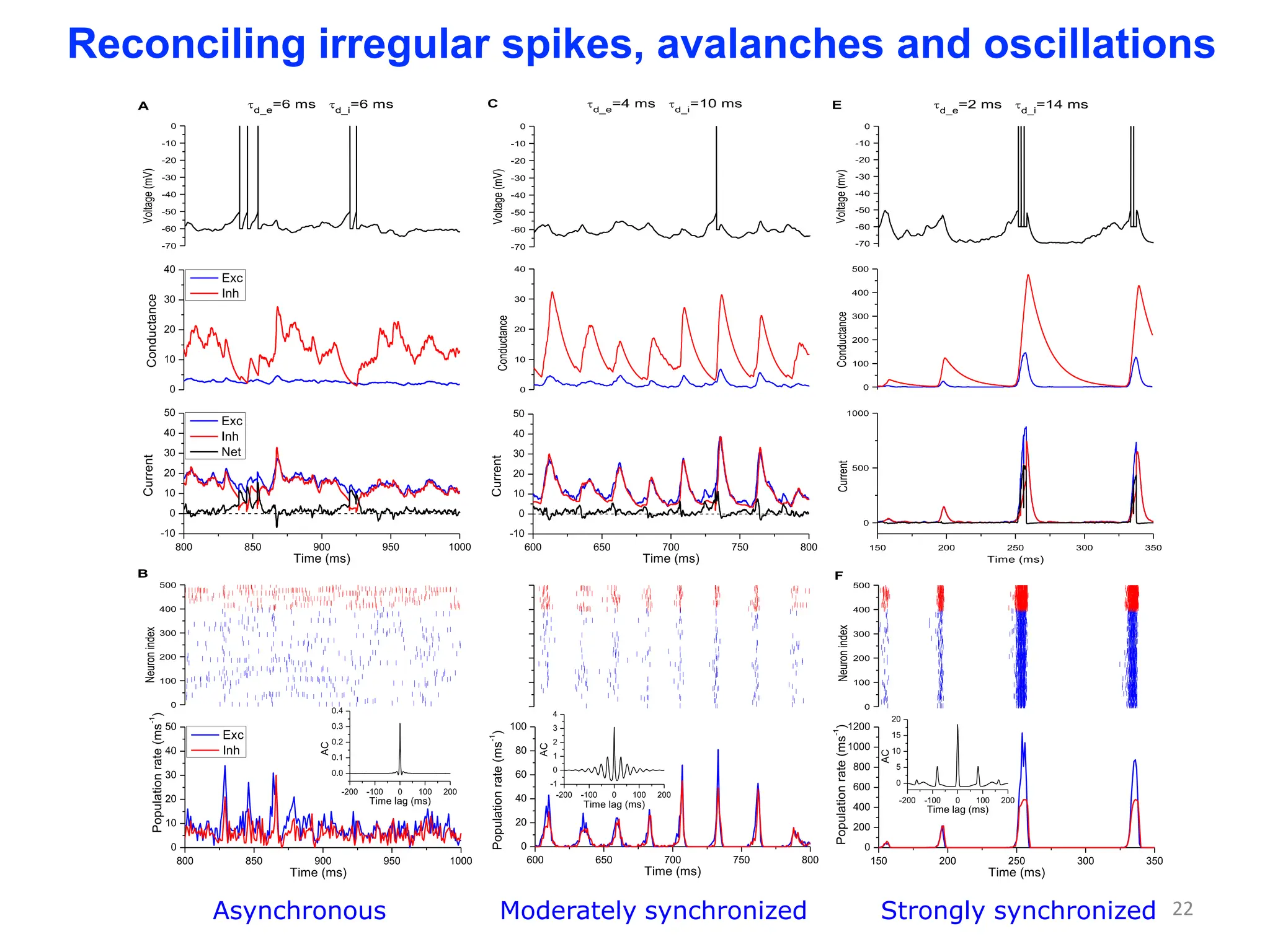
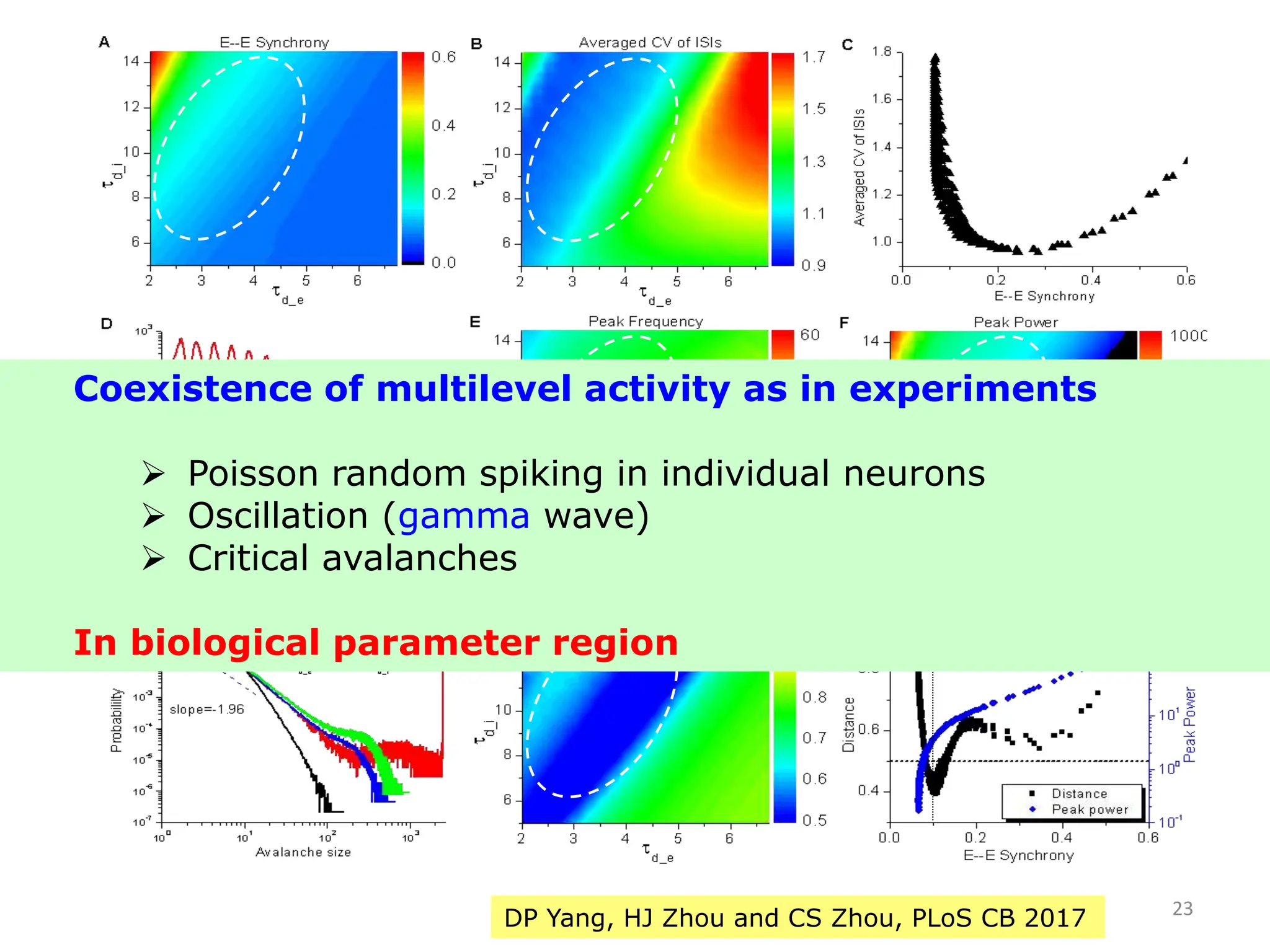
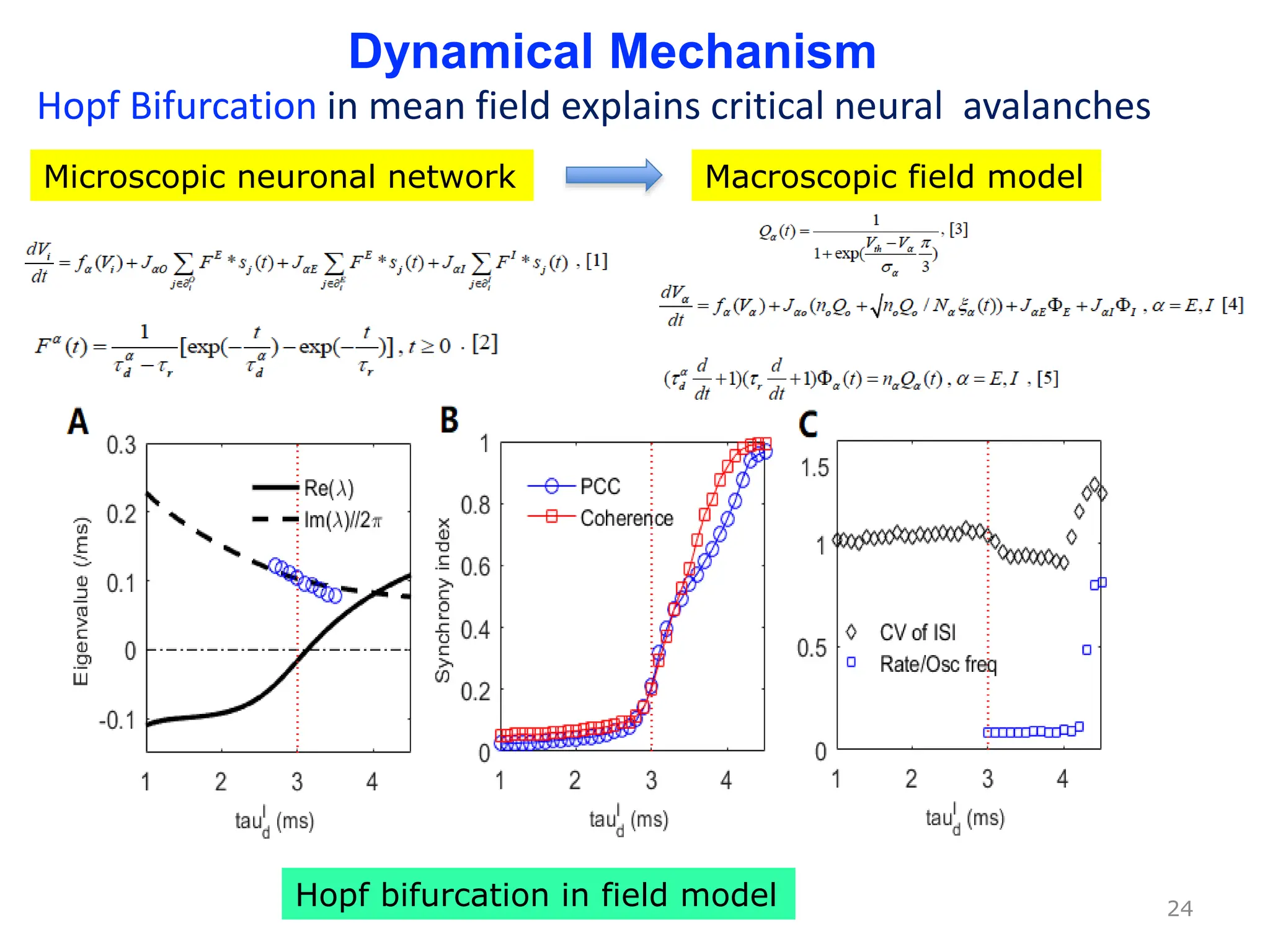
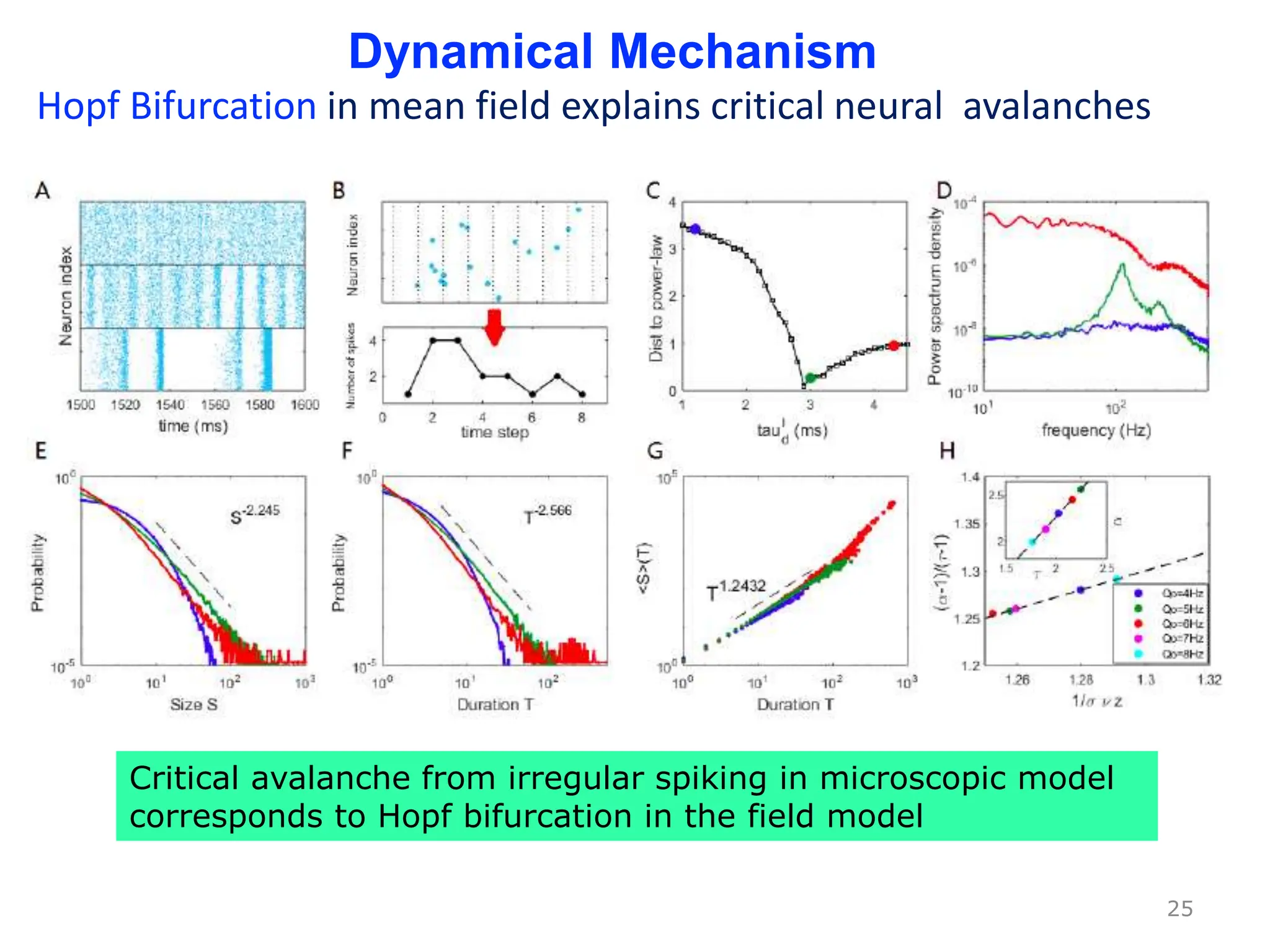
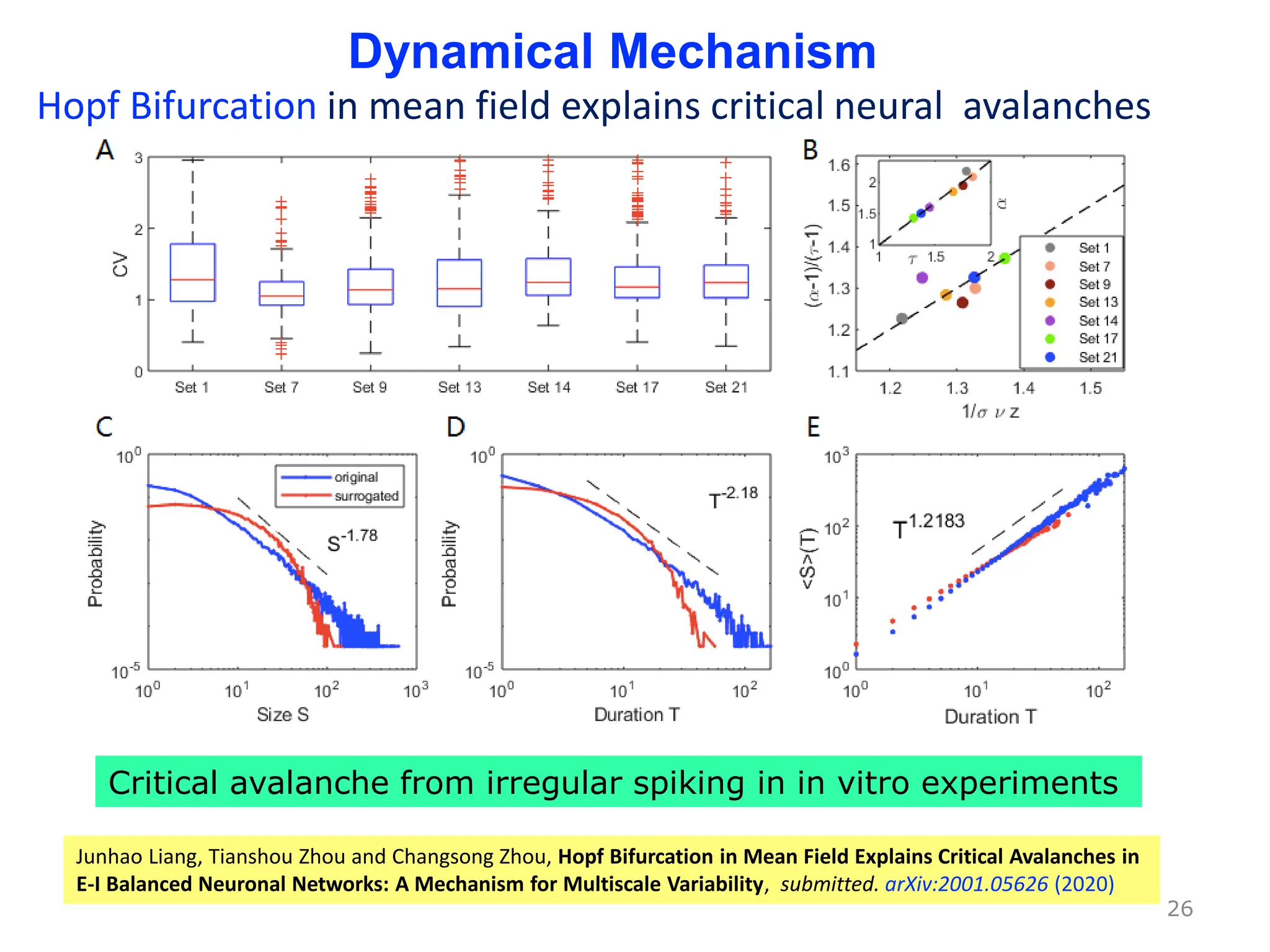
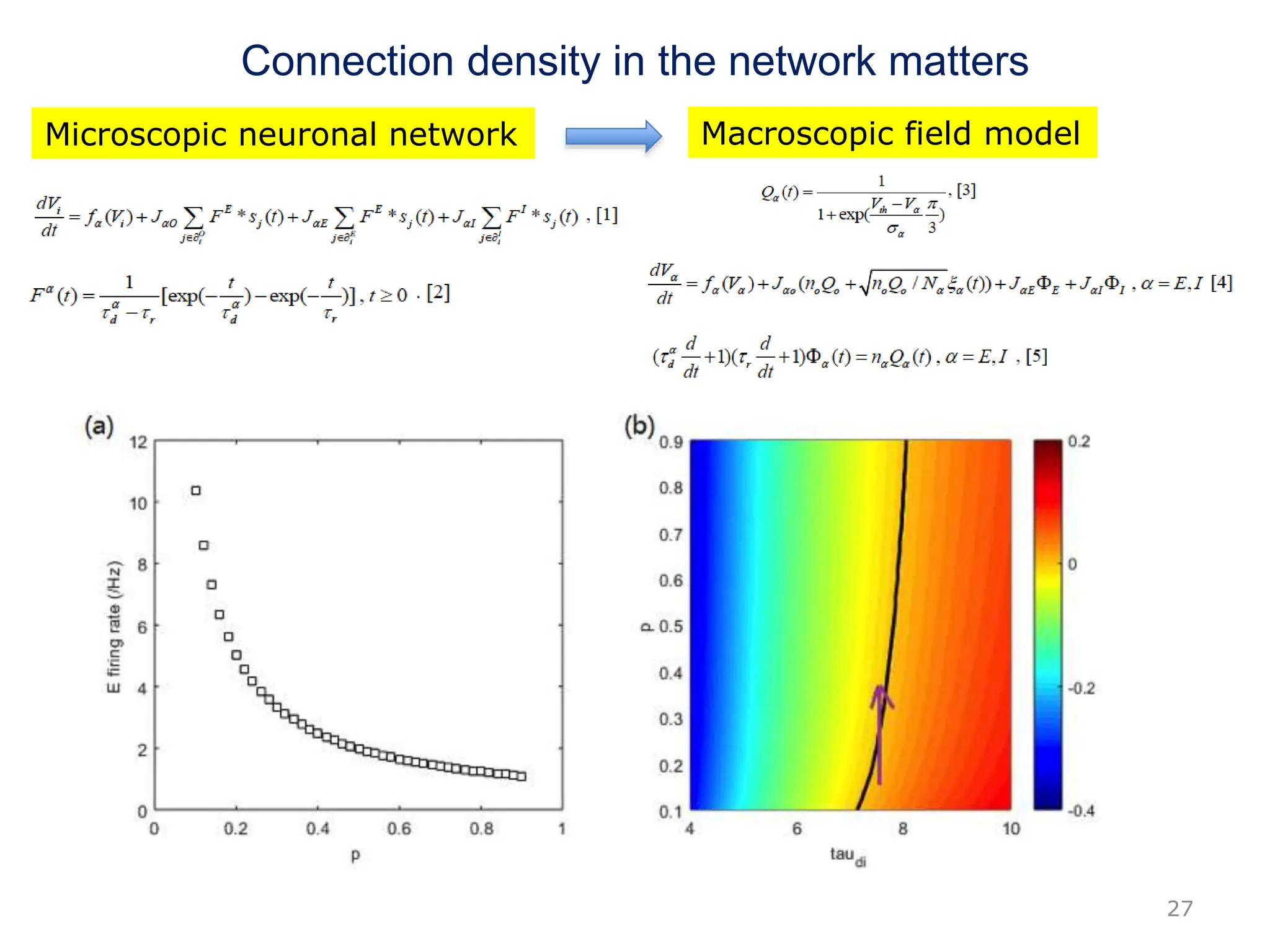
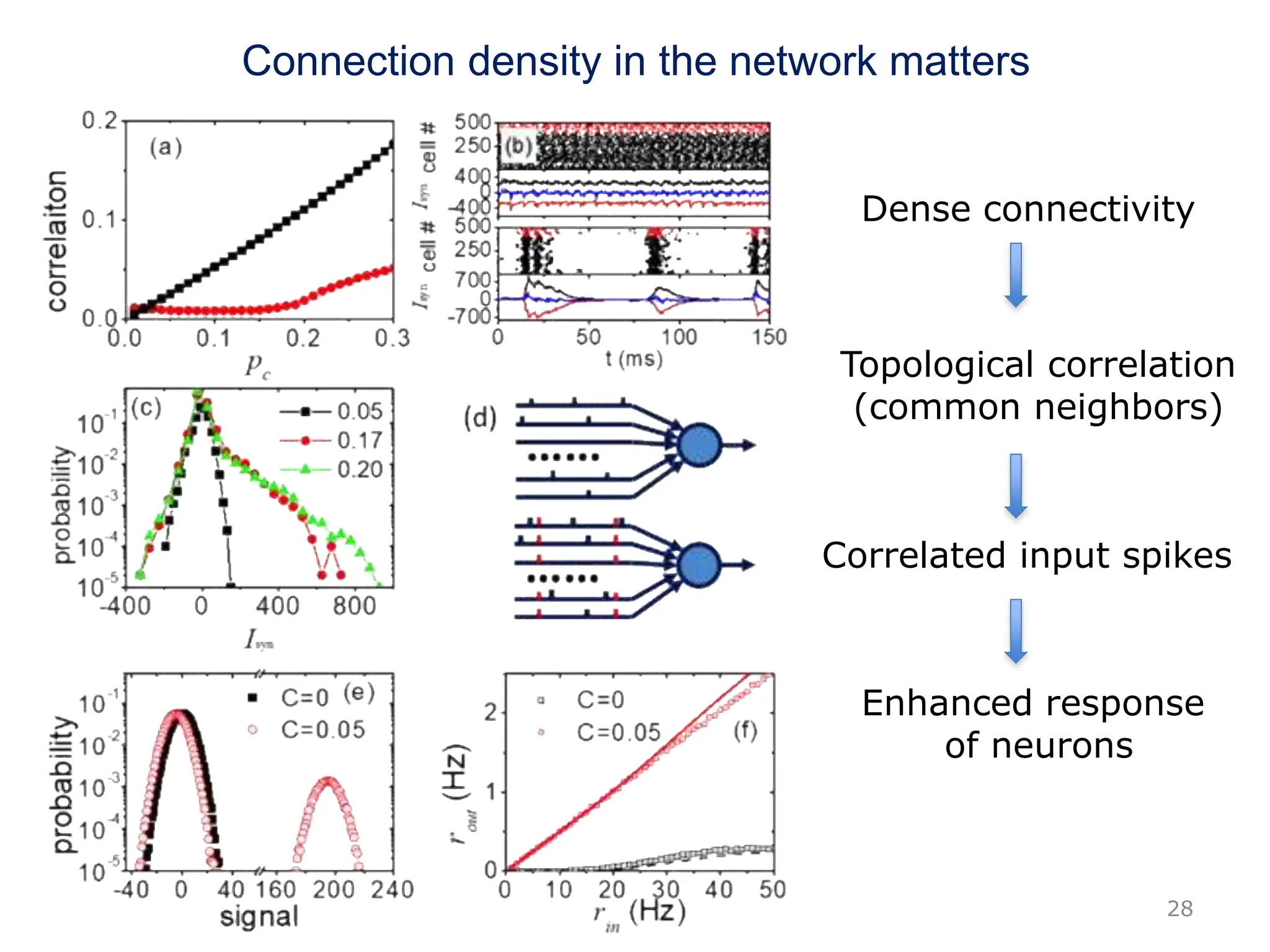
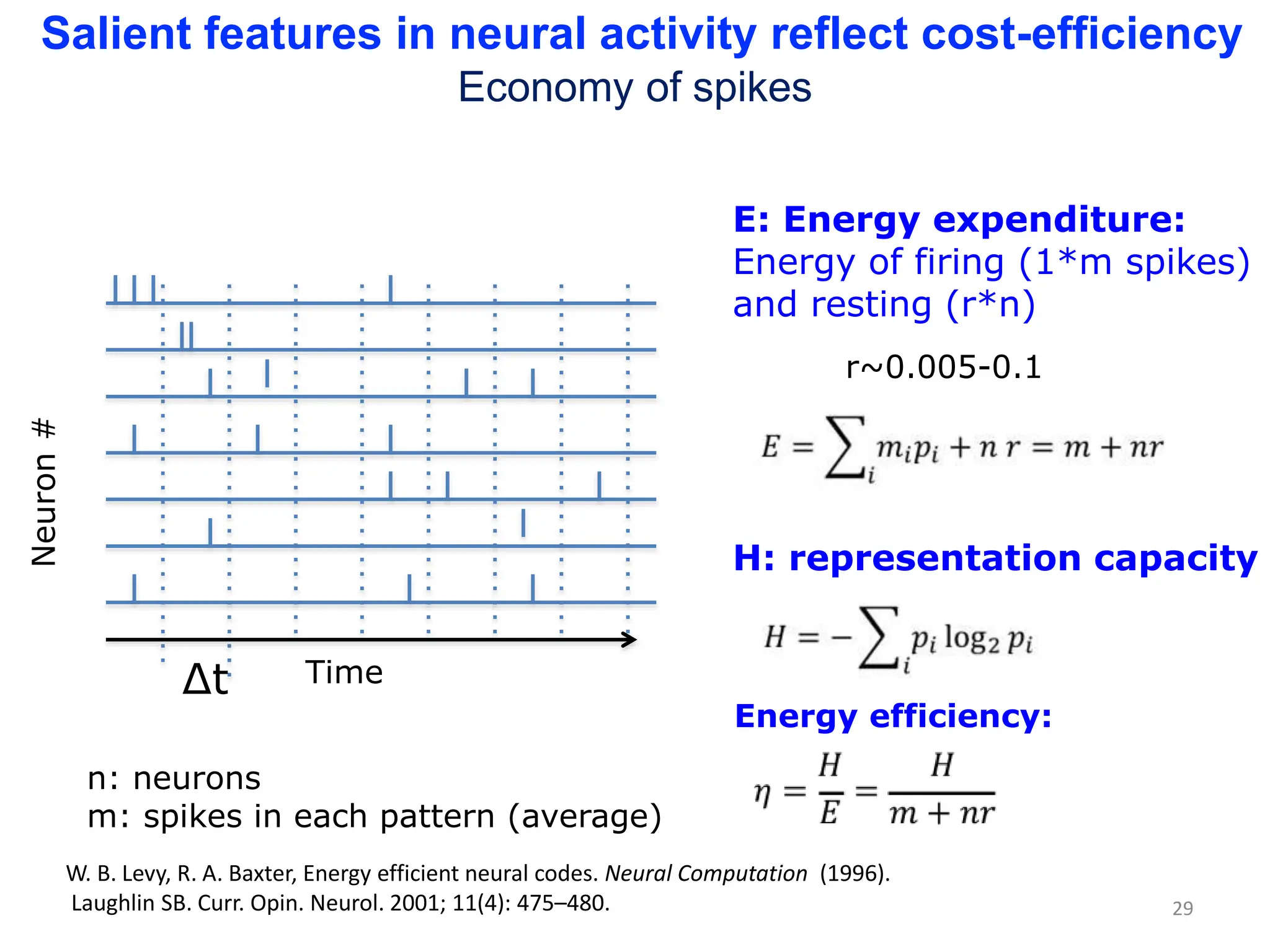
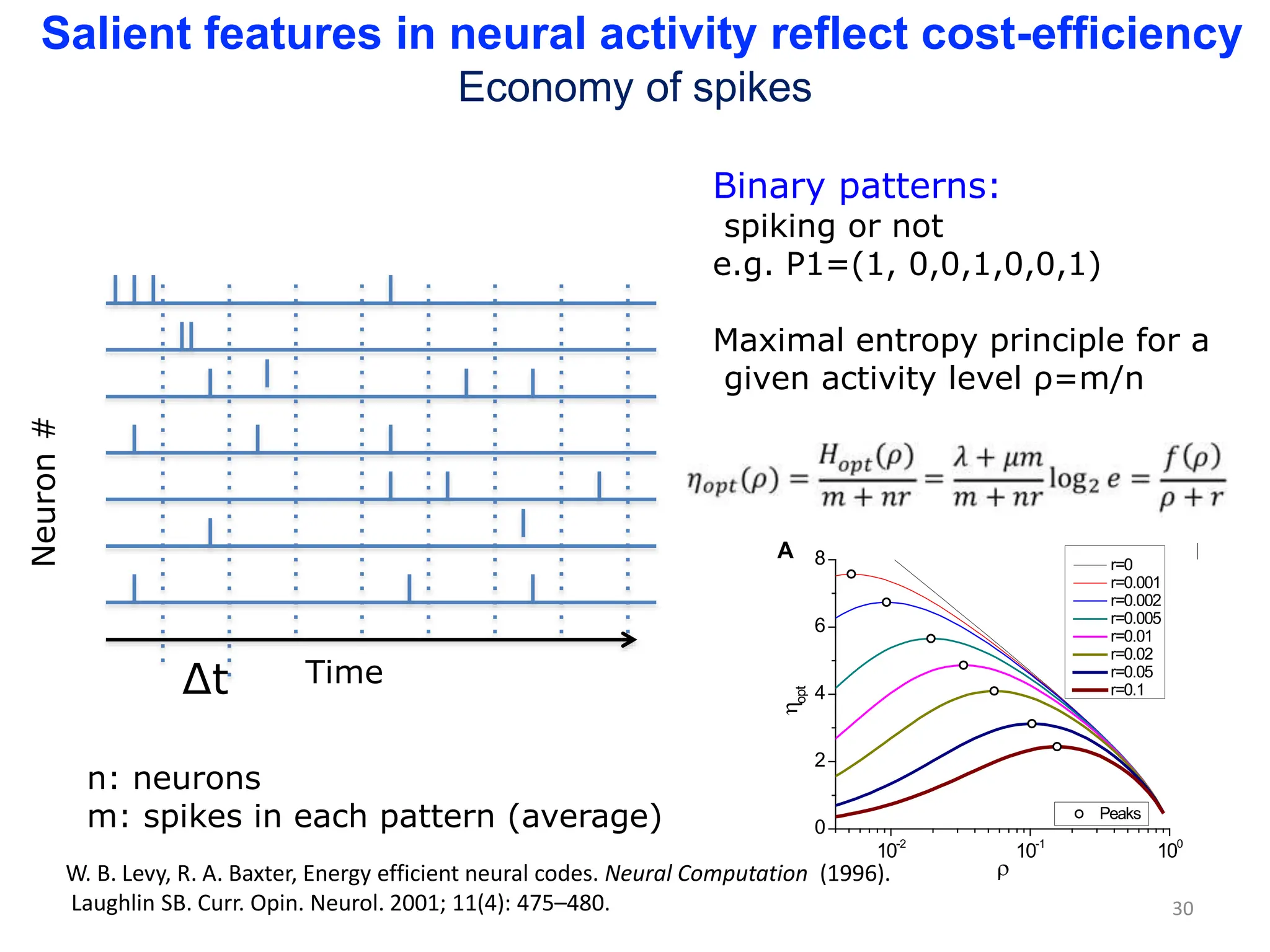
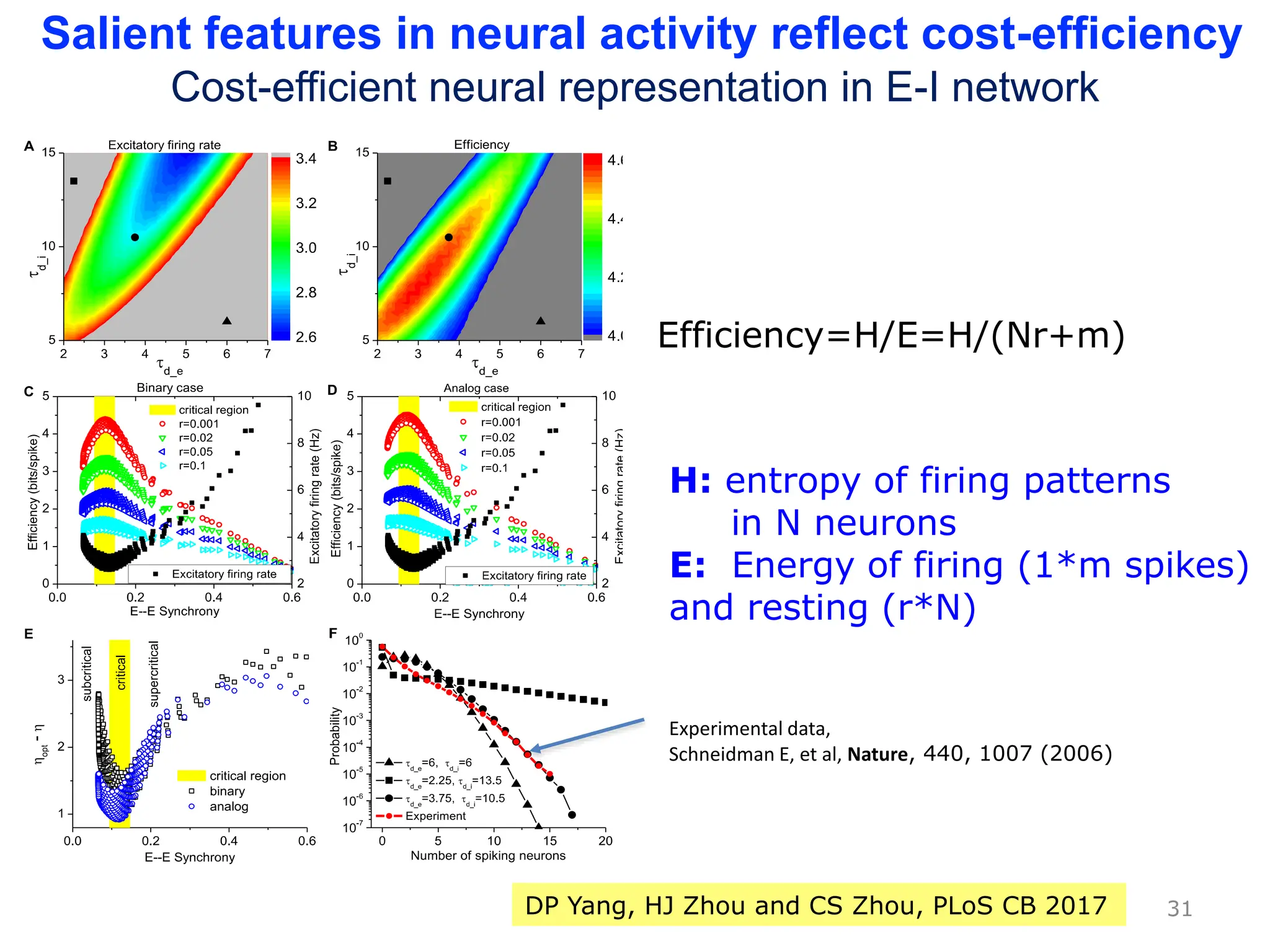
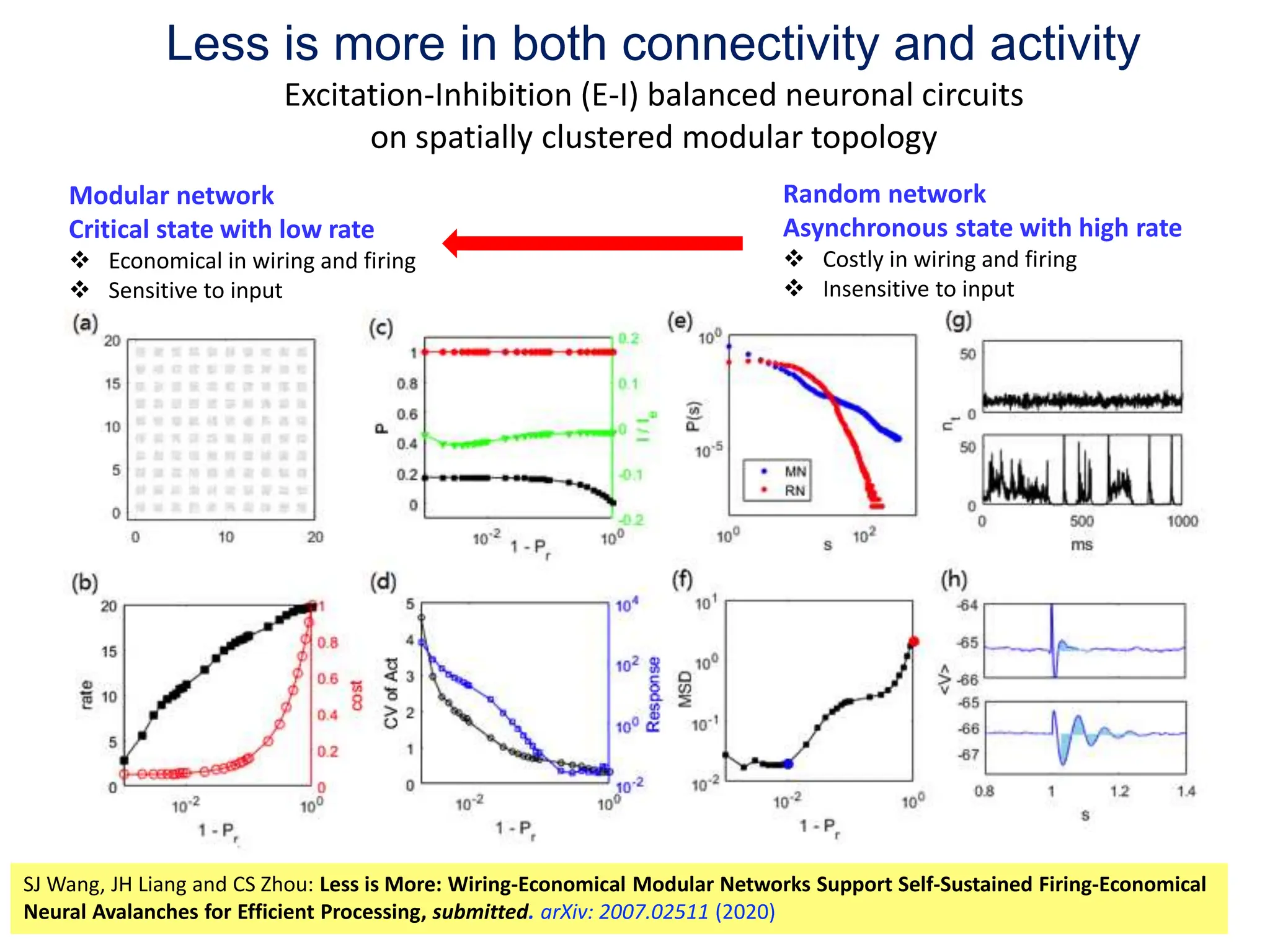
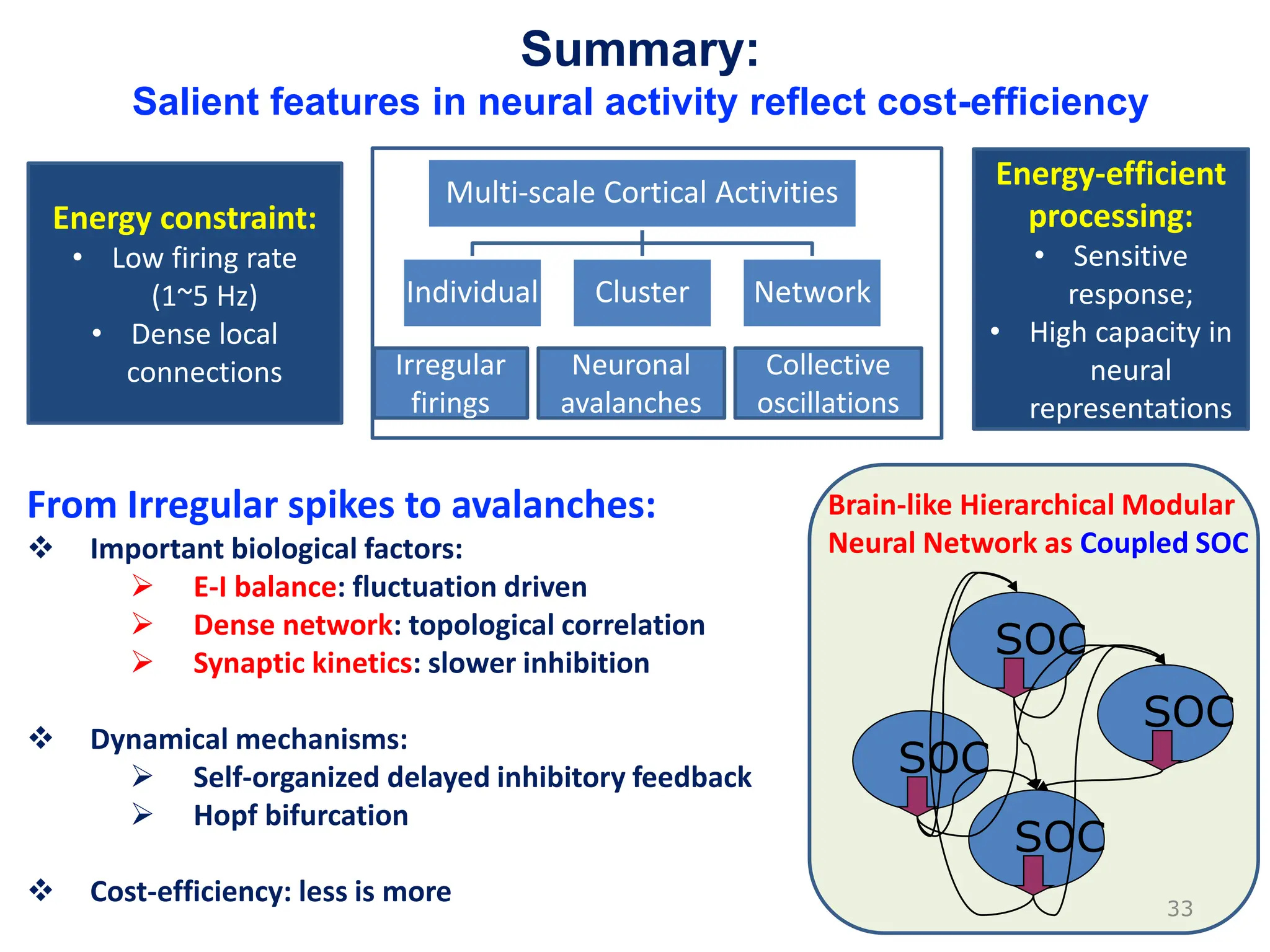
Zhou Changsong presents a document discussing the brain as a complex dynamical network system subject to constraints of cost and function. It aims to reconcile irregular neuronal spiking with neural avalanches through a biologically plausible neuronal network model and statistical physics analysis. The key findings are that the model shows coexistence of irregular spiking, oscillations, and critical avalanches through a dynamical mechanism of Hopf bifurcation in the mean field model that explains critical neural avalanches corresponding to irregular spiking in the microscopic neuronal network model. This multiscale variability in brain activity reflects principles of cost-efficient neural representation and dynamics.

1. ZHOU Changsong (周昌松）
Department of Physics
Centre for Nonlinear Studies
Institute of Computational and Theoretical Studies
Hong Kong Baptist University
0
From Sparse Irregular Spikes to Critical Avalanches:
Cost-Efficient Neural Dynamics

2. 1
Outline
Brain as complex dynamical network system;
cost-efficiency trade-off
Reconcile irregular neuronal spiking and neural
avalanches
Less is more

3. Brain as Dynamical Complex System
D.R. Chialvo “Critical Brain Networks” Physica A 340 (2004)
 High degree of freedom
 Strong nonlinearity
 Complex Connectivity
2
Human brain:
 Highly costly:
2% of the body’s weight
20% of resting metabolism
 Remarkably efficient:
Power density (0.01W/cm2) 1/104 of CPU (50-100 W/cm2)
Merolla, P.A., et al. A million spiking-
neuron integrated circuit with a scalable
communication network and interface,
Science, 2014. 345, 668.

4. Brain is a functional Complex System:
Designed by Great Nature through evolution
Subject to multiple constraints
Optimization of multiple functions
The trade-off must be reflected in the architecture,
activity and their interactions
Shall brain-inspired intelligence be constrained by
cost/function as in neural system?
Cost-efficiency trade-off
3

5. Energy cost of communication in the brain
Energy demands (50—80%) of spiking:
• Restoration of ion movements
• Propagation of action potentials
• Neurotransmitter uptake
Energy constraint: low firing rate (1~5Hz);
minimizing fiber length
4
Laughlin, S.B., Energy as a constraint on the coding and processing
of sensory information. Current opinion in neurobiology, 2001.

6. Columns and layers
Local neuronal circuits
Connectivity and Complexity
5
• Connection Architecture/Topology

7. Connectome Structure: Network of Networks
Hierarchy of Complex Modular Interaction
6
Complex Networks:
• Small-world
• Scale-free
• Modular
• Hierarchy
Cat Human

8. Connectome Structure: Network of Networks
Connectivity:
Local: dense (0.1-0.2)
Global: sparse (10-7-10-6)
Excitatory: Inhibitory~ 4:1
Hierarchy of Complex Modular Interaction
7
Complex Networks:
• Small-world
• Scale-free
• Modular
• Hierarchy
Cat Human
Challenge for network science and statistical physics:
hierarchical modular network
Markov, et al., 2012 Neuron
Highly heterogeneous weight

9. – Individual activity:
• low-rate firing
• irregularity
– Collective dynamics:
• network oscillations
• Critical neuronal avalanches
8
Salient features in brain activity

10. Irregularity of neuronal discharge
9
recorded from area MT (V5) of an alert monkey
Softky, W.R. and C. Koch J Neurosci, 1993. 13, 334-350
Shadlen M N and Newsome W T, J Neurosci, 1998. 18, 3870–3896
Different trials
with identical
stimulus

11. The origin of irregularity: E-I balanced state
E-I balance:
equal average amounts of
de- and hyperpolarizing
membrane currents
Shu, Y.S., et. al. Nature, 2003. 423, 288
Robert C. F, et. al. Nature, 2007. 450, 425
Van Vreeswijk, C. , Science, 1996. 274, 1724-1726.
Properties:
• Sparse network connectivity
• Stable at low rate with high fluctuation
• Display asynchronous irregular dynamics
10
Patch clamp technique
External
E
I
Binary (Ising) neuron
network model
4/3/2024

12. Instantaneous Balance:
Tight Coupling of Excitation & Inhibition
 Instantaneous correlation of excitation and inhibition
 Inhibition lags behind excitation
In rat somatosensory cortex in vivo
M. Okun, I. Lampl, Nat. Neurosci. 11, 535 (2008).
during ongoing and sensory-evoked activities
11

13. Weak pairwise correlation is crucial for
strongly correlated the firing patterns
Boltzmann distribution under
maximum entropy assumption:
Schneidman E, et al, Nature, 2006, 440, 1007
12

14. N. Friedam et al
PRL 108, 208102 (2012)
Fontenele et al
PRL 122, 208101 (2019)
Salient Feature of Brain Dynamics
Neural Avalanches: Self-Organized Criticality (SOC):
13
Neuronal Spikes

15. J. Beggs, D. Plenz, 2003.
J. Neurosci. 23 (35), 11167.
Salient Feature of Brain Dynamics
Neural Avalanches: Self-Organized Criticality (SOC):
E. Gireech, D. Plenz, 2008.
PNAS, 105, 7576
T. Petemann, et al, D. Plenz,
2009. PNAS, 106, 15921
14
Local field potential

16. 15
SOC in slow fMRI cluster of point-process
E. Tagliazucchi, et al.,Front. In Physio. 2012
Zhang and Raichle (2010) Nat Rev Neurosci
Functional Magnetic Resonance Imaging (fMRI)
Human resting fMRI
Salient Feature of Brain Dynamics
Neural Avalanches: Self-Organized Criticality (SOC):

17. Critical neuronal avalanches are crucial
for efficient information processing
Dynamic range Information Capacity Variability of Phase
Synchrony
Neuronal Avalanches imply
maximum dynamic range in
Cortical Networks at Criticality
Shew, W.L., H.D. Yang, T.
Petermann, R. Roy, and D. Plenz. J
Neurosci, 2009. 29, 15595-15600
Information Capacity and
Transmission Are Maximized in
Balanced Cortical Networks with
Neuronal Avalanches
Shew, W.L., H. Yang, S. Yu, R. Roy,
and D. Plenz. J Neurosci, 2011. 31,
55-63
Maximal variability of phase
synchrony in cortical
networks with neuronal
avalanches
Yang, H., W.L. Shew, R. Roy, and D.
Plenz. J Neurosci, 2012. 32, 1061-
1072 16

18. Collective oscillations
17
strong gamma (30–40 Hz)
oscillation
of the LFP, together with low
(2 Hz) and irregular firing in
pyramidal cells.
a single pyramidal cell fires
only once in every 15–20
cycles of the population
rhythm.
Fisahn A, et. al. Nature 394: 186–189, 1998.
Human Brain
Oscillations
(EEG/MEG)
Hippocampus in vitro
Local field potential (LFP)
Linkenkaer-Hansen K, J. Neurosci, 2001, 21: 1370
Theta:
4-7 Hz
Alpha:
8-12 Hz
Beta:
12-30 Hz
Gamma:
30-100 Hz
Delta:
up to 4 Hz

19. 18
Saccade eye movement of Monkey: Prof. Zhang Mingsha, BNU
+ .  Eye track; LFP;
 Multiple trials;
 Spike sorting;
Multilevel
Dynamics:
 Irregular spiking
 Oscillations
 Critical
avalanches
 Event-related
potential (ERP)
M. Chen, Y. Liu, L. Wei, and M. Zhang, J. Neurosci. 33,
814 (2013).
SJ Wang, G Ouyang, G Jing, MS Zhang, M Wong,
CS Zhou, Phys. Rev. Lett. 2016

20. Questions
19
How irregular spiking, neural avalanches and
oscillations can be reconciled?
What are the important factors?
What is the dynamical mechanism?
Is it cost-efficient?
We try to address these questions using
biologically plausible neuronal network model
and statistical physics analysis

21. Conductance-based neuronal network model
Brunel, N. and X.J. Wang, J Neurophysiol, 2003.
90, 415-430
Random E-I recurrent network
Time course of synaptic conductance:
Slow inhibitory synaptic current (5~10ms)
Exc
Inh
External
excitatory
input Iex
=( )+ ( ) ( )
+ ( )
=( )+ ( ) ( )
+ ( )
gee
gii
gei
gie
gee
gei
Evolving Equations for potentials:
(t)=
(t)=
Time courses of synaptic conductance:
Fast excitatory synaptic current (2~5 ms)
 N=2500 neurons (80% exc)
 Random network
 Connectivity p=0.2
 Poisson input
20

22. Dynamical Equations
Exc
Inh
External
excitatory
input Iex
=( )+ ( ) ( )
+ ( )
=( )+ ( ) ( )
+ ( )
gee
gii
gei
gie
gee
gei
Evolving Equations for potentials:
(t)=
(t)=
Time courses of synaptic conductance:
Exc
Inh
3ms
C
spike
coming
l r
d_e
d_i
spike threshold
resting potential
2 ms
10 mV
B
refractory period
21

23. Reconciling irregular spikes, avalanches and oscillations
Asynchronous Moderately synchronized Strongly synchronized 22

24. Coexistence of multilevel activity as in experiments
 Poisson random spiking in individual neurons
 Oscillation (gamma wave)
 Critical avalanches
In biological parameter region
23
DP Yang, HJ Zhou and CS Zhou, PLoS CB 2017

25. 24
Dynamical Mechanism
Hopf Bifurcation in mean field explains critical neural avalanches
Microscopic neuronal network Macroscopic field model
Hopf bifurcation in field model

26. 25
Critical avalanche from irregular spiking in microscopic model
corresponds to Hopf bifurcation in the field model
Dynamical Mechanism
Hopf Bifurcation in mean field explains critical neural avalanches

27. 26
Critical avalanche from irregular spiking in in vitro experiments
Junhao Liang, Tianshou Zhou and Changsong Zhou, Hopf Bifurcation in Mean Field Explains Critical Avalanches in
E-I Balanced Neuronal Networks: A Mechanism for Multiscale Variability, submitted. arXiv:2001.05626 (2020)
Dynamical Mechanism
Hopf Bifurcation in mean field explains critical neural avalanches

28. 27
Connection density in the network matters
Microscopic neuronal network Macroscopic field model

29. 28
Connection density in the network matters
Dense connectivity
Topological correlation
(common neighbors)
Correlated input spikes
Enhanced response
of neurons

30. Time
Neuron
#
Δt
E: Energy expenditure:
Energy of firing (1*m spikes)
and resting (r*n)
H: representation capacity
n: neurons
m: spikes in each pattern (average)
Energy efficiency:
r~0.005-0.1
W. B. Levy, R. A. Baxter, Energy efficient neural codes. Neural Computation (1996).
Laughlin SB. Curr. Opin. Neurol. 2001; 11(4): 475–480. 29
Salient features in neural activity reflect cost-efficiency
Economy of spikes

31. Time
Neuron
#
Δt
n: neurons
m: spikes in each pattern (average)
W. B. Levy, R. A. Baxter, Energy efficient neural codes. Neural Computation (1996).
Laughlin SB. Curr. Opin. Neurol. 2001; 11(4): 475–480. 30
Salient features in neural activity reflect cost-efficiency
Economy of spikes
Binary patterns:
spiking or not
e.g. P1=(1, 0,0,1,0,0,1)
Maximal entropy principle for a
given activity level ρ=m/n

32. 31
H: entropy of firing patterns
in N neurons
E: Energy of firing (1*m spikes)
and resting (r*N)
Efficiency=H/E=H/(Nr+m)
DP Yang, HJ Zhou and CS Zhou, PLoS CB 2017
Salient features in neural activity reflect cost-efficiency
Cost-efficient neural representation in E-I network
Experimental data,
Schneidman E, et al, Nature, 440, 1007 (2006)

33. Less is more in both connectivity and activity
Excitation-Inhibition (E-I) balanced neuronal circuits
on spatially clustered modular topology
Random network
Asynchronous state with high rate
 Costly in wiring and firing
 Insensitive to input
Modular network
Critical state with low rate
 Economical in wiring and firing
 Sensitive to input
32
SJ Wang, JH Liang and CS Zhou: Less is More: Wiring-Economical Modular Networks Support Self-Sustained Firing-Economical
Neural Avalanches for Efficient Processing, submitted. arXiv: 2007.02511 (2020)

34. Summary:
Salient features in neural activity reflect cost-efficiency
33
Energy constraint:
• Low firing rate
(1~5 Hz)
• Dense local
connections
Energy-efficient
processing:
• Sensitive
response;
• High capacity in
neural
representations
Multi-scale Cortical Activities
Individual Cluster Network
Irregular
firings
Neuronal
avalanches
Collective
oscillations
From Irregular spikes to avalanches:
 Important biological factors:
 E-I balance: fluctuation driven
 Dense network: topological correlation
 Synaptic kinetics: slower inhibition
 Dynamical mechanisms:
 Self-organized delayed inhibitory feedback
 Hopf bifurcation
 Cost-efficiency: less is more
SOC
SOC
SOC
SOC
Brain-like Hierarchical Modular
Neural Network as Coupled SOC

35. Thank you for your
attention!
Thanks to collaborators:
Dongping Yang; Haijun Zhou;
Shengjun Wang; Junhao Liang
Funding:
Hong Kong RGC
NSFC
NSFC-RGC Joint Scheme
34
Our works on neural avalanches, brain criticality and signal complexity:
• JH Liang, TS Zhou and CS Zhou, arXiv:2001.05626 (2020)
• SJ Wang, JH Liang and CS Zhou, arXiv: 2007.02511 (2020)
• MX Liu, XY Liu, A Hildebrandt and CS Zhou, Cerebral Cortex Communication (2020)
• R Wang, P Lin, MX Liu, Y Wu, T Zhou and CS Zhou, Physical Review Letters (2019)
• MX Liu, CC Song, T Knopfel and CS Zhou, NeuroImage (2019)
• DP Yang, HJ Zhou and CS Zhou, PLoS Computational Biology (2017)
• SJ Wang, G Ouyang, G Jing, MS Zhang, M Wong, CS Zhou, Physical Review Letters (2016).
• SJ Wang, CS Zhou, New Journal Physics (2012 Highlight)
• SJ Wang, C Hilgetag, CS Zhou, Frontiers in Computational Neuroscience (2010)