Talk was given in the Statistical Physics group of Faculty of Sciences, University of Granada

1. A double homeostatic
mechanism to get
self-organized quasi-criticality
Osame Kinouchi
Ludmila Brochini
Ariadne A. Costa
Tawan T. A. Carvalho
Maurício Girardi-Schappo

2. 2

3. Previous Literature
3
Dynamical synapses causing self-
organized criticality in neural
networks.
A. Levina, J. M. Herrmann & T. Geisel
Nature Physics volume 3, pages 857–
860 (2007).

4. 4
J.Stat.
ournal of Statistical Mechanics:
J Theory and Experiment
Self-organization without conservation:
are neuronal avalanches generically
critical?
Juan A Bonachela, Sebastiano de Franciscis,
Joaqu´ın J Torres and Miguel A Mu˜noz
Departamento de Electromagnetismo y F´ısica de la Materia and Instituto de
F´ısica Te´orica y Computacional Carlos I, Facultad de Ciencias, Universidad de
J.Stat.Mech.(2009)P090
ournal of Statistical Mechanics:
An IOP and SISSA journalJ Theory and Experiment
Self-organization without conservation:
true or just apparent scale-invariance?
Juan A Bonachela and Miguel A Mu˜noz
Departamento de Electromagnetismo y F´ısica de la Materia and Instituto de
F´ısica Te´orica y Computacional Carlos I, Facultad de Ciencias, Universidad de
Granada, 18071 Granada, Spain
E-mail: jabonachela@onsager.ugr.es and mamunoz@onsager.ugr.es
Received 12 May 2009
Accepted 2 August 2009
Published 17 September 2009
Online at stacks.iop.org/JSTAT/2009/P09009
doi:10.1088/1742-5468/2009/09/P09009
Abstract. The existence of true scale-invariance in slowly driven models of self-
organized criticality without a conservation law, such as forest-fires or earthquake
automata, is scrutinized in this paper. By using three different levels of
description—(i) a simple mean field, (ii) a more detailed mean-field description
in terms of a (self-organized) branching processes, and (iii) a full stochastic
representation in terms of a Langevin equation—it is shown on general grounds
that non-conserving dynamics does not lead to bona fide criticality. Contrary to
the case for conserving systems, a parameter, which we term the ‘re-charging’
rate (e.g. the tree-growth rate in forest-fire models), needs to be fine-tuned in
non-conserving systems to obtain criticality. In the infinite-size limit, such a
fine-tuning of the loading rate is easy to achieve, as it emerges by imposing
2009
2010

5. 5
Article
Self-Organized Supercriticality and Oscillations in
Networks of Stochastic Spiking Neurons
Ariadne A. Costa 1,2, Ludmila Brochini 3 and Osame Kinouchi 4,*
1 Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN 47405, USA;
ad.andrade.costa@gmail.com
2 Instituto de Computação, Universidade de Campinas, Campinas-SP 13083-852, Brazil
3 Departamento de Estatística, Instituto de Matemática e Estatística (IME), Universidade de São Paulo,
São Paulo-SP 05508-090, Brazil; ludbrochini@gmail.com
4 Departamento de Física, Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto (FFCLRP),
Universidade de São Paulo, Ribeirão Preto-SP 14040-901, Brazil
* Correspondence: osame@ffclrp.usp.br; Tel.: +55-16-3315-3693
Received: 23 May 2017; Accepted: 31 July 2017; Published: 2 August 2017
Abstract: Networks of stochastic spiking neurons are interesting models in the area of theoretical
neuroscience, presenting both continuous and discontinuous phase transitions. Here, we study
fully-connected networks analytically, numerically and by computational simulations. The neurons
have dynamic gains that enable the network to converge to a stationary slightly supercritical state
(self-organized supercriticality (SOSC)) in the presence of the continuous transition. We show that
SOSC, which presents power laws for neuronal avalanches plus some large events, is robust as
a function of the main parameter of the neuronal gain dynamics. We discuss the possible applications
of the idea of SOSC to biological phenomena like epilepsy and Dragon-king avalanches. We also find
that neuronal gains can produce collective oscillations that coexist with neuronal avalanches.
1Scientific RepoRts
Phase transitions and self-
organized criticality in networks of
stochastic spiking neurons
Ludmila Brochini ,Ariadne deAndradeCosta , MiguelAbadi ,AntônioC. Roque , Jorge
&Osame Kinouchi
Phase transitions and critical behavior are crucial issues both in theoretical and experimental
neuroscience.We report analytic and computational results about phase transitions and self-organized
probability given by a smooth monotonic function Φ(V) of the membrane potential V, rather than a
Φ. In particular, we
encounter both continuous and discontinuous phase transitions to absorbing states.At the continuous
transition critical boundary, neuronal avalanches occur whose distributions of size and duration
are given by power laws, as observed in biological neural networks.We also propose and test a new
mechanism to produce SOC: the use of dynamic neuronal gains – a form of short-term plasticity
probably located at the axon initial segment (AIS) – instead of depressing synapses at the dendrites
(as previously studied in the literature).The new self-organization mechanism produces a slightly
supercritical state, that we called SOSC, in accord to some intuitions ofAlanTuring.
“Another simile would be an atomic pile of less than critical size: an injected idea is to correspond to a neutron
entering the pile from without. Each such neutron will cause a certain disturbance which eventually dies away. If,
however, the size of the pile is sufficiently increased, the disturbance caused by such an incoming neutron will very
likely go on and on increasing until the whole pile is destroyed. Is there a corresponding phenomenon for minds, and
is there one for machines? There does seem to be one for the human mind. The majority of them seems to be subcrit-
ical, i.e., to correspond in this analogy to piles of subcritical size. An idea presented to such a mind will on average
give rise to less than one idea in reply. A smallish proportion are supercritical. An idea presented to such a mind may
give rise to a whole “theory” consisting of secondary, tertiary and more remote ideas. (…) Adhering to this analogy
we ask, “Can a machine be made to be supercritical?”” Alan Turing (1950)1
.
The Critical Brain Hypothesis2,3
states that (some) biological neuronal networks work near phase transitions
because criticality enhances information processing capabilities4–6
and health7
. The first discussion about criti-
cality in the brain, in the sense that subcritical, critical and slightly supercritical branching process of thoughts
could describe human and animal minds, has been made in the beautiful speculative 1950 Imitation Game paper
by Turing1
. In 1995, Herz & Hopfield8
noticed that self-organized criticality (SOC) models for earthquakes were
mathematically equivalent to networks of integrate-and-fire neurons, and speculated that perhaps SOC would
occur in the brain. In 2003, in a landmark paper, these theoretical conjectures found experimental support
by Beggs & Plenz9
and, by now, more than half a thousand papers can be found about the subject, see some
reviews2,3,10
. Although not consensual, the Critical Brain Hypothesis can be considered at least a very fertile idea.
The open question about neuronal criticality is what are the mechanisms responsible for tuning the network
towards the critical state. Up to now, the main mechanism studied is some dynamics in the links which, in the
biological context, would occur at the synaptic level11–17
.
Here we propose a whole new mechanism: dynamic neuronal gains, related to the diminution (and recovery)
of the firing probability, an intrinsic neuronal property. The neuronal gain is experimentally related to the well
known phenomenon of firing rate adaptation18–20
. This new mechanism is sufficient to drive neuronal networks
Universidade de
Universidade de São Paulo, Departamento
r
a
P
OPEN
www.nature.com/scientificreports
Stochastic oscillations and dragon
king avalanches in self-organized
quasi-critical systems
Osame Kinouchi , Ludmila Brochini ,AriadneA.Costa , JoãoGuilherme FerreiraCampos &
MauroCopelli
In the last decade, several models with network adaptive mechanisms (link deletion-creation, dynamic
synapses, dynamic gains) have been proposed as examples of self-organized criticality (SOC) to explain
neuronal avalanches. However, all these systems present stochastic oscillations hovering around the
critical region that are incompatible with standard SOC. Here we make a linear stability analysis of
corresponds to a stable focus that loses stability at criticality.We argue that when this focus is close
Received: 19 October 2018
Accepted: 28 January 2019
Published: xx xx xxxx
OPEN
2016
2017
2019

6. 6
PHYSICAL REVIEW RESEARCH 2, 012042(R) (2020)
Rapid Communications
Synaptic balance due to homeostatically self-organized quasicritical dynamics
Mauricio Girardi-Schappo ,1,*,†
Ludmila Brochini,2
Ariadne A. Costa,3
Tawan T. A. Carvalho ,4
and Osame Kinouchi 1,*,‡
1
Universidade de São Paulo, FFCLRP, Departamento de Física, Ribeirão Preto, SP, 14040-901, Brazil
2
Universidade de São Paulo, Instituto de Matemática e Estatística, São Paulo, SP, 05508-090, Brazil
3
Universidade Federal de Goiás - Regional Jataí, Unidade Acadêmica Especial de Ciências Exatas, Jataí, GO, 75801-615, Brazil
4
Universidade Federal de Pernambuco, Departamento de Física, Recife, PE, 50670-901, Brazil
(Received 30 July 2019; accepted 23 January 2020; published 20 February 2020)
Recent experiments suggested that a homeostatic regulation of synaptic balance leads the visual system to
recover and maintain a regime of power-law avalanches. Here we study an excitatory/inhibitory (E/I) mean-
field neuronal network that has a critical point with power-law avalanches and synaptic balance. When short-
term depression in inhibitory synapses and firing threshold adaptation are added, the system hovers around
the critical point. This homeostatically self-organized quasicritical (SOqC) dynamics generates E/I synaptic
current cancellation in fast timescales, causing fluctuation-driven asynchronous-irregular (AI) firing. We present
the full phase diagram of the model without adaptation varying external input versus synaptic coupling. This
system has a rich dynamical repertoire of spiking patterns: synchronous regular (SR), asynchronous regular
(AR), synchronous irregular (SI), slow oscillations (SO), and AI. It also presents dynamic balance of synaptic
currents, since inhibitory currents try and compensate excitatory currents over time, resulting in both of them
scaling linearly with external input. Our model thus unifies two different perspectives on cortical spontaneous
activity: both critical avalanches and fluctuation-driven AI firing arise from SOqC homeostatic adaptation and
are indeed two sides of the same coin.
DOI: 10.1103/PhysRevResearch.2.012042
Experimental and theoretical evidence suggests that spon-
taneous cortical activity happens in the form of asynchronous
irregular firing patterns (AI). This could be generated by
the balance of excitatory/inhibitory (E/I) synaptic currents
independent homeostatic mechanisms to generate the SOqC
dynamics: plasticity in the inhibitory synapses [18] and adap-
tive firing thresholds [19].
As for the second point, we will show that our homeo-

7. The model
• N neurons (all-to-all graph)
• N
E
excitatory neurons, p = N
E
/N
• N
I
inhibitory neurons, q = N
I
/N p+q = 1
• a = E (excitatory) or I (inhibitory)
• Xi
a
= 1 (i-th neuron spikes)
• Xi
a
= 0 (i-th neuron remains silent)
• Vi
a
[t] = membrane potential at (discrete) time t
• Wij
ab
= synapses
• Ii = input
• 𝛉 = firing threshold
• 𝛍 = leakage parameter
7

8. Excitatory/Inhibitory (E/I) network with
stochastic integrate-and-fire neurons
8
E I
WIE
WEI
WEE
WII

9. Stochastic firing function 𝚽(V)
9

10. Order and control parameters
10
𝛒a[t] = < Xa
j>[t] density of firing sites
Wab = < Wij
ab > average synaptic weight

11. The quiescent (Q) or absorbing (𝛒0) phase
11
𝛒E = 𝛒I = 𝛒0 = 0
V[t+1] = 𝛍V[t] + I
Stationary: (1 - 𝛍) V* = I
Maximum V* for 𝛒0 = 0 is Vmax = 𝛉
Thus, Imax = (1 - 𝛍) 𝛉
Define field h = I - Imax = I - (1 - 𝛍) 𝛉
Thus transition to the absorbing state occurs at h = 0

12. Mean-field calculation (𝛍 = 0)
12
W = pWEE/IE - q WII/EI = weighted synaptic weight

13. Stationary solutions
13
𝛒E = 𝛒I = 𝛒 by symmetry
Three solutions:
𝛒0 = 0 (absorbing state) for h < 0,
𝛒+ (stable) and 𝛒- (unstable) from:

14. Comparison with model A of Brunel
(2000) (1343 citations)
14
Excitatory:
p = NE/N = 0.8
WEE = WIE = J
Inhibitory:
q = NI/N = 0.2
WII = WEI = gJ
Normal coordinates: W = p J - q g J
h = I - (1 - 𝛍) 𝛉
Brunel coordinates: g = WII/WEE = p/q - W/qJ
Y = I / 𝛉 = h/𝛉 + (1 - 𝛍)

15. Phase diagram in the LIF limit of large 𝚪J
15
Brunel (2000)
Brunel coordinates:
g = p/q - W/Jq
Y = I / 𝛉 = h/𝛉 + (1 - 𝛍)
Brunel notation:
High (H) or Low (L) = 𝛒+
Intermediary (I) = 𝛒-
Quiescente (Q) = 𝛒0

16. Bifurcation diagram (𝛍 = 0)
16
𝛒+ or H
𝛒- or L
𝛒+, 𝛒- , 𝛒0
for Y < 1
Brunel (2000)
g = p/q - W/Jq = 4 - 5 W/J
Small W or large J: gc → 4
𝛒+

17. Continuous phase transition: (Wc = 1/𝚪, hc = 0)
or (gc,Yc = 1 - 𝛍)
17

18. Critical point at (Wc,hc = 0) or (gc,Yc = 1-𝛍)
18
For:
For:
Mean-field Directed Percolation

19. General phase diagram: gc = 4 - 1/(q𝚪J)
19

20. Changing parameters J and 𝚪
20
All the lines are analytic

21. Critical point neuronal avalanches
21

22. Has Brunel model a DP
critical point?
22
196 Brunel
Table 1. Comparison between simulations and theory in the
inhibition-dominated irregular regimes: Average firing rates and
global oscillation frequency.
Firing rate Global frequency
Simulation Theory Simulation Theory
B. SI, fast 60.7 Hz 55.8 Hz 180 Hz 190 Hz
C. AI 37.7 Hz 38.0 Hz — —
D. SI, slow 5.5 Hz 6.5 Hz 22 Hz 29 Hz
varying firing rate ν(t). Thus, the analysis developed
in the present article is not adequate to describe such
states. However, the analysis does predict the transition
toward such synchronized states as soon as the excita-
Brunel (2000)Figure 3. Frequency of the global oscillation (imaginary part of the
solution of Eq. (46) with the largest real part, in the regions in which
the real part is positive) as a function of the external inputs νext, for
several values of the delay and g. Full lines: D = 1.5 ms. Long-
dashed lines: D = 2 ms. Short-dashed lines: D = 3 ms. For each
value of D, three curves are shown, corresponding to g = 8, 6, 5
(from top to bottom). Note that the frequencies for high νext are
close to 1/4D (167, 125, and 83 Hz, respectively), while all curves
gather in the low νext region at around 20 Hz. In this region the
frequency essentially depends on the membrane time constant. For
short delays there is a large gap between slow and fast frequency
ranges, since these regions are well separated by the asynchronous
region. For large delays and g large enough, the frequency increases
continuously from the slow regime to the fast regime.
r Even a very small increase in the width of the dis-
tribution stabilizes the stationary state in the whole
low g region. Thus, in this whole region, the network
settles in a AR (asynchronous regular) state.
One might ask the question whether the irregularity
of the network dynamics is caused by the external
noise or by the intrinsic stochasticity generated by the
quenched random structure of the network. To check
that the irregularity in the AI and SI states is not an
effect of the external noise generated by the random
arrival of spikes through external synapses, the stabil-
ity region of the asynchronous state has been obtained
when the external input has no noise component (by
setting σext = 0). The comparison between noisy and
noiseless external inputs is shown in Fig. 5. It shows
that the region of stability of the AI (asynchronous ir-
regular) state is only weakly modified by the absence
of external noise. The CV in the AI region is also
only weakly modified by the removal of the external
noise. Numerical simulations confirm that in both AI
and SI regions single neurons show highly irregular
firing. Thus, the irregularity of spike trains in this re-
gion is an intrinsic effect of the random wiring of the
network.
= Conjecture

23. .
23
2 3 4 5 6
0.8
1
1.2
AR
500 520 560 580
0
0.5
SR
0
0.5
AI
500 520 560 580
0
0.5
SI
0
0.5
SO
0
0.05
0 200 400 600 800 1000 1200 1400
0
0.01
0 2 4 6 8
-10 100
102
10-6
10-3
(c)
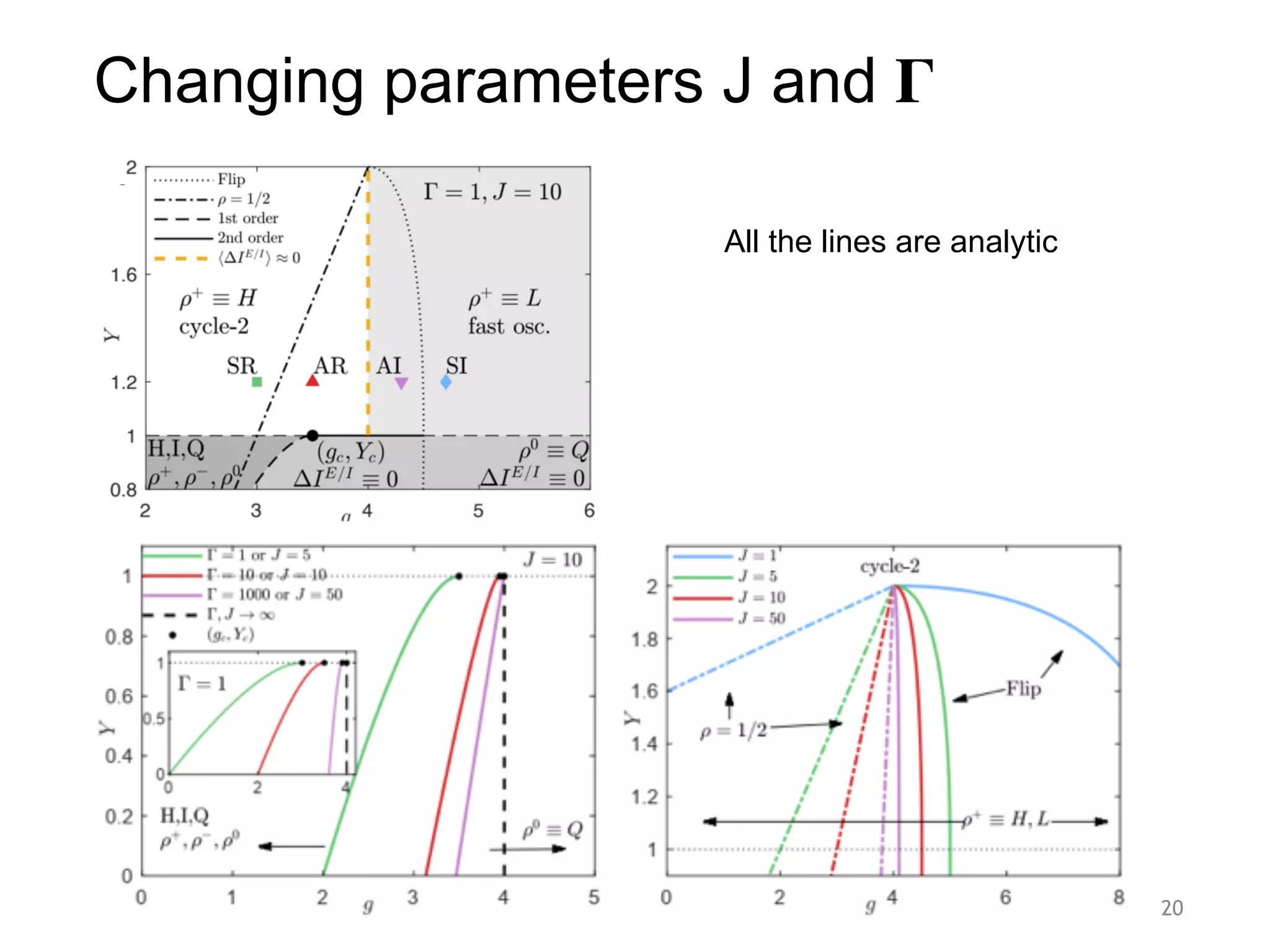
FIG. 2. Avalanches and firing patterns. (a) Phase diagram for µ = 0, and J = 10; a critical line starts at gc = 3.5, see Eq. (13), for Y = 1.
The critical point, the subcritical region with g > gFold; Y 1, and the supercritical region g = 4; Y > 1 have balanced synaptic currents, such
that the net current is IE/I
= IE
+ II
≈ 0. At Y = 1.2, from left to right: SR/cycle-2 (g = 3), AR/High (g = 3.5), AI/Low (g = 4.3), and
SI/fast oscillations (g = 4.7). SR and AR are separated by a bifurcation tho cycle-2 due to the refractory period; SI and AI are separated by
a flip bifurcation. (b) Distribution of avalanche sizes (main plot, τ = 1.5) and duration (bottom inset, τt = 2) at the critical point. Top inset:
size and duration scaling law s ∼ T a
has a crossover with a = 2.5 for small avalanches (a finite-size effect) and a = 2 for the rest of the
data. (c) Network simulation results (N = 106
neurons), ρ[t], for the points in (a). From the top left to the bottom right panel: critical point
absorbing-state avalanches (peaks); SR, AR, SO (slow waves for Y Yc = 1 − µ, µ = 0.9, Y = 0.101), SI, and AI. The background shows
the raster plot of 1,000 randomly selected neurons.
The variable ρ ≈ ρ1 = IE
/(pJ) is shown in the inset of
Fig. 1(b). These currents saturate for large enough J. This
linear scaling highlights the dynamic balance of synaptic
inputs, as inhibition tracks excitation over time [25,35].
Phase diagram. The soft threshold neurons’ phase diagram
is shown in Fig. 2(a). The curves are bifurcations of the stable
avalanches also respect the scaling law 1/(σνz) = (τt −
1)/(τ − 1) [inset in Fig. 2(b)], as expected for the DP uni-
versality class [30,36,37], and observed in experiments [38].
The simulated network activity in all the six dynami-
cal regimes is shown in Fig. 2(c). The critical point (gc =
3.5,Y = 1) displays avalanches sparked by a vanishing
PHYSICAL REVIEW RESEARCH 2, 012042(R) (2020)
6
R
R
AI
500 520 560 580
0
0.5
SI
0
0.5
SO
0
0.05
0
0 2 4 6 8
-10
-5
0
100
102
10-6
10-3
100
100
102
100
105
(b)
= 0, and J = 10; a critical line starts at gc = 3.5, see Eq. (13), for Y = 1.
Figure 8. Simulation of a network of 10,000 pyramidal cells and 2,500 interneurons, with connection probability 0.1 and JE = 0.1 mV. For
each of the four examples are indicated the temporal evolution of the global activity of the system (instantaneous firing frequency computed in
bins of 0.1 ms), together with the firing times (rasters) of 50 randomly chosen neurons. The instantaneous global activity is compared in each
SO
SISR
AI

24. Critical networks and
Balanced networks
• What is the relation between synaptic balance, balanced currents and critical networks?
• The DP critical point gc = p/q - 1/(q 𝚪J ) with power laws avalanches converges to the
synaptic balanced point gb = p/q = 4 in the large 𝚪J limit.
• Since Wc = 1/𝚪 and Wc = pJ - q gc J = IE
- II
, we have quasi-balanced currents:
IE
= II
+ 1/𝚪
• Not all critical networks are balanced, not all balanced networks are critical, but there exist
networks both critical and balanced (large 𝚪).
• What are the minimum requirements for SR, AR, AI, SI phases?
• Intrinsic noise, refractory period, finite variance for 𝚪i, Wij , Ii and 𝛉i. Continuous time,
leakage and network sparseness are not necessary to obtain the phases and the critical
point.
• Open question: There is a DP critical point in Brunel phase diagram? Exactly where?
24

25. Homeostatic mechanisms generate
(quasi-)critical and (quasi-)balanced networks
25
Quasi is nice!

26. Homeostatic set point
26
In the W,h coordinates:
W* = [Wc+A/(𝛕WuW)/(1+1/(𝛕WuW)]
h* = 1/(c 𝛕 𝛉 u 𝛉)2
In the g, Y coordinates:
g* = gc / (1+1/(𝛕WuW))
+1/q (p-A/J) / (1+𝛕WuW)
Y* = Yc [1-1/( I c𝛕 𝛉 u 𝛉)2]
For large separation of time scales
(𝛕W , 𝛕 𝛉 > 100 ms):
W*, h*, g*, Y* → Wc , hc , gc , Yc

27. The SOqC system hovers around the fixed point (a focus) due to finite
size noise (demographic noise). The variance of the oscillations
diminishes with N
27
AI

28. The time scale 𝛕 can be used to fit different experimental data
28
Version July 10, 2017 submitted to Entropy 10 of 16
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
τ = 2560
Ps(s)
s
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Ps(s)
τ =640 τ = 1280
τ = 160
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
s
τ = 5120
τ = 320
Ps(s)
Dragon kings
Bumps
Avalanches

29. Alternative homeostatic mechanisms
(only 𝛕 parameter)
• Wij[t+1] = Wij[t] + 1/𝛕 Wij[t] - Wij[t] Xj[t]
• Wij[t+1] = Wij[t] + 1/𝛕 - Wij[t] Xj[t]
• 𝚪i[t+1] = 𝚪i[t] + 1/𝛕 𝚪i - 𝚪i[t] Xi[t]
• 𝚪i[t+1] = 𝚪i[t] + 1/𝛕 - 𝚪i[t] Xi[t]
• 𝛉i[t+1] = 𝛉i[t] - 1/𝛕 + 𝛉i[t] Xi[t]
29

30. Conclusions …
• Homeostatic mechanisms in inhibitory synaptic weights + firing thresholds
-> SOqC fully compatible with the results of Ma et al. Cortical circuit
dynamics are homeostatically tuned to criticality in vivo, Neuron, (2019).
• SOqC = gross tuning of A, 𝛕W, 𝛕 𝛉, uW, u 𝛉 , not fine-tuning of g and Y (or W
and h).
• SOqC generates a fluctuation-driven AI-like spiking activity (stochastic
oscillations from a noise perturbed focus).
• The critical point gc (power-law avalanches) converges to the balanced
point gb (E/I synapses/currents) in the limit of hard LIF thresholds.
• We unified SOqC with Brunel phenomenology (fully ?).

31. … and Perspectives
(colaboration with Mauro Copelli group)
• Tawan T. A. Carvalho: Subsampling (in our model) explains
anomalous avalanche exponents of Fontenele et al. (2019).
• Jheni Gonsalves: Directed Percolation critical point and
avalanches found in the Potjans-Diesmann model!

32. 32
Contact:
okinouchi@gmail.com
Ludmila BrochiniAriadne A. Costa Maurício Girardi-Schappo Tawan T. A. Carvalho