1. Republica bolivariana de Venezuela
Ministerio del poder popular para la educación superior
Instituto universitario de tecnología
Antonio José de sucre
Ejercicios
Alumno
Morelia García CI:24.385.336

2. 1/ Hallar el área de la región encerradas por los gráficos
a) 푓(푥) = 푥2 − 4, 푔(푥) = 푥 − 4
y
y= x2 - 4
1 x
Y= x- 4
퐼푛푡푒푟푠푒푐푐푖표푛: 푥2 − 4 = 푋 − 4 → 푋2 − 푋 = 0
푋(푋 − 1) = 0
푋 = 0 ; 푋 = 1
1
퐴 = ∫ (푥 − 4) − ( 푥2
0
1
− 4) 푑푥 = ∫ 푋 − 4 − 푥2 + 4 푑푥
0
1
퐴 = ∫ 푋 − 푋2
0
푑푥 =
푥2
2
−
푋3
3
⃒ 푑푒 표 푎 1
퐴 =
12
2
−
13
3
표2
2
− [
−
표3
3
]
퐴 =
1
6
푈2

3. b) 푦 = 푥 3, 푦 = 4푥
푋3 = 4푋
푋3 − 4푋 = 0
푋 (푋2 − 4) = 0
푋 (푋 + 2)(푋 − 2) = 0
푋 = 0 ; 푋 = 2 ; 푋 = −2
Y=x3 Y=4x
-2 2 Y=
Solución:
퐴푇 = 2 퐴1
퐴1 → 0 ≤ 푋 ≤ 2; 푋3 ≤ 푌 ≤ 4푋
2
퐴1 = ∫ 4푋 − 푋3 푑푥
0
Integrando
퐴1 = 4
푋2
2
−
푋4
4
⃒ de 0 a 2
퐴1 = 2 (2)2 −
24
4
= 4 푢2
퐴푇 = 2 ∗ 4 푢2 ; 퐴푇 = 8 푢2

4. c) 푥 =
12
푦
, 푥 = 0, 푦 = 1, 푦 = 푒2
푋 =
12
푌
; 푋 = 0 ; 푌 = 0 ; 푌 = 푒2
Y
X=12/y
y=e2
y=1
x
Tipo II
퐴 = 1 ≤ 푌 ≤ 푒2 ; 0 ≤ 푋 ≤
12
푌
퐴 = ∫
12
푦
푒2
1
푑푦 = 12 ln〈푌〉 ⃒ 푑푒 1 푎 푒2
퐴 = 12 [푙푛 푒2 − ln(1)]
퐴 = 12 ∗ 2
퐴 = 24 푢2

5. d) 푓(푥) = tan
푥
2
, 푒푙 푒푗푒 푥 푦 푙푎푠 푟푒푐푡푎푠 푥 = 0, 푥 =
1
2
휋
A: Tipo I
0 ≤ 푋 ≤
휋
2
; 0 ≤ 푌 ≤ 푡푎푛
푋
2
y y=tan(x/2)
x=π/2 x
퐴 = ∫ 푡푎푛
푋
2
휋
2
0
푑푥 ; 퐶표푚표 ∫ 푇푎푛 퐾푥푑푥 =
1
퐾
ln 푆푒푐 퐾 푋 + 퐶
퐴 =
1
1
2
퐿푛 |푆푒푐
1
2
푥| ⃒ 푑푒 0 푎
휋
2
1
cos
퐴 = 2 [퐿푛 |
휋
4
| − Ln |
1
|]
cos(0)
퐴 = 2 퐿푛 |
1
√2
2
| = 2 퐿푛 2 = 퐿푛 √2
2
= 퐿푛 (2) 푢2

6. 2/ hallar el volumen del solido de revolución generado por la región encerrada por
las curvas dadas (utilice el método del disco, arandelas y cortezas cilíndricas)
a) Un arco de y=cos2x, alrededor del eje x
Solución
Método Disco
0 ≤ 푋 ≤
휋
4
; 0 ≤ 푌 ≤ cos 2푌
y y=cos2x
x
π/4
휋
4
푉 = 휋 ∫ (cos 2푋)2
0
푑푥 = 휋 ∫ [
1 + cos 4푋
2
]
휋
4
0
푑푥
푉 =
휋
2
∫
휋
4
0
푑푥 +
휋
2
휋
4
∫ cos 4푋
0
푑푥 =
휋
2
푋 +
휋
2
푠푒푛 4푋
4
⃒ 푑푒 0 푎
휋
4
푉 = [
휋
2
휋
4
(
) +
휋
8
푠푒푛 4
휋
4
] − [0 +
휋
8
푠푒푛 0] =
휋2
8

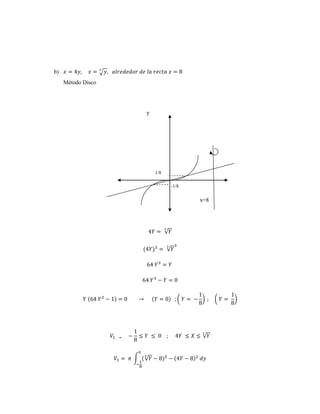
7. b) 푥 = 4푦, 푥 = √푦 3 , 푎푙푟푒푑푒푑표푟 푑푒 푙푎 푟푒푐푡푎 푥 = 8
Método Disco
y
1/8
-1/8
x=8
4푌 = √푌 3
(4푌)3 = √푌 3 3
64 푌3 = 푌
64 푌3 − 푌 = 0
푌 (64 푌2 − 1) = 0 → (푌 = 0) ; ( 푌 = −
1
8
) ; ( 푌 =
1
8
)
푉1 → −
1
8
≤ 푌 ≤ 0 ; 4푌 ≤ 푋 ≤ √푌 3
0
푉1 = 휋 ∫ ( √푌 3 − 8)2
−
1
8
− (4푌 − 8)2 푑푦

8. 푉1 = 휋 ∫ 푌
2
3
0
−
1
8
− 16 푌
1
3 + 64 − 16 푌2 + 64 푌 − 64 푑푦
푉1 = 휋 [
5
3
5
3
푌
− 16
4
3
4
3
푌
− 16
푌3
3
+ 64
푌2
2
] ⃒ 푑푒 −
1
8
푎 0
푉1 = 휋 {[0] − [
3
5
− (
1
8
5
⁄3
)
− 12 (−
1
8
4
⁄3
)
+ 32 (−
1
8
)2] −
−1
8
16 (
)3
3
}
푉1= 휋 [
3
160
+
3
4
−
1
96
−
1
2
] =
31
120
휋
푉2 → 0 ≤ 푌 ≤
1
8
; √푌 3 ≤ 푋 ≤ 4푌
1
8
푉2 = 휋 ∫ (4푌 − 8)2 − ( √푌 3 − 8)2
0
푑푦
푉2 = 휋 ∫ 16 푌2 − 64 푌 + 64 − 푌
2
3
1
8
0
− 16 푌
1
3 − 64 푑푦
푉2 = 휋 ∫ 16 푌2 − 64 푌 − 푌
2
3
1
8
0
− 16 푌
1
3 푑푦
푉2 = 휋 [16
푌3
3
− 64
푌2
2
−
5
3
5
3
푌
+ 16
4
3
4
3
푌
] ⃒ 푑푒 0 푎
1
8
푉2 = 휋 {
1
8
)3
3
16 (
1
8
− 32 (
)2 −
3
5
(
1
8
5
⁄3
)
1
8
+ 12 (
4
⁄3
)
− (0)}
푉2= 휋 [
1
96
−
1
2
−
3
160
+
3
4
] =
29
120
휋
푉푇=
31
120
휋 +
29
120
휋 =
휋
2
푢2

9. c) Hallar el volumen del sólido que se genera al rotar alrededor del eje x la
elipse
푥2
푎2 +
푦2
푏2 = 1
Capa Cilíndricas
Por Simetría
y
b
x
-a a
푉푇 = 2 푉1
푑표푛푑푒 푉1 푒푠푡푎 푑푎푑표 푝표푟
0 ≤ 푌 ≤ 푏 ; 0 ≤ 푋 ≤
푎
푏
√푏2 − 푌2
퐷푒푠푝푒푗푎푛푑표 푋:
푋2
푌2
= 1 −
푎2 푏2
푏2 − 푌2
푋2 = 푎2 [
푏2 ]
푎2
푏2 (푏2 − 푌2)) =
푋 = √(
푎
푏
√(푏2 − 푌2)
푉1 = 2휋 ∫ 푦 ∗
푎
푏
푏
0
√푏2 − 푌2 푑푦 = 2
푎
푏
푏
휋 ∫ 푦
0
√푏2 − 푌2 푑푦
Cambio de Variable
푢 = 푏2 − 푌2 ; 푑푢 = −2푌 푑푦 → −
푑푢
2
= 푌푑푦
푆푖 푌 = 푏 → 푢 = 0
푆푖 푌 = 0 → 푢 = 푏2

10. 푉1 = 2
푎
푏
휋 (
1
2
) ∫ 푢
1
2 푑푢 =
0
푏2
−
푎
푏
휋 [
3
2
3
2
푢
] 푑푒 푏2 푎 0
푽ퟏ = −
풂
풃
휋 ∗
2
3
[√03 − √(푏2)3] = −
풂
풃
휋 ∗
2
3
[−푏3] =
2
3
푎 푏2휋
푽푻 = ퟐ [
ퟐ
ퟑ
푎 푏2휋] =
4
3
푎 푏2휋
d) Hallar el volumen del sólido que genera la región encerrada por.
푦 = 4 − 푥2, 푒푗푒 푥, 푎푙 푔푖푟푎푟 푎푙푟푒푑푒푑표푟 푑푒 푙푎 푟푒푐푡푎 푥 = 3
y
x
X=3
푆푖 푌 = 0 ; 4 − 푋2 = 0 → 푋2 = 4 → √푋2 = √4 → |푋| = 2 → (푋 = −2); (푋 = 2)
Radio 푅(푋) = 3 − 푋 푀é푡표푑표 푑푒 푐표푟푡푒푧푎푠 퐶푖푙푖푛푑푟푖푐푎
푏
푉 = 2 휋 ∫ 푅(푋)
푎
[퐹(푋) − 퐺(푋)] 푑푥
2
푉 = 2 휋 ∫ (3 − 푋)
−2
[(4 − 푋2) − 0] 푑푥
2
푉 = 2 휋 ∫ (3 − 푋) (4 − 푋2)
−2
푑푥
2
푉 = 2 휋 ∫ 12 − 3푋2 − 4푋 + 푋3
−2
푑푥
푉 = 2 휋 [12푋 − 3
푋3
3
− 4
푋2
2
+
푋4
4
] 푑푒 − 2 푎 2

11. 푉 = 2 휋 {[12(2) − 23 − 2(2)2 +
(2)4
4
] − [12(−2) − (−2)3 − 2(−2)2 +
(−2)4
4
] }
푉 = 2 휋 [12 − (−20)]
푉 = 64 휋 푢3
3/ Hallar la longitud de la curva dada
a) 푦 =
푥3
6
+
1
2푥
, 푑푒푠푑푒 푥 = 1 ℎ푎푠푡푎 푥 = 3
푏
퐿 = ∫ √1 + 퐹′푥2
푎
푑푥
y
1 2 3
Derivando
푦′ =
3푥2
6
+
1
2
−1
푥2 ) =
(
푥2
2
−
1
2푥2 =
2푥4 − 2
4푥2
2푥4 − 2
4푥2 )2
3
퐿 = ∫ √1 + (
1
푑푥
퐿 = ∫ √1 +
4푥8 − 8푥4 + 4
16푥4
3
1
푑푥
16푥4 − 4푥8 − 8푥4 + 4
퐿 = ∫ √
16푥4
3
1
푑푥

12. 퐿 = ∫
√4푥8 + 8푥4 + 4
4푥2
3
1
푑푥
퐿 = ∫
√(2푥4 + 2)2
4푥2
3
1
푑푥 = ∫
2푥4 + 2
4푥2
3
1
푑푥
퐿 = ∫
1
2
3
1
푥2 +
1
2
푥−2 푑푥 =
1
2
푥3
3
+
1
2
푥−1
−1
⃒푑푒 1 푎 3
퐿 =
1
6
푥3 −
1
2푥
⃒ 푑푒 1 푎 3
퐿 = [
1
6
33 −
1
2(3)
] − [
1
6
−
1
2
] =
14
3
b) 푦 = 푙푛푠푒푐푥, 푑푒푠푑푒 푥 = 0, ℎ푎푠푡푎 푥 =
휋
3
푦 = ln(sec 푥) 퐷푒푠푑푒 푥 = 0 ℎ푎푠푡푎 푥 =
휋
3
y
휋
3
퐿 = ∫ √1 + ((ln sec 푥)′)2
0
푑푥
퐿 = ∫ √1 + [
1
sec 푥
∗ (푆푒푐 푥 ∗ 푡푔푥)]
2
휋
3
0
푑푥
휋
3
퐿 = ∫ √1 + 푡푔2푥
0
푑푥

13. 휋
3
퐿 = ∫ √sec2 푥
0
푑푥
휋
3
퐿 = ∫ sec2 푥
0
푑푥 = 푙푛|푆푒푐 푥 ∗ 푡푔푥| 푑푒 표 푎
휋
3
1
푐표푠
퐿 = 푙푛 |
휋
3
+
푠푒푛
휋
3
푐표푠
휋
3
| − ln |
1
푐표푠0
+
푠푒푛 0
푐표푠0
|
퐿 = ln |
1
1
2
+
√3
2
1
2
| − ln(1)
퐿 = ln(2 + √3)