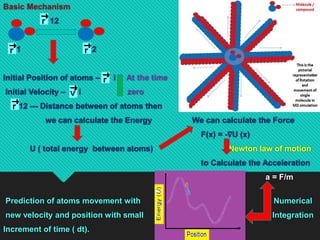
Molecular dynamics (MD) simulations calculate particle trajectories by integrating Newton's equations of motion. This document discusses the history and basic principles of MD, force fields, the NAMD simulation package, and applications. NAMD is a parallelized MD program for biomolecular simulations that uses spatial decomposition and multithreading. It supports features like CHARMM force fields, ensembles, and interactive modeling with VMD for structure visualization. MD simulations are useful for modeling protein structures, comparing protein templates, and predicting protein behavior through refinement of simulation approaches.

1. Molecular Dynamics
and NAMD simulation
PRESENTED BY – SHOAIB KHAN , B.PHARM
Research Intern
Nyro Research India
Zastra Innovations
Galgotias University

2. OVERVIEW
History
Introduction
Basic Mechanism/Principle
Types of MD
NAMD Simulation
Applications

3. MOLECULAR DYNAMICS
History
MD Simulation was firstly started from 1950 along with various successes
with Monte Carlo simulation .
In the back of 18th century themselves popularized for statistical
Mechanics ,in Buffon’s Needle Problem that known as Metropolis-
Hastings algorithm ( also known as Markov chain Monte Carlo method ).

4. In 1791 Verlet integration algorithm was used by Jean Baptiste
Delambre.
Now a day this is most common integration algorithm use that is
numerical method used to integrate Newton’s equations of motion and
that calculate the trajectories of particles in MD simulation and their
computer graphics.

5. Introduction
Molecular Dynamics is the integration of the
Newtonian Equation of motion ,trajectories of
Individual atoms and obtaining their thermo-
dynamics properties via using the principle of statistical mechanics .
That technique also used widely in the field of Computational biology.

6. Basic Mechanism
12
1 2
Initial Position of atoms – i At the time
Initial Velocity – i zero
12 --- Distance between of atoms then
we can calculate the Energy We can calculate the Force
F(x) = -∇U (x)
U ( total energy between atoms) Newton law of motion
to Calculate the Acceleration
a = F/m
Prediction of atoms movement with Numerical
new velocity and position with small Integration
Increment of time ( dt).

7. Force Field (FF)
Force field is the mathematically express the Energy in dependence
manner of a system on the coordinate of its particles.
It is composed in an analytical form of interatomic potential energy
U(r1,r2,r3….rN ) and a set of parameters that entering into this form.
These parameters generally obtained from either semi-empirical quantum
mechanical calculations or through fitting to the experimental data like
neutron, electron diffraction and X-ray , NMR , Raman ,infrared and
neutron spectroscopy, etc.
That defined the molecules are simply occur as a set of atoms which held
together simple elastic force like harmonic and the FF that replaces the
true potential with the help of simplified model that valid in the region of
being simulated.

8. CHARMM FORCE FIELD
Where ;
Kb – Bond force constant
b-b0 – is the distance from equilibrium that the atom has moved.
Kθ – angle force constant
θ-θ0 – is the angle from equilibrium between 3 bonded atoms.
kφ – dihedral force constant
φ– dihedral angle
δ– is the phase shift

9. n – the multiplicity of the function.
Kw – is the force constant.
w-w0 – out of plane angle.
Ku – respective force constant
U – is the distance between the 1,3 atoms in the harmonic potential.
In the last two term that represent the Non-bond interaction between
the pairs of atom (i,j).
Through definition , the non-bond force applied where the atoms pairs
should separated by at least 3 bonds.
To van Der Waal (VDW) energy that calculated from the standard 12-6
Lennard-Jones potential and Coulombic potential calculated with
electrostatic energy.
In the given equation of Rminij is not the minimum potential but rather
where Lennard-Jones potential cross the x-axis mean where the
Lennard-Jones potential become zero.

10. MD Simulation Packages
AMBER -- Assisted Model Building with Energy Refinement
GROMACS -- GROningen MAchine for Chemical Simulations
NAMD -- nanoscale molecular dynamics
GRACE – GRaphing , Advanced Computation and Exploration of data
VMD -- Visual Molecular Dynamics

11. NAMD (nanoscale molecular
dynamics)
NAMD is a molecular dynamic program that designed to high
performance simulation in a large Biomolecular system on parallel
computers.
For object-oriented design that using C++ to facilitates the
incorporation of new algorithm into the program.
This dynamic uses the spatial decomposition that coupled with
multithreaded programs that require to precise understanding of the
behavior of memory system in the respect of reading and writing
operation from their multiple processors.

12. NAMD features
NAMD perform various feature that necessary in molecular dynamics
simulation with MD package.
The features include are the following:
CHARMM19 and CHARMM22 parameter support,
NVE ensemble dynamics,
Langevin dynamics,
velocity rescaling,
harmonic atom restraints, file compatibility with X-PLOR and
energy minimization.
There is currently two form of boundaries condition that provided by
NAMD such as one is vacuum that is infinite vacuum to accessible
model and second one is a spherical boundary for the harmonic
potential to restrain the atoms within in given sphere by user-defined
radius.

13. Interactive Modeling
Interactive Modeling is a system consist the MDScope that perform the
interactive MD simulation.
In this modeling combines the molecular graphic program VMD in
computational power of NAMD that using communication package MDCOMM.
MDScope is an essential requirement of NAMD to high computation
performance that use ten femtoseconds of simulation for effective interactive
modeling during each second of viewing time.

14. Molecular graphic program
VMD
In the molecular graphic program VMD that showing not only flexibility of
static structure instead of that viewing and modification of running
simulation.
The key features of VMD are :-
1. They have flexibility selection of language to choosing atom subsets to a
variety of rendering and their coloring option.
2. It also showing the image in stereo by using a side byside format or it also
provide Crystal-Eyes stereo mode in the suitable equipped system.
3. It also contain a spatial tracking devices in supportive that provide a 3 D
pointer that accompany the user to interface in a stereo displaying
Environment.

15. Applications
It helps to design the theoretical model of protein structure.
It also helps to selection of those protein template regions that showing
reasonable degree of similarity in between of various 3D protein structures.
To the prediction of various numbers of conclusions by the refinement of
different MD approaches.
For the prediction process in last step in most cases that implies the
relaxation of structure by using normally molecular mechanics.

16. References
1. Bernal, J. D. (January 1997). "The Bakerian Lecture, 1962 The structure of
liquids". Proceedings of the Royal Society of London. Series A.
Mathematical and Physical Sciences. 280 (1382): 299–322.
2. La bildo estas kopiita de wikipedia:en. La originala priskribo estas:
Demonstration of Metropolis Hastings Algorithm.
3. Wang, Y., Harrison, C.B., Schulten, K. and McCammon, J.A., 2011.
Implementation of accelerated molecular dynamics in
NAMD. Computational science & discovery, 4(1), p.015002.
4. González, M.A., 2011. Force fields and molecular dynamics
simulations. École thématique de la Société Française de la
Neutronique, 12, pp.169-200.
5. https://www.ks.uiuc.edu/Training/Tutorials/science/forcefield-
tutorial/forcefield-html/node5.html

17. 6. Nelson, M.T., Humphrey, W., Gursoy, A., Dalke, A., Kalé, L.V., Skeel, R.D.
and Schulten, K., 1996. NAMD: a parallel, object-oriented molecular
dynamics program. The International Journal of Supercomputer
Applications and High Performance Computing, 10(4), pp.251-268.
7. https://snl.no/fysikkens_historie
8.
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4655909/#:~:text=Molecul
ar%20dynamics%20simulations%20have%20evolved,structure%2Dto%2Dfun
ction%20relationships.&text=Specific%20application%20of%20the%20techni
que,and%20structure%20refinement)%20is%20discussed.
9. Energy functions and their relationship to molecular conformation
CS/CME/BioE/Biophys/BMI 279 Sept. 22 and 24, 2020 Ron Dror .
10. https://youtu.be/ipRnvs7_CxA
11. https://www.sciencedirect.com/topics/computer-
science/multithreaded-program