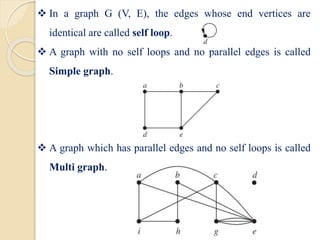
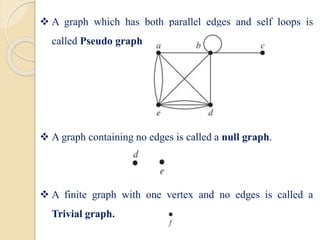
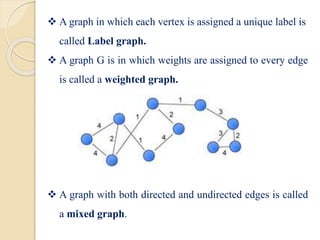
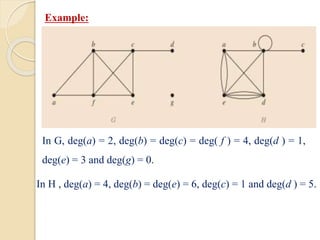
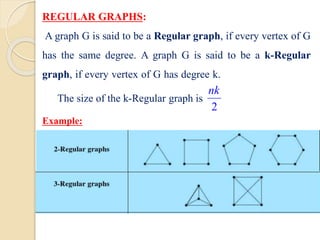
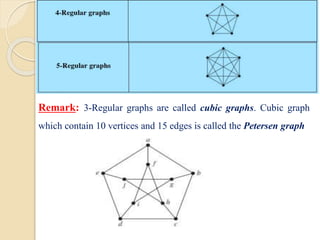
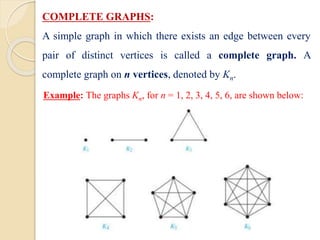
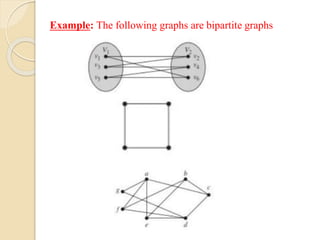
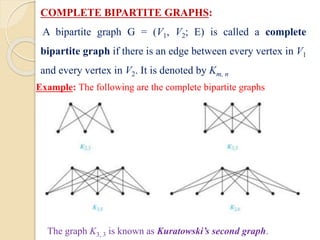
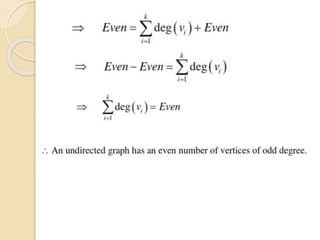This document serves as an introduction to graph theory, defining key concepts such as vertices, edges, types of graphs (directed, undirected), and various terminologies related to graph structures. It discusses properties of vertices, including degree, in-degree, and out-degree, and elaborates on specific types of graphs like regular, complete, bipartite, and weighted graphs. Additionally, it presents the handshaking theorem, which highlights relationships between vertex degrees and edges, as well as solving example problems related to these concepts.

1. Module - 5
Part – 1
Introduction to Graph Theory

2. Definition:
A graph G is a pair of finite sets (V, E), where
V = {v1 , v2 , ......, vn } is non empty set, whose elements are
called vertices (or nodes) and E = {e1 , e2 , ......, en } is a set
whose elements are called edges of G.
Each edge has either one or two vertices associated with it,
called its endpoints. An edge is said to connect its endpoints.
G
A graph with three vertices and
three edges.

3. ORDER AND SIZE OF A GRAPH:
In a finite graph G (V, E), the number of vertices
denoted by V (G) is called the order of the graph G and the
number of edges denoted by E (G) is called the size of the
graph G.
Example:
Remark: The set of vertices V of a graph G may be infinite. A
graph G (V, E) is called a finite graph if it has finite number
of vertices and edges. Otherwise it is called an infinite graph.

4. DIRECTED AND UNDIRECTED GRAPHS:
Let G (V, E) be a graph. If the elements of E are ordered pair of
vertices of G, then the Graph G is called a directed graph. Each
directed edge is associated with an ordered pair of vertices. The
directed edge associated with the ordered pair (u, v) is said to start at
u and end at v.
If the elements of E are unordered pair of vertices of G, then the
Graph G is called an undirected graph.

5. BASIC TERMINOLOGIES:
 Two vertices u and v in an undirected graph G are called
adjacent (or neighbors) in G if u and v are endpoints of
an edge e of G. Such an edge e is called incident with
the vertices u and v and e is said to connect u and v.
 In other words, if ‘v’ is an end vertex of an edge ‘e’ of
G, then e is an incident to the vertex v. Two vertices in a
graph are said to be adjacent, if they are the end vertices
of the same edge. Two parallel edges are said to be
adjacent edges, if they incident on a common vertex.

6.  The set of all neighbors of a vertex v of G = (V, E),
denoted by N (v), is called the neighborhood of v. If A is a
subset of V, we denote by N (A) the set of all vertices in G
that are adjacent to at least one vertex in A.
 In a directed graph G, when (u, v) is an edge, u is said to be
adjacent to v and v is said to be adjacent from u. The
vertex u is called the initial vertex of (u, v), and v is called
the terminal or end vertex of (u, v). The initial vertex and
terminal vertex of a loop are the same.
 In a graph G (V, E),the edges having the same pair of end
vertices are called parallel edges or multiple edges.

7.  In a graph G (V, E), the edges whose end vertices are
identical are called self loop.
 A graph with no self loops and no parallel edges is called
Simple graph.
 A graph which has parallel edges and no self loops is called
Multi graph.

8.  A graph which has both parallel edges and self loops is
called Pseudo graph.
 A graph containing no edges is called a null graph.
 A finite graph with one vertex and no edges is called a
Trivial graph.

9.  A graph in which each vertex is assigned a unique label is
called Label graph.
 A graph G is in which weights are assigned to every edge
is called a weighted graph.
 A graph with both directed and undirected edges is called
a mixed graph.

10. DEGREE OFA VERTEX:
The degree of a vertex in an undirected graph is the number
of edges incident with it, except that a loop at a vertex
contributes twice to the degree of that vertex. The degree of
the vertex v is denoted by deg (v).
 If the degree of vertex v is zero, then v is called an
isolated vertex.
 If the degree of vertex v is one, then v is called pendent
vertex.
 A vertex in a graph G is said to be even or odd vertex
according as its degree is an even or odd number.

11. Example:
In G, deg(a) = 2, deg(b) = deg(c) = deg( f ) = 4, deg(d ) = 1,
deg(e) = 3 and deg(g) = 0.
In H , deg(a) = 4, deg(b) = deg(e) = 6, deg(c) = 1 and deg(d ) = 5.

12. IN-DEGREE AND OUT-DEGREE:
In a directed graph, the in-degree of a vertex v, denoted by
deg- (v), is the number of edges with v as their terminal
vertex. The out-degree of v, denoted by deg+ (v), is the
number of edges with v as their initial vertex.
(Note that a loop at a vertex contributes 1 to both the
in-degree and the out-degree of this vertex.)
Example: The in-degrees in G are deg- (a) = 2, deg- (b) = 2,
deg- (c) = 3, deg- (d) = 2, deg- (e) = 3 and
deg- ( f ) = 0.
The out-degrees in G are deg+ (a) = 4, deg+ (b) =
1, deg+ (c) = 2, deg+ (d) = 2, deg+ (e) = 3 and
deg+ ( f ) = 0.

13. REGULAR GRAPHS:
A graph G is said to be a Regular graph, if every vertex of G
has the same degree. A graph G is said to be a k-Regular
graph, if every vertex of G has degree k.
The size of the k-Regular graph is
2
nk
Example:

14. Remark: 3-Regular graphs are called cubic graphs. Cubic graph
which contain 10 vertices and 15 edges is called the Petersen graph

15. COMPLETE GRAPHS:
A simple graph in which there exists an edge between every
pair of distinct vertices is called a complete graph. A
complete graph on n vertices, denoted by Kn.
Example: The graphs Kn, for n = 1, 2, 3, 4, 5, 6, are shown below:

16. The graph K5 is known as Kuratowski’s first graph.
A simple graph for which there is at least one pair of distinct
vertex not connected by an edge is called noncomplete.
BIPARTITE GRAPHS:
A simple graph G is called bipartite if its vertex set V can be
partitioned into two disjoint sets V1 and V2 such that every
edge in the graph connects a vertex in V1 and a vertex in V2.
i.e., no edge in G connects either two vertices in V1 or two
vertices in V2.

17. Example: The following graphs are bipartite graphs

18. COMPLETE BIPARTITE GRAPHS:
A bipartite graph G = (V1, V2; E) is called a complete
bipartite graph if there is an edge between every vertex in V1
and every vertex in V2. It is denoted by Km, n
Example: The following are the complete bipartite graphs
The graph K3, 3 is known as Kuratowski’s second graph.

19. THE HANDSHAKING THEOREM:
The sum of degrees of all the vertices in a graph is an even
number. This number is equal to twice the number of edges in
the graph. That is, for any undirected graph G = (V, E),
 
1
deg 2
n
i
i
v E
=
=

Proof:
Every edge of G incident with two vertices.
 Every edge of G contributes 2 to the sum of degrees of
vertices of G
i.e., Every edge of G contributes 2 to the  
1
deg
n
i
i
v
=


20. Note: This property is called hand shaking property
because every people shake hands, then total number
of hands shaken must be even. This property is also known
as the first theorem of graph theory.

21. Theorem: An undirected graph has an even number of
vertices of odd degree.
(By using hand shaking
theorem)

23. Determine 𝑉 for the graph 𝐺 = (𝑉, 𝐸) in the following cases:
a) G has 9 edges and all the vertices of degree 3
b) G has 10 edges with two vertices of degree 4 and the others
of degree 3.
c) G is a cubic graph with 9 edges.
d) G is a regular graph with 15 edges.
e) 16 edges and all vertices of degree 4.
f) 21 edges, 3 vertices of degree 4 and other vertices of degree
3.
g) 12 edges, 6 vertices of degree 3 and other vertices of degree
less than 3.

24. ⇒ 3 + 3 + ⋯ 𝑛 𝑡𝑖𝑚𝑒𝑠 = 2(9)
⇒ 3𝑛 = 18
⇒ 𝑛 = 6
Therefore, 𝑉 = 6.
By data, deg 𝑣1 = deg 𝑣2 = ⋯ = deg 𝑣𝑛 = 3, 𝐸 = 9.
To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

a) G has 9 edges and all the vertices of degree 3

25. ⇒ 4 + 4 + 3 + 3 + ⋯ + (𝑛 − 2) 𝑡𝑖𝑚𝑒𝑠 = 2(10)
⇒ 3 𝑛 − 2 = 20 − 8
⇒ 𝑛 − 2 = 4
⇒ 𝑛 = 6
Therefore, 𝑉 = 6.
By data, 𝑑𝑒𝑔 𝑣1 = deg 𝑣2 = 4, deg 𝑣3 = ⋯ = deg 𝑣𝑛 = 3,
𝐸 = 10. To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

b) G has 10 edges with two vertices of degree 4 and the others
of degree 3.

26. ⇒ 3 + 3 + ⋯ + 𝑛 𝑡𝑖𝑚𝑒𝑠 = 2(9)
⇒ 3𝑛 = 18
⇒ 𝑛 = 6
Therefore, 𝑉 = 6.
By data, deg 𝑣1 = deg 𝑣2 = ⋯ = deg 𝑣𝑛 = 3, 𝐸 = 9.
To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

c) G is a cubic graph with 9 edges.

27. ⇒ 𝑘 + 𝑘 + ⋯ + 𝑛 𝑡𝑖𝑚𝑒𝑠 = 2(15)
⇒ 𝑘𝑛 = 30
⇒ 𝑛 = 30/𝑘
Possible values of 𝑘 = 1,2,3,5, 6, 10, 15, 30
Possible values of 𝑛 = 30, 15, 10, 6, 5, 3, 2, 1
 𝑉 = 30 𝑜𝑟 15 𝑜𝑟 10 𝑜𝑟 6 𝑜𝑟 5 𝑜𝑟 3 (𝑜𝑟) 2 (𝑜𝑟) 1
By data, deg 𝑣1 = deg 𝑣2 = ⋯ = deg 𝑣𝑛 = 𝑘, 𝐸 = 15.
To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

d) G is a regular graph with 15 edges.

28. ⇒ 4 + 4 + ⋯ + 𝑛 𝑡𝑖𝑚𝑒𝑠 = 2(16)
⇒ 4𝑛 = 32
⇒ 𝑛 = 8
Therefore, 𝑉 = 8
By data, deg 𝑣1 = deg 𝑣2 = ⋯ = deg 𝑣𝑛 = 4, 𝐸 = 16.
To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

e) 16 edges and all vertices of degree 4.

29. ⇒ 4 + 4 + 4 + 3 + 3 + ⋯ + (𝑛 − 3) 𝑡𝑖𝑚𝑒𝑠 = 2(21)
⇒ 3 𝑛 − 3 = 42 − 12
⇒ 𝑛 − 3 = 10
⇒ 𝑛 = 13
Therefore, 𝑉 = 13
By data, 𝑑𝑒𝑔 𝑣1 = deg 𝑣2 = deg 𝑣3 = 4, deg 𝑣4 = ⋯ = deg 𝑣𝑛 =
3, 𝐸 = 21. To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

f) 21 edges, 3 vertices of degree 4 and other vertices of degree 3.

30. By data,
deg 𝑣1 = deg 𝑣2 = ⋯ = deg 𝑣6 = 3, deg 𝑣7 < 3, … deg 𝑣𝑛 < 3
𝐸 = 12. To find 𝑉 =?
By hand shaking theorem, we
have
 
1
deg 2
n
i
i
v E
=
=

g) 12 edges, 6 vertices of degree 3 and other vertices of degree less than 3.
⇒ 3 6 + 3 𝑛 − 6 > 2(12)
⇒ 3𝑛 > 24
⇒ 𝑛 > 8
Therefore, 𝑉 is at least 9.

31. Show that there is no graph with 28 edges and 12 vertices in
the following cases:
(a) The degree of a vertex is either 3 or 4
(b) The degree of a vertex is either 3 or 6
(a) By data, 𝑛 = 12, 𝐸 = 28.
By hand shaking property, we have
⇒ 3𝑘 + 4 𝑛 − 𝑘 = 2|𝐸|
⇒ 3𝑘 + 4 12 − 𝑘 = 2(28)
⇒ 𝑘 = −8, which is impossible.
Therefore, there is no such graph.
 
1
deg 2
n
i
i
v E
=
=


32. Show that there is no graph with 28 edges and 12 vertices in
the following cases:
(a) The degree of a vertex is either 3 or 4
(b) The degree of a vertex is either 3 or 6
(b) By data, 𝑛 = 12, 𝐸 = 28.
By hand shaking property, we have
⇒ 3𝑘 + 6 𝑛 − 𝑘 = 2|𝐸|
⇒ 3𝑘 + 6 12 − 𝑘 = 2(28)
⇒ 𝑘 = 16/3, which is impossible.
Therefore, there is no such graph.
 
1
deg 2
n
i
i
v E
=
=


33. Show that in a complete graph of n vertices
a) Degree of every vertex is 𝑛 − 1
b) The total number of edges is
𝑛 𝑛−1
2
(a) In a complete graph of n vertices, each edge is incident
with n -1 edges.
Therefore, degree of every vertex is 𝑛 − 1.
(b) By hand shaking property, we have
⇒ 𝑛 − 1 + 𝑛 − 1 + ⋯ 𝑛 𝑡𝑖𝑚𝑒𝑠 = 2 𝐸 .
⇒ 𝑛 𝑛 − 1 = 2 𝐸
⇒ 𝐸 =
𝑛 𝑛−1
2
.
 
1
deg 2
n
i
i
v E
=
=
