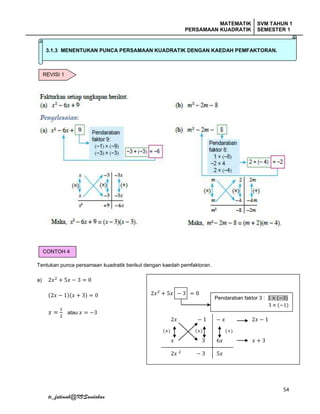
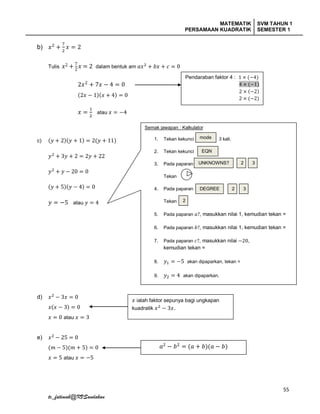
Dokumen ini membincangkan tentang persamaan kuadratik dalam satu pemboleh ubah, termasuk ciri-ciri, maksud punca, dan kaedah penyelesaian melalui pemfaktoran. Pelbagai aktiviti dan contoh disediakan untuk membantu pelajar memahami cara mengenal pasti dan menyelesaikan ungkapan kuadratik. Terdapat juga masalah berbentuk praktikal yang memerlukan pelajar untuk memformulasi dan menyelesaikan persamaan kuadratik.

1. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
46
tc_fatimah@KVSandakan
UNIT 3.0 : PERSAMAAN KUADRATIK DALAM SATU
PEMBOLEH UBAH
Objektif Am : Mempelajari serta mengetahui cara-cara menyelesaikan masalah yang
melibatkan persamaan kuadratik.
Objektif Khusus : 3.1.1 Mengenal pasti dan menerangkan ciri-ciri ungkapan kuadratik
dalam satu pemboleh ubah.
3.1.2 Menerangkan maksud punca suatu persamaan kuadratik.
3.1.3 Menentukan punca suatu persamaan kuadratik dengan kaedah
pemfaktoran.
3.1.4 Menyelesaikan masalah yang melibatkan persamaan kuadratik.

2. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
47
tc_fatimah@KVSandakan
3.1 PERSAMAAN KUADRATIK
UNGKAPAN KUADRATIK
1. Ungkapan kuadratik dalam satu pemboleh ubah ialah ungkapan yang berbentuk 𝑎𝑥2
+ 𝑏𝑥 + 𝑐,
dengan a, b dan c sebagai pemalar, a ≠ 0 dan x sebagai pemboleh ubah.
2. Ciri-ciri ungkapan kuadratik dalam satu pemboleh ubah:
(a) Kuasa tertinggi bagi x ialah 2.
(b) Hanya mengandungi satu pemboleh ubah.
Contoh :
(i) 3𝑥2
+ 5 (iii) 2𝑚2
+ 4𝑚 + 7
(ii) 2𝑥2
− 3𝑥 (iv) −2𝑦2
Tentukan sama ada setiap yang berikut ialah ungkapan kuadaratik dalam satu pemboleh ubah atau
bukan. Nyatakan sebabnya.
a) 2𝑦2
+ 4
b) 𝑚4
+ 4𝑚2
+ 7
c) 𝑚2
+ 4𝑛 +
1
5
d) 2(𝑚2
− 1)
3.1.1 MENGENAL PASTI DAN MENERANGKAN CIRI-CIRI UNGKAPAN KUADRATIK DALAM SATU
PEMBOLEH UBAH.
CONTOH 1
Ungkapan kuadratik, satu pemboleh ubah 𝑦, 𝑏 = 0 dan
𝑐 = 4.
Bukan ungkapan kuadratik, kuasa tertinggi bagi 𝑚 𝑖alah 4.
Bukan ungkapan kuadratik, lebih dari satu pemboleh ubah,
𝑚 dan 𝑛.

3. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
48
tc_fatimah@KVSandakan
Objektif : Mengenal pasti ungkapan kuadratik.
Langkah-langkah : 1. Bentukkan kumpulan yang terdiri daripada empat orang.
2. Lengkapkan jadual di bawah secara berpasangan.
3. Bandingkan keputusan dengan pasangan yang lain dalam kumpulan.
Ungkapan Kuasa tertinggi
pemboleh ubah
Bilangan
pemboleh ubah
Adakah ini suatu ungkapan kuadratik?
𝑥2
– 4𝑥 + 3
8𝑝2
+ 10
5𝑥 + 6
2𝑥2 + 4𝑦 + 14
16 − 𝑡2
−3𝑥2
𝑚2
+ 4𝑚
3(𝑝2
+ 4)
1
𝑥2
+ 4𝑥 − 1
Objektif : Mengenal pasti nilai pemalar, 𝑎, 𝑏, dan 𝑐.
Langkah-langkah : 1. Lakukan aktiviti ini secara berpasangan.
2. Lengkapkan jadual di bawah.
3. Tentukan sama ada terdapat ungkapan kuadratik yang mempunyai nilai
pemalar
(i) 𝑎 = 0 (ii) 𝑏 = 0 atau 𝑐 = 0
4. Tentukan sama ada terdapat ungkapan kuadratik yang mempunyai nilai
pemalar
(i) 𝑏 = 0 (ii) 𝑐 = 0 (iii) 𝑏 = 𝑐 = 0
Ungkapan
kuadratik
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 𝑎 𝑏 𝑐
2 − 2𝑥 + 3𝑥2
3𝑥2
− 2𝑥 + 2 3 −2 2
5𝑥 − 6𝑥2
8 + 2𝑥2
3𝑥2
3𝑥(𝑥 − 4)
PENEROKAAN 1
PENEROKAAN 2

4. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
49
tc_fatimah@KVSandakan
PERSAMAAN KUADRATIK
1. Persamaan kuadratik ialah satu persamaan algebra yang mempunyai ciri-ciri berikut:
(a) Terdapat hanya satu pemboleh ubah,
(b) Kuasa tertinggi pemboleh ubah ialah 2,
(c) Terdapat tanda kesamaan, ‘=’.
2. Persamaan kuadratik dalam bentuk am
𝑎, 𝑏 dan 𝑐 ialah pemalar,𝑎 ≠ 0 dan 𝑥 ialah pemboleh ubah.
Cik Emi merancang untuk membuat dua jenis kad untuk digunakan dalam aktiviti Kelab Matematik. Ukuran
bagi kad-kad tersebut adalah seperti yang ditunjukkan dalam rajah di bawah.
a) Bentuk satu ungkapan kuadratik bagi jumlah luas kedua-dua kad ini, L cm2
, dalam sebutan 𝑥.
b) Diberi jumlah luas kedua-dua kad ialah 114 cm2
, bentuk satu persamaan kuadratik dalam sebutan 𝑥.
Penyelesaian
a) L = 𝑥2
+ 𝑥(2𝑥 + 1) b) 3𝑥2
+ 𝑥 = 114
= 𝑥2
+ 2𝑥2
+ 𝑥 3𝑥2
+ 𝑥 − 114 = 0
= 3𝑥2
+ 𝑥
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0
CONTOH 2
𝑥 𝑐𝑚
𝑥 𝑐𝑚 𝑥 𝑐𝑚
(2𝑥 + 1) 𝑐𝑚

5. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
50
tc_fatimah@KVSandakan
No. Soalan Penyelesaian
1 Panjang sebuah segi empat tepat melebihi
lebarnya sebanyak 3 cm. Diberi bahawa luas
segi empat tepat itu ialah 130 cm2
.
2 Luas segi empat tepat P ialah 8 cm2
lebih
besar daripada luas segi empat tepat Q.
1. Nilai-nilai bagi pemboleh ubah yang memuaskan suatu persamaan kuadratik dikenali sebagai punca-
punca bagi persamaan kuadratik tersebut.
Tujuan: Menentukan nilai pemboleh ubah yang memuaskan suatu persamaan kuadratik.
Langkah:
1. Lengkapkan jadual di bawah. Seterusnya, kenal pasti nilai-nilai x yang memuaskan persamaan
kuadratik yang diberikan.
LATIHAN 1
3.1.2 MENERANGKAN MAKSUD PUNCA SUATU PERSAMAAN KUADRATIK.
P
Q(𝑥 + 3) 𝑐𝑚
8 𝑐𝑚
(𝑥 − 1) 𝑐𝑚
(𝑥 + 2) 𝑐𝑚
PENEROKAAN 3
𝑥2
− 3𝑥 + 2 = 0
Nilai 𝑥 Nilai 𝑥2
− 3𝑥 + 2
0 (0)2
− 3(0) + 2 = 2
1 0
2 0
3 2
4 6
Nilai 𝑥 ialah 1, 2
𝑥2
− 5𝑥 + 4 = 0
Nilai 𝑥
0
1
2
3
4
Nilai 𝑥 ialah

6. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
51
tc_fatimah@KVSandakan
2. Perbincangan: Bagaimanakah anda dapat menentukan nilai pemboleh ubah yang memuaskan suatu
persamaan kuadratik?
Kesimpulan : 1. Terdapat satu atau dua nilai pemboleh ubah yang memuaskan suatu persamaan kuadratik.
2. Nilai-nilai pemboleh ubah yang memuaskan suatu persamaan kuadratik dikenali sebagai
punca bagi persamaan kuadratik tersebut.
𝑥2
− 2𝑥 + 1 = 0
Nilai 𝑥
0
1
2
3
4
Nilai 𝑥 ialah
𝑥2
+ 𝑥 − 2 = 0
Nilai 𝑥
0
1
2
3
4
Nilai 𝑥 ialah
𝑥2
+ 2𝑥 − 2 = 1
Nilai 𝑥
0
1
2
3
4
Nilai 𝑥 ialah
𝑥2
− 4𝑥 + 5 = 2
Nilai 𝑥
0
1
2
3
4
Nilai 𝑥 ialah

7. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
52
tc_fatimah@KVSandakan
Tentukan sama ada setiap nilai berikut merupakan punca bagi persamaan kuadratik yang diberikan atau
bukan.
a) 2𝑥2
− 7𝑥 + 3 = 0; 𝑥 = 1, 𝑥 = 3
(i) 𝑥 = 1
Kiri: Kanan:
2( )2
− 7( ) + 3 0
(ii) 𝑥 = 3
Kiri: Kanan:
2( )2
− 7( ) + 3 0
b) 3𝑥2
− 7𝑥 + 5 = 3; 𝑥 = 1, 𝑥 =
1
3
(i) 𝑥 = 1
Kiri: Kanan:
3( )2
− 7( ) + 5 3
(ii) 𝑥 =
1
3
Kiri: Kanan:
3( )2
− 7( ) + 5 3
c) Tentukan sama ada setiap nilai yang berikut ialah punca persamaan kuadaratik 3𝑥2
+ 10𝑥 − 8 = 0 atau
tidak.
(i) 𝑥 = 4 (ii) 𝑥 = −2 (iii) 𝑥 =
2
3
CONTOH 3

8. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
53
tc_fatimah@KVSandakan
Tentukan sama ada setiap nilai berikut merupakan punca bagi persamaan kuadratik yang diberikan atau
bukan.
a) 2𝑥2
+ 2𝑥 − 24 = 0; 𝑥 = 3
𝑥 = 3
Kiri: Kanan:
b) 𝑥2
= 5𝑥 − 7; 𝑥 = −1
𝑥 = −1
Kiri: Kanan:
c) (2𝑛 + 1)(𝑛 + 2) = 5; 𝑥 =
1
2
𝑥 =
1
2
Kiri: Kanan:
d) (𝑥 − 1)(𝑥 + 4) = 0; 𝑥 = 2
𝑥 = 2
Kiri: Kanan:
e) 2(𝑥 − 3)(𝑥 − 5) = 0; 𝑥 = 5
𝑥 = 5
Kiri: Kanan:
f) 𝑥2
− 3𝑥 + 2 = 0; 𝑥 = 1
𝑥 = 1
Kiri: Kanan:
LATIHAN 2

9. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
54
tc_fatimah@KVSandakan
Tentukan punca persamaan kuadratik berikut dengan kaedah pemfaktoran.
a) 2𝑥2 + 5𝑥 − 3 = 0
(2𝑥 − 1)(𝑥 + 3) = 0
𝑥 =
1
2
atau 𝑥 = −3
2𝑥2 + 5𝑥 − 3 = 0
3.1.3 MENENTUKAN PUNCA PERSAMAAN KUADRATIK DENGAN KAEDAH PEMFAKTORAN.
REVISI 1
Pendaraban faktor 3 : 1 × (−3)
3 × (−1)
2𝑥 − 1 − 𝑥 2𝑥 − 1
𝑥 3 6𝑥 𝑥 + 3
2𝑥 2
− 3 5𝑥
(×) (×) (+)
CONTOH 4

10. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
55
tc_fatimah@KVSandakan
b) 𝑥2
+
7
2
𝑥 = 2
Tulis 𝑥2 + 7
2
𝑥 = 2 dalam bentuk am 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0
2𝑥2
+ 7𝑥 − 4 = 0
(2𝑥 − 1)(𝑥 + 4) = 0
𝑥 =
1
2
atau 𝑥 = −4
c) (𝑦 + 2)(𝑦 + 1) = 2(𝑦 + 11)
𝑦2
+ 3𝑦 + 2 = 2𝑦 + 22
𝑦2
+ 𝑦 − 20 = 0
(𝑦 + 5)(𝑦 − 4) = 0
𝑦 = −5 atau 𝑦 = 4
d) 𝑥2
− 3𝑥 = 0
𝑥(𝑥 − 3) = 0
𝑥 = 0 atau 𝑥 = 3
e) 𝑥2
− 25 = 0
(𝑚 − 5)(𝑚 + 5) = 0
𝑥 = 5 atau 𝑥 = −5
Pendaraban faktor 4 : 1 × (−4)
4 × (−1)
2 × (−2)
2 × (−2)
Semak jawapan : Kalkulator
1. Tekan kekunci 3 kali.
2. Tekan kekunci
3. Pada paparan
Tekan
4. Pada paparan
Tekan
5. Pada paparan 𝑎?, masukkan nilai 1, kemudian tekan =
6. Pada paparan 𝑏?, masukkan nilai 1, kemudian tekan =
7. Pada paparan 𝑐?, masukkan nilai −20,
kemudian tekan =
8. 𝑦1 = −5 akan dipaparkan, tekan =
9. 𝑦2 = 4 akan dipaparkan.
mode
EQN
e
UNKNOWNS? 2 3
DEGREE 2 3
2
𝑥 ialah faktor sepunya bagi ungkapan
kuadratik 𝑥2
− 3𝑥.
𝑎2
− 𝑏2
= (𝑎 + 𝑏)(𝑎 − 𝑏)

11. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
56
tc_fatimah@KVSandakan
1. Tentukan punca bagi setiap persamaan kuadratik berikut dengan kaedah pemfaktoran.
a) 𝑥2
− 3𝑥 − 10 = 0 b) 3𝑥2
− 5𝑥 + 2 = 0
c) 2𝑥2
+ 8𝑥 − 24 = 0 d) 2𝑥2
+ 3𝑥 − 9 = 0
e) 4𝑥2
− 3𝑥 − 10 = 0 f) −3𝑥2
− 𝑥 + 14 = 0
g) 𝑥2
− 5𝑥 = 0 h) 𝑥2
− 4 = 0
LATIHAN 3

12. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
57
tc_fatimah@KVSandakan
2. Tulis setiap persamaan kuadratik yang berikut dalam bentuk am. Seterusnya selesaikan persamaan
kuadratik tersebut.
a) 𝑚(𝑚 + 2) = 3 b) 3𝑝(11 − 2𝑝) = 15
c)
1
2
𝑦2
= 12 − 𝑦 d) 𝑎 +
5
𝑎
= 6
e)
8
𝑘
= 2 + 𝑘 f) (ℎ − 2)(ℎ − 1) = 12
g) (2𝑥 − 1)2
= 3𝑥 − 2 h) (𝑟 + 1)(𝑟 + 9) = 16𝑟

13. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
58
tc_fatimah@KVSandakan
Marina ingin membuat rangka sebuah kotak berbentuk kuboid dengan menggunakan rod kayu. Harga rod
kayu ialah RM5 per meter. Tapak kuboid tersebut berbentuk segi empat sama. Tinggi kuboid ialah 30 cm
lebih daripada panjang tapak. Jumlah luas permukaan kotak ini ilah 4 800 cm2
. Bajet Marina untuk
membina rangka sebuah kotak ialah RM15. Tentukan sama ada Marina mempuyai bajet yang mencukupi
atau tidak.
Penyelesaian
3.1.4 MENYELESAIKAN MASALAH YANG MELIBATKAN PERSAMAAN KUADRATIK.
CONTOH 5
Panjang tapak = 𝑥 cm
Tinggi kuboid = (𝑥 + 30) cm
Jum. luas permukaan = 4 800 cm2
Bajet = RM15 sebuah kotak
Memahami masalah
 Tentukan ungkapan
luas permukaan kuboid.
 Bentuk persamaan
kuadratik.
 Selesaikan persamaan
kuadratik berkenaan.
 Tentukan ukuran kotak
dan bajet.
Merancang strategi
𝑥 cm
(𝑥+30)cm
Jum. luas permukaan = 2(𝑥)(𝑥) + 4(𝑥)(𝑥 + 30)
= 2𝑥2
+ 4𝑥2
+ 120𝑥
= 6𝑥2 + 120𝑥
6𝑥2
+ 120𝑥 = 4 800
6𝑥2
+ 120𝑥 − 4 800 = 0
𝑥2
+ 20𝑥 − 800 = 0
(𝑥 + 40)(𝑥 − 20) = 0
𝑥 = −40 atau 𝑥 = 20
𝑥 = −40 tidak diterima, maka 𝑥 = 20.
Marina tidak mempunyai bajet yang mencukupi untuk membina rangka kotak itu.
Melaksanakan strategi
Ukuran kotak ialah 20 cm × 20 cm × 20 cm
Panjang sisi kotak
= 8 × 20 cm + 4 × 20 cm
= 360 cm
= 3.6 m
Bajet = RM15 × 3.6 = RM18
Kesimpulan

14. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
59
tc_fatimah@KVSandakan
Selesaikan setiap masalah yang berikut.
1. Sebuah segi tiga mempunyai panjang tapak 𝑥 cm dan tinggi (𝑥 − 3) cm. Diberi luas segi tiga itu ialah
54 cm2
,
a) Bentukkan satu persamaan kuadratik
b) Cari nilai 𝑥 c) Nyatakan tinggi segi tiga itu
2. Rajah berikut menunjukkan segi empat tepat 𝐴𝐵𝐶𝐷.
Perimeter segi empat tepat itu ialah 220 cm. Jika panjang dan luas bagi segi empat tepat itu masing-
masing ialah 𝑥 cm dan 3000 cm2
,
a) Bentukkan satu persamaan kuadratik
b) Cari nilai 𝑥 c) Nyatakan panjang dan lebar segi empat
tersebut.
LATIHAN 4
𝑥 cm
𝐴 𝐵
𝐷𝐶

15. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
60
tc_fatimah@KVSandakan
3. Sebuah segi segi empat tepat mempunyai panjang 8 cm lebih daripada lebarnya, x cm. Jika luas segi
empat tepat itu ialah 209 cm2
,
a) Bentukkan satu persamaan kuadratik
b) Cari nilai 𝑥 c) Nyatakan perimeter segi empat tepat tersebut
4. Rajah berikut menunjukkan segi empat tepat 𝐴𝐵𝐶𝐷 dan 𝐸𝐹𝐺𝐻.
Diberi bahawa kedua-dua segi empat tepat itu mempunyai luas yang sama.
a) Bentukkan satu persamaan kuadratik
b) Cari nilai 𝑥
(2𝑥 + 4) m𝐷 𝐶
𝐵𝐴
(2𝑥 + 5) m
(4𝑥 + 1) m
2𝑥 m
𝐸 𝐹
𝐺𝐻

16. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
61
tc_fatimah@KVSandakan
1. Tentukan sama ada setiap ungkapan berikut merupakan ungkapan kuadratik dalam satu pemboleh
ubah atau bukan.
a) 𝑝2
− 4𝑝 + 1 b)
1
2
𝑦2
− 4𝑦 + 9 c)
1
3
− 2𝑏 + 𝑎2
d) −𝑚 + 1 e) 𝑏2
+ 2
f)
𝑎2+2𝑎+1
3
2. Sebuah bas dipandu dengan laju (5𝑥 − 3) 𝑘𝑚𝑗−1
. Cari jarak yang dilalui oleh bas tersebut jika masa
yang diambil ialah (3 + 𝑥) jam.
3. Diberi salah satu punca bagi persamaan kuadratik 𝑥2
+ 𝑝𝑥 − 18 = 0 ialah 2. Hitung nilai 𝑝.
4. Selesaikan persamaan   mmm  2
26
3
2
.
LATIHAN PENGUKUHAN

17. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
62
tc_fatimah@KVSandakan
5. Tunjukkan bahawa persamaan kuadratik (𝑚 − 6)2
= 12 − 2𝑚 boleh ditulis sebagai 𝑚2
− 10𝑚 +
24 = 0. Seterusnya selesaikan persamaan (𝑚 − 6)2
= 12 − 2𝑚.
6. Rajah 5.1 menunjukkan sebuah bekas air berbentuk kiub penuh berisi air. Air tersebut dicurahkan ke
dalam bekas berbentuk silinder seperti yang ditunjukkan dalam Rajah 5.2. Diberi bahawa tinggi silinder
tersebut adalah dua kali ganda jejarinya.
Carikan tinggi , dalam cm, silinder itu.

18. MATEMATIK
PERSAMAAN KUADRATIK
SVM TAHUN 1
SEMESTER 1
63
tc_fatimah@KVSandakan
7. Selesaikan persamaan kuadratik berikut:
a) −
1−2𝑥
5𝑥
=
𝑥−1
6
b) (𝑥 + 3)2
= 𝑥 + 5
8. Persatuan Sejarah Kolej Vokasional Sandakan telah melukis dua buah mural yang berbentuk segi
empat tepat sempena Hari Kemerdekaan Malaysia.
a) Ungkapkan beza luas antara kedua-dua buah mural, 𝐿 m2
dalam sebutan 𝑥.
b) Diberi beza luas antara dua buah mural tersebut ialah 10 m2
, hitung nilai 𝑥
c) Hitung perimeter bagi mural yang lebih kecil.
(3𝑥 + 1) 𝑚
(𝑥 − 3) 𝑚
(2𝑥 − 1) 𝑚
(𝑥 − 1) 𝑚