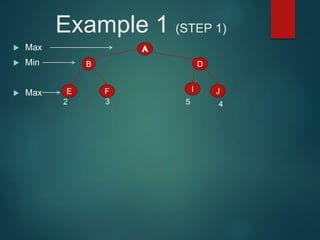
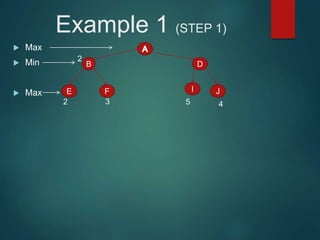
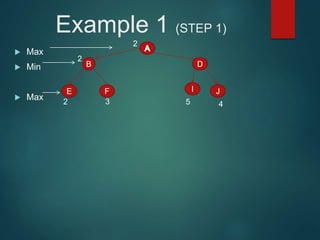
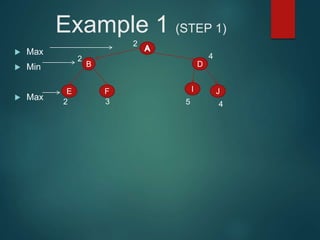
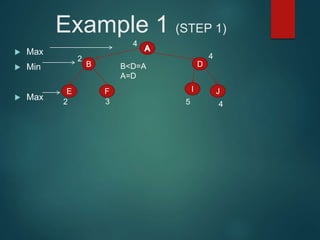
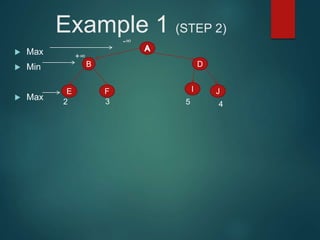
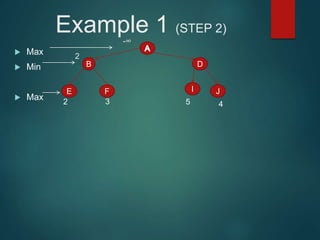
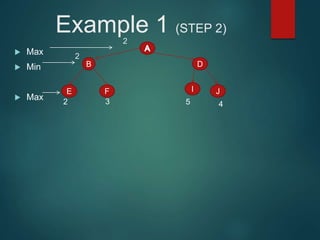
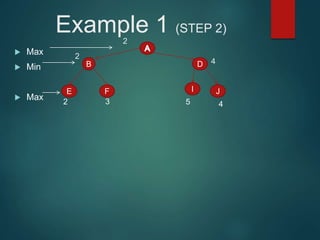
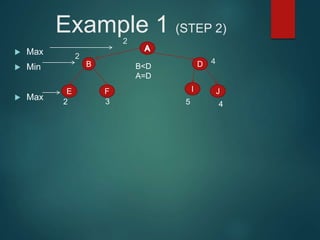
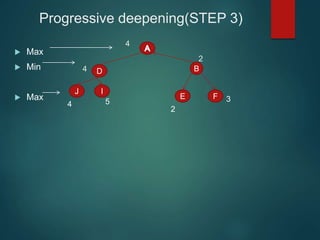
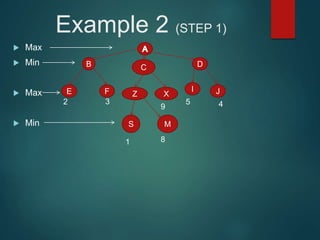
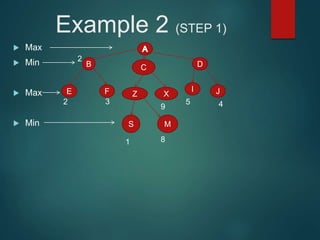
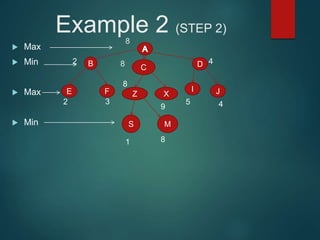
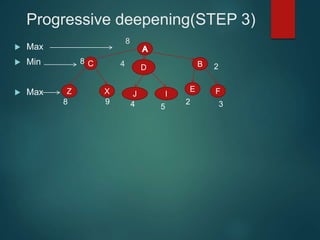
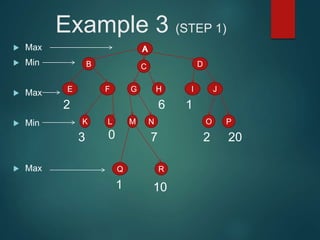
The minimax algorithm is used to determine the best possible move for a player in two-player zero-sum games like chess. It works by having each player assume their opponent will make the best counter-move. The algorithm searches the game tree by alternately maximizing and minimizing at each level to assign a value to leaf nodes, then backing up values towards the root. This process determines the move with the highest minimum value from the player's perspective.

1. Minimax Algorithm
PRESENTED BY: SULAIMAN M. KARIM
STUDENT NO: 4013031617
E-MAIL: SULAIMAN_MUSARIA@YAHOO.COM

2. Introduction
 Minimax is one of the oldest heuristic in IT.
 In 1950, the first chess programs were written by
C.Shannon & A.Tuting based on this algorithm.
 IBM’s Deep blue supercomputer defeats the chess
grandmaster kasparov in 1997.

3. -In two players games with perfect information,
the minimax algorithm can determine the best
move for a player by evaluating (enumerating)
the entire game tree.
-Player 1 is called Max. : Maximizes result.
-Player 2 is called Min.
Minimizes opponent’s
result.
Two persons games

4. Properties of minimax
 It is complete (if the tree is finite).
 It is Optimal (against an optimal
opponent).
 d=depth of the tree .
 b=legal moves.
1-Time complexity : bᵈ .
2-Space complexity : b*d .

5. MinMax Algorithm types
1. Game theory.
2. Combinatorial game theory.
3. Minimax for individual decisions.
4. Maximin in philosophy.

6. Minimax steps
The minimax algorithm consists of 5
steps:-
1-Generate the whole game tree.
2-Apply the utility function to leaf
nodes to get their values.
3-Use the utility of nodes at level N to
determine the utility of nodes at level
N-1 in the search tree.

7. Minimax steps
4-Continue backing up values
towards the root , layer at a time.
5-Eventually the backed values
reach the top of the tree , at that
point Max chooses the move that
leads to the highest value .

8. MinMax Algorithm code
Int MinMax (state s, int depth, int type)
{
if( terminate(s)) return Eval(s);
if( type == max ) {
for ( child =1, child <= NmbSuccessor(s); child++) {
value = MinMax(Successor(s, child), depth+1, Min)
if( value > BestScore) BestScore = Value; } }
if( type == min ) {
for ( child =1, child <= NmbSuccessor(s); child++) {
value = MinMax(Successor(s, child), depth+1, Max)
if( value < BestScore) BestScore = Value;
} }
return BestScore; }

9. Game theory
-In general games:-The maximin value of
a player is the largest value that the player
can be sure to get without knowing the
actions of the other players. Its formal
definition is:-

10. Example 1 (STEP 1)
 Max
 Min
 Max
B D
E F I J
52 3 4

11. Example 1 (STEP 1)
 Max
 Min
 Max
B D
E F I J
52 3 4
2

12. Example 1 (STEP 1)
 Max
 Min
 Max
B D
E F I J
52 3 4
2
2

13. Example 1 (STEP 1)
 Max
 Min
 Max
B D
E F I J
52 3 4
2
2
4

14. Example 1 (STEP 1)
 Max
 Min
 Max
B D
E F I J
5
B<D=A
A=D
3 4
2
4
4
2

15. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
We use Alpha= -∞,and Beta= +∞
maximizer=alpha,Minimizer=beta
+∞
-∞

16. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
+∞
-∞

17. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
2
-∞

18. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
2
2

19. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
2
2
+∞

20. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
2
2
4

21. Example 1 (STEP 2)
 Max
 Min
 Max
B D
E F I J
53 42
2
2
4
B<D
A=D

22. Progressive deepening(STEP 3)
 Max
 Min
 Max
BD
E F
IJ
354
2
2
4
4

23. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9

24. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2

25. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
2
8

26. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
2
8
8

27. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
B<C
A=C

28. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
4

29. Example 2 (STEP 1)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
4
C>D
A=C

30. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
We use Alpha= -∞,and Beta= +∞
maximizer=alpha,Minimizer=beta
+∞
-∞

31. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
+∞
-∞

32. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
-∞

33. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
2

34. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
2
+∞

35. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
2
+∞
8

36. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
2
8
8

37. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
B<C
A=C

38. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
∞+

39. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
4

40. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
C>D
A=C
4

41. Example 2 (STEP 2)
 Max
 Min
 Max
 Min
B D
E F I J
52 3 4
C
Z X
MS
81
9
2
8
8
8
4
Here we will use prune for the nodes that’s we
don’t need it again like node (S).

42. Progressive deepening(STEP 3)
 Max
 Min
 Max
C B
Z X E F
28 9 3
D
J I
5
8
8
4
4
2

43. Example 3 (STEP 1)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6

44. Example 3(STEP 1)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
2
3

45. Example 3 (STEP 1)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
2<6=6
1
7
6
3

46. Example 3 (STEP 1)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
6>1=6
1
7
6
20
1
3

47. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
We use Alpha= -∞,and Beta= +∞
maximizer=alpha,Minimizer=beta
+∞
-∞

48. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
We use Alpha= -∞,and Beta= +∞
maximizer=alpha,Minimizer=beta
+∞
-∞

49. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
-∞
3

50. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
2
3
-∞

51. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
2<6=6
3
6
1
7

52. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
6
3
6
1
7
-∞

53. Example 3(STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
6>1=6
3
6
1
7
1
20

54. Example 3 (STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
6
3
6
1
7
1
20

55. Example 3 (STEP 2)
 Max
 Min
 Max
 Min
 Max
B C D
E F G H I J
K L M N O P
Q R
1 10
202703
12 6
2
6
3
6
1
7
1
20
Here we will use prune for the nodes that’s we
don’t need it again

56. Progressive deepening(STEP 3)
 Max
 Min
 Max
B C D
E F G H I J
2
6
3
6
7
1
2012 6

57. Progressive deepening(STEP 3)
 Max
 Min
 Max
BC D
E FGH
I J
2
6
3
6
7
1
201
26