Minimax algorithm ex.pptx
•Download as PPTX, PDF•
0 likes•75 views
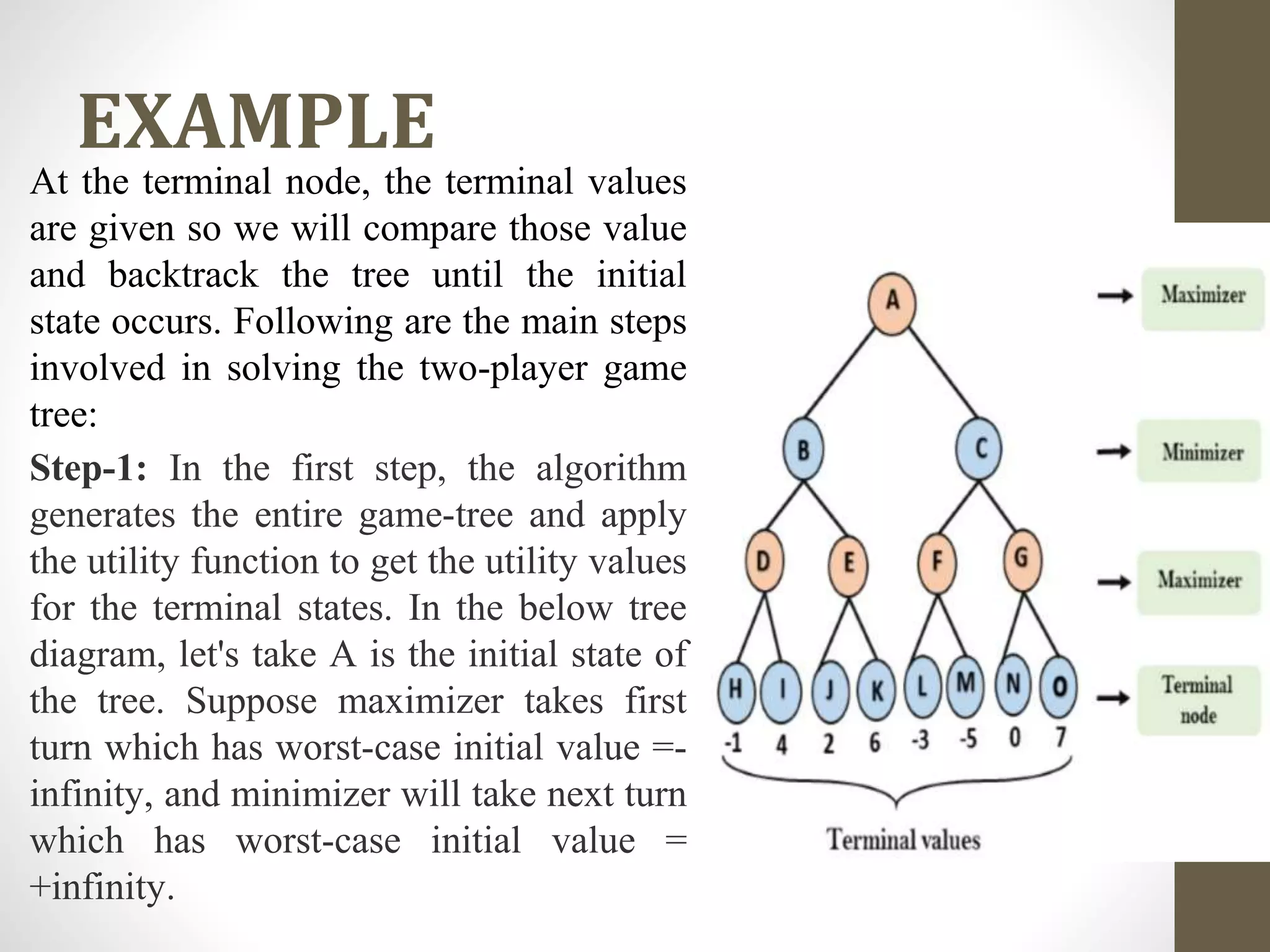
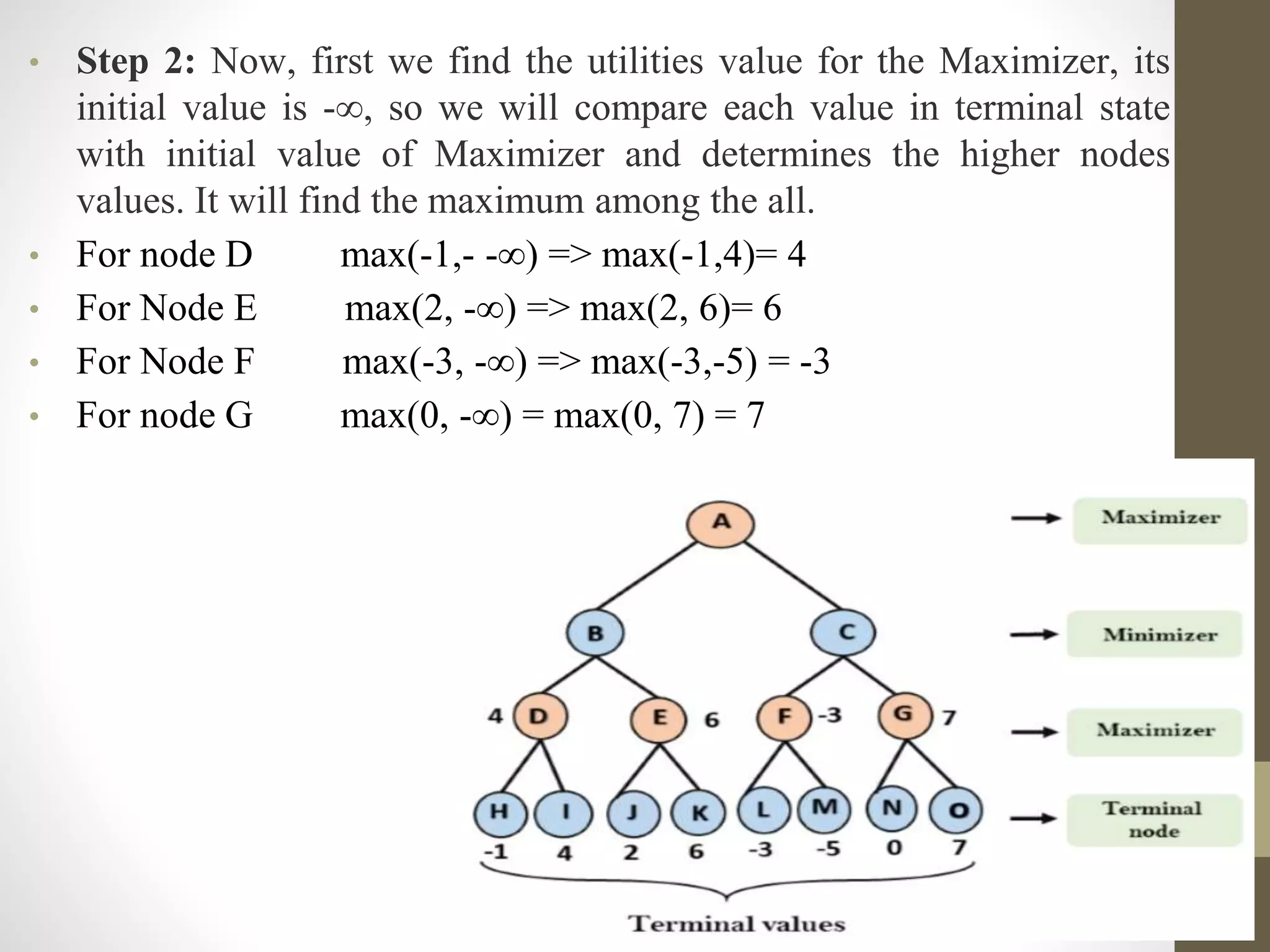
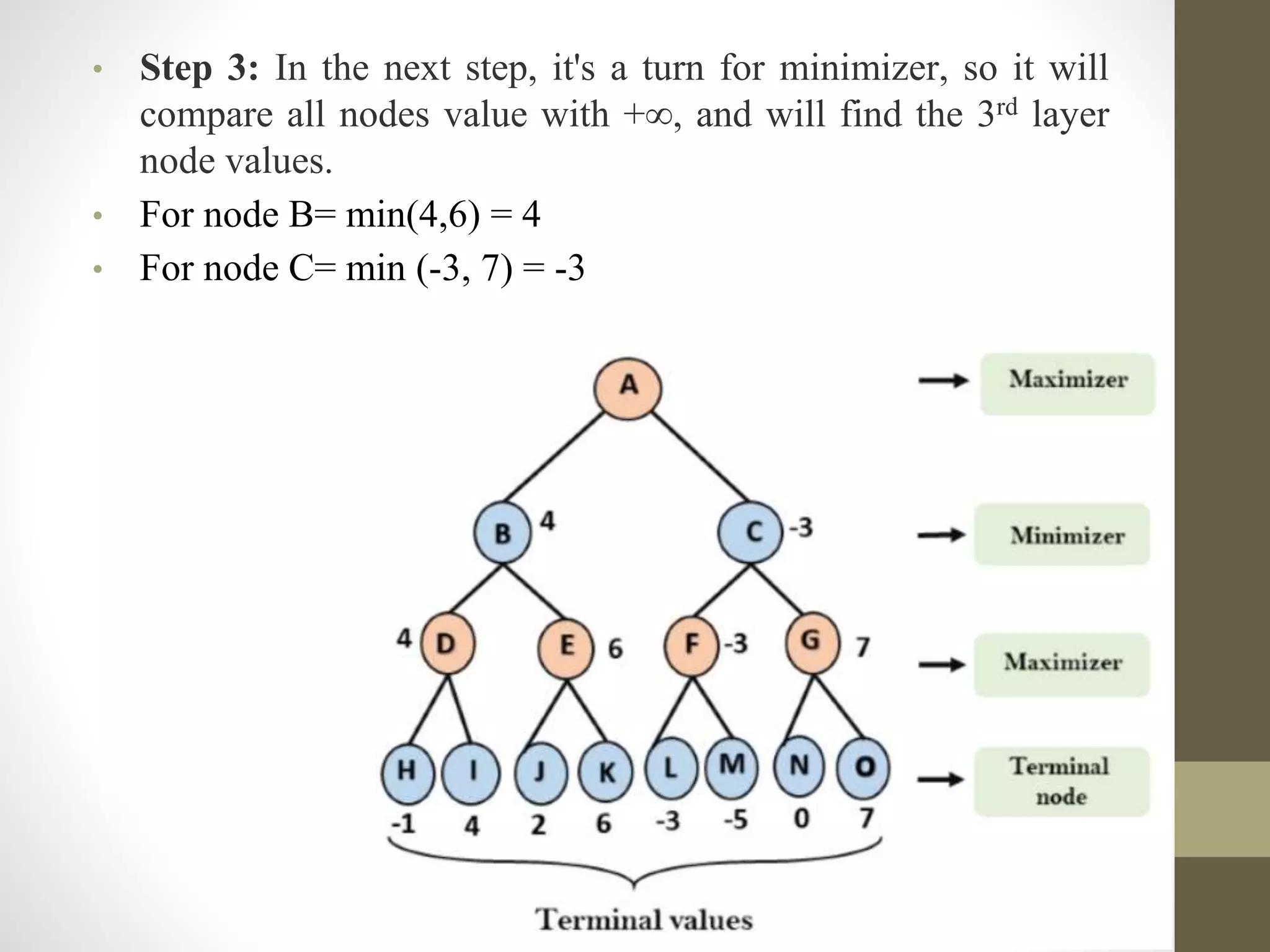
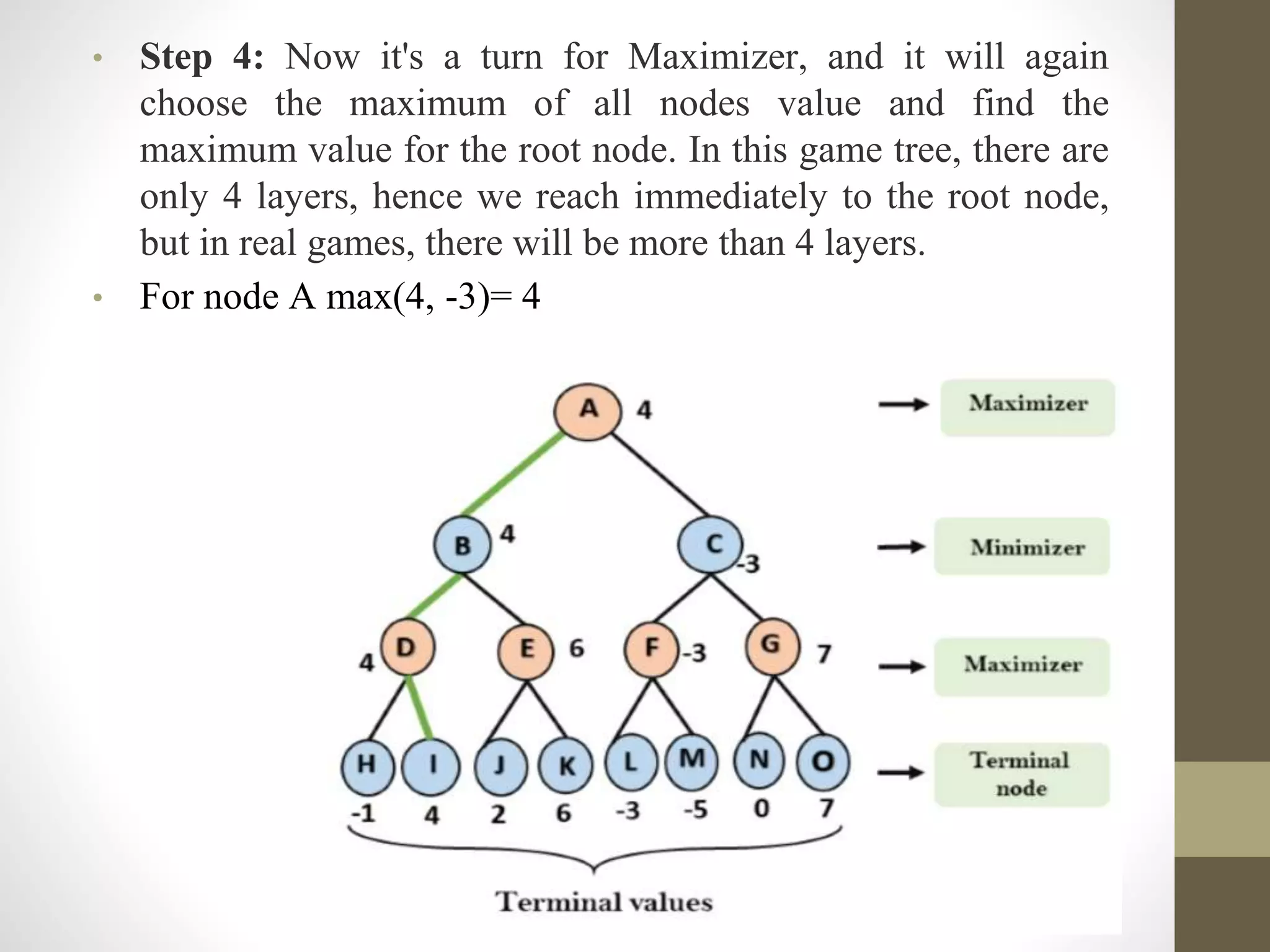
The document describes the 4 main steps to solve a two-player game tree: 1) Generate the entire game tree and assign utility values to terminal nodes. 2) For the maximizer, compare each terminal node value to -infinity and select the maximum. 3) For the minimizer, compare each value to infinity and select the minimum. 4) For the maximizer, compare values from the previous step and select the maximum value for the root node.
Report
Share
Report
Share
Recommended
Programed I/O Modul..
This document discusses programmed input/output (I/O) mode for data transfer. It explains that programmed I/O involves (1) the program waiting for the device to signal ready status by repeatedly testing status bits before each transfer, and (2) data is only transferred once the other end is ready. While this ensures the processor is dedicated to I/O, it can result in prolonged wait states which are inappropriate for asynchronous devices that can trigger events unpredictably, like keyboards. The document provides examples of reading and writing data using programmed I/O mode.
Finite Automata in compiler design
This document discusses deterministic finite automata (DFAs) and nondeterministic finite automata (NFAs). It defines DFAs and NFAs, describes their components and representations using transition graphs and tables. It also discusses converting NFAs to equivalent DFAs, which is important for implementing pattern matching software using finite state machines.
Introduction to Algorithms Complexity Analysis
The document provides an overview of algorithms, including definitions, types, characteristics, and analysis. It begins with step-by-step algorithms to add two numbers and describes the difference between algorithms and pseudocode. It then covers algorithm design approaches, characteristics, classification based on implementation and logic, and analysis methods like a priori and posteriori. The document emphasizes that algorithm analysis estimates resource needs like time and space complexity based on input size.
Min-Max algorithm
The minmax algorithm is used in two-player turn-based games to determine the optimal move for a player assuming the opponent plays optimally. It works by having one player act as the maximizer trying to maximize their score, and the other as the minimizer trying to minimize the score. The algorithm analyzes all possible moves and countermoves to determine the outcome with the best score for the maximizer. It is optimal if both players play optimally but has limitations due to its exhaustive search of all possibilities.
Polygon filling
The document discusses different techniques for filling polygons, including boundary fill, flood fill, and scan-line fill methods. It provides details on how each technique works, such as using a seed point and filling neighboring pixels for boundary fill, replacing all pixels of a selected color for flood fill, and drawing pixels between edge intersections for each scan line for scan-line fill. Examples are given to illustrate the filling process for each method.
Status register
The document discusses status registers and shift registers used in digital circuits. A status register contains status bits that indicate the result of arithmetic logic unit (ALU) operations, including carry (C), sign (S), zero (Z), and overflow (V) bits. The carry bit is set if there is an output carry from the ALU, the sign bit is set if the highest order bit is 1, the zero bit is set if the ALU output is all zeros, and the overflow bit is set if the result is out of the ALU's range. Shift registers are used to shift data in digital circuits.
CO Module 5
The document discusses parallel processing and provides classifications of parallel computer architectures. It describes Flynn's classification of computer architectures as single instruction stream single data stream (SISD), single instruction stream multiple data stream (SIMD), multiple instruction stream single data stream (MISD), and multiple instruction stream multiple data stream (MIMD). It also discusses pipeline computers, array processors, and multiprocessor systems as different architectural configurations for parallel computers. Pipelining is described as a technique to decompose a process into sub-operations that execute concurrently in dedicated segments to achieve overlapping computation.
Overview of Shift register and applications
Shift registers are used for temporary storage and can store multiple bits. There are two types: serial load and parallel load. Serial load registers shift data in or out one bit at a time on each clock cycle, while parallel load registers allow loading/output of all bits simultaneously. Common applications of shift registers include ring counters, Johnson counters, and pseudo-random pattern generators. A ring counter shifts data through the register and back to the first stage, counting through a fixed number of states. A Johnson counter also shifts data through the stages but with the last stage complement fed back to first, allowing it to count through more states than a ring counter.
Recommended
Programed I/O Modul..
This document discusses programmed input/output (I/O) mode for data transfer. It explains that programmed I/O involves (1) the program waiting for the device to signal ready status by repeatedly testing status bits before each transfer, and (2) data is only transferred once the other end is ready. While this ensures the processor is dedicated to I/O, it can result in prolonged wait states which are inappropriate for asynchronous devices that can trigger events unpredictably, like keyboards. The document provides examples of reading and writing data using programmed I/O mode.
Finite Automata in compiler design
This document discusses deterministic finite automata (DFAs) and nondeterministic finite automata (NFAs). It defines DFAs and NFAs, describes their components and representations using transition graphs and tables. It also discusses converting NFAs to equivalent DFAs, which is important for implementing pattern matching software using finite state machines.
Introduction to Algorithms Complexity Analysis
The document provides an overview of algorithms, including definitions, types, characteristics, and analysis. It begins with step-by-step algorithms to add two numbers and describes the difference between algorithms and pseudocode. It then covers algorithm design approaches, characteristics, classification based on implementation and logic, and analysis methods like a priori and posteriori. The document emphasizes that algorithm analysis estimates resource needs like time and space complexity based on input size.
Min-Max algorithm
The minmax algorithm is used in two-player turn-based games to determine the optimal move for a player assuming the opponent plays optimally. It works by having one player act as the maximizer trying to maximize their score, and the other as the minimizer trying to minimize the score. The algorithm analyzes all possible moves and countermoves to determine the outcome with the best score for the maximizer. It is optimal if both players play optimally but has limitations due to its exhaustive search of all possibilities.
Polygon filling
The document discusses different techniques for filling polygons, including boundary fill, flood fill, and scan-line fill methods. It provides details on how each technique works, such as using a seed point and filling neighboring pixels for boundary fill, replacing all pixels of a selected color for flood fill, and drawing pixels between edge intersections for each scan line for scan-line fill. Examples are given to illustrate the filling process for each method.
Status register
The document discusses status registers and shift registers used in digital circuits. A status register contains status bits that indicate the result of arithmetic logic unit (ALU) operations, including carry (C), sign (S), zero (Z), and overflow (V) bits. The carry bit is set if there is an output carry from the ALU, the sign bit is set if the highest order bit is 1, the zero bit is set if the ALU output is all zeros, and the overflow bit is set if the result is out of the ALU's range. Shift registers are used to shift data in digital circuits.
CO Module 5
The document discusses parallel processing and provides classifications of parallel computer architectures. It describes Flynn's classification of computer architectures as single instruction stream single data stream (SISD), single instruction stream multiple data stream (SIMD), multiple instruction stream single data stream (MISD), and multiple instruction stream multiple data stream (MIMD). It also discusses pipeline computers, array processors, and multiprocessor systems as different architectural configurations for parallel computers. Pipelining is described as a technique to decompose a process into sub-operations that execute concurrently in dedicated segments to achieve overlapping computation.
Overview of Shift register and applications
Shift registers are used for temporary storage and can store multiple bits. There are two types: serial load and parallel load. Serial load registers shift data in or out one bit at a time on each clock cycle, while parallel load registers allow loading/output of all bits simultaneously. Common applications of shift registers include ring counters, Johnson counters, and pseudo-random pattern generators. A ring counter shifts data through the register and back to the first stage, counting through a fixed number of states. A Johnson counter also shifts data through the stages but with the last stage complement fed back to first, allowing it to count through more states than a ring counter.
Restoring & Non-Restoring Division Algorithm By Sania Nisar
Restoring division algorithm ,non restoring division algorithm ,restoring division algorithm for unsigned integer ,restoring division flowchart ,non-restoring division for unsigned integer ,non-restoring division flowchart
Quantization.pptx
Quantization is the process of converting a continuous analog signal into a discrete digital signal. It involves sampling the analog signal at regular intervals and assigning the signal amplitude at each sample point to the nearest of a finite set of discrete values. This results in a loss of information from the original analog signal. The quality of the quantized signal depends on the number of discrete quantization levels used. There are two main types of quantization - uniform, where the quantization levels are spaced evenly, and non-uniform, where they are spaced unequally often in a logarithmic relationship. The difference between the original analog amplitude and the quantized value at each sample point is known as quantization error.
Particle swarm optimization
A presentation on PSO with videos and animations to illustrate the concept. The ppt throws light on the concept, the algo, the application and comparison of PSO with GA and DE.
Stack organization
This document discusses stack organization and operations. A stack is a last-in, first-out data structure where items added last are retrieved first. It uses a stack pointer to track the top of the stack. Common operations are push, which adds an item to the top of the stack, and pop, which removes an item from the top. Stacks can be implemented with registers, using a stack pointer and data register. Reverse Polish notation places operators after operands, making it suitable for stack-based expression evaluation.
Character generation techniques
There are three main methods for generating characters using software: the stroke method, vector/bitmap method, and starbust method. The stroke method uses a sequence of line and arc drawing functions defined by starting and end points. The starbust method uses a fixed pattern of 24 bit line segments to represent characters. The bitmap method stores characters as arrays of 1s and 0s representing pixels, allowing for variable font sizes by increasing the array size. All the methods can create aliased characters, and the starbust method requires extra memory to store the 24 bit segment codes.
Unit 4-booth algorithm
Booth's algorithm is a method for multiplying two signed or unsigned integers in binary representation more efficiently than straightforward algorithms. It uses fewer additions and subtractions by representing the multiplicand as 2's complement numbers. The algorithm loads the multiplicand and multiplier into registers, initializes a third register to 0, and performs bitwise shifts and arithmetic operations (addition/subtraction of the multiplicand) on the registers based on the values of bits from the multiplier. This process builds up the product one bit at a time in a third register.
Types of grammer - TOC
This ppt will give you an idea about types of grammar in TOC.
Learn from it and share it to share knowledge
Clock Triggering
There are four types of clock triggering that determine when a sequential circuit responds to input changes: negative level triggering, positive level triggering, positive edge triggering, and negative edge triggering. Negative level triggering occurs when a flip flop is triggered at the negative/low level of the clock pulse. Positive level triggering occurs when a flip flop is triggered at the positive/high level of the clock pulse. Positive edge triggering occurs when the output responds to input changes only at the rising edge of the clock pulse. Negative edge triggering occurs when the output responds to input changes only at the falling edge of the clock pulse.
Compiler Design Lecture Notes
FellowBuddy.com is an innovative platform that brings students together to share notes, exam papers, study guides, project reports and presentation for upcoming exams.
We connect Students who have an understanding of course material with Students who need help.
Benefits:-
# Students can catch up on notes they missed because of an absence.
# Underachievers can find peer developed notes that break down lecture and study material in a way that they can understand
# Students can earn better grades, save time and study effectively
Our Vision & Mission – Simplifying Students Life
Our Belief – “The great breakthrough in your life comes when you realize it, that you can learn anything you need to learn; to accomplish any goal that you have set for yourself. This means there are no limits on what you can be, have or do.”
Like Us - https://www.facebook.com/FellowBuddycom
Frame buffer
This presentation contains -
- Frame Buffer
- Digital-to-Analog ( DAC ) Converter
- Single bit plane frame buffer
- N-bit plane frame buffer
- 3-bit color frame buffer
- 24-bit color frame buffer
Coa module2
This document discusses the fundamental concepts and organization of the central processing unit (CPU). It describes how the CPU fetches, decodes, and executes instructions through a multi-step process. It explains that the CPU uses a program counter to keep track of the next instruction, and increments it after fetching and decoding each one. It also details how the CPU performs operations like fetching data from memory, storing to memory, transferring between registers, and performing arithmetic/logic functions using the ALU.
Shift Registers
Shift registers are digital circuits composed of flip-flops that can shift data from one stage to the next. They can be configured for serial-in serial-out, serial-in parallel-out, parallel-in serial-out, or parallel-in parallel-out data movement. Common applications include converting between serial and parallel data, temporary data storage, and implementing counters. MSI shift registers like the 74LS164 and 74LS166 provide 8-bit shift register functionality.
Closure properties of context free grammar
Context free language
Context free Grammar
Closure properties of context free language.
Closure properties of context free grammar.
Union, Concatenation, Kleene closure, Intersection, Complement, Applications of CFL
State Space Search in ai
Artificial Intelligence: Introduction, Typical Applications. State Space Search: Depth Bounded
DFS, Depth First Iterative Deepening. Heuristic Search: Heuristic Functions, Best First Search,
Hill Climbing, Variable Neighborhood Descent, Beam Search, Tabu Search. Optimal Search: A
*
algorithm, Iterative Deepening A*
, Recursive Best First Search, Pruning the CLOSED and OPEN
Lists
Lecture 11 Informed Search
Heuristic search algorithms use heuristics, or problem-specific knowledge, to guide the search for a solution. Some heuristics guarantee completeness while others may sacrifice completeness to improve efficiency. A heuristic function estimates the cost to reach the goal state from the current state. For example, in the 8-puzzle problem the Manhattan distance heuristic estimates this cost as the sum of the distances each misplaced tile would need to move to reach its goal position. The example shows applying the Manhattan distance heuristic to guide the search for a solution to instances of the 8-puzzle problem.
Anti- aliasing computer graphics
Anti-aliasing is a technique used to reduce aliasing, which makes curved or slanted lines appear jagged when displayed on a lower resolution output device like a monitor. Aliasing occurs because the device lacks enough resolution to smoothly represent curved lines. Anti-aliasing works by adding subtle color changes around lines, which causes jagged edges to blur together when viewed from a distance. There are several anti-aliasing techniques, including increasing the display resolution, area sampling to shade pixels based on the area covered by thickened lines, and post-filtering by generating a higher resolution virtual image and averaging it down.
carry look ahead adder
It is the adder used to eliminate the wastage of time occur at each stage of parallel binary adder.In this , by using only carry input signal , we can calculate the the carry output without going to calculate carry at each stage.it is commonly used only for 4 bit addition because further calculation will be more complex.
Chomsky Hierarchy.ppt
This document discusses the Chomsky hierarchy and different types of automata and grammars. It begins by describing applications of different automata like Turing machines, linear bounded automata, pushdown automata, and finite automata. It then discusses recursive and enumerable sets and linear bounded automata. It provides examples of languages accepted by LBAs and notes that LBAs have more power than PDAs but less than TMs. It also discusses unrestricted grammars, context-sensitive grammars, and places language classes in the Chomsky hierarchy. It concludes by asking questions about left linear versus right linear grammars.
Turing machine
This presentation summarizes Turing machines, including:
- Turing machines were introduced by Alan Turing in 1936 as a mathematical model of computation.
- A Turing machine consists of a finite state control, a tape divided into cells, and a tape head that can read and write symbols on the tape and move the tape left and right.
- Turing machines are formally defined by a 7-tuple that specifies the states, tape alphabet, transition function, blank symbol, start state, and accepting states.
Graph theory narsingh deo
This document provides details on a new software update that will be installed on all company computers. The update includes security patches that fix vulnerabilities, improved compatibility with newer operating systems, and new features to enhance the user experience. The update will be automatically pushed out to all devices overnight on Friday and should take less than 30 minutes to complete on most machines. Users are advised to make sure their computers have a backup battery or are plugged in to avoid power interruptions during installation.
I. Mini-Max Algorithm in AI
Artificial Intelligence: Introduction, Typical Applications. State Space Search: Depth Bounded
DFS, Depth First Iterative Deepening. Heuristic Search: Heuristic Functions, Best First Search,
Hill Climbing, Variable Neighborhood Descent, Beam Search, Tabu Search. Optimal Search: A
*
algorithm, Iterative Deepening A*
, Recursive Best First Search, Pruning the CLOSED and OPEN
Lists
MINI-MAX ALGORITHM.pptx
The Mini-Max algorithm is a recursive algorithm used in game theory and decision making to find the optimal move for a player assuming the opponent also plays optimally. It works by having two players, MAX and MIN, where MAX aims to maximize their score and MIN aims to minimize MAX's score. The algorithm performs a depth-first search of the game tree, evaluating each terminal node and backing up values until it reaches the initial state node to determine the optimal first move.
More Related Content
What's hot
Restoring & Non-Restoring Division Algorithm By Sania Nisar
Restoring division algorithm ,non restoring division algorithm ,restoring division algorithm for unsigned integer ,restoring division flowchart ,non-restoring division for unsigned integer ,non-restoring division flowchart
Quantization.pptx
Quantization is the process of converting a continuous analog signal into a discrete digital signal. It involves sampling the analog signal at regular intervals and assigning the signal amplitude at each sample point to the nearest of a finite set of discrete values. This results in a loss of information from the original analog signal. The quality of the quantized signal depends on the number of discrete quantization levels used. There are two main types of quantization - uniform, where the quantization levels are spaced evenly, and non-uniform, where they are spaced unequally often in a logarithmic relationship. The difference between the original analog amplitude and the quantized value at each sample point is known as quantization error.
Particle swarm optimization
A presentation on PSO with videos and animations to illustrate the concept. The ppt throws light on the concept, the algo, the application and comparison of PSO with GA and DE.
Stack organization
This document discusses stack organization and operations. A stack is a last-in, first-out data structure where items added last are retrieved first. It uses a stack pointer to track the top of the stack. Common operations are push, which adds an item to the top of the stack, and pop, which removes an item from the top. Stacks can be implemented with registers, using a stack pointer and data register. Reverse Polish notation places operators after operands, making it suitable for stack-based expression evaluation.
Character generation techniques
There are three main methods for generating characters using software: the stroke method, vector/bitmap method, and starbust method. The stroke method uses a sequence of line and arc drawing functions defined by starting and end points. The starbust method uses a fixed pattern of 24 bit line segments to represent characters. The bitmap method stores characters as arrays of 1s and 0s representing pixels, allowing for variable font sizes by increasing the array size. All the methods can create aliased characters, and the starbust method requires extra memory to store the 24 bit segment codes.
Unit 4-booth algorithm
Booth's algorithm is a method for multiplying two signed or unsigned integers in binary representation more efficiently than straightforward algorithms. It uses fewer additions and subtractions by representing the multiplicand as 2's complement numbers. The algorithm loads the multiplicand and multiplier into registers, initializes a third register to 0, and performs bitwise shifts and arithmetic operations (addition/subtraction of the multiplicand) on the registers based on the values of bits from the multiplier. This process builds up the product one bit at a time in a third register.
Types of grammer - TOC
This ppt will give you an idea about types of grammar in TOC.
Learn from it and share it to share knowledge
Clock Triggering
There are four types of clock triggering that determine when a sequential circuit responds to input changes: negative level triggering, positive level triggering, positive edge triggering, and negative edge triggering. Negative level triggering occurs when a flip flop is triggered at the negative/low level of the clock pulse. Positive level triggering occurs when a flip flop is triggered at the positive/high level of the clock pulse. Positive edge triggering occurs when the output responds to input changes only at the rising edge of the clock pulse. Negative edge triggering occurs when the output responds to input changes only at the falling edge of the clock pulse.
Compiler Design Lecture Notes
FellowBuddy.com is an innovative platform that brings students together to share notes, exam papers, study guides, project reports and presentation for upcoming exams.
We connect Students who have an understanding of course material with Students who need help.
Benefits:-
# Students can catch up on notes they missed because of an absence.
# Underachievers can find peer developed notes that break down lecture and study material in a way that they can understand
# Students can earn better grades, save time and study effectively
Our Vision & Mission – Simplifying Students Life
Our Belief – “The great breakthrough in your life comes when you realize it, that you can learn anything you need to learn; to accomplish any goal that you have set for yourself. This means there are no limits on what you can be, have or do.”
Like Us - https://www.facebook.com/FellowBuddycom
Frame buffer
This presentation contains -
- Frame Buffer
- Digital-to-Analog ( DAC ) Converter
- Single bit plane frame buffer
- N-bit plane frame buffer
- 3-bit color frame buffer
- 24-bit color frame buffer
Coa module2
This document discusses the fundamental concepts and organization of the central processing unit (CPU). It describes how the CPU fetches, decodes, and executes instructions through a multi-step process. It explains that the CPU uses a program counter to keep track of the next instruction, and increments it after fetching and decoding each one. It also details how the CPU performs operations like fetching data from memory, storing to memory, transferring between registers, and performing arithmetic/logic functions using the ALU.
Shift Registers
Shift registers are digital circuits composed of flip-flops that can shift data from one stage to the next. They can be configured for serial-in serial-out, serial-in parallel-out, parallel-in serial-out, or parallel-in parallel-out data movement. Common applications include converting between serial and parallel data, temporary data storage, and implementing counters. MSI shift registers like the 74LS164 and 74LS166 provide 8-bit shift register functionality.
Closure properties of context free grammar
Context free language
Context free Grammar
Closure properties of context free language.
Closure properties of context free grammar.
Union, Concatenation, Kleene closure, Intersection, Complement, Applications of CFL
State Space Search in ai
Artificial Intelligence: Introduction, Typical Applications. State Space Search: Depth Bounded
DFS, Depth First Iterative Deepening. Heuristic Search: Heuristic Functions, Best First Search,
Hill Climbing, Variable Neighborhood Descent, Beam Search, Tabu Search. Optimal Search: A
*
algorithm, Iterative Deepening A*
, Recursive Best First Search, Pruning the CLOSED and OPEN
Lists
Lecture 11 Informed Search
Heuristic search algorithms use heuristics, or problem-specific knowledge, to guide the search for a solution. Some heuristics guarantee completeness while others may sacrifice completeness to improve efficiency. A heuristic function estimates the cost to reach the goal state from the current state. For example, in the 8-puzzle problem the Manhattan distance heuristic estimates this cost as the sum of the distances each misplaced tile would need to move to reach its goal position. The example shows applying the Manhattan distance heuristic to guide the search for a solution to instances of the 8-puzzle problem.
Anti- aliasing computer graphics
Anti-aliasing is a technique used to reduce aliasing, which makes curved or slanted lines appear jagged when displayed on a lower resolution output device like a monitor. Aliasing occurs because the device lacks enough resolution to smoothly represent curved lines. Anti-aliasing works by adding subtle color changes around lines, which causes jagged edges to blur together when viewed from a distance. There are several anti-aliasing techniques, including increasing the display resolution, area sampling to shade pixels based on the area covered by thickened lines, and post-filtering by generating a higher resolution virtual image and averaging it down.
carry look ahead adder
It is the adder used to eliminate the wastage of time occur at each stage of parallel binary adder.In this , by using only carry input signal , we can calculate the the carry output without going to calculate carry at each stage.it is commonly used only for 4 bit addition because further calculation will be more complex.
Chomsky Hierarchy.ppt
This document discusses the Chomsky hierarchy and different types of automata and grammars. It begins by describing applications of different automata like Turing machines, linear bounded automata, pushdown automata, and finite automata. It then discusses recursive and enumerable sets and linear bounded automata. It provides examples of languages accepted by LBAs and notes that LBAs have more power than PDAs but less than TMs. It also discusses unrestricted grammars, context-sensitive grammars, and places language classes in the Chomsky hierarchy. It concludes by asking questions about left linear versus right linear grammars.
Turing machine
This presentation summarizes Turing machines, including:
- Turing machines were introduced by Alan Turing in 1936 as a mathematical model of computation.
- A Turing machine consists of a finite state control, a tape divided into cells, and a tape head that can read and write symbols on the tape and move the tape left and right.
- Turing machines are formally defined by a 7-tuple that specifies the states, tape alphabet, transition function, blank symbol, start state, and accepting states.
Graph theory narsingh deo
This document provides details on a new software update that will be installed on all company computers. The update includes security patches that fix vulnerabilities, improved compatibility with newer operating systems, and new features to enhance the user experience. The update will be automatically pushed out to all devices overnight on Friday and should take less than 30 minutes to complete on most machines. Users are advised to make sure their computers have a backup battery or are plugged in to avoid power interruptions during installation.
What's hot (20)
Restoring & Non-Restoring Division Algorithm By Sania Nisar
Restoring & Non-Restoring Division Algorithm By Sania Nisar
Similar to Minimax algorithm ex.pptx
I. Mini-Max Algorithm in AI
Artificial Intelligence: Introduction, Typical Applications. State Space Search: Depth Bounded
DFS, Depth First Iterative Deepening. Heuristic Search: Heuristic Functions, Best First Search,
Hill Climbing, Variable Neighborhood Descent, Beam Search, Tabu Search. Optimal Search: A
*
algorithm, Iterative Deepening A*
, Recursive Best First Search, Pruning the CLOSED and OPEN
Lists
MINI-MAX ALGORITHM.pptx
The Mini-Max algorithm is a recursive algorithm used in game theory and decision making to find the optimal move for a player assuming the opponent also plays optimally. It works by having two players, MAX and MIN, where MAX aims to maximize their score and MIN aims to minimize MAX's score. The algorithm performs a depth-first search of the game tree, evaluating each terminal node and backing up values until it reaches the initial state node to determine the optimal first move.
AI_unit3.pptx
The document discusses game theory and algorithms for game playing in artificial intelligence, including minimax, alpha-beta pruning, and Monte Carlo tree search. Minimax is a decision-making algorithm that works by choosing the option that maximizes the minimum payoff. It assumes both players play optimally. Alpha-beta pruning improves on minimax by pruning branches that cannot affect the outcome. Monte Carlo tree search is a technique that builds a search tree using random simulations rather than exhaustive search.
Unit_I_Introduction(Part_III).ppt
1) The document discusses adversarial search problems, which arise in competitive multi-agent environments modeled as games. It describes optimal strategies in two-player zero-sum games using the minimax algorithm and game trees.
2) The minimax algorithm recursively computes the minimax value of each node in the game tree by considering optimal play from both players. This allows it to determine an optimal strategy for the first player.
3) Alpha-beta pruning improves upon minimax by pruning subtrees from consideration once it determines they cannot influence the final decision, allowing optimal strategies to be found more efficiently.
Two player games
Two player games involve two players alternating turns trying to maximize or minimize the outcome of a game. The MiniMax algorithm is commonly used to choose the best move for a player in two player games by recursively evaluating all possible future moves. Alpha-beta pruning improves upon MiniMax by pruning branches that cannot influence the final outcome, allowing deeper search of the game tree within the same time limit.
Chess engine presentation
This document summarizes the key components of a chess engine project. It discusses the objective to checkmate the opponent's king, the scope of allowing two players to play each other or a player against the computer. It then covers the building blocks like the board representation, move generation for each piece type, and introducing AI algorithms like mini-max and alpha-beta pruning to allow the computer to choose optimal moves. Tools like Python and Pygame are used to develop the GUI and handle game logic and AI.
AI3391 Artificial Intelligence UNIT III Notes_merged.pdf
The document provides information about game playing and constraint satisfaction problems (CSP). It discusses adversarial search techniques like minimax algorithm and alpha-beta pruning that are used for game playing. The minimax algorithm uses recursion to search through the game tree and find the optimal move. Alpha-beta pruning improves on minimax by pruning parts of the tree that are guaranteed not to affect the outcome. The document also mentions other topics like Monte Carlo tree search, stochastic games with elements of chance, and formalization of game state, actions, results, and utilities.
12 adversal search
This document discusses adversarial search techniques for two-agent games with perfect information. It introduces the minimax procedure and how it recursively assigns values to nodes in a game tree by maximizing the value for the maximizing agent and minimizing for the minimizing agent. The alpha-beta pruning technique is described which improves search efficiency by pruning subtrees that cannot alter the minimax value of the root. Examples of applying minimax and alpha-beta to tic-tac-toe are provided. The document also discusses handling games of chance using expectimax search and learning effective evaluation functions from self-play.
Juegos minimax AlfaBeta
The document discusses game theory and algorithms used in game-playing programs such as Minimax and Alpha-Beta pruning. It provides examples of how Minimax works to evaluate all possible moves in a game tree and select the optimal move. Alpha-Beta pruning improves on Minimax by avoiding exploring subtrees that cannot affect the outcome, reducing computation time.
ACI-Webinar-3-MinMaxAlphaBetaPruning-TicTacToe.pptx
The document describes the minimax algorithm and alpha-beta pruning for a Tic Tac Toe game. It explains that minimax finds the best possible move by assuming the opponent plays optimally to minimize utility. Alpha-beta pruning improves upon minimax by pruning branches that cannot influence the final decision. It then provides pseudocode for the minimax and alpha-beta algorithms. Finally, it shows code for implementing a Tic Tac Toe game that uses minimax with alpha-beta pruning to choose moves.
ch_5 Game playing Min max and Alpha Beta pruning.ppt
Game-Playing & Adversarial Search was covered in two lectures. Minimax search finds the optimal strategy but is impractical for large games. Minimax with alpha-beta pruning improves search efficiency by pruning subtrees that cannot affect the result. Iterative deepening allows more search within time limits by incrementally increasing search depth. Heuristics help guide search and handle limited lookahead.
I. Alpha-Beta Pruning in ai
Alpha-beta pruning is a modification of the minimax algorithm that optimizes it by pruning portions of the search tree that cannot affect the outcome. It uses two thresholds, alpha and beta, to track the best values found for the maximizing and minimizing players. By comparing alpha and beta at each node, it can avoid exploring subtrees where the minimum of the maximizing player's options will be greater than the maximum of the minimizing player's options. This allows it to often prune branches of the tree without calculating their values, improving the algorithm's efficiency.
Game playing.ppt
Game playing problems can be modeled as game trees to apply search techniques like minimax and alpha-beta pruning. Minimax searches a game tree to determine the move that maximizes the minimum payoff against an optimal opponent. It recursively evaluates nodes based on the minimax rule. Alpha-beta pruning improves performance by avoiding evaluating subtrees that cannot impact the result. Chance nodes in games like Backgammon use expected values to model uncertainty from dice rolls.
It is an artificial document, please. regarding Ai topics
Game playing can be studied to understand problems involving adversarial agents. Games define large search spaces that require minimal initial structure to study. Typical perfect games have two players who alternate moves in a zero-sum game with complete information and no chance elements. To play such a game, one considers all legal moves and evaluates the resulting positions to determine the best move. Minimax search evaluates positions and uses the minimax rule to select the move that maximizes the guaranteed payoff. Alpha-beta pruning improves minimax search by avoiding evaluating unpromising moves.
21CSC206T_UNIT3.pptx.pdf ARITIFICIAL INTELLIGENCE
1) Adversarial search involves searching game trees to find the best move in games with competitive players like tic-tac-toe and chess. Important concepts include pruning unwanted search tree portions and heuristic evaluation functions.
2) A game tree represents all possible game states, moves, and outcomes. Elements of game playing search include the initial state, players, legal moves, game results, end states, and payoffs for winning, losing, or drawing.
3) The minimax algorithm searches game trees to determine the best guaranteed outcome against an optimal opponent. It recursively evaluates nodes using the minimax rule to maximize the minimum payoff for the maximizing player.
1.game
Games provide well-defined test beds for developing AI techniques. They have clear rules and allow direct comparison of algorithms against humans. Game playing involves searching game trees to find optimal strategies, taking into account opponents' possible moves. The minimax algorithm and its improved version alpha-beta pruning are commonly used to search game trees and select the best next move.
cai
Minimax is an algorithm that is commonly used for game playing. It works by constructing a game tree that represents all possible future game states up to a certain depth, and uses an evaluation function to assign a value to each state. The minimax algorithm traverses the tree and "backs up" values from the leaves to the root by maximizing values at MAX nodes and minimizing values at MIN nodes. Alpha-beta pruning improves upon minimax by pruning branches that cannot affect the final output value.
Min Max Artificial Intelligence algorithm
The Mini-Max algorithm is a recursive algorithm used in decision making and game theory. It uses a depth-first search to explore the game tree, with one player trying to maximize their score (MAX) and the other trying to minimize it (MIN). At each node, it recursively evaluates the possible moves down to a terminal node, then backtracks to assign scores. It is complete, optimal if both players play optimally, and has time and space complexity of O(bm) for a branching factor b and maximum depth m. However, it is slow for complex games with large branching factors.
Lecture 8 dynamic programming
This document discusses algorithms for finding minimum and maximum elements in an array, including simultaneous minimum and maximum algorithms. It introduces dynamic programming as a technique for improving inefficient divide-and-conquer algorithms by storing results of subproblems to avoid recomputing them. Examples of dynamic programming include calculating the Fibonacci sequence and solving an assembly line scheduling problem to minimize total time.
Similar to Minimax algorithm ex.pptx (20)
AI3391 Artificial Intelligence UNIT III Notes_merged.pdf
AI3391 Artificial Intelligence UNIT III Notes_merged.pdf
ACI-Webinar-3-MinMaxAlphaBetaPruning-TicTacToe.pptx
ACI-Webinar-3-MinMaxAlphaBetaPruning-TicTacToe.pptx
ch_5 Game playing Min max and Alpha Beta pruning.ppt
ch_5 Game playing Min max and Alpha Beta pruning.ppt
It is an artificial document, please. regarding Ai topics
It is an artificial document, please. regarding Ai topics
Recently uploaded
bank management system in java and mysql report1.pdf
truth is high but higher still is truth full living
22CYT12-Unit-V-E Waste and its Management.ppt
Introduction- e - waste – definition - sources of e-waste– hazardous substances in e-waste - effects of e-waste on environment and human health- need for e-waste management– e-waste handling rules - waste minimization techniques for managing e-waste – recycling of e-waste - disposal treatment methods of e- waste – mechanism of extraction of precious metal from leaching solution-global Scenario of E-waste – E-waste in India- case studies.
DEEP LEARNING FOR SMART GRID INTRUSION DETECTION: A HYBRID CNN-LSTM-BASED MODEL
As digital technology becomes more deeply embedded in power systems, protecting the communication
networks of Smart Grids (SG) has emerged as a critical concern. Distributed Network Protocol 3 (DNP3)
represents a multi-tiered application layer protocol extensively utilized in Supervisory Control and Data
Acquisition (SCADA)-based smart grids to facilitate real-time data gathering and control functionalities.
Robust Intrusion Detection Systems (IDS) are necessary for early threat detection and mitigation because
of the interconnection of these networks, which makes them vulnerable to a variety of cyberattacks. To
solve this issue, this paper develops a hybrid Deep Learning (DL) model specifically designed for intrusion
detection in smart grids. The proposed approach is a combination of the Convolutional Neural Network
(CNN) and the Long-Short-Term Memory algorithms (LSTM). We employed a recent intrusion detection
dataset (DNP3), which focuses on unauthorized commands and Denial of Service (DoS) cyberattacks, to
train and test our model. The results of our experiments show that our CNN-LSTM method is much better
at finding smart grid intrusions than other deep learning algorithms used for classification. In addition,
our proposed approach improves accuracy, precision, recall, and F1 score, achieving a high detection
accuracy rate of 99.50%.
Recycled Concrete Aggregate in Construction Part III
Using recycled concrete aggregates (RCA) for pavements is crucial to achieving sustainability. Implementing RCA for new pavement can minimize carbon footprint, conserve natural resources, reduce harmful emissions, and lower life cycle costs. Compared to natural aggregate (NA), RCA pavement has fewer comprehensive studies and sustainability assessments.
CHINA’S GEO-ECONOMIC OUTREACH IN CENTRAL ASIAN COUNTRIES AND FUTURE PROSPECT
The rivalry between prominent international actors for dominance over Central Asia's hydrocarbon
reserves and the ancient silk trade route, along with China's diplomatic endeavours in the area, has been
referred to as the "New Great Game." This research centres on the power struggle, considering
geopolitical, geostrategic, and geoeconomic variables. Topics including trade, political hegemony, oil
politics, and conventional and nontraditional security are all explored and explained by the researcher.
Using Mackinder's Heartland, Spykman Rimland, and Hegemonic Stability theories, examines China's role
in Central Asia. This study adheres to the empirical epistemological method and has taken care of
objectivity. This study analyze primary and secondary research documents critically to elaborate role of
china’s geo economic outreach in central Asian countries and its future prospect. China is thriving in trade,
pipeline politics, and winning states, according to this study, thanks to important instruments like the
Shanghai Cooperation Organisation and the Belt and Road Economic Initiative. According to this study,
China is seeing significant success in commerce, pipeline politics, and gaining influence on other
governments. This success may be attributed to the effective utilisation of key tools such as the Shanghai
Cooperation Organisation and the Belt and Road Economic Initiative.
Harnessing WebAssembly for Real-time Stateless Streaming Pipelines
Traditionally, dealing with real-time data pipelines has involved significant overhead, even for straightforward tasks like data transformation or masking. However, in this talk, we’ll venture into the dynamic realm of WebAssembly (WASM) and discover how it can revolutionize the creation of stateless streaming pipelines within a Kafka (Redpanda) broker. These pipelines are adept at managing low-latency, high-data-volume scenarios.
Electric vehicle and photovoltaic advanced roles in enhancing the financial p...
Climate change's impact on the planet forced the United Nations and governments to promote green energies and electric transportation. The deployments of photovoltaic (PV) and electric vehicle (EV) systems gained stronger momentum due to their numerous advantages over fossil fuel types. The advantages go beyond sustainability to reach financial support and stability. The work in this paper introduces the hybrid system between PV and EV to support industrial and commercial plants. This paper covers the theoretical framework of the proposed hybrid system including the required equation to complete the cost analysis when PV and EV are present. In addition, the proposed design diagram which sets the priorities and requirements of the system is presented. The proposed approach allows setup to advance their power stability, especially during power outages. The presented information supports researchers and plant owners to complete the necessary analysis while promoting the deployment of clean energy. The result of a case study that represents a dairy milk farmer supports the theoretical works and highlights its advanced benefits to existing plants. The short return on investment of the proposed approach supports the paper's novelty approach for the sustainable electrical system. In addition, the proposed system allows for an isolated power setup without the need for a transmission line which enhances the safety of the electrical network
KuberTENes Birthday Bash Guadalajara - K8sGPT first impressions
K8sGPT is a tool that analyzes and diagnoses Kubernetes clusters. This presentation was used to share the requirements and dependencies to deploy K8sGPT in a local environment.
International Conference on NLP, Artificial Intelligence, Machine Learning an...
International Conference on NLP, Artificial Intelligence, Machine Learning and Applications (NLAIM 2024) offers a premier global platform for exchanging insights and findings in the theory, methodology, and applications of NLP, Artificial Intelligence, Machine Learning, and their applications. The conference seeks substantial contributions across all key domains of NLP, Artificial Intelligence, Machine Learning, and their practical applications, aiming to foster both theoretical advancements and real-world implementations. With a focus on facilitating collaboration between researchers and practitioners from academia and industry, the conference serves as a nexus for sharing the latest developments in the field.
Literature Review Basics and Understanding Reference Management.pptx
Three-day training on academic research focuses on analytical tools at United Technical College, supported by the University Grant Commission, Nepal. 24-26 May 2024
Technical Drawings introduction to drawing of prisms
Method of technical Drawing of prisms,and cylinders.
IEEE Aerospace and Electronic Systems Society as a Graduate Student Member
IEEE Aerospace and Electronic Systems Society as a Graduate Student Member
A SYSTEMATIC RISK ASSESSMENT APPROACH FOR SECURING THE SMART IRRIGATION SYSTEMS
The smart irrigation system represents an innovative approach to optimize water usage in agricultural and landscaping practices. The integration of cutting-edge technologies, including sensors, actuators, and data analysis, empowers this system to provide accurate monitoring and control of irrigation processes by leveraging real-time environmental conditions. The main objective of a smart irrigation system is to optimize water efficiency, minimize expenses, and foster the adoption of sustainable water management methods. This paper conducts a systematic risk assessment by exploring the key components/assets and their functionalities in the smart irrigation system. The crucial role of sensors in gathering data on soil moisture, weather patterns, and plant well-being is emphasized in this system. These sensors enable intelligent decision-making in irrigation scheduling and water distribution, leading to enhanced water efficiency and sustainable water management practices. Actuators enable automated control of irrigation devices, ensuring precise and targeted water delivery to plants. Additionally, the paper addresses the potential threat and vulnerabilities associated with smart irrigation systems. It discusses limitations of the system, such as power constraints and computational capabilities, and calculates the potential security risks. The paper suggests possible risk treatment methods for effective secure system operation. In conclusion, the paper emphasizes the significant benefits of implementing smart irrigation systems, including improved water conservation, increased crop yield, and reduced environmental impact. Additionally, based on the security analysis conducted, the paper recommends the implementation of countermeasures and security approaches to address vulnerabilities and ensure the integrity and reliability of the system. By incorporating these measures, smart irrigation technology can revolutionize water management practices in agriculture, promoting sustainability, resource efficiency, and safeguarding against potential security threats.
6th International Conference on Machine Learning & Applications (CMLA 2024)
6th International Conference on Machine Learning & Applications (CMLA 2024) will provide an excellent international forum for sharing knowledge and results in theory, methodology and applications of on Machine Learning & Applications.
Presentation of IEEE Slovenia CIS (Computational Intelligence Society) Chapte...
Presentation of IEEE Slovenia CIS (Computational Intelligence Society) Chapte...University of Maribor
Slides from talk presenting:
Aleš Zamuda: Presentation of IEEE Slovenia CIS (Computational Intelligence Society) Chapter and Networking.
Presentation at IcETRAN 2024 session:
"Inter-Society Networking Panel GRSS/MTT-S/CIS
Panel Session: Promoting Connection and Cooperation"
IEEE Slovenia GRSS
IEEE Serbia and Montenegro MTT-S
IEEE Slovenia CIS
11TH INTERNATIONAL CONFERENCE ON ELECTRICAL, ELECTRONIC AND COMPUTING ENGINEERING
3-6 June 2024, Niš, SerbiaRecently uploaded (20)
bank management system in java and mysql report1.pdf
bank management system in java and mysql report1.pdf
DEEP LEARNING FOR SMART GRID INTRUSION DETECTION: A HYBRID CNN-LSTM-BASED MODEL
DEEP LEARNING FOR SMART GRID INTRUSION DETECTION: A HYBRID CNN-LSTM-BASED MODEL
Recycled Concrete Aggregate in Construction Part III
Recycled Concrete Aggregate in Construction Part III
CHINA’S GEO-ECONOMIC OUTREACH IN CENTRAL ASIAN COUNTRIES AND FUTURE PROSPECT
CHINA’S GEO-ECONOMIC OUTREACH IN CENTRAL ASIAN COUNTRIES AND FUTURE PROSPECT
Generative AI leverages algorithms to create various forms of content
Generative AI leverages algorithms to create various forms of content
Harnessing WebAssembly for Real-time Stateless Streaming Pipelines
Harnessing WebAssembly for Real-time Stateless Streaming Pipelines
Electric vehicle and photovoltaic advanced roles in enhancing the financial p...
Electric vehicle and photovoltaic advanced roles in enhancing the financial p...
2. Operations Strategy in a Global Environment.ppt
2. Operations Strategy in a Global Environment.ppt
KuberTENes Birthday Bash Guadalajara - K8sGPT first impressions
KuberTENes Birthday Bash Guadalajara - K8sGPT first impressions
International Conference on NLP, Artificial Intelligence, Machine Learning an...
International Conference on NLP, Artificial Intelligence, Machine Learning an...
Literature Review Basics and Understanding Reference Management.pptx
Literature Review Basics and Understanding Reference Management.pptx
Technical Drawings introduction to drawing of prisms
Technical Drawings introduction to drawing of prisms
IEEE Aerospace and Electronic Systems Society as a Graduate Student Member
IEEE Aerospace and Electronic Systems Society as a Graduate Student Member
A SYSTEMATIC RISK ASSESSMENT APPROACH FOR SECURING THE SMART IRRIGATION SYSTEMS
A SYSTEMATIC RISK ASSESSMENT APPROACH FOR SECURING THE SMART IRRIGATION SYSTEMS
ML Based Model for NIDS MSc Updated Presentation.v2.pptx
ML Based Model for NIDS MSc Updated Presentation.v2.pptx
6th International Conference on Machine Learning & Applications (CMLA 2024)
6th International Conference on Machine Learning & Applications (CMLA 2024)
Presentation of IEEE Slovenia CIS (Computational Intelligence Society) Chapte...
Presentation of IEEE Slovenia CIS (Computational Intelligence Society) Chapte...
Minimax algorithm ex.pptx
- 1. EXAMPLE At the terminal node, the terminal values are given so we will compare those value and backtrack the tree until the initial state occurs. Following are the main steps involved in solving the two-player game tree: Step-1: In the first step, the algorithm generates the entire game-tree and apply the utility function to get the utility values for the terminal states. In the below tree diagram, let's take A is the initial state of the tree. Suppose maximizer takes first turn which has worst-case initial value =- infinity, and minimizer will take next turn which has worst-case initial value = +infinity.
- 2. • Step 2: Now, first we find the utilities value for the Maximizer, its initial value is -∞, so we will compare each value in terminal state with initial value of Maximizer and determines the higher nodes values. It will find the maximum among the all. • For node D max(-1,- -∞) => max(-1,4)= 4 • For Node E max(2, -∞) => max(2, 6)= 6 • For Node F max(-3, -∞) => max(-3,-5) = -3 • For node G max(0, -∞) = max(0, 7) = 7
- 3. • Step 3: In the next step, it's a turn for minimizer, so it will compare all nodes value with +∞, and will find the 3rd layer node values. • For node B= min(4,6) = 4 • For node C= min (-3, 7) = -3
- 4. • Step 4: Now it's a turn for Maximizer, and it will again choose the maximum of all nodes value and find the maximum value for the root node. In this game tree, there are only 4 layers, hence we reach immediately to the root node, but in real games, there will be more than 4 layers. • For node A max(4, -3)= 4