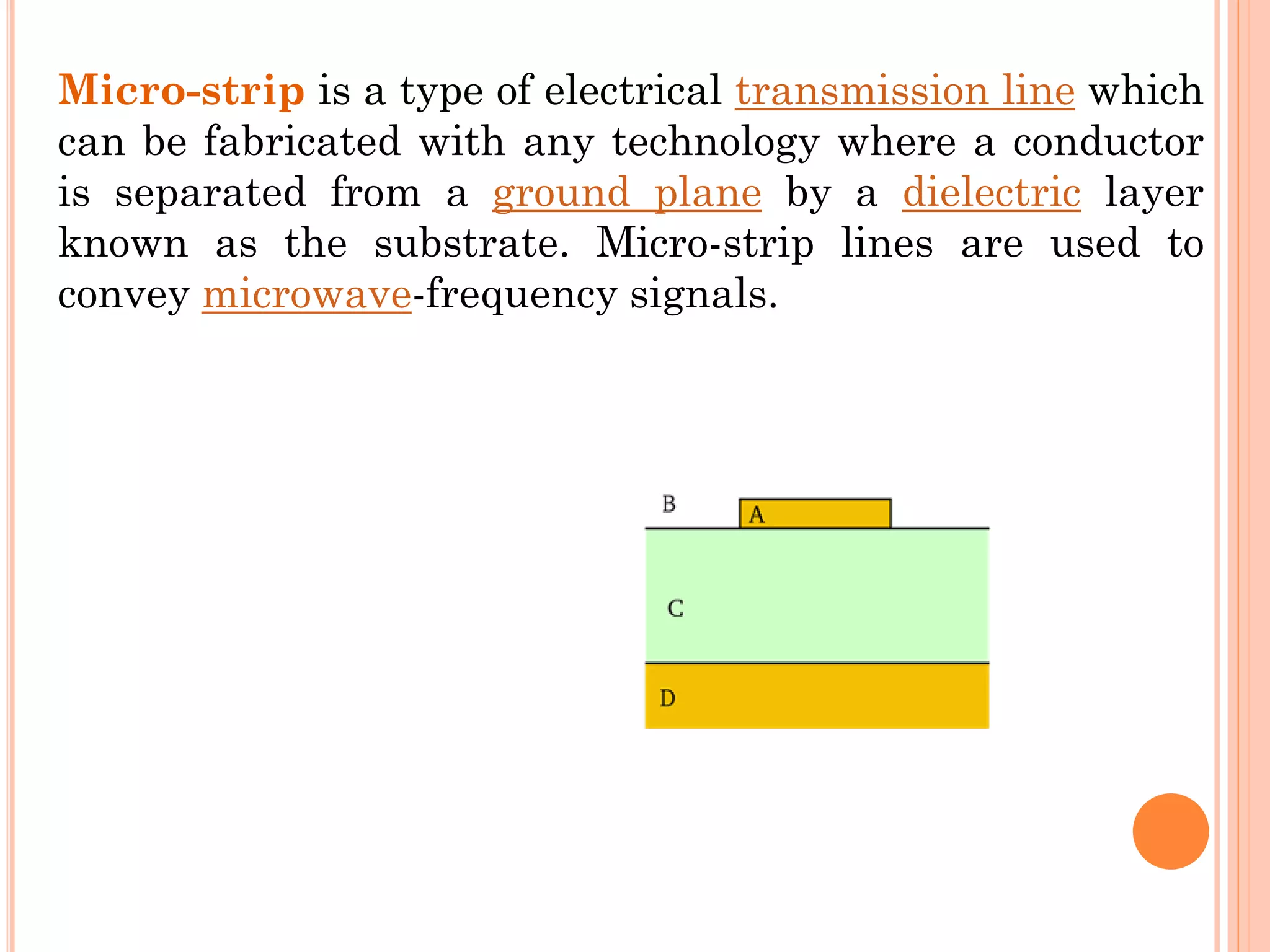
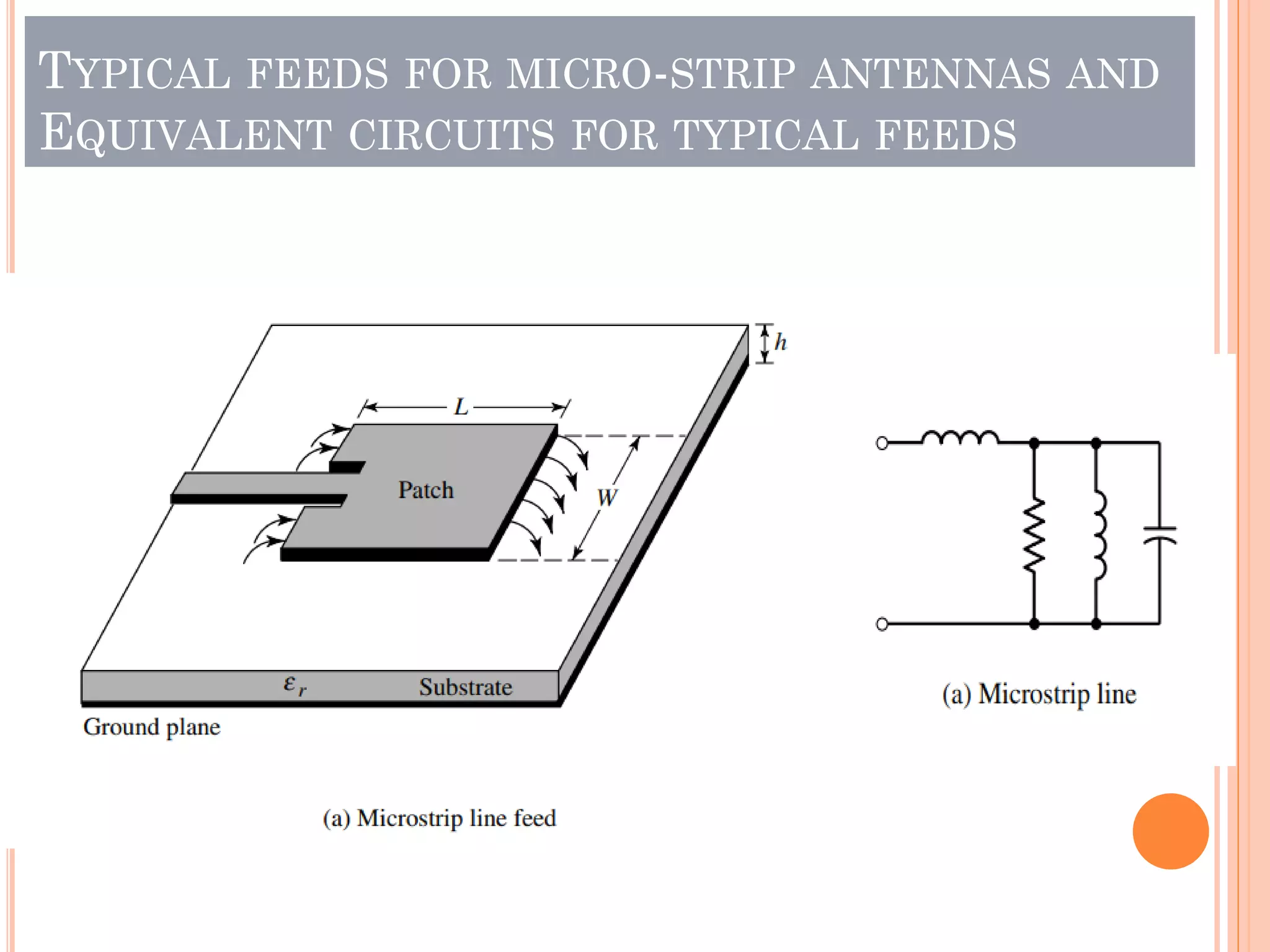
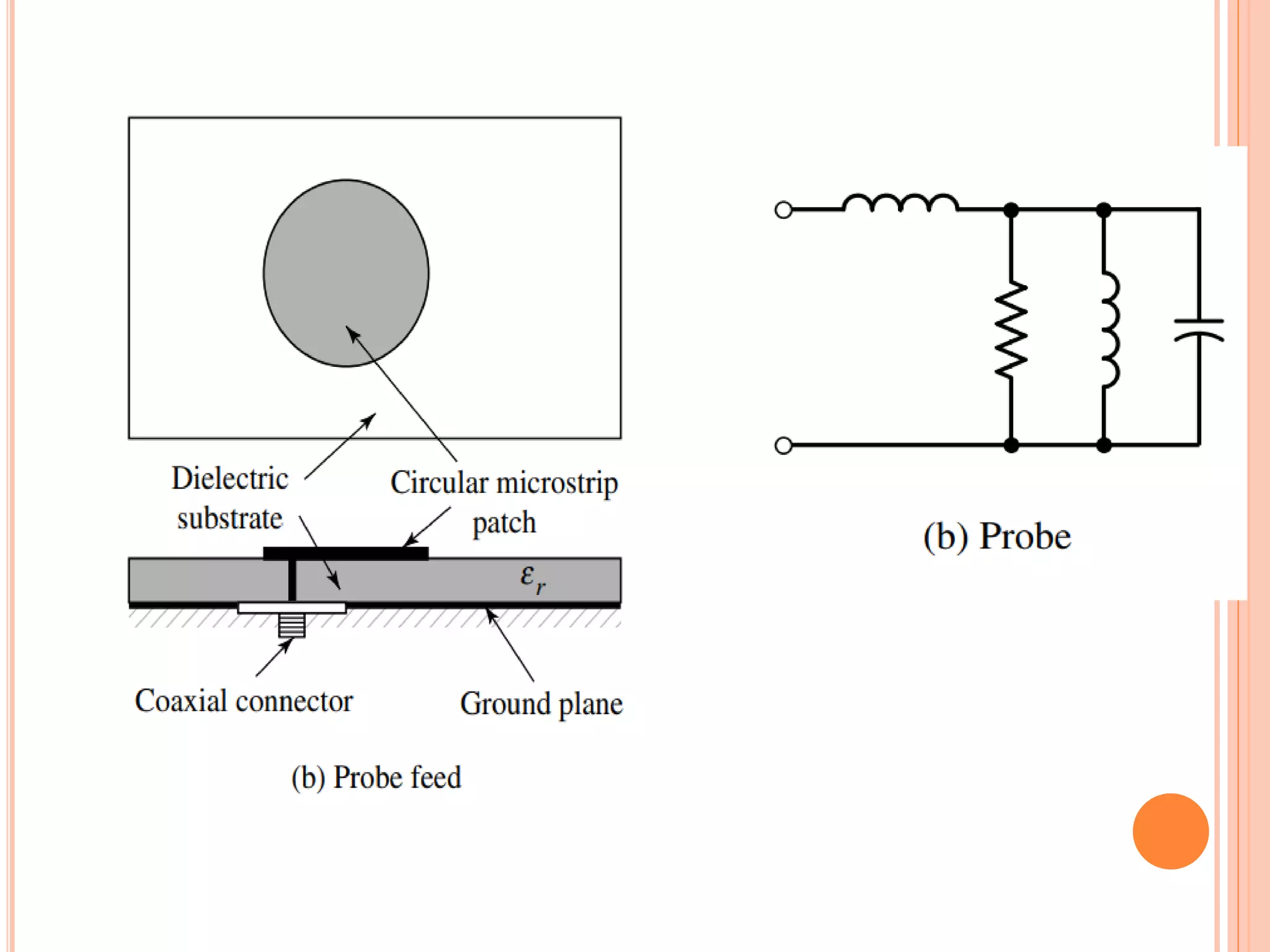
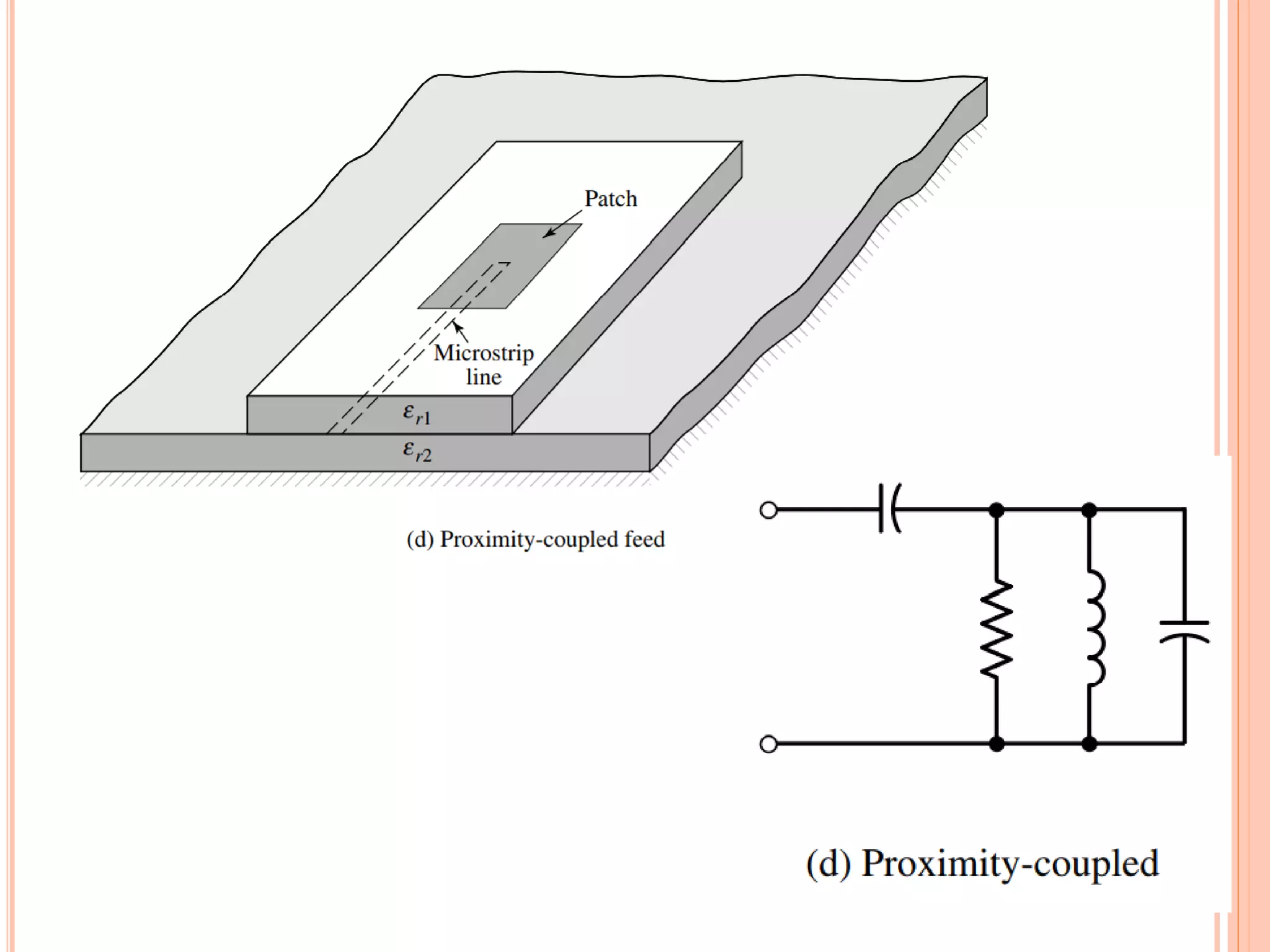
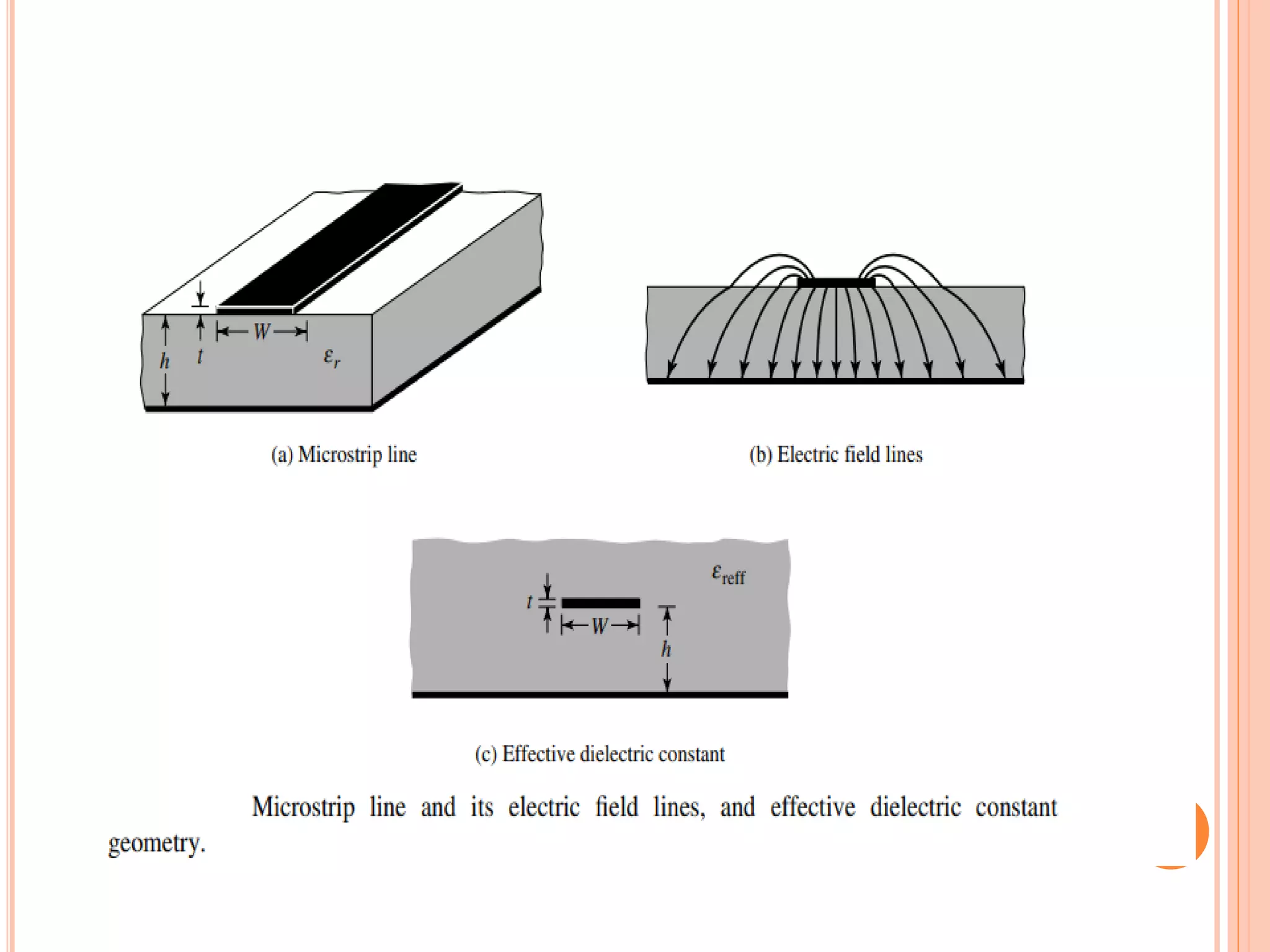
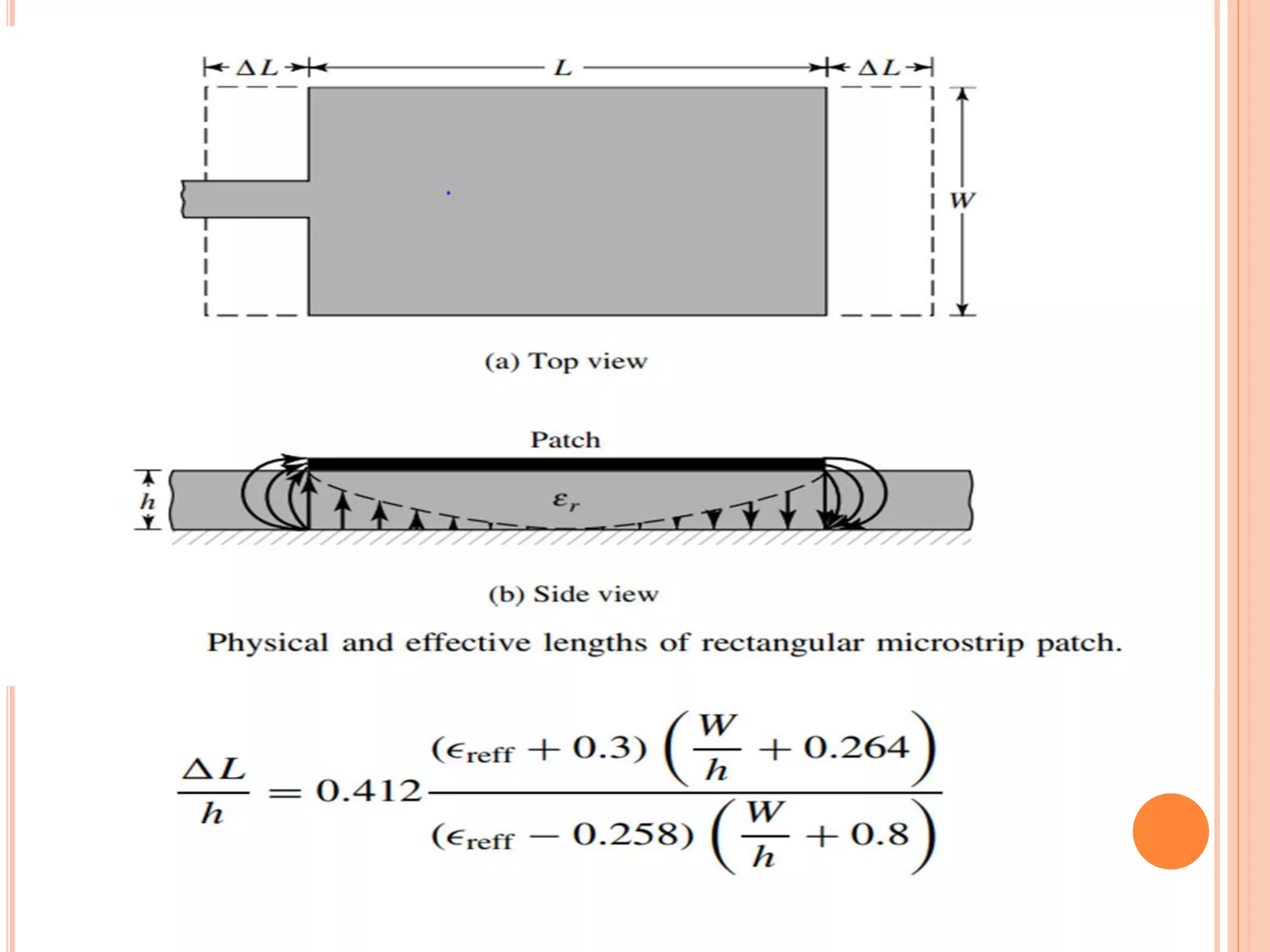
Micro-strip antennas consist of a conducting patch on a dielectric substrate backed by a ground plane. They are inexpensive to produce and can be fabricated using printed circuit board technology. The patch shape is typically rectangular and can be analyzed using transmission line models. Key design considerations include the effective dielectric constant which influences the resonant frequency, as well as fringing effects along the patch edges which affect the patch length. A common design procedure specifies the resonant frequency, substrate properties, and calculates the appropriate patch dimensions.

1. MICRO-STRIP ANTENNAS

2. Micro-strip is a type of electrical transmission line which
can be fabricated with any technology where a conductor
is separated from a ground plane by a dielectric layer
known as the substrate. Micro-strip lines are used to
convey microwave-frequency signals.

4. Microwave components such as antennas, couplers,
filters, power dividers etc. can be formed from microstrip,
with the entire device existing as the pattern of
metallization on the substrate. Micro-strip is thus much
less expensive than traditional waveguide technology.
Micro-strip antennas are one of the most popular
antennas in the wireless communication market.
Micro-strip antennas (AKA patch antennas) were first
proposed in 1950s. The greatest interest in micro-strip
antennas, leading to development and research, started
in 1970s.

8. Basic Characteristics
A micro-strip antenna (MSA) basically consists of radiating
patch, dielectric substrate, feed and ground plane. Patch and
ground plane made of material such as copper or gold. The
structure of the MSA and its electric field distribution
excited in its fundamental mode is shown in Figure, consist
of a very thin (t ≪ 𝛌𝟎, where 𝛌𝟎 is the free-space wavelength)
metallic strip (patch) placed a small fraction of a wavelength
(h ≪ 𝛌𝟎, usually 0.003𝛌𝟎 ≤ h ≤ 0.05𝛌𝟎) above a ground plane.
For a rectangular patch, the length L of the element is
usually 𝛌𝟎∕3 < L < 𝛌𝟎∕2. There are numerous substrates that
can be used for the design of micro-strip antennas, and their
dielectric constants are usually in the range of 2.2 ≤ 𝜺𝒓 ≤ 12.
The strip (patch) and the ground plane are separated by a
dielectric sheet (referred to as the substrate), as shown in
Figure.

10. PATCH SHAPES

11. TYPICAL FEEDS FOR MICRO-STRIP ANTENNAS AND
EQUIVALENT CIRCUITS FOR TYPICAL FEEDS

15. Methods of Analysis
There are many methods of analysis for micro-strip antennas.
The most popular models are the transmission-line, cavity,
and full wave (which include primarily integral
equations/Moment Method). The transmission-line model is
the easiest of all, it gives good physical insight, but is less
accurate and it is more difficult to model coupling. Compared
to the transmission-line model, the cavity model is more
accurate but at the same time more complex. However, it also
gives good physical insight and is rather difficult to model
coupling, although it has been used successfully. In general
when applied properly, the full-wave models are very
accurate, very versatile, and can treat single elements, finite
and infinite arrays, stacked elements, arbitrary shaped
elements, and coupling. However they are the most complex
models and usually give less physical insight.

16. RECTANGULAR PATCH
Transmission-Line Model
It was indicated earlier that the transmission-line model
is the easiest of all but it yields the least accurate results
and it lacks the versatility. A rectangular micro-strip
antenna can be represented as an array of two radiating
narrow apertures (slots), each of width W and height h,
separated by a distance L. Basically the transmission-line
model represents the micro-strip antenna by two slots,
separated by a low-impedance Zc transmission line of
length L

17. A. Fringing Effects
For the principal E-plane (xy-plane) fringing is a
function of the ratio of the length of the patch L to the
height h of the substrate (L/h) and the dielectric
constant 𝜺𝒓 of the substrate. Since for micro-strip
antennas L/h ≫ 1, fringing is reduced.
W/h ≫ 1 and 𝜺𝒓 ≫ 1
The effective dielectric constant is defined as the
dielectric constant of the uniform dielectric material ,
the effective dielectric constant has values in the range
of 1 < 𝜺𝒓𝒆𝒇𝒇 < 𝜺𝒓 .

19. The initial values (at low frequencies) of the
effective dielectric constant are referred to as the
static values, and they are given by

20. B. EFFECTIVE LENGTH, RESONANT
FREQUENCY, AND EFFECTIVE WIDTH
Because of the fringing effects, electrically the patch of
the microstrip antenna looks greater than its physical
dimensions. For the principal E-plane (xy-plane), this is
demonstrated in Figure where the dimensions of the
patch along its length have been extended on each end by
a distance ΔL, which is a function of the effective
dielectric constant 𝜺𝒓𝒆𝒇𝒇 and the width-to-height ratio
(W/h). A very popular and practical approximate relation
for the normalized extension of the length is

23. The q factor is referred to as the fringe
factor (length reduction factor). As the
substrate height increases, fringing also
increases and leads to larger separations
between the radiating edges and lower
resonant frequencies.
Where q

24. C. Design
Based on the simplified formulation that has been
described, a design procedure is outlined which leads to
practical designs of rectangular micro-strip antennas. The
procedure assumes that the specified information includes
the dielectric constant of the substrate (𝜺𝒓 ), the resonant
frequency (𝒇𝒓 ), and the height of the substrate h. The
procedure is as follows:

26. Example: Design a rectangular micro-strip
antenna using a substrate (RT/duroid 5880) with
dielectric constant of 2.2, h = 0.1588 cm (0.0625
inches) so as to resonate at 10 GHz.