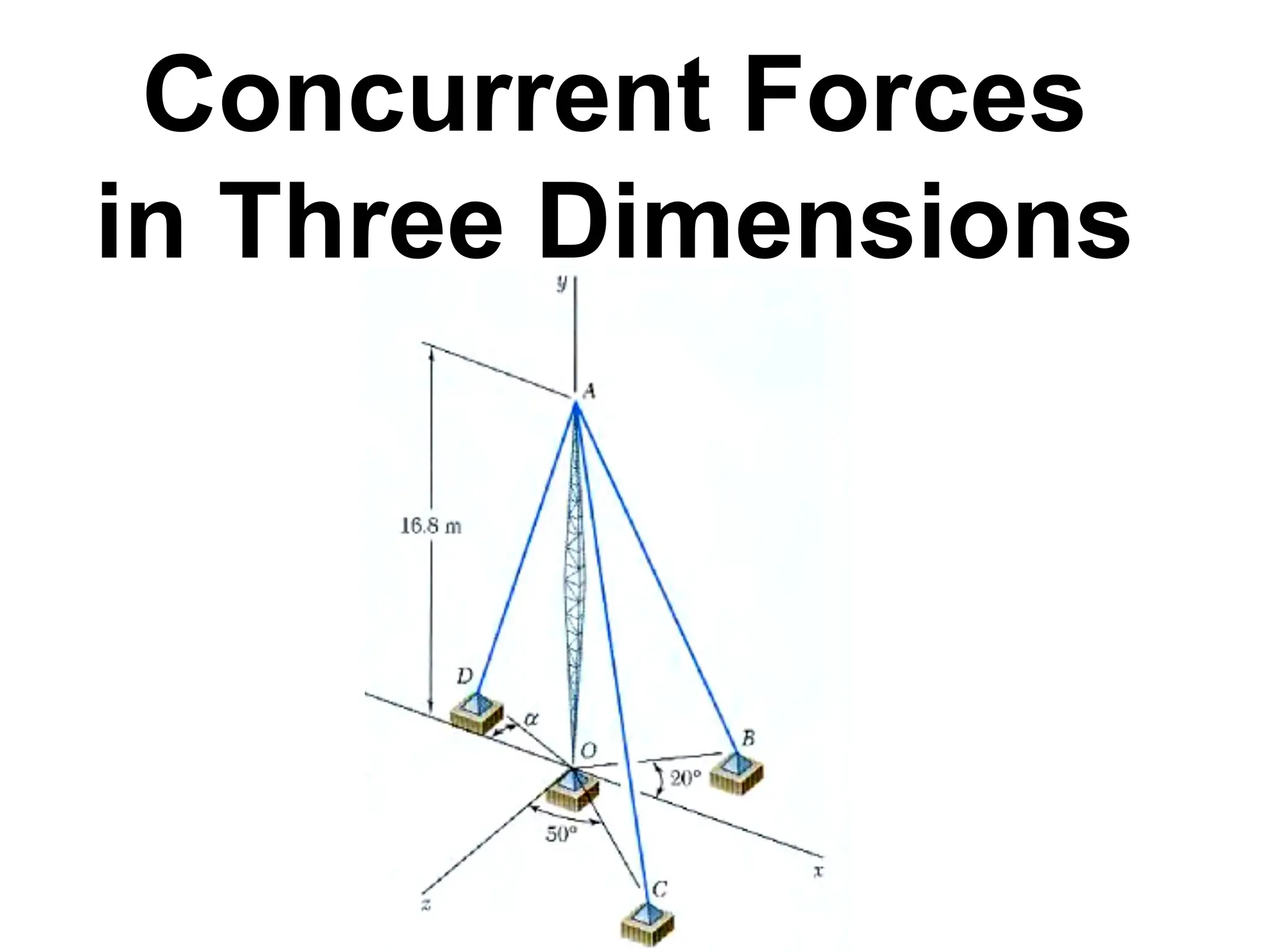
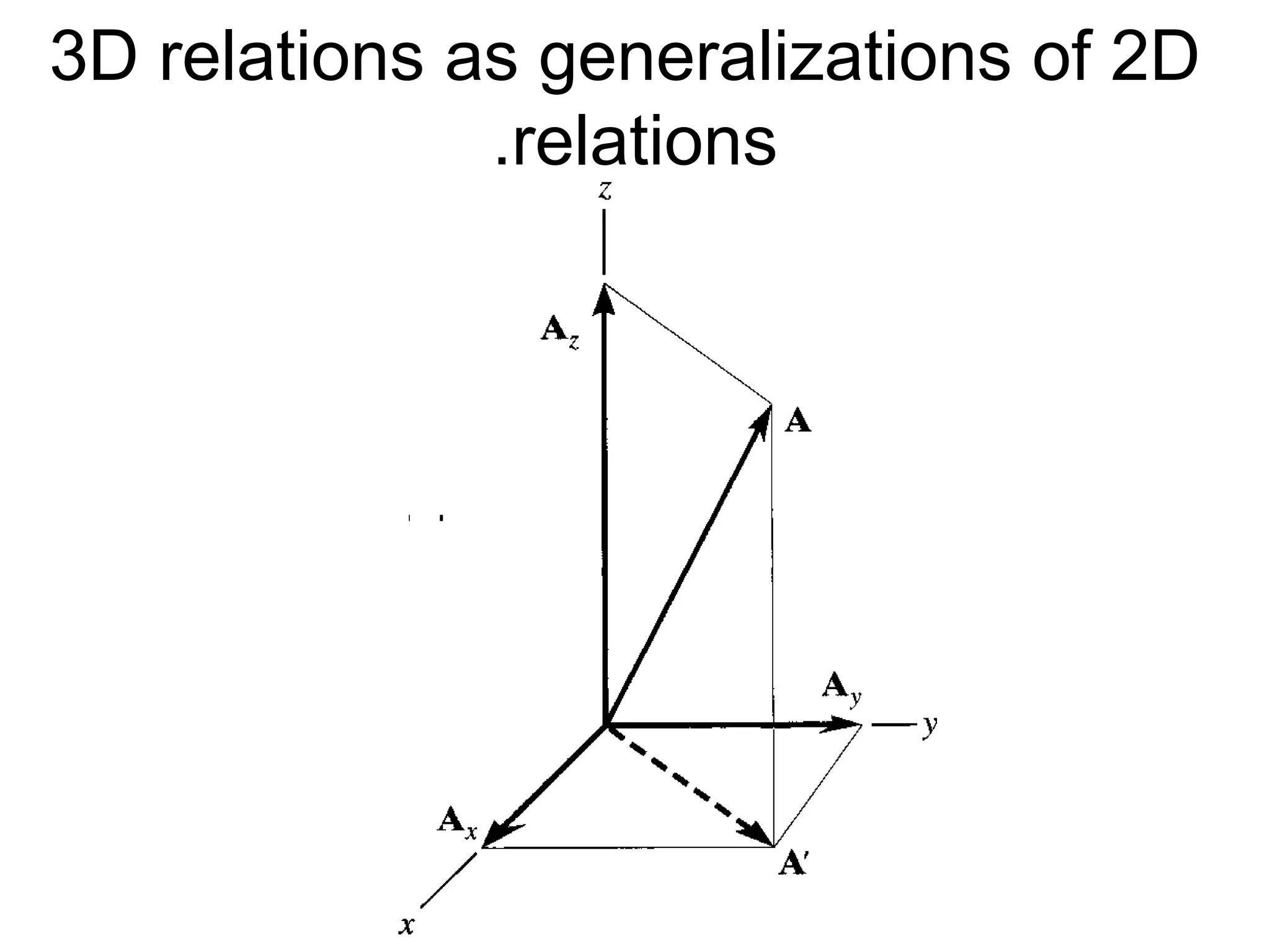
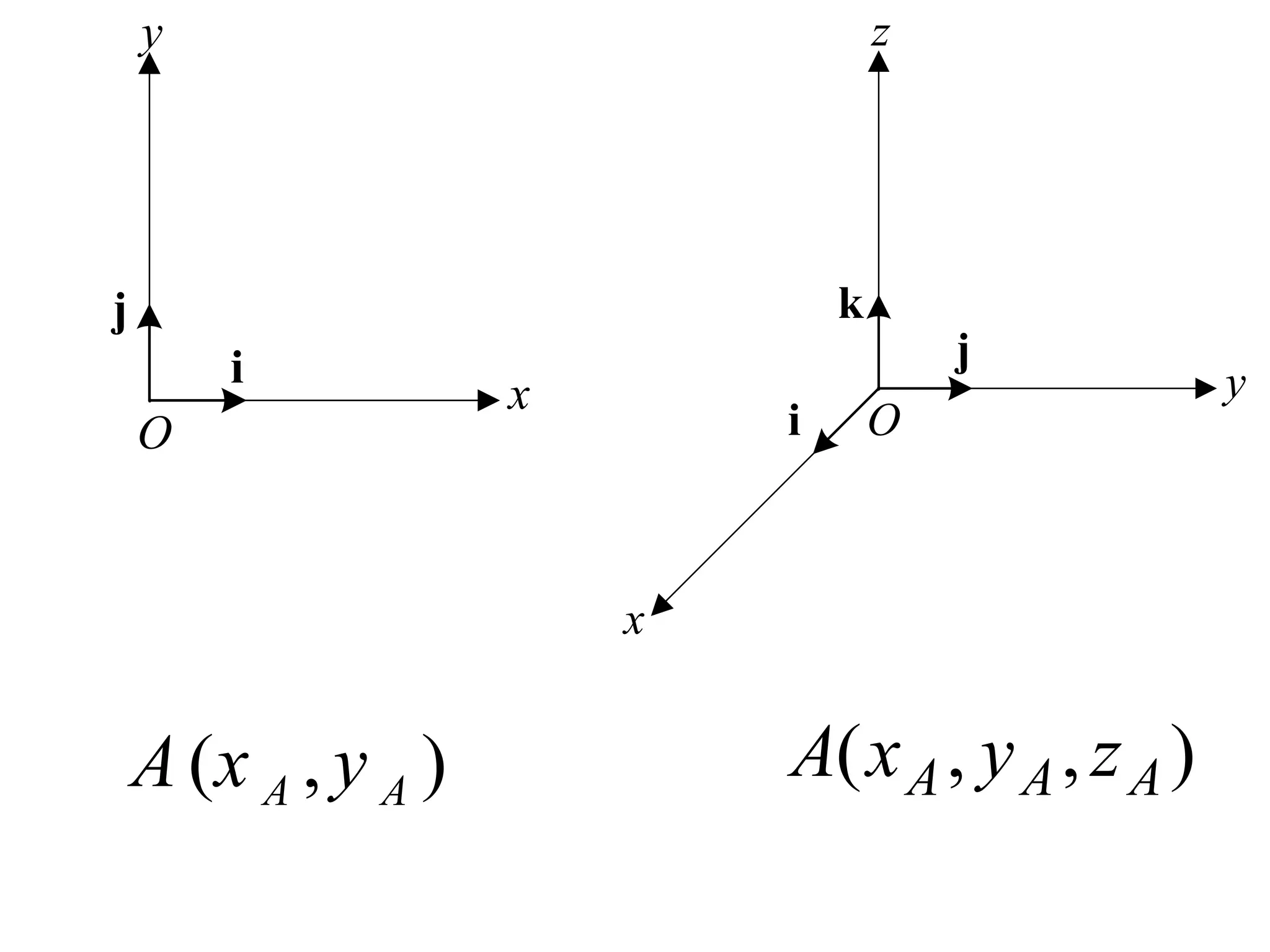
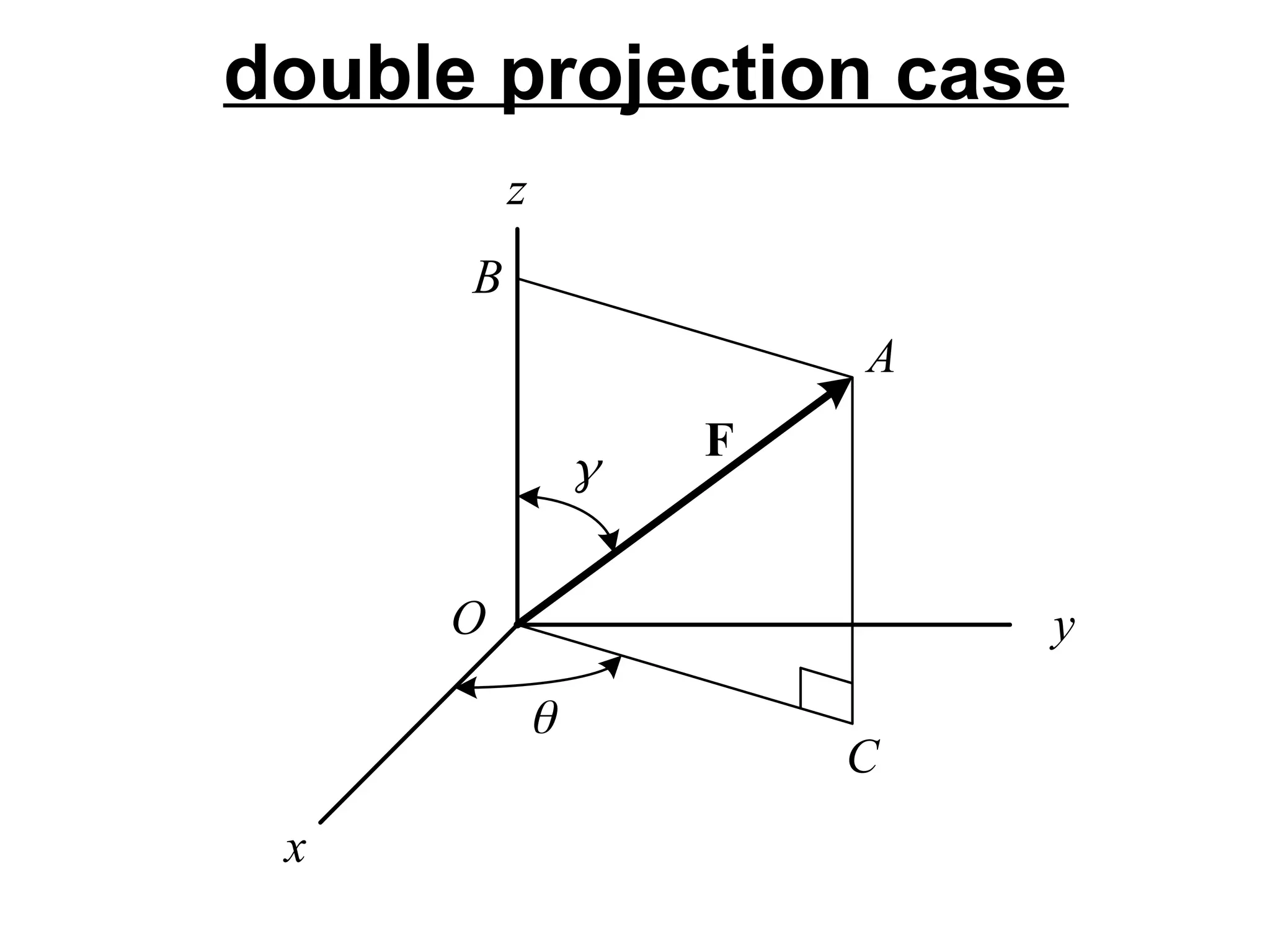
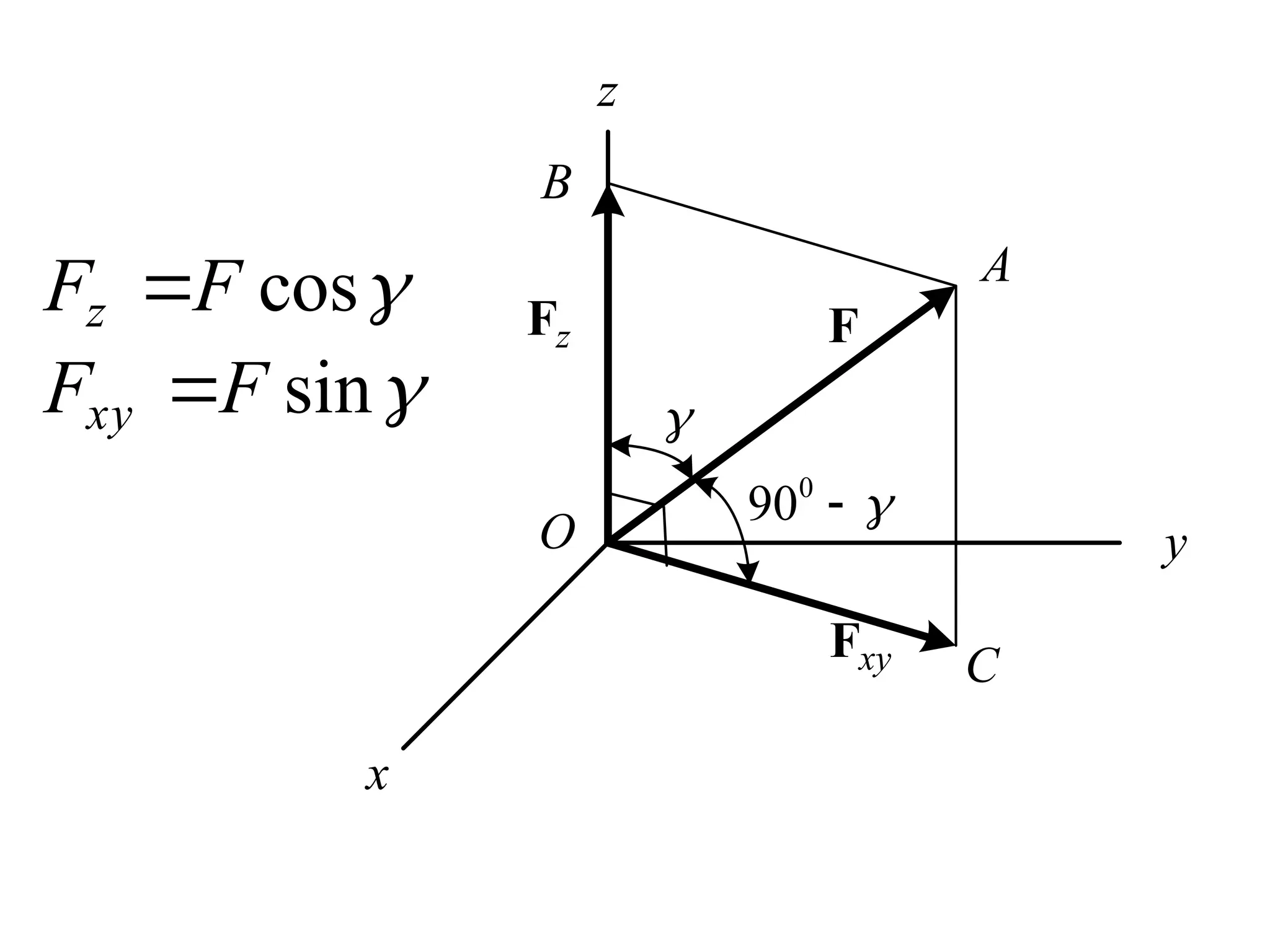
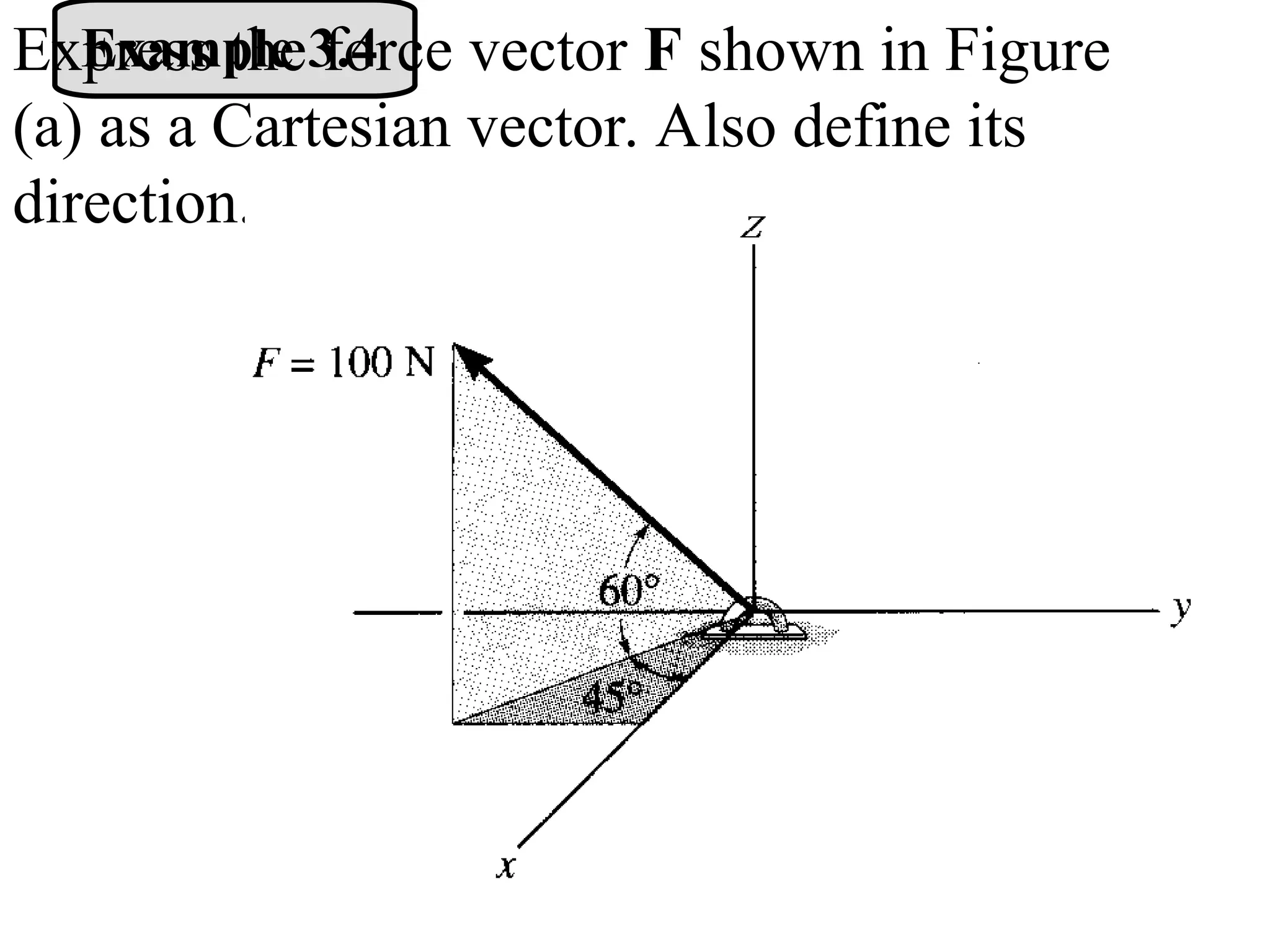
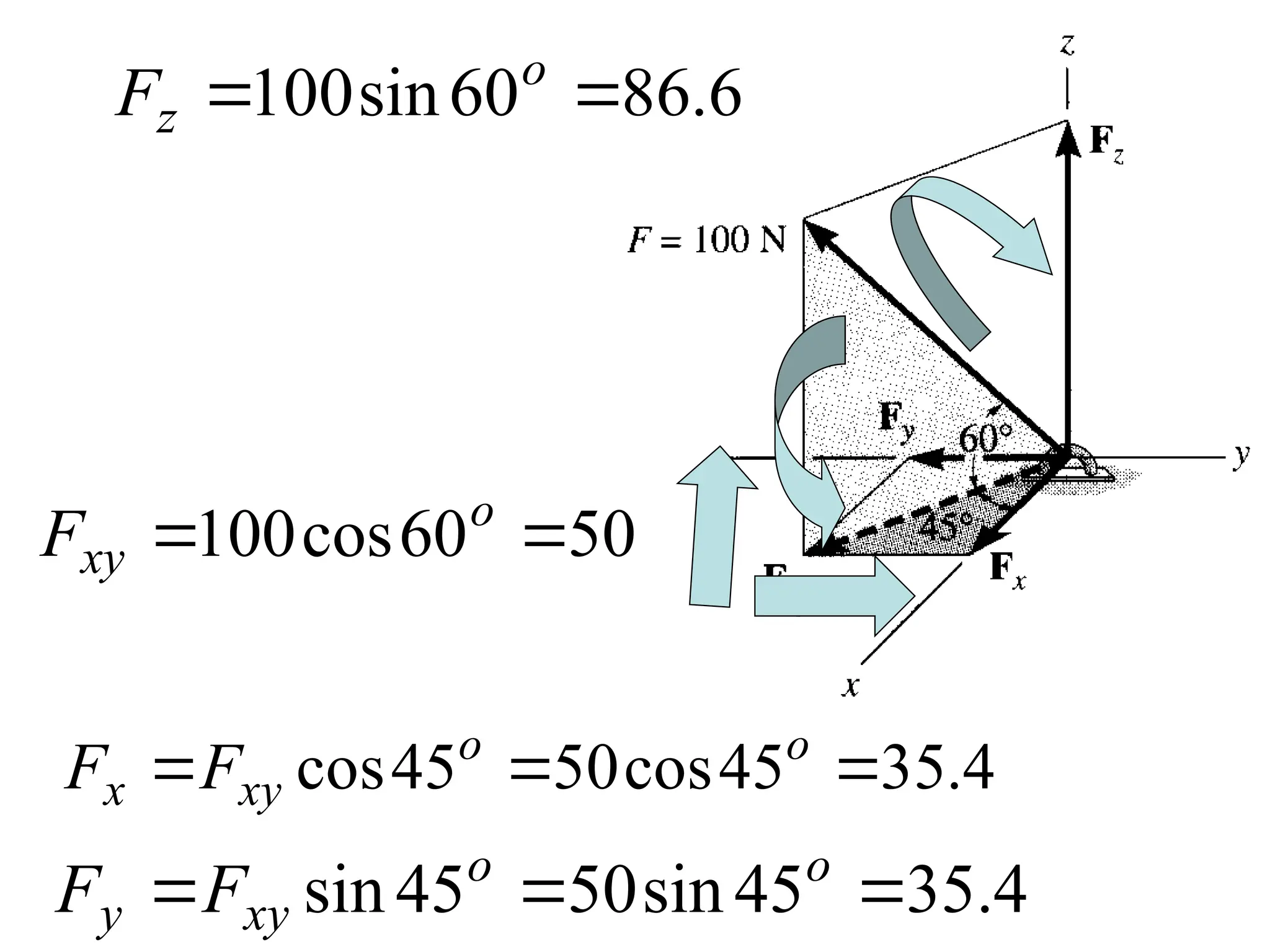
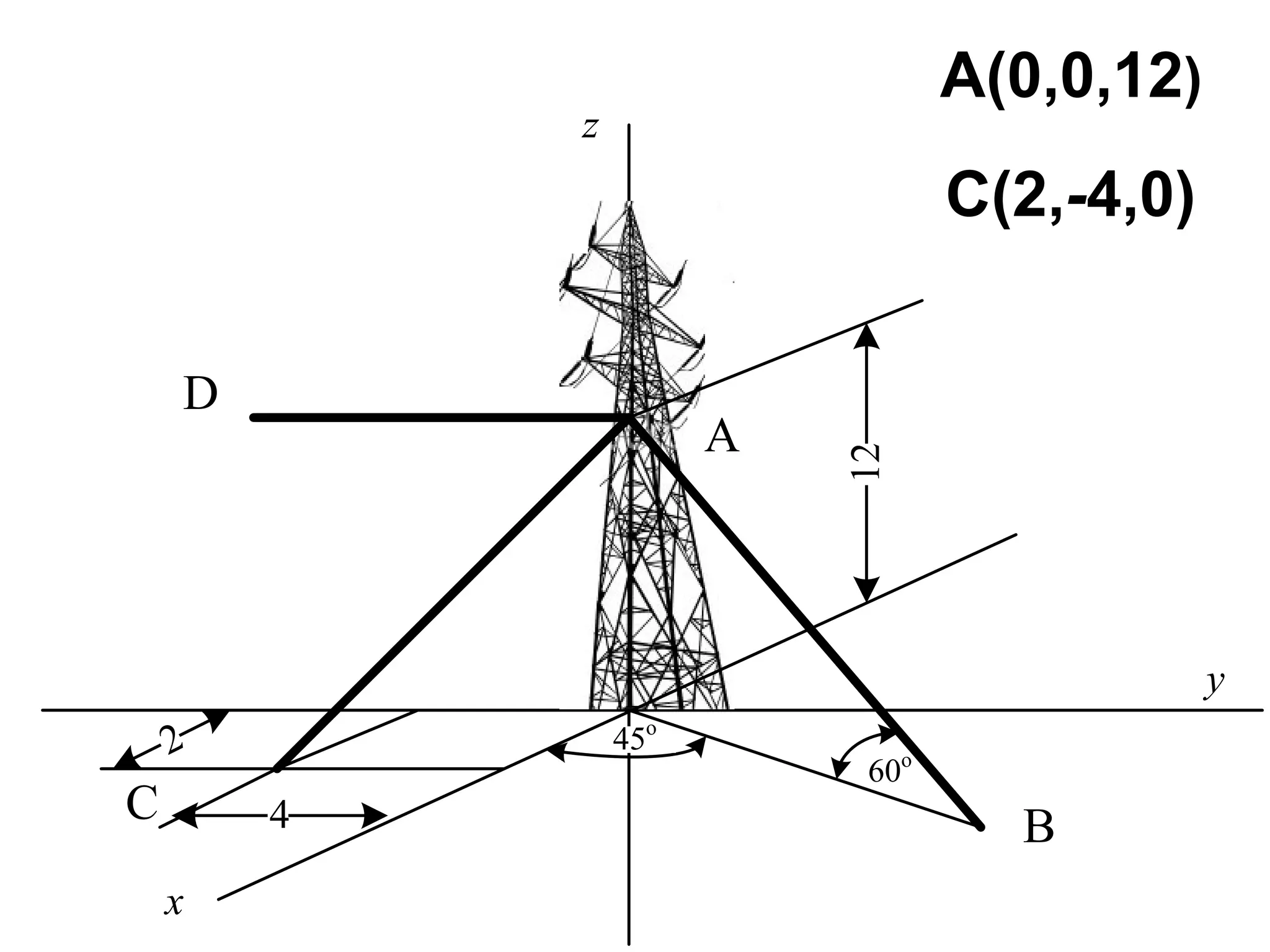
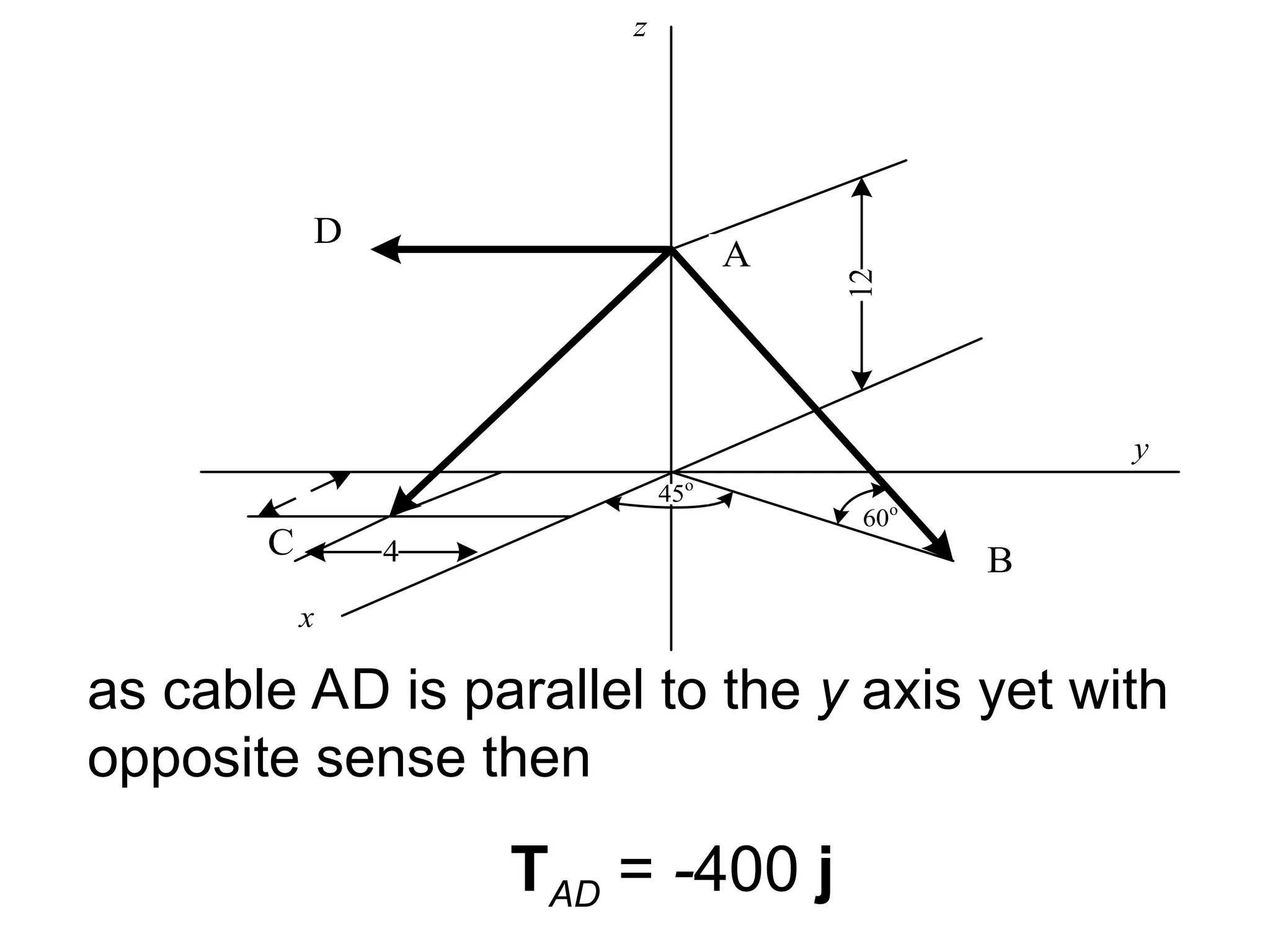
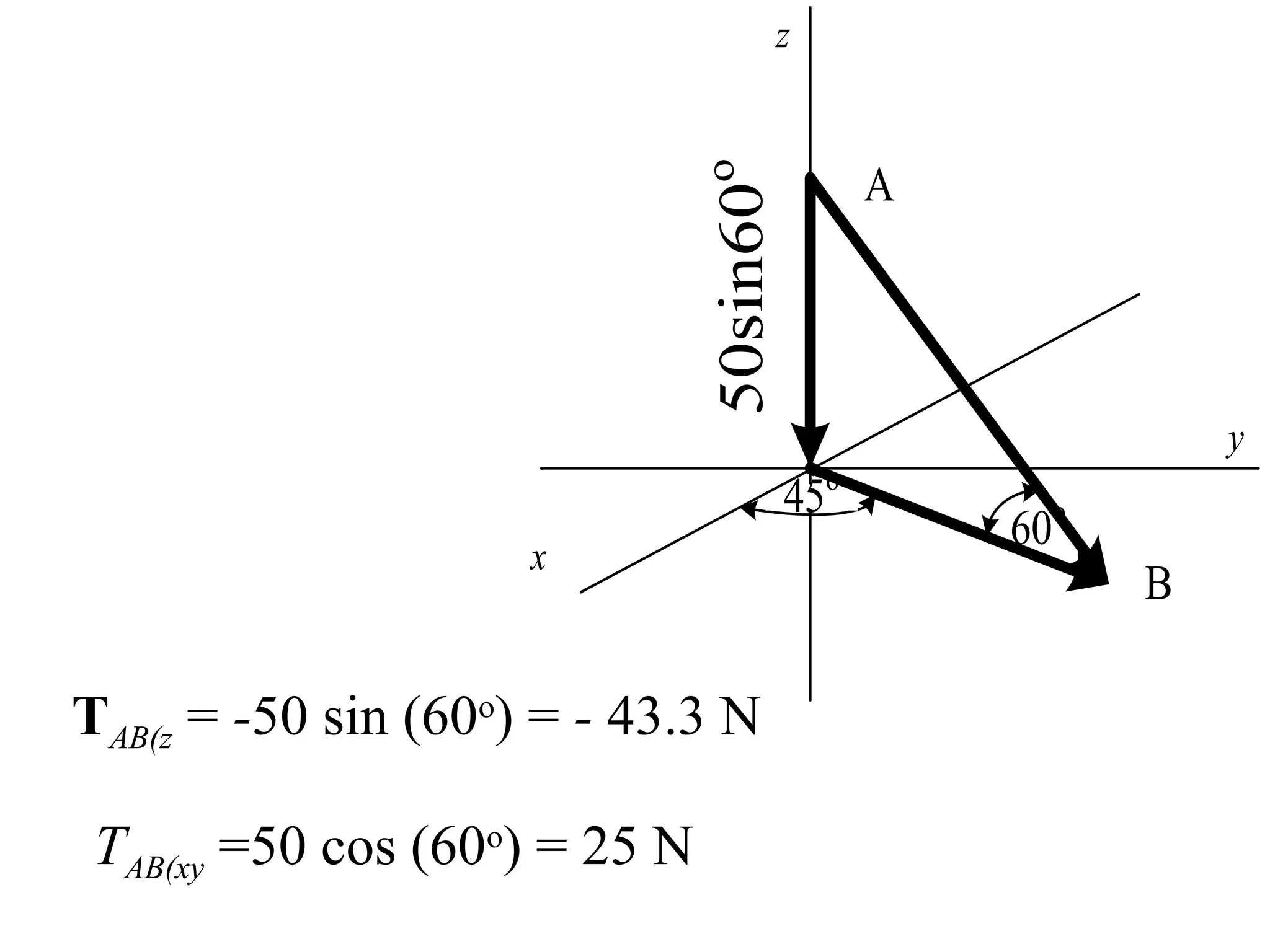
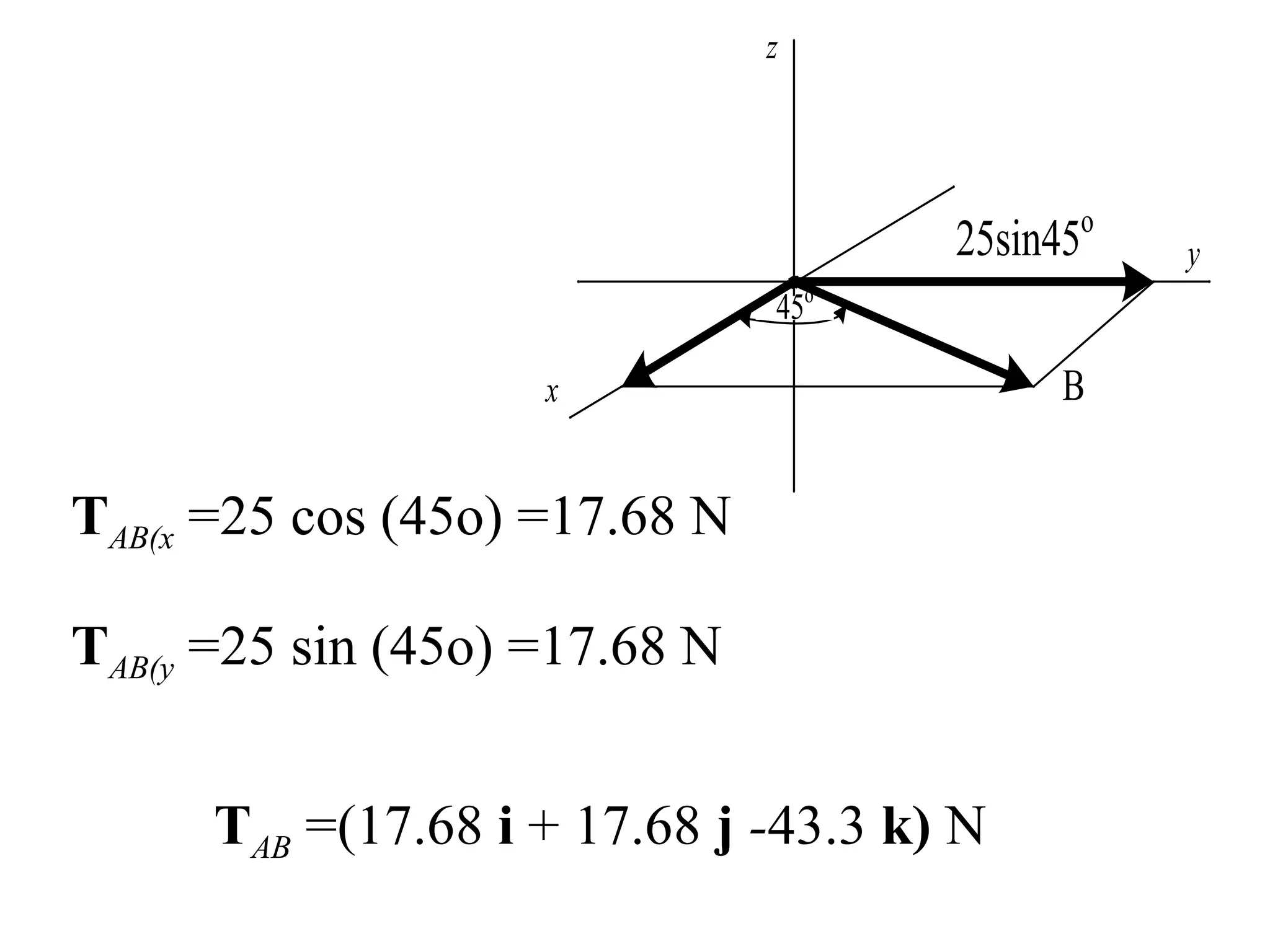
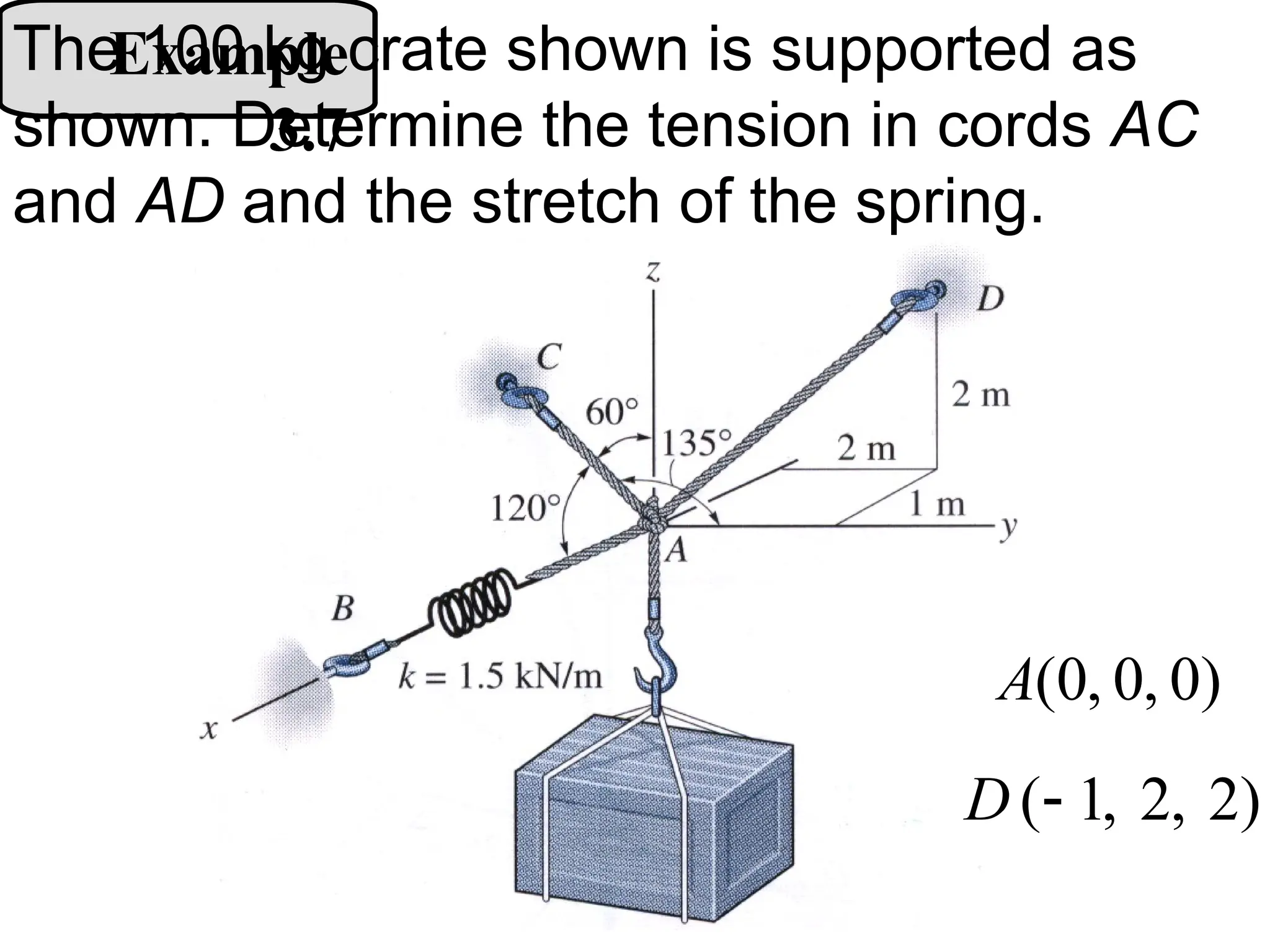
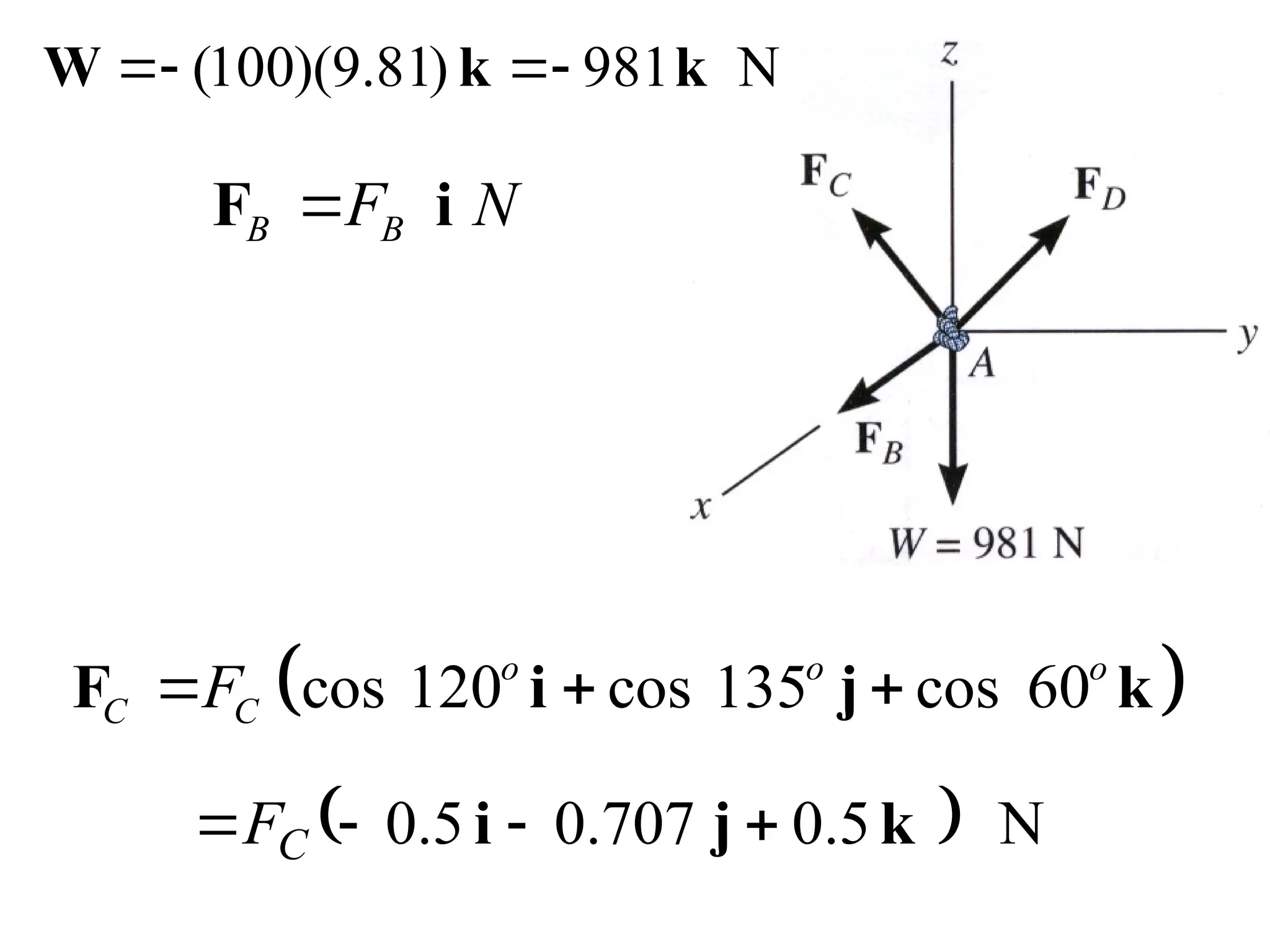
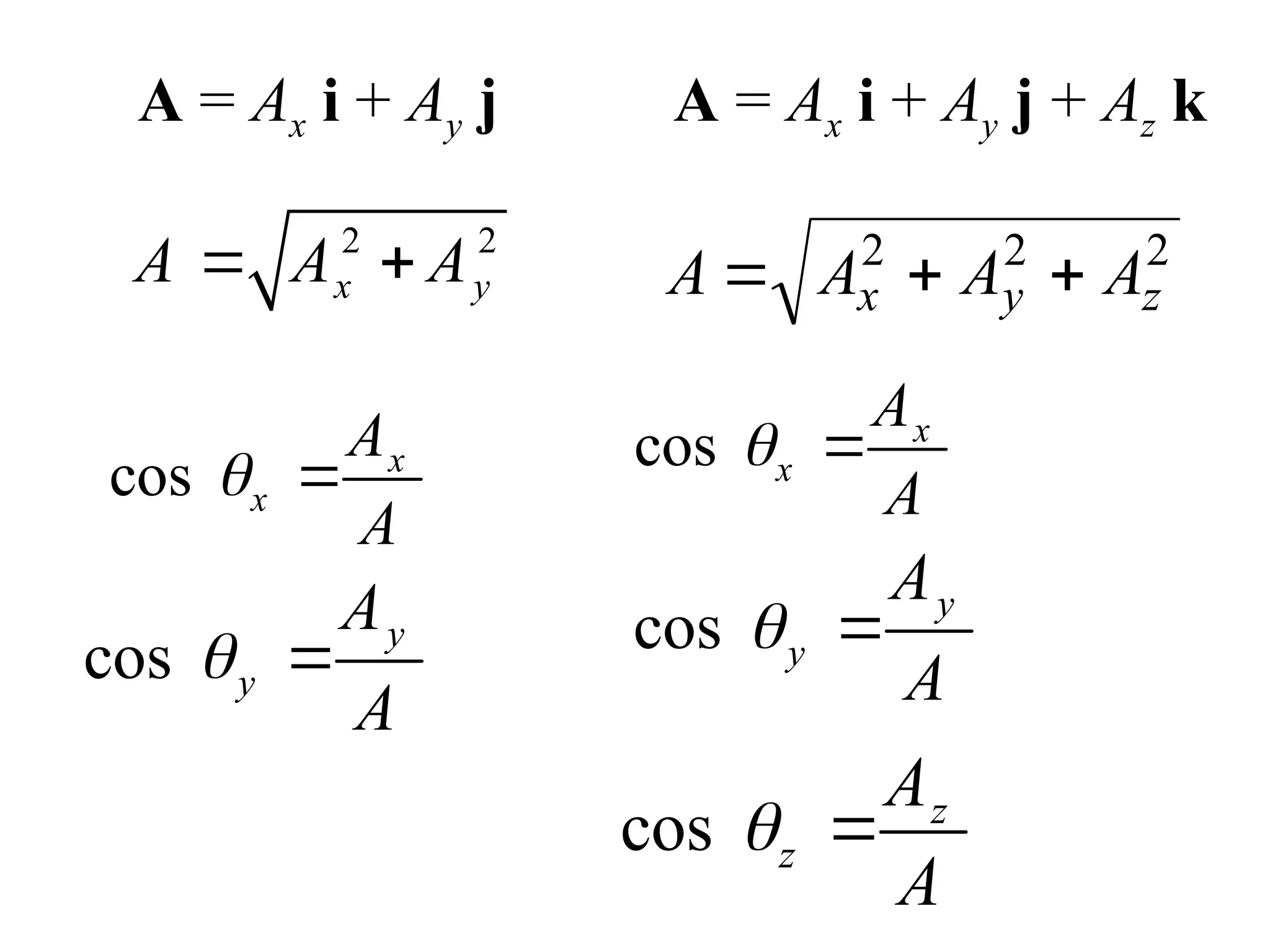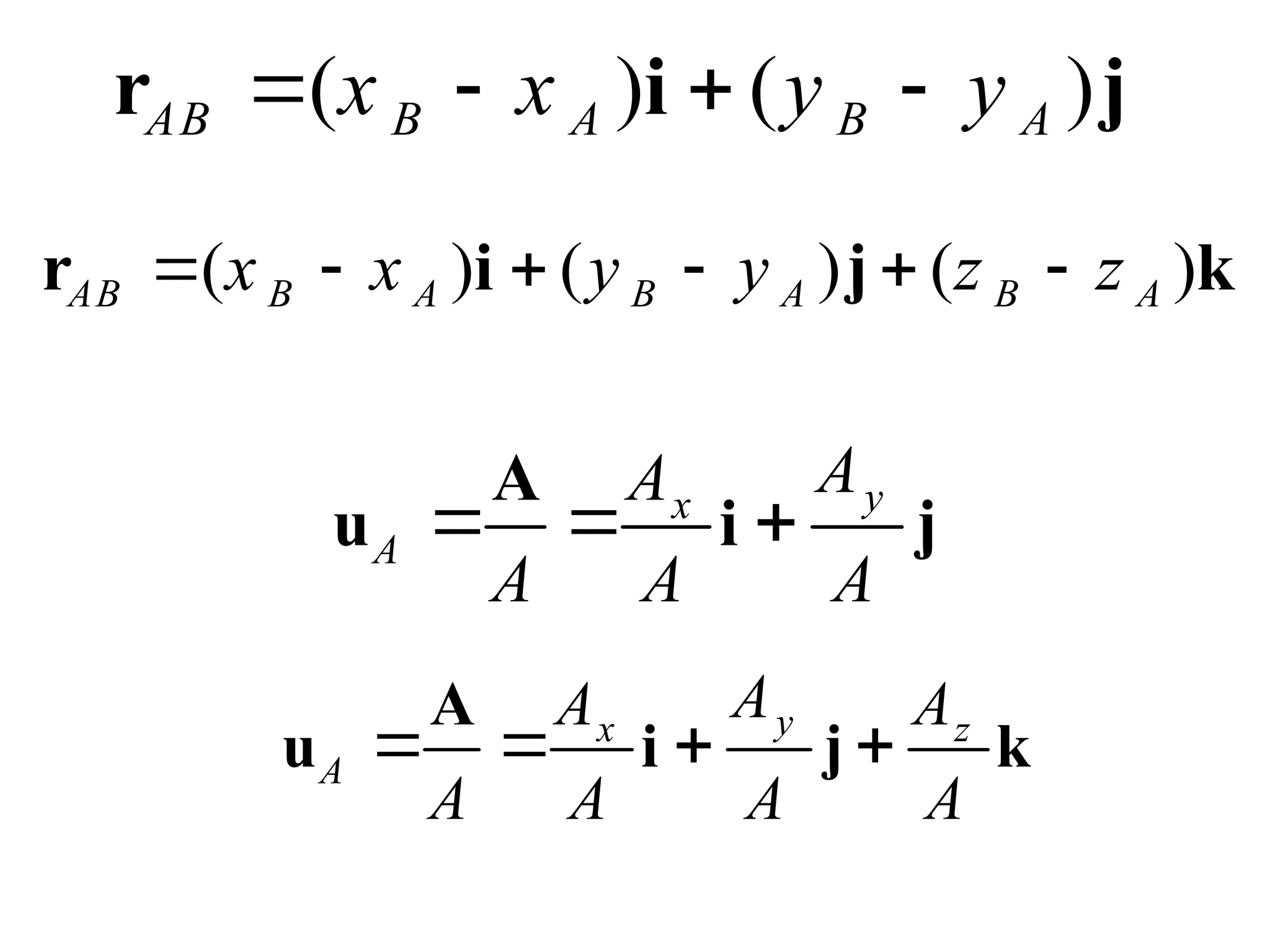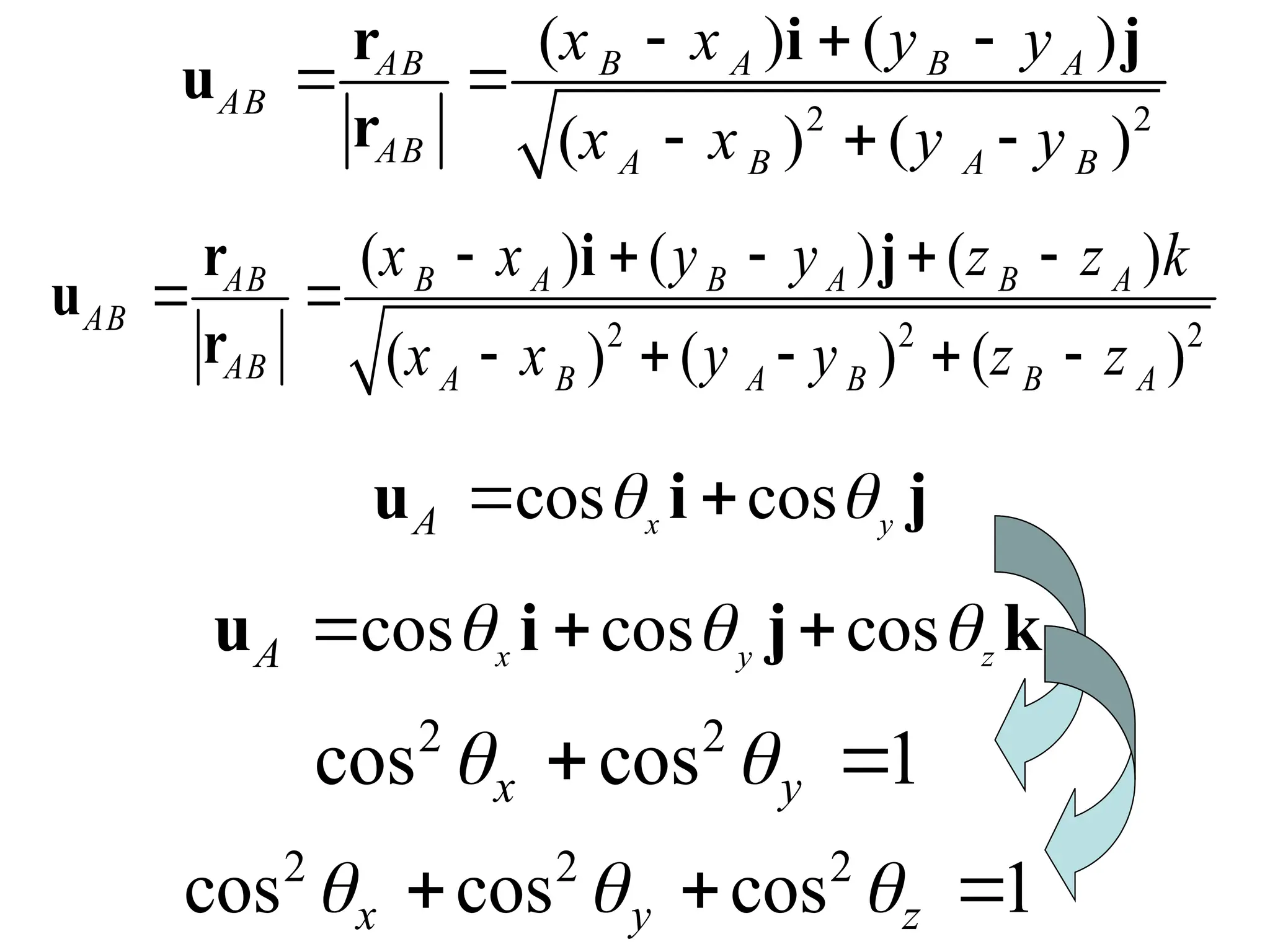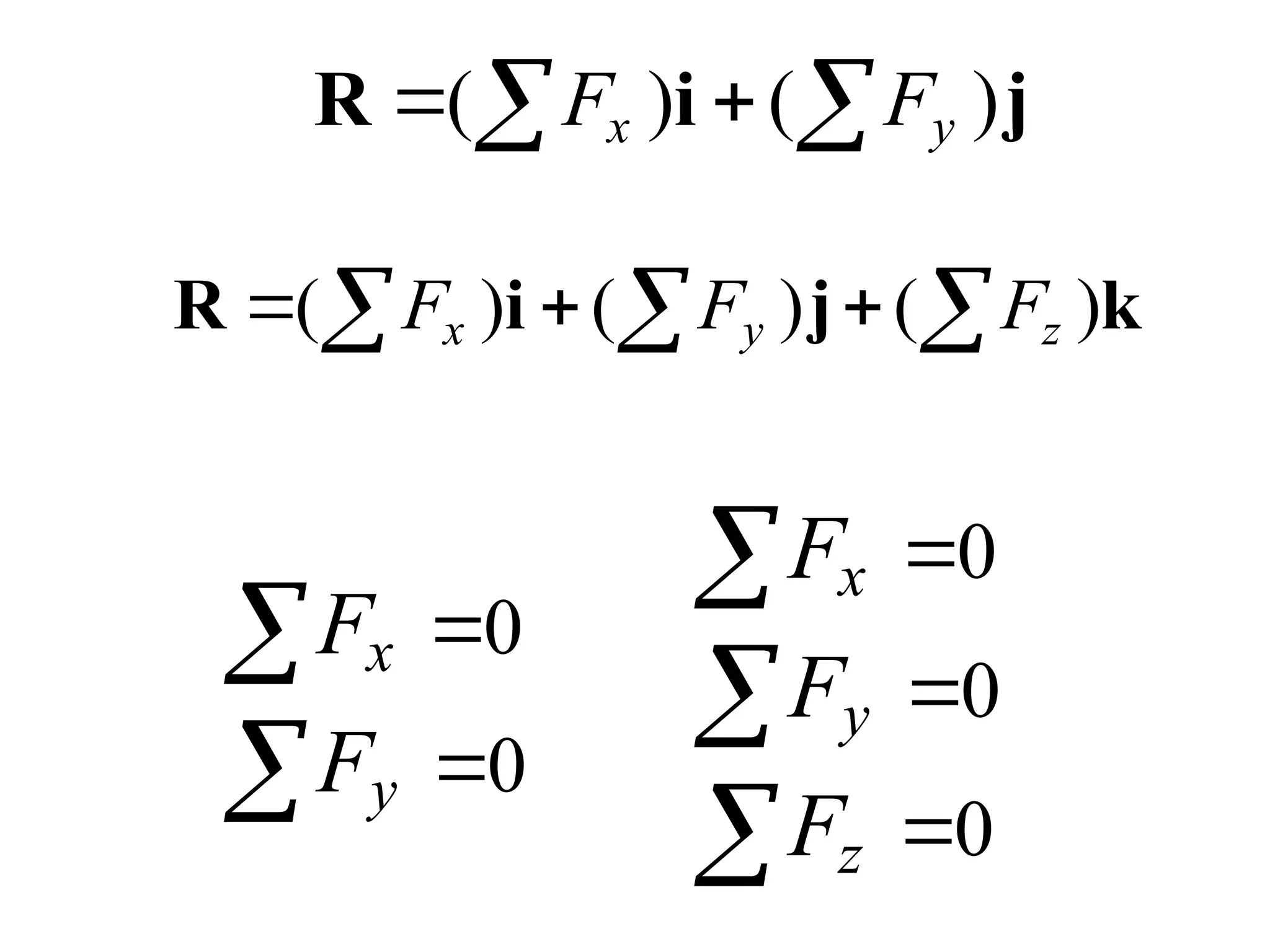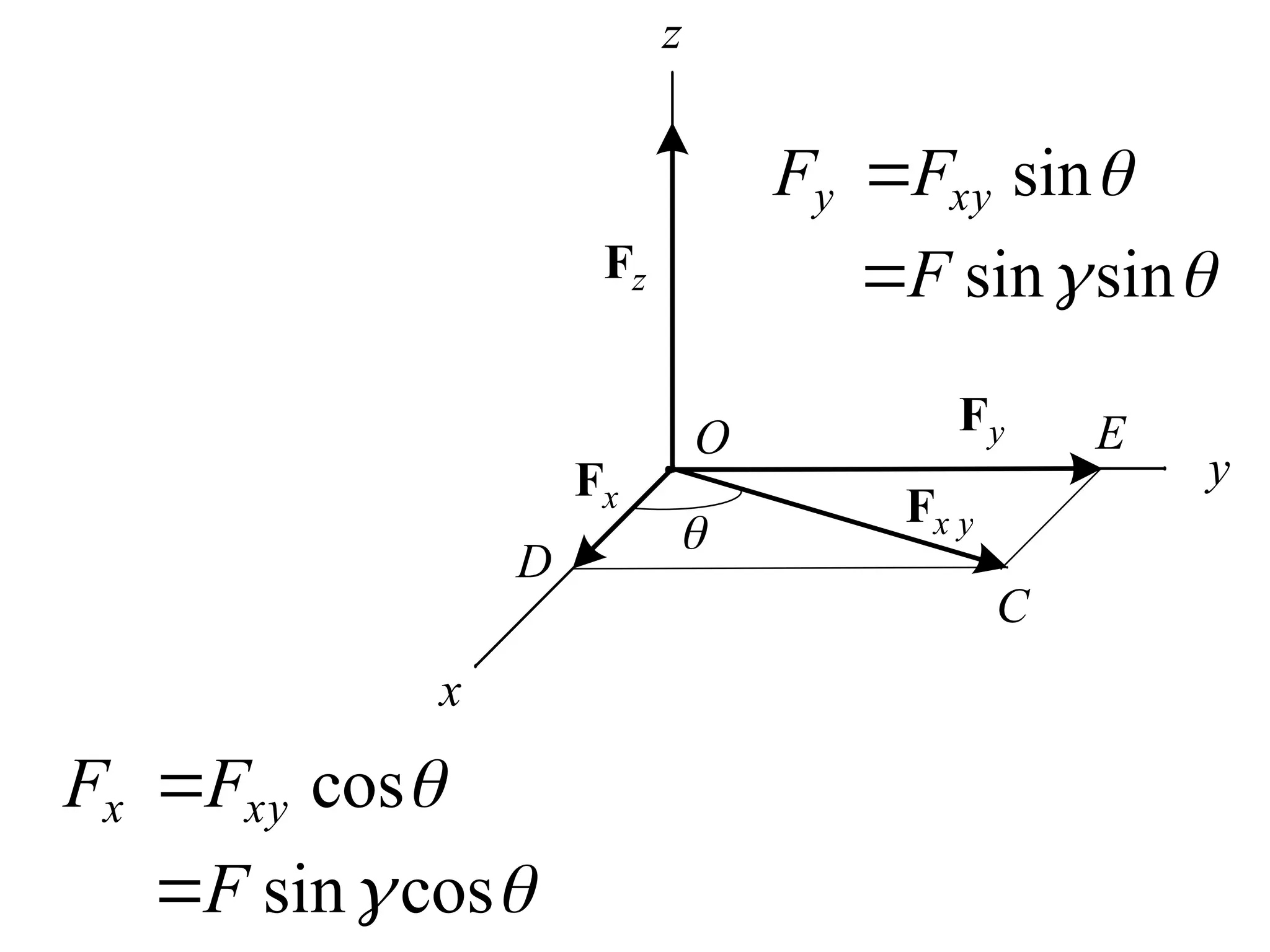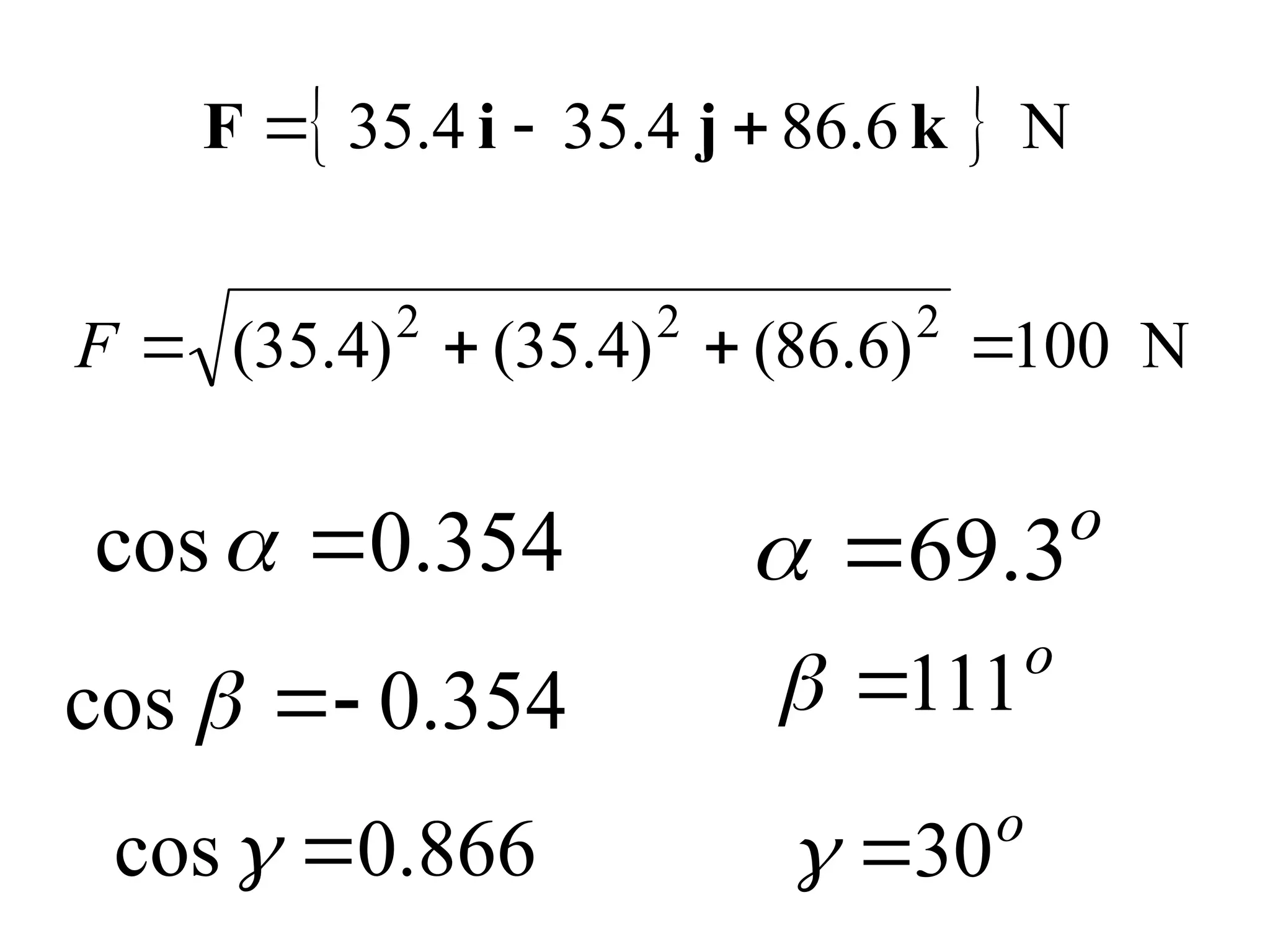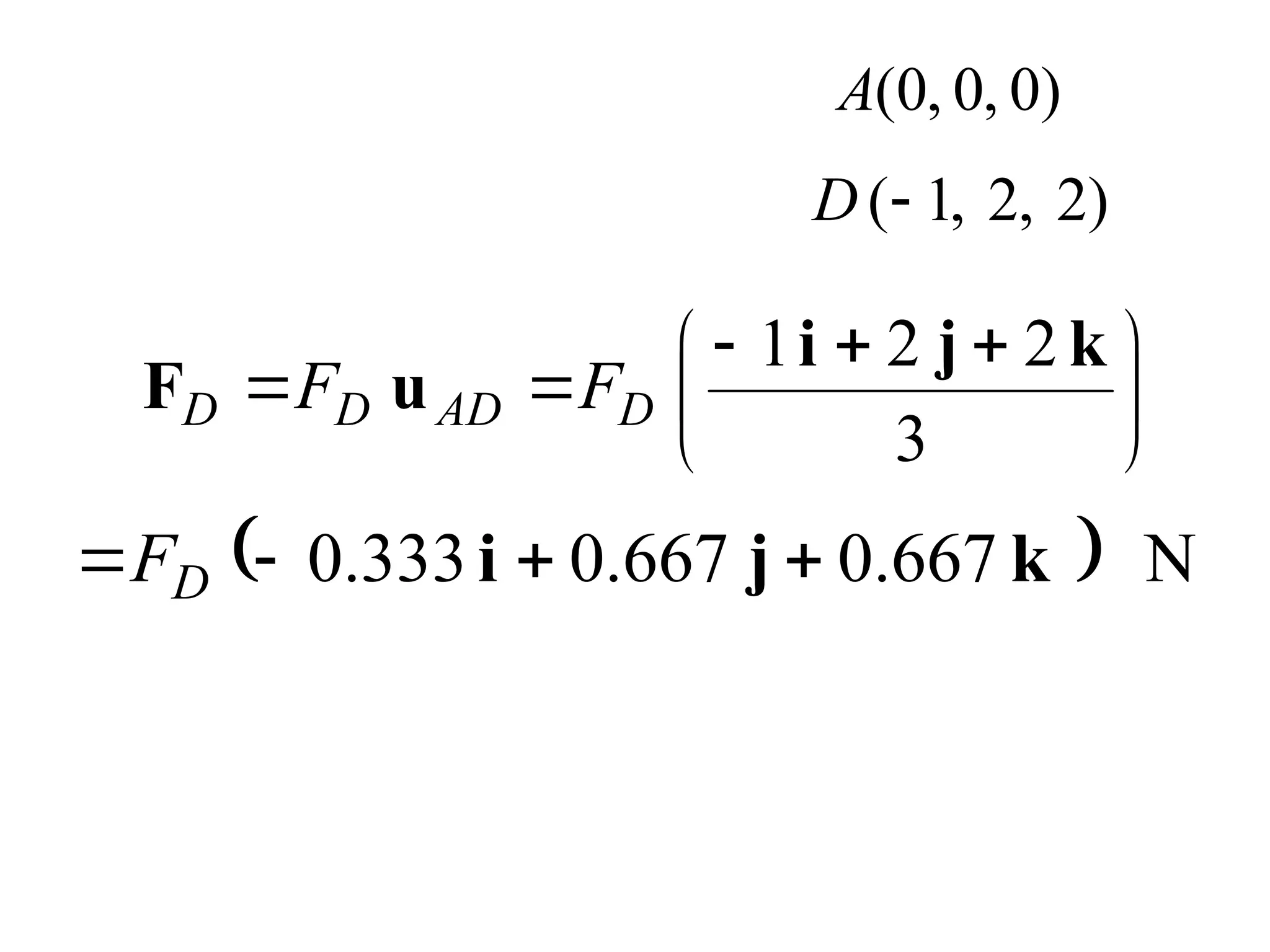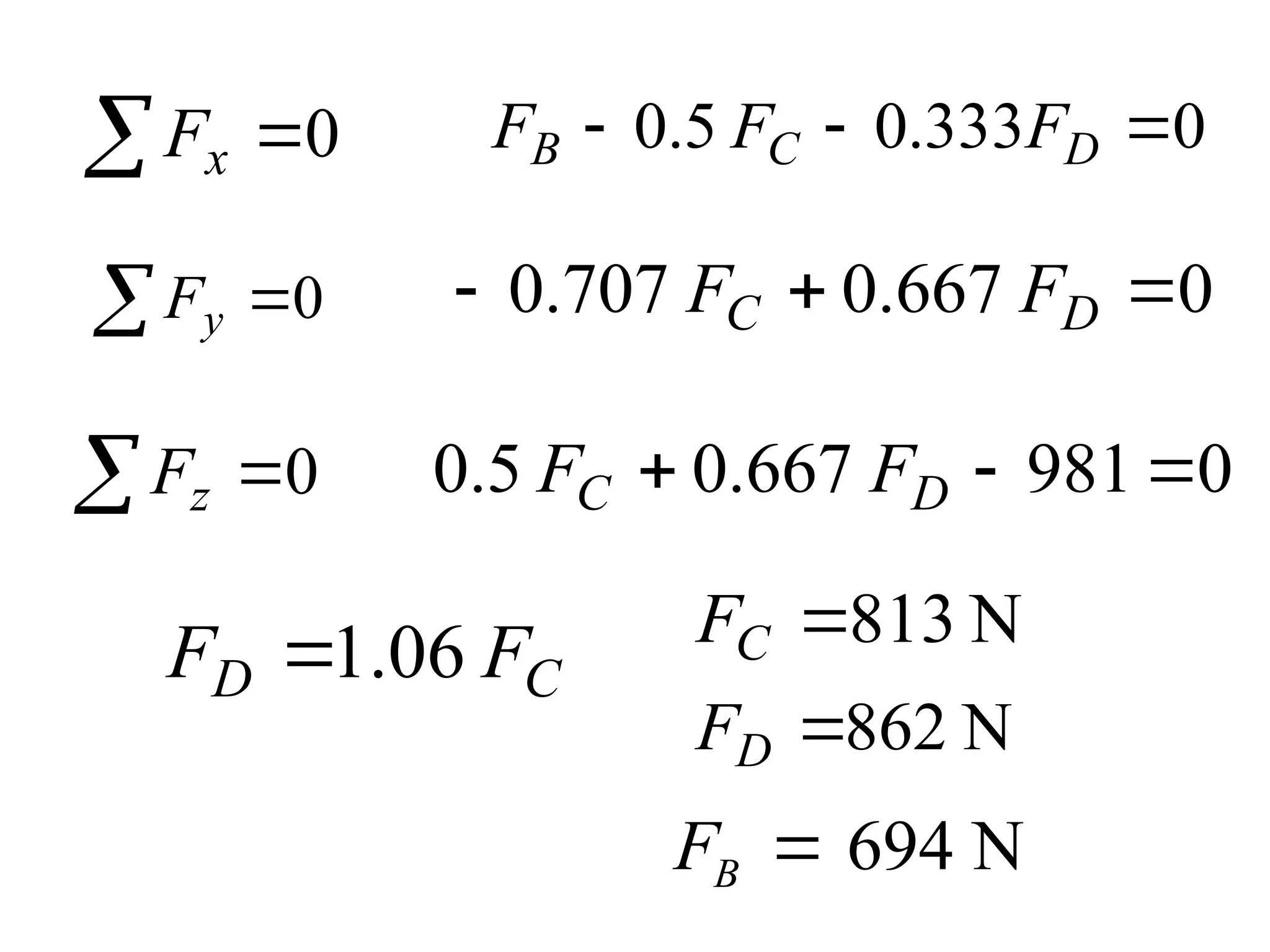The document discusses the analysis of concurrent forces in three dimensions and their representation as Cartesian vectors. It provides mathematical formulations for force components, direction angles, and resultant forces, with examples illustrating the application of these principles in calculations involving tensions in cables and the support of weights. Key examples involve determining forces acting on specific points and the resultant direction and magnitude of tensions in various configurations.